Magnetic Susceptibility Anisotropy of Human Brain in vivo and its Molecular Underpinnings

Abstract

Frequency shift of gradient-echo MRI provides valuable information for assessing brain tissues. Recent studies suggest that the frequency and susceptibility contrast depend on white matter fiber orientation. However, the molecular underpinning of the orientation dependence is unclear. In this study, we investigated the orientation dependence of susceptibility of human brain in vivo and mouse brains ex vivo. The source of susceptibility anisotropy in white matter is likely to be myelin as evidenced by the loss of anisotropy in the dysmyelinating shiverer mouse brain. A biophysical model is developed to investigate the effect of the molecular susceptibility anisotropy of myelin components, especially myelin lipids, on the bulk anisotropy observed by MRI. This model provides a consistent interpretation of the orientation dependence of macroscopic magnetic susceptibility in normal mouse brain ex vivo and human brain in vivo and the microscopic origin of anisotropic susceptibility. It is predicted by the theoretical model and illustrated by the experimental data that the magnetic susceptibility of the white matter is least diamagnetic along the fiber direction. This relationship allows an efficient extraction of fiber orientation using susceptibility tensor imaging. These results suggest that anisotropy on the molecular level can be observed on the macroscopic level when the molecules are aligned in a highly ordered manner. Similar to the utilization of magnetic susceptibility anisotropy in elucidating molecular structures, imaging magnetic susceptibility anisotropy may also provide a useful tool for elucidating the microstructure of ordered biological tissues.

Introduction

Frequency shift (phase scaled by echo time) in gradient-echo MRI has offered unique biological sensitivity and superior contrast-to-noise ratio (CNR) for brain tissues (Duyn, 2010; Duyn et al., 2007; Rauscher et al., 2005). Previously, frequency shift resulting from paramagnetic blood in the vascular system has been utilized extensively to generate susceptibility weighting (Haacke et al., 2004). However, frequency shift in the white matter is still not well understood. For example, frequency shift of the white matter may not be solely explained by its volume susceptibility due to the highly anisotropic microstructure of the brain white matter (He and Yablonskiy, 2009). To address the structural compartmentalization of the cells in the brain white matter, He and Yablonskiy (2009) introduced the concept of a cylindrically shaped Lorentzian boundary. The generalized Lorentzian model attributed the orientation dependence of frequency shift in the white matter to the non-spherical susceptibility inclusions within the elongated structures at cellular and subcellular levels (He and Yablonskiy, 2009). Subsequently, concepts of anisotropic white matter susceptibility and susceptibility tensor in brain tissue were proposed and demonstrated using human corpus callosum sections in vitro, mouse brains ex vivo, and human brains in vivo (Lee et al., 2010; Li et al., 2011; Liu, 2010). Although both approaches – non-spherical Lorentzian model and anisotropic magnetic susceptibility – provide a reasonable characterization of the frequency shift-susceptibility relationship in brain white matter, the molecular underpinning for the angular dependence of susceptibility and frequency shift and their interrelationships is still not well understood.

At the molecular level, most biomolecules are known to have anisotropic magnetic susceptibility, which has been widely used to elucidate molecular structures using NMR and EPR spectroscopy (Opella, 1997; Prestegard, 1998; Prosser et al., 1996; Tjandra and Bax, 1997). The investigation of the contribution of anisotropic molecular magnetic properties to the MRI-observable macroscopic magnetic susceptibility is of particular importance for the understanding of frequency shift and susceptibility contrast between gray and white matter. Recently, Lee et al. have evaluated frequency shift and susceptibility of human corpus callosum samples, and suggested that the observed frequency shift variation is better interpreted by the model of susceptibility anisotropy (Lee et al., 2010). They also suggested that one possible source of this susceptibility anisotropy is the phospholipid bilayers in myelin (Lee et al., 2010). Similarly, structurally constrained macromolecules along axons were also suggested as the potential source of this anisotropy by Liu (2010). Subsequently, Liu et al reported that the frequency and susceptibility contrast between gray and white matter are nearly absent in brains of the dysmyelinating shiverer mice (Liu et al., 2011a). In the shiverer mouse brain, the axon structure is intact as demonstrated by the presence of strong diffusion anisotropy (though slightly reduced) and unaltered fiber orientations; however, the amount of myelin sheath surrounding the axon is greatly impaired as visualized in electron micrograph (Liu et al., 2011a). These results demonstrate the importance of myelin in generating susceptibility contrast, and further suggest myelin as the potential source of susceptibility anisotropy. However, the quantitative relationship between the MRI-measured susceptibility anisotropy and molecular magnetic properties of myelin components, especially myelin lipids, remains to be elucidated, especially in the human brain in vivo.

In this study, we further explored the cellular and molecular underpinnings of MRI observed susceptibility anisotropy using established physical principles. The source of susceptibility anisotropy is most likely to be myelin, as shown by the near-complete loss of susceptibility anisotropy in the shiverer mouse brains. A biophysical model is developed to investigate the impact of spatially ordered myelin components, especially membrane lipids, to the bulk magnetic susceptibility anisotropy. The model-predicted macroscopic susceptibility anisotropy, based on known values of molecular susceptibility anisotropy of membrane lipids, agrees with the MRI-determined susceptibility anisotropy in the control-mouse brains. We further evaluated the susceptibility anisotropy of the human brain in vivo using susceptibility tensor imaging (STI). The obtained susceptibility anisotropy of human brain white matter is also consistent with model predictions. Furthermore, the fiber orientation determined by STI largely agrees with that determined by diffusion tensor imaging (DTI) (Basser et al., 1994). These results suggest that the macroscopic susceptibility anisotropy is intrinsically related to the content and the structure of the myelin on the microscopic level and the architecture of fiber pathways on the system level.

Materials and Methods

Susceptibility tensor model: linking molecular and bulk susceptibility anisotropy

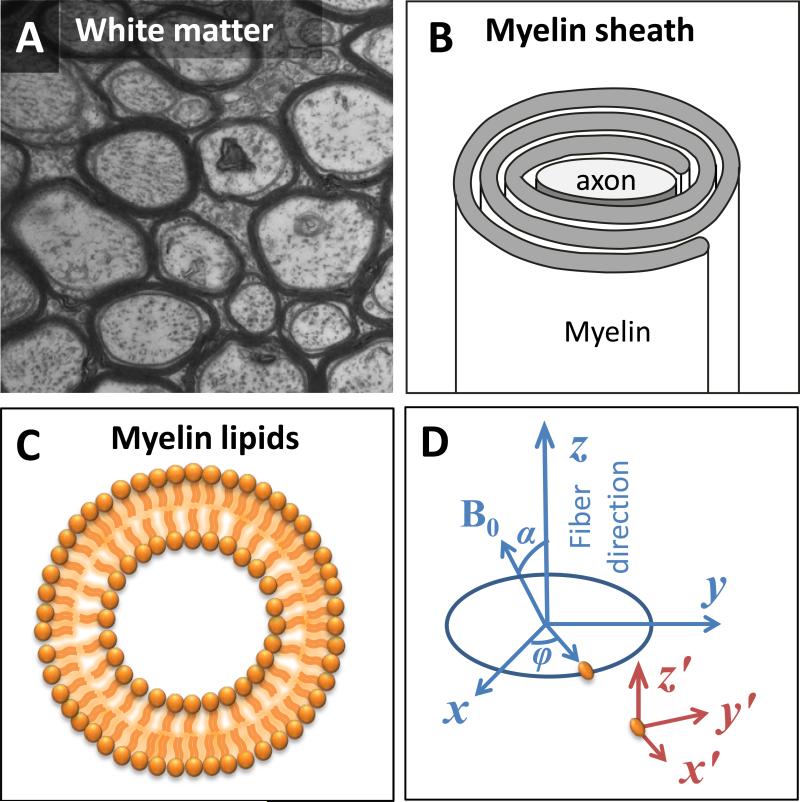
Nerve axons in the central nervous system are insulated by the multilayered myelin sheath as commonly illustrated by the dense lines in the cross sectional electron micrograph (EM) of axons (Fig. 1A). Myelin is rich in lipids (~70% dry weight) and proteins (~30% dry weight) (Baumann and Pham-Dinh, 2001). It is composed of spiraling sheaths of double bilayers separated by aqueous layers of 3-4 nm thickness that alternate between cytoplasmic and extracellular cell membranes (Inouye and Kirschner, 1988) (Fig. 1B). In this complex structure, water molecules in myelin experience fast molecular tumbling (τ_c ~ 10^-12 sec) and are not expected to contribute to the anisotropy. The abundant lipids in the myelin membranes, on the other hand, are strongly anisotropic at the molecular level and are highly organized around the axons but with limited mobility (τ_c~10^-8 sec) (Pu et al., 2009).

Fig. 1. The axon and molecular coordinate systems.

A. An electron-micrograph of the white matter fiber architecture of a wild-type mouse (The EM figure is courtesy of Gabriel Corfas, PhD, of Harvard University). B. A schematic representation of the myelin sheath. C. A schematic representation of the radial alignment of membrane lipid molecules. D. The axon coordinate system (x, y and z) and the molecular coordinate system (x′, y′ and z′). The z-axis is parallel to the fiber direction, and the x-axis is in the plane defined by z-axis and H₀ direction. The z′-axis is parallel to the z-axis. The angle between x′ and x axes is φ.

Previous studies have documented the susceptibility anisotropy of model lipid bilayers and crystals, such as egg lecithin (Kawamura et al., 1981; Sakurai et al., 1980; Scholz et al., 1984). Susceptibility anisotropy of the membrane lipids from isolated human lipoproteins was also reported, which was estimated at 0.223 ppm using NMR spectroscopy (Lounila et al., 1994). This value is an order of magnitude larger than the observed gray-white matter susceptibility contrast of -0.013 to -0.029 ppm in control mice (Liu et al., 2011a). Given the strong anisotropy and the abundance of lipid molecules in the myelin, we hypothesize that the magnetic susceptibility anisotropy in the white matter arises mainly from ordered myelin lipids, while the quantitative relationship between the two is determined by the density of myelin lipids and the way these lipid molecules are spatially organized. As a first attempt to analyze analytically the relationship between lipid molecules and bulk anisotropy, an idealized model of the axonal membrane is utilized as illustrated in Fig. 1C. Specifically, the axon is modeled with a perfect cylinder and the myelin sheaths are modeled with concentric cylindrical shells with molecules radially aligned within these membranes (Fig. 1C).

Two coordinate systems are defined: an axon coordinate system (x, y, z) and a molecular coordinate system (x′, y′, z′) (Fig. 1D). Notice that the z- and z′-axis are parallel. The transformation matrix between these two coordinate systems is denoted as R_z which is a rotation matrix around the z-axis with a rotation angle of φ. The fiber angle, denoted as α, is defined as the angle between the z-axis and the H₀ direction. Hence, the applied magnetic field is $\overrightarrow{\mathbf{H}}={[H_0\text{sin}\alpha ,0,H_0\text{cos}\alpha ]}^T$ in the axon coordinate system. The magnetic moment ${\overrightarrow{\mathbf{m}}}_m$ of a single molecule in response to the applied field $\overrightarrow{\mathbf{H}}$ is related to its rank-2 susceptibility tensor χ_m following

$${\overrightarrow{\mathbf{m}}}_m={\mathbf{R}}_z{\chi }_m{{\mathbf{R}}_z}^T\overrightarrow{\mathbf{H}}$$ [1]

where χ_m is defined in the molecular frame of reference. In the molecular frame of reference, the molecular susceptibility tensor is diagonalized, that is, ${\chi }_m=diag({\chi }_m^r,{\chi }_m^c,{\chi }_m^l)$, where ${\chi }_m^r$, ${\chi }_m^c$ and ${\chi }_m^l$ represent the molecular susceptibility in the radial (x′-axis), the circumferential (y′-axis) and the longitudinal direction (z′-axis) of the axon, respectively.

To relate the bulk magnetic susceptibility anisotropy to the molecular anisotropy, we further assume that the interactions of electron clouds across neighboring molecules are negligible so that the superposition rule holds. This assumption is valid as the bilayer structure is formed by the self-assembling of lipids through the hydrophobic effect. In other words, a lipid bilayer is typically held together by entirely non-covalent forces that do not involve the formation of chemical bonds between individual molecules. Thus, the induced magnetization density can be estimated by integrating over all molecules within the imaging voxel of interest:

$$\overrightarrow{\mathbf{M}}={\int }_V{\overrightarrow{\mathbf{m}}}_{m}dV=\frac{f_{lipid}}{2\pi }{\int }_{\phi =0}^{2\pi }{\mathbf{R}}_z{\chi }_m{\mathbf{R}}_z^T\overrightarrow{\mathbf{H}}d\phi$$ [2]

Here, f_lipid is the volume fraction of myelin lipids. The induced magnetization generates a perturbation field to the applied external field. However, in gradient-echo MRI, only the z-component (i.e. in the Ĥ direction, which is the unit vector in the direction of $\overrightarrow{\mathbf{H}}$) of the perturbation field can be detected by measuring the resulting frequency shift. After integration of Eq. 2, the MRI detectable magnetization in the Ĥ direction can be calculated as:

$$M_z=\overrightarrow{\mathbf{M}}\cdot \widehat{\mathbf{H}}=f_{lipid}{H}_0\left[\left(\frac{{\chi }_m^r+{\chi }_m^c}{2}-{\chi }_m^l\right){\text{sin}}^2\alpha +{\chi }_m^l\right]$$ [3]

By definition, the macroscopic susceptibility (χ) of each imaging voxel is the ratio of the observed magnetization and the applied magnetic field:

$$\chi =M_z∕H_0=f_{lipid}\left(\frac{{\chi }_m^r+{\chi }_m^c}{2}-{\chi }_m^l\right){\text{sin}}^2\alpha +{\chi }_0$$ [4]

Here, the last term is changed from $f_{lipid}{\chi }_m^l$ to χ₀. This generalization is made because the absolute susceptibility of tissue is not available, so χ₀ is used to include any baseline changes due to the choice of susceptibility reference and the aforementioned isotropic susceptibility elements in the white matter. The detailed derivation from Eq. 2 to Eq. 4 was included in supplementary materials.

For lipid molecules, the differences between ${\chi }_m^c$ and ${\chi }_m^l$ are typically assumed to be small, so both components can be represented by a common term ${\chi }_m^{\perp }$. On the other hand, ${\chi }_m^r$ is parallel to the long axis of the molecular chain and can be represented as ${\chi }_m^{\parallel }$. Here, ${\chi }_m^{\perp }$ and ${\chi }_m^{\parallel }$ are defined with respect to the longitudinal direction of a lipid molecule. Since the longitudinal direction of a lipid molecule is perpendicular to the axon fiber direction, ${\chi }_m^{\parallel }$ is perpendicular to the axon fiber direction. Eq. 4 can be simplified as:

$$\chi =f_{\text{lipid}}\left(\frac{{\chi }_m^{\parallel }-{\chi }_m^{\perp }}{2}\right){\text{sin}}^2\alpha +{\chi }_0$$ [5]

Eq. 5 suggests a simple sine-squared relationship between the macroscopic susceptibility and the susceptibility anisotropy of an individual lipid molecule. If the macroscopic susceptibility anisotropy is defined as the susceptibility difference between parallel (α = 0°) and perpendicular (α = 90°) orientations, Eq. 5 predicts that magnetic susceptibility anisotropy or the maximum variation of macroscopic susceptibility (Δχ_max) is $-f_{\text{lipid}}({\chi }_m^{\parallel }-{\chi }_m^{\perp })∕2$.

This model can be easily expanded to model the macroscopic effect of proteins and other molecules that may not align with the surface norm of the membrane (Supplementary materials). It can be shown that as long as the cylindrical symmetry of myelin is assumed, the sine-squared relationship between macroscopic susceptibility anisotropy and fiber angle can be obtained regardless of their orientation with respect to the surface norm, given the freedom of rotation around the surface norm.

Experimentally, the apparent magnetic susceptibility (AMS) of each voxel can be spatially resolved from measured 3D frequency maps (Δf) by inverting the following relationship (Marques and Bowtell, 2005; Salomir et al., 2003)

$$\Delta f=\gamma {\mu }_0{H}_0\cdot F{T}^{-1}\left[\left(1∕3-k_z^2∕k^2\right)\cdot FT\left(\chi \right)\right]$$ [6]

where γ is the gyromagnetic ratio of water proton, k is the spatial frequency vector, μ₀ is the vacuum permeability, FT represents the Fourier Transform, FT^-1 represents the inverse Fourier Transform and the term 1/3 corresponds to the sphere of Lorentz. For anisotropic susceptibility, the relationship between the resonance frequency shift and macroscopic susceptibility tensors is given by (Liu, 2010):

$$\Delta f=F{T}^{-1}\left[\frac{1}{3}{\widehat{\mathbf{H}}}^{\mathrm{T}}FT\left(\chi \right)\widehat{\mathbf{H}}-{\mathbf{k}}^{\mathrm{T}}\widehat{\mathbf{H}}\frac{{\mathbf{k}}^{\mathrm{T}}FT\left(\chi \right)\widehat{\mathbf{H}}}{k^2}\right]\gamma {\mu }_0{H}_0$$ [7]

where the macroscopic susceptibility tensor χ is expressed as a 3×3 matrix, and the term Ĥ^TFT(χ)Ĥ/3 corresponds to the sphere of Lorentz. Given a set of independent measurements, the susceptibility tensors can be spatially resolved by solving Eq. 7 in the k-space. A minimum of 6 independent measurements in different directions are required to solve Eq. 7 to obtain all the susceptibility tensor elements.

MRI of mouse brain ex vivo

Male wild-type control (CTRL) mice (C3HeB/FeJ, n = 2) of 10-weeks old were scanned at 9.4 T to assess the orientation dependence of macroscopic susceptibility of brain white matter. Age- and sex-matched dysmyelinating shiverer (SHVR) mice (C3FeSWV-Mbp-Shi, n = 2) were also scanned with identical protocol to evaluate the role of myelin in susceptibility anisotropy. The number of orientations was 7 and 19 for the two control mice and 6 and 11 for the two shiverer mice. Both mouse strains were obtained from the Jackson Laboratory (Bar Harbor, ME). Prior to scanning, mice were anesthetized and perfused with formalin following the procedures described by Johnson et al. (Johnson et al., 2002). The perfused mouse brain was kept within the skull to prevent any potential damage to the brain and was scanned within a few days after perfusion to minimize the alteration in tissue properties. Previous studies have confirmed that formalin-perfused mouse brains yield comparable phase and susceptibility contrast to saline-perfused brains (Liu et al., 2011a). The perfusion-fixed mouse brains were scanned on a 9.4 T (400 MHz) 89-mm-diameter vertical bore Oxford magnet with a GE EXCITE MR imaging console (GE Healthcare, Waukesha, WI). A solenoid radiofrequency coil developed in-house was used to achieve desirable SNR. Due to the spatial constraints of this coil, the mouse brain can only be rotated around the anterior-posterior axis, i.e., the long axis. This setup is sufficient for evaluating the susceptibility anisotropy, but not sufficient for calculating the full susceptibility tensor, since rotations about two axes perpendicular to H₀ are required for calculating the full susceptibility tensor using Eq. 7. 3D spoiled-gradient-recalled (SPGR) images were acquired using the following imaging parameters: matrix size = 256×128×128, field-of-view = 22×11×11 mm³, flip angle = 40°, TE = 20 ms, and TR = 200 ms. Shimming of magnet was performed at each head orientation to achieve higher image quality, while its effect on tissue phase is completely eliminated during the background phase removal procedure. The total scanning time was 55 min per orientation. After each acquisition, the brain was rotated to a different orientation and the acquisition was repeated. To determine the fiber orientations, diffusion tensor images were also acquired on the same scanner with a diffusion-weighted 3D spin-echo sequence (Jiang and Johnson, 2010) and the following parameters: FOV = 22×11×11 mm³, matrix = 164×82×82, TE = 12 ms, TR = 4s. One image without diffusion weighting and six diffusion weighted images were acquired with a b-value of 1500 s/mm². The encoding directions were (1 0 1), (1 0 -1), (1 1 0), (1 -1 0), (0 1 1) and (0 1 -1). All animal studies were approved by the Institutional Animal Care and Use Committee (IACUC) of Duke University.

MRI of human brain in vivo

One healthy adult volunteer (male, 33-years old) was scanned on a GE MR750 3.0 T scanner (GE Healthcare, Waukesha, WI). A quadrature head coil was employed for the gradient echo imaging to allow a wider range of head orientations inside the coil. Gradient-echo images with various head orientations with respect to the main magnetic field were acquired using a standard flow-compensated 3D SPGR sequence with the following parameters: TE = 40 ms, TR = 60 ms, flip angle = 20°, FOV = 256×256×256 mm², matrix size = 128×128×128. Shimming was performed at each head orientation. A total of 16 orientations were acquired to achieve the rotation angle of -42~52° (around the anterior-posterior direction) and -43~39° (around the left-right direction). Diffusion tensor images were also acquired using an 8-channel head coil and a standard single-shot EPI sequence with a parallel-imaging acceleration factor of 2. The parameters were as follows: TE = 82 ms, TR = 8 s, FOV = 256×256 mm², matrix size = 128×128, slice thickness = 2 mm without gap, b-value = 800 s/mm², 5 non-diffusion weighted images and 25 diffusion encoding directions. 75 slices were acquired to cover the whole brain. All human studies were approved by Institutional Review Board of Duke University.

Image Analysis

Image phase was unwrapped with a Laplacian-based phase unwrapping algorithm (Li et al., 2011; Schofield and Zhu, 2003) and filtered with the sphere mean value filtering (Schweser et al., 2011), with a radius of 25 voxels for both mouse and human brain studies with radius decreasing towards the brain boundary (Li et al., 2011; Wu et al., 2011). Phase value was normalized by the TE to yield the frequency shift. AMS was first quantified at each brain orientation with respect to the main magnetic field using the LSQR method with the addition of first-order k-space derivative to improve the numerical stability (Li et al., 2011). The multi-orientation gradient echo images were linearly registered to the non-diffusion weighted DTI images using FSL-FLIRT (Oxford Center for Functional MRI of the Brain, Oxford, UK). The resulting transformation matrix was used to rotate the phase and susceptibility maps and to determine the brain orientation with respect to the main magnetic field.

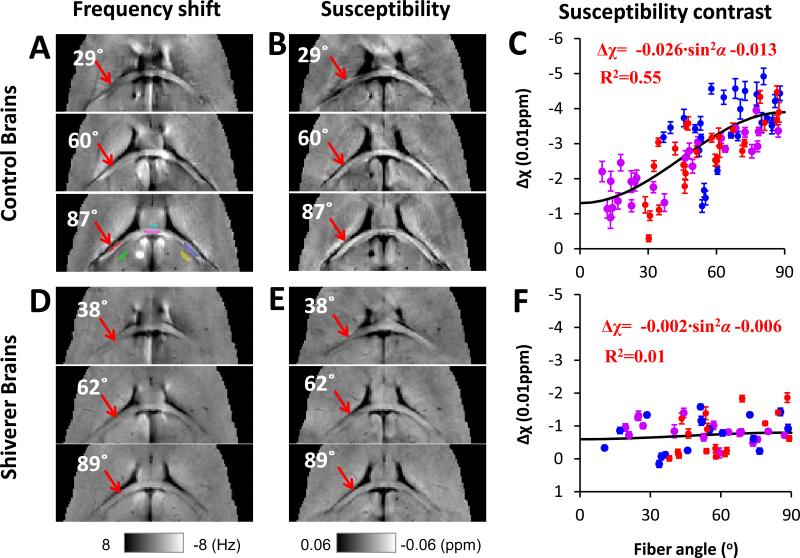
For mouse brains, three regions of interest (ROI) within the hippocampal commissure (Fig. 2A) were manually drawn using a Matlab-based ROI tool developed in-house. Another three regions of interest were also drawn within the adjacent gray matter. AMS contrast was calculated as the AMS difference between white matter and the adjacent gray matter. The angular dependence of AMS contrast was fitted to Eq. 5 using a nonlinear least-square fitting.

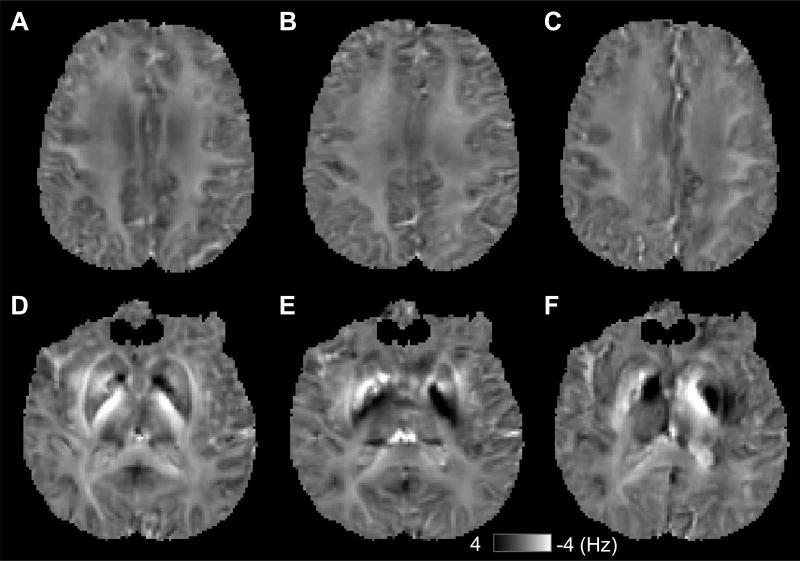
Fig. 2. Orientation dependence of AMS in normal and dysmyelinating shiverer mice.

A and D: frequency maps from 3 selected brain orientations. A representative selection of ROI is shown in the lower panel of A. ROIs in the white matter are labeled by red, magenta, and blue colors; ROIs in the corresponding adjacent gray matter are labeled by green, cyan, and yellow colors. B and E: AMS corresponding to the frequency shifts shown in A and D. C and F: AMS difference between white and gray matter. All data points are shown as mean ± standard error. Susceptibility anisotropy is observed in the control mice but not in shiverer mice. The angles shown on the images are the angles between the directions of the white matter segment (red ROI pointed by a red arrow) determined by DTI and the main field, e.g., 0° means that the selected fiber segment is parallel to the main magnetic field. The ROI color in panel A corresponds to the data point color in panel C and F.

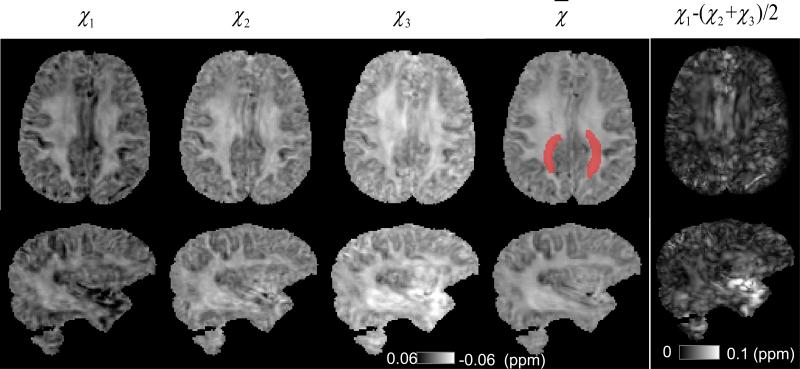
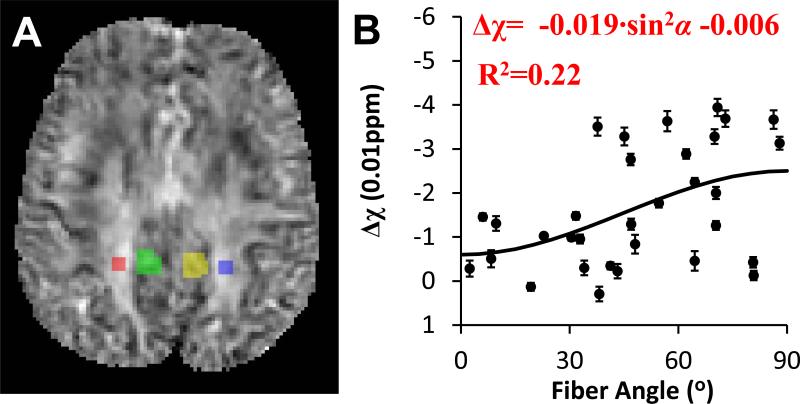
For the human brain, susceptibility tensors were calculated from the multi-orientation frequency shift data using Eq. 7, in which a regularization approach was added to the original method (Liu, 2010) to reduce the sensitivity to imperfect image registration (Liu et al., 2011b). Similar to DTI analysis, the susceptibility tensors were decomposed into their eigenvalues (χ₁, χ₂ and χ₃), which are coordinate-system independent. To determine the susceptibility anisotropy of in vivo human brain using STI, a region of interest within the white matter fiber bundle was selected (Fig. 5, highlighted with red color), which includes segments of the corpus callosum, the corticopontine tract and the posterior thalamic radiation). A reasonable amount of gray matter exists in their vicinity, allowing comparison with AMS contrast determined with single-orientation method. According to Eq. 5, white matter is the most paramagnetic in the fiber direction (corresponding to χ₁), while equally diamagnetic in the other two orthogonal directions (corresponding to χ₂ and χ₃). Hence, the susceptibility anisotropy was calculated as Δχ_max = χ₁ – (χ₂ + χ₃)/2. To assess the orientation dependence of AMS, smaller ROIs, labeled with red and blue color, were selected in order to obtain a mean angle for the specified white matter fiber bundles (Fig. 6A). Two ROIs, labeled with green and yellow color, were selected in the gray matter for the AMS contrast calculation.

Fig. 5. Principal, mean susceptibilities and susceptibility anisotropy in the human brain.

The three principal susceptibilities of the same two slices in Fig. 4 are shown from left to right in a descending order. The increasing image intensity show strong susceptibility anisotropy in the white matter. A reduced level anisotropy is also observed in the gray matter. The region in mean susceptibility map labeled with red color is used for calculation of susceptibility anisotropy.

Fig. 6. Orientation dependence of AMS in human brain in vivo.

A: the overlay of the ROI of white matter (red and blue) and gray matter (green and yellow) on top of the AMS map. B: AMS difference between white and gray matter.

Diffusion tensor images were analyzed as described previously (Basser et al., 1994). The computation was implemented in Matlab R2010a (Mathworks, Natick, MA) and carried out on a Linux cluster comprised of 61 computing nodes with 8 CPU cores and 32 GB RAM per node. Although we were able to take advantage of the high-end computing facility, all calculations can be handled by typical desktop computers (Li et al., 2011).

Results

Myelin is the main source of susceptibility anisotropy in white matter

Following the established convention of displaying frequency shift in NMR spectroscopy, frequency and susceptibility values were displayed with a reversed axis. Specifically, higher image intensity was used to represent lower frequency shifts or more diamagnetic susceptibility. Fig. 2A and D shows the processed image frequency shift, from which the AMS were calculated (Fig. 2 B and E). In the control mice, the AMS contrast increases significantly with fiber angle (arrows in Fig. 2B), whereas in the shiverer mouse, such directionality is clearly absent (arrows in Fig. 2E). More specifically, in the control mice, the AMS of the white matter relative to adjacent gray matter decreases monotonically (i.e. becoming more diamagnetic) with increasing fiber angles, and reaches the minimum (or maximum in absolute values) at 90° (Fig. 2G). In other words, the AMS of the white matter is least diamagnetic along the fiber direction (α = 0°). The same data was also plotted against sin²α (Fig. S2 in supplementary materials). The relationship could be fitted using a sine-squared function (Eq. 5). The magnetic susceptibility anisotropy of the white matter, as defined by Δχ_max, is estimated to be 0.026 ppm, while the baseline AMS contrast is -0.013 ppm (R²=0.55). In contrast to the clear anisotropy in the control mice, the directionality of the AMS contrast is completely missing in the shiverer mice (Fig. 2H). The magnetic susceptibility anisotropy of the white matter, Δχ_max, is determined to be only 0.002 ppm, while the baseline AMS contrast is also decreased (-0.006 ppm) (R²=0.01). As the primary structural difference between the two types of mice is the loss of myelin sheath in the shiverer (Chernoff, 1981), these results provide strong evidence supporting that the magnetic susceptibility anisotropy observed in previous studies (Lee et al., 2010; Li et al., 2011; Liu, 2010) arises mainly from myelin.

Model prediction of susceptibility anisotropy

According to Lounila et al (Lounila et al., 1994) ${\chi }_m^{\parallel }-{\chi }_m^{\perp }$ is -0.223 ppm for membrane lipids. A wide range of values (10~20%) have been reported in the literature for the volume fraction of lipids (Baumann and Pham-Dinh, 2001; Lee et al., 2010; Sutor et al., 2000; Woodard and White, 1986). In the current study, a lipid volume fraction (f_lipid) of 16% is employed, the same number used by Lee et al (Lee et al., 2010). Based on Eq. 5, the aligned lipid molecules in the membrane structures give rise to a macroscopic susceptibility anisotropy (Δχ_max) of 0.018 ppm. Furthermore, Eq. 5 also predicts that the susceptibility of the white matter is more paramagnetic when the fiber is along with the field, since the term in front of sin² α, i.e. $f_{\text{lipid}}({\chi }_m^{\parallel }-{\chi }_m^{\perp })∕2$, is negative. Considering the extensive heterogeneity of the lipid fraction and the idealized model of the myelin structure, the predicted value is considered to be in good agreement with the MRI-determined susceptibility anisotropy of 0.026 ppm in the mouse hippocampal commissure.

Susceptibility anisotropy of human brain in vivo

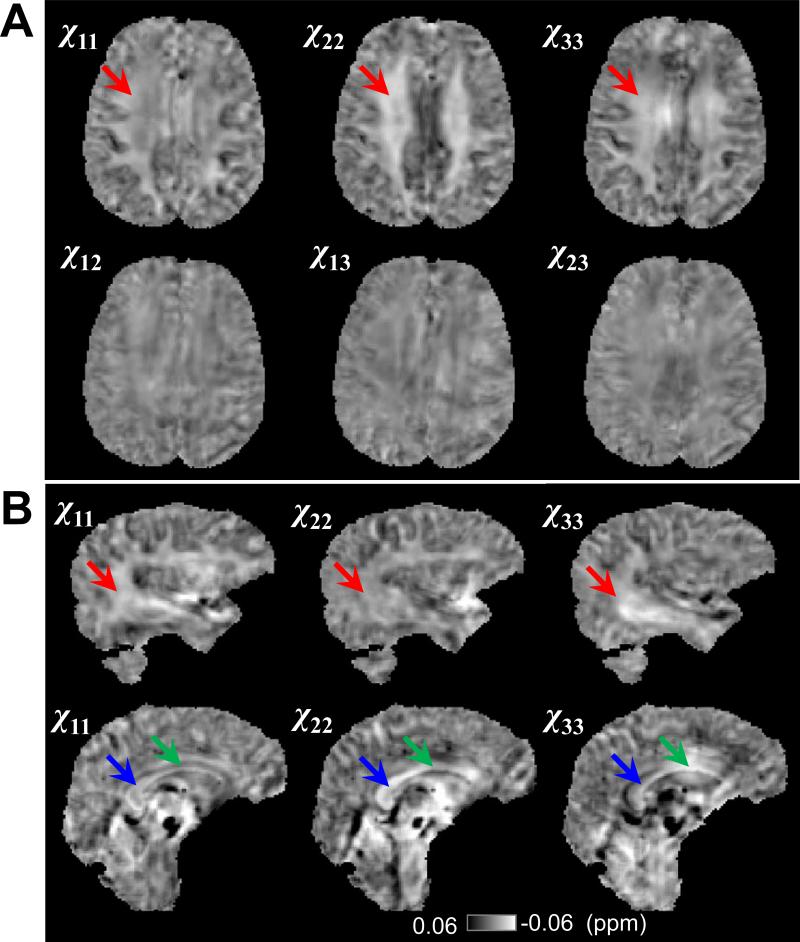
Fig. 3 shows the representative frequency maps from different brain orientations after phase processing. The calculated susceptibility tensors were shown in Fig. 4A. The diagonal components of the susceptibility tensor, i.e. χ₁₁ (in left-right direction), χ₂₂ (in anterior-posterior direction) and χ₃₃ (in superior-inferior direction), in the major fiber bundles (red arrow) exhibit significantly different susceptibility contrast relative to the gray matter. These differences between the diagonal tensor elements directly demonstrate the susceptibility anisotropy of human brain in vivo. More evidence of anisotropic susceptibility is shown in Fig. 4B. Fig. 5 shows the principal susceptibilities, the mean susceptibility calculated by $\overline{\chi }=({\chi }_1+{\chi }_2+{\chi }_3)∕3$ as well as the susceptibility anisotropy map calculated by Δχ_max = χ₁ – (χ₂ + χ₃)/2.

Fig. 3. Frequency maps from different head orientations.

A-C shows the frequency maps from one axial slice, and D-F shows frequency maps from another axial slice.

Fig 4. Susceptibility tensors and evidence of susceptibility anisotropy.

A: Maps of all 6 elements of the susceptibility tensor of a representative axial slice. The red arrows point to a white matter fiber bundle, which shows significantly different susceptibility along different image axis. B. The diagonal tensor elements in two different sagittal slices. Red arrows point to the sagittal striatum, green and blue arrows point to two segments of corpus callosum, which show different image contrast along different image axis.

The susceptibility anisotropy of a selected white matter fiber bundle (Fig. 5) was determined to be 0.022 ± 0.008 ppm using STI. This susceptibility anisotropy of 0.022 ppm in human brain is slightly larger than the model-predicted value of 0.018 ppm. Consistent with the diagonal elements of susceptibility tensors, a trend of orientation dependence of AMS could be observed despite the large data scattering. This data scattering was probably due to the tissue heterogeneity and complex fiber structures. A susceptibility anisotropy value of 0.019 ppm was obtained by fitting the AMS contrast to Eq. 5, which was similar to that determined by STI, supporting the validity of the proposed STI-based approach for susceptibility anisotropy calculation. Comparing to the single orientation method, STI calculates susceptibility tensor (6 elements) from all 16 directions using a more comprehensive physical model (Eq. 7), and is expected to provide more reliable determination of susceptibility anisotropy.

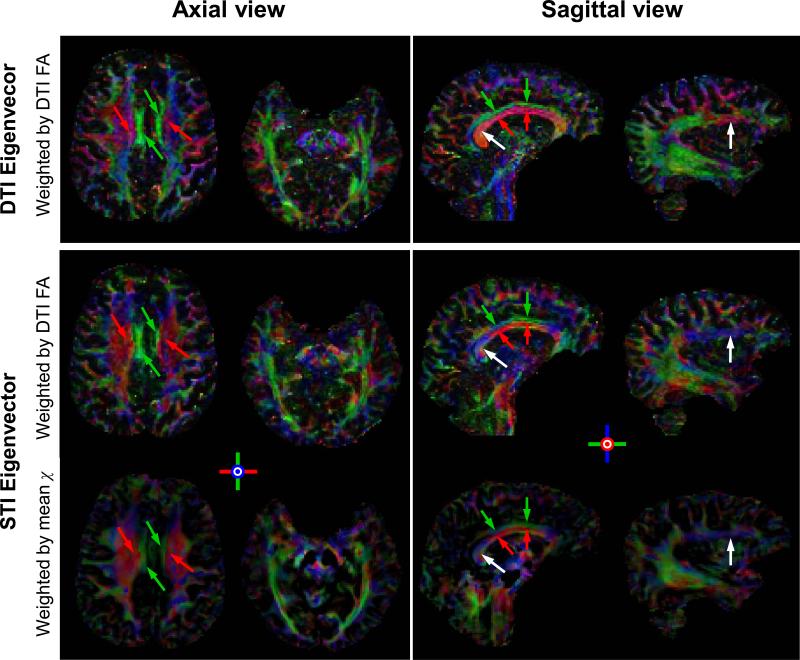
Susceptibility tensor decomposition also gives eigenvectors, which indicate the tensor orientation. To visualize tensor orientations, the eigenvectors of the susceptibility tensor and the diffusion tensor are color-coded following the same scheme with red representing left-right direction, green representing anterior-posterior and blue representing superior-inferior. To avoid biases caused by the color intensity, both DTI and STI eigenvectors were also weighted by the same diffusion FA map (Fig. 7 top and middle rows). To obtain a similar color map using exclusively STI data, STI eigenvectors were also weighted by the rescaled mean susceptibility (Fig. 7, bottom row). Overall, the colormap of the STI shows good agreement with that of DTI. There are also noticeable differences between DTI and STI especially at the edges of the fiber bundles that are more susceptible to errors in image registration (white arrows). Nevertheless, the capability of STI in separating two fiber bundles in close contact but of different orientations is striking. For example, both STI and DTI are able to differentiate between the corpus callosum (red arrows) and the cingulate gyrus (green arrows).

Fig. 7. Comparison of the eigenvectors of diffusion and susceptibility tensors in the human brain.

In the first two rows, both DTI and STI color maps are weighted by the same fractional anisotropy map of DTI for an unbiased comparison. In the bottom row, the STI eigenvector map is weighted by the rescaled mean susceptibility. The corpus callosum/superior corona radiata and the cingulate gyrus (in axial view), as well as the corpus callosum and the cingulate gyrus (in sagittal view) are clearly separated with consistent orientations between STI and DTI (red and green arrows). Differences also exist (white arrows) which may be caused by imperfect image registration.

Discussion

In this study, we provided the first demonstration of susceptibility tensor imaging in thehuman brain in vivo and explored the molecular underpinnings of MRI-observed bulk susceptibility anisotropy. The source of the bulk susceptibility anisotropy in brain white matter is identified as myelin, as shown by the loss of susceptibility anisotropy in brains of dysmyelinating shiverer mice. We further proposed the spatially ordered lipids in myelin structures as the main source of the susceptibility anisotropy. A biophysical model was developed, which related the macroscopic susceptibility anisotropy to the microscopic magnetic susceptibility anisotropy of the lipid molecules in the myelin of the white matter. The predictions by the model based on known molecular magnetic properties of lipid molecules agree well with the susceptibility anisotropy of mouse brain ex vivo and human brain in vivo. The model is further supported by the overall consistency of fiber orientations determined independently by DTI and STI. Together, these results provide good evidence for myelin as the main source of susceptibility anisotropy, and suggested that the spatially aligned membrane lipids in myelin are the molecular underpinning for the MRI observed susceptibility anisotropy.

The existence of magnetic susceptibility anisotropy on the molecular level is well-documented and utilized to determine molecular structures (Bertini et al., 2002; Pervushin et al., 1997; Tolman et al., 1995). However, bulk susceptibility anisotropy is rarely significant except in a few limited cases where spatial ordering exists, such as crystallized samples (Prestegard, 1998; Tjandra and Bax, 1997) and the residual dipole coupling at ultra-high fields (Lohman and Maclean, 1978; Tolman et al., 1995; Van Zijl et al., 1984). The bulk susceptibility anisotropy observed in proton-MRI, however, is not a result of the spatial ordering of water molecules. Rather, it is a consequence of the interaction between water molecules and an ordered surrounding medium, in this case, the lipid bilayers in the myelin sheath. This interpretation is consistent with the experimental data. First, compared to the control mice, the susceptibility anisotropy (Δχ_max) of the brain white matter dropped by an order of magnitude in the shiverer mouse (CTRL: 0.026 ppm v.s. SHVR: 0.002 ppm) while the baseline susceptibility contrast is reduced only by a factor of 2 (CTRL: -0.013 ppm v.s. SHVR: -0.006 ppm), suggesting that the myelin sheath is the main source of the magnetic susceptibility anisotropy. Second, the model predicted Δχ_max (0.018 ppm) due to membrane lipids accounts for the majority of the measured magnetic susceptibility anisotropy (0.026 ppm) in mice. Third, the predicted anisotropy induced by membrane lipids (0.018 ppm) can interpret >80% of the measured susceptibility anisotropy (0.019 by ROI analysis and 0.022ppm by STI) in human brain in vivo. It should be noted that this estimated ratio could be influenced by the uncertainties in the measured susceptibility anisotropy and the spatial variation of chemical composition in the white matter. Our data is considered consistent with the reported value of 0.012 ppm in human brain specimen by Lee et al (Lee et al., 2010), given the differences in sample preparation, imaging parameters, data analysis and biological variations. Finally, the fiber orientation estimated by STI agrees largely with DTI for human brain.

Although our study focused on the contribution of lipid bilayers to susceptibility anisotropy, a few other factors need to be noted. First, the brain white matter contains a complex composition of lipids, not only phospholipids, but also glycolipids and cholesterol (in the ratio of about 4:2:3) (Baumann and Pham-Dinh, 2001). The structure of glycolipids is similar to phospholipids with a long hydrophobic tail and a hydrophilic head, whereas the structure of cholesterol is significantly different. Although the exact contribution of cholesterol to the overall susceptibility anisotropy is difficult to evaluate, the addition of cholesterol does increase the degree of ordering in magnetically aligned phospholipid bilayers (Lu et al., 2004). Second, besides membrane lipids, there are also other macromolecules that are aligned along the radial direction of the axon fibers, especially transmembrane proteins. For example, the proteolipid protein (PLP) is believed to bind the lipid bilayer as the myelin sheath wraps come together while the myelin basic protein (MBP) is sandwiched in the extracellular space between two adjacent bilayers (Barkovich, 2000). Although the direction of the anisotropy of these proteins may vary (PLP in the radial direction and MBP in the circumferential direction), they share the same cylindrical symmetry of the myelin sheath. As a result, the same sine-squared relationship is expected to apply to these proteins (see supplementary materials, 2). Furthermore, in the white matter, the mass of proteins is ~64% of that of the lipids (Woodard and White, 1986), and the peptide segments of the proteins are much less aligned than those of the lipids. As a result, the contribution of proteins to susceptibility anisotropy is expected to be significantly less than that of lipids. Given the limited knowledge of the magnetic anisotropy values of myelin proteins, the exact contribution of proteins to macroscopic susceptibility anisotropy remains to be investigated.

In addition to molecules in the myelin, brain tissues also contain many other compounds with magnetic susceptibilities different from that of water, e.g., tissue iron, and deoxy-hemoglobin. The anisotropic effect of these molecules is expected to cancel out on the macroscopic scale due to the lack of spatial coherence. Nevertheless, they do contribute to the mean susceptibility (trace of the susceptibility tensor) and the T2*-relaxation rate. There are also growing evidence supporting the contribution of chemical exchange between macromolecules and mobile protons to the frequency shift contrast between gray and white matter (Luo et al., 2010; Shmueli et al., 2011; Zhong et al., 2008). Chemical exchange is not expected to be dependent on the magnetic field orientation. Thus, it is not expected to contribute to the anisotropy.

Previously, He and Yablonskiy (2009) have employed a Lorentzian cylinder approach to describe the dependence of phase contrast on white matter fiber orientation. In the Lorentzian cylinder model, the frequency of a molecule moving in a cylinder is expressed as:

$$\frac{\Delta f}{f_0}=2\cdot \pi \cdot {\chi }_a\cdot {\text{sin}}^2\vartheta$$ [8]

Taking the influence of nearby spins into account, the orientation dependence of resonance frequency shift of white matter (WM) is related to magnetic susceptibility of the longitudinal structures (χ_a) as:

$$\frac{\Delta f_{WM}}{f_0}=\frac{4}{3}\cdot \pi \cdot {\chi }_{WM}-2\cdot \pi \cdot {\chi }_a\cdot \left({\text{cos}}^2\vartheta -\frac{1}{3}\right)$$ [9]

The model is further refined in a recent study by Denk et al. (Denk et al., 2011) in order to fit their data. The Lorentzian cylinder model attributed the orientation dependence of frequency shift to the effect of compartmentalized but isotropic susceptibility in elongated domains. As demonstrated by the loss of frequency contrast in the shiverer mice, the non-spherical Lorentz effect, if significant, should also originate from the myelin sheath. Our study, on the other hand, models the cumulative effect of molecular susceptibility anisotropy and its macroscopic manifestation in spatially resolved magnetic susceptibility. While frequency shift may provide a reasonable description for simple structures, its quantitative value for complicated brain architecture is limited due to the long range dipolar effect (supplementary materials). Although the Lorentzian cylinder model (Eq. 8) and the model proposed in this study (Eq. 4) were not separated because they both predict a sine-squared relationship, emerging evidence suggests that the susceptibility anisotropy of lipids may play a more important role than the non-spherical Lorentz effect: (1) the frequency shift at the boundaries and outside of corpus callosum preparations was observed, which cannot be explained with the Lorentzian cylinder model (Lee et al., 2010); (2) the orientation dependence of R₂* on fiber angle was better explained by the dominance of anisotropic susceptibility in human brain specimen, with a ratio of 1.59 between anisotropic and isotropic susceptibility (Lee et al., 2011). A similar ratio of 2 is also observed in control mouse brains of this study (anisotropic: -0.026 ppm v.s. isotropic: -0.013 ppm); and (3) the susceptibility (and frequency shift) contrast and susceptibility anisotropy is nearly absent in the shiverer mice, although the cylindrical structures of axon are still present as revealed by DTI (Liu et al., 2011a). These findings may suggest that, although the MRI-measured susceptibility anisotropy can be a combination of molecular magnetic anisotropy and non-spherical Lorentz effects, myelin lipids appear to be the main source of the macroscopic susceptibility anisotropy. Since the anisotropy due to molecular magnetic anisotropy and non-spherical Lorentz effects are aligned in exactly the same direction, their combination will not cause discrepancy between DTI and STI eigenvectors.

This is the first demonstration of extracting fiber orientation in vivo using anisotropic susceptibility. The purpose is to elucidate the molecular mechanism of an important biophysical phenomenon in the brain. Routine application of STI in vivo is still non-trivial, due to, e.g., the difficulties in the experimental setup and subsequent data processing. For the interpretation of STI data, a few important factors also need to be noted. First, the selection of phase or susceptibility reference is critical for STI. In this study, the background phase is removed using sphere mean value filtering, which essentially sets susceptibility reference to the mean susceptibility of the brain tissue. Hence, the susceptibility references are consistent among different orientations. Second, different principal susceptibility is observed in the gray matter. Given the lack of coherent tissue microstructures in the gray matter and the large voxel size, it is likely that susceptibility of gray matter is isotropic, and the observed difference is caused by partial volume effect. This was supported by a recent mouse brain study that the susceptibility anisotropy was mainly found in white matter fibers (Liu et al., 2011b). However, the possibility of anisotropic susceptibility in gray matter still exists. If susceptibility anisotropy can be accurately measured and validated in the gray matter, it may provide a useful tool to study the microstructure of the gray matter. Despite the difficulties in STI, the clear separation of large fiber bundles that are in close contact but of different orientations, for example, the corpus callosum and the cingulate gyrus, is very encouraging, which demonstrates that the orientation of the susceptibility tensor is indeed related to the white matter micro-architecture.

The overall consistency between diffusion and susceptibility tensor orientations for large fiber bundles indicate the existence of common biological bases to STI and DTI, in particular, with respect to the structural support of axon. There are also important differences, for example, with respect to the contribution of myelin sheath. There are growing evidence suggesting that myelin per se does not play a dominant role in diffusion anisotropy (Beaulieu, 2002; Liu et al., 2011a). On the other hand, myelin appears to be the primary source of susceptibility anisotropy. The frequency shift and susceptibility has a unique chemical sensitivity, e.g. to myelin and iron, which can be much more sensitive than DTI-derived parameters. Single-orientation susceptibility mapping has been used for the assessment of brain myelination (Liu et al., 2011a). The image interpretation, however, can sometimes be confounded by the orientation dependence of susceptibility in the white matter. According to the model presented here, susceptibility anisotropy, on the other hand, is linearly proportional to the amount of myelin. However, measurement of susceptibility anisotropy by STI alone is nontrivial. The combination of STI and DTI may potentially overcome this difficulty and allow for a reduced number of orientation sampling and more accurate measurement of susceptibility anisotropy and mean susceptibility. The combination of DTI and STI may also potentially allow a more accurate determination of complex white matter fiber structures that have largely eluded the capability of DTI.

Conclusion

In summary, this study demonstrated that the spatially resolved bulk susceptibility anisotropy in brain tissue is likely to originate from myelin, and further suggested that the cylindrically aligned lipid molecules in myelin are the main source of bulk susceptibility anisotropy. Our results suggest that magnetic susceptibility anisotropy can be used as a potential endogenous marker for myelination, as is predicted by the model that the susceptibility anisotropy is linearly proportional to the lipid concentration. Finally, it is now possible to estimate fiber orientation solely from bulk magnetic susceptibility tensor in the human brain in vivo.

Research Highlights.

1. A biophysical model that links the MRI-observed susceptibility anisotropy to the anisotropic molecular magnetic susceptibility.

2. Agreement between model predictions and experimental susceptibility anisotropy in both in vivo human brain and ex vivo mouse brains.

3. The first demonstration of extracting fiber orientation in vivo using anisotropic magnetic susceptibility.