Abstract
Several applications of fMRI at high field have taken advantage of the increased BOLD contrast to increase spatial resolution, but the potential benefits of higher fields for detecting and analyzing functional connectivity have largely been unexplored. We measured the influence of spatial resolution at 7T on estimates of functional connectivity through decreased partial volume averaging. Ten subjects were imaged at 7T with a range of spatial resolutions (1×1×2mm to 3×3×2mm) during performance of a finger tapping task and in the resting state. We found that resting state correlations within the sensory-motor system increase as voxel dimensions decreased from 3×3×2mm to 1×1×2mm, whereas connectivity to other brain regions was unaffected. This improvement occurred even as overall signal to noise ratios decrease. Our data suggest that this increase may be due to decreased partial volume averaging, and that functional connectivity within the primary seed region is heterogeneous on the scale of single voxels.
Keywords: fMRI, functional connectivity, 7T, motor
1. INTRODUCTION
Derivations of resting state functional connectivity from intervoxel correlations of Blood Oxygen Level Dependent (BOLD) signals across the brain are now routinely obtained by functional magnetic resonance imaging (fMRI), but there is continuing interest in technical advances that may improve the quality of these measurements. In principle the higher signal to noise ratio and stronger BOLD effects obtained at high fields such as 7T should permit more reliable estimates of connectivity. Here we evaluate some advantages and challenges of using 7T BOLD fMRI to measure connectivity within the motor system and illustrate how the use of smaller voxels can significantly affect estimates of intervoxel correlations, suggesting that functional connectivity is heterogeneous within primary motor areas on the millimeter scale.
Transitioning fMRI techniques to higher magnetic fields brings several advantages as well as some disadvantages. The quadratic increase in signal intensity with field can be leveraged to decrease voxel volume while maintaining signal-to-noise ratio (SNR). In addition, BOLD contrast also increases at least linearly as susceptibility variations produce amplified dephasing effects. However, phase accumulations due to inhomogeneities in the static magnetic field are also increased, resulting in considerable degradation of echo planar images. Nonetheless, successful high resolution BOLD fMRI can be accomplished by appropriate design of the imaging protocol and pulse sequence, especially with the use of parallel imaging and multi-shot techniques (Poser et al., 2010; Speck et al., 2008; Stringer et al., 2011; Yacoub et al., 2001).
Although decreases in voxel volume reduce the SNR, in regions where the BOLD activation is heterogeneous on the scale of a voxel or smaller, the BOLD contrast-to-noise ratio (CNR) may still increase because of reduced partial volume averaging. Several reports have shown that fMRI images acquired at 7T with voxel volumes 1mm3 or smaller (Poser et al., 2010; Speck et al., 2008; Stringer et al., 2011; Yacoub et al., 2008) maintain detectable BOLD contrast. This can be compared to typical 3T fMRI voxel volumes of 27mm3. If activations are smaller than 27mm3 in size, their CNR are reduced by partial volume dilution. Similarly, if connectivity from one region to another is heterogeneous on the scale of millimeters, then increased spatial resolution may improve estimates of resting state functional connectivity. The aim of the present study is to test whether decreasing voxel volume increases estimates of resting state functional connectivity within the motor system through decreasing partial volume averaging despite the expected decrease in SNR of the resulting images.
2. METHODS
2.1 (Image Acquisition)
Ten subjects were imaged on a Philips Achieva 7T MRI scanner with a volume transmit RF coil and a SENSE receive coil (16 channels, Nova Medical). Each subject had a series of five functional imaging series acquired, in addition to high resolution structural images. Subjects initially performed a block designed finger tapping task while images were acquired over 19 axial slices (single shot gradient echo EPI, 90 volumes, FOV=192mm, 19 slices, TR/TE = 2000/28ms, θ = 70°, voxel size = 1×1×2mm, SENSE factor = 3.92). A standard linear regression of the block-designed task was performed at the imaging console using IView BOLD software to identify the sensorimotor network. The task consisted of 20s finger tapping with the left hand (LeftTap: thumb pressed to each finger sequentially, self paced), 20s tapping with the right hand (RightTap: same scheme), and 20s resting with their eyes open. This sequence was repeated three times. The left and right primary motor cortices, as well as the supplementary motor area were identified by immediately contrasting right tapping versus rest and left tapping versus rest. Seven contiguous axial slices covering these structures were identified for further imaging.
Four resting state acquisitions were then recorded with a range of voxel sizes covering these seven slices. Subjects began each series by repeating the finger tapping task, after which they were instructed to close their eyes and rest. The post-task resting state lasted for 500s for each run. Images were acquired again using single shot gradient echo EPI (680 volumes, FOV = 192mm, θ = 54°, TR/TE = 1000/28ms, SENSE factor = 3.92, full k-space acquisition). The voxel volumes used were 2mm3, 4.5mm3, 8mm3, and 18mm3 corresponding to resolutions of 1×1×2mm, 1.5×1.5×2mm, 2×2×2mm, and 3×3×2mm. The bandwidth in the frequency encoding direction was 1203.4Hz, 1146.0Hz, 1492.8Hz, and 2280.8Hz for each of the resolutions respectively. Gradient limits were reduced for the highest resolution images in order to reduce peripheral nerve stimulation among the subjects. Seven slices were imaged at the highest resolution, while all three other resolutions spanned 13 slices with the central seven matching those slices imaged at 1×1×2mm resolution, allowing for the maximum amount of data possible to be gathered at each resolution. The order of image acquisition at different resolutions was counterbalanced across subjects such that half had images gathered from lowest to highest resolution, while the other half had images acquired from highest to lowest resolution.
2.2 (Initial Processing)
All functional images were corrected for slice timing and motion artifacts using SPM5 (http://www.fil.ion.ucl.ac.uk/spm/software/spm5/) prior to any further analysis. Prior to functional connectivity analyses, each voxel’s BOLD time course underwent linear regression of the six estimated motion parameters and the global time course calculated across the whole brain. All voxels’ time courses were also linearly detrended, the means were subtracted and they were both low pass filtered (0.1Hz) and high pass filtered (0.0078Hz).
At each spatial resolution, individual subject activation maps were calculated from the block designed data using SPM5. General linear models of the data were constructed from the timing of the two finger tapping conditions as well as the six estimated motion parameters and the mean value of the data. Contrasts were established to identify those voxels activated by either left or right handed finger tapping, and maps were thresholded at the individual voxel p<0.05 level using a family-wise error correction for multiple comparisons.
2.3 (Connectivity Map Analysis)
In order to test for the effects of voxel volume on functional connectivity data, we measured our ability to distinguish an established network of resting state functional connectivity (the sensorimotor network) from the rest of the brain. We measured the differences in correlation coefficients between seed voxels and both motor and non-motor voxels in functional connectivity maps generated from images acquired at each specified resolution.
This analysis began with calculation of functional connectivity maps at the individual subject level by manually selecting a single activated voxel along the central sulcus on the right hand side of the brain as the seed voxel (FWE corrected, p<0.05, minimum cluster size = 1 voxel). The specific voxel chosen was different from subject to subject and was identified at the highest spatial resolution. The corresponding larger voxel at every other resolution was then identified. Thus all connectivity maps were constructed from the same single voxel seed region, where the only variable between resolutions is the size of the voxels in the images. We verified that the voxel chosen for each subject was appropriate by inspecting initial connectivity maps to confirm bilateral representation of the motor network, and in any cases where the bilateral motor network was not identified, a new seed voxel was chosen. Seed voxel locations were also reviewed across all resolutions in each subject to confirm that the location of the seed voxel was not shifted by residual registration errors or distortion.
Functional connectivity maps consisted of the Pearson’s correlation coefficient between every voxel and the seed voxel. This generated a distribution of correlations across the brain that potentially contain multiple false-positive (spurious) correlations. These connectivity maps were then segmented into two classes of voxels, the conventional motor network, and the non-motor voxels within the brain. Motor network voxels were identified for each subject at the highest resolution as those voxels significantly activated during either left or right handed finger tapping according to the blocked task data (FWE corrected, p<0.05, no minimum cluster size), and were resized to each of the lower resolutions by identifying the larger voxels containing those identified at the highest resolution. All voxels in the brain, excluding the motor voxels, were considered non-motor voxels. This was done to ensure that the same network definitions were used across runs for each subject. Histograms of functional connectivity measurements across subjects were calculated at each resolution for both motor and non-motor voxels, where voxel counts were normalized by the total number of voxels at each resolution. Finally, the contrast to noise ratio between the motor network and the rest of the brain was calculated within the maps of functional connectivity (CNRrmap) as defined by equation 1, where ‘r’ is the Pearson’s correlation coefficient, ‘’ is the average correlation across the specified set of voxels, and N is the number of voxels.
| (1) |
A 2-way ANOVA testing for significant effect of voxel volume on CNRrmap measurements across subjects was performed, followed by paired t-tests to identify which resolutions were significantly different from each other.
2.4 (Connectivity Matrix Analysis)
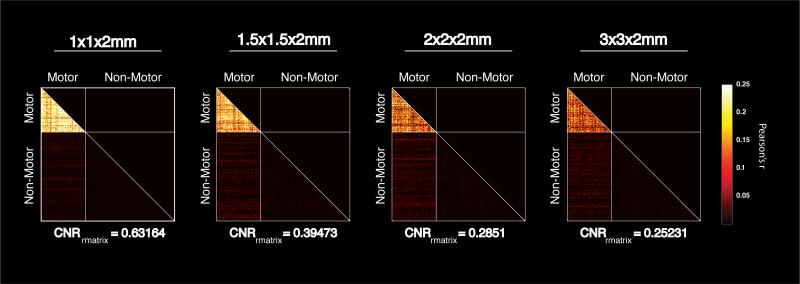
In order to test whether any effects of increased spatial resolution were dependent on the specific seed voxel chosen, we calculated a matrix of pair-wise correlations between voxels in the brain. We randomly selected 100 voxels from the motor network and 200 voxels from the non-motor network for analysis in each subject and at each resolution. We then calculated the pair-wise correlations between all 300 voxels, creating a matrix of correlation coefficients. In order to quantify any improvement in the contrast between the motor and non-motor network, we measured the mean correlation between all pairs of motor voxels, and the mean correlation between all pairs of motor and non-motor voxels. We defined the contrast to noise ratio (CNRrmatrix) to be the difference between these means divided by the standard deviation of the correlations between motor and non-motor voxels. This is meant to be conceptually similar to equation 1, working with pair-wise correlations instead of correlations to a single seed voxel, and yields one CNRrmatrix value per subject and per resolution. We then tested for a significant effect of voxel volume on CNRrmatrix using a 2-way ANOVA with factors for spatial resolution and subjects.
2.5 (tSNR Measurement)
The temporal SNR (tSNR) decreases as voxel sizes decrease, and in principle this might be expected to cause correlation values between connected regions to appear smaller. The tSNR was calculated for each subject using the resting state images acquired at each spatial resolution after slice timing and motion correction. tSNR was calculated on a voxel-by-voxel basis as the mean signal divided by the standard deviation across time. In order to focus the measurement on the most relevant voxels, the distribution of tSNR measurements was calculated for all activated voxels (motor voxels above) measured for each subject (FWE corrected, p<0.05, no minimum cluster size). In order to compare one distribution to another, the mean distribution across subjects was plotted at each resolution. Each distribution was smoothed with a five point moving average filter.
2.6 (Measuring Partial Volume Effects)
Changes in functional connectivity measurements are expected to arise from underlying differences in partial volume averaging. To test whether this was the case, we focused on those images acquired during the finger tapping task. Two analyses were performed to test whether decreasing voxel volume leads to increased functional contrast due to decreased partial volume averaging. The first analysis identified whether task activation in the sensory-motor network became more focal as images were acquired with increasingly high spatial resolution. To this end, the percent of within-brain voxels that were significantly activated by the finger tapping task was calculated across all subjects and plotted as a function of spatial resolution.
However, decreases in this ratio are expected to occur as the SNR decreases. Looking for a second measure of partial volume effects in our functional images, we noted that the significance of activation should decrease in a predictable manner as voxel volume decreases (due to decreases in SNR) assuming that the magnitude of the signal change is held constant. Therefore, we also looked at whether the significance of activation varied more than would be predicted by changes in the noise alone as voxel volume decreased. To test this, the most active voxels across all resolutions were identified as those voxels that were significantly active at the lowest resolution (FWE p<0.05, minimum cluster size = 5), and that contained at least one significantly active voxel (same criteria as above) within its boundaries at each of the three higher spatial resolutions. T-statistics were plotted against the standard deviation of the model error for all active voxels at each resolution, and were compared to theoretical decreases (Friston et al., 1995). This decrease is described by equation 2 below,
| (2) |
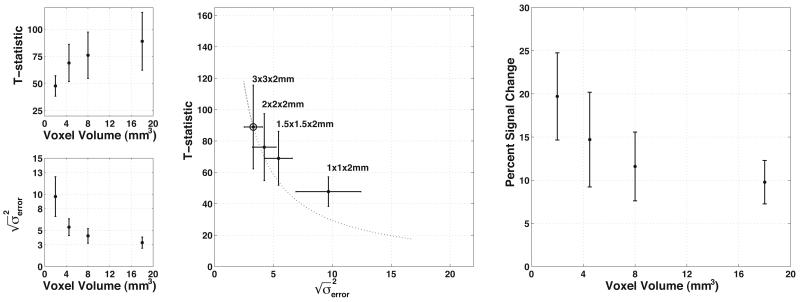
where ‘c’ is the contrast matrix, ‘b’ is the matrix of beta weights, ‘G’ is the design matrix describing the task, and ‘ε2’ represents the model error terms. As voxel volumes decrease, T-statistics will be affected both by changes in signal and by changes in the noise. The change in noise as a function of voxel volume is related to the fact that total noise has both a thermal and a physiological component, the latter of which is signal dependent. To predict the theoretical changes in activation T-statistics as voxel volume decreased, it was necessary to account for this change in the composition of the noise from one resolution to the next. Thus, we turned to empirical measurements of model error, which include both physiological noise and thermal noise. Measurements of model error at each resolution were used to predict the theoretical change in T-statistic, assuming no change in the activity-related signal variance (i.e. beta weights, contrast matrix, or regression matrix). This prediction used the initial starting point T-statistic measured at 3×3×2mm resolution and predicted the expected significance of activation using the measured model error at each of the other resolutions. These were then compared to the measured T-statistics at each resolution (see Figure 6). Any discrepancy between the predicted and measured T-statistics in this analysis would likely be attributable to changes in the task related variance (i.e. percent signal change), so we also calculated the percent signal change at each resolution as a more direct measure of this effect. This was calculated as the amplitude of the average signal change across active voxels (selection described above) divided by the mean signal across conditions. If partial volume averaging decreases as voxel volume decreases, then we expect that measured T-statistics would fall less than would be predicted by the noise alone, and that this would be due to increased functional contrast measured as percent signal change.
Figure 6.
The effect of decreased partial volume averaging on task-related activation, the residual model error, and voxel volume. All points/bars represent the mean/standard deviation across subjects of the average value across active voxels. (top left) T-statistics decrease with decreasing voxel volume in a nonlinear fashion. (bottom left) The deviation of the model error decreases as voxel volume increases. (center) The decrease in the T-statistic as a function of model error is less than would be predicted by theory. The dotted line represents the theoretical decrease given the initial point measured with 3×3×2mm voxels, marked by an additional circle. (right) Functional contrast increases as voxel volume decreases, indicating less dilution of the functional signals by partial volume averaging.
3. RESULTS
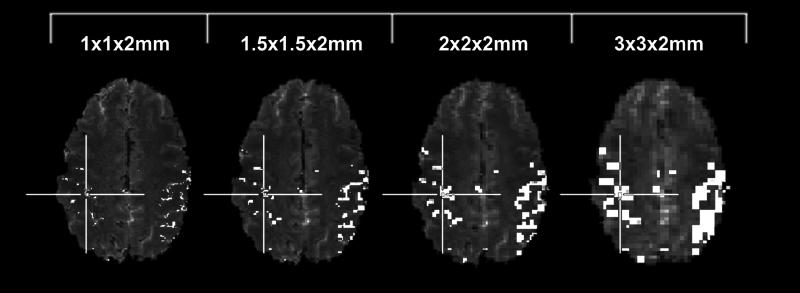
Significant activation was measured in the sensorimotor network in all ten subjects imaged at 7T with all four resolutions. The motor network was defined based upon activation measured in the highest resolution data, which were used to locate the correspondingly larger voxels in lower resolution images (Figure 1). The activated regions consisted of both primary motor and somatosensory cortices, and the supplementary motor area (SMA).
Figure 1.
An example of the network definitions across resolution. Cross hairs highlight the seed voxel location chosen in this subject.
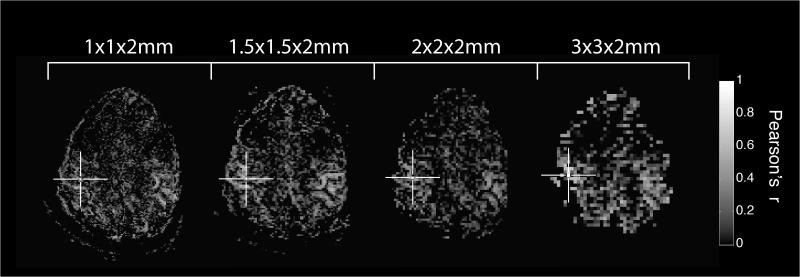
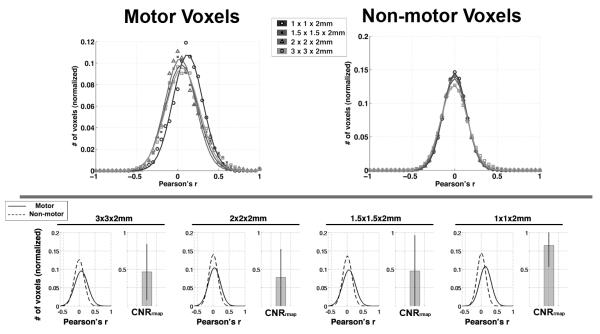
Maps of functional connectivity showed the expected bilateral sensorimotor network for each subject at each resolution, an example of which can be seen in Figure 2. Qualitatively, distortion over the region of the brain imaged here was not different across resolutions. The distribution of correlations among both motor and non-motor voxels was well described by Gaussian profiles, and goodness of fit metrics for the profiles shown in Figure 3 can be seen in Table 1. The distribution of correlation measurements among motor voxels showed increased correlation as voxel dimensions decreased to 1×1×2mm, as shown in Figure 3. Correlations measured throughout the rest of the brain remained unchanged as a function of voxel volume, and the comparison of the distributions between motor and non-motor voxels can also be seen in Figure 3. There is increased separation between the motor and non-motor distributions when the maximum spatial resolution was used, confirmed through measurement of the CNRrmap between motor and non-motor voxels. There was a significant effect of voxel volume on measurements of CNRrmap (p=0.0395) measured via 2-way ANOVA, and the subsequent results of paired T-tests between resolutions are shown in Table 2. The CNRrmap measurements made at the highest resolution were significantly different from those made at the two lowest resolutions, with the difference between the 1×1×2mm and the 2×2×2mm voxels remaining significant even when correcting for multiple comparisons across the six tests (p<0.05).
Figure 2.
Examples of individual subject connectivity maps illustrating increased specificity associated with mapping functional connectivity with higher spatial resolution. The cross hairs indicate the location of the seed voxel.
Figure 3.
(top) The distributions of functional connectivity (correlation) among MOTOR and NON-MOTOR voxels at each resolution. A Gaussian curve was fit to the mean distribution across subjects at each resolution. (bottom) A direct comparison of the distributions of correlation among motor and non-motor voxels at each resolution. Note the increase in separation between the motor and non-motor distributions (i.e. contrast) as voxel volume approach 1×1×2mm.
Table 1.
Goodness of Fit for Gaussian Distributions in Figure 3
| 1×1×2mm | 1.5×1.5×2mm | 2×2×2mm | 3×3×2mm | |
|---|---|---|---|---|
| R2motor | 0.9907 | 0.9797 | 0.9882 | 0.9868 |
| R2non-motor | 0.9997 | 0.9988 | 0.9996 | 0.9974 |
Table 2.
Probability of No Significant Difference in CNRrmap Across Resolutions (p-values from paired t-tests)
| resolution | 1×1×2 | 1.5×1.5×2 | 2×2×2 | 3×3×2 |
|---|---|---|---|---|
| 1×1×2 | --- | |||
| 1.5×1.5×2 | 0.081 | --- | ||
| 2×2×2 | 0.011** | 0.17 | --- | |
| 3×3×2 | 0.014* | 0.8 | 0.52 | --- |
marks values below 0.05
significant after multiple comparison correction (Tukey-Kramer method)
This improvement is not dependent on the specific seed voxel chosen, as evidenced by Figure 4, where multiple motor and non-motor voxels were selected and this selection was randomized from subject to subject and from resolution to resolution. There was a significant effect of voxel volume on CNRrmatrix (p<10−5) measured via 2-way ANOVA. The distributions of tSNR shown in Figure 5 suggest that this improvement occurs despite a decrease in resting state tSNR associated with imaging using smaller voxel volumes.
Figure 4.
Pair-wise correlation matrices measuring the correlation between 100 randomly selected motor voxels and 200 randomly selected non-motor voxels. Each plot represents the average correlation matrix across subjects. Only the bottom half of the matrix is shown to avoid redundancy, and lines are inserted to aid in identifying the transitions between motor and non-motor voxels within the matrix. Note the significant improvement in contrast between the within network correlations (i.e. motor to motor) over those to the rest of the brain (i.e. motor to non-motor).
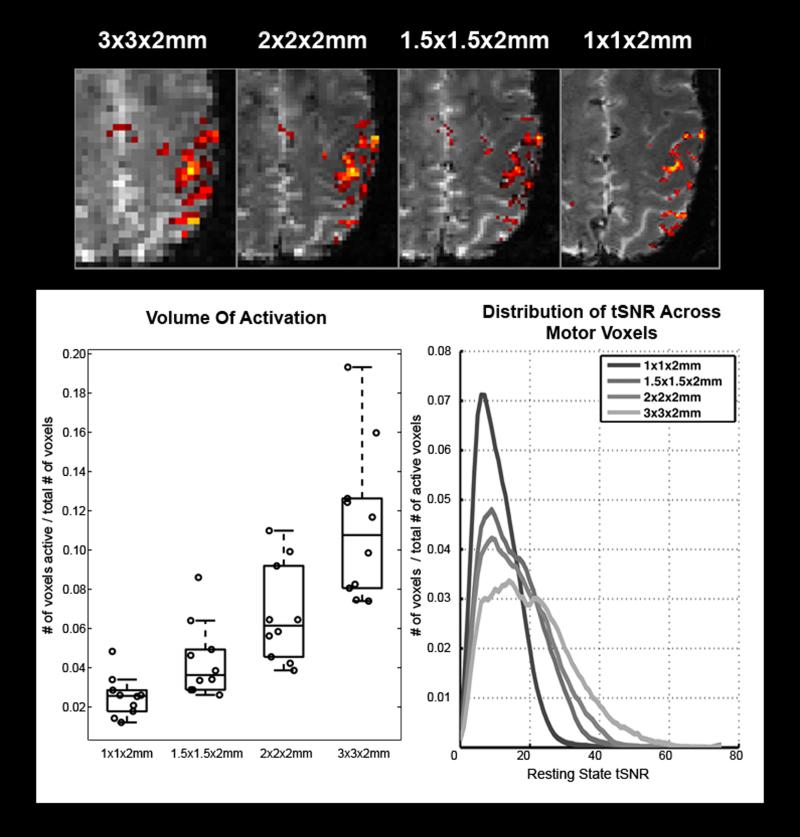
Figure 5.
(top) An example of activation changes as a function of spatial resolution. Note that activity becomes more focal as voxel volume decreases. (bottom left) A plot of the estimated activated volume measured at each available spatial resolution. Circles represent individual measurements made in each subject. Box lines are at the lower quartile, median, and upper quartile of the data. Whiskers extend from each end of the box to the adjacent values in the data. (bottom right) The average distribution of resting state tSNR measured among motor voxels, averaged across subjects. Note the expected increase in tSNR as voxel volume increases. Voxel counts were normalized by the total number of voxels in the image to adjust for the changing total number of active voxels from one resolution to another.
The volume of tissue activated by the finger tapping task decreased as a function of voxel volume, suggesting a more focal representation of the motor network, also shown in Figure 5. When looking at the most active voxels, the strength of activation decreased as a function of voxel volume, though less than would be predicted by the measured noise (residual model error) alone. The contrast, measured as percent signal change, increased among these voxels as voxel volume decreased, as shown in Figure 6.
4. DISCUSSION
In this study, we have demonstrated that imaging at very high spatial resolution (1×1×2mm) allows for improved functional connectivity analyses. This improvement was observed despite the accompanying decrease in SNR, and resulted in an increased ability to distinguish the sensorimotor network as defined by a finger tapping task from the rest of the brain in resting state functional connectivity maps.
Improvements in measures of resting state functional connectivity may be due in part to decreased partial volume averaging. By looking at images acquired during a finger tapping task, we demonstrated that activity becomes more focal as voxel volume decreases (Figure 5). This suggests that the true representation of the sensory-motor network is more focal than can be resolved with the larger voxel volumes used here. However, this could be explained either by decreasing partial volume averaging or by decreased sensitivity as voxels become smaller and only the most robust activations remain significant. As we looked at the strength of activation across resolutions (Figure 6), we see that the significance of activation decreased as voxel volume decreased. When compared to the theoretical decrease in T-statistic based on the measured model error, the observed T-statistics decreased more slowly than could be predicted by the noise alone (Figure 6, center), suggesting that functional contrast increased. Contrast directly measured as percent signal change increased as voxel volume decreased, supporting the view that decreased partial volume averaging of the sensory-motor network resulted in increased functional contrast. Assuming that task driven activity reflects underlying functional connectivity, these results support the view that the improvements in measurements of resting state functional connectivity shown by Figure 3 are due to decreased partial volume averaging of the motor network.
When measuring resting state functional connectivity, we observe the expected decrease in temporal signal to noise as voxel volume decreases (Figure 5, right), though we also observe an improvement in the contrast between the motor network and the rest of the brain in maps of functional connectivity (Figure 2,3). Looking at the data in Figure 3, the improvement in CNRrmap was significant when comparing the highest resolution data to others, suggesting that the benefits of decreased partial volume averaging outweigh the loss of signal associated with imaging with smaller voxels. However, a reliable continuous improvement in connectivity measurements as voxel volume decreased was not observed, shown by the fact that the only statistically significant improvement was observed when comparing the highest resolution data to the others. Addressing any concerns of what effects linear regression of the global time course might have on these results, we repeated the measurement of CNRrmap both with and without this regression and found the effect of voxel volume on CNRrmap to be significant in both cases (p<0.04).
Comparing this finding to previous reports, data from (Van Dijk et al., 2010) suggest that decreasing voxel volume does not improve interregional correlations. However, they studied this effect only between two voxel dimensions, 3×3×3mm and 2×2×2mm. Our data also did not find significant differences at these scales but our results suggest that significant changes are observed as voxel dimensions continue to decrease to 1×1×2mm . The limit of this improvement is a topic deserving further study.
Measuring seed region functional connectivity maps using single voxel seed regions presents several challenges that should be considered. First, in order to maintain the same seed voxel across multiple resolutions, the seed voxel must be defined in the highest resolution data first. Voxels of 3×3×2mm are capable of spanning gray matter, white matter and cerebrospinal fluid simultaneously, so choosing an inappropriate high resolution voxel within these large, low resolution voxels could bias the data against high resolution imaging. By choosing the seed in the highest resolution first, this ambiguity was eliminated because there is only one voxel at each lower resolution that contains the initial seed chosen. Second, accurate identification of an appropriate voxel for each subject requires mapping of the functional network using a traditional task paradigm. Without accounting for subject to subject variability in the functional network representation, there could be increased variability in the quality of the resulting connectivity maps, reducing sensitivity to other factors affecting the strength of interregional correlations. Alternative methods such as independent component analysis may allow for similar measurements to be made without the complication of identifying specific seed voxels in each subject. However, those methods would face different challenges such as ensuring that variance was split consistently across components as spatial resolution was manipulated, and that any apparent effect of spatial resolution was not dependent on the number of components chosen for the analysis.
Changes in the ratio of physiological to thermal noise also need to be considered in evaluating the benefits of increased spatial resolution. Physiological noise can robustly create widespread, non-specific correlations that confound functional connectivity analyses. For this reason, we employed global time course correction as a method for partially removing these effects. While global time course correction continues to be debated for studies of functional connectivity (Murphy et al., 2009), evidence suggests that global time courses do contain physiological noise signals (Chang and Glover, 2009), and that the linear regression of these signals reduces physiological noise throughout the brain (Fox et al., 2009). Even so, removal of physiological noise will likely be incomplete and residual physiological noise should still be considered. Because physiological noise scales with overall signal, its relative contribution to fMRI signal variance will also change with increasing spatial resolution (Kruger and Glover, 2001; Triantafyllou et al., 2005). On one hand, global physiological noise will decrease relative to thermal noise with decreasing voxel volume, which could contribute to improved spatial specificity of functional connectivity measurements. However neuronally driven BOLD fluctuations will also decrease with decreasing signal, weakening interregional correlations. We observe that correlations within the motor network increase as voxel volume decreases. This suggests that the balance of decreased partial volume effects, decreased physiological/thermal noise ratio, and decreased overall signal results in more spatially specific measurements of functional connectivity. Furthermore, the results of our analysis of task-driven data support the role of decreased partial volume averaging in contributing to this increase in spatial specificity, though other factors may play a role as well and deserve further study.
In order for functional connectivity studies to transition to imaging with the resolutions suggested here, new strategies for acquiring data are required. This is because whole brain data acquired with traditional single shot EPI at millimeter resolution will suffer several limitations. Single shot EPI shows considerable distortion near regions of large susceptibility, and those distortions will continue to worsen as echo train lengths increase for increased spatial resolution. Using thin slices to maintain high through-plane resolution will require a significant increase in the number of slices required for full brain coverage, lengthening the acquisition time per volume. However, continuing hardware developments such as stronger gradient coils, and advanced acquisition strategies such as spatial and temporal multiplexing (Feinberg et al., 2002; Moeller et al., 2010) and improved 3D acquisitions (Barry et al., 2011) may help address these concerns.
It may be noted that the functional imaging parameters used here were held as constant as possible across resolutions in order to isolate the effects of decreasing voxel volume. However, future studies may be able to improve the performance of low resolution acquisitions relative to those used here though complete optimization of those individual protocols. For example, shorter EPI echo trains associated with low resolution image acquisitions would likely require less SENSE acceleration, leading to an improvement in signal-to-noise. We chose not to manipulate the SENSE acceleration from one resolution to the next for this study as this would systematically introduce different levels of SENSE-related noise from one resolution to the next (Lutcke et al., 2006; Preibisch et al., 2003), and would make interpreting the effects of decreasing voxel volume alone difficult. Likewise, shorter echo trains could allow for decreased repetition times, potentially providing more temporal samples within a given scan duration. This could result in improved statistical sensitivity, though the penalty of decreased steady state magnetization would need to be considered too. While these issues and others would likely be considered in optimizing an image acquisition for future measurements of functional connectivity, our data suggest that the improved functional contrast provided by decreasing voxel volume should also be considered in this optimization process.
Previous imaging studies have described the effects of partial volume dilution in a variety of contexts including classifying multiple sclerosis lesions (Firbank et al., 1999), tissue segmentation (Bullmore et al., 1995), and T2 measurements of vasculature (Stainsby and Wright, 1998). It is also accepted that issues of partial volume averaging are not unique to MRI data (Fazio and Perani, 2000). With respect to measurements of connectivity, most attention has been paid to partial volume effects on measurements of structural connectivity using diffusion tensor imaging in combination with fiber tracking analyses (Alexander et al., 2001; Frank, 2001; Tuch DS, 1999) where fibers of different orientations cross, partial volume effects can cause an apparent decrease in diffusion anisotropy. Our finding that resting state functional connectivity maps more closely mirror typical activity maps as images are acquired at higher spatial resolutions suggests that the underlying source of low frequency correlations in resting state data is more focal than may be revealed using lower resolution images. Supporting this, there is an increasing number of examples of functional organization of the brain on spatial scales approaching 1mm, observed in imaging studies of the subdivisions of the thalamus (Gilbert et al., 2001), optical dominance columns of the visual cortex (Yacoub et al., 2008), and recently in the digit separation of the somatosensory cortex (Sanchez-Panchuelo et al., 2010; Stringer et al., 2011).
5. CONCLUSIONS
We have demonstrated that measurements of functional connectivity may be improved through acquisition of high resolution images (i.e. 1×1×2mm voxels). Our studies at 7T show that these high resolution images, which decrease partial volume effects, help separate the sensorimotor network from the rest of the brain in typical maps of functional connectivity.
Highlights.
Increasing spatial resolution improves measurements of functional connectivity.
Improvements are likely due to decreased partial volume averaging.
Increased functional contrast outweighs the loss in terms of signal to noise ratio.
ACKNOWLEDGMENTS
This work was supported by the National Institutes of Health [T32 EB03817, R01 EB00461].
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
7. REFERENCES
- Alexander AL, Hasan KM, Lazar M, Tsuruda JS, Parker DL. Analysis of partial volume effects in diffusion-tensor MRI. Magn Reson Med. 2001;45:770–780. doi: 10.1002/mrm.1105. [DOI] [PubMed] [Google Scholar]
- Barry RL, Strother SC, Gatenby JC, Gore JC. Data-driven optimization and evaluation of 2D EPI and 3D PRESTO for BOLD fMRI at 7 Tesla: I. Focal coverage. Neuroimage. 2011;55:1034–1043. doi: 10.1016/j.neuroimage.2010.12.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Brammer M, Rouleau G, Everitt B, Simmons A, Sharma T, Frangou S, Murray R, Dunn G. Computerized brain tissue classification of magnetic resonance images: a new approach to the problem of partial volume artifact. Neuroimage. 1995;2:133–147. doi: 10.1006/nimg.1995.1016. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH. Effects of model-based physiological noise correction on default mode network anti-correlations and correlations. Neuroimage. 2009;47:1448–1459. doi: 10.1016/j.neuroimage.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazio F, Perani D. Importance of partial-volume correction in brain PET studies. J Nucl Med. 2000;41:1849–1850. [PubMed] [Google Scholar]
- Feinberg DA, Reese TG, Wedeen VJ. Simultaneous echo refocusing in EPI. Magn Reson Med. 2002;48:1–5. doi: 10.1002/mrm.10227. [DOI] [PubMed] [Google Scholar]
- Firbank MJ, Coulthard A, Harrison RM, Williams ED. Partial volume effects in MRI studies of multiple sclerosis. Magn Reson Imaging. 1999;17:593–601. doi: 10.1016/s0730-725x(98)00210-0. [DOI] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank LR. Anisotropy in high angular resolution diffusion-weighted MRI. Magnetic Resonance in Medicine. 2001;45:935–939. doi: 10.1002/mrm.1125. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Poline JB, Grasby PJ, Williams SC, Frackowiak RS, Turner R. Analysis of fMRI time-series revisited. Neuroimage. 1995;2:45–53. doi: 10.1006/nimg.1995.1007. [DOI] [PubMed] [Google Scholar]
- Gilbert AR, Rosenberg DR, Harenski K, Spencer S, Sweeney JA, Keshavan MS. Thalamic volumes in patients with first-episode schizophrenia. Am J Psychiatry. 2001;158:618–624. doi: 10.1176/appi.ajp.158.4.618. [DOI] [PubMed] [Google Scholar]
- Kruger G, Glover GH. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn Reson Med. 2001;46:631–637. doi: 10.1002/mrm.1240. [DOI] [PubMed] [Google Scholar]
- Lutcke H, Merboldt KD, Frahm J. The cost of parallel imaging in functional MRI of the human brain. Magnetic Resonance Imaging. 2006;24:1–5. doi: 10.1016/j.mri.2005.10.028. [DOI] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010;63:1144–1153. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poser BA, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. Neuroimage. 2010;51:261–266. doi: 10.1016/j.neuroimage.2010.01.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preibisch C, Pilatus U, Bunke J, Hoogenraad F, Zanella F, Lanfermann H. Functional MRI using sensitivity-encoded echo planar imaging (SENSE-EPI) Neuroimage. 2003;19:412–421. doi: 10.1016/s1053-8119(03)00080-6. [DOI] [PubMed] [Google Scholar]
- Sanchez-Panchuelo RM, Francis S, Bowtell R, Schluppeck D. Mapping human somatosensory cortex in individual subjects with 7T functional MRI. J Neurophysiol. 2010;103:2544–2556. doi: 10.1152/jn.01017.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speck O, Stadler J, Zaitsev M. High resolution single-shot EPI at 7T. MAGMA. 2008;21:73–86. doi: 10.1007/s10334-007-0087-x. [DOI] [PubMed] [Google Scholar]
- Stainsby JA, Wright GA. Partial volume effects on vascular T2 measurements. Magn Reson Med. 1998;40:494–499. doi: 10.1002/mrm.1910400322. [DOI] [PubMed] [Google Scholar]
- Stringer EA, Chen LM, Friedman RM, Gatenby C, Gore JC. Differentiation of somatosensory cortices by high-resolution fMRI at 7 T. Neuroimage. 2011;54:1012–1020. doi: 10.1016/j.neuroimage.2010.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triantafyllou C, Hoge RD, Krueger G, Wiggins CJ, Potthast A, Wiggins GC, Wald LL. Comparison of physiological noise at 1.5 T, 3 T and 7 T and optimization of fMRI acquisition parameters. Neuroimage. 2005;26:243–250. doi: 10.1016/j.neuroimage.2005.01.007. [DOI] [PubMed] [Google Scholar]
- Tuch DS, W.R., Belliveau JW, Wedeen VJ. High angular resolution diffusion imaging of the buman brain. Proceedings of the 7th Annual Meeting of ISMRM; Philadelphia, PA. 1999. p. 321. [Google Scholar]
- Van Dijk KR, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. J Neurophysiol. 2010;103:297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yacoub E, Harel N, Ugurbil K. High-field fMRI unveils orientation columns in humans. Proc Natl Acad Sci U S A. 2008;105:10607–10612. doi: 10.1073/pnas.0804110105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yacoub E, Shmuel A, Pfeuffer J, Van De Moortele PF, Adriany G, Andersen P, Vaughan JT, Merkle H, Ugurbil K, Hu X. Imaging brain function in humans at 7 Tesla. Magn Reson Med. 2001;45:588–594. doi: 10.1002/mrm.1080. [DOI] [PubMed] [Google Scholar]