Dynamic Bayesian network modeling for longitudinal brain morphometry

Abstract

Identifying interactions among brain regions from structural magnetic-resonance images presents one of the major challenges in computational neuroanatomy. We propose a Bayesian data-mining approach to the detection of longitudinal morphological changes in the human brain. Our method uses a dynamic Bayesian network to represent evolving inter-regional dependencies. The major advantage of dynamic Bayesian network modeling is that it can represent complicated interactions among temporal processes. We validated our approach by analyzing a simulated atrophy study, and found that this approach requires only a small number of samples to detect the ground-truth temporal model. We further applied dynamic Bayesian network modeling to a longitudinal study of normal aging and mild cognitive impairment — the Baltimore Longitudinal Study of Aging. We found that interactions among regional volume-change rates for the mild cognitive impairment group are different from those for the normal-aging group.

1. Introduction

Magnetic-resonance (MR) imaging provides high-resolution structural brain images in vivo, and has been widely adopted for the delineation of brain structure and function. The majority of MR-based morphometric studies are cross-sectional case-control comparison in design; that is, these studies measure morphological attributes, such as gray-matter volumes, in samples at a particular point in time. In contrast, longitudinal studies are more informative about evolving processes and time-related changes. MR-based longitudinal morphometric studies have been conducted to better understand changes due to normal aging (Raz et al. (1997); Resnick et al. (2003)), alcoholism (Rohlfing et al. (2006)), mild cognitive impairment(Jack et al. (1999)), rapid conversion in mild cognitive impairment (Chetelat et al. (2005)) and normal development (Thompson et al. (2000)); in addition, other researchers have used longitudinal changes in MR features to predict subsequent clinical conversion in normal elderly and amnestic mild cognitive impairment(Jack et al. (2005)).

There exists a vast body of literature regarding the quantification of evolving brain morphometry (Jack et al. (1999); Thompson et al. (2000); Scahill et al. (2002); Resnick et al. (2003); Rohlfing et al. (2006)). Most of these studies are based on general linear mixed models (GLMMs). One widely used GLMM-based method models interactions by computing a t statistic between scans of the same subject across time points. Another GLMM-based approach is based on a regression model, in which volume change of a brain region is the dependent variable, and a clinical variable is the independent variable. In this approach, associations among clinical variables and rates of change in brain measurements are estimated by coefficients of the resulting regression model.

Although widely used, GLMM-based methods have important limitations. First, GLMM-based methods cannot describe the dynamics of interactions among brain regions; that is, they cannot model how multivariate interactions change across time. Second, GLMM-based methods often assume normality. This assumption may not be valid in some applications.

A central principle of brain organization is functional integration, in which the observed changes in a brain region can be explained by the changes in other regions or itself (Friston (2002)). There are two requirements of a plausible model of interactions among brain regions using longitudinal data: the model must be dynamic and nonlinear (Harrison and Friston (2003)). A dynamic model represents a temporally evolving system; a nonlinear model is capable of representing nonlinear associations among brain regions. GLMM-based approaches are limited in that they cannot model nonlinear, dynamic systems.

To capture evolving multivariate associations, we propose a dynamic Bayesian network (DBN) representation. DBNs have three principal features that make them well suited to the analysis of dynamic interactions among regions. First, DBNs encode uncertainty; this feature is particularly important if the underlying process is stochastic, or if we cannot perfectly measure all variables. Second, a discrete DBN can represent any probabilistic distribution over a set of variables, which is important in cases in which variables manifest nonlinear multivariate interactions. Third, there exist efficient algorithms for delineating these interactions by generating DBNs from a data set.

The DBN model was introduced in (Dean and Kanazawa (1989); Murphy (2002)); DBNs have been used to infer transcriptional regulatory networks from gene-expression data (Dojer et al. (2006); Geier et al. (2007)), to infer brain region interactions from functional MR data (Zhang et al. (2006); Rajapakse and Zhou (2007); Burge et al. (2009)), and to reconstruct functional neuronal networks from spike-train ensembles (Eldawlatly et al. (2010)). However, the use of DBNs to model inter-regional associations in a longitudinal morphometric study has not been explored.

In subsequent sections, we describe our DBN-based approach to modeling inter-regional associations in a longitudinal study of brain morphometry. We then evaluate our implementation using simulated and clinical data.

2. Background: Dynamic Bayesian Networks

A Bayesian network (BN) is a probabilistic graphical model that compactly represents a joint distribution over n random variables = {X₁ … X_n}. A BN B includes two components: a structure , and parameters Θ. = { , 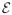} is a directed acyclic graph, in which 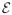is a set of directed edges. If there exists an edge X_i → X_j, then we call X_i a parent of X_j; we denote the parent set of X_j by pa(X_j). The structure encodes a set of conditional-independence statements. The joint distribution over can be represented as

$$P(\mathcal{V})=\prod _{i}P(X_i\mid pa(X_i)).$$ (1)

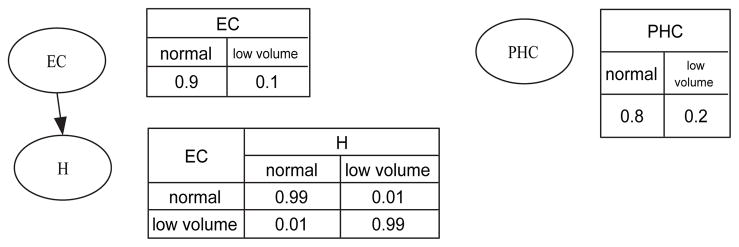
Figure 1 shows a simple example of a BN; this BN represents probabilistic associations among three brain structures: parahippocampal cortex (PHC), entorhinal cortex (EC), and hippocampus (H). = {PHC, EC, H}. If a structure has low regional volume, it assumes the state ‘low volume’; otherwise, it assumes the state ‘normal’. The graph in Figure 1 indicates that the volume of parahippocampal cortex is independent of the volumes of entorhinal cortex and hippocampus. That is, knowing the state of parahippocampal cortex provides no information regarding the states of entorhinal cortex and of the hippocampus. In this BN, the edge between hippocampus and entorhinal cortex indicates that the volumes of hippocampus and entorhinal cortex are associated.

Figure 1.

An example of a Bayesian network. PHC = parahippocampal cortex; EC = entorhinal cortex; H = hippocampus.

In this paper, we assume that variables are discrete; therefore, we represent the conditional-probability distribution for X_i as a conditional-probability table (CPT). Figure 1 shows CPTs to the right of each variable in the BN. For example, in the CPT for hippocampus, P(H = low volume | EC = low volume) = 0.99 means that the conditional probability of hippocampus having low volume given that entorhinal cortex has low volume is 0.99. Let θ_ijk represent the probability of X_i = j given that pa(X_i) = k. Then Θ = {θ_ijk} constitutes the BN’s parameters.

A dynamic Bayesian network (DBN) is an extension of a BN that can model interactions among temporal processes (Dean and Kanazawa (1989); Murphy (2002)). Consider a discrete-time stochastic process, in which a random vector X_t = {X_1,t, …, X_n,t} follows the distribution P(X_t), where t is an integer that indexes the period, and X_i,t is the i^th variable at time t. A DBN is defined as a pair, (B₁, B_→), where B₁ is a BN that defines the baseline probability distribution P(X₁); and B_→ defines the transition probability P(X_t+1 | X_t). B₁ is a regular BN model, which may represent any initial distribution.

B_→, which represents system dynamics, is a crucial part of a DBN model. We assume that inter-slice dependencies do not change over time. That is, the transition probability P(X_t+1 | X_t) is independent of t. In other words, the stochastic process of interest is a first-order stationary Markov process. We can represent the transition probability P(X_t+1 | X_t) as a two-slice temporal BN (2TBN). A 2TBN contains two time points, with an instance of each variable in each time slice (t and t + 1). Edges are added from nodes at time t to the nodes with which they are associated at t + 1. Note that these associations are not necessarily causal; they are merely temporal associations (Burge et al. (2009)). In B_→, we assume that there are no intra-slice edges. The variables in the first slice of B_→ do not have parameters associated with them, while those in the second slice have associated transition-probability tables.

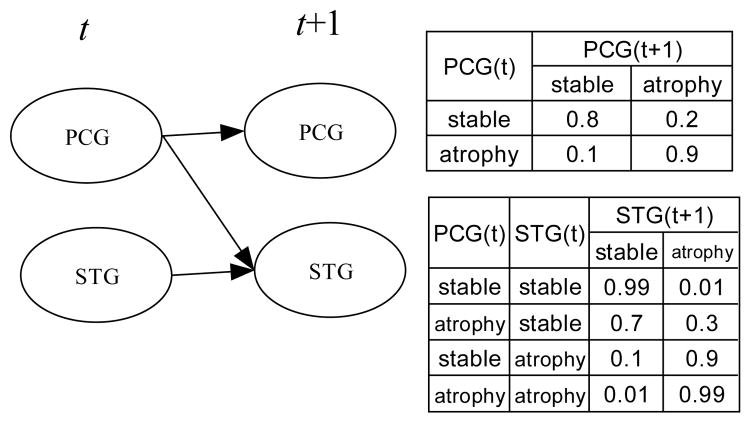
Figure 2 depicts a simple 2TBN modeling hypothetical brain-volume changes with aging. This model represents the interactions among three temporal processes: trajectories of volumes of the parahippocampal cortex, entorhinal cortex, and hippocampus. Each region assumes a state in {volume loss, stable}. The model in Figure 2 is a hypothetical stochastic process in which morphological changes in entorhinal cortex are associated with subsequent changes in the hippocampus and entorhinal cortex (edges EC(t) → EC(t + 1) and EC(t) → H(t + 1)), morphological changes in hippocampus are associated with subsequent changes in hippocampus (edge H(t) → H(t + 1)), and morphological changes in parahippocampal cortex are associated with subsequent changes in parahippocampal cortex (edge PHC(t) → PHC(t + 1)). In this model, the probability P(EC(t + 1) = volume loss|EC(t) = stable) = 0.2 indicates that when entorhinal cortex volume is stable, there is a 20% chance that it will undergo volume loss when measured at the next time point. Note that P(EC(t+1) = stable|EC(t) = stable) = 1.0 − P (EC(t+1) = volume loss|EC(t) = stable).

Figure 2.

An example of a two-slice temporal Bayesian network for modeling brain-volume changes with aging. PHC, parahippocampal cortex; EC, entorhinal cortex; H, hippocampus.

3. Methods

Our DBN-based approach is a two-stage model-generation algorithm. Stage 1 centers on selecting the morphological features to be analyzed for a longitudinal data set. Stage 2 uses data from these features to generate a DBN that models the underlying dynamic system. Figure 3 provides an overview of this algorithm.

Figure 3.

An overview of the DBN-based algorithm for delineating temporal associations.

Stage 1 consists of five steps: skull-stripping, segmentation, registration, regional-volume calculation, and morphological-attribute generation. First, we use a semi-manual approach for skull-stripping (Goldszal et al. (1998)). We then manually edit the resulting MR volume to remove residual non-brain tissue and cerebellum. In the second step, we employ a fuzzy c-mean algorithm with intensity non-uniformity correction to segment the brain into gray matter, white matter, and cerebrospinal fluid (Goldszal et al. (1998)). The third step is registration; we use hierarchical attribute-matching mechanism for elastic registration (HAMMER) to warp each subject’s brain structures to a common stereotaxic space (Shen and Davatzikos (2002)), typically a brain atlas with labeled anatomical structures. This registration process generates a deformation field that maps among voxels in the subject’s brain volume and voxels in the atlas. In the fourth step, we perform Regional Analysis of Volumes Embedded in a Stereotaxic Space (RAVENS) on the deformation field (Davatzikos et al. (2001)). This step generates a RAVENS map, de-fined on the stereotaxic space, for each MR image. In a RAVENS map, the voxel-wise sum of signal intensity for a structure is equal to the volume of that structure in the subject’s brain before deformation.

After RAVENS-map generation, we generate a time series, S^j(t, i), for each atlas structure i. After completing the four steps in Stage 1 of our analysis, we can calculate the volume-change rate, r(t, i), to quantify the volume change for each structure i at time t:

$$r(t,i)=\frac{\mathrm{\Omega }(t,i)-\mathrm{\Omega }(t-1,i)}{TI(t-1,t)},$$ (2)

where TI(t − 1, t) is the time interval between time point t − 1 and t, Ω(t, i) is the volume of structure i at time t. If r(t, i) is less than a threshold, this structure manifests volume loss, so we set the value of S^j(t, i) to ‘1’; otherwise, we set S^j(t, i) = 0. Alternatively, we can use the volume-change ratio, ρ(t, i), for each structure i at time t:

$$\rho (t,i)=\frac{\mathrm{\Omega }(t,i)-\mathrm{\Omega }(t-1,i)}{\mathrm{\Omega }(t-1,i)TI(t-1,t)},$$ (3)

If ρ(t, i) is less than a threshold, this structure manifests volume loss, so we set the value of S^j(t, i) to be ‘1’; otherwise, we set S^j(t, i) = 0. Both the volume-change rate and the volume-change ratio are variables that describe temporal changes. ¹

The resulting data set D = {S^j(t, i)} (1 ≤ t ≤ T, 1 ≤ i ≤ m_i, 1 ≤ j ≤ m_j), where T, m_i, m_j comprises the numbers of time points, structures of interest, and subjects, respectively, and constitutes the input to the second stage of our algorithm.

Stage 2 generates the structure and parameters of a 2TBN. A 2TBN does not have intra-slice edges; therefore, the goal is to detect inter-slice edges, i.e., associations among variables across time points. For a problem involving m_i variables {X_i}, a 2TBN, which by definition models only two time points t and t + 1, includes 2m_i variables: { $X_i^{(1)}$} and { $X_i^{(2)}$} are the variables at time points 1 and 2, respectively. In this framework, detecting inter-slice edges is equivalent to finding the parent set of variable $X_i^{(2)}$. We use the K2 score (Cooper and Herskovits (1992); Herskovits (1991)) to measure how well a variable’s parent set fits the data:

$$K2(\mathcal{G},\text{D})=\prod _{j=1}^{q_i}\frac{(r_i-1)!}{(N_{ij}+r_i-1)!}\prod _{k=1}^{r_i}{N}_{\mathit{ijk}}!,$$ (4)

where r_i and q_i are the numbers of possible states of $X_i^{(2)}$ and $pa(X_i^{(2)})$, respectively, and N_ijk is the number of instances in which the variable $X_i^{(2)}$ assumes state k and $pa(X_i^{(2)})$ assumes state j. We used the REVEAL algorithm (Liang et al. (1998)) to find a parent set that maximizes each variable’s K2 score.

After detecting the parent set of $X_i^{(2)}$, the algorithm computes the maximum-likelihood estimation of the 2TBN parameters (i.e., the CPT of $X_i^{(2)}$):

$${\widehat{\theta }}_{\mathit{ijk}}=\frac{N_{\mathit{ijk}}+1}{N_{ij}+r_i}.$$ (5)

4. Experimental Results

4.1. Simulated atrophy data

4.1.1. Materials

We obtained high-resolution (0.9375 × 0.9375 × 1.25 mm³) T1-weighted spoiled gradient-echo (SPGR) brain images from 11 normal elderly subjects (axial acquisition; repetition time = 35; echo time = 5; flip angle = 45; field of view = 24; matrix = 256 × 256; number of excitations = 1) (Resnick et al. (2003)). For each subject, we manually delineated the right precentral gyrus (PCG) and the left superior temporal gyrus (STG), using DISPLAY software (the Brain Imaging Center, Montreal Neurological Institute). We used the STAR4 algorithm (Davatzikos (1996)) to induce a uniform contraction of the labeled gyri. By varying parameters in STAR4, we generated MR volumes with different degrees of atrophy in these gyri (atrophy rate τ = 3%, 6%, 9%, 11%, 15%, 19%). These 77 image volumes constituted the simulated-atrophy data set, denoted by D_atrophy. Thus, for each subject, there were seven volumes. Using MR volumes without simulated atrophy as baseline images, and introducing approximately 3% volume reduction in the PCG and STG, we generated an MR volume with τ = 0.03; introducing an additional approximately 3% volume reduction in these gyri resulted in a volume with τ = 0.06; we continued this process until τ =0.19. An example of simulated atrophy is shown in Figure 4.

Figure 4.

Simulated development of atrophy in the right precentral gyrus and in the left superior temporal gyrus.

To test our DBN-modeling approach, we simulated an aging process based on the DBN in Figure 5. The ground-truth DBN modeled an aging process involving two regions: PCG and STG. Our goal was to generate simulated time-series MR data for two structures: PCG(t, i) and STG(t, i), where t represents a time point, and i represents a subject.

Figure 5.

The 2TBN model used to generated the simulated data. PCG = right precentral gyrus; STG = the left superior temporal gyrus. ‘0’ indicates no atrophy and ‘1’ indicates atrophy.

First, we generated a time series with seven time points for each subject, S(t, i), by randomly sampling the DBN depicted in Figure 5. Table 1 (top) lists the sampled time series for subject 2. Second, if S^PCG(t, i) = stable (2 ≤ t ≤ 7), we knew there was no volume change in PCG between time t and t − 1, and we therefore set PCG(t, i) to PCG(t − 1, i) which was the PCG data in the previous time point; otherwise, we introduced approximately 3% atrophy to PCG(t − 1, i) to generate PCG(t, i), representing atrophy. For t = 1, PCG(1, i) was initialized to baseline PCG data in D_atrophy. We similarly generated the series STG(t, i). Table 1 (bottom) lists the volumes of PCG(t, i) and STG(t, i) for subject i = 2.

Table 1.

Simulated PCG and STG time series for subject 2. Top, random sample generated from the DBN in Figure 5. Bottom, the volumes constituting the simulated PCG and STG series

	t1	t2	t3	t4	t5	t6	t7
PCG	stable	stable	stable	stable	atrophy	atrophy	stable
STG	stable	atrophy	atrophy	atrophy	atrophy	atrophy	atrophy

volume(t, i)	t1	t2	t3	t4	t5	t6	t7
PCG	359372	359372	359372	359372	343586	334807	334807
STG	406654	397202	390860	379987	376902	362009	360299

The simulated longitudinal data D_simu, in which PCG(t, i) and STG(t, i) are instantiations of a process represented by the DBN in Figure 5, constituted the input to our DBN-modeling method, to determine whether it could recover the ground-truth DBN used to generate the simulated data.

4.1.2. Results

We applied our DBN-modeling algorithm to the simulated data D_simu described in Section 4.1.1. D_simu consists of observations at seven time points for 11 subjects; each observation corresponds to a T1-weighted MR volume.

In the morphological-feature–extraction stage, the template, which de-fines a common stereotaxic space, was a T1-weighted MR image of an elderly subject with approximately average ventricular sizes (relative to those of the rest of the subjects). We selected two structures, the right precentral gyrus and the left superior temporal gyrus, as the regions of interest. We set the discretization threshold for ρ(t, i) to −0.01.

Let $B_{\to }^{\ast }$ and B̂_→ denote the ground-truth DBN (Figure 5) and the DBN generated by the our DBN-generation algorithm, respectively. We computed the structure error, err, to evaluate the structural similarity between $B_{\to }^{\ast }$ and B̂_→:

$$\mathit{err}={\mathit{err}}_{\mathit{missing}}+{\mathit{err}}_{\mathit{extra}},$$ (6)

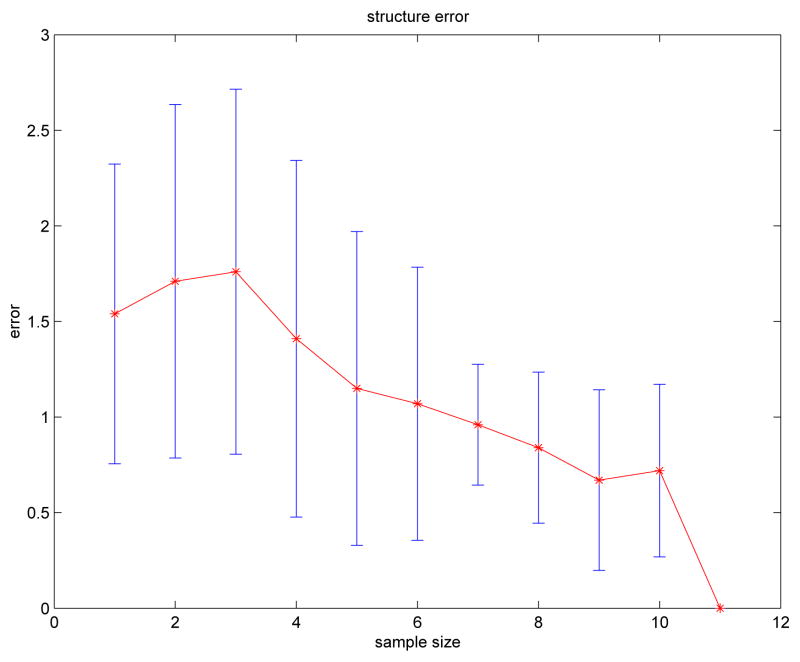
where err_missing represents the number of inter-slice edges that are in $B_{\to }^{\ast }$ but not in B̂_→ (i.e., false-negative associations), and err_extra represents the number of inter-slice edges that are in B̂_→ but not in $B_{\to }^{\ast }$ (i.e., false-positive associations). The numbers of false-positive and false-negative associations, and therefore the value of err, depends on the number of subjects in the study. To determine a more robust estimate for err for a given number of subjects m_j, we can randomly choose m_j subjects from D_simu, generate a DBN, and calculate err. By repeating this process, we can use the average err as an estimate of the true numbers of false-positive and false-negative edges (and therefore associations) in the recovered DBN model. Figure 6 plots mean(err) with error bars [mean(err) − std(err), mean(err)+std(err)] versus the number of subjects. As expected, Figure 6 shows that err tends to decrease as the number of subjects increases. The structure of $B_{\to }^{\ast }$ is correctly identified by our algorithm when m_j ≥ 11.

Figure 6.

Structure error versus subject number.

For m_j = 11, the CPTs of PCG and STG in B̂_→ are listed in Table 2. The CPTs of PCG and STG in B̂_→ are similar to those in $B_{\to }^{\ast }$. For example,

Table 2.

Conditional probability tables for PCG and STG in the simulated-data study

PCG(1)	P(PCG(2) | PCG(1))
	stable	atrophy
stable	0.80	0.20
atrophy	0.33	0.67

PCG(1)	STG(1)	P(STG(2) | PCG(1), STG(1))
		stable	atrophy
stable	stable	0.93	0.07
atrophy	stable	0.33	0.67
stable	atrophy	0.50	0.50
atrophy	atrophy	0.16	0.84

CPT of STG in B̂_→ indicates that PCG temporally affects STG, however the converse is not true. This assertion is also found in $B_{\to }^{\ast }$. However, some entries in the CPTs of B̂_→ are different from those of $B_{\to }^{\ast }$. Either the noise in the morphological feature-extraction stage, or the limited number of samples, could cause this discrepancy.

4.2. The Baltimore Longitudinal Study of Aging

The Baltimore Longitudinal Study of Aging (BLSA) (Resnick et al. (2003); Driscoll et al. (2009)) investigates age-related brain changes in normal aging and MCI. All participants were in good general health at entrance. Exclusion criteria included central nervous system disease, severe cardiovascular disease, severe pulmonary disease, metastatic cancer, and current depression. The study was approved by the local institutional review boards, and all participants gave written informed consent prior to each assessment (Driscoll et al. (2009)).

The complete BLSA study includes 138 participants (ages 64 – 86 years) who were free of dementia at initial evaluation and were prospectively followed annually for up to 10 years (Driscoll et al. (2009)). During the course of this study, some of the subjects developed mild cognitive impairment (MCI), which was diagnosed using criteria consistent with those defined by Petersen (Petersen et al. (1999)). Only participants with a stable MCI diagnosis (i.e., subjects did not revert back to normal in subsequent years) were included in the MCI group. Of these 138 subjects, three subjects underwent only 2 MR examinations; since DBN analysis requires at least 3 MR measurements in order to generate the minimum required two change rates, we excluded these three subjects from DBN analysis. The sample that we analyzed thus included 135 subjects (117 normal aging individuals, and 18 subjects diagnosed with stable MCI). The labels NC-NC and NC-MCI denote these two groups.

At each annual visit, each subject underwent T1-weighted spoiled gradient-echo MR examination of the brain (axial acquisition; repetition time = 35; echo time = 5; flip angle = 45; field of view = 24; matrix = 256 × 256; number of excitations = 1). In this analysis, we focused on modeling temporal interactions among seven brain regions. Four of them—the hippocampal formation (H), entorhinal cortex (E), parahippocampal gyrus (PARAH), and frontal cingulate region (CING)—are in or near the medial temporal lobe and the limbic system. These brain regions are known to be affected by Alzheimer’s disease (AD). The other three structures—the medial frontal-orbital gyrus (MFOG), middle frontal gyrus (MFG), and medial frontal gyrus (MEFG)—are in the prefrontal region, which demonstrates changes with normal aging (Dennis and Cabeza (2008)).

In Section 3 we describe how we calculated regional gray-matter (GM) volumes. We adjusted these volumes by intracranial volumes, and then calculated volume-change rates using Equation (2). For each brain region, the thresholding process converted the volume-change rate into a binary variable. Following our clinical expert’s recommendation, we thresholded the regional GM volume-change rate by 1 standard deviation (SD) below the sample mean.

The data set D that we used as input to our DBN-modeling algorithm included seven structure variables for each subject, as described in the previous section. We performed DBN analyses of the normal aging and MCI groups.

We used resampling approaches for model validation. In particular, for a data set D, we re-sampled it using the jackknife resampling method, and obtained a new data set D^r. Then we generated a DBN model based on this new data set. The collection of DBNs generated from D^r formed a model ensemble. From this model ensemble we calculated model frequencies and the model mode (i.e., the most frequently appearing model). If the DBN generated from D had the same structure as that of the model mode, we concluded that this model was stable under data perturbation and therefore was not likely to represent a statistical artifact.

4.2.1. Results for the NC-NC Group

The structure of B̂_→ for the NC-NC group is shown in Figure 7. In this network, structures with index 1 (such as H1) are variables at time point 1; similarly, structures with index 2 are variables at time point 2. Jackknife resampling yielded one model in the ensemble; the mode had frequency = 1.0, i.e., no other model resulted from resampling. The model generated using the original data corresponded to the mode of the ensemble.

Figure 7.

The DBN structure for the NC-NC group.

4.2.2. Results for the NC-MCI group

Figure 8 shows the structure of B̂_→ for the NC-MCI group. Jackknife resampling yielded 11 models in the ensemble, and the mode had frequency = 0.27. The model generated using the original data corresponded to the mode of the ensemble.

Figure 8.

Bayesian network structure for the NC-MCI group.

4.2.3. Results for different regional volume thresholds

In the above analysis, we chose the threshold (one SD below sample mean) based on our clinical expert’s recommendation. To determine the effects of changing the threshold, we re-analyzed the data five using different thresholds: 0.7 SD below sample mean, 0.9 SD below sample mean, 1.0 SD below sample mean, 1.1 SD below sample mean, 1.3 SD below sample mean.

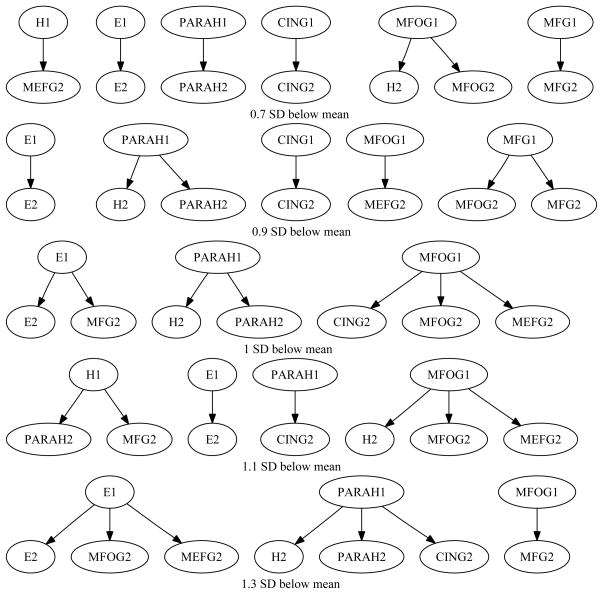
For the NC-NC group, there was no change in the 2TBN structure. For the NC-MCI group, there was some variability, due to the 6-fold smaller number of subjects in this group. Figure 9 shows the 2TBN structures for different thresholds for the NC-MCI group. Table 3 lists the summary statistics of the 2TBN structures for the MCI group. A between-structure interaction is an edge from a structure at time 1 to another structure at time 2. For example, E1 → MFG2 is a between-structure interaction. Table 3 lists the total number of edges and the total number of between-structure interactions.

Figure 9.

The 2TBN structures for different thresholds. From top to bottom, the threshold is 0.7, 0.9, 1, 1.1, and 1.3 SD below mean.

Table 3.

Summary statistics for the 2TBN structures for different thresholds

Threshold (SD below mean)	Total number of edges	Total number of between structure interactions
0.7	7	2
0.9	7	3
1.0	7	4
1.1	7	5
1.3	7	5

The collection of DBNs generated from different thresholds forms a model ensemble. We performed stability analysis based on edge frequencies for this ensemble (Chen and Herskovits (2005)), with edge frequency defined as

$$f(L)=\frac{N_L}{N_{\mathit{total}}},$$ (7)

where N_L is the number of occurrences of edge L, and N_total is the total number of models in the model ensemble. If an edge has edge frequency 1.0, it means this edge appears in all models.

The model ensemble across different thresholds included five models, which together contained 18 unique edges. Five edges had edge frequency greater than 0.5; that is, they were included in the majority of models. We consider these edges to be stable across models. The five edges with edge frequency greater than 0.5 are: E1 → E2 (f = 1.0), PARAH1 → H2 (f = 0.6), PARAH1 → PARAH2 (f = 0.8), MFOG1 → MFOG2 (f = 0.6), MFOG1 → MEFG2 (f = 0.6). Among these five edges, two of them are between-structure interactions.

5. Conclusion and Discussion

We have described a DBN-based approach to modeling an evolving process in a longitudinal study of brain morphometry. Our model-generation algorithm consists of two stages: feature extraction and data mining. The first stage extracts morphological features (features describing volume change for a region between two consecutive time points), and then thresholds this feature to generate a data set containing variables representing whether or not regions undergo volume loss during a period. The second stage generates a DBN model that approximates the underlying discrete time-series process that generated the data. The major strengths of this approach are (1) DBNs explicitly model dynamic systems, and are therefore well suited to analyzing discrete time-series data; and (2) a DBN can model arbitrary multivariate inter-regional associations among categorical variables, whether linear or nonlinear. As shown in the simulated-atrophy study, even with a limited number of subjects, this approach can correctly identify the structure of the underlying dynamic system.

To more realistically evaluate our approach, we analyzed a subset of the BLSA data. We used a 2TBN to model temporal interactions among these seven brain regions. The 2TBN structures for the NC-NC group and the NC-MCI group are different. In particular, for the NC-NC group (Figure 7), there are no between-structure interactions: all temporal processes evolve independently of each other. In contrast, for the NC-MCI group (Figure 8), there are many between-structure interactions. For the NC-MCI group, the 2TBN model has 7 edges. Four of them (E1 → MFG2, PARAH1 → H2, MFOG1 → CING2, MFOG1 → MEFG2) represent between-structure interactions. Note that these edges are not necessarily causal, they merely indicate temporal associations.

We found that there are important differences between the 2TBN structures for the NC-NC and NC-MCI groups. In particular, there are no between-structure interactions for the NC-NC group while there are many between-structure interactions for the NC-MCI group. This is expected. Several previous studies have reported regional atrophy rate differences between MCI and normal-aging groups (e.g., Jack et al. (2005); Sluimer et al. (2009); Driscoll et al. (2009)). Jack et al. found that atrophy rates of hippocampus, entorhinal cortex, and whole brain for the MCI cohort were significantly greater than those for the healthy elderly cohort (Jack et al. (2005)). Our results also suggest that we may build diagnostic or prognostic models based on interactions among temporal processes (the 2TBN structure). For example, we found that the defining feature of normal aging was that all temporal processes evolve independently. Alteration of this pattern could suggest early pathology.

To determine the effects of changing the threshold, we re-analyzed the data using different thresholds. For the NC-NC group, there is no change in the 2TBN structure. For the NC-MCI group, there was some variability, due to the smaller number of subjects in this group (Table 3). However, the major finding — differences between the 2TBN structure for the NC-NC group and that for the NC-MCI group — holds across different thresholds.

In this paper, we modeled brain region volume changes using DBNs in which all variables are categorical. We made this choice for several reasons: (1) a categorical DBN can represent arbitrary multivariate inter-slice associations among structure variables. If variables in a DBN are continuous, the most common parameterized distribution for such variables is the Gaussian distribution, and inter-slice associations are restricted to be linear. (2) For a categorical DBN, there exist algorithms to identify complex inter-slice associations based on observed data (Liang et al. (1998)). For a DBN containing continuous variables, no such algorithms exist. One disadvantage of using discrete variables to model regional volume changes is the potential loss of information resulting from discretization; however, the results for our simulated data indicate that such information loss is modest.

In this paper, we employed computer algorithms to delineate the structure of a 2TBN from data. However, experts could also specify the structure based on their expertise. For example, if we wanted to know the transition probabilities P(GM_t+1|GM_t), we can construct a 2TBN with GM_t → GM_t+1, then estimate the transition probabilities using Equation (5).

One of the limitations of the image-preprocessing pipeline described in Section 3 is that it does not use a longitudinal warping algorithm. Longitudinal warping algorithms incorporate temporal information (Shen and Davatzikos (2003); Hua et al. (2011)), and may increase statistical power.

The 2TBN represents a first-order stationary Markov process. If the dependencies in the underlying process change over time, our method generates a model that is an average over the different (t, t + 1) dependency structures; this is a limitation of 2TBN, or of any method that assumes a stationary stochastic process. We used the 2TBN representation due to the limited number of time points. For longitudinal morphometric studies, the number of time points is typically very small (often fewer than 5), whereas functional MR or spike train data could have hundreds of time points. When working with data collected at a small number of time points, if we use a DBN model with a similar number of time points, the model-generation process becomes unstable and may generate an over-fitted model. When a study has a large number of time points, we can use a method such as (Tucker and Liu (2004)) to generate a DBN with changing dependencies from longitudinal data. As might be expected, this method requires a larger sample size to compute the increased number of DBN parameters.

Highlights.

• Our method uses a dynamic Bayesian network to represent evolving inter-regional dependencies.

• This Bayesian approach can model evolving multivariate associations which cannot be modeled by GLMM-based approaches.

• We validate our approach by analyzing a longitudinal study of normal aging and mild cognitive impairment.