RESOLUTION OF CROSSING FIBERS WITH CONSTRAINED COMPRESSED SENSING USING DIFFUSION TENSOR MRI

Abstract

Diffusion tensor imaging (DTI) is widely used to characterize tissue micro-architecture and brain connectivity. In regions of crossing fibers, however, the tensor model fails because it cannot represent multiple, independent intra-voxel orientations. Most of the methods that have been proposed to resolve this problem require diffusion magnetic resonance imaging (MRI) data that comprise large numbers of angles and high b-values, making them problematic for routine clinical imaging and many scientific studies. We present a technique based on compressed sensing that can resolve crossing fibers using diffusion MRI data that can be rapidly and routinely acquired in the clinic (30 directions, b-value equal to 700 s/mm²). The method assumes that the observed data can be well fit using a sparse linear combination of tensors taken from a fixed collection of possible tensors each having a different orientation. A fast algorithm for computing the best orientations based on a hierarchical compressed sensing algorithm and a novel metric for comparing estimated orientations are also proposed. The performance of this approach is demonstrated using both simulations and in vivo images. The method is observed to resolve crossing fibers using conventional data as well as a standard q-ball approach using much richer data that requires considerably more image acquisition time.

Introduction

Diffusion tensor imaging (DTI) provides non-invasive contrasts which are sensitive to in vivo cellular organization as modeled by local diffusivity, anisotropy, and tissue orientation (Basser and Jones, 2002; Le Bihan et al., 2001; Le Bihan and van Zijl, 2002). The tensor model represents one independent, dominant direction per voxel, so that the estimated orientation may be ambiguous or misleading in voxels with complex fiber structure (Wiegell et al., 2000). Substantial efforts have been made to address this “crossing fiber” problem and one fruitful approach has been to acquire more detailed information through additional sensitized scans (e.g., diffusion spectrum (Wedeen et al., 2000), multi-tensor analysis (Tuch et al., 2002), high angular resolution (Frank, 2002), q-ball (Tuch, 2004), and high b-value (Tournier et al., 2004) imaging techniques). Scan time and hardware constraints limit widespread adoption of these methods in clinical research, however. In this paper we characterize tissue regions with potential crossing fibers using data acquired in conventional DTI protocols (i.e., low b-value, moderate angular resolution with ~30 directions).

Recently, there have been several indications that it is possible to resolve crossing-fibers from conventional DTI acquisitions provided that sufficient a priori information is available. Independent component analysis can exploit spatial information to fit a prolate tensor mixture (Kim et al., 2005), while cylindrically constrained two-tensor models have been numerically amenable to fitting using regularization techniques (Peled et al., 2006; Stamatios et al., 2008; Tuch et al., 2002). Direct deconvolution with a discrete tensor basis set has also been used (Ramirez-Manzanares et al., 2007). A major obstacle confronting these approaches is the complexity of representing heterogeneous intra-voxel structure. Using restricted two-component models (Peled et al., 2006; Stamatios et al., 2008) greatly reduces variability, but risks over- or under-fitting. Alternatively, substantial spatial regularization and probability models have been suggested to stabilize a more general approach (Ramirez-Manzanares et al., 2007). As these approaches are highly sensitive to noise, the authors typically suggest limiting application to areas of known fiber crossing (e.g., planar tensor estimates) to avoid erroneous detections.

To address the crossing fiber problem, we suggest that one is interested in a parsimonious and reproducible explanation of the observed signals and these goals are best achieved using a finite set of possible intra-voxel components. Although initially developed as an alternative to Nyquist sampling, compressed sensing (Donoho, 2006) offers a simple and elegant solution to the problem of regularized fitting of tensor models which does not require explicit model selection. Compressed sensing is one variant of many popular regularized regression methods (often referred to as least absolute shrinkage and selection operator – LASSO - techniques) (Efron et al., 2003; Tibshirani, 1996b) and has been widely used for signal reconstruction, denoising, and image reconstruction (Lustig et al., 2008).

Our approach, Crossing Fiber Angular Resolution of Intra-Voxel structure (CFARI) (Landman et al., 2008; Landman et al., 2010a, b; Landman et al., 2010c), has been the first systematic attempt to use compressed sensing to infer complex tissue micro-architecture through estimation of the local diffusion characteristics. With CFARI, we posit a set of canonical diffusion functions for representative tissue classes and potential orientations, and estimate the representative mixture fraction for voxel using compressive sensing optimization criteria. In this manuscript, we present the CFARI framework for estimating diffusion inferred structure and demonstrate accurate and reliable quantification of intra-voxel orientations using both simulated and in vivo data. We describe the advantages of incorporating positivity constraints on the mixture model which forms the basis for our compressed sensing reconstruction and demonstrate substantial runtime improvements through a novel hierarchical approach to compressed sensing. Finally, we compare the estimated intra-voxel structure using CFARI with that which can be achieved using analytic q-ball (Descoteaux et al., 2007). CFARI is implemented in the JIST (Java Image Science Toolkit) framework and is available in open source (http://www.nitrc.org/projects/jist/) (Lucas et al., 2010).

Materials and Methods

Theoretical Framework

The proposed approach models each voxel as a discontinuous (i.e., non-exchanging) collection of tissue compartments wherein each compartment describes a particular tissue type at a particular orientation. It is assumed that there are a finite number of tissue types, each being modeled by a particular diffusion model (Cory and Garroway, 1990), and that there are a finite number of fixed and known orientations to which these compartments can be aligned (see Figure 1). The overall objective of the CFARI approach is to determine the fractional contributions (mixture fractions) of the compartments such that when they are combined via an imaging equation, the measurements are optimally predicted. Importantly, the number of compartments that are determined to contribute to the predictor should be minimal, so that the final description of each voxel consists of a small collection of tissue compartments, each corresponding to a tissue type with a particular orientation. In the case of two crossing fibers, for example, only two among hundreds of possible mixture fraction coefficients are (ideally) non-zero. The novelty of this overall approach is its exclusive focus on the parsimonious estimation of mixture fractions, which is made possible by providing a fixed, finite basis of possible tissue compartments.

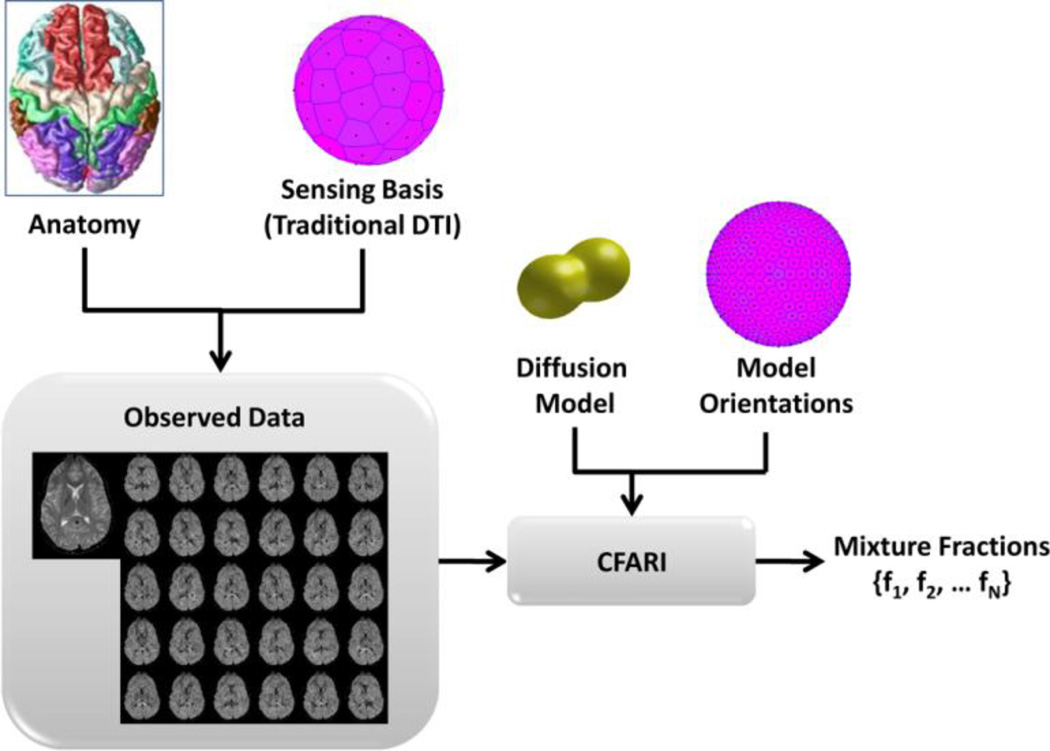
Figure 1.

Overview of the CFARI Method. A traditional DTI acquisition is used to acquire data. For analysis, a mixture model consisting of a tensor model oriented along a large number of directions is fit to the observed data using a regularized regression approach.

Although the above framework is quite general and there are many possible alternative models to explore, in this initial presentation we focus on a fairly restricted model that works quite well in practice and is intuitive and straightforward to explain. In particular, we use a multi-compartment model in which each component is a traditional tensor model of diffusion (Kim et al., 2005; Peled et al., 2006; Ramirez-Manzanares et al., 2007; Stamatios et al., 2008). We also assume that the diffusion measurements are made with a fixed diffusion sensitization strength (b-value) over an assortment of different diffusion gradient directions. Accordingly, the observed signal intensity S_k at a voxel is a finite mixture of signals, each one of which is described by the Stejskal-Tanner tensor formulation (Stejskal and Tanner, 1965) as follows

$$S_k=S_0{\displaystyle \sum _i^N}{f}_i{e}^{-b{\mathit{g}}_k^T{\mathbf{D}}_i{\mathit{g}}_k}+\eta$$ (1)

Here, g_k is the diffusion gradient direction, b is the diffusion sensitization strength, S₀ is a noise-free reference signal in the absence of diffusion weighting (the so-called b0 image), N is the number of possible compartments (tensors) within each voxel, f_i is the (unknown) mixture fraction for each compartment, D_i is the tensor associated with the i^th compartment, and η is a noise term that follows a signal-dependent, Rician distribution. While magnitude noise in MRI is Rician distribution, Rician distributions are approximately Gaussian above an SNR of approximately 5:1 (Gudbjartsson and Patz, 1995). In the following framework, we pursue a regularized least-squares approach which does not explicitly account for the differences between Rician and Gaussian noise structure.

In compressed sensing terminology, we identify the sensing basis as the set of diffusion measurements that are observed and the reconstruction basis as the set of N compartmental models that are to be used in linear combination to best fit these observations. These concepts and how they fit within the overall CFARI framework are illustrated in Figure 1. In the simulations and experiments considered in this paper, we use a fixed b-value and acquire images using K different gradient orientations spread over the sphere. This sensing basis is general enough to include conventional DTI acquisition strategies like the Jones-30 protocol (Jones et al., 1999; Skare et al., 2000) as well as HARDI and q-ball protocols. According to Eq. (1), the reconstruction basis is determined by our choice of N tensors D_i, i = 1,…N. Even within this already restricted (multi-tensor) model, we could choose to include a large collection of tensors having different shapes (e.g., sphere, prolate, and planar), different values of fractional anisotropy (FA) and mean diffusivity, and different orientations. To focus on models representative of single fiber populations, we have chosen prolate tensors (also known as linear) such that λ₂ = λ₃ = 0.5 × 10⁻³ mm²/s and with λ₁ selected to yield a fixed FA for all tensors in the reconstruction basis. We have found that FA approximately equal to 0.7 generally yields good results for white matter imaging in the brain and that the tensors included in the reconstruction basis should comprise hundreds of orientations—i.e., the principal eigenvectors of these tensors—over the unit sphere (see Figure 1). Effects of various tradeoffs in these choices are revealed in our simulation experiments (below). For compressed sensing optimality (e.g., least number of observations required for exact reconstruction), the forward projection of any sparse representation in the reconstruction basis should be incoherent with the sensing basis (i.e., the representation of any signal in the two basis sets should be minimally related). Randomized construction of a sampling basis is optimal; however, in practice, arbitrary or pseudo-random construction yields sufficiently low coherence for functions of interest such that compressed sensing methods are reasonably efficient. Herein, we rely on regular sampling of orientations with the underlying tissue assumed to be randomly oriented with respect to the sampling basis.

Compressed Sensing Algorithm: CFARI

Given the framework outlined above, we can now present the optimization problem to be solved and its solution. We define the vector y to be the K attenuation observations each scaled by the b0 image—i.e., y_k = S_k / S₀. From Eq. (1), we see that the observations can be written in matrix form as

$$\mathit{y}=\mathit{\text{Sf}}+\mathit{\eta }$$ (2)

where the K × N matrix S comprises a set of attenuation terms for each element of the reconstruction basis and each diffusion weighted experiment, f is the N × 1 vector of mixing coefficients, and η̃ is a K × 1 vector of scaled noise terms. Given the model in Eq. (2), we may write a compressed sensing criterion for the estimation of f as follows

$$\widehat{\mathit{f}}=\underset{\mathit{f}:{\mathit{f}}_i\in [0,\infty )}{\text{argmin}}\{\mathbf{S}\mathit{f}-{\mathit{y}}_{L2}+\beta {\mathit{f}}_{L1}\}$$ (3)

This formulation seeks mixing coefficients that are non-negative and minimize a criterion that simultaneously tries to match the data (first term in (3)) with as few non-zero coefficients as possible (second term in (3)). This formulation has many variants and goes by many names—e.g., l1-regularized logistic regression (Koh et al., 2007), LASSO (Tibshirani, 1996a) and its variants (Kim et al., 2006; Tibshirani et al., 2005), L2-L1 or least mixed-norm minimization (Fu et al., 2006), and many other areas in machine learning and signal processing (Candes et al., 2006a; Candes et al., 2006b; Chen et al., 2001). In our formulation, the elements of f are required to be strictly non-negative so that when normalized to sum to unity, they can be interpreted as mixture fractions. Non-negativity is somewhat unusual in the compressed sensing literature, but has been investigated in image processing applications, for example, to satisfy image intensity non-negativity assumptions (Fu et al., 2006).

In Eq. (3), β is a sparsity regularization parameter controlling the tradeoff between the precision of model fitting (the L2 norm) and the sparsity requirement (L1 norm). As β approaches zero, the estimate tends toward unregularized least-squares regression. As β increases, the sparsity term dominates. The specific choice of regularization parameter β can dramatically affect the behavior of the compressed sensing estimator, however. At some large β, for example, the differential penalty for any non-zero f_i will outweigh the model-mismatch penalty and the best estimate will be f̂ = 0, an obviously undesirable result. The lowest β at which this occurs is denoted β^* and is called the breakdown point. The magnitude of β that is required to achieve a particular tradeoff between the L2 and L1 norms depends on the scale-dependent factors including the units of S, the number of observations, and the number of basis functions, and β^* represents a consistent point for determining a specific behavior. As has been previously advocated (Kim et al., 2007), we characterize and optimize the numeric value of β relative to the empirically determined β^* so that our findings are robust to choice of units and the particular model representation.

Performance Optimization

Computational complexity is a major limitation of compressed sensing techniques for diffusion-inferred intra-voxel structure. Efficient numerical techniques are available for the nonlinear optimization problem in compressed sensing; however, these techniques are still far more involved than linear tensor estimation or the common Levenberg-Marquardt nonlinear tensor fitting methods. To allow CFARI to be computationally competitive with tensor-based analysis, we propose a technique for accelerated compressed sensing of diffusion-inferred intra-voxel structure utilizing adaptive refinement of a multi-resolution basis set.

There are efficient numerical methods to address optimization problems of the form of Eq. (3); in this work, we use the interior point method of Kim et al. (Kim et al., 2007) which includes the ability to enforce positivity constraints. The computational complexity of this L2-L1 optimization routine is approximately proportional to the square of the size of the reconstruction basis, which is therefore a key limiting factor in algorithm speed. In order to provide sufficient directional resolution, we define the orientations in our reconstruction basis π₀ by the vertices of a sixth order tessellation of a dodecahedron, yielding 376 unique orientations distributed over the halfsphere. In order to reduce computation time, our adaptive approach uses two passes, each designed to focus on a small set of possible orientations from π₀. The first pass applies CFARI using a small basis set π₁ comprising only 55 of these orientations (distributed uniformly over the halfsphere), producing a coarse estimate of the intra-voxel structure. Voxels having all estimated mixture coefficients below a threshold ε (herein, 0.1) are interpreted as isotropic and are not reprocessed.

A second pass is performed on the remaining voxels using a modified basis set π₂ derived by combining orientations from π₁ with selected additional orientations from π₀. In particular, for each direction in π₁ that produces a mixture fraction greater than ε in the first pass, all directions in π₀ within 12 degrees of that direction are added to the basis set. This process is carried out on a per-voxel basis, so while π₀ and π₁ are static basis sets, π₂ is unique to each voxel. As an added precaution, if the number of directions that exceed ε is greater than a set threshold (herein, 5), then that voxel is reprocessed using the full π₀. In the experiments that we have carried out, this procedure adds an average of seven extra directions for each direction in π₁ with a mixture fraction that exceeds ε. With appropriate choices of π₀, π₁, and the various thresholds we find that our adaptive CFARI algorithm yields similar accuracy to the full CFARI with a tenfold reduction in computational complexity.

To increase empirical efficiency, we further reduce the number of voxels to be analyzed using intensity driven masking to exclude background and non-brain tissues (e.g., by using an automated brain extraction technique (Carass et al., Submitted 2010; Smith, 2002)). It may be possible to perform model selection based on characterization of the diffusion weighted MRI signal in manner of (Alexander et al., 2002). However, CFARI is premised on resolving structure within voxels that could be isotropic as perceived with tensor analysis, so we are cautious with these approaches and have hitherto erred on the side additional computation.

Assessment of Error

Rather than estimating a tensor and its implied direction through an eigenanalysis as in conventional DTI, CFARI estimates a set of directions and their mixture fractions at each voxel. In order to assess the performance of CFARI, we must specify a meaningful metric for these particular estimated parameters, and this turns out to be harder than it would seem at first glance. Traditional mean squared error on the partial fraction estimates alone does not work well because their “correctness” relative to the problem as a whole depends critically on the discrete angular structure of the reconstruction basis. Instead, a more logical starting point is the average angular error between the detected directions and the closest true directions in the model framework as we have used in preliminary reports on CFARI:

$${\text{Err}}_{\mathit{\text{FP}}}={\displaystyle \sum _i}{\widehat{f}}_i\underset{j\in \text{model}}{\text{min}}\angle ({\mathit{v}}_i,{\mathit{w}}_j)$$ (4)

Here, f̂_i is the estimated model fraction for the i^th indexed direction v_i in the reconstruction basis, and w_j is the j^th indexed direction of the true component model. For completeness, let t_j be the true fraction associated with true basis element w_j. Err_FP can be interpreted as the false positive (“FP”) angular error rate — e.g., the average directional error between a detected direction and a corresponding true direction.

Although highly intuitive, Err_FP is not ideal because it does not properly characterize the effect of errors in the mixture fractions nor does it account for the absence of directions in the estimated dataset. As an example of this failing, consider a true basis set that has some contribution from every component in the reconstruction basis (as one would use to model an “isotropic” component of diffusion in our chosen reconstruction basis). In this case, the error would be zero regardless of the estimated mixture fractions because the angle between the estimated direction and the nearest true direction is always zero. In the following, we present a more balanced error metric that considers both false positive (FP) and false negative directions along with the errors in mixture fractions.

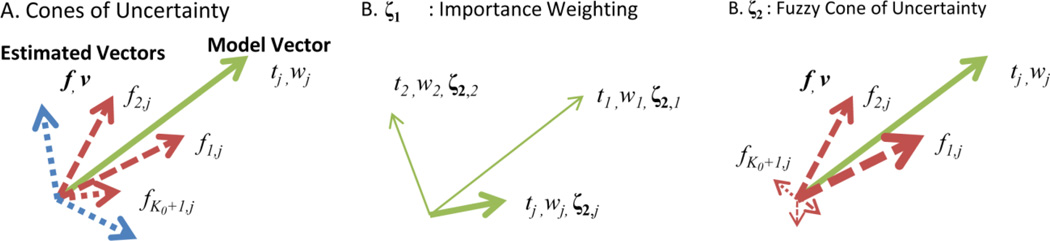
Consider the relationship between two sets of directions and weightings, E: {f_i, v_i} and M: {t_j, w_j}, as illustrated in Fig. 2. The sets of directions could be the same (as could be the case in assessing reproducibility), or they could be different (as could be the case for assessing error relative to a truth model). In analogy with the method used to assess of fiber reproducibility in (Jones, 2003), we will define a cone of uncertainty that characterizes an overall mismatch between the multiple orientations existing in the two sets while also considering the differences in their respective partial fractions. We start by recognizing that, unlike the definition of Err_FP, a proper metric should consider all directions in the model set M and ask whether the estimated directions in set E have correctly approximated each model direction w_j. But we only care about the estimated directions up to the true partial fraction t_j of the model direction. Therefore, the fundamental cone that we consider is that defined by the collection of estimated directions closest to a particular model direction whose total estimated partial fractions do not exceed the true model fraction of the model direction. Accordingly, consider a reordering of the estimated directions such that vⁱ_k,j is the k^th closest estimated vector to model vector w_j. Then we find the maximum integer K_j such that the estimated mixture fractions satisfy ${\displaystyle \sum _{k=1}^{K_j}}{{\widehat{f}}^i}_{k,j}\le t_j$, as illustrated in Figure 2A. In order to achieve equality, we add one more estimated direction, but reduce its estimated partial fraction: ${\displaystyle \sum _{k=1}^{K_j+1}}{{\widehat{f}}^i}_{k,j}=t_j$. The average angular distance between the model vector and this collection of estimated directions can therefore be defined as

$${\tilde{\theta }}_j={\displaystyle \sum _{k=1}^{K_j+1}}{{\widehat{f}}^i}_{k,j}\angle \left({\mathit{v}}_{k,j},{\mathit{w}}_j\right)$$ (5)

Figure 2.

Illustration of error metric between a model vector sets (solid lines) and an estimated vector (dashed). A cone of uncertainty (A) is calculated as the average angular distance between the estimated the K₀^th+1 closest directions (red dashed) to each vector j in the model set which sum to the corresponding partial fraction t_j. Other estimated directions (blue dotted) are not considered. The importance weighting (ζ₁,B) deemphasized direction with low partial fraction that may have high error (as indicated by line width) as these are less relevant to goodness of fit. Noise in the estimation process may introduce estimated direction with low partial fraction and high angular error which are still within the sharp cone of uncertainty and lead to unreasonable error measures. The fuzzy cone of uncertainty (ζ₂,C) weights the cone of uncertainty by the proportion of unexplained partial fraction (indicated by line width) up to or less than each angle, which reduces the impact of small, outlier contributions (such a the three small dashed vectors).

With Eq. (5), we have a set of “cones of uncertainty” defined for each model direction w_j. We could simply define a metric as the sum of these angles; but this neglects the fact that some angles are more important than others. In particular, the model directions whose partial fractions are larger are more important, and getting those directions “wrong” should weigh more heavily in the error metric. Based on this logic, we can write the following metric:

$$\epsilon ={\displaystyle \sum _j}{t}_j\left({\displaystyle \sum _{k=1}^{K_j+1}}{{\widehat{f}}^i}_{k,j}\angle \left({\mathit{v}}_{k,j},{\mathit{w}}_j\right)\right)$$ (6)

which can be qualitatively interpreted as the mean cone of uncertainty between the estimated directions in E and the model directions in M.

Our experiments reveal that Eq. (6) is still lacking in a few ways. First, we note that ε is not symmetric and in particular may not consider the error associated directions that are found in E but do not exist in the model M. Therefore, we should “symmetrize” this definition. Second, we find that the linear weighting by both the estimated and true mixture fractions puts too much weight on directions having small mixture fractions. For example, consider a discrete model basis set of 241 directions in which there are three true directions with equal partial fraction. If the directions are estimated accurately but there is 1% noise on the mixture fractions, then the resulting average angular error is more than 16°, which seems unreasonable. However, if we weight by the square of the estimated mixture fractions, this error reduces to less than a degree, which is more consistent with visual interpretation. Even with this change, the same 1% noise on mixture fraction on one of two basis sets results in greater than 14% error in ε, which implies that the linear weighting by the true mixture fractions should also be modified. This problem is illustrated in Figure 2C.

All three of these problems are addressed by defining a symmetric metric of the following form:

$$\epsilon =\frac{\psi (E,M)+\psi (M,E)}{2}$$ (7)

where

$$\psi (E,M)={\zeta }_1\left({\displaystyle \sum _{k=1}^{K_j+1}}{\zeta }_2(\angle \left({\mathit{v}}_{k,j},{\mathit{w}}_j\right),\mathit{f},\mathit{t}),\mathit{t}\right)$$ (8)

Here ζ₁ (x, u) is a scalar valued function of a similarity vector x and vector u of mixture fractions and ζ₂ (y, z, u) is a vector valued function of a similarity vector y, and two vectors z and u containing mixture fractions. Note that the similarity measure x corresponds to same basis set as the mixture fraction vector u, and the similarity measure y corresponds to same basis set as the mixture fraction vector z. ζ₁ is an importance weighting for the errors computed in the reference frame of the first basis set, while ζ₂ is an importance weighting for calculation of the cone of uncertainty.

At present, we are choosing the two importance weighting functions empirically—i.e., by what works well in practice. In the case of ζ₁, we find that squaring the mixture fractions while normalizing to a unit weighting across all directions works well in practice:

$${\zeta }_1\left(\mathit{x},\mathit{u}\right)=\frac{{\displaystyle {\sum }_m}{u}_m^2{\mathit{x}}_m}{{\displaystyle {\sum }_m}{u}_m^2}$$ (9)

where x is a vector indexed by m. We define the importance weighting ζ₂ based on the proportion of partial fraction quantity explained by vectors at a larger separation:

$${\zeta }_2\left(\mathit{y},\mathit{z},\mathit{u}\right)=\frac{{\displaystyle {\sum }_{k=1}^{Z_0+1}}{z}_{k,j}{\displaystyle {\sum }_{n=k+1}^{Z_0+1}}{z}_{k,j}{y}_n}{{\displaystyle {\sum }_{k=1}^{Z_0+1}}{z}_{k,j}{\displaystyle {\sum }_{n=k}^{Z_0+1}}{z}_{k,j}}$$ (10)

Here z_k,j is defined as the k^th closest element of the basis set for z to the j^th element corresponding to u, and Z₀ is defined as the maximal indexed direction for the cone of uncertainty between the two direction sets (as K₀ is above). The result of ζ₂ is a vector of similarity measures of the same size as the basis set u (note z_k,j indexed by j). Both ζ₁ and ζ₂ preserve the intuitive interpretation that a moderate rotation from one set to the other set results an error equal to the degree of rotation times the partial fraction of that vector.

Tractography

Tractography is not the primary focus of this paper, but since fiber visualization is a useful qualitative outcome of a diffusion imaging experiment, we implemented a straightforward approach which is loosely based on FACT (Mori and van Zijl, 2002) and whose results can be visualized in DTIStudio (Johns Hopkins University, Baltimore, MD). Our approach, called INtravoxel Fiber Assignment by Continuous Tractography (INFACT), initializes fiber tracking at every voxel in the dominant direction determined by the largest mixture coefficient f_i. Tracking proceeds in both directions by continuous piecewise linear assignment as in FACT. At each step, the orientation was selected as the dominant direction with the nearest neighbor voxel that minimized the following importance weighting, w_i = f_i|v_i · v_last|^γ where v_i is the principle eigenvector of tensor D_i, v_last is the unit vector representing the last step in tracking, and γ is a regularization parameter that emphasizes continuity of the tracked fibers. Ad hoc experiments showed that γ = 4 yielded reasonable results.

Experiments and Results

The CFARI formulation is not dependent on the specific form of the diffusion weighted data to be analyzed—the data could be from a low b-value DTI study, from a high angular resolution diffusion imaging (HARDI) study, or from a multi-b-value, multi-shell diffusion spectrum imaging study. In this paper, however, we are primarily interested in the estimation of multiple intra-voxel directions using fairly standard clinical and research DTI scans. To explore this potential we carried out both simulations and experiments using acquired data, as described next.

Simulations

Simulation of Crossing Fibers

Two fiber tracts comprising tensors having FA=0.7 (λ₁=2×10⁻³ mm²/s, λ₂ = λ₃ =0.5×10⁻³ mm²/s) were simulated so that they cross at 90 degrees, as shown in Figure 3. The tracts each have a maximum partial fraction along a diagonal of the image and are “blended” with an isotropic component moving away from the diagonal such that the tract cross-section has a Gaussian profile. The two tracts were combined and scaled so that the partial fractions at each voxel add to unity. A typical clinical DTI sequence with the following parameters was simulated: 30 diffusion weighting directions, b-value of 700 s/mm², five b0 images, and Rician noise. The SNR of the simulations was defined as the ratio of the (noise-free) unweighted signal intensity to the noise standard deviation on the complex signal. Complete simulations were performed at SNRs of 15:1 and 25:1. The finest grain reconstruction basis of CFARI was made from identical prolate tensors each having FA=0.7 oriented toward the 376 vertices of a sixth order tessellation of a dodecahedron, as previously described. The compressed sensing regularization coefficient was defined as β = 10⁻¹ β^*, where β^*is the breakdown point computed independently at each voxel. The minimum angle between a true direction and any direction in the basis set was 1.63°. The maximum minimum angle between any vector in the basis set and its nearest neighbor was 8.69°.

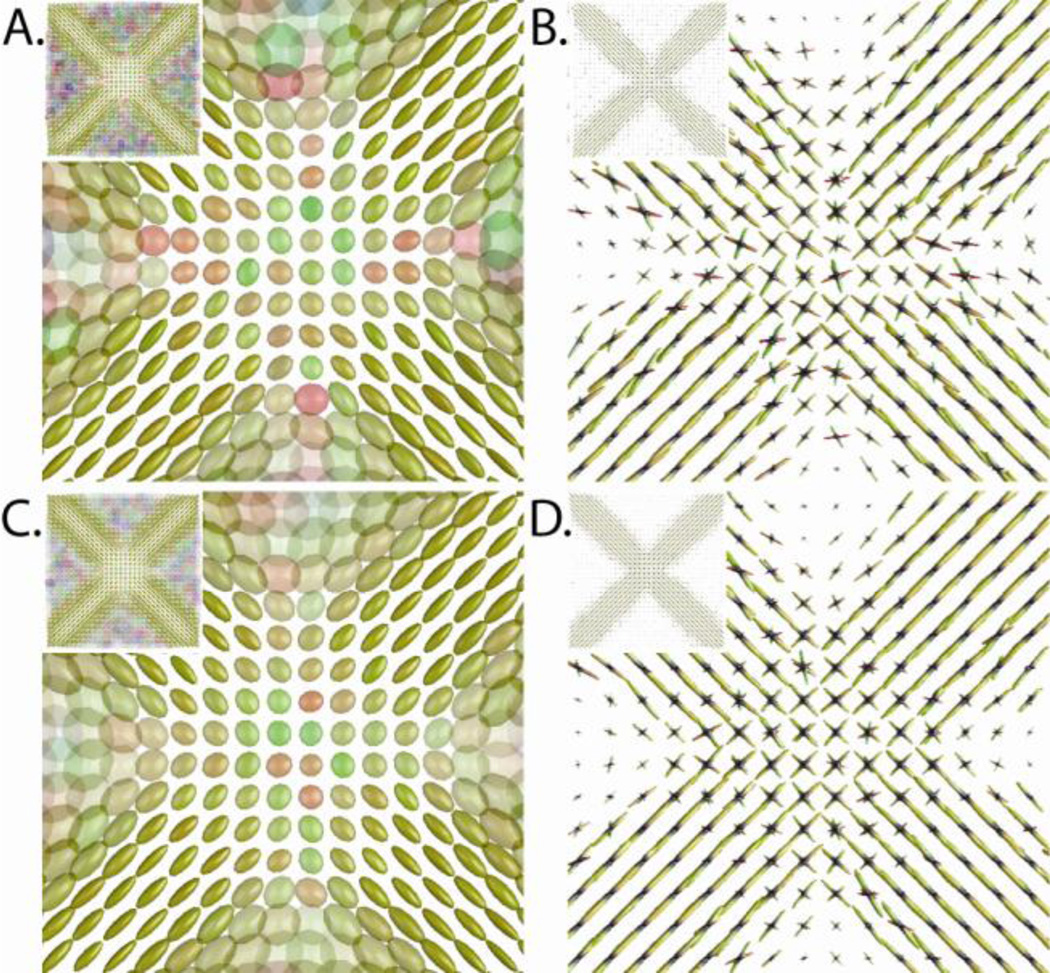
Figure 3.

Simulation of crossing fibers at an SNR of 15:1 (A&B) and 25:1 (C&D). Tensor fits to a DTI acquisition of a fiber crossing region (left: A&C) results in a zone of planar tensors (enlarged for detail) where directional orientation is ambiguous. CFARI estimate (right: B&D) are able to identify the underlying structure using the same simulated dataset. For each voxel, the five CFARI directions with the highest partial fraction are shown weighted by partial fraction. Tensors (A&C) are colored by principle eigenvector (red=horizontal, green=vertical, blue=out of plane) and rendered with shading. Fiber orientation plots (B&D) show a surface mesh where each point is colored by the normalized coordinate (red/green/blue as with tensors; zero is at the origin of each glyph), and the distance from the origin is proportional to the estimated partial fraction.

Figure 3 shows the results of this simulation. The results of standard tensor computations on the simulated data are shown in Figures 3A and 3C. Here it is evident that tensors are representative of the underlying truth only in areas for which the fibers are not substantially overlapping. The higher SNR present in the measurements leading to Figure 3C does not lead to a better result in the crossing region over that of Figure 3A. The results in Figures 3B and 3D demonstrate the ability of CFARI to capture the crossing fiber information that is reflected in the data. As well, it is evident by visual comparison of Figures 3B and 3D that increasing the SNR improves the quality of the CFARI estimate.

Dependence on β and reconstruction basis

Simulations were carried out to explore the interdependence of the CFARI estimation parameters: β, the reconstruction basis, and the ground truth. At an SNR of 25:1, 1024 Monte Carlo simulations were performed with an equal mixture of crossing fibers having three true FA’s: FA=0.55 (λ₁ =1.3×10⁻³ mm²/s), FA=0.71 (λ₁ =2×10⁻³ mm²/s), and FA=0.81 (λ₁ =3×10⁻³ mm²/s). For each simulation set, a CFARI basis was constructed for each of 50 linearly spaced axial diffusivities from 0.5×10⁻³ (FA=0) to 3×10⁻³ (FA=0.81) and β was swept in 50 logarithmic steps from 10⁻⁴ β^* to β^*.

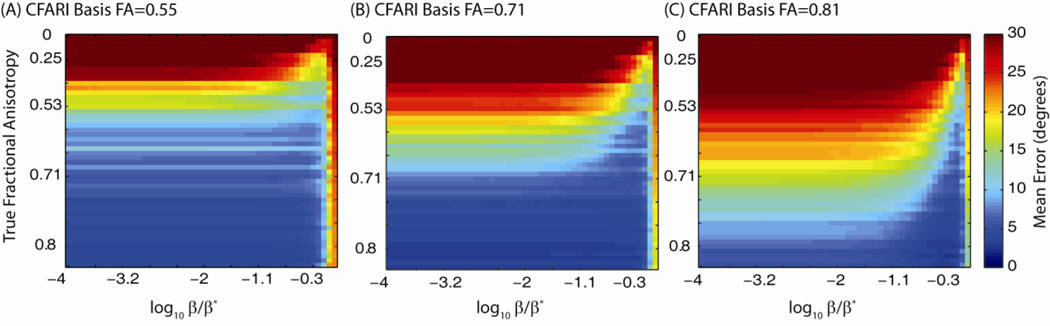
Note that this experiment involved 7,680,000 simulations, the results of which are presented in terms of the mean error for each combination of parameters: 3 Model FA’s (subplot in Fig. 4) × 50 True FA (rows in Fig. 4) × 50 choices of β / β^* (columns in Fig 4) × 1024 Monte Carlo iterations. Increasing β improved accuracy, especially with moderate (Figure 4B) and high model anisotropy (Figure 4C); yet reduced reliability at high β was apparent near β^* for all simulations. Achievable error generally decreased with higher model anisotropies, but the error increased when the model anisotropy was lower than the true, underlying anisotropy.

Figure 4.

Selection of CFARI model basis and scale parameter. Increasing basis anisotropy reduced the lowest possible error; however, increasing anisotropy increased error when the truth is of lower anisotropy (compare A->B->C). Increasing β also resulted in lower error; yet as β became very close to β^*, error dramatically increased.

Impact of Reconstruction Resolution

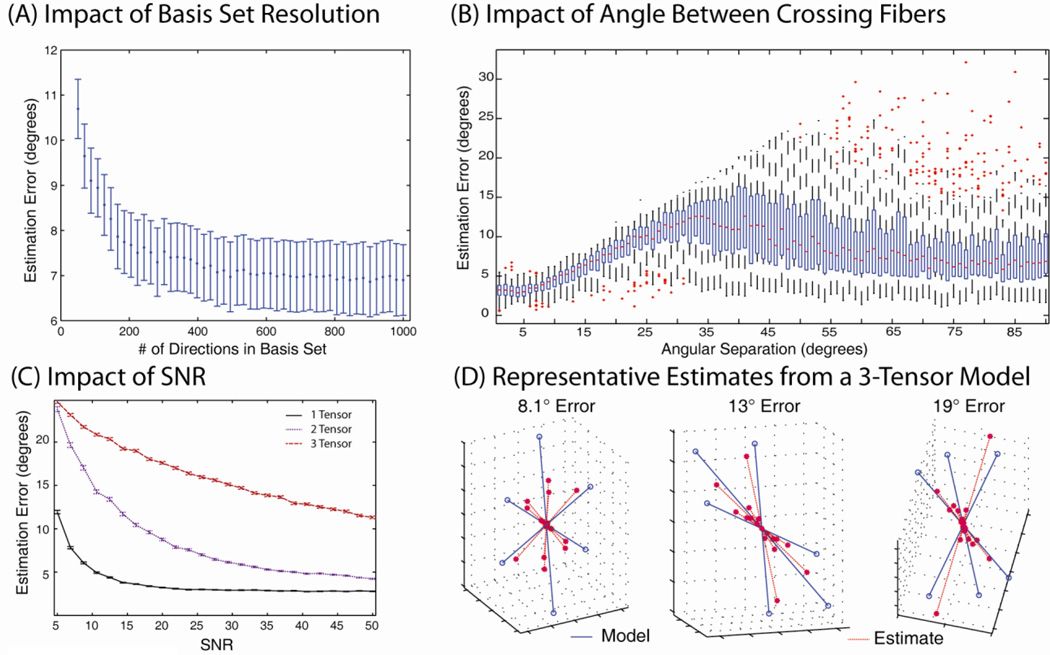
The impact on the directional resolution of basis set was examined by CFARI fitting of an equal partial fraction crossing fiber model (as in Fig. 3) with 1000 Monte Carlo iterations, but replacing the directional of the basis set a minimum potential energy distribution (Skare et al., 2000) with between 50 and 1000 unique directions (corresponding to an angular separation of between 19.45° and 3.6°, respectively) with all other parameters held constant. Larger reconstruction basis sets resulted in reduced error (Figure 5A). However, the marginal improvement was negligible (well less than a degree) once at least 400 directions were included in the reconstruction basis (e.g., a mean separation between the basis and true vector of 3.4°).

Figure 5.

Fiber crossing simulations for true FA of 0.7. Error was reduced by increasing the directional resolution of the basis set (A), but stabilized near 400 directions with an SNR of 25:1. Mean estimation error was sensitive to the angle between crossing fibers (B) and to the SNR of the observed data (C). The box plot in (B) shows median (magenta center line), quartiles (range of center blue boxes), two standard deviation interval (extent of dashed vertical lines) and extreme values (magenta + symbols beyond the standard deviation lines) of estimated error by simulated angular separation. For qualitative interpretation of the error metric, (D) illustrates three examples in which CFARI achieved three different error levels based on a ground truth, three compartment model.

Impact of Fiber Crossing Angle

The effects of crossing fiber angle on estimation accuracy were evaluated by randomly generated 100 directional pairs of tensors with FA 0.7 (as above) for each of 90 linear separations ranging from 1° to 90°. For each pair, one direction was selected uniformly on the sphere and a second direction was selected uniformly at random on the circle at a particular radius. For both simulations, CFARI was performed with the same parameters as in the initial crossing fiber simulation.

For all fiber crossing angles, the median error was less than 15° (Figure 5B) at an SNR of 25:1. Error peaked at a separation of around 30° (estimation error of ±13°) and improved with increasing separation (to ±7° error at a separation of 90°).

Impact of SNR

The impact of SNR on CFARI estimation was evaluated for simulated tracts corresponding to a single tensor, two tensors whose tracts crossing at 90° and three tensors crossing at 60°. For these simulations, true FA was equivalent to reconstruction FA (i.e., 0.7). For each model, 1000 observations were simulated for 25 linearly spaced SNRs from 5:1 to 50:1.

Single tensor models could be estimated reliably at the resolution of the basis set (±3°) at an SNR of 15:1 and higher, while two and three tensor crossing could also be resolved, but with higher error (Figure 5C). At an SNR of 25:1, the mean estimation errors were 3° for a single tensor, 7° for two tensors, and 16° for three tensors. For qualitative comparison, Figure 5D illustrates representative estimates from a three tensor model for three error levels.

Impact of Partial Volume Effects

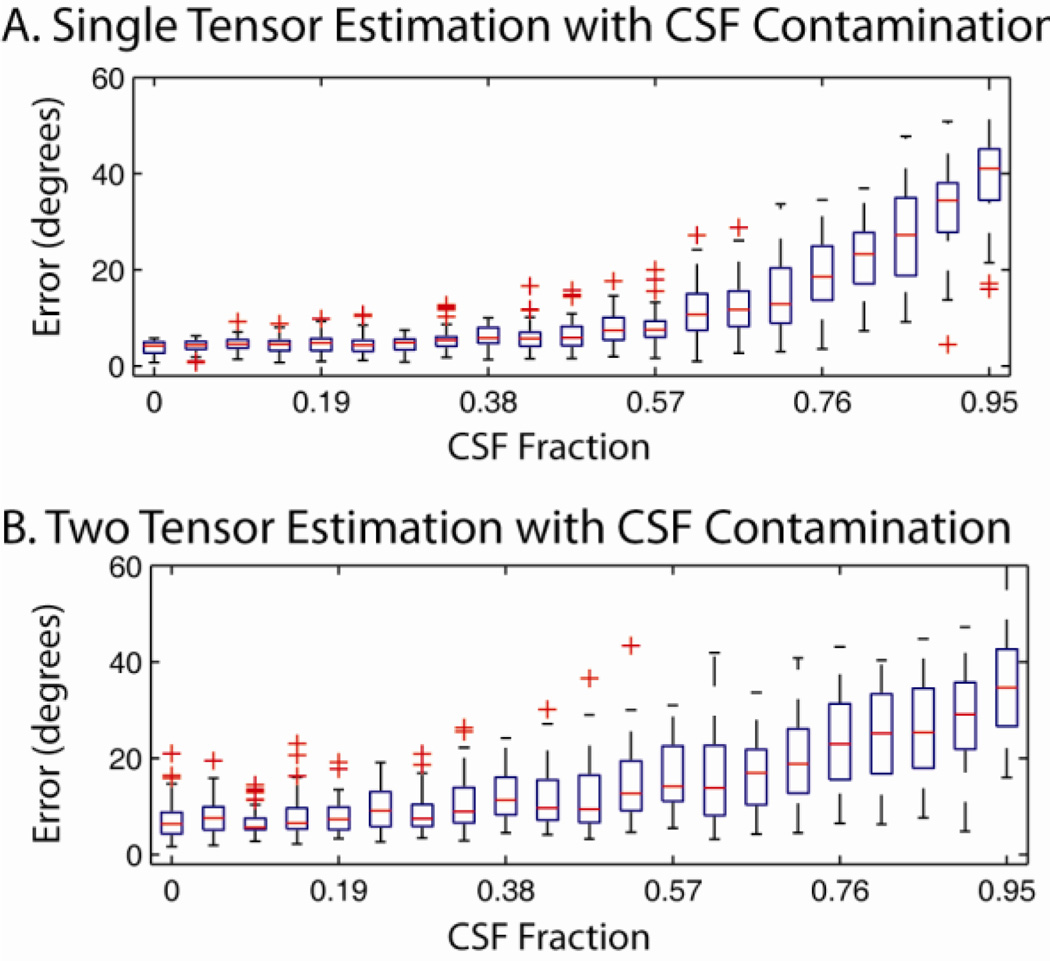
The impact of CSF partial volume effects on CFARI estimation were evaluated for single tensors and two tensors whose tracts crossing at 90°. For these simulations, true FA was equivalent to reconstruction FA (i.e., 0.7). For each model, 50 observations were simulated at an SNR of 25:1 for 21 linearly spaced CSF partial fraction components from 0% to 95%. A reconstruction basis consisting of a 7^th order tessellated icosahedrons augmented with isotropic tensor component (246 unique tensors) was used with the same simulated acquisition sequence as above.

Estimation of both single tensor (Figure 6A) and two tensor (Figure 6B) models was robust to CSF contamination of up to 50%. Error rapidly increased after 60% CSF partial fraction. Notably, the maximum partial fraction estimated for the CSF component was less than 10⁻⁶ for any simulation. Hence, the current framework is not a surrogate to directly estimating free water fraction (such as the “ball and stick” model (Behrens et al., 2003)), but the directional estimates are robust to partial fraction contamination.

Figure 6.

Impacts of CSF partial fraction contamination on CFARI directional estimates. Single (A) and two (B) tensor models were simulated with a CSF component representing from 0% to 95% of the partial fraction.

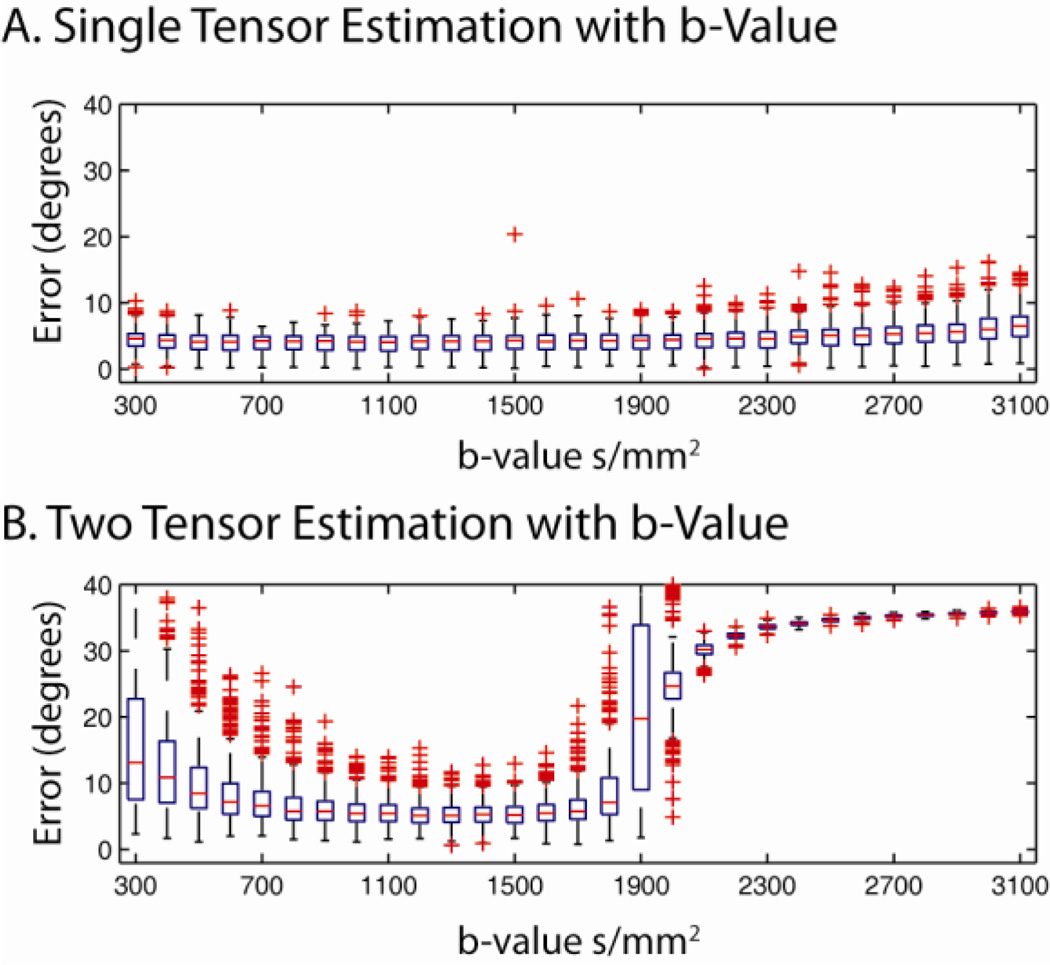
Impact of b-Value

The impacts of b-value on CFARI estimation were evaluated for single tensors and two tensors whose tracts crossing at 90°. For these simulations, true FA was equivalent to reconstruction FA (i.e., 0.7). For each model, 500 observations were simulated at an SNR of 25:1 (defined on the b=0 s/mm² data) for b-values from 300 s/mm² to 3100 s/mm². A reconstruction basis consisting of a 7^th order tessellated icosahedrons augmented with isotropic tensor component (246 unique tensors) was used with the same simulated acquisition sequence as above. Estimation of single tensor components was remarkably stable across b-values, while error in two tensor models was stable from 700 s/mm² to 1700 s/mm² (Figure 7). For the two tensor model, the observed minimum error was at 1300 s/mm2 (5.3 ° versus 7.3 ° at 700 s/mm2, significantly different with two-sided t-test at p<0.001). At very high b-value, more outliers were observed with the single tensor model and errors were extreme with the two tensor model.

Figure 7.

Impacts of b-value on CFARI directional estimates. Single (A) and two (B) tensor models were simulated with a b-value ranging from 300 s/mm² to 3100 s/mm² with an SNR on the b=0 s/mm² image equal to 25:1.

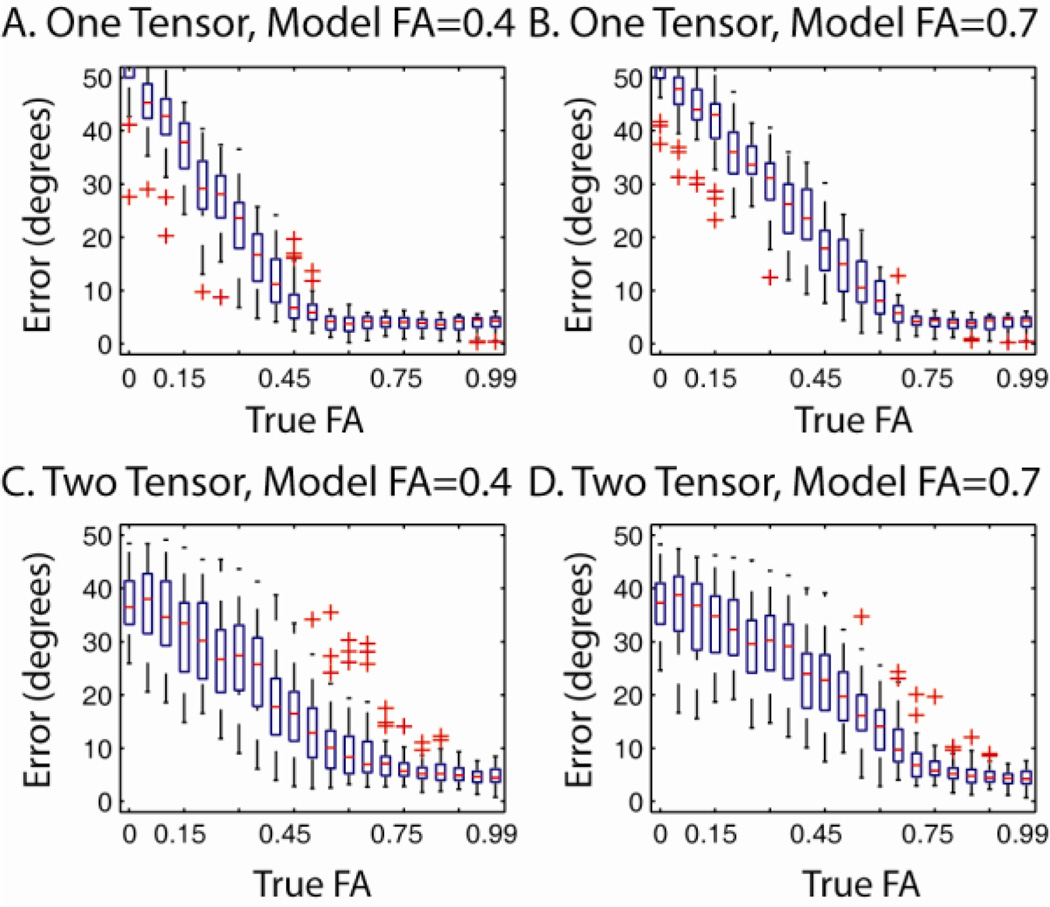
Isolating the Effects of FA

The interaction between CFARI model FA and true tensor FA (illustrated in Figure 4) explored in additional detail for single tensors and two tensors whose tracts crossing at 90°. For these simulations, true FA for prolate tensors was varied between 0 and 0.999 in 21 steps while reconstruction FA was either 0.4 or 0.7. In both cases, maximum diffusivities were 2×10⁻³ s/mm². For pair of true FA and model FA, 50 observations were simulated at an SNR of 25:1 (defined on the b=0 s/mm² data) for a b-value of 700 s/mm². A reconstruction basis consisting of a 7^th order tessellated icosahedrons augmented with isotropic tensor component (246 unique tensors) was used with the same simulated acquisition sequence as above. As Figure 8 illustrates, when the true FA is higher than the model FA, errors are low and nearly constant for varying FA. With decreasing true FA below the model FA, error rates increase.

Figure 8.

Interaction of true FA with reconstruction model FA. Single tensor (A,B) and two tensor models (C,D) were simulated with varying true FA. Reconstruction was performed with either a low FA (0.4) reconstruction basis (A,C) or a high FA reconstruction basis (B,D).

Empirical Data

Data

A healthy volunteer (M/20 years old) with no history of neurological conditions was recruited. Local institutional review board approval and written informed consent were obtained prior to examination. All data were acquired using a 3T MR scanner (Achieva, Philips Medical Systems, Best, The Netherlands) with body coil excitation and an eight channel phased array SENSitivity Encoding (SENSE (Pruessmann et al., 1999)) head-coil for reception. In a single scan session, a full repetition of a DTI and q-ball dataset was acquired. The dataset consisted of two DTI datasets acquired with a multi-slice, single-shot, echo-planar imaging (EPI), spin echo sequence (TR/TE = 6410/69 ms, SENSE factor = 2.5). Sixty-five transverse slices were acquired parallel to the line connecting the anterior commissure-posterior commissure (AC-PC) with no slice gap and 2.2 mm nominal isotropic resolution (FOV = 212 × 212, data matrix = 96 × 96, reconstructed to 256 × 256). Fat suppression as performed with Spectral Presaturation with Inversion Recovery (SPIR) and the phase encoding direction was anterior-posterior. Diffusion weighting was applied along 30 directions (Jones30; other vendor specific parameters were set to achieve maximum gradient magnitudes: gradient overplus = no, gradient mode = enhanced) with a b-value of 700 s/mm². For each DTI dataset, five minimally weighted images (5 b0’s) (b ≈ 33 s/mm²) were acquired and averaged on the scanner. The total scan time to acquire one DTI dataset was 4 min 4s. No cardiac or respiratory gating was employed. A standard q-ball sequence at a b-value of 3000 s/mm² and 99 diffusion directions with the same resolution and coverage as the DTI dataset was acquired (TR/TE = 15348/77 ms, SENSE factor = 2.5). Three sets of five scanner averaged reference scans were acquired. Total scan time for the q-ball dataset was 31 min 27 s.

Analysis

Motion compensation and eddy current distortion correction were performed prior to analysis with JIST-CATNAP (Landman et al., 2007). Both CFARI and q-ball analysis were performed independently for each repetition of the pairs of 30 direction datasets and for the high b-value 99 direction datasets. For q-ball analysis, a regularized 6th order spherical harmonic fit was estimated with analytical q-Ball using Laplace–Beltrami regularization with the recommended regularization term of 0.006 (Descoteaux et al., 2007). Intra-voxel orientations were estimated as the local maxima of the spherical harmonic model projected onto a discrete basis set of 289 directions as described in (Descoteaux et al., 2007). CFARI analysis was performed with an adaptive basis set (55 directions in the initial pass and 376 directions in the larger set) with a canonical tensor with FA of 0.71, as described above. As in the simulation experiment, the compressed sensing regularization coefficient was defined as β = 10⁻¹ β^*, where β^* is the breakdown point computed independently at each voxel.

Results

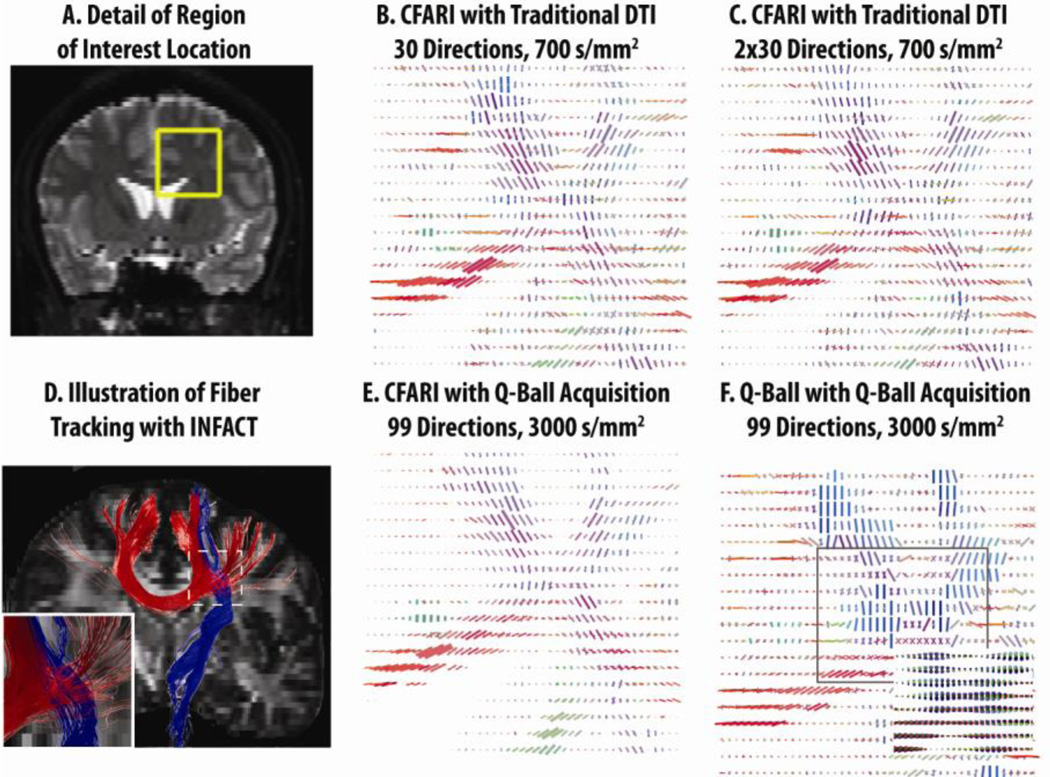
Figures 9 and 10 show the results of the human subject experiments. No ground truth is available with real data, so we emphasize a qualitative comparison of CFARI and q-ball. With only 30 directions at low b-value, CFARI maps structure that is consistent with the crossing of the internal capsule and corpus callosum (Figure 9B). This estimate visually improves with multiple repetitions and at higher b-values (Figure 9C,E). The maximal directions from analytic q-ball were qualitatively reasonable when applied to the intended sequence (Figure 9F). Figure 9D illustrates that INFACT tractography is capable of tracking through the region of crossing fibers illustrated in this figure. Figure 10 presents a detailed view of CFARI on two representative slices. Although applying CFARI on the q-ball acquisition produces excellent results, it is qualitatively apparent that the results are largely the same when only 30 directions and low b-values are used.

Figure 9.

Qualitative inspection of intra-voxel orientations estimated with in vivo data show patterns consistent with anatomy, which can be clearly appreciated in the region of the corpus callosum and internal capsule (highlighted in A). CFARI directions are visually consistent even with what one would expect from anatomical consideration while analytic q-ball (F) show shows consistency using higher b-value data. Note that the maximal directions for q-ball were extracted from the parameterized orientation distributions function (inlay of F). Fiber tracking with the data in (D) show results that are visually consistent with the crossing of major fiber tracts.

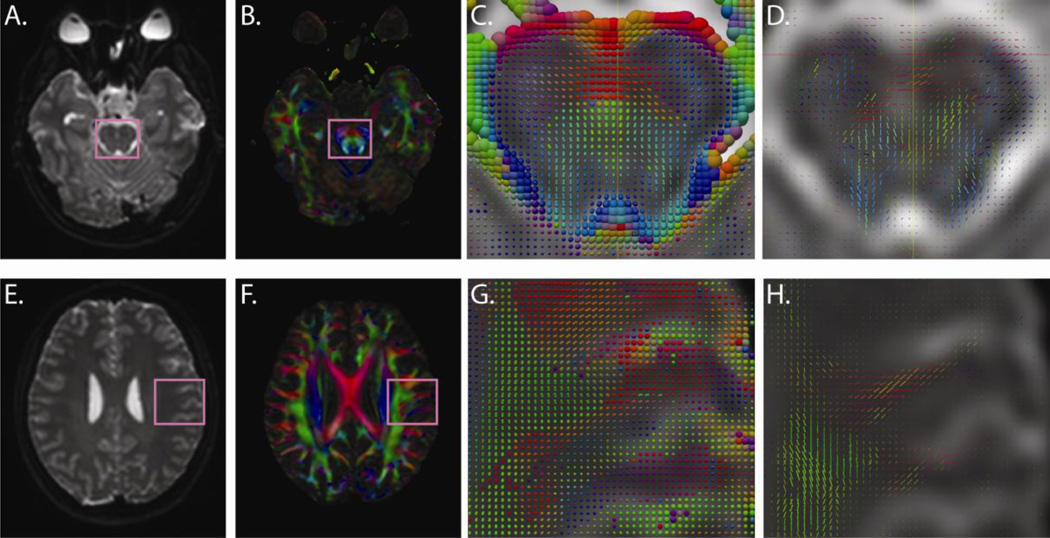
Figure 10.

Comparison of DTI and HARDI direction estimates. Mean unweighted scans (A,E) and DTI colormap images (B,F) are shown for two representative slices. Enlargements show estimated diffusion tensors (C,G) alongside CFARI directions (D,H) based on two repetitions of 30 directions at a b-value of 700 s/mm² (with parameters corresponding to C in Figure 9).

Discussion

CFARI provides a robust framework for estimating intra-voxel structure from conventional diffusion-weighted acquisitions and shows great promise in helping to resolve the crossing fiber problem. The multiple intravoxel directions could be used for probabilistic or deterministic fiber tracking in place of multi-orientation structures inferred by other methods. Because CFARI is driven only by information from individual voxels, one could exploit spatial regularization either in the subsequent fiber tracking or through direct incorporation of smoothing (e.g., (Assemlal et al., 2007)). Calculation of generalized contrast measures, such as generalized fractional anisotropy (GFA) (Tuch, 2004), is also straightforward.

CFARI is sensitive to the choice of reconstruction basis. Figure 4 illustrates that error for high FA tensors decreases with a higher reconstruction basis FA. However, when the true FA is lower than the reconstruction FA, the error rapidly decreases (compare the slow darkening of blue right A–C of Figure 4 to the rapid intensity change across the horizontal point in each plot where reconstruction FA equals true FA). Hence, choice of a reconstruction basis is an important design criterion and must be tuned to the types of tissues one is interested in querying. Herein we have chosen an FA of 0.7, which appears to be a conservative FA for representing fibers in the spinal cord columns or corpus callosum white matter. Intersections of extensions of these structures have historically been of primary interest for resolving crossing fibers. Basis set optimization based on physiological criteria would be a fascinating area of continuing investigation. The compressed sensing regularization criterion is empirically found to offset the typical curses of dimensionality when using large reconstruction basis sets. However, computation time scales super-linearly with the size of the basis set. Hence, for efficiency reasons, the marginal improvement in estimation accuracy with increasing basis set must be weighed against the feasibility of achieving these results. Note that we did not evaluate very large basis sets (>10⁴) so additional stability concerns may arise.

The single voxel simulations demonstrate that the resulting angular resolution is comparable to previously reported findings for both q-ball peak detection and deconvolution approaches (e.g., 10–20 degrees precision). We note that CFARI makes no attempt to model the full richness of the orientation distribution functions possible with q-ball analysis; rather CFARI directly extracts “dominant” orientation contributions and is able to do so with far less information. The q-ball error metrics are disconcertingly high, yet are consistent with the 12–16° error reported in Table 5 of [4] for a biological phantom. Visually, q-ball contains additional information than local maxima and it seems possible to use the representation to find other definitions of mixture components, yet, as shown herein, this information is not well-captured by local maxima. In summary, CFARI enables evaluation of intra-voxel structure (e.g., for advanced fiber tracking and tissue classification) in studies that have hitherto been limited to tensor analysis due to scan time availability or others limitations on acquiring a full q-ball dataset. Here we have shown that estimated mixture directions can be determined with approximately the same accuracy as traditional q-ball analysis using only 13% of the scan time.

The multi-compartment framework hints at other possibilities for characterizing tissue characteristics. It might be possible to associate specific basis component coefficients with different biophysical basis (e.g., types of tissue). Currently, the CFARI basis components vary only by orientation. In previous work, we saw that within this framework CFARI is robust to model mismatch. Lowering the FA of the basis set to improve robustness increases overall error. The CFARI numerical estimation framework readily supports a non-tensor model for individual compartments, such as with the ball and stick diffusion model (Behrens et al., 2003). It would be fascinating to use either simulated or empirical observations of biological compartments of interests as a basis set. The utility of such an approach is, as yet, unproven and will be an exciting area of future research.

In summary, the simulations demonstrate that the positivity constraints in CFARI lead to stable and precise estimates of multiple intra-voxel compartmental directions. For the majority of models and SNR’s explored, the additional constraint improved error over the unconstrained estimates and lead to more computational efficient estimates.