Summary
We present the codimensional PCA, a novel and straightforward method for resolving sample heterogeneity within a set of cryo-EM 2D projection images of macromolecular assemblies. The method employs Principal Component Analysis (PCA) of resmapled 3D structures computed using subsets of 2D data obtained with a novel hypergeometric sampling scheme. PCA provides us with a small subset of dominating “eingevolumes” of the system, whose reprojections are compared with experimental projection data to yield their factorial coordinates constructed in a common framework of the 3D space of the macromolecule. Codimensional PCA is unique in the dramatic reduction of dimensionality of the problem, which facilitates rapid determination of both the plausible number of conformers in the sample and their 3D structures. We applied the codimensional PCA to a complex data set of T. thermophilus 70S ribosome, and we identified four major conformational states and visualized high mobility of the stalk base region.
INTRODUCTION
Single particle cryo-electron microscopy (EM) is an experimental technique uniquely suited to imaging of macromolecular assemblies and machines in their native, unconstrained state. Due to a relatively rapid freezing (~5 ms) of the specimen during sample preparation, time resolution is sufficient to capture a mixture of complexes in varied conformational states, as the sample may contain macromolecular complexes differentiated by non-stoichiometry of ligand binding or conformational variability. Intrinsic conformational heterogeneity in functionally defined complexes is biologically of utmost importance and when revealed, it provides a fascinating insight into the function of protein complexes. However, structural heterogeneity of sample invalidates the basic principle of the single particle technique, according to which collected projection images should represent the macromolecular assemblies with identical structure (Frank, 2006). Thus, heterogeneity, both compositional and conformational, constitutes a major methodological challenge. Dedicated computational methods should be developed, which will be capable of identifying the heterogeneity and then separating the data set into homogeneous subsets (Spahn and Penczek, 2009).
Examination of 2D projection data is the most straightforward and robust computational approach to the analysis of sample heterogeneity. Principal Component Analysis (PCA) proved to be indispensable in clustering of 2D images that differ only slightly (van Heel and Stoffler-Meilicke, 1985). Regrettably, unequivocal interpretation of 2D results in the terms of structural variability of a 3D complex is difficult. Therefore, preference is usually given to methods that operate directly in the 3D space, comparing EM projection data with the re-projections of a number of candidate 3D structures, as in the multiparticle (or multireference) refinement (Rye et al., 1999; Schuette et al., 2009). While the approach has been shown to be robust for a particular specimen, its general applicability is not known. Moreover, the computational challenges are formidable, particularly in the implementation inspired by the Maximum Likelihood methodology (Scheres et al., 2007), as one has to simultaneously determine class membership and orientation parameters of 2D projection images, whose number is often of the order of 105 – 106, using multiple reference structures.
We have originally introduced bootstrap as a resampling method suitable for analysis of conformational variability that allows real-space variance estimation in single particle reconstruction (Penczek et al., 2006a; Zhang et al., 2008). In bootstrap, we randomly select with replacement a set of n images from the available set of n EM projection images. In the resampled set some images appear more than once, and some are omitted. For each resampled set of projections a 3D reconstruction is computed resulting in a ‘bootstrap structure’. We showed that the variance of the bootstrap structures is related in a simple manner to that of the unknown source structures from which the projection images originated. We also proposed to use the information about localized variance to initiate a multireference refinement procedure called the “focused classification” (Penczek et al., 2006b). However, bootstrap resampling has shortcomings when applied to a set of EM projection images with a non-uniform distribution of projection directions, as typically encountered in EM. Directional overabundance of projections causes some angular regions to be sampled with effectively higher frequencies and results in streaking artifacts in the variance field and spurious correlations in the resampled volumes. While other ad hoc resampling methods have been introduced in the EM field for the purpose of sorting inhomogeneous data sets, their properties were not studied (Fischer et al., 2010; Simonetti et al., 2008).
In the present work, we propose the codimensional PCA; a computational approach that allows to untangle the conformational states present in the EM sample using PCA of the maps computed from the resampled sets of 2D projection data. In order to eliminate artifacts due to non-uniform distribution of projections, we introduce a novel resampling strategy, the HyperGeometric Stratified Resampling (HGSR) scheme. It differs from the previously used bootstrap resampling in two important ways: (a) in the HGRS resampling is stratified, i.e., the set of projection images is divided into subsets that share similar angular directions and resampling is performed independently within each subset; (b) the angular distribution of the resampled projections is kept uniform, which is accomplished by drawing the same number of images from each stratum. The main innovation is that we provide a way for rapidly clustering 2D projection data in the factorial space constructed in the common framework of a 3D space of the macromolecule under investigation. More specifically, we compute eigenvectors (henceforth referred to as “eigenvolumes”) of the 3D structures resulting from resampling of the projection data set using a novel stratified resampling strategy, and compute the factorial coordinates as inner products between the re-projections of these eigenvolumes into directions of the original 2D projection data and the 2D projection data themselves. This circumvents the problem created by the fact that while the data is 2D and it has the form of the projections of original structures, we are interested in the variability of the 3D structure. The solution proposed justifies the name codimensional PCA. The main gain of the approach is the dramatic reduction of dimensionality of the problem, which makes it possible to rapidly determine both the plausible number of conformers in the sample and their 3D structures.
In application to the cryo-EM data, we re-analyzed a set of projection images of a ribosomal Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex, where the ternary complex (EF-Tu•aminoacyl-tRNA•GDP) was stalled on the ribosome using the antibiotic kirromycin. Previous application of the multiparticle refinement had already demonstrated intrinsic conformational heterogeneity in this complex (Schuette et al., 2009). We show that the new method allows a rapid identification of the major conformational states of the complex present in the sample, and the results are in a general agreement with those previously obtained. When the analysis was focused on the stalk base region of one of the thus obtained groups, we identified the conformational variability of the stalk base and of the stalk itself that is even more complex than previously anticipated, which clearly demonstrates superiority of our new approach.
RESULTS
Codimensional PCA
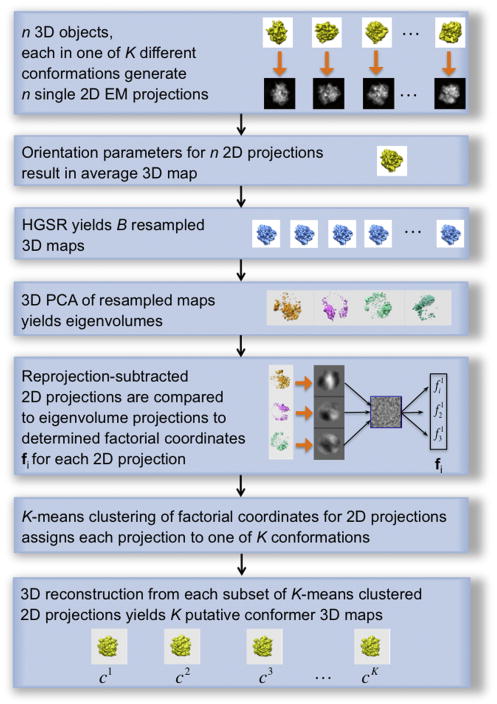
The method is directed at identification of the conformers within a cryo-EM sample of 2D projection data. It includes six main stages (Fig. 1): (1) the entire projection data set undergoes a 3D projection alignment, which results in determining the overall, “average” 3D structure, (2) the 2D projections are resampled yielding a large number of 3D structures, (3) which undergo eigenanalysis (PCA), and (4) a small number of thus obtained dominating eigenvolumes are used to compute factorial coordinates of 2D projection data; (5) the factorial coordinates undergo cluster analysis, and (6) based on the resulting class assignments for the projection data, the 3D structures of conformers are computed.
Figure 1.
The sequence of steps constituting codimensional PCA. The analysis requires a set of 2D cryo-EM projection images that are aligned within the common framework of reference yielding an “average” 3D structure of the molecule. As a result of eigenanalysis of resampled structures and calculation of factorial coordinates of 2D projection images, and clustering separation of the projection data set into subsets, the procedure eventually provides structures of putative conformers. See also Figure S1.
Resampling of projection data was recognized as a leading method for the analysis of variability in a structure reconstructed from the set of its projection images (Penczek, 2002; Penczek et al., 2006a; Zhang et al., 2008). Here we introduce a HyperGeometric Stratified Resampling (HGSR) scheme, designed to address the challenges of the cryo-EM data distribution of projection directions and requirements of the 3D reconstruction algorithms. Given a set of n 2D projection images and their angular directions, we begin with creating a tessellation of the unitary sphere resulting in R approximately equal-size areas. As each angular direction can be represented as a point on the unit sphere, it appears sufficient to find a set of reference points that are uniformly distributed on the surface of the unit sphere so that these define centers of the areas sought. Except for trivial cases, a sphere cannot be uniformly covered by points (Saff and Kuijlaars, 1997), so an approximate solution has to be found. Whereas various possible solutions can be adopted, we select the one designed so that the distances between each point and its nearest neighbors are approximately equal and the angular step size of the tilt angle is constant while the steps of the azimuth angle vary in proportion to the sine of the tilt angle (Baldwin and Penczek, 2007). These R angular directions, each specified by a normal vector defined by the tilt and azimuth angles, define a set of tessellations. We assign images to respective tessellations by selecting assignments corresponding to the maximum of the inner products computed between projection direction of a given image (again specified by the tilt and azimuth angles of this image) and each of the normal vectors defining tessellations. The procedure yields R subsets each with nr images, respectively ( ). Next, we select the number of images m to be retained in each tessellation such that m is between 1 and the number of images in the least populated area (1 < m < minr nr).
We proceed with resampling by randomly selecting, without replacement, m out of nr images for r-th tessellation (i.e., in r-th stratum). The choice of resampling strategy is dictated by the requirement of assigning the same number of projection images to each tessellation and thus of imposing an approximately uniform distribution of projection directions over the entire angular range. While conceivably other within-stratum resampling strategies could be used, such as the bootstrap or the jackknife, they would result in the overall uneven distribution of projection data. Selection of m images per tessellation results in a quasi-uniformly distributed resampled set of mR projection images. Subsequently, we compute the corresponding resampled 3D structure. Resampling is independently repeated B times in each stratum (Supplemental Figure S1). Based on these B resamplings, we obtain voxel-by-voxel values of the HGSR variance estimator S2 which, using the Theorem in the Supplement, can be recalculated to yield the voxel-by-voxel variance σ2 , or the “variance volume field”. Briefly, the number of elements shared by each pair out of B m-samples is a hypergeometric random variable. The distribution variance σ2 is related to the expected value of the HGSR variance S2 by the following expression
| (1) |
For details and a derivation, see the Supplemental Information. The variance volume field, in turn, can be used to identify the variance component due to structural variability of the macromolecule (Penczek et al., 2006a). When the variance field reveals localized variability, we follow-up with eigenanalysis of the resampled volumes, which constitutes the first step of the codimensional PCA. Importantly, as both variance and covariance of the resampled volumes are related to those of the sample by the same multiplicative factor, we obtain eigenvectors of the original unknown molecular complexes. For a typical EM structure, the number of elements of the covariance matrix equals the number of voxels in 3D structure squared, i.e., ~(1003)2 = 1012, which is very large. However, we are interested in a very small subset of dominating eigenvectors, which we compute using our MPI-parallelized implementation of the implicitly restarted “out-of-core” Lanczos iterative algorithm (Parlett, 1980), which does not require explicit formation of the covariance matrix. The selected eigenvectors, after rearrangement of the elements into a 3D space, become eigenvolumes that are used in the second step of the codimensional PCA to compute factorial coordinates of 2D projection images. This is accomplished by re-projecting the eigenvolumes in the directions of the original EM projection images (determined using 3D projection matching) and computing the inner product between the re-projections and the EM projection data. In Fourier space, it follows from the Central Section Theorem that the so-computed factorial coordinates correspond to the inner products of the Fourier transforms (FTs) of the 2D projection data and appropriate central sections of FTs of eigenvolumes. In a “focused” variant analysis, a 3D mask that defines the region of interest in the structure is also projected in the same directions and the inner products resulting in factorial coordinates, are computed only within the 2D region outlined by the projection of the mask.
Using the procedure described, we accomplish two goals: (1) we obtain factorial coordinates of the 2D data in a common 3D framework of reference spanned by the 3D structure of the molecule; therefore in this representation we can use clustering techniques to split projection data set into subsets corresponding to the 3D conformers of the molecule, and (2) dimensionality of the data set is dramatically reduced as the number of pixels in 2D projections is of the order of 104, while the number of eigenvolumes ordinarily does not exceed 10. In effect, we can rapidly explore various possibilities of splitting the projection data set with the use of the clustering algorithm and, after within-group 3D reconstruction from the projections, investigate the resulting structures. For the structures with reveal features deemed promising, a multi-reference 3D projection alignment is initialized. In the fourth step of analysis, this latter alignment refines both initial group assignments and alignment parameters of projection data, and yields the final structures of the conformers.
Proof of principle
Codimensional PCA contains a number of parameters that have to be determined for each particular data set. In HGSR, we have to set the number of angular regions R (in practice, the angular step that spans them) and the number of projections m to retain per region. The choice is mainly dictated by the non-uniformity of the particular distribution of projection directions. Also, there is a preference to compute the resampled volumes using a possibly large number of projections, i.e., to keep mR close to n, and at the same time to have the projections distributed as uniformly as possible, which requires R to be large. The two requirements are contradictory as for a non-uniform distribution of projections, a large number of approximately equal-sized angular regions results in some of them having very few projections assigned, resulting in small m and small mR, and in the effect in noisy resampled structures. On the other extreme, very small R results in distributions of resampled projections reflecting the original possibly nonuniform distribution, which usuall produces artifactual results. While it is difficult to provide rigorous rules, we established that the choice of R is related to the expected “resolution” of eigenanalysis; this follows from the relation between angular sampling and the resolution of the reconstructed object (Penczek, 2008), which leads to preferable settings of mR ≅ 0.9n and m ≅ 0.9minr nr, whenever possible.
To test the proposed method we generated a test data set based on the atomic coordinates of the ribosome in two different states that differed by the ratchet-like subunit rearrangement (RSR), i.e. the X-ray structure of a ribosomal complex with EF-G in the post-translocational (POST) state (Gao et al., 2009) and the cryo-EM structure of the EF-G containing a pre-translocational intermediate (TiPRE) (Ratje et al., 2010). The latter structure is based on the former and was flexibly docked into the cryo-EM map using the MDFit method. Whereas the POST complex is in the classical ribosome configuration, the TiPRE ribosome is in the rotated configuration with the 30S subunit rotated counterclockwise by ~6° relative to the 50S subunit (Ratje et al., 2010). In addition to this conformational mode we omitted the coordinates of selected ligands to introduce compositional heterogeneity. As a result we obtained a “realistic” mixture of five 70S ribosome structures that differed with respect to conformation and ligands. Specifically, we created three versions of the PRE 70S: one that contained E-site tRNA and had EFG bound, one with E-site tRNA, and one with EFG bound only. For POST 70S we created two versions: first one with two tRNAs (in E-site and P-site) and second one, vacant, with no ligands (Supplemental Table S1). The atomic models were converted to discretized EM electron densities using the voxel size of 4.3Å and the box size of 753 voxels (Supplemental Figure S2).
In order to determine what results could be obtained using Principal Component Analysis (PCA) should the 3D structures of conformers be directly available, we applied PCA to test the structures of the ribosome. We generated 100 copies of the structures, each represented in proportions as specified in Table S1, we added to them white noise resulting in the SNR of 8.0, and then we low-pass filtered them to the 10.7Å resolution (at the Nyquist frequency, the resolution was 8.6Å). PCA yielded two dominant eigenvolumes (i.e., eigenvectors of the problem mapped back into original 3D space), as the eigenvalues for the first four were (in arbitrary units) 113.2, 21.8, 3.6, and 2.7, respectively. The first eigenvalue corresponds to the RSR, the second to the presence/absence of the bound ligands (Supplemental Figure S3). Variance computed directly from the test volumes is quite noisy (Supplemental Figure S3b), as it represents variability due to RSR, substoichiometry of tRNAs and EFG, and the localization of the loop in the back of the 50S subunit. While the locations of tRNAs can be recognized as areas of high variance, their appearance is partly obscured by the residual variability due to RSR. In contrast, the first two eigenvolumes (Supplemental Figure S3c-f) satisfactorily separate two sources of variability, which in our test structures are only weakly coupled: the RSR and binding of ligands. Moreover, the second eigenvolume very sharply represents tRNAs and EFG leaving no doubt as for the two ligands’ substoichiometric binding (Supplemental Figure S3f). K-means clustering was carried out using factorial coordinates corresponding to the first two eigenvolumes and yielded groups that completely agreed with the initial assignments of test volumes.
For the tests of resampling strategies we decided not to add noise to the simulated data in order to have pure representations of the variance and eigenvolumes and recognizing that the 3D reconstruction algorithm itself was a source of “noise” in the resampled volumes. Moreover, the backprojection step induces correlations between voxels of the reconstructed object that manifest themselves in the PCA results and thus are likely to have a major impact on the ability of the codimensional PCA to properly identify variability of the sample (Penczek et al., 2006a). In addition, to obtain a non-uniform distribution of the projection directions typical of ribosome projects, we used Eulerian angles from one of the previously determined structures (Supplemental Figure S4).
The proper test of codimensional PCA began with generating 9,453 noise-free 2D projection images of five test 70S structures. For tessellation we set the angular step to 10.0 degrees yielding R = 211 angular regions and we chose to retain 80% of data in the least populous region, which for the given distribution of angular directions amounted to 3 projection images per region. These setting resulted in resampled volumes computed using 633 projection images each. We used the direct Fourier inversion 3D reconstruction algorithm that employs nearest-neighbor interpolation and 2× oversampling and which allows to calculate rapidly (using the MPI parallelization) of a large number of high-quality reconstructions (Zhang et al., 2008). We generated 11,200 resampled volumes and we computed the average volume, its variance, and eigenvolumes using the resampled volumes low-pass filtered to a 14.3Å resolution (Supplemental Figure S5). The first four eigenvalues were (in arbitrary units) 10.5, 3.4, 3.0, 2.9, which justified using the first two only. The results are in a general agreement with those obtained from the direct analysis of test volumes and demonstrate that the proposed resampling method works properly and, most importantly, yields the same eigenvolumes in the same order as that determined by the eigenvalues obtained using the direct approach.
We note that the variance obtained from the resampled volumes (Supplemental Figure S5b) is of significantly lower quality than the variance obtained directly from the test structures, even taking into account that the latter is quite fragmented (compare with Supplemental Figure S4b). The former is bulky in its central part and the details present in the latter are not resolved. Based on these results we generally conclude that the 3D real space variance as obtained using resampling techniques (bootstrap including), while it provides some indication about localized variability, is not particularly useful to answer detailed questions about the conformational changes in the cryo-EM structures. The reason is the loss of resolving power in the variance field obtained from resampled volumes: any well localized variable region which indeed yields strong variance will be surrounded by a region of increased variability masking any details, as demonstrated by the appearance of bulky region in Supplemental Figure S3b. The fundamental reason is that the resampling approach yields variance that includes, as a major component, the reconstruction algorithm variance (Penczek et al., 2006a), which tends to be high in the regions of sharp edges or isolated features in the reconstructed object. The problem is all but eliminated by the application of the eigenanalysis of the resampled volumes, as evidenced by the excellent agreement between dominating eigenvolumes obtained directly from test structures and from resampled structures. Therefore, in codimensional PCA described here we entirely rely on eigenanalysis and clustering of projections’ factorial coordinates to analyze conformational variability in macromolecules images by EM.
We continued our analysis of test data by computing factorial coordinates corresponding to the first two HGSR eigenvolumes and we performed K-means clustering assuming K = 5 groups. Then we compared the resulting assignment of 2D projections to groups with the original one and determined that 8,042 were assigned properly, which constitutes 85% of the total number (Supplemental Table S2). The main problem was with mixing of projections belonging to the first and the third group, which both contain EFG and differ only by the presence of P-site tRNA (Supplemental Table S1). Clearly, this is a minor difference in comparison to massive RSR-related conformational changes or even to substoichiometry of the EFG, which has much larger molecular mass than the tRNA. However, it is reassuring that the 3D structures computed using K-means assignments were visually indistinguishable from the correct ones. Therefore, we proceeded with multireference alignment accomplished without changing the original Eulerian angles, thus constituting a “pure” form of 3D K-means (Penczek et al., 2006b). As a result, we obtained 100% assignment agreement of 2D projection data with original assignments.
Since the codimensional PCA results presented here were obtained using noise-free projection data with correct Euler angles, and thus no alignment errors, they may indicate practical limits of what can be accomplished using the method. It is difficult to generalize findings as they are certainly influenced by the particular distribution of the Eulerian angles selected for the tests. For example, the poorly resolved presence of the P-site tRNA by cluster analysis of factorial coordinates might be caused by the fact that in addition to a relatively low mass this tRNA is buried within a dense and bulky ribosome, and thus requires high frequency information to be properly identified. Finally, in other applications, the limit of responsiveness of the codimensional PCA will be most likely set by the distribution of projection directions, which is impossible to predict and, if highly non-uniform, will reduce the number of projections used to calculate the resampled volumes, and thus adversely impact the overall resolution of the results. This is further discussed in the Section “Test of stratification settings of HGSR” of the Supplemental Information. However, the main findings are that (1) we were able to obtain the same and identically ordered eigenvolumes as those obtained from direct calculations and that (2) the codimensional PCA results are of sufficient quality to serve as a starting point to multireference alignment. The second point is of utmost importance, as the naïve applications of the K-means algorithm, found in various implementations of the multireference alignment, may be biased by incorrect initial seed volumes, become trapped in local minima and yield artifactual results.
Functional states of T. Thermophilus 70S ribosome complex determined by codimensional PCA
After the encouraging results obtained using the simulated data we tested our new codimensional PCA method using the cryo-EM data. We analyzed a previous data set of 586,329 cryo-EM projection images of the Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex (Schuette et al., 2009). The set was originally processed using a multi-particle refinement strategy (Connell et al., 2008; Penczek et al., 2006b), and shown to contain a conformationally heterogeneous specimen. From the major sub-population (323,688 projection images) a cryo-EM map of the complex could be determined at a 6.4Å resolution (Schuette et al., 2009). However, despite the improvement of the structure by multi-particle refinement leading to a high fidelity map as evidenced by the comparison with the X-ray structure of a very similar complex (Schmeing et al., 2009), residual localized heterogeneity was still present, as indicated by weaker density of E-site tRNA and a disordered and fragmented L1 stalk and the L7/L12 stalk base (SB) region.
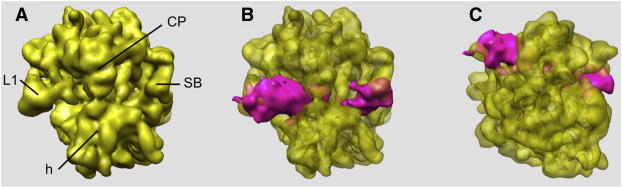
Initially, we decimated the data such that the pixel size was 4.3Å and the window size 75×75 pixels, we realigned them using 3D projection matching, and we used HGSR to compute eigenvolumes. We set the angular step for tessellation to 7.5 degrees, which resulted in R=377 angular regions and we selected to retain 90% of data in the least populous region, which for the given distribution of angular directions amounted to m=365 projection images. These setting resulted in resampled volumes computed using 137,605 projection images each, i.e. 23.5% of the total data. We calculated 100,000 resampled volumes and we computed the average volume, its variance and eigenvolumes using the resampled volumes low-pass filtered to 12Å resolution (Fig.2). We performed K-means clustering using the factorial coordinates derived from the first three dominating eigenvolumes and determined that separation into six groups yields distinguishable and interpretable initial structures (Fig.3). The number of projections images associated were 84,822, 81,037, 99,830, 108,028, 106,452, and 106,160.
Figure 2.
Variance analysis of cryo-EM structure of the Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex. (a) The average structure of resampled volumes computed using HGSR and the data set of 586,329 cryo-EM projections shown in top view. Regions of high variance (magenta) of the 70S complex seen in (b) top view and (c) 30S subunit view. The variability is localized on L1 protein, tRNA within intersubunit space, and the stalk region. CP, central protuberance; SB, stalk base; L1, protein L1; h, head. See also Figures S2-S7 and Tables S1 and S2.
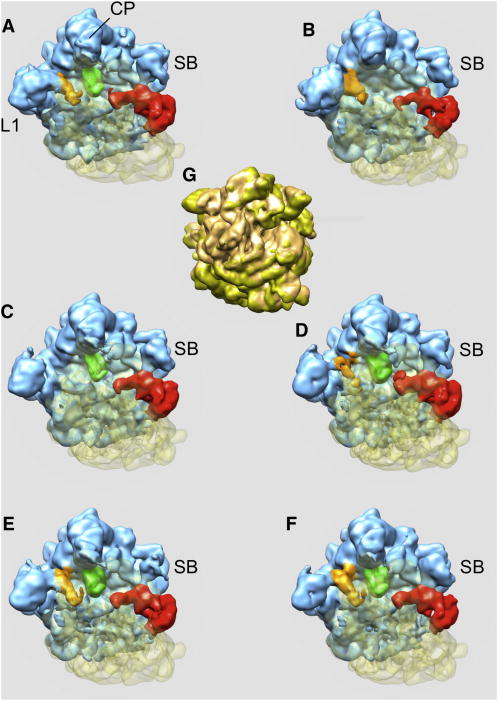
Figure 3.
Six structures derived from the data set of 586,329 cryo-EM projection images of the Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex obtained with K-means clustering using factorial coordinates derived from the first three dominating eigenvolumes and 3D reconstruction according to 2D projection assignments to clusters (a-f). Structures (a,c-f) of the ribosome are in classical conformation, while sub-population (b) is in the rotated conformation (RTS). (g) - RTS between structure (b) shown in light brown and structure (c) shown in gold. CP, central protuberance; SB, stalk base; L1, protein L1. Blue – 50S subunit, transparent yellow – 30S subunit, brown – E-site tRNA, green – P-site tRNA, red – EFG. See also Figures S2-S7 and Tables S1 and S2.
Already at this stage, the main sources of heterogeneity can be recognized. In good overall agreement with our previous multiparticle analysis (Schuette et al., 2009), most of the ribosomes are in a classical unrotated conformation, while one sub-population of ribosomes is found in the rotated conformation, with a tRNA in a P/E hybrid state and the SB in an outer position (Fig. 3b). Also, the weaker density of the SB in another sub-population indicates mobility of this element. Importantly, while the E-site tRNA density in our previous map (Schuette et al., 2009) was weak, this heterogeneity was not resolved by the multi-particle refinement methodology applied at that time. Here, we have one sub-population in the main conformation with EF-Tu and three tRNAs in A/T, P and E sites (Fig.3a) and a second one with EF-Tu and only two tRNAs in A/T, and P sites (Fig.3c). Thus, codimensional PCA clearly distinguishes the populations due to the presence or absence of the E-site tRNA demonstrating a superior resolving power of our new approach.
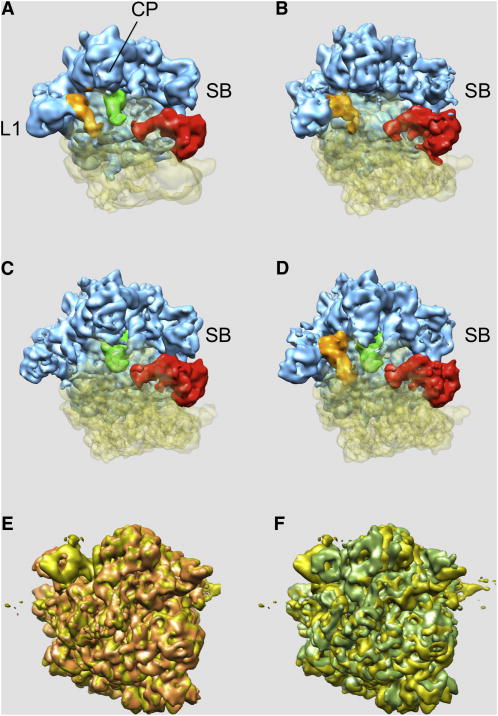
After the initial classification of the data, the E-site tRNA density remained weak in two subpopulations of the main conformation indicating that they still contained mixtures of projection images of ribosomes with and without bound E-site tRNA. We addressed this problem by using the data decimated using a smaller pixel size of 2.44Å and a larger window size of 132×132 pixels and proceeding with multireference alignment initialized with six structures obtained in the previous step. As a result, we obtained four major groups (number 1, 2, 4, and 5) that contained 138,900, 87,641, 133,757, and 113,743 3 projection images, respectively, while groups number 3 and 6 were too small to yield interpretable structures and corresponding images were eliminated from further analysis. The resolution of the four retained groups was 8.9Å, 9.8Å, 8.9Å, and 9.5Å (FSC @0.5 cut-off), respectively (Fig. 4). Two of these final maps represent the Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex in the main conformation with the presence or absence of E-site tRNA density as a distinguishing feature (Fig. 4a,c). As in previous complexes, the presence of the E-site tRNA appears coupled with an inward-movement of the L1 protuberance to allow for the well-established interaction of the L1 protuberance with the elbow of the E-site tRNA. The second sub-population represents the complex in the rotated conformation with a P/E hybrid site tRNA (Fig. 4b). As in the initial map for this sub-population, the SB is in an outer position. Lower density for this feature hints at remaining flexibility.
Figure 4.
Four structures (a-d) derived from the data set of 586,329 cryo-EM projection images of the Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex obtained using multi-particle refinement with six structures shown in Fig. 3 as seeds. Two groups were eliminated, as the number of assigned EM projection data was insufficient to obtain reliable 3D reconstructions. (a, c) - complex in the main conformation distinguished by the presence or absence of E-site tRNA density, also shown as overlap in (e): gold – conformation (a), light brown – conformation (c). (b) -complex in the rotated conformation with a P/E hybrid site tRNA, also shown as overlap in (f): gold – conformation (a), light green – conformation (b). CP, central protuberance; SB, stalk base; L1, protein L1. Blue – 50S subunit, transparent yellow – 30S subunit, brown – E-site tRNA, green – P-site tRNA, red – EFG. See also Figures S2-S7 and Tables S1 and S2.
Interestingly, the SB region is largely disordered in the fourth sub-population and has a very fragmented appearance even at low contour levels (Fig. 4d). Otherwise, the cryo-EM map of the fourth sub-population resembles the main state of the 70S•tRNA•EF-Tu•GDP•kirromycin complex as it includes the E-site tRNA. The major constituents of the stalk base are helices 42, 43 and 44 of 23S rRNA and thus the stalk base is covalently connected to the body of the 50S subunit. Therefore, compositional heterogeneity can be largely excluded and a high mobility of this element remains as the most likely source of the observed disorder. To visualize the conformational mode of the SB region we applied the second phase of codimensional PCA to the data set of this fourth sub-population, this time in a focused mode (Penczek et al., 2006b). We outlined a stalk region using a binary 3D mask and restricted to this region the computation of eigenvectors and subsequent comparisons of projection data with re-projections of the structure in a multiparticle refinement. We computed 23,808 resampled volumes (angular step 7.5 degrees and d=0.1, so that each resampled volume was computed using 5,278 projection images) and we performed K-means clustering using the factorial coordinates derived from the first three dominating eigenvolumes. We used the corresponding 3D structures as seeds in a multireference alignment scheme in which, in order to prevent collapsing of groups we enforced the same number of projection data per structure (18,949 images). Finally, we performed a within-group 3D projection alignment. As a result, we obtained six structures with resolutions ranging between 15.3 and 17.9Å (FSC @0.5 cut-off), in which the 70S complex is nearly identical, but which reveal mobility of the stalk base region (Fig. 5).
Figure 5.
Mobility of the stock base (SB) imaged by the focused codimensional PCA and multiparticle alignment of the sub-population shown in Fig. 4d (a-f). (g) - Thermus Thermophilus 70S•tRNA•EF-Tu•GDP•kirromycin complex shown in Fig. 4a with the reference orientation of SB outlined by the dashed blue circle. (a-f) regions of six sub-population of complex shown in Fig.4d corresponding to blue circle in (g) with structure from Fig.4a shown in semi-transparent blue. CP, central protuberance; SB, stalk base; EF-Tu, elongation factor Tu; h - head. See also Figures S2-S7 and Tables S1 and S2 and Supplemental Movie.
The success of the second phase of codimensional PCA in the focused mode is demonstrated by the appearance of a distinct density for the SB region and sometimes even for the attached L7-stalk in the resulting cryo-EM maps. The comparison of the maps reveals mobility of the SB region that is larger and more complex than the previously anticipated two states (the inner and the outer position) (Fig. 5 and the Supplemental Movie). The SB can be seen in outer positions compared to the main state, but also in more inward positions. One sub-population indicates upward movement (Fig. 5f). Movement of the SB region results in dynamic interactions between the SB and the ternary complex. In an extreme inward position (Fig. 5c) with the SB touching the central protuberance of the 50S subunit we note an extended arc-like connection to EF-Tu, similar to that shown in an early cryo-EM work on 70S•EF-G complexes (Agrawal et al., 1999). In an extreme outward position the SB loses its interaction with the elbow of the A/T tRNA (Fig. 5e); instead, we note two interactions with domains 1 and 3 of EF-Tu, respectively.
DISCUSSION
We demonstrated that under test conditions codimensional PCA can recover both the information about variability of the data and the proper assignment of projection data to 3D structures. The former is contained in eigenvolumes derived from PCA of the resampled structures while the latter results from clustering of factorial coordinates. We showed that the results obtained from codimensional PCA performed on projection images match closely those that could be obtained by PCA directly on original 3D structures. This provides clear evidence that when applied to EM data, codimensional PCA can capture variability of biological macromolecules imaged in an electron microscope.
The limitation of the proposed analysis is the signal-to-noise ratio of the EM data. As shown previously, the resampling technique yields estimate of the covariance of the sample, thus the only way to improve the reliability and resolution of the results is to increase the number of collected EM images (Zhang et al., 2008). We anticipate that the recent progress in automation of EM data collection (Lyumkis et al., 2010; Zhang et al., 2009) will make possible to increase he EM data sets such that the potential of codimensional PCA can be fulfilled.
Compared to other computational approaches to sorting the heterogeneous sets of 2D EM projection data, codimensional PCA simplifies the analysis by relying on an initial alignment of the entire data set. Thus, the approach is aimed at single-particle data sets for which the overall 3D structure determination is sensible, i.e., the magnitude of conformational changes or molecular mass of substoichiometric components of the complex is not “too large”. When this is not the case and the sample does not represent structures of the same basic complex, the methodology of single particle as such does not apply and one has to resort to “classify first, align second” strategies. They can either involve biochemical separation of various states present, or initial sorting out of 2D class averages possibly supported by Random Conical Tilt reconstruction (Spahn and Penczek, 2009). If good guesses of initial structures are available, it is also possible to use the multireference alignment schemes, which however introduce a possibility of bias. In the codimensional PCA, as long as the initial alignment of the entire data set is possible, the seed structures emerge from largely objective steps of resampling, eigenanalysis of resampled volumes, calculation of factorial coordinates and clustering, so the risk of a bias towards preconceived notions about the number and structures of conformers is controlled. Given relatively small computational requirements, we anticipate codimensional PCA to become a method of choice in identification and analysis of conformational variability in single particle structural EM.
The ultimate challenge of the codimensional PCA is to detect and visualize conformational variability with the temporal and spatial resolution sufficient to relate the results to those obtained from molecular dynamics simulations using X-ray molecular models and followed by PCA. The eigenvolumes derived from EM analysis reveal possible conformational modes of the structure directly from the experimental data. In order to discern their physical meaning, they need to be related to the eigenvolumes obtained using model calculations. Taken together and possibly augmented by FRET experiments, such analyses will result in a comprehensive picture of large-scale dynamics of macromolecular assemblies.
EXPERIMENTAL PROCEDURES
T. Thermophilus 70S Ribosome Complex Electron Microscopy and Structure Determination
Ribosomal complexes were prepared as described previously (Schuette et al., 2009; Selmer et al., 2006). The sample was frozen onto Quantifoil grids using a Vitrobot (FEI) device. The data ere collected on film on an Tecnai G2 Polara (FEI) electron microscope operating at 300 kV and 39,000× magnification under low dose conditions (~19 e-/Å2). The micrographs were scanned on a D8200 Primscan drum scanner (Heidelberger Druckmaschinen) with a step size of 4.758 μm corresponding to 1.26 Å on the specimen scale.
The Contrast Transfer Function (CTF) defocus values for the micrographs were determined with CTFind (Mindell and Grigorieff, 2003) and subsequently corrected during the structure determination process (Mouche et al., 2001). Ribosomal projection images were automatically identified using the program Signature (Chen and Grigorieff, 2007) and were subsequently screened visually or automatically. The entire data set comprised 586,329 cryo-EM projection images collected from 452 micrographs with assigned defocus values in the range of 0.6–4.0 μm. The published EF-Tu complex had a resolution of 6.4 Å (FSC@0.5 cout-ff) and was generated using projection matching procedures as implemented in the SPIDER software package (Frank et al., 1996) from the major sub-population of 323,688 projection images (Schuette et al., 2009). Codimensional PCA analysis of was performed using implementation in SPARX software package (Hohn et al., 2007).
Implementation
Codimensional PCA described above was implemented in the SPARX package (Hohn et al., 2007) available at http://sparx-em.org/sparxwiki/ together with its essential dependency, EMAN2 (Tang et al., 2007). The system makes use of C++ for compute-intensive code, while Python is used to implement complex higher-level image processing tasks. The link between C++ and Python is generated using the Boost Python Library (Abrahams and Grosse-Kunstleve, 2003). The code is parallelized on a Python level using the Message Passing Interface (MPI). The most computationally intensive part of codimensional PCA is computation of resampled volumes. We use a fast direct Fourier inversion 3D reconstruction algorithm that is based on nearest neighbor interpolation in reciprocal space and incorporates Wiener filter-type correction for the CTF effects and weighting that compensates for uneven distribution of 2D sampling points in Fourier space (Zhang et al., 2008). For efficiency, we begin with padding images with zeroes to twice the size and computing 2D FFTs of input data. The result is stored in a disk buffer (for 100,000 2D projections 64×64 pixels, the size of the buffer is 6.6GB). The resampling is simply parallelizable as each CPU accesses the buffer independently, inserts 2D projection data as needed into 3D Fourier volume, finally computes inverse 3D FFT and stores the resampled volume in a disk file associated with this CPU. Assuming total of 128,000 resampled volumes and 128 CPUs, each file will occupy 1GB of disk space, total ~130GB, and the time of calculations for data sets analyzed here was ~12h. Finally, these files serve as input to Principal Component Analysis implemented as a parallel version (using MPI) of the implicitly restarted Lanczos iterative algorithm for “out-of-core” computation of dominant eigenvectors (Parlett, 1980). We typically restrict ourselves to no more than 10 eigenvectors and the time of calculations did not exceed 0.5h.
Supplementary Material
Highlights.
Codimensional PCA was developed for analysis of EM sample heterogeneity
The method is based on hypergeometric stratified resampling of 2D EM data
It yields correct eigenvectors of 3D data set as represented by its 2D projections
Codimensional PCA correctly indentifies conformers in the EM sample
Acknowledgments
The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing High Performance Computing resources that have contributed to the research results reported in this paper. This work was supported by the National Institutes of Health, grant R01 GM 60635 (to P.A.P.) and the Deutsche Forschungsgemeinschaft (DFG), grant SFB 740 TP (to C.M.T.S.)
Footnotes
SUPPLEMENTAL INFORMATION Supplemental Information includes the proof of relation between the expected value of the HGSR variance and the distribution variance (Eq.1) and description of the tests of codimensional PCA performed using simulated data. Simulated data and test programs described in the Supplemental Information together with detailed tutorial are available at http://sparx-em.org/sparxwiki/codim.
References
- Abrahams D, Grosse-Kunstleve RW. Building hybrid systems with Boost Python. CC Plus Plus Users Journal. 2003;21:29–36. [Google Scholar]
- Agrawal RK, Heagle AB, Penczek P, Grassucci RA, Frank J. EF-G-dependent GTP hydrolysis induces translocation accompanied by large conformational changes in the 70S ribosome. Nat Struct Biol. 1999;6:643–647. doi: 10.1038/10695. [DOI] [PubMed] [Google Scholar]
- Baldwin PR, Penczek PA. The Transform Class in SPARX and EMAN2. Journal of Structural. Biology. 2007;157:250–261. doi: 10.1016/j.jsb.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Chen JZ, Grigorieff N. SIGNATURE: A single-particle selection system for molecular electron microscopy. Journal of Structural Biology. 2007;157:168. doi: 10.1016/j.jsb.2006.06.001. [DOI] [PubMed] [Google Scholar]
- Connell SR, Topf M, Qin Y, Wilson DN, Mielke T, Fucini P, Nierhaus KH, Spahn CM. A new tRNA intermediate revealed on the ribosome during EF4-mediated back-translocation. Nat Struct Mol Biol. 2008;15:910–915. doi: 10.1038/nsmb.1469. [DOI] [PubMed] [Google Scholar]
- Fischer N, Konevega AL, Wintermeyer W, Rodnina MV, Stark H. Ribosome dynamics and tRNA movement by time-resolved electron cryomicroscopy. Nature. 2010;466:329–333. doi: 10.1038/nature09206. [DOI] [PubMed] [Google Scholar]
- Frank J. Three-Dimensional Electron Microscopy of Macromolecular Assemblies. New York: Oxford University Press; 2006. [Google Scholar]
- Frank J, Radermacher M, Penczek P, Zhu J, Li Y, Ladjadj M, Leith A. SPIDER and WEB: processing and visualization of images in 3D electron microscopy and related fields. Journal of Structural Biology. 1996;116:190–199. doi: 10.1006/jsbi.1996.0030. [DOI] [PubMed] [Google Scholar]
- Gao YG, Selmer M, Dunham CM, Weixlbaumer A, Kelley AC, Ramakrishnan V. The structure of the ribosome with elongation factor G trapped in the posttranslocational state. Science. 2009;326:694–699. doi: 10.1126/science.1179709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hohn M, Tang G, Goodyear G, Baldwin PR, Huang Z, Penczek PA, Yang C, Glaeser RM, Adams PD, Ludtke SJ. SPARX, a new environment for cryo-EM image processing. Journal of Structural Biology. 2007;157:47–55. doi: 10.1016/j.jsb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- Lyumkis D, Moeller A, Cheng A, Herold A, Hou E, Irving C, Jacovetty EL, Lau PW, Mulder AM, Pulokas J, et al. Automation in single-particle electron microscopy connecting the pieces. Methods Enzymol. 2010;483:291–338. doi: 10.1016/S0076-6879(10)83015-0. [DOI] [PubMed] [Google Scholar]
- Mindell JA, Grigorieff N. Accurate determination of local defocus and specimen tilt in electron microscopy. Journal of Structural Biology. 2003;142:334–347. doi: 10.1016/s1047-8477(03)00069-8. [DOI] [PubMed] [Google Scholar]
- Mouche F, Boisset N, Penczek PA. Lumbricus terrestris hemoglobin - The architecture of linker chains and structural variation of the central toroid. Journal of Structural Biology. 2001;133:176–192. doi: 10.1006/jsbi.2001.4362. [DOI] [PubMed] [Google Scholar]
- Parlett BN. A new look at the Lanczos-Algorithm for solving symmetric-systems of linear-equations. Linear Algebra and Its Applications. 1980;29:323–346. [Google Scholar]
- Penczek PA. Variance in three-dimensional reconstructions from projections. In: Unser M, Liang ZP, editors. Proceedings of the IEEE International Symposium on Biomedical Imaging. Washington, DC: 2002. pp. 749–752. [Google Scholar]
- Penczek PA. Single Particle Reconstruction. In: Shmueli U, editor. International Tables for Crystallography. New York: Springer; 2008. pp. 375–388. [Google Scholar]
- Penczek PA, Chao Y, Frank J, Spahn CMT. Estimation of variance in single particle reconstruction using the bootstrap technique. Journal of Structural Biology. 2006a;154:168–183. doi: 10.1016/j.jsb.2006.01.003. [DOI] [PubMed] [Google Scholar]
- Penczek PA, Frank J, Spahn CMT. A method of focused classification, based on the bootstrap 3-D variance analysis, and its application to EF-G-dependent translocation. Journal of Structural Biology. 2006b;154:184–194. doi: 10.1016/j.jsb.2005.12.013. [DOI] [PubMed] [Google Scholar]
- Ratje AH, Loerke J, Mikolajka A, Brunner M, Hildebrand PW, Starosta AL, Donhofer A, Connell SR, Fucini P, Mielke T, et al. Head swivel on the ribosome facilitates translocation by means of intra-subunit tRNA hybrid sites. Nature. 2010;468:713–716. doi: 10.1038/nature09547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rye HS, Roseman AM, Chen S, Furtak K, Fenton WA, Saibil HR, Horwich AL. GroEL-GroES cycling: ATP and nonnative polypeptide direct alternation of folding-active rings. Cell. 1999;97:325–338. doi: 10.1016/s0092-8674(00)80742-4. [DOI] [PubMed] [Google Scholar]
- Saff EB, Kuijlaars ABJ. Distributing many points on a sphere. Mathematical Intelligencer. 1997;19:5–11. [Google Scholar]
- Scheres SH, Gao H, Valle M, Herman GT, Eggermont PP, Frank J, Carazo JM. Disentangling conformational states of macromolecules in 3D-EM through likelihood optimization. Nature Methods. 2007;4:27–29. doi: 10.1038/nmeth992. [DOI] [PubMed] [Google Scholar]
- Schmeing TM, Voorhees RM, Kelley AC, Gao YG, Murphy FVt, Weir JR, Ramakrishnan V. The crystal structure of the ribosome bound to EF-Tu and aminoacyl-tRNA. Science. 2009;326:688–694. doi: 10.1126/science.1179700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuette JC, Murphy FVT, Kelley AC, Weir JR, Giesebrecht J, Connell SR, Loerke J, Mielke T, Zhang W, Penczek PA, et al. GTPase activation of elongation factor EF-Tu by the ribosome during decoding. EMBO J. 2009;28:755–765. doi: 10.1038/emboj.2009.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selmer M, Dunham CM, Murphy FV, Weixlbaumer A, Petry S, Kelley AC, Weir JR, Ramakrishnan V. Structure of the 70S ribosome complexed with mRNA and tRNA. Science. 2006;313:1935–1942. doi: 10.1126/science.1131127. [DOI] [PubMed] [Google Scholar]
- Simonetti A, Marzi S, Myasnikov AG, Fabbretti A, Yusupov M, Gualerzi CO, Klaholz BP. Structure of the 30S translation initiation complex. Nature. 2008;455:416–420. doi: 10.1038/nature07192. [DOI] [PubMed] [Google Scholar]
- Spahn CM, Penczek PA. Exploring conformational modes of macromolecular assemblies by multiparticle cryo-EM. Curr Opin Struct Biol. 2009;19:623–631. doi: 10.1016/j.sbi.2009.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang G, Peng L, Baldwin PR, Mann DS, Jiang W, Rees I, Ludtke SJ. EMAN2: An extensible image processing suite for electron microscopy. Journal of Structural Biology. 2007;157:38–46. doi: 10.1016/j.jsb.2006.05.009. [DOI] [PubMed] [Google Scholar]
- van Heel M, Stoffler-Meilicke M. Characteristic views of E. coli and B. stearothermophilus 30S ribosomal subunits in the electron microscope. EMBO Journal. 1985;4:2389–2395. doi: 10.1002/j.1460-2075.1985.tb03944.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Nakamura N, Shimizu Y, Liang N, Liu X, Jakana J, Marsh MP, Booth CR, Shinkawa T, Nakata M, Chiu W. JADAS: a customizable automated data acquisition system and its application to ice-embedded single particles. J Struct Biol. 2009;165:1–9. doi: 10.1016/j.jsb.2008.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Kimmel M, Spahn CM, Penczek PA. Heterogeneity of large macromolecular complexes revealed by 3D cryo-EM variance analysis. Structure. 2008;16:1770–1776. doi: 10.1016/j.str.2008.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.