Abstract
Visual motion cues are one of the most important factors for eliciting animal behaviour, including predator-prey interactions in aquatic environments. To understand the elements of motion that cause such selective predation behaviour, we used a virtual plankton system where the predation behaviour in response to computer-generated prey was analysed. First, we performed motion analysis of zooplankton (Daphnia magna) to extract mathematical functions for biologically relevant motions of prey. Next, virtual prey models were programmed on a computer and presented to medaka (Oryzias latipes), which served as predatory fish. Medaka exhibited predation behaviour against several characteristic virtual plankton movements, particularly against a swimming pattern that could be characterised as pink noise motion. Analysing prey-predator interactions via pink noise motion will be an interesting research field in the future.
For many predatory animals, survival depends on their ability to properly and rapidly identify objects, such as high-value prey. While hunting, a predator has to distinguish living prey from other environmental objects in real time. Naturally, all sensory information is used in this predator-prey interaction, including visual cues, which are an especially important factor in many cases1,2,3,4,5,6. In aquatic ecosystems, for example, selective visual predation by planktivorous fish greatly affects the composition of the zooplankton community7,8. Planktivorous fish select prey based upon numerous visual factors, including the size, visibility, colour, shape, and motion of the plankton9,10,11,12,13. Several previous studies have postulated that the visual motion of zooplankton is the most important for inducing predatory behaviour8,14,15,16.
Only a few studies have examined predation behaviour based on prey swimming patterns; this is mainly due to the difficulty of controlling zooplankton swimming behaviour. In 1995 and 2005, a virtual plankton system, in which computer-generated prey was used to investigate vision in predator animals, overcame such problems and clarified the visual motion patterns affecting the induction of predation behaviour14,15. Bluegill sunfish (Lepomis macrochirus) preferred virtual plankton displaying higher speeds14 or particular temporal motion patterns, such as a spinning motion15. However, mathematical modelling for the underlying spatiotemporal structure of the entire prey motion has not yet been attempted. Therefore, we have statistically analysed the swimming patterns of zooplankton (the water flea Daphnia magna) and determined the validity of the modelling. The predation behaviour of fish (the medaka Oryzias latipes) against computer-generated virtual plankton was studied.
Medaka are known to have highly acute vision, as demonstrated by previous studies on the optomotor response17,18 and open-field testing19. Medaka are omnivorous fish, but dissection studies of their alimentary tracts have revealed that the gastric contents of medaka living in a natural pool contained up to 30% zooplankton and small aquatic insects, suggesting that medaka act as predators of self-moving small animals20. In the freshwater environment of Japan, small Crustacea, including Daphnia, comprise the largest zooplankton population after Rotatoria21, and they play an important role in nourishing invertebrate and vertebrate predators, including medaka. Therefore we used medaka and water fleas (D. magna) as model organisms to study predator-prey interactions.
The majority of zooplankton is known to swim in a random fashion22 with irregular changes in speed and trajectory. This randomly complicated time-series of movements can be analysed by Fourier analysis, in which different wave sources are transformed to different characteristic statistical properties. These properties are called power spectrum densities (PSDs, power distributions in the frequency spectrum) and can be used to distinguish different types of waves. This classification by PSD is named using “colour” terminology, such as white noise (a signal with a flat frequency spectrum), pink noise (a density proportional to the inverse of its frequency) and blue noise (a density that is proportional to its frequency). Colour noises are widely found in nature. Pink noise, for example, has been found in neuron dynamics23. Retinal cells are arranged in a blue noise-like pattern, which yields good visual resolution24. In the present study, zooplankton swimming was classified using Fourier analysis. Computer models of zooplanktons were then generated using an inverse Fourier transformation. Our data suggest an important role for the spatiotemporal motion patterns that are characterised as pink noise.
Results
Motion analysis of D. Magna
Figure 1A shows the swimming pattern of 1 plankton that travelled 334.40 mm from its start position to its end position over a 57 s period (1700 frames, mean speed = 5.87 mm/s). The swimming pattern of D. magna appeared to be a type of irregular walk; the moving distance and direction per frame changed constantly. Occasionally, D. magna suddenly stopped all motion, behaved like a dead particle, and appeared to sink due to gravity.
Figure 1. Motion analysis of D. magna.
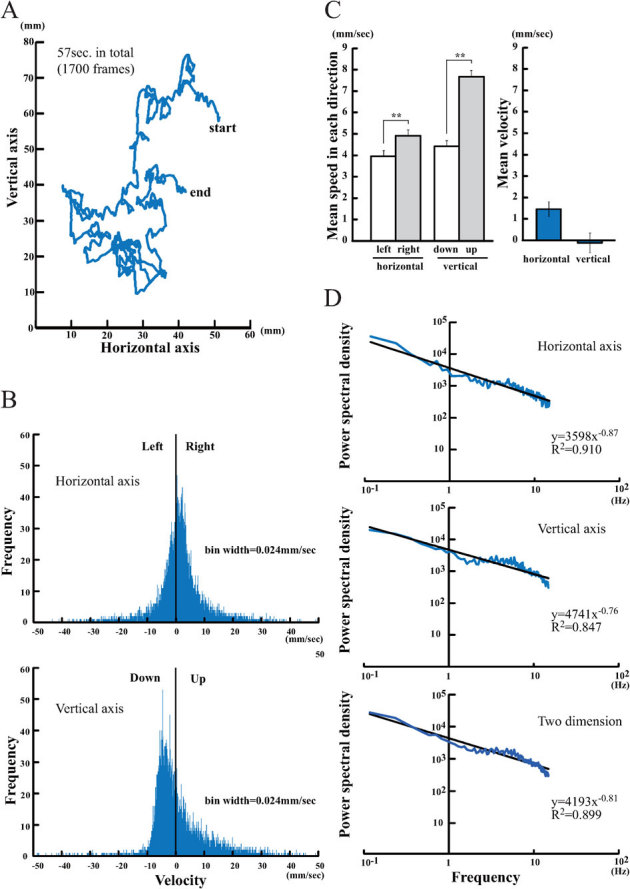
(A) A time series plot of the swimming trajectory of D. magna. In total, 1700 consecutive coordinates (57 s in total) of the calculated mass centre of single representative D. magna were plotted in the vertical-horizontal axes. (B) A frequency histogram of the swimming velocity derived from 12,288 vectors (256 vectors × 48 D. magna). The swimming velocity was calculated separately in the horizontal (right direction as positive value) and vertical (up direction as positive value) axes. (C) Left graph: The mean speed in each direction. Left, right, up-, and downward speeds are shown separately. Right graph: The mean velocity in the horizontal and vertical axes. (D) A log-log plot of the mean PSD of the swimming velocity in the horizontal (top), vertical (middle), and two-dimensional (bottom) axes. The PSDs were extracted from 256 consecutive vectors and averaged (n = 48). Best-fit lines using a power-law approximation are shown in black.
To quantify the swimming pattern of the plankton, coordinate data from the first 257 frames (256 vectors of swimming velocity) of observation were taken for 48 plankton and summarised in Fig. 1B as a frequency distribution of the swimming velocity (12,288 vectors in total). The results clearly illustrate that the frequency distribution has a single peak with wide tails located at either side. However, an asymmetric frequency distribution pattern was found in the vertical direction. Although the distribution frequencies gradually decreased as the speed increased in the upward direction, the distribution frequencies in the downward direction were concentrated at low speeds and formed a single peak around −8.0 mm/s. In contrast, a symmetric frequency distribution pattern was found in the horizontal direction. The distribution frequency gradually decreases as the speed increases in both the left and right directions. These conclusions were also supported by the mean speed in each direction (Fig 1C, left graph). An approximately 2-fold difference in speed was found between the mean speeds in the downward and upward directions (downward, 4.41 ± 0.28 mm/s; upward, 7.67 ± 0.30; p < 0.01, unpaired t-test). A smaller difference was observed between the mean speeds in the left and right directions (left, 3.95 ± 0.27 mm/s; right, 4.92 ± 0.29; p < 0.01, unpaired t-test). A similar result was also found for freshwater copepods (Cyclops abyssorum praealpinus)15. This asymmetric zooplankton motion pattern, including the one shown here for daphnids, reflects a bias to sink rather than to swim downwards25. A pair of swimmerets (the second antennae of D. magna) generates a preferential driving force in the upward direction, and as a result, the main cause of downward motion must be a passive fall due to gravity during akinesis25.
The mean velocity in the vertical direction was not significantly greater than 0 (−0.11 ± 0.46, right panel of Fig. 1C), indicating that plankton neither emerged from the water surface nor sank to the bottom. In the horizontal direction, the mean velocity exhibited a slight preference to the right (1.44 ± 0.34, right panel of Fig. 1C) for an unknown reason. The mean PSD of the swimming velocity is shown in Fig. 1D. Log-log plots of the PSD were inversely proportional to frequency in both the horizontal and vertical directions. The slope values of the PSDs calculated by a power-law approximation were −0.87 and −0.76 in the horizontal and vertical directions, respectively (−0.81 on average).
Behavioural test of medaka
Based on the coordinate data derived from swimming D. magna, we generated a raw data model of virtual plankton in which the swimming patterns of real plankton were faithfully reflected. This model was then used to study the attraction and predation behaviour of fish (Fig. 2). The attraction behaviour of medaka is summarised (n = 13) in Fig. 3A, and the predation behaviour is summarised in Fig. 3B. In the figures, the white bars represent an internal control, which was the mean score of the first minute without visual stimuli in each trial. The effects of visual stimuli presented during the second minute are shown in percentages (the score for the first minute = 100%). In the blank control, no visual stimulus was presented during the second minute either; no significant increase was observed in the second minute compared to the value for the internal control (paired t-test).
Figure 2. Experimental setup and quantification of medaka behaviour.
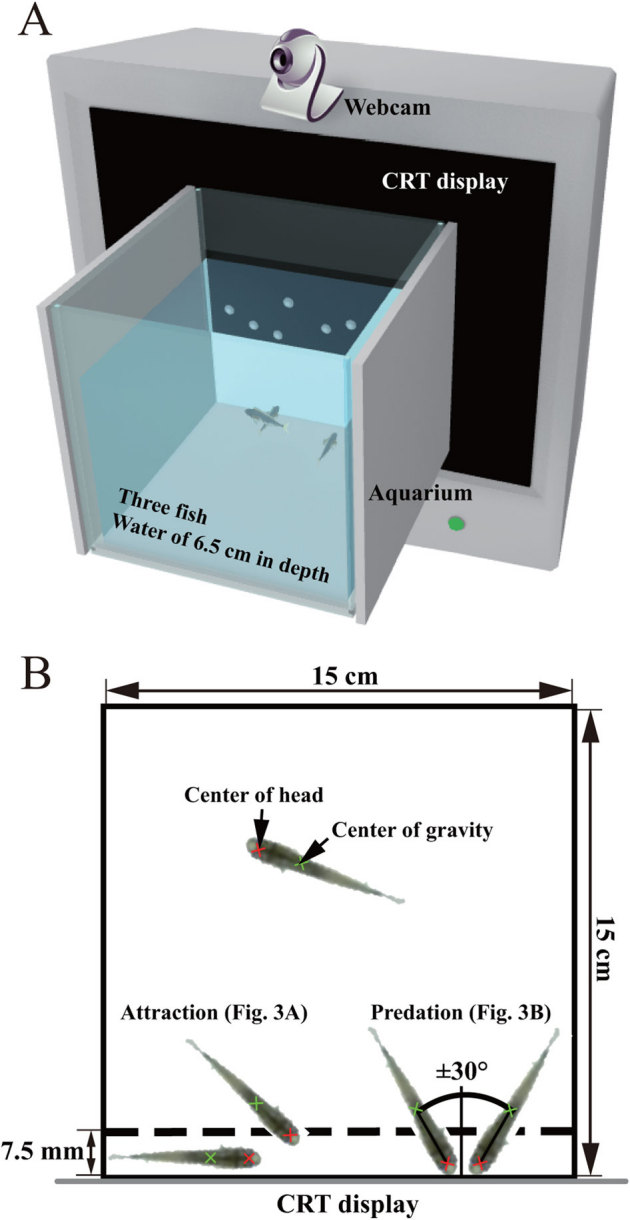
(A) Experimental setup. The test aquarium was attached to a CRT display on which virtual plankton were shown. The behaviours of the 3 fish in the test aquarium as recorded by a webcam placed above the test aquarium. (B) Quantification of medaka behaviour. Motion capture and analysis of the medaka in the recorded movies were performed using computer software. The centres of the head and mass of fish were determined automatically. The angle of the body axis against a line orthogonal to the CRT display side was calculated from the 2 centres. An area 7.5 mm in width from the CRT display was defined as the prey zone. The residence time of the centre of the head in the prey zone was calculated as the measure of the attraction behaviour. The time when the head centre was in the prey zone and the angle of the body axis was within ± 30° was used to calculate the residence time as a measure of predation behaviour.
Figure 3. Attraction and predation behaviour.

Nine types of virtual plankton (raw data, D. magna, slope, speed, 1/f-noise, Gaussian noise, blue noise, constant speed, and stationary dot models) were presented to medaka, and the attraction and predation behaviours were calculated. In the blank control, no virtual plankton were presented. The data shown represents the mean ± SEM. *p < 0.05, **p < 0.01 (2-tailed unpaired t-test with Bonferroni correction). (A) The mean scores of the attraction behaviour. The values are shown as percentages of the mean score of the first minute, in which no visual stimulus was presented. (B) The mean scores of the predation behaviour. The values are shown as percentages of the mean score of the first minute, in which no visual stimulus was presented.
The effects of the raw data model were evaluated by comparisons to the blank control. With regard to predation behaviour, the raw data model score was significantly and drastically higher than that of the blank control (Fig. 3B, unpaired t-test, p = 0.0002, t26 = −4.284), but this was not the case with regard to the attraction behaviour (Fig. 3A). These results indicated that the lingering time for fish at close range to the cathode ray tube (CRT) display did not significantly increase in response to zooplankton movement, although a slight increase was observed. This may be dependent on the visual acuity of fish17,18,19. Predation behaviour better assesses the effect of feeding stimulants as well as the selection method14,15.
We next generated 8 additional types of virtual plankton models in keeping with the characteristic parameters found in the swimming patterns of D. magna: D. magna, slope, speed, 1/f noise, Gaussian noise, blue noise, constant speed, and stationary dots models (refer to Methods). The frequency distributions for the swimming velocity (Fig. 1B), mean speed (Fig. 1C), and/or PSD slope value (Fig. 1D) were used to generate virtual plankton with a circular shape. With regard to attraction behaviour (Fig. 3A), none of the scores from the virtual plankton models were significantly higher than the blank control, again suggesting a lesser potency of attraction behaviour when studying feeding behaviour.
Fig. 3B shows the relative frequency of predation behaviour in each experimental group. A comparison of the frequency of predation behaviour to that of the blank control using an unpaired t-test did not detect significant differences between the Gaussian noise (p = 0.117, t27 = −1.617), blue noise (p = 0.092, t28 = −1.745), constant speed (p = 0.055, t27 = −2.005), and stationary dot (p = 0.243, t28 = −1.193) groups. On the contrary, the D. magna (p < 0.0001, t26 = −5.186), slope (p = 0.0014, t27 = −3.573), speed (p = 0.0004, t27 = −4.04), and 1/f-noise (p < 0.0001, t26 = −5.48) model groups exhibited remarkably high frequencies of predation behaviour towards the virtual plankton. The scores for predation behaviour of these 4 effective virtual plankton were comparable to those from the raw data model.
When the value for the second 1-minute time bin was compared to the value for the internal control of the first 1-minute time bin, a significant increase was observed under every condition except for the blank control and the stationary dots (paired t-test). This statistical analysis indicates whether the moving objects, which suddenly appeared on the display, were more or less attractive to the medaka. Of all of the visual stimuli, the pink noise-containing models had the lowest p-values for predation behaviour (e.g. p = 5.83×10−6, t13 = −7.320 for the D. magna model; p = 8.02×10−6, t13 = −7.103 for the 1/f-noise model; p = 0.041, t13 = −2.274 for the Gaussian noise model; and p = 0.047, t14 = −2.174 for the stationary dots).
Discussion
Signals with PSD slope values close to −1.0 are termed 1/f noise or pink noise. The name arises from falling between white noise (1/f 0) and red noise (1/f2). White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any centre frequency. Red noise is commonly known as Brownian noise, which is the type of signal noise that is produced by Brownian motion, hence its additional name of “random walk noise”. Pink noise is detected from numerous signals that are generated by various natural and artificial processes, and it has been extensively studied in various fields such as electronics26,27, economics28, and psychology29,30. In biological fields, heartbeats31,32, electrocorticograms33,34,35, and current flow in ion channels36,37 exhibit pink noise. Although the mean speed of D. magna was in line with that reported in recent studies38,39,40,41, no prior studies have reported pink noise in D. magna; a random element to Daphnia swimming was previously reported, however15,40.
The common term for the 5 effective types of virtual plankton including the raw data model was pink noise. In particular, the 1/f noise model was reconstructed as a pure mathematical model generated by the phase-locked loop method42, suggesting that pink noise is one of the key components for triggering predation behaviour in medaka. The asymmetric frequency distribution of the swimming velocity found in the vertical direction may not be applicable to predation behaviour, however (Fig. 1B).
Pink noise literally includes noise or random elements. To investigate the effect of such noise and random elements, we examined Gaussian (Gaussian white noise) and blue noise models. Blue noise has a frequency spectrum such that the power spectral density is proportional to the frequency. The scores of predation behaviour for the Gaussian and blue noise models were surprisingly not significantly higher than for the blank control (Fig. 3B) suggesting that noise elements are not critical for predation behaviour. Stochastic resonance is a phenomenon that occurs in a threshold measurement system when an appropriate measure of information transfer is maximised in the presence of a non-zero level of stochastic input noise thereby lowering the response threshold. The resulting system resonates at a particular noise level43. Mechanisms for determining the response threshold of predation behaviour may not be satisfied by only stochastic resonance.
Is predation behaviour tuned to proper specific frequencies within pink noise? This hypothesis was supported by a recent study with virtual plankton15 in which bluegill sunfish (Lepomis macrochirus) preferred a hop-and-sink motion with a fixed hopping rate at a single frequency. Our motion analysis of brine shrimp (Artemia salina), which are commonly used as prey for medaka in aquaria, also indicated that the movement speed was concentrated at a single frequency (10.74 Hz) in both the horizontal and vertical directions (unpublished data). However, the veracity of a hypothesis based only on response to specific frequencies was doubtful. Strickler et al. reported that a significant preference for the hop-and-sink motion was not observed when compared with a liner motion at a constant speed15. The pink noise effect was notably higher than the liner motion model with constant speed (constant speed model), as shown in Fig. 3B. Although care should be taken in interpreting data from one species of fish, fish may not simply prefer a specific frequency. These lines of evidence suggest a view that a matrix of variables with a wide range of low frequencies, represented by pink noise, is important for predation behaviour.
Random motion has been found throughout different species of zooplankton in both fresh water and marine settings44. Along with other species, the velocity fluctuations in the marine zooplankton dinoflagellate (Oxyrrhis marina) appear to indicate pink noise45. The pink-noise model, derived from the prey-predator interactions between D. magna and medaka, may be applicable to prey-predator interactions in wide range of fresh water and marine species. In addition, pink noise phenomena were also found in the trajectories of zebrafish46 and Escherichia coli47,48, suggesting that visual motion with pink noise is one characteristic of biological signals. Therefore, it is intriguing that predators use biological signals that are ubiquitously found in living organisms for effective hunting. Furthermore, the pink-noise idea can be extended to the fishing lure of anglerfish or even the prey-predator interactions of terrestrial animals. Discrete mathematics, as represented by Fourier analysis or fractal analysis49, have been successfully used to express several important natural phenomena. Prey-predator interactions via pink-noise motion are an encouraging field for future research.
Methods
Animals
Medaka (Oryzias latipes, black variety50) were purchased from a local pet shop (Jumbo Encho, Aichi, Japan). They were housed in a 60 L glass aquaria system for at least 7 days before being transferred to the experimental system. The stock populations (50 fish per aquarium) were kept in aerated and filtered water at 26 ± 1°C on a 12/12 h light/dark cycle (lighting on from 08:00–20:00) and were fed an artificial dry diet (Tetra Killifish Food, Tetra Japan, Tokyo, Japan). The fish were fed at 08:30. The holding water was prepared by mixing de-ionised H2O and artificial sea salt (18 g/60 L; Tetra Marine Salt Pro, Tetra Japan, Tokyo, Japan). Adult fish (body weight 250 ± 50 mg) were used for all experiments. After the study, the fish were transferred to a retirement aquaria and are being maintained for another research project. D. magna were kindly donated by Prof. Taisen Iguchi51. The donated plankton were housed immediately after hatching in a 30 L aquarium (20 L of housing water) for 4 days prior to the experiment. The stock populations were maintained in the same conditions as the medaka but without aeration and filtration. A Chlorella suspension (0.3 ml/10 L, Chlorella Industry, Tokyo, Japan) was added to the housing tank as a food source once a day at 08:30. This study was approved by the committee for Animal Experimentation at the National Institutes of Natural Sciences, Japan (approval numbers: 10A044 and 11A019).
Motion analysis of D. Magna
Cuboid glass aquaria [length of inner side: 9.5 cm (horizontal width) × 1.0 cm (horizontal depth) × 9.5 cm (vertical depth)] were used as test tanks for the motion analysis of D. Magna. The aquaria were filled with housing water (with a vertical depth of 8.0 cm). The temperature of the tank water was maintained at 26°C ± 1°C by air conditioning in the experiment room. The bottom of each tank was coated with 1% agarose gel (Nacalai Tesque, Kyoto, Japan) to prevent a reflection of the illumination. The lateral sides of the tanks, excluding the side where the video camera was positioned, were covered with black rubber to prevent excessive illumination. The test tank was placed in a dark room. Illumination at the surface of the water was adjusted to 3000 lux using 3 white florescent lamps placed just outside each vertical tank surface, excluding the side where the video camera was positioned. Ten to 20 D. magna were transferred to the tank, and a digital camera was used to record the motion of the plankton (EXILIM EX-F1, Casio Computer, Tokyo, Japan). The video images (30 fps, 1280 pixels × 720 pixels) were analysed using DIPP-Motion 2D software (DITECT, Tokyo, Japan). The coordinates of the centre of mass of the plankton were automatically tracked in each video frame. Data points where plankton collided against each other or the tank walls were excluded. To accommodate the dimensional limits of the virtual plankton reconstituted on a computer display only two-dimensional coordinates (horizontal-vertical axes) were analysed. The movement distance per frame was calculated from a series of coordinates and converted into the swimming velocity (mm/sec), which was calculated separately for the horizontal axis (right direction as positive value) and vertical axis (up direction as positive value). The swimming speed was calculated as the absolute value of the swimming velocity. A power spectral density (PSD) was extracted from a sequence of 256 swimming velocities and calculated using Fast Fourier Transformation (FFT). The result is shown as the mean PSD of 48 plankton. The slope of the mean PSD (log-log plot) was calculated by a power-law approximation.
Making the virtual plankton
Virtual planktons were presented on a 15-in CRT display with a refresh rate of 70 Hz and a resolution of 1024 × 768 pixels. All stimuli were controlled by Psychlops software (C++ library for developing psychophysical visual stimulus, http://psychlops.sourceforge.jp/en/; please refer to our previous paper52), running on a Windows PC. Visual stimuli were presented within an area of 500 × 230 pixels (130 × 60 mm2; interpixel distance: 0.26 mm) located in the centre of the display. The coordinate at the bottom-left corner of the area was defined as (0, 0). The virtual plankton were drawn using 6 white round dots (80 cd·m−2, Psychlops oval function of 3 pixels in diameter) on a black background. The starting coordinates of the centres of the dots were (65, 100), (145, 100), (225, 100), (275, 100), (355, 100), and (435, 100). The positions of the moving dots were updated every 2 video frames according to numerical sequences in data files in which timeline data for the moving distance per video frame were described (see below). If the virtual plankton exited the area, they re-entered the presentation area from a position diagonal to their exit. The positions of the moving dots were reset to the starting position every 10 s.
To reconstruct virtual plankton on a CRT display, 9 types of numerical sequences were prepared using the following procedure. A value less than the interpixel interval was added to the next value in the progression. New numerical sequences were generated for each trial. The validity of numerical sequences was also examined by motion analysis of virtual plankton as described previously for the motion analysis of D. magna.
1) Raw data model: The raw velocity data of 71 D. magna were randomly connected, and 2 progressions (1 each for the horizontal and vertical axes), each of which consisted of 26,624 numbers, were prepared. In total, 4096 consecutive numbers were randomly clipped from the progressions, and 12 progressions (6 each for the horizontal and vertical directions) were generated. The binding order of the raw data and the 12 progressions were replaced for each trial.
2) D. magna model: Progressions were generated by the Wichmann-Hill algorithm53 referencing the discrete probability distributions of the raw velocity data from D. magna (refer to Fig. 1B). Then, the PSD of each progression was calculated by FFT and transformed to fit a function of y = x−N (N = −0.87 for the horizontal axis and −0.76 for the vertical axis) with a convolution filter54. The mean speed in the horizontal and vertical directions was adjusted to 4.42 and 5.76 mm/s, respectively.
3) Slope model: Progressions consisting of Gaussian random numbers were generated by the Wichmann-Hill algorithm. Then, the PSD of each progression was calculated by FFT and transformed to fit a function of y = x−N (N = −0.87 for the horizontal axis and −0.76 for the vertical axis) with a convolution filter. The mean speed in both the horizontal and vertical directions was adjusted to 5.09 mm/s.
4) Speed model: Progressions consisting of Gaussian random numbers were generated by the Wichmann-Hill algorithm. Next, the PSD of each progression was calculated by FFT and transformed to fit a function of y = x−N (N = −0.81 for both axes) with a convolution filter. The mean speed in the horizontal and vertical directions was adjusted to 4.42 and 5.76 mm/s, respectively.
5) 1/f noise: Progressions for which the slopes of the PSDs (power-law approximation) equalled −1.0 were generated by the phase-locked loop method42. The mean speed in both the horizontal and vertical directions was adjusted to 5.09 mm/s.
6) Gaussian noise: Progressions consisting of Gaussian-distributed random numbers were generated by the Wichmann-Hill algorithm. The mean speed in both the horizontal and vertical directions was adjusted to 5.09 mm/s.
7) Blue noise: Blue noise sequences were generated using Gaussian-distributed random numbers and a convolution filter. The value of N was adjusted to 3.0, and the mean speed in both the horizontal and vertical directions was adjusted to 5.09 mm/s.
8) Constant speed: Each virtual plankton moved with a speed of 5.09 mm/s in a constant direction. The direction of motion was decided by a uniform random number generator (linear congruential generator55).
9) Stationary dot: All virtual plankton maintained their starting positions during the stimulation periods.
Behavioural test for medaka
The experimental setup is shown in Fig. 2A. Cubic glass aquaria (inner side length of 15 cm) were used as test tanks in the medaka behavioural experiments. To restrict the exterior visual stimulation of the fish, 2 lateral sides were covered with white styrene sheets. The test tanks were filled with 1.46 L of medium; the water make up was the same as the housing tank. The vertical depth of the water was 6.5 cm. The tank water was maintained at a temperature of 26°C ± 1°C by air conditioning the experiment room. A total of 142 naïve fish were used for ten types of visual stimuli (the number of fish in each condition is shown in Fig. 3).
First, the test tanks were placed in an anterior area of the recording room. Three naïve fish were randomly selected from stock populations and carefully transferred to the test tank (from 09:00–15:00). Twenty-four hours later, the test tank was moved to the recording room and attached to the CRT display, and the animals were allowed to acclimate for 1 h. The illumination at the bottom of test tank was adjusted to 1500 lux with 2 white florescent lamps that were placed just outside the vertical tank surface. After the acclimation period, the animals' behaviour was recorded from above using a web camera (Qcam-130E; Logicool, Tokyo, Japan) for 2 min. Visual stimuli were presented on the CRT display during the last minute. The resulting video images were stored in the AVI file format (15 fps, 960 × 720 pixels), and analysed using DIPP-Motion 2D software.
A brief overview of the quantification criteria for the fish behaviour is shown in Fig. 2B. The coordinates of the head and mass centres of the fish were automatically tracked in each video frame. The head centre was defined as the centre position of the 2 mass centres of the eyes. The angle of the body axis against a line orthogonal to the inner surface of the tank on the CRT display side was calculated from the coordinates of head and mass centres. An area 7.5 mm in width from the inner surface of the tank on the CRT display side was defined as the prey zone. The width of the area was approximately comparable to the length from the front edge to the root of the pectoral fins of the fish (mean full length of fish: 25.5 ± 3.4 mm, n = 134). The staying time of the centre of the head in the prey zone was calculated as a measure of the attraction behaviour. When the head centre was present in the prey zone and the angle of the body axis was within ± 30°, the residence time was calculated as a measure of predation behaviour. The results of each trial were calculated as the mean values for 3 fish. The statistical significance of the results was determined using paired (2-tailed) or unpaired (2-tailed with Bonferroni correction) t-tests. A cut off of p < 0.05 was used as the threshold for statistical significance. All values are reported as the mean ± SEM.
Author Contributions
W.M. performed and designed the experiments and performed the data analysis. E.W. designed and supervised the experiments and wrote the manuscript. All of the authors reviewed and approved the manuscript.
Acknowledgments
We are grateful to Drs. Taisen Iguchi, Hajime Watanabe, Yasuhiko Kato, and Kenji Toyota for the generous gift of D. magna; to Drs. Hiroshi Hosokawa, Hiroaki Kobayashi and Tomohiro Nakayasu for helpful comments on this manuscript; and to Ms. Mie Watanabe for her technical assistance with preparing the manuscript. The Ministry of Education, Culture, Sports, Science, and Technology of Japan supported this work.
References
- Miklósi A., & Andrew R. J. Right eye use associated with decision to bite in zebrafish. Behav. Brain Res. 105, 199–205 (1999). [DOI] [PubMed] [Google Scholar]
- New J. G., Alborg Fewkes L., & Khan A. N. Strike feeding behaviour in the muskellunge, Esox masquinongy: contributions of the lateral line and visual sensory systems. J. Exp. Biol. 204, 1207–1221 (2001). [DOI] [PubMed] [Google Scholar]
- New J. G., & Kang P. Y. Multimodal sensory integration in the strike-feeding behaviour of predatory fishes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355, 1321–1324 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prete F. R. Stimulus configuration and location in the visual field affect appetitive responses by the praying mantis, Sphodromantis lineola (Burmeister). Vis. Neurosci. 10, 997–1005 (1993). [DOI] [PubMed] [Google Scholar]
- Prete F. R. Hurd L. E., Branstrator D., & Johnson A. . Responses to computer-generated visual stimuli by the male praying mantis, Sphodromantis lineola (Burmeister). Anim. Behav. 63, 503–510 (2002). [Google Scholar]
- Prete F. R. & Mahaffey R. J. Appetitive responses to computer-generated visual stimuli by the praying mantis Sphodromantis lineola (Burmeister). Vis. Neurosci. 10, 669–679 (1993). [DOI] [PubMed] [Google Scholar]
- Black A. R. Predator-induced phenotypic plasticity in Daphnia pulex: Life history and morphological responses to Notonecta and Chaoborus. Limnol. Oceanogr. 38, 986–996 (1993). [Google Scholar]
- Brewer M. C., Dawidowicz P., & Dodson S. I. Interactive effects of fish kairomone and light on Daphnia escape behaviour. J. Plankton Res. 21, 1317–1335 (1999). [Google Scholar]
- Egger D. M. The nature of prey selection by planktivorous fish. Ecology , 58, 46–59 (1977). [Google Scholar]
- Gerking S. D. Feeding Ecology of Fish. Academic Press, New York (1994). [Google Scholar]
- Ingle D. Vision: the experimental analysis of visual behaviour. In W.S. Hoar & D. J. Randall (Eds.), .Fish physiology, Vol. V. (pp. 59–77). Academic Press, New York (1971). [Google Scholar]
- Li K. T., Wetterer J. K., & Hairston N. G. Fish size, visual resolution, and prey selectivity. Ecology 66, 1729–1735 (1985). [Google Scholar]
- Ware D. M. Risk of epibenthic prey to predation by rainbow trout (Salmo gairdneri). J. Fish. Res. Board Can. 30, 787–797 (1973). [Google Scholar]
- Brewer M. C., & Coughlin J. N. Virtual plankton: A novel approach to the investigation of aquatic predator-prey interactions.Mar. Freshwat. Behav. Physiol. 26, 91–100 (1995). [Google Scholar]
- Strickler J. R. et al. A. Visibility as a factor in the copepod - planktivorous fish relationship. Scientia Marina, 69, 111–124 (2005). [Google Scholar]
- Zaret T. M. The effect of prey motion on planktivore choice. In W. C. Kerfoot, (Eds.), .Evolution and Ecology of Zooplankton Communities, (pp. 594–603). The University Press of New England, Hanover, NH (1980). [Google Scholar]
- Beck J. C., Gilland E., Tank D. W., & Baker R. Quantifying the ontogeny of optokinetic and vestibuloocular behaviours in zebrafish, medaka, and goldfish. J. Neurophys. 92, 3546–3561 (2004). [DOI] [PubMed] [Google Scholar]
- Carvalho P. S. M., Noltie D. B., & Tillitt D. E. Ontogenetic improvement of visual function in the medaka Oryzias latipes based on an optomotor testing system for larval and adult fish. Anim. Behav. 64, 1–10 (2002). [Google Scholar]
- Matsunaga W., & Watanabe E. Habituation of medaka (Oryzias latipes) demonstrated by open-field testing. Behav. Processes 85, 142–150 (2010). [DOI] [PubMed] [Google Scholar]
- Watanabe K., Azuma A., & Mizota C. Effect of difference habitat for growth and food habit of medaka, Oryzias latipes. [in Japanese] .The Japanese Society of Irrigation, Drainage and Rural Engineering, sppl. 968–969 (2008). [Google Scholar]
- Morishita C., & Ohtaka A. Zooplankton community structure in the Byobu-san Lakes, Aomori Prefecture, northern Japan [in Japanese]. Bulletin of the Faculty of Education, Hirosaki University, 101, 41–53 (2009). [Google Scholar]
- Seuront L., Brewer M. C. & Strickler J. R. Quantifying zooplankton swimming behavior: the question of scale. Handbook of scaling methods in aquatic ecology: Measurement, Analysis, Simulation. CRC Press, New York, NY. 33–359 (2003). [Google Scholar]
- Sobie C., Babul A., & de Sousa R. Neuron dynamics in the presence of 1/f noise. Phys. Rev. E 83, 051912 (2011). [DOI] [PubMed] [Google Scholar]
- Yellott J. I. Jr. Spectral consequences of photoreceptor sampling in the rhesus retina. Science 221, 382–385 (1983). [DOI] [PubMed] [Google Scholar]
- Haury L., & Weihs D. Energetically Efficient Swimming Behaviour of Negatively Buoyant Zooplankton. Limnol. Oceanogr. 21, 797–803 (1976). [Google Scholar]
- Rubiola E., & Giordano V. On the 1/f frequency noise in ultra-stable quartz oscillators. IEEE Trans Ultrason. Ferroelectr. Freq. Control 54, 15–22 (2007). [DOI] [PubMed] [Google Scholar]
- Weissman M. B. 1/f noise and other slow, nonexponential kinetics in condensed matter. Rev. Mod. Phys. 60, 537–571 (1988). [Google Scholar]
- Gontis V., & Kaulakys B. Modeling long-range memory trading activity by stochastic differential equations. Physica A: Statistical Mechanics and its Applications, 382, 114–120 (2006). [Google Scholar]
- Farrell S., Wagenmakers E. J., & Ratcliff R. 1/f noise in human cognition: Is it ubiquitous, and what does it mean? Psychon. Bull. Rev. 13, 737–741 (2006). [DOI] [PubMed] [Google Scholar]
- Thornton T. L., & Gilden D. L. Provenance of correlations in psychological data. Psychon. Bull. Rev. 12, 409–411 (2005). [DOI] [PubMed] [Google Scholar]
- Aoyagi N., Struzik Z. R., Kiyono K., & Yamamoto Y. Autonomic imbalance induced breakdown of long-range dependence in healthy heart rate. Methods Inf. Med. 46, 174–178 (2007). [PubMed] [Google Scholar]
- Beckers F., Verheyden B., & Aubert A. E. Aging and nonlinear heart rate control in a healthy population. Am. J. Physiol. Heart Circ. Physiol. 290, H2560–H2570 (2006). [DOI] [PubMed] [Google Scholar]
- Allegrini P. et al. Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E: Stat. Nonlin. Soft Matter Phys 80, 061914 (2009). [DOI] [PubMed] [Google Scholar]
- Freeman W. J., & Zhia J. Simulated power spectral density (PSD) of background electrocorticogram (ECoG). Cogn. Neurodyn. 3, 97–103 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- West B. J., Geneston E. L., & Grigolini P. . Maximizing information exchange between complex network. Phys. Rep. 468, 1–99 (2008). [Google Scholar]
- Bezrukov S. M., & Winterhalter M. Examining noise sources at the single-molecule level: 1/f noise of an open maltoporin channel. Phys. Rev. Lett. 85, 202–205 (2000). [DOI] [PubMed] [Google Scholar]
- Kobayashi M., & Musha T. 1/f fluctuation of heartbeat period. IEEE Trans. Biomed. Eng. 29, 456–457 (1982). [DOI] [PubMed] [Google Scholar]
- Baillieul M., de Wachter B., & Blust R. Effect of salinity on the swimming velocity of the water flea Daphnia magna. Physiol. Zool. 71, 703–707 (1998). [DOI] [PubMed] [Google Scholar]
- Garcia R. et al. Optimal foraging by zooplankton within patches: the case of Daphnia. Math. Biosci. 207, 165–188 (2007). [DOI] [PubMed] [Google Scholar]
- Komin N., Erdman U., & Schimansky-Geier L. Random walk theory applied to daphnia motion. Fluctuation and Noise Letters, 4, L151–L159 (2004). [Google Scholar]
- Ordemann A., Balazsi G., & Moss F. Pattern formation and stochastic motion of the zooplankton Daphnia in a light field. Physica A: Statistical Mechanics and its Applications, 325, 260–266 (2003). [Google Scholar]
- de Bellescize H. La réception synchrone. L'Onde Électrique 11, 230–240 (1932). [Google Scholar]
- Moss F., Ward L. M. & Sannita W. G. Stochastic resonance and sensory information processing: a tutorial and review of application. Clin. Neurophysiol. 115, 267–281 (2004). [DOI] [PubMed] [Google Scholar]
- Seuront L., Hwang J. S., Tseng L. C., Schmitt F. G., Souissi S., Wong C. K. Individual variability in the swimming behavior of the sub-tropical copepod Oncaea venusta (Copepoda: Poecilostomatoida). Mar. Ecol. Prog. Ser. 283, 199–217 (2004). [Google Scholar]
- Bartumeus F., Peters F., Pueyo S., Marrase C., & Catalan J. Helical Levy walks: adjusting searching statistics to resource availability in microzooplankton. Proc. Natl. Acad. Sci. U. S. A. 100, 12771–12775 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nimkerdphol K., & Nakagawa M. Effect of sodium hypochlorite on zebrafish swimming behaviour estimated by fractal dimension analysis. J. Biosci. Bioeng. 105, 486–492 (2008). [DOI] [PubMed] [Google Scholar]
- Bray D., & Bourret R. B. Computer analysis of the binding reactions leading to a transmembrane receptor-linked multiprotein complex involved in bacterial chemotaxis. Mol. Biol. Cell 6, 1367–1380 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zonia L., & Bray D. Swimming patterns and dynamics of simulated Escherichia coli bacteria. J. R. Soc. Interface 6, 1035–1046 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandelbrot B. B. The Fractal Geometry of Nature. W.H. Freeman, New York (1977). [Google Scholar]
- Tanaka M., Kinoshita M., Kobayashi D., & Nagahama Y. Establishment of medaka (Oryzias latipes) transgenic lines with the expression of green fluorescent protein fluorescence exclusively in germ cells: a useful model to monitor germ cells in a live vertebrate. Proc. Natl. Acad. Sci. U. S. A. 98, 2544–2549 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatarazako N., Oda S., Watanabe H., Morita M., & Iguchi T. Juvenile hormone agonists affect the occurrence of male Daphnia. Chemosphere, 53, 827–833 (2003). [DOI] [PubMed] [Google Scholar]
- Watanabe E., Matsunaga W. & Kitaoka A. Motion signals deflect relative positions of moving objects. Vision Res. 50, 2381–2390 (2010). [DOI] [PubMed] [Google Scholar]
- Wichmann B. A., & Hill I. D. Algorithm AS 183: An Efficient and Portable Pseudo-Random Number Generator. Appl. Stat. 31, 188 –190 (1982). [Google Scholar]
- Doetsch G. Die Integrodifferentialgleichungen vom Faltungstypus. Mathematische Annalen 89, 192–207 (1923). [Google Scholar]
- Lehmer D. H. Mathematical methods in large-scale computing units. In: Proceding 2nd Symposium on Large-Scale Digital Calculating Machinery, Cambridge, MA, 141–146 (1949). [Google Scholar]


