A novel survival multifactor dimensionality reduction method for detecting gene–gene interactions with application to bladder cancer prognosis

Abstract

The widespread use of high-throughput methods of single nucleotide polymorphism (SNP) genotyping has created a number of computational and statistical challenges. The problem of identifying SNP–SNP interactions in case–control studies has been studied extensively, and a number of new techniques have been developed. Little progress has been made, however, in the analysis of SNP–SNP interactions in relation to time-to-event data, such as patient survival time or time to cancer relapse. We present an extension of the two class multifactor dimensionality reduction (MDR) algorithm that enables detection and characterization of epistatic SNP–SNP interactions in the context of survival analysis. The proposed Survival MDR (Surv-MDR) method handles survival data by modifying MDR’s constructive induction algorithm to use the log-rank test. Surv-MDR replaces balanced accuracy with log-rank test statistics as the score to determine the best models. We simulated datasets with a survival outcome related to two loci in the absence of any marginal effects. We compared Surv-MDR with Cox-regression for their ability to identify the true predictive loci in these simulated data. We also used this simulation to construct the empirical distribution of Surv-MDR’s testing score. We then applied Surv-MDR to genetic data from a population-based epidemiologic study to find prognostic markers of survival time following a bladder cancer diagnosis. We identified several two-loci SNP combinations that have strong associations with patients’ survival outcome. Surv-MDR is capable of detecting interaction models with weak main effects. These epistatic models tend to be dropped by traditional Cox regression approaches to evaluating interactions. With improved efficiency to handle genome wide datasets, Surv-MDR will play an important role in a research strategy that embraces the complexity of the genotype–phenotype mapping relationship since epistatic interactions are an important component of the genetic basis of disease.

Introduction

With the advent of genome-wide analyses, the view that the genetic basis of a common human disease can be explained by sequence variation in a few discrete genes has been recently replaced by a new appreciation for the complexity of the biological networks and the interplay between proteins that jointly influence phenotypes. The recent advances in high-throughput genotyping techniques have made large quantities of genotype data commonplace in genetic epidemiology studies. Single nucleotide polymorphisms (SNPs) can modify many phenotypes, including cancer risk, responses to varying levels of drugs, and survival outcomes. Researchers have analyzed these data for single SNP effects and are now embracing the challenge of identifying SNP–SNP interactions.

The problem of identifying multiple SNP effects in a case–control study, which can be formulated as predicting binary outcomes, has been studied extensively and demonstrated great promise in recent years (Ritchie et al. 2001; Park and Hastie 2008; Huang et al. 2004). Comparative studies (He et al. 2009; Ritchie et al. 2003) through extensive simulation showed that multifactor dimensionality reduction (MDR) has the best performance when the true multi-SNP effects are non-additive (Ritchie et al. 2001, 2003; Hahn et al. 2003; Hahn and Moore 2004; Moore 2004, 2007; Moore et al. 2006, 2010; Moore and Williams 2009). MDR was developed as a nonpara-metric and model-free data mining method for detecting, characterizing, and interpreting epistasis in the absence of significant main effects in genetic and epidemiologic studies of complex traits such as disease susceptibility. The goal of MDR is to change the representation of the data using a constructive induction algorithm to make non-additive interactions easier to detect using any clas-sification method such as naïve Bayes or logistic regression. In 2006, Generalized MDR (Lou et al. 2007) was proposed to extend MDR algorithm to be applicable to continuous phenotypes.

There have been very few attempts to develop methods that systematically identify SNP–SNP interactions in relation to censored time-to-event data, such as a patient’s survival time following cancer diagnosis or time to cancer relapse. It would be desirable to have models to efficiently detect non-linear high-order interactions in the context of survival analysis. Due to large variability in time to cancer recurrence among cancer patients, studying possibly censored survival phenotypes can be more informative than treating the phenotypes as binary variables.

In a previous study (Andrew et al. 2009), we explored a population-based bladder cancer case–control study dataset using MDR to identify single SNPs and SNP combinations associated with cancer risk. We also identified a few single SNPs that were related to bladder cancer survival using the Cox-regression model. However, due to limitations in the available methods, we were not able to find the SNP–SNP combinations that are associated with bladder cancer survival.

In the current paper, we presented an extension of the MDR algorithm (Hahn et al. 2003) to detect and characterize epistatic interactions in the context of survival analysis. We evaluated the type-I error and power of the proposed method using simulated datasets under different epitasis models. We then applied it to identify SNP–SNP interactions in relation to survival of bladder cancer cases using the population-based study (Andrew et al. 2009) in New Hampshire.

Method

In this section, we introduce log-rank statistics and describe how they can be used in the MDR framework in the context of survival data.

Log-rank test

The log-rank test statistic compares estimates of the hazard functions of two groups at each observed event time. It is constructed by computing the observed and expected number of events in one of the groups at each observed event time. These events are added to obtain an overall summary across all of the time points where there is an event.

Let j = 1,…, J be the distinct times of observed events in either group. For each time j, let N_1j and N_2j be the number of subjects “at risk” (have not yet had an event or been censored) at the start of period j in the two groups, respectively. Let N_j = N_1j + N_2j. O_1j and O_2j are defined as the observed number of events in these two groups, respectively, at time j, and define O_j = O_1j + O_2j. Given that O_j events happened across both groups at time j, under the null hypothesis O_1j has the hyper-geometric distribution with parameters N_j, N_1j, and O_j. The expected value $E_{1j}=O_j\frac{N_{1j}}{N_j}$, with variance $V_j=\frac{(N_j-O_j)O_j{N}_{1j}{N}_{2j}}{(N_j-1)N_j^2}$.

The log-rank statistic compares each O_j to its expected value E_j under the null hypothesis and is defined as:

$$C=\frac{{\sum }_{j=1}^J(O_{1j}-E_{1j})}{\sqrt{{\sum }_{j=1}^J{V}_j}}\sim N(0,1).$$ (1)

MDR algorithm

Traditional MDR is a data reduction (i.e., constructive induction) approach that seeks to identify multi-locus combinations of genotypes that are associated with either high risk or low risk of disease. Thus, MDR defines a single variable that incorporates information from several loci that can be divided into high risk and low risk combinations.

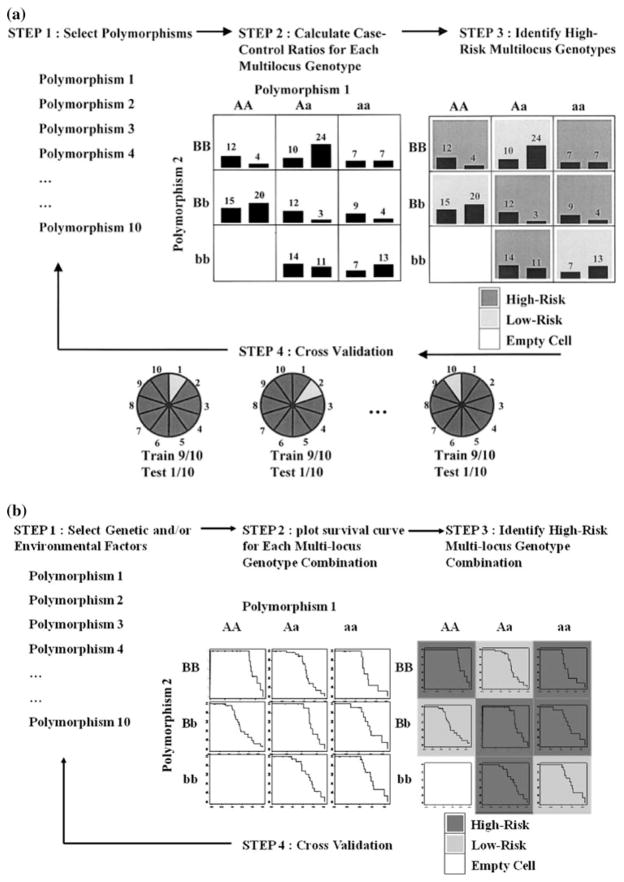
The general process of defining a new attribute as a function of two or more other attributes is referred to as constructive induction or attribute construction and was first described by Michalski 1983. Constructive induction using MDR for binary outcomes (e.g., case–control status) is accomplished in the following way (Fig. 1a, steps 1–3):

Fig. 1.

a MDR attribute construction. Here, we use a threshold T = 1 to determine the high and low risk groups. A new binary attribute is created with those two levels. b Surv-MDR attribution construction. Survival curve in each genotype combination is compared to other genotype combinations to determine the high and low risk groups

1. Assume there are P SNPs in the dataset, for a given number of loci K, select K SNPs from the P SNPs.

2. Construct a contingency table using these K SNPs and calculate case–control ratios for each multi-locus genotype.

3. Let T be the ratio of cases to controls in the whole dataset. For each multi-locus genotype, if the ratio of cases to controls exceeds T, then it is considered high-risk. Otherwise, it is considered low-risk. Once all genotypes are labeled ‘high-risk’ and ‘low-risk’, a new binary attribute is created constructed by pooling the “high risk” genotype combinations into one group and the “low risk” into another group.

The MDR uses a simple probabilistic classifier that is similar to naïve Bayes (Hahn and Moore 2004) to model the relationship between variables constructed using MDR and case–control status. Naïve Bayes classifiers were assessed using balanced accuracy as recommended by Velez et al. (2007). Balanced accuracy is defined as the arithmetic mean of sensitivity and specificity:

$$1/2(\text{TP}/(\text{TP}+\text{FN})+\text{TN}/(\text{TN}+\text{FP}))=(\text{sensitivity}+\text{specificity})/2,$$ (2)

where TP are true positives, TN are true negatives, FP are false positives, and FN are false negatives. For each data-set, MDR evaluates all possible K-way interactions and identifies the best model using balanced accuracy. MDR uses tenfold cross-validation to determine the K loci that give the best model overall (Fig. 1a, step 4):

1. Divide the dataset into ten parts. Use nine-tenth of the data as training set and the rest as testing set.

2. Compute training balanced accuracy for each K-way interaction in the training set.

3. Create a MDR attribute for the testing set using the K SNPs that have the largest training balanced accuracy.

4. Repeat the procedure ten times so that each sample is included in testing set once.

5. Compute the testing balanced accuracy using the new MDR attribute and the case–control status. For the K-way models that are chosen from the training set, record how many times (cross-validation consistency) each is identified as the best model.

The best MDR model was selected as that with the maximum testing accuracy and highest cross-validation consistency. The latter is used as a tie break. If both statistics are tied, then the more parsimonious model is chosen as the best model.

Survival MDR algorithm

Survival MDR (Surv-MDR) extends the MDR algorithm described above to work with censored survival phenotypes. Instead of comparing the case–control ratio of each multi-locus genotype to a fixed threshold T, we propose to use log-rank test statistics to compare the survival distributions of each multi-locus genotype combination and its complement. Constructive induction by Surv-MDR is done as follows (Fig. 1b, steps 1–3):

1. Assume there are P SNPs in the dataset, for a given number of loci K, select K SNPs from the P SNPs.

2. For each multi-locus genotype combination defined by the K SNPs, calculate log-rank test statistics comparing the survival time between samples with and without the genotype combination.

3. If the log-rank test statistic is positive, the corresponding genotype is considered high-risk. Otherwise, it is considered low-risk. Once all genotypes are labeled ‘high-risk’ and ‘low-risk’, a new binary attribute is created by pooling the “high risk” genotype combinations into one group and the “low risk” into another group.

Using log-rank test statistics to determine high or low risk group in a survival setting resembles comparing case–control ratio in the binary outcome setting. When the log-rank test statistic is positive, there are more events observed in the subset defined by the multi-locus genotype combination than expected. Therefore, this genotype is defined as high-risk group. Following the same logic, if the test statistic is negative, the corresponding genotype combination is defined as a low-risk group. Since the log-rank test is model-free, Surv-MDR is also a non-parametric method like MDR. We expect it to have good performance when the true SNP effect is non-additive.

With survival time, we cannot use balanced accuracy to characterize the relationship between the Surv-MDR attribute and phenotype. Instead, we compare the survival time between high and low risk groups defined by the Surv-MDR attribute and use H = C² (C has been defined in Eq. 1) as the score to choose the best model. The cross-validation procedure for Surv-MDR is similar to that used in traditional MDR. The difference is that we define the training score from the log-rank test as H_train (replacing the training balanced accuracy) to determine the best K-order interaction model and use H_test (the testing score) to identify the best overall model. When there is no SNP effect, Surv-MDR attributes from the testing set are randomly assigned to the high or low risk group. Therefore, we expect that H_test’s distribution is close to χ²(1) We tested this hypothesis with simulated data as described below.

The R-functions for Surv-MDR are available upon request.

Simulation study

To demonstrate the strength of the proposed method, we generated simulation datasets with censored survival outcome and two functional interacting SNPs embedded within a set of ten independent SNPs.

We first generated datasets based on different penetrance functions. We developed a total of 40 different penetrance functions that define a probabilistic relationship between a status indicator of high or low risk and SNPs where the outcome is dependent on genotypes from two loci in the absence of any marginal effects. These purely epistatic models were distributed evenly across four broad-sense heritabilities (0.1, 0.2, 0.3, and 0.4) and two different minor allele frequencies (0.2 and 0.4), where all functional SNPs in that data set have either one or the other minor allele frequencies. A total of five models for each of the eight heritability–allele frequency combinations were generated for a total of 40 models. The details of the 70 penetrance functions have been described previously (Velez et al. 2007).

Let f_ij be the element from the ith row and jth column ofa penetrance function. SNP1 and SNP2 are the two functional interacting SNPs. We have:

$$P(\text{high}\text{risk}\mid \text{SNP}1=i,\text{SNP}2=j)=f_{ij}.$$ (3)

We sampled 200 high risk patients and 200 low risk patients from the above probabilistic model to create one simulated dataset and repeat 100 times to get 100 datasets for each model.

Then we simulate the survival time using Cox model:

$$\lambda (t)={\lambda }_0(t)exp(x\beta ).$$ (4)

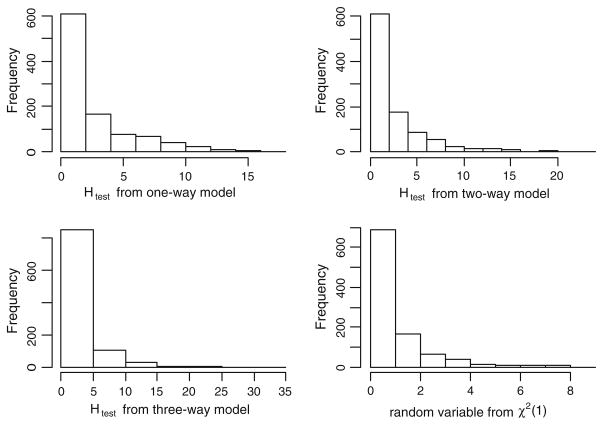
Here x is the status indicator with value 1 for high risk patients, 0 for low risk patients, and β = 1. A Weibull distribution with the shape parameter of 5 and the scale parameter of 2 was used for the baseline hazard function,λ₀(t). A uniform U(0,4) was used to simulate the censoring times. Based on this setting, we would expect about 40% censoring. Finally, we merge survival time and censoring status with the SNP data and remove the status indicator which is treated as a latent variable to associate the SNP effect with the survival time. The goal of this simulation study was to evaluate the type-I error and power of the proposed method. To calculate the type-I error, we randomly picked 25 datasets from each model and removed the functional SNPs to create a total of 1,000 null datasets. We ran Surv-MDR on these datasets and obtained H_test for the top one-, two-, and three-way interaction models. We plotted the histogram of these statistics and compared it with the histogram of 1,000 random variables generated from χ²(1).

To estimate the power of the proposed method, we ran Surv-MDR on all simulated datasets and searched over all possible one-, two-, and three-way interaction models. Then we determined the best model based on the testing score, H_test. We also used the 95th percentile of the testing score from the null models as a threshold to guard against any non-significant findings. The power was estimated as the percentage of times Surv-MDR correctly included the two functional interacting SNPs in the chosen model out of each set of 100 datasets. This result is significant at the 0.05 level. We also ran Cox-regression on the simulated dataset and defined the power as the percentage of times that both the two functional SNPs had univariate p value<0.1. Since many of the high-order interactions have sparse or empty cells, Cox regression has convergence issues when the interaction term is included. The traditional prerequisite for the Cox algorithm to consider an interaction model is the presence of a main effect. In our simulation study, we similarly considered joint detection of the two SNPs with main effects to be successful detection of the functional interaction model.

Real data analysis

We then applied Surv-MDR to a population-based epide-miologic study conducted in New Hampshire to identify SNP–SNP interactions in relation to cancer survival. We identified all cases of bladder cancer among New Hamp-shire residents, ages 25–74 years, diagnosed from July 1, 1994 to December 31, 2001 from the State Cancer Registry. Briefly, we interviewed a total of 857 bladder cancer cases, which was 85% of the cases confirmed to be eligible for the study. Death of cases was determined as of June 15, 2009 using the Social Security and the National Death Indices (NDI). Survival time was calculated using the difference between the earliest date of primary tumor diagnosis and the date of death. The median duration of follow-up was 9.3 years.

Informed consent was obtained from each participant, and all procedures and study materials were approved by the Committee for the Protection of Human Subjects at Dartmouth College. Consenting participants underwent a detailed in-person interview. Questions covered sociod-emographic information, lifestyle factors, such as use of tobacco, and medical history prior to the diagnosis date of the bladder cancer.

We isolated DNA using Qiagen genomic DNA extraction kits (QIAGEN Inc, Valencia, CA, USA) from peripheral circulating blood lymphocyte specimens harvested at the time of the interview. Buccal samples were requested in the case of a refusal. Genotyping was performed on all DNA samples of sufficient concentration using the Cancer Panel on the GoldenGate Assay system by Illumina’s Custom Genetic Analysis service (Illumina Inc., San Diego, CA, USA). The Cancer Panel contains 1,421 SNPs in approximately 400 hypothesized cancer-related genes from the SNP500 database. The assayed SNPs included a combination of the tagging and coding SNPs for each gene. Genotype data were available on 617 of interviewed cases. Samples repeated on multiple GoldenGate plates yield the same call for 99.9% of SNPs, and 99.5% of samples submitted were successfully genotyped. We excluded patients with more than 154 missing genotypes (10%), leaving a set of 532 patients for analysis. We focused this analysis on 203 SNPs that were involved in DNA repair processes by implementing the Database for Annotation, Visualization, and Integrated Discovery (DAVID) Gene Ontology (GO) search engine (http://www.geneontology.org/GO.tools.microarray.shtml).

We then applied our novel Surv-MDR method to this DNA repair SNP dataset to identify the top ten one-way SNP models based on training score, H_train. Then for each of the top ten models, we ran tenfold cross-validation to get the testing score, H_test. Finally, we estimated the empirical p value for these models using the null scores generated from the simulation.

Results

Simulation results

Figure 2 plots the histogram of the test statistics H_test from the one-, two-, and three-way simulated models. We also plotted a histogram of random variables generated from χ²(1)as a comparison. The distributions of H_test from the three models resemble χ²(1) but have larger value than χ²(1) High-order models generated even larger test statistics than the low-order models. The reason lies in cross-validation procedure itself. Since each training set takes 90% of the samples, there is an 80% overlap between any two training sets. Therefore, the Surv-MDR attributes in the testing sets, which are determined by the corresponding training model, are not independent of each other. Moreover, this dependency increases with the model complexity. This shows that we cannot use χ²(1) to estimate the p value of the Surv-MDR model; instead, we should use the empirical distribution.

Fig. 2.

Histograms of the log-rank test statistics from cross-validation. The upper left plot is the statistics from one-way model. The upper right plot is the statistics from two-way model. The lower left plot is the statistics from three-way model. The lower right plot is the random variables from χ²(1)

In Table 1, we summarize the power for Surv-MDR and Cox regression under each minor allele frequency and heritability combination tested in our simulation study. Surv-MDR has good power when heritability is at 0.3 and 0.4. The power for models with heritability at 0.1 and 0.2 is low. Note that the survival time is correlated with the two SNPs combination through a latent risk indicator variable. Therefore, it is much harder to identify the true SNPs pairs than using traditional MDR in the context of a risk analysis when the case–control variable is specified. The Cox regression models had poor power to detect the interactions in all situations. In most cases, the detection is just little better than random selection which has an expected power of 0.1 9 0.1 = 0.01. This result was expected because all SNPs are simulated to have no main effect.

Table 1.

Power comparison on 40 epitasis models

Minor allele frequency	Heritability	Surv-MDR	Cox-regression
0.2	0.4	0.70	0.02
0.2	0.3	0.46	0.014
0.2	0.2	0.18	0.008
0.2	0.1	0.05	0.012
0.4	0.4	0.44	0.016
0.4	0.3	0.32	0.006
0.4	0.2	0.11	0.008
0.4	0.1	0.04	0.004

Bladder cancer study results

We went on to apply our novel survival SNP–SNP interaction detection method Surv-MDR in follow-up data from a population-based study of bladder cancer. In Table 2, we summarize the top one- and two-way models identified by the Surv-MDR. We first used the H_train score to find the top ten one- and two-way models. Then we removed redundant SNPs that were in linkage disequilibrium and identified the two models with the best testing score. We observed that the gene PMS1 was represented in both the one- and two-way models. This indicates that PMS1 has a strong main effect on bladder cancer survival. It also implies that the two-way model is the result of an additive effect of independently associated SNPs, rather than true epistasis effect.

Table 2.

Top two models identified by Surv-MDR

	Training score	Testing score	Empirical p value
One-way models
PMS1_48 rs1233284	10.08	10.08	0.04
PARP1_13 rs747657	6.78	6.78	0.121
Two-way models
FANCA_34 rs2159116 and PMS1_27 rs1233288	24.27	23.52	0.001
ERCC1_05 rs11615 and MSH2_08 rs1863332	21.98	24.90	<0.001

Like MDR, Surv-MDR does not distinguish between multiplicative and additive effects. In an attempt to identify the true epistasis models (i.e., multiplicative effects), we removed the SNPs with significant main effects from the dataset (Cox regression p < 0.05) and re-ran Surv-MDR to detect epistatic effects among the remaining SNPs. In Table 3, we list the top two-way combinations of SNPs without a significant individual main effect. These top two models were obtained using the training and testing scores as in Table 2. We then used Cox regression to assess the main effects and multiplicative interactions for these SNP combinations. The individual Cox regression p values for CCNH_04 (rs3093816) and PCNA_10 (rs17352) are 0.31 and 0.08, respectively, but their combined Surv-MDR testing score through tenfold cross-validation has an empirical p value of 0.006. The likelihood ratio test for the interaction term in the Cox model had a p value of 0.04, indicating a multiplicative effect for this SNP combination (hazard ratio 1.54, 95% CI 1.02–2.32). Thus, Surv-MDR identified an interaction model associated with survival in real data from a human population. Likewise, most of the other Surv-MDR top ranked SNP combinations had multiplicative effects as demonstrated by the likelihood ratio of the interaction term p value: FANCA_34 and PMS1_27 p = 0.004; ERCC1_05 and MSH2_08 p = 0.06; BLM_03 and XRCC4_07 p = 0.04.

Table 3.

Top 2 two-way models restricted to SNPs without significant main effects

Top two-way models	Training score	Testing score	Empirical p value
CCNH_04 rs3093816 and PCNA_10 rs17352	19.56	18.07595	0.006
BLM_03 rs2270132 and XRCC4_07 rs2662238	18.23	11.76173	0.033

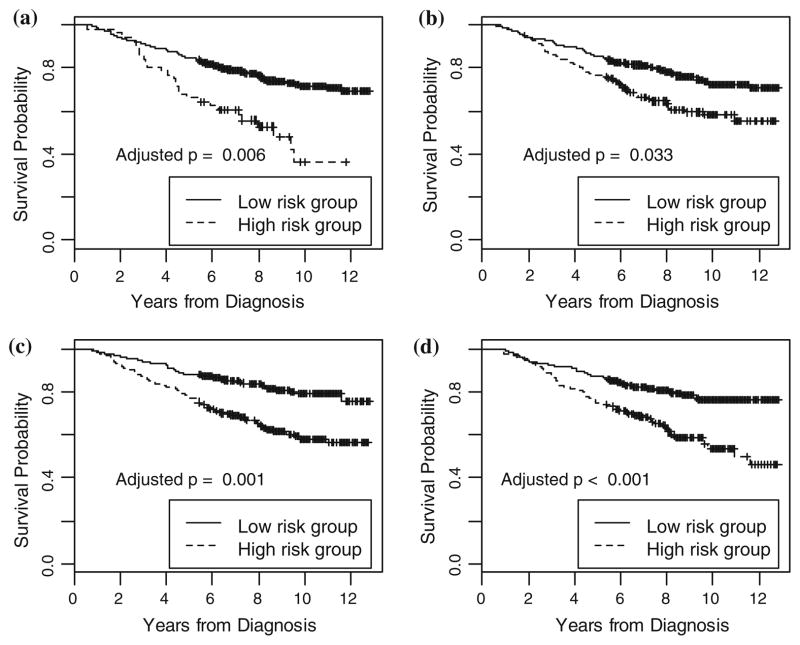
In Fig. 3, we plot the survival curves for the high-risk versus low-risk group patients defined by the Surv-MDR attribute for SNP pairs with significant empirical p values from Tables 2 and 3. We used tenfold cross-validation to first build a training model only using the SNP pair of interest on the training set. Then we applied the model to assign patients into the high or low risk group in the testing set. We repeated this procedure ten times to assign every patient into an appropriate group. Then we constructed the Kaplan–Meier plot of the patients in the high and low risk groups. Figure 3a, b shows CCNH_04 and PCNA_10, and BLM_03 and XRCC4_07, which were selected from Table 3 to represent interaction models with non-additive effect. In Fig. 3c, d, we select two SNP pairs, FANCA_34 and PMS1_27, and ERCC1_05 and MSH2_08 to represent interaction models that have an additive effect. We pooled the patients with different genotype combinations into high or low risk groups to enable simple representation and interpretation of the data. The groups representing these pairs of SNPs separate the two survival curves and are significantly associated with patients’ survival time.

Fig. 3.

Bladder cancer survival in relation to Surv-MDR attribute defined by four SNP pairs. The Surv-MDR attribute in a is defined by SNP CCNH_04 and PCNA_10. The attribute in b is defined by SNP BLM_03 and XRCC4_07. The attribute in c is defined by SNP FANCA_34 and PMS1_27. The attribute in d is defined by SNP ERCC1_05 and MSH2_08

Discussion

In this paper, we present a novel algorithm to identify SNP interactions associated with censored survival outcome or other time-to-event data. To the best of our knowledge, this is the first attempt to extend the well-known MDR method to survival setting. The clear advantage of Surv-MDR is that it uses a non-parametric approach to determine the high or low risk group for genotype combinations. This gives the algorithm the flexibility to handle complex, nonlinear relationships between survival time and SNP effects.

The Surv-MDR also changes the representation of the data by pooling different genotype combinations into a two-level single attribute. This challenges the traditional analysis method of using many dummy variables to represent every genotype combination. Due to limitations in sample size, some of the dummy variables used in traditional models can be very sparse or empty. This makes the modeling of high-order combinations very difficult. Surv-MDR solves this dilemma elegantly by collapsing all high-risk genotypes and all low-risk genotypes into a two-level attribute. This not only makes it easier for the higher order interaction term to be detected, but also makes it possible to incorporate the Surv-MDR attribute into other statistical and machine learning algorithms, such as boosting and neural networks. This will allow us to build more powerful models that involve multiple genotype combinations in the future.

The Surv-MDR also offers a cross-validation procedure to pick the best model based on the testing score. Since high-order interactions tend to have better training scores than low-order interactions, these cross-validation procedures can ensure that the finding is truly an association. The Surv-MDR algorithm also explores the empirical distribution of the testing score from the null models and applies it to estimate the significance of the selected model. From the simulation and real data analysis, we demonstrate that Surv-MDR can detect the presence of multiplicative interaction models even when the main effects are not statistically sig-nificant. These epistatic combinations tend to be missed or dropped when using traditional Cox regression approaches.

The Surv-MDR method identified a number of biologically plausible SNP–SNP interactions that influence the survival of bladder cancer patients in our study. PMS1 is involved in mismatch repair of damaged DNA. Fanconi anemia is an inherited syndrome characterized by defective DNA repair that is associated with genetic variants of FANC family members, including FANCA. The FANCA and PMS1 interactions could be explained by inadequate repair when both of these mechanisms are impaired. Likewise, ERCC1 and MSH2 are involved in the nucleotide excision and mismatch repair processes, respectively. Jointly, low ERCC1 and low MSH2 protein levels were significantly associated with lung cancer survival following chemotherapy treatment, suggesting that a combination of SNPs in these genes may also have a plausible prognostic impact (Kamal et al. 2010).

The top epistatic interactions included cyclin H (CCNH), which controls the mitotic checkpoint during cell division. Proliferating cellular nuclear antigen (PCNA) is involved in the synthesis of DNA during replication in preparation for cell division, as well as in a DNA damage tolerance pathway. PCNA-related proliferation of mammary carcinomas correlated with increased cyclin H protein levels (Qiu et al. 2003). Combined, defects in these two genes might decrease survival by allowing cells to divide through mitosis without proper DNA synthesis or response to damage.

XRCC4 is involved in the non-homologous end joining pathway of repairing double strand breaks in DNA. Sequence variations in the DNA helicase BLM (RECQL2), which unwinds DNA, are associated with chromosome breaks. Inhibited DNA repair would exacerbate the consequences of disrupted unwinding activity as seen in XRCC3 deleted cells with BLM deficiency. A SNP in the BLM-related helicase RECQL1 is associated with reduced pancreatic cancer survival (Seki et al. 2008).

Despite the advantages stated above, Surv-MDR is more computationally demanding than MDR. The current Surv-MDR algorithm is carried out using R (http://www.r-project.org). Run time for Surv-MDR is around 120 min for the analysis of 100 datasets exhaustively exploring all possible one-, two-, and three-way interactions. For the analysis of our bladder cancer study data, it took 20 min to search over all two-way models with 201 SNPs and 532 patients. Considering the anticipated escalation in run time when we increase the number of SNPs and order of interactions, Surv-MDR needs further optimization to make processing data from a genome-wide association study or exploring more than three-way interactions for thousands of SNPs practical. One approach would be to implement Surv-MDR in a more efficient computing language such as C++ or Java to make large-scale implementation feasible in the future.

Another limitation is that the Surv-MDR method does not have a way to adjust for covariate effects such as age, gender, and smoking status. Since those are known to be risk factors for many cancers and other complex diseases, including them in the model would yield better power to efficiently detect SNP combinations without confounding. The incorporation of adjustment for potential confounders could be achieved using Cox regression’s Wald test statistics as a post-hoc analysis, or could be incorporated directly into Surv-MDR instead of log-rank test statistics to determine the high or low risk group in the future.

We anticipate that Surv-MDR will be used to find interactions among other variables, in addition to genotypes. For example, Surv-MDR will facilitate pharmaco-genomic analyses by identifying combinations of drug treatments and genotypes that affect time to progression.

In summary, we demonstrate that Surv-MDR is a promising dimension reduction method for the efficient identification of SNP interactions in a survival setting. We believe that it will play an important role as part of a research strategy to understand genetic influences on disease outcomes that embrace the complexity of the genotype–phenotype mapping relationship.