Phase-sensitive imaging of the outer retina using optical coherence tomography and adaptive optics

Abstract

The cone photoreceptor’s outer segment (OS) experiences changes in optical path length, both in response to visible stimuli and as a matter of its daily course of renewal and shedding. These changes are of interest, to quantify function in healthy cells and assess dysfunction in diseased ones. While optical coherence tomography (OCT), combined with adaptive optics (AO), has permitted unprecedented three-dimensional resolution in the living retina, it has not generally been able to measure these OS dynamics, whose scale is smaller than OCT’s axial resolution of a few microns. A possible solution is to take advantage of the phase information encoded in the OCT signal. Phase-sensitive implementations of spectral-domain optical coherence tomography (SD-OCT) have been demonstrated, capable of resolving sample axial displacements much smaller than the imaging wavelength, but these have been limited to ex vivo samples. In this paper we present a novel technique for retrieving phase information from OCT volumes of the outer retina. The key component of our technique is quantification of phase differences within the retina. We provide a quantitative analysis of such phase information and show that–when combined with appropriate methods for filtering and unwrapping–it can improve the sensitivity to OS length change by more than an order of magnitude, down to 45 nm, slightly thicker than a single OS disc. We further show that phase sensitivity drops off with retinal eccentricity, and that the best location for phase imaging is close to the fovea. We apply the technique to the measurement of sub-resolution changes in the OS over matters of hours. Using custom software for registration and tracking, these microscopic changes are monitored in hundreds of cones over time. In two subjects, the OS was found to have average elongation rates of 150 nm/hr, values which agree with our previous findings.

1. Introduction

Since the emergence of single-cell imaging in the living human retina [1], much of which has employed adaptive optics (AO) [2, 3], the cone photoreceptor has been the most extensively studied cell in the living human retina. AO flood illumination and scanning laser ophthalmoscopy (SLO) have been used to study many properties of the cones, such as: arrangement and packing in normal and defective retinas; changes in reflectance over time; and sampling of the ocular image. The combination of AO with optical coherence tomography (OCT) has permitted cones to be resolved in depth as well, facilitating study of cones’ three dimensional structure [4, 5, 6, 7, 8, 9], waveguiding properties [10], polarization behavior [11, 12], and volumetric changes over time [13].

Recently, AO was combined with temporally coherent flood illumination (AOCFI), effectively turning the bright reflectors that cap the ends of the cylindrical cone outer segment (OS) into an interferometer. This technique, by encoding changes in optical path length as changes in reflectance, permitted observation of OS length changes smaller than the wavelength of the imaging source (800 – 900 nm)–both those in response to visible stimuli [14] and those occurring as part of the cone’s daily cycle of renewal [15].

While sensitive to length changes, AOCFI is unable directly to identify the involved reflections. OCT, by contrast, has the capacity to locate these reflections with a precision of a few microns; both en face time-domain OCT [16] and AO-OCT [17] have been used to detect changes on a corresponding scale. Still, most subcellular changes of interest occur on a much finer scale and go undetected with these OCT methods.

An alternative strategy is to take advantage of the fact that the OCT signal encodes both the intensity and phase of reflections from the retina. Phase-sensitive OCT has been used in ex vivo studies of stabilized samples [18, 19, 20], but has not been applied in the living human retina, since axial motion of the retina–much larger than the wavelength of the imaging source–decorrelates phase between measurements. Other forms of OCT employ phase information as well, but in specific, restrictive ways. Doppler OCT, for example, uses phase differences between neighboring A-lines to compute flow velocity in retinal blood vessels [21, 22, 23], correcting for axial motion by monitoring bulk phase distribution. We propose a method–inspired by AOCFI–that quantifies the phase difference between reflective layers in the retina, which, unlike absolute phase, is immune to decorrelation due to axial motion. We refer to this technique as referenced phase imaging.

Successful application of referenced phase imaging–to measure changes in OS length–requires concerted application of a number of sub-strategies: choice of a suitable reference reflection, spatial phase unwrapping, inclusion criteria for phase averaging, segmentation and registration of OCT volumes, cone identification and tracking, and handling temporal phase wrap.

In this paper we propose and validate such techniques. First, we apply statistical analysis of referenced phase across the cone aperture to determine the instrument’s sensitivity to changes in OS length. Second, we show that phase sensitivity is a function of retinal eccentricity, being higher in the narrower cones near the fovea. Third, we apply the referenced phase method to measurement of length changes in OS over hours. We show that significant phase changes are present, and moreover that they correspond with our previous findings using AOCFI. Fourth, we successfully apply the method outside of the OS, suggesting its potential to measure sub-resolution displacements in other retinal cells and structures. These four goals are addressed by four experiments, detailed in the methods and results sections. An appendix describes additional technical aspects of image processing and phase retrieval.

2. Methods

2.1. Imaging system and protocol

The imaging system has been described in detail elsewhere [7, 24, 13]. In short, the system consisted of an ultra-high resolution spectral-domain OCT (UHR-SD-OCT) system, which provided cellular axial resolution, combined with a woofer-tweeter AO system, which provided cellular lateral resolution. Together they achieved a three-dimensional resolution of 3 × 3 × 3 μm. The AO system incorporated a Shack-Hartmann wavefront sensor, consisting of a CCD (Matrox; Dorval, Quebec, Canada) and a lenslet array (20 × 20), cascaded with an 37-actuator bimorph mirror (AOptix Technologies, Inc.; Campbell, CA, U.S.A.) and a 140-actuator MEMS mirror (Boston Micromachines Corp.; Boston, MA, U.S.A.)–the woofer and tweeter, respectively. The OCT system included a spectrometer, consisting of a transmissive grating and CMOS two-line detector (Sprint; Basler; Ahrensburg, Germany), and a spectrally broadband light source. During the present study, the light source of the OCT system was upgraded, from an SLD (Broadlighter; Superlum Inc.; Moscow, Russia; Δλ = 110 nm, λ_c = 840 nm) to a bandpass-filtered ultrafast Ti:saphhire laser (Integral; Femtolasers; Vienna, Austria; Δλ = 160 nm, λ_c = 800 nm; with filter, Δλ = 81 nm, λ_c = 809 nm). For the SLD and laser, respectively, the line acquisition rates were 125 kHz and 167 kHz. The improved line rate was facilitated by the narrower bandwidth of the filtered Ti:saphhire spectrum, which required readout of a smaller region of the linescan detector. The same narrow spectrum could not be achieved with the SLD due to its lower total output power. Some of the data sets were collected using the SLD and others with the Ti:saphhire laser, as indicated in Table 1.

Table 1.

Subjects imaged in experiments, along with imaging source used. See text for details on which subjects were imaged in which experiments.

Subject	Age	Eye	Rx Sph/Astig (D)★	Imaging source
S1†	23	OD‡	0/0	SLD and Ti:saphhire laser
S2	33	OD	−3.0/0	SLD
S3	21	OD	0/0	Ti:saphhire laser
S4	37	OD	−2.5/0	Ti:saphhire laser

^★Prescription of sphere/astigmatism in diopters.

^†Subject was imaged on multiple occasions.

^‡Oculus dexter (“right eye”).

Four subjects without known eye disease, aged 21 – 37, were imaged. Each subject’s eye was cyclopleged with a single drop of Tropicamide 1% each hour. The subject’s head was stabilized with a bite bar, and defocus and astigmatism were corrected using trial lenses. An illuminated LCD screen, conjugate to the subject’s retina, was used to provide a target for fixation. Unless otherwise noted, volumes were collected at 1.5°, temporal to the fovea along the horizontal meridian. Analyzed volumes subtended 0.6° × 0.6° (180 μm × 180 μm) in lateral dimensions, and were sampled at 1 pixel/μm in each dimension. The eccentricity was selected as a compromise between the number of cones visible (approximately 1300 in the imaged patch) and adequate lateral sampling of each cone (cone area of approximately 22 μm², yielding 21 A-lines for each cone).

The woofer-tweeter system was operated sequentially, with the AOptix mirror frozen after reaching a stable correction, after which the BMC mirror operated in closed loop mode during acquisition of OCT volumes. The large stroke of the AOptix mirror was used to focus the beam on the photoreceptor layer. In all experiments, dynamic correction and focus were sufficient to visualize cone photoreceptors. Volumes were acquired at rates of 3.3 Hz (SLD) and 4.4 Hz (laser) and each acquisition consisted of a series of 15 volumes.

2.2. Image processing and analysis (see appendix for detail)

Software tools for image processing and analysis were developed using Python/NumPy/SciPy (with extensions written in C++) and MATLAB (Mathworks; Nattick, MA, U.S.A.). OCT volumes were segmented and layers identified that corresponded to external limiting membrane (ELM), inner segment outer segment junction (ISOS), posterior tips of outer segment (PT), and retinal pigment epithelium (RPE). En face (“bird’s eye”) projections of the cone mosaic were generated by co-adding intensities from the ISOS and PT layers. The en face projections were used to register volumes to one another, which allowed cones to be tracked over volumes, in spite of the lateral shifts and warp induced, respectively, by motion between and within volumes. Cones were automatically identified in en face projections, and cone coordinates in each volume were recorded. The segmentation, registration, and identification procedures are detailed in the appendix (§A.1, §A.2, and §A.3, respectively). Once a cone’s coordinates were known, A-lines belonging to the cone were selected using multiple conjunct inclusion criteria (detailed in appendix §A.4 and Fig. 10).

Next, we quantified the phase difference between ISOS and PT for individual cones. The optical path length between these layers can be expressed as a distance, as a number of waves (at the imaging wavelength, e.g. 809 nm), or as an angle (number of waves multiplied by 2π radians per wave). The phase of any retinal reflection–or the difference between two such phases–is given as an angle only, and cannot be interpreted as a physical length in the absence of other assumptions. Thus the phase difference between ISOS and PT is the angular separation between the two. We refer to this phase difference as θ_OS, computed as follows:

$${\theta }_{\text{OS}}=\text{mod}\left({\theta }_{\text{PT}}-{\theta }_{\text{ISOS}},2\pi \right)$$ (1)

where θ_PT and θ_ISOS were extracted from the OCT signal. In SD-OCT, the spectrum of the source, which is modulated by interference with structures in the retina, is Fourier transformed. The result of this transformation is a complex A-line, where each complex pixel a + bi represents a phasor Ae^−iθ at a particular depth in the retina. The amplitude of the reflection is computed for all pixels, using $A=\sqrt{a^2+b^2}$, and the resulting A-lines are assembled into a volume as shown in Fig. 1. Next, using the segmented locations of ISOS and PT, the phase of those reflections is retrieved using θ = arctan(b/a).

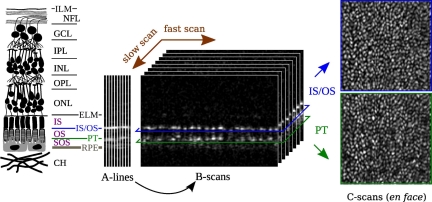
Fig. 1.

Conceptual diagram of OCT imaging. OCT is principally a depth imaging modality. (Left) A diagram showing the layered structure of the retina. The layers pertinent to the present work are the external limiting membrane (ELM), inner segment (IS), inner segment outer segment junction (IS/OS), outer segment (OS), posterior tip of the outer segment (PT), sub-outer segment space (SOS), and retinal pigment epithelium (RPE). (Center) In SD-OCT, each exposure of the detector generates one A-line. These A-lines are assembled, along the dimension of the fast galvo scanner, into B-scans, which in turn are assembled, along the slow scan dimension, into volumetric images. (Right) After axial registration of A-lines, transverse sections of the volumetric image can be extracted, corresponding to en face views of the retina, at various depths. Shown here, for example, are such projections of the ISOS and PT layers.

Because the range of possible observed phase is [0,2π), single phase measurements cannot be unambiguously interpreted as physical lengths. This ambiguity is known as phase wrap, and it impacted the present study in two distinct ways.

First, when computing θ_OS for a single cone, we wanted to average over the cone’s A-lines to reduce the impact of phase noise. If, however, the length of a cone is close to a whole multiple of waves, some A-lines will have phase near 0 and others near 2π. We refer to this as spatial phase wrap, and across A-lines within a cone it complicates statistical analysis and averaging. We describe a technique for spatial unwrapping in the appendix (§A.4). The difference computed in Eqn. 1 compounds the problem of spatial wrap by increasing the range of wrapped differences to 4π, which is why we use mod 2π.

Second, when examining phase changes over time, if two consecutive measurements contain a large jump in phase (close to 2π rad), it is impossible to determine, in the absence of interpretative assumptions, whether the jump represents a large change in the true phase or a small change in the true phase, with the opposite sign. We refer to this ambiguity as temporal phase wrap. In order to assess phase changes over time, we developed methods to overcome temporal phase wrap as well (see appendix §A.5 for details).

Spatial wrap affects both the mean and variance of phase within a cone. Phase standard deviation within a cone is an indication of phase sensitivity, since two measurements on the same cone are generally distinguishable when their difference exceeds the noise within the cone. As such, we define phase sensitivity, σ_θ as the standard deviation of spatially unwrapped phase within a cone. To assess phase sensitivity over a set of cones, we computed the RMS of the phase sensitivities of individual cones. Using the wavelength of the imaging source, λ, and the refractive index of the OS, n_OS (estimated to be 1.43, following [25]), sensitivity to changes in length was calculated as

$${\sigma }_{\text{L}}={\sigma }_{\theta }\lambda /\left(4\pi n_{\text{OS}}\right).$$ (2)

The standard deviation of a random uniform distribution in the range [0,2π) is ${\sigma }_{\text{uncorrelated}}=\sqrt{{\pi }^2/3}=1.814\text{rad}$. We regarded observed standard deviations smaller than this value as being meaningfully interpretable as OS length sensitivities, while the same could not be said of standard deviations close to σ_uncorrelated. The standard deviation of a finite sample of a uniform distribution itself is normally distributed, with a variance related to the number of samples. As such, a 95% confidence interval α can be defined, with respect to σ_uncorrelated, such when σ_OS < σ_uncorrelated – α, we can be 95% confident that the distribution of σ_OS is nonuniform. While we expected σ_θ within cones to be smaller than that of a random, uniform distribution, we expected the distribution of θ_OS across cones to be uniform and random, since there was no reason to expect clustering of OS lengths close to any particular multiple(s) of the imaging wavelength.

2.3. Experiments

Experiment 1. Phase sensitivity in the cone outer segment

σ_θ was measured within cones to assess the instrument’s sensitivity to changes in OS length, σ_L. All four subjects were imaged, each at 1.5° eccentricity, temporal to the fovea. For each subject, a series of 15 volumes was acquired. Cones were automatically identified, A-lines belonging to each cone were selected, θ_OS was computed for each A-line, and these were spatially unwrapped. The effectiveness of unwrapping in improving phase sensitivity was assessed by comparing σ_θ of the wrapped and unwrapped cases. To determine if the distribution of θ_OS within cones was meaningful (i.e. nonuniform), it was compared to a uniform, random phase distribution within [0,2π) using a χ² test. To test if phase variance was significantly larger among cones than within cones, we used ANOVA. Finally, within-cone phase correlation was qualitatively assessed by comparison between two dimensional autocorrelations of en face projections of intensity and referenced phase.

Experiment 2. Eccentricity dependence of phase sensitivity

We sought to determine the eccentricity-dependence of θ_OS sensitivity. One subject (S3) was imaged at five eccentricities, 1.5°, 2.0°, 3.0°, 4.0°, and 5.0° temporal to the fovea, with a series of 15 volumes acquired at each eccentricity. Based on contrast of the projected cone mosaic (quantified as the power spectrum at the cones’ expected spatial frequency), one volume was selected from each series for analysis. Cones were automatically identified, and phase sensitivity within cones (σ_θ) was assessed as in Experiment 1. Assuming each volume was centered about the intended retinal eccentricity, the distance from the foveal center was computed for each cone in each volume, and cones were binned according to distance from the foveal center, in 100 μm increments. The RMS of σ_θ was computed for each bin, giving an indication of phase sensitivity for cones across the volume.

Experiment 3. Phase changes over hours

We sought to observe changes in θ_OS over hours, as such changes are predicted by both our understanding of outer segment renewal and our previous measurements [15]. Two subjects were imaged repeatedly over three or four hours (S1 and S4, respectively, both using the Ti:sapphire source). The first data sets were collected at 9:55 p.m. and 10:41 a.m. for S1 and S4, respectively.

For each measurement, a series of 15 volumes was acquired, and from these a single volume was selected using visual assessment of en face cone mosaic, in terms of low distortion and high cone contrast. The selected volumes, after cone identification and volume registration, represented a time series, in which single cones could be monitored over time. For each cone at each time, a set of values of θ_OS were selected, spatially unwrapped (as in Experiment 1), and recorded for further analysis.

As a first step, for sets of θ_OS within each cone we computed an ANOVA over time, to determine whether statistically significant phase changes occurred. We felt this was an important preliminary step, as it would serve to establish whether subsequent analysis of the rate of phase change was meaningful.

As a second step, we sought to determine the rate of phase change. The major hurdle for assessing the rate of phase change was the presence of temporal phase wrap. We approached this problem with two distinct tacks: (1) unwrapping by fitting to a family of probable linear equations and (2) Lomb-Scargle sinusoidal fitting to the sine of the observed phase. The details of these methods are given in the appendix (§A.5). Once a rate of phase change Δθ_OS/Δt was measured, it, along with the imaging wavelength λ and OS refractive index n_OS, was used to calculate a rate of length change, as follows:

$$\Delta L_{\text{OS}}/\Delta t=\frac{\Delta {\theta }_{\text{OS}}\lambda }{4\pi n_{\text{OS}}}\frac{1}{\Delta t}$$ (3)

Experiment 4. Phase sensitivity outside OS

Thus far, we have described application of referenced phase imaging to the narrow scope of the OS. We are interested, as well, in its application to other cells and structures in the retina. To determine whether it may be applied outside of the OS, we quantified phase sensitivity of the inner segment (IS)–between ELM and ISOS–and sub-outer segment space, between PT and RPE (SOS). Images were acquired on all four subjects and analyzed, much as described in Experiment 1. However, instead of computing referenced phase of the outer segment, we computed referenced phase of the IS and SOS instead. Sensitivity was assessed as described in Experiment 1.

3. Results

3.1. Image processing and analysis

Segmentation of the OCT volume, performed on each A-line, permitted us to generate en face projections of the cone mosaic by co-adding the intensity values found at ISOS and PT for each A-line in the volume. Fig. 2 (left, center) shows examples of these projections, from two volumes in a single acquisition (S1). Registration of volumes to one another allowed en face projections to be averaged. Such averaging improved signal to noise ratio (SNR) and, when an en face image without visible motion artifacts was used as a reference image, removed motion artifacts from the average, improving visibility of the cones. Fig. 2 (right) shows a registered average of the 15 en face images, i.e. 15 images such as the one shown in Fig. 2 (center), using Fig. 2 (left) as a reference. Improved image quality in the average image provides qualitative evidence that the volumes were registered correctly–a key first step in the subsequent tracking of cones.

Fig. 2.

En face projections of the cone mosaic. (Left and center) Single en face projections of the cone mosaic, produced by co-adding the segmented images of ISOS and PT from single volumes, acquired at 1.5°. A registered average (right) using the image on the left as a reference. Scale bars represent 50 μm.

Combining (1) A-line inclusion criteria, (2) spatial unwrapping, (3) registration, and (4) cone tracking permits θ_OS to be monitored for all cones in a series of volumes. Fig. 3 ( Media 1 ^{(5.4MB, AVI)} ) shows a subset of the cones tracked, in intensity (upper left) and phase (upper right). Due to eye motion, not all cones are present in all frames of the video. Cones appearing in a large number of frames were selected for this display, and these are naturally clustered in a portion of the mosaic mostly present in all frames. For quantitative analysis, however, all cones in each frame were tracked. Fig. 3 (bottom) shows stabilized views of the selected cones, arranged in two rows. The top box in each row contains the intensity image (labeled I) and the bottom box in each row contains the θ_OS image (labeled θ). In the stabilized view it appears that θ_OS is correlated among pixels inside the cone aperture in the intensity view.

Fig. 3.

( Media 1 ^{(5.4MB, AVI)} ). Tracking intensity and phase of individual cones over time. (Upper left) An en face projection of the cone mosaic (S1), constructed by co-adding intensities of ISOS and PT pixels for each A-line in the volume. Video shows en face projections from each volume in a series collected over two hours. Colored boxes designate locations of example cones, as they are tracked through the time series. (Upper right) An en face projection of θ_OS, constructed as shown in Equation 1. Colored boxes designate locations of the same example cones shown in the intensity projection. Roughly circular patches of correlated phase are clearly visible in the phase projection. (Bottom) Stabilized views of the example cones shown in the en face intensity and phase projections. In each row of box pairs, the top box shows an enlarged view of the intensity projection and the bottom box shows an enlarged view of the phase projection, as indicated by the I and θ symbols at the left. In the stabilized phase projections excluded pixels are not shown; correlation among included pixels is visually apparent. In the enlarged, stabilized phase projections, many cones do not appear circular. The reasons for this are, presumably, eye motion–which often warps the image of the cone–and segmentation errors–which may cause spurious exclusion of A-lines, leading to shape irregularities and discontinuities.

3.2. Experiment 1. Phase sensitivity in the cone outer segment

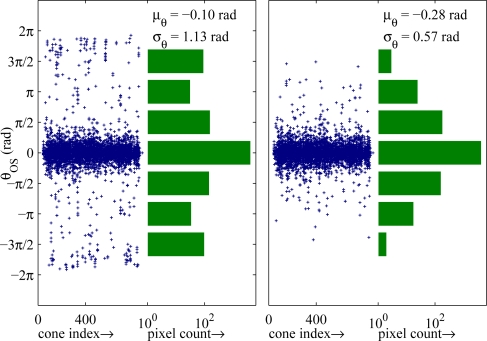
Fig. 4 shows the phase distribution of all cones in a single volume (S2) before (left) and after (right) spatial unwrapping. In each case, the plot shows θ_OS for all A-lines in all cones in the volume, grouped by cones such that each column of points represents the median-subtracted set of θ_OS values from a single cone. In the wrapped distribution (Fig. 4, left) it is evident that in many cones θ_OS is clustered near the edges of the ±2π range, indicating the presence of phase wrap. These are not present in the spatially unwrapped case (Fig. 4, right). The log-scale bar graphs show the marginal phase distribution, and indicates a standard deviation of 1.13 rad in the wrapped case and 0.57 rad in the unwrapped case. Among all subjects and all volumes, the standard deviation of the wrapped phase distribution ranged from 1.1 rad to 1.8 rad. That is, without unwrapping phase, in the worst case the correlation of phase within cones is equal to that of a random uniform distribution (1.814 rad). In the best case, without unwrapping, phase measurements may be pooled from large numbers of cones. However, meaningful measurements cannot be made from a few cones without a robust unwrapping procedure. A clear demonstration of the unwrapping problem is given in Fig. 10 in the appendix. The range of unwrapped standard deviations was 0.48 rad to 1.5 rad, in all cases smaller (p<0.05) than that of a uniform random distribution. The RMS of unwrapped standard deviations, over all cones in all subjects (considering a total of 255,531 A-lines in 26,898 cones), was 1.0 rad. Applying Equation 1 this average σ_θ suggests an OS length sensitivity, σ_L, of 45 nm. In the best single volume σ_L = 23 nm, and over all volumes acquired from the best subject (S1), σ_L = 30 nm.

Fig. 4.

Within-cone phase distributions (S2). (Left, scatter plot) The median-subtracted phase of each pixel in each cone. Each column of points depicts θ_OS within a cone. Spatial phase wrapping is evident in the cluster of points near the ±2π edges of the plot. (Left, bar graph) The marginal histogram of the distribution on left, shown in log scale. The tails of the histogram near ±2π indicate spatial phase wrapping. (Right, scatter plot) The normalized phase of each pixel in each cone, after spatial unwrapping. (Right, bar graph) The marginal histogram of the unwrapped distribution, with noticeable reduction in the tails, which indicates the effect of unwrapping. The wrapped and unwrapped standard deviations correspond to length sensitivities (σ_L) of 53 nm and 27 nm, respectively. μ_θ represents average, median-normalized phase, over all cones.

The distributions of θ_OS in Fig. 4 are visibly nonuniform, and this was confirmed using a χ² test for uniformity. The χ² statistic was computed for the observed θ_OS distribution and an expected uniform distribution over the same range. The χ² statistic was very large, ranging from 410 to 11000, with p < 10⁻⁶ (the probability that θ_OS represents a uniform, random distribution) for all volumes from all subjects. By contrast, the same test for uniformity applied to wrapped phase, yielded a χ² statistic as low as 1.1 (p = 0.79), suggesting that the distribution of wrapped θ_OS, even when median-subtracted and averaged over cones, may be uniform.

We used ANOVA to test whether the differences in θ_OS among cones was significant in comparison to the variance of θ_OS within cones. The F-statistic was very large, ranging from 11.5 to 173, yielding a p < 10⁻⁶ for all volumes from all subjects. This suggests that the observed differences in θ_OS from cone to cone are meaningful, and not due to phase noise. It should also be noted that the F-statistic is highly conservative in this case, since between-group variance is artificially reduced by the [0,2π) wrapped range.

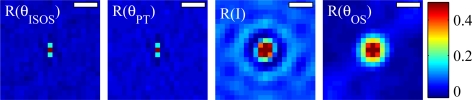
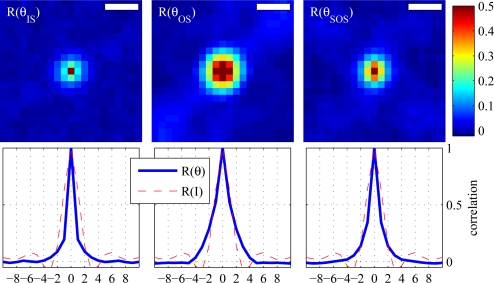
For confirmation that θ_OS was correlated within cones, we computed the autocorrelations of the intensity and phase images. These are shown in Fig. 5. The first two images (far left, near left) show the autocorrelations of en face projections of θ_ISOS and θ_PT, respectively, which are the absolute phase at the corresponding reflections. It is clear from these images that very little phase correlation exists among A-lines, though a small amount can be seen at the pixels above and below the midpoint, parallel to the fast scan direction. This brief vertical phase correlation is likely a consequence of the vertical orientation of the fast scan. Neighboring pixels along the fast scan are acquired in quick succession, separated by only 6 – 8 μs. Axial eye motion–responsible for decorrelating phase across much of the image–must be sufficiently small over these brief time intervals to preserve correlation of phase between neighboring pixels. Two pixels away from the midpoint, the correlation disappears completely.

Fig. 5.

Autocorrelations of ISOS phase, PT phase, intensity, and θ_OS, from left to right; autocorrelations clipped at 0.5 to enhance visibility of correlation tails and zero crossings. The autocorrelations of absolute phase, at ISOS and PT (far left and near left) show a small correlation between neighboring pixels in the direction of the fast scan (vertical), likely due to the brief (6 – 8 μs) interval between acquisition of successive A-lines and correspondingly small amount of axial eye motion. The autocorrelation of intensity (near right) shows a central peak with concentric rings surrounding it, characteristic of the uniformly packed cone mosaic. The spacing of the rings agrees with the expected cone spacing at this eccentricity (1.5°). The autocorrelation of referenced phase, θ_OS (far right) has a central peak similar to that of the intensity autocorrelation, suggesting that θ_OS is correlated among Alines within a cone, but not with neighboring cones. These images provide confirmation of the instrument’s sensitivity to θ_OS. Scale bars represent 5 μm.

Fig. 5 (near right) shows the autocorrelation of an en face intensity projection (S1). It has the stereotypical appearance of a uniformly packed mosaic. The distance between concentric peaks agrees with the predicted cone row spacing of approximately 5 μm [26]. Fig. 5 (far right) shows the autocorrelation of an en face projection of θ_OS. There is substantial agreement between the central peaks of the intensity and phase autocorrelations, but while the intensity autocorrelation has bright, concentric rings surrounding the central peak, the phase autocorrelation lacks any such features. The similarity between central peaks suggests that both intensity and phase are correlated among pixels within the cone, while the dissimilarity between the tails of the autocorrelation suggests that periodicity exists in the intensity image but not in the phase image, which is consistent with our predictions.

3.3. Experiment 2. Eccentricity dependence of phase sensitivity

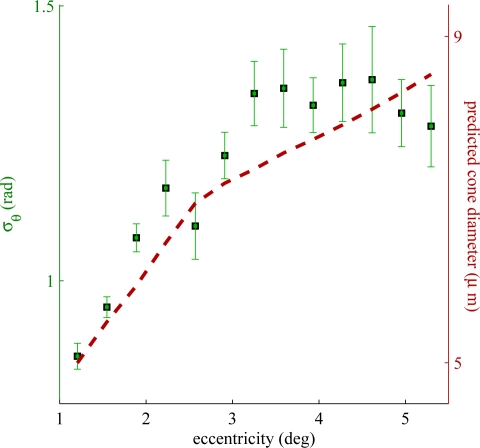
We sought to determine if phase sensitivity in the OS varied with retinal eccentricity, and in particular at eccentricities greater than the 1.5° at which the data in Experiment 1 were collected. Fig. 6 depicts this relationship. The black squares (left axis) show phase sensitivity as a function of retinal eccentricity, indicating a generally positive relationship that appears to plateau around 3.5°.

Fig. 6.

Phase sensitivity as a function of retinal eccentricity, as measured in one subject (S3). Phase sensitivity (black squares) is better near the foveal center, which may be due to structural differences among cones at different eccentricities. It is known that cone diameter increases with retinal eccentricity (see dotted red line), which may be related to the observed differences in sensitivity.

The dotted red line (right axis) shows predicted cone diameter [26] as a function of retinal eccentricity. Up to 4° the two curves show similar eccentricity-dependence–strong near the fovea and weaker outside the fovea.

3.4. Experiment 3. Phase changes over hours

We imaged two subjects (S1 and S4) over several hours, calculating θ_OS for all cones in all volumes, as in Experiment 1. Automated cone identification and tracking permitted θ_OS to be monitored over time.

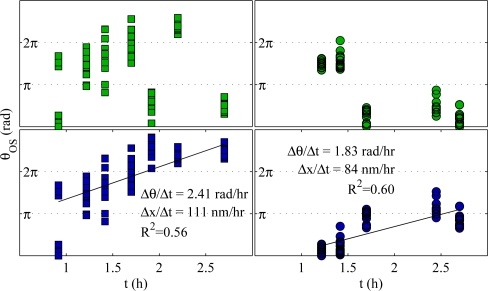
As a first pass, to determine whether statistically significant phase changes were present over time, we employed ANOVA for each cone in each subject. ANOVA, employed this way with respect to time, determines whether differences in average phase over time are significant (α = .01), in comparison to variance of phase within cones at single time points. We found that 97% (S1) and 88% (S4) cones underwent significant phase changes over time.

Figure 7 shows plots of θ_OS over time for two cones from subject S1. For each cone, the temporally wrapped (top) and unwrapped (bottom) values are shown. Temporal unwrapping was performed using the linear fitting method described in the appendix (§A.5). For these two cones, rates of elongation were 111 nm/hr and 84 nm/hr, reasonably consistent with previous findings [15]. Measurements were absent when, in a given volume, the cone was out of view or suffered from a motion artifact. Also, it must be pointed out that at any given time as many as 21 points are shown in the plots (corresponding to the 21 pixels in the circular footprint of the OS); as a result, the precise average phase may be difficult to discern visually.

Fig. 7.

Representative phase changes in two single cones (S1). For each cone, the temporally wrapped data are shown in the top plot (green markers) and temporally unwrapped data shown in the bottom plot (blue markers). In the unwrapped data, linear fits were performed, and the slopes of these fits are shown, expressed as Δθ_OS/Δt and ΔL_OS/Δt. The elongation rates of these two cones, 111 nm/hr and 84 nm/hr, are within the range of our previous findings. Data were temporally unwrapped using a linear model fitting approach, described in the appendix (§A.5).

In these two cones, instances of phase wrapping are apparent (1.9 h and 2.7 h, left, and 1.7 h, right). The linear fitting technique readily identified such instances of wrapping and corrected them accordingly. This was true for many cones in each data set, but examples of unwrapping error were common, and the bulk rate of renewal was consequently indeterminate by this method.

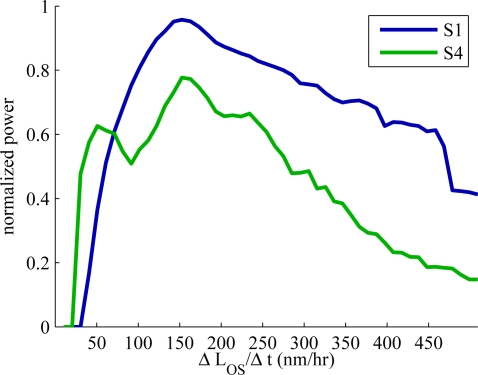
In order to assess the average rate of change over all cones, we performed Lomb-Scargle fitting of the sine of measured phase. In short, it involves computing sin(θ_OS) for each cone, generating its frequency spectrum by sinusoidal fitting, and averaging these spectra. The spectra for S1 and S4 are shown in Fig. 8. The frequency (x) axis of the plot is expressed in terms of rate of length change, ΔL_OS/Δt. The spectra from both subjects have clear peaks at approximately 150 nm/hr. These rates are higher than what was typically observed using AOCFI [15] but within the range of observations made over a larger number of subjects and broader range of retinal eccentricities [27].

Fig. 8.

Frequency spectra of sin(θ_OS), averaged over all cones in each of the two over-hours data sets. The frequency (x) axis has been expressed in terms of rate of OS length change, using Equation 3. Peaks at approximately 150 nm/hr can be seen in both spectra. It is uncertain whether the breadth of the peaks is due to a large range of true frequencies or to fitting noise. Previous experiments [27] found a narrower range of frequencies, which suggests the breadth here may be due to fitting noise.

3.5. Experiment 4. Phase sensitivity outside OS

We applied the same methods described in Experiment 1 to investigate phase sensitivity outside of the OS, in the inner segment (IS) between ELM and ISOS, and the extracellular matrix (SOS) between PT and RPE. We found the distribution of phase in these layers, confined to the same cone apertures used in Experiment 1, to be significantly nonuniform, with σ_θ values of 1.24 rad and 0.88 rad for IS and SOS, respectively, corresponding to σ_L of 56 nm and 40 nm in the best subject (S1). Over all subjects, σ_L was 72 nm and 58 nm for IS and SOS, respectively.

Additionally, we examined autocorrelations of the IS and SOS en face phase projections, which are shown in Fig. 9 (top left and top right, respectively), in comparison to the autocorrelation of the OS en face phase projection (top center). As expected from the phase sensitivities above, the autocorrelations of these projections show local phase correlation. It is clear that SOS exhibits less local autocorrelation than OS, and IS still less, but in both cases the local autocorrelation of phase is better than random, i.e. correlated over more than 1 pixel. The profile of each image is plotted below (blue lines). Superimposed on each profile is the profile of the intensity projection (red, dashed). The important feature in these plots is the first zero. The first zero for θ_OS (center, blue) is at 5 μm. For θ_IS (left, blue) and θ_SOS (right, blue), the first zero occurs at 4 μm.

Fig. 9.

Autocorrelations of θ_IS (left) and θ_SOS (right), as compared to that of θ_OS (center), and profile plots below (blue). Profiles of the intensity autocorrelation (red, dashed) are superimposed on each profile, for comparison. The first zero in each profile plot can be thought of as the correlation width. For θ_OS, the correlation width is 5 μm. For θ_IS and θ_SOS, the correlation widths are both 4 μm. Scale bars represent 5 μm.

4. Discussion

Phase-sensitive AO-OCT is a potentially powerful tool for measuring sub-resolution axial changes in the retinal microstructure. We demonstrated a sensitivity to OS length changes, averaged over subjects, in the cone outer segment of 45 nm–slightly thicker than a single OS disc–and as low as 23 nm in one subject. We demonstrated analogous sensitivities in the IS and SOS of 72 nm and 58 nm, respectively.

4.1. Image analysis and phase retrieval

We developed a set of tools for processing AO-OCT volumes–segmenting and registering them, and identifying and tracking features. The en face projections shown in Fig. 2 qualitatively validate our segmentation technique, since it has been previously noted [7] that only the ISOS and PT reflections possess the characteristic periodic, hexagonally packed appearance of the cone mosaic. Improved image quality in the registered average confirms that volumes were correctly registered to one another.

In the present study a total of 26,898 cones were identified in the projections. As it was impractical to manually verify that the cones were all correctly identified and tracked, a subset of four randomly selected cones was visually checked for each data set. In all cases, the sample cones were confirmed to be correctly tracked by the tracking software.

An example of cone tracking is shown in Fig. 3. For such a large number of cones, efficient and automated algorithms for tracking were critical. These tools will doubtless enable many more studies of cones, and other structures, over time–phase sensitive or otherwise.

4.2. Phase sensitivity and the importance of unwrapping

Before applying referenced phase imaging to the measurement of sub-resolution changes over time we sought to demonstrate that the OS referenced phase θ_OS was a meaningful quantity–namely that θ_OS could be averaged over A-lines within a cone to reduce the impact of phase noise. We determined that the average phase sensitivity over all subjects was σ_θ = 1.0 rad, corresponding to 45 nm. This is a factor of 67 smaller than the 3 μm axial resolution of UHR-OCT.

The problems of distinguishing two reflections in the retina and detecting the movement of one reflection, however, are slightly different, and may be described as problems of resolution and localization, respectively. If the structure of the reflector and coherence function of the OCT are known, and the OCT spectrum is adequately sampled, the precision of localization is limited not by optical resolution but rather by SNR. In a previous study [13] we performed repeated measurements of cone OS length using AO-OCT. In images with SNR of approximately 27 dB we found the standard deviation of such measurements (termed σ_intra–cone) to be 1.41 μm. Those measurements included no fitting or oversampling of the cone’s axial reflectance profile, so a portion of σ_intra–cone may have been due to discretization. Still, these results suggest intensity-based localization precision more than one order of magnitude larger than the present sensitivity of 45 nm.

Figs. 4 and 10 suggest that in order to observe sub-resolution changes in the retina, a method for spatially unwrapping phase is necessary. We demonstrated that spatial unwrapping led to a twofold improvement in sensitivity, averaged over cones, and that in single cones failure to unwrap could generate the worst possible phase errors. We observed further that A-line outer segment length, given by a custom segmentation algorithm, can assist greatly in deciding which A-lines should be used for phase analysis.

4.3. Eccentricity dependence of phase sensitivity

The results of Experiment 2 show that phase sensitivity in the OS varies greatly with retinal eccentricity. Fig. 6 shows that the most precise measurements of θ_OS can be made near the fovea, and also suggests that variations in cone structure (such as OS diameter) may impact phase sensitivity. Interestingly, this result accounts for the resolution tradeoff at low eccentricities–the smaller cone diameter near the fovea is closer to the diffraction limit, but does not appear to negatively impact phase correlation, at least down to 1°.

Low phase variance is likely intimately related to the waveguide properties of the inner and outer segments of the cone, properties that define the wave pattern that propagates in each segment. Using optical waveguide theory, the wave pattern is usually represented as a decomposition of optical modes, the number supported related to the waveguide diameter, in our case the diameter of the cone IS and OS. While we do not know the explicit relation between our phase variance measurements and the actual waveguide properties of the cones imaged, we nevertheless can make coarse predictions. As an example, we expect a cone with low phase variance to support few optical modes (simple wave pattern), and conversely one with a high phase variance to support many optical modes (complex wave pattern). Based on this expectation, Fig. 6 indicates that cones near the fovea support fewer modes than those in the periphery, at least over the retinal eccentricities imaged (1° to 5°). This prediction is consistent with optical waveguide theory that shows the number of modes increases linearly as a function of waveguide diameter, in this case cone segment diameter. The relation, however, is more complex than this. The number of modes also depends on the refractive indices of the IS, OS, and interphotoreceptor matrix–values which are subject to debate. Moreover, cones probably do not behave like ideal step index fibers as assumed by these theoretical calculations. Additionally, recent measurements of the optical Stiles-Crawford effect using OCT indicates the waveguiding properties imprinted on the ISOS and PT reflections are noticeably different, differing by roughly a factor of two in directionality [10]. The true relation between phase variance and waveguide properties of cones will not be known until these complexities are addressed. This is future work.

Regardless of these uncertainties, our findings do show that the most precise measurements of phase can be made close to the fovea. As such, it highlights the significant role played by AO, which enables imaging of these tiny (< 5 μm) cells, which cannot generally be seen without it.

4.4. Measuring OS renewal using reference phase imaging

We demonstrate that θ_OS can be monitored in each of thousands of cones over hours. When phase is monitored for intervals longer than its angular period, temporal phase wrapping occurs, which prevents standard approaches to handling time-series data, such as regression or curve fitting. For visualizing temporal wrap–and unwrapping–in individual cones we developed an unwrapping scheme that minimized phase variance around a family of linear models, selecting the model that generated the smallest variance. For analysis of all cones, we sidestepped the issue of temporal wrap, by looking at Lomb-Scargle sine fitting, which showed elongation rates around 150 nm/hr (Fig. 8).

Several caveats to this approach must be stated. First, we assume that phase changes due to OS renewal are linear and monotonic, largely based on our previous AOCFI findings. Those methods employed Fourier transformation based estimates of frequency, which may better resist irregularities in frequency, other nonlinearities, and even some sorts of nonmonotonicities, than the method employed here. One clear potential source of nonmonotonicity in OS length change is disc shedding. It is thought that the cone OS sheds its outer tip once per day–the portion regrown by the constant process of disc renewal. This event probably results in a sudden OS length change of several waves. It might be visible as a sudden change in θ_OS. However, applying referenced phase to detect shedding would require additional technical finesse, especially due to the potential ambiguity between shedding-related phase changes and phase wrap.

Second, it is worth mentioning the presence of a smaller, but significant, peak in the Lomb-Scargle spectrum for subject S4, around 50 nm/hr. We do not have an explanation for this peak, but if it reflects a true, slower change in the cone OS (either in a subset of cones or over a portion of the experiment’s duration), it would clearly impact our interpretation of the spectrum and subsequent determination of ΔL_OS/Δt.

4.5. Referenced phase imaging outside the cone outer segment

The phase sensitive method was also successfully applied outside of the COS, offering a tantalizing glimpse into what other retinal structures could potentially be probed using this technique. In the cases of both θ_IS and θ_SOS, one of the reflections used to calculate referenced phase was a possibly waveguided reflection originating from an end of the outer segment. We are intrigued by the possibility of using these reflections to detect sub-resolution structural features and changes throughout the retina. θ_SOS, for instance, presumably reflects the distance between PT and a bright reflection in or near the RPE layer. Electron microscopy has been used to show that stacks of somewhat intact discs can sometimes be found in the SOS, en route to the underlying RPE cell [28]. Our demonstrated phase sensitivity in SOS suggests that the transport of these packets of discs could be monitored using our phase technique.

5. Conclusion

We have successfully demonstrated a phase imaging technique based on AO and OCT for resolving structural changes in the living human retina more than one order of magnitude smaller than previously reported with OCT. Critical to our technique is the ability to measure phase differences between reflective layers located at different retinal depths. We demonstrated the technique is sensitive to changes in cone OS length of about 45 nm. We showed that a number of preliminary analytical steps are necessary for achieving this subcellular resolution. The most important of these are careful selection of A-lines for analysis and spatial unwrapping of phase within the structures (or regions) of interest. Without these, the capacity to detect average changes in depth is greatly reduced, and measurements of changes in single cells are unreliable. We further used this technique to measure length changes in the cone OS over hours, and found rates of change consistent with our previous, flood illumination-based findings [15].

Appendix A. A detailed description of image processing and analysis methodology

A.1. Segmentation

From each volume, a subvolume containing the outer retina (external limiting membrane (ELM), inner-outer segment junction (IS/OS), outer segment posterior tips (PT) and retinal pigment epithelium (RPE)) was extracted, and the layers corresponding to ELM, IS/OS, PT, and RPE were labeled in each A-line, using an automated algorithm based on multiple one dimensional cross-correlations, first between neighboring A-lines to establish local, small axial shifts; and second between single A-lines and a global model representing the axial intensity profile of the retina at the given eccentricity. The model was based on a coarsely aligned average of all the A-lines in a volume. The labels of peaks (ELM, IS/OS, PT, and RPE) in the model were checked and corrected by a trained technician, when necessary.

A.2. Registration

For experiments in which cones were monitored over time, volumes in a time series were registered as follows. For each volume an en face image of the cone mosaic was generated by locating the IS/OS and PT layers, and co-adding these two. From this series, a reference image was automatically selected by choosing the en face image with the highest contrast at the expected spatial frequency of the cones. If the selected reference image contained an obvious motion artifact, the image with the next highest contrast was used instead. Each target en face image in the series was then divided into narrow strips (approximately the width of a single cone), parallel to the fast scan direction, which were then cross correlated with the reference image to determine local shifts. Peaks from the cross correlations were used to construct a cubic Vandermonde matrix, the eigenvalues of which were used to define polynomials which bound a maximum likelihood neighborhood, viz. the region along the fast scan dimension (defined in the space of the reference image) in which the structures in the target image are most likely to be found. On a second pass, each line in each target image is cross correlated with the reference image, and peaks within the maximum likelihood neighborhood are located. These peaks are used to generate a location for each target line in each target image in the coordinate system of the reference image. Lines whose cross correlation peaks do not exceed a chosen threshold (0.3) are excluded from registration and considered to be missing data. The threshold can be adjusted to reflect the goals of registration: if minimizing missing data and maximizing image quality is the goal, a small threshold (e.g. < 0.1) can be used; if registration correctness is the goal (as in the case of quantifying phase changes over time), a larger threshold (e.g. > 0.2) can be used.

A.3. Cone identification

Cones were identified using a custom algorithm, which operated by applying a Gaussian bandpass filter to the en face images, computing the watershed [29] of the complement (negative) image, and filtering the watershed basins by basin size and basin total intensity. Miss and false positive rates were less than 3% and corrected manually. By combining automated cone identification with automated registration, coordinates of any cone could be determined in all volumes in which it appeared in a sufficiently well-correlated region. It was then straightforward to track any cone over time.

Once a cone was identified and tracked, we determined which A-lines in each volume belonged to that cone. A-line selection was performed by finding all A-lines within a fixed radius from the cone center (using expected cone diameter [26]) and selecting those whose OS length matched the most frequent OS length of the region. This inclusion criterion was motivated by the observation of strongly unimodal OS length distributions within single cone regions. While length distributions were unimodal, mismatches within the circular region were common, due possibly to image warp (which results in non-circular images of the cones), segmentation error, or blur. The circular region of interest at 1.5°. consisted of 21 A-lines with a radius of 2.5 pixels. On average, of these 21 pixels, 9.5 were included for analysis.

A.4. Phase retrieval and spatial unwrapping

Phase at the IS/OS (θ_ISOS) and PT (θ_PT) were computed for A-lines within each cone, from the segmented, complex-valued volumes. Phase values, such as these are bounded by a 2π interval [0,2π), the range of the complex arctangent function used to calculate phase. Consequently, referenced phase θ_PT – θ_ISOS is bounded by a 4π interval, [−2π,2π). Because for a single pixel there is no meaningful difference between values in [−2π,0) and [0,2π), we wrap θ_OS back into a [0,2π]) range using mod 2π in Equation 1.

Values of θ_OS were observed to be spatially wrapped within cones. Spatial wrapping manifested as two distinct clusters of phase values, one near 0 and one near 2π, and may be due to phase noise or real phase variation among pixels within a cone.

θ_OS within single cones was spatially unwrapped by sequentially, in descending order, subtracting 2π from each value and computing the phase variance. The minimum variance was used to select the correct unwrapping point for each cone, above which values were reduced by 2π and below which values remained intact. This method dramatically reduced variance in wrapped cones, but did not greatly impact variance in cones without wrapping or in sets of uniformly distributed random phase values. The choice to subtract, and not add, 2π was arbitrary. One consequence of the choice is that in an en face phase projection (such as in Fig. 3), pixels within cones tend to be darker than pixels between cones.

At many stages of processing and analyzing images, expected cone diameter was used. These values were typically taken from [26], interpolating when necessary. Automated identification of cone centers, combined with expected cone diameter, allowed A-lines potentially belonging to individual cones to be readily identified.

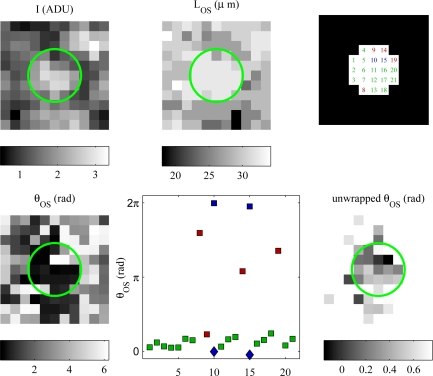
Once a cone’s A-lines were found, segmentation information was used to generate intensity images of each cone, along with corresponding maps of OS length and θ_OS. Fig. 10 (top left, top center, and bottom left) show these maps, respectively, for a single cone. Visual examination of cones’ OS length maps revealed that some A-lines within the cone’s region appeared not to match the most common OS length in the region. The source of these mismatches is unknown, but may be due to eye motion (which results in imperfectly circular en face cone projections), true variations in cone aperture size, optical blur, or segmentation error. The OS length map of the cone provides important information–complementary to the cone’s en face intensity profile–that can be used to include and exclude A-lines for analysis. Fig. 10 (bottom center) shows a plot of θ_OS for A-lines in the cone’s region. The x-axis of the plot indicates the numerical index of the A-line, and the positions of the numbered A-lines are shown (top right). From the plot and phase map (bottom left) it is clear that most of the A-lines in the cone have θ_OS values close to 0, while two of the A-lines (indices 10 and 15) have phase values close to 2π. The proximity of these A-lines to the cone’s center, along with their matching OS length, provide supportive evidence that these A-lines belong to the cone. Four other A-lines (indices 8, 9, 14, and 19) appear not to belong to the cone OS, as their lengths do not match the OS length of the cone. OS length mismatch is a useful criterion for excluding A-lines from the phase analysis of this cone.

The most parsimonious interpretation of the observations in Fig. 10 is that the wrapped Alines (10 and 15) should be shifted downward by 2π and that the mismatch A-lines (8, 9, 14, and 19) should be excluded from analysis. In so doing, we dramatically alter the average value of θ_OS for this cone. If we use all the A-lines, intact, θ_OS = 1.5 rad and σ_θ = 2.1 rad; if we unwrap A-lines and exclude mismatches, θ_OS = 0.33 rad and σ_θ = 0.24 rad. It is evident that phase unwrapping is a critical step for uncovering the correct phase separation between IS/OS and PT, and that failing to unwrap correctly may lead to serious phase errors. Generally, if the true phase is near 2π rad, and half the observed values are near 2π rad with the other half near 0 rad, the average across A-lines will be close to π rad, corresponding to an error of π rad–the worst possible error in the phase domain. Whether validating phase measurements by computing statistics over A-lines or averaging over A-lines to reduce the impact of phase noise, a method for unwrapping spatially wrapped phase measurements is critical.

In Figs. 3 and 10, it can be observed that intensity varies among A-lines within a single cone. Phase noise is known to be related to the inverse square root of SNR [19], which suggests that phase, in the dimmer pixels, may have higher noise. It is possible that further restricting phase measurements to only the brightest A-lines in the cone may improve phase sensitivity–a possibility meriting further investigation.

Fig. 10.

An example of spatial unwrapping and OS length-based exclusion, applied to Alines in a single cone. (Top left) En face view of a cone’s intensity, projected by summing the intensities of the ISOS and PT reflections in each A-line in an 11 × 11 μm (1 μm/px) subvolume at 1.5°, centered about the automatically identified x- and y-coordinate of the cone. The green circle indicates the cone’s region of interest (ROI), defined as all the pixels within a fixed radius of the cone center; the radius was D/2, where D is the predicted center-to-center spacing of the cones, and varied with retinal eccentricity. (Top center) OS lengths for each A-line in the ROI, determined by the automatic segmentation of retinal layers. (Top right) Indices, arbitrarily assigned, for each of the 21 pixels (A-lines) in the cone’s ROI. (Bottom left) En face projection of θ_OS. Each pixel is computed by applying Eqn. 1 to the complex A-lines in the subvolume. It is clear in the θ_OS projection that many of the pixels in the ROI have values close to 0 rad, with the exceptions of pixels 10 and 15, which have values close to 2π, and pixels 8, 14, and 19, which have values somewhere between. (Bottom center, square markers) Phase values from the ROI plotted by pixel index. This plot confirms what was visually apparent in the θ_OS projection, that most pixels are close to 0 rad, while two are near 2π rad and three are between π and 1.8π. From the length map (top center) it is evident that four of these pixels (8, 9, 14, and 19, specifically) do not have OS lengths matching the rest of the pixels, which suggests they should be excluded from the phase analysis. Spatial unwrapping (based on variance minimization) shifts pixels 10 and 15 by −2π. The unwrapped values are shown with blue diamonds on the plot. (Bottom right) θ_OS plotted from the subvolume, scaled between the minimum and maximum unwrapped θ_OS values.

A.5. Temporal unwrapping

Qualitative observation of single cone phase traces indicated the clear presence of temporal phase wrap: cones with increasing θ_OS would jump from near 2π to near 0 over short intervals. We employed two methods for visualizing and quantifying phase changes in which temporal wrapping was present.

For traces of θ_OS in which phase wrapping was visibly evident, we employed an unwrapping technique that searched for unwrapping points that best fit linear models within a finite range of slopes, corresponding to [−200 nm/hr, 200 nm/hr]. The algorithm proceeded as follows. Linear models were subtracted from the measured phase, and the residual phase values were unwrapped using the variance minimization technique employed for spatial unwrapping, and the minimum variance was recorded for each linear model. The linear model resulting in the smallest residual, unwrapped variance was determined, and used to temporally unwrap phase. We chose this range of slopes based on previous AO flood findings that indicated cones renew at rates between 80 and 150 nm/hr [27].

For the analysis of all cones, we employed an alternate method to overcome the challenges imposed by temporal phase wrap in the over-hours data: fitting sinusoids to sin(θ_OS). sin(θ_OS) has the virtue of being impervious to phase wrap in θ_OS, since, for any angle θ, sin(θ) = sin(θ + 2π) = sin(θ + 4π).... We used the Lomb-Scargle algorithm to compute a frequency spectrum for each cone’s sin(θ_OS) time series. These spectra were averaged, producing the plot in Fig. 8.