A hematoma detector—a practical application of instrumental motion as signal in near infra-red imaging

Abstract

Abstract: In this paper we discuss results based on using instrumental motion as a signal rather than treating it as noise in Near Infra-Red (NIR) imaging. As a practical application to demonstrate this approach we show the design of a novel NIR hematoma detection device. The proposed device is based on a simplified single source configuration with a dual separation detector array and uses motion as a signal for detecting changes in blood volume in the dural regions of the head. The rapid triage of hematomas in the emergency room will lead to improved use of more sophisticated/expensive imaging facilities such as CT/MRI units. We present simulation results demonstrating the viability of such a device and initial phantom results from a proof of principle device. The results demonstrate excellent localization of inclusions as well as good quantitative comparisons.

1. Introduction

Over the past decade Near Infra-Red (NIR) imaging has demonstrated increasing utility as a neuro-imaging modality [1–7]. It is commonplace as a spectroscopic [6] and tomographic [3] model for functional imaging. In the area of structural imaging it is also making progress, particularly for neo-natal [8–10] and stroke monitoring [11]. NIR has also been used spectroscopically to monitor (though not as a detection tool) for cerebrovascular reactivity in traumatic brain injury subjects [12,13].

A challenge of NIR imaging is avoiding motion at the detectors when acquiring data. Typically, the positions of optodes need to be known and constant and detectors must be kept perpendicular (fiber)/parallel (CCD) to the surface, since a moving detector results in visible motion artifacts, which mask the data. Some work has been done [14] to model (and hence remove) this motion as a form of noise. Other approaches have been to eliminate noise by using techniques such as independent component analysis [15]. Here, we consider the idea that detector fiber motion is a useful signal, and not just noise. This concept is not the same as Laser Doppler Imaging, nor is it a scanning technology where a light is passed across the object (e.g., [16]).

The usefulness of a “motion signal” can be demonstrated in a structural imaging application for NIR in intracranial hematoma detection. For NIR imaging, absolute imaging is normally used at a superficial depth, and differential imaging for all other depths. The problem then with hematoma imaging is how to create a difference image on what is essentially a static hematological event (as we are not considering imaging the process of hematoma formation here). Some simplified devices have already been discussed in the literature, e.g., [17–19], which utilize an approach based on comparing to a contra-lateral measurement to create a difference image. Therefore they examine sparse non-symmetrical effects which, as we shall discuss, may prevent correct clinical diagnosis. Some authors have suggested diffuse optical tomography for hematoma detection; however, this approach is costly, requires large instrumentation, and is not as available as a handheld, real-time solution on the full adult head. Another recent approach uses 3D localization to register multiple images collected with a handheld device [20]; this is a similar idea to that presented here, but is still effectively concerned with using static imaging. Other, so called moving, devices do exist (such as [21]), but they are also designed to make static measurements at discrete locations, as opposed to taking measurements as the device itself tracks.

It is clear from clinical discussions that one primary use of any such device will be the rapid screening (triage) of traumatic brain injury (TBI) patients before the use of more expensive and intensively used imaging techniques, i.e., CT and MRI. Often the queue for such imaging is long and currently patients without focal neurological signs are prioritized by common measures of overall neurological function, such as the Glasgow Coma Scale (GCS). In the case where CT and MRI imaging facilities are not readily available (e.g., battlefield), NIR imaging could help determine the relative urgency of patient transport. NIR could also be used to monitor known hematomas at the bedside or outpatient clinic.

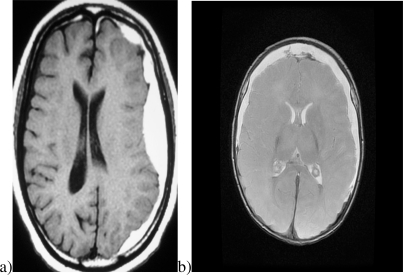
There are many types of intracranial and extracranial hematomas. In addition to extra-calvarial (outside the skull) hemorrhage, the most important collections of blood are intracranial. Extra-axial (outside the brain) hemorrhage is usually either “epidural hematoma” (EDH) [22] or “subdural hematoma” (SDH) [23]. Epidural hematomas are usually unilateral. In contrast, blood in the subdural space may be unilateral or bilateral. Figure 1 illustrates typical examples of unilateral and bilateral hematomas. Existing NIR technology may not detect the presence of symmetrical bilateral hematomas. A new NIR device will only be useful in clinical application if it can reliably diagnose all types of hematoma.

Fig. 1.

Typical hematomas: (a) unilateral and (b) bilateral.

In this work we consider moving a device across the head to detect a hematoma, using the changing signal as a differential measure. A single depth, or source detector separation, (such as used in previous studies [18]) will clearly vary with the heterogeneity of the head; however, if we use two detectors—one to probe the skin and skull and one to probe the dural region—we should be able to normalize for changes due to superficial heterogeneity. This assumption is based on the fact that we are not, as is usual in NIR imaging, looking for hemodynamic changes, but actually detecting the presence of a large inclusion of blood in the dural region. The presence of whole blood should provide a larger than normal change in absorption due to the concentrations of blood involved. Normally in NIR imaging we are looking at changes in blood volume/oxygenation at a blood volume of around 3% in brain [2,24]; here we are looking at a volume swing from around this 3% level to 100% in a significantly sized region. Thus, a detection threshold should exist for hematomas.

Here we will demonstrate using the accepted theory for diffuse optical imaging (the diffusion approximation) that such a device is viable. We include to this end a brief description of the theoretical model used. We note that many models are available, but we have opted for the familiar finite element model of the diffusion approximation and have implemented our simulations on a mathematician’s head (a sphere).

We will go on to describe the instrument used as a proof of concept device. To enable a thorough assessment of the potential of the imaging technique, the instrument used in this study is much more sophisticated than required for the final device. We have used a fiber based system, more familiar to functional imaging (based on [3]). The system also has an integrated high resolution motion tracking device derived from the latest gaming mouse hardware to allow us to monitor position; this tracking method has been validated by including a computer controlled rotating stage where the phantoms are mounted for study. Solid resin phantoms with tissue-like optical properties, on loan from University College London (see below for details), were used in this study.

We will demonstrate that, as expected, the theoretical model suggests that we can detect inclusions based on the appropriate selection of the two source detector separations and that the method will have limitations based on the optical contrast of the anomaly. The experimental data goes on to validate the numerical results, showing excellent localization of inclusions and quantitative measures that are in good agreement with the optical contrast of the different inclusions. As such we demonstrate a novel approach to NIR imaging that would be applicable to the case of imaging hematomas in traumatic brain injury patients and which would alleviate one of the current limitations to sensitivity of existing devices.

2. Theoretical model

The theoretical model is based on the diffusion approximation (DA) [25]. There is some debate over whether a more sophisticated model should be used to handle light transport in certain regions of the head (particularly near the cerebrospinal fluid (CSF) [26,27]). However, it is also clear in [27], that when using a difference image, any change in the size of a hematoma would be apparent in a normalized difference image. As the instrumental design relies on a ratio of signals, or normalized difference, the DA is sufficient in this case.

The diffusion approximation is given by

$$-\nabla \cdot \kappa (r)\nabla \Phi (r)+{\mu }_a(r)\Phi (r)=q(r)$$

where κ(r) is the diffusion coefficient at point r (κ(r) = 1/3 (μ_a(r) + μ_s'(r))), Φ(r) is the intensity at point r, q(r) is the source function, μ_a(r) is the absorption coefficient at point r, and μ_s'(r) is the reduced scattering coefficient at point r (μ_s'(r) = (1 – cos(Θ))μ_s(r), where cos(Θ) is the average scattering angle). A selection of boundary conditions are offered in the literature, including those of Dirichlet, Neumann, and Robin [28]. For this work we have used the Robin condition and a finite element model similar to that proposed in [29] for numerical solutions. The finite element solution, not derived here, for the forward problem is given as [29]

$$(K(\kappa )+C({\mu }_a)+\frac{1}{2\alpha }A)\Phi =Q$$

where

$$\begin{array}{l}{K}_{ij}={\displaystyle \underset{\Omega }{\int }k(\text{r})\nabla u_i(\text{r}).\nabla u_j(\text{r})}d\text{r}\\ C_{ij}={\displaystyle \underset{\Omega }{\int }{\mu }_a(\text{r})u_i(\text{r})u_j(\text{r})}d\text{r}\\ A_{ij}={\displaystyle \underset{\partial \Omega }{\int }{u}_i(\text{m})u_j(\text{m})}d\text{m}\\ {\Phi }_{ij}={\displaystyle \underset{\Omega }{\int }{\phi }_i{u}_i(\text{r})}d\text{r}\\ Q_i={\displaystyle \underset{\Omega }{\int }{q}_i{u}_i(\text{r})}d\text{r}\end{array}$$

and K_ij, C_ij, A_ij, Φ_ij and Q_i are the matrix/vector components; u_i and u_j are the basis functions associated with the nodes; and ϕ_i and q_i are the intensity and source terms at the nodes of the mesh. We also define m as a point on the boundary of the domain and α as a term defined by the refractive index mismatch at the boundary; further details are given in [28], but for the purposes of this paper the boundary is matched giving α = 2.

3. Instrumental design

The design of this instrument is based on changing the imaging paradigm compared to most state-of-the-art diffuse optical imaging, which emphasizes creating stable (or static) sources and detectors. These approaches aim to image small changes in the hemodynamics present in a medium or, in the case of structural imaging, to create an image of the absolute or steady state structure of an object. Given the difficulties of absolute imaging, such as uncertainties in whether non-scattering or anisotropic regions will be detectable or effect images, these approaches are far from being ready to use for the development of a hematoma imaging device. Similarly, a hematoma does not represent a “changing” medium in the sense of hemodynamic changes over time, as there is no metabolic event causing oxygenation or volume change on a physiological level.

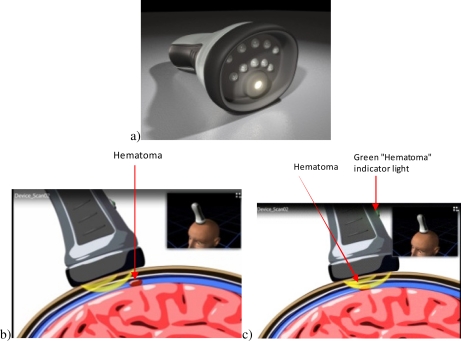
It has been shown [17] that some hematomas can be detected by using a contra-lateral difference image. However, in the case of a symmetric bilateral hematoma this method can result in a false negative diagnosis, i.e., missing the trauma. Further, as this approach uses sub-sampling, it can miss potentially localized events, again causing a false negative indication. In this work we present a model, which is based on using a moving optical head imaging system such as that illustrated in Fig. 2 , to create the difference signal and detect the hematoma at its boundaries. Additionally, since the device can move over the whole patient head (see the final envisaged design in Fig. 2); there is no risk of missing hematomas.

Fig. 2.

(a) The design of the device and its use scanning over the head in (b) the absence and (c) presence of a hematoma in the field of view—where the green light on the device indicates presence of a hematoma (Media 1 ^{(1.6MB, AVI)} ).

Our hypothesis is that by moving the imaging probe across the head and probing at one depth sensitive to the superficial layers and comparing to a probe sensitive to the dural layer, we should see a marked contrast shift in the presence of blood in the dural layer (i.e., a subdural or epidural hematoma).

To test our hypothesis we have developed a specialized holder for a functional brain imaging instrument. An array of fibers from the instrument, mounted on a phantom, enables tracking of the holder. The instrument has also been modified to accept additional input from a motion tracker mounted on the holder to determine the location of the instrument simultaneously with the data collection. The holder has many detector separations to select the correct separation distances and will allow us to characterize, at a later date, the depth sensitivity and specificity of the device with further phantom studies.

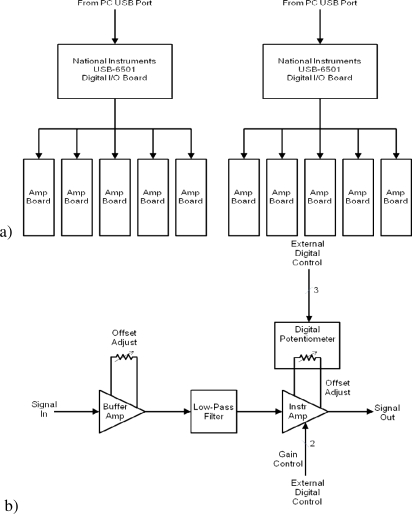
The fiber-based system developed is based on the instrument described in [3]. It uses 10 mW LED sources and the sampling rate at the detectors is set at ~100Hz. Our minor modifications to the design are catalogued here. The modified instrument uses trifurcated instead of bifurcated fibers for the source positions to allow us to use three instead of two wavelengths. The device uses 750/800 and 850 nm sources; we selected the 750 source for this study. This change from bifurcated to trifurcated fibers will allow us (in future) to use three wavelengths to discriminate the three types of hemoglobin expected in hematomas (oxy, deoxy, and, in the case of chronic hematoma, met). Three diode wavelengths will be used: the first two will be chosen based on work in submission on wavelength optimization [30] to discriminate for oxy- and deoxy- hemoglobin and a third will be added to assess for methemoglobin to allow the imaging of chronic rather than acute hematomas. The second change to the system is the introduction of in-house amplifiers after the avalanche photodiodes for increased dynamic range. The amplifier box can be used to amplify up to ten inputs. Each channel consists of a single board that contains a unity gain amplifier, followed by a low-pass filter, and an instrumentation amplifier with programmable gain inputs. A digitally-controlled potentiometer is connected to the offset adjust pins of the amplifier to minimize any DC offset associated with the amplifier. The gain of the instrumentation amplifier and the value of the digital potentiometer are controlled by inputs from a National Instruments USB-6501 Digital I/O board. Two digital lines set the gain of the amplifier (with gain options of 1X, 10X, 100X, and 1000X) and three digital lines are used as a serial interface to the digital potentiometer to set its value. For each gain setting, the offset adjust has a specific value that would minimize the DC offset at the output of the amplifier. There are two USB-6501 boards in the instrument, each controlling five of the amplifier boards. The design schematic for this box is given in Fig. 3 .

Fig. 3.

(a) An overall block diagram of the programmable ten-channel amplifier box showing computer control configuration and (b) a block diagram of a single channel amplifier unit with five control lines to set gain and minimize amplifier offset.

The fibers from this instrument are coupled to a holder built using a 3D printer designed to hold one source and six detector fibers arranged in an array as (S, D1, D2, D3, D4, D5, D6). These are set to minimum separation based on the fiber diameter and the mechanics of attachment to the device, giving an inter fiber spacing of 8.816 mm. The component is designed to fit 70 mm diameter cylindrical phantoms and is illustrated in Fig. 4 , below, with fibers and mounting unit for the phantom. The scanning head is fixed to a height-adjustable stem allowing us to probe the phantom at different layers with a computer-controlled rotational stage for validating the motion detection.

Fig. 4.

The instrument imaging head’s seven fibers (one source and six detectors) and a high resolution mouse sensor for positioning. Also present is a computer-controlled motorized stage to check positioning data.

The final component of the system is the built-in motion tracker/position sensor. The position sensor is a Philips PLN2020 twin-eye laser sensor extracted from a computer mouse. This sensor has a resolution of 5600 dpi (~4.5 µm per count) in both the X and Y directions and is effective at rates up to 500 mm/s. The USB interface of the mouse was used to connect the sensor to the computer. A driver was created for the mouse (NI-VISA driver developed by National Instruments) and the position data was read directly into the test software. In this manner, a regular mouse can still be used with the computer while reading data from the position sensor. The current position is updated every 10 ms to ensure an accurate position is available each time an optical measurement takes place.

4. Phantoms

4.1. Numerical phantoms

The basic numerical phantom is a sphere of radius 70 mm, constructed as a tetrahedral mesh with 34049 nodes. It has optical properties of µ_s’ = 1.0 mm⁻¹ and µ_a = 0.01 mm⁻¹. It contains a 5X absorption contrast inclusion (radius 10 mm) centered at 25 mm below the surface. The model is not congruent with a human head or hematoma, but is sufficient to demonstrate the principle. It is also not congruent with the experimental phantom as we are not providing validation of the numerical model— this was previously done in the literature—but are demonstrating the underlying principles of the technique.

Four other numerical phantoms are used. Based on the same mesh, we created a smaller inclusion phantom (radius 5mm) and a larger inclusion phantom (two touching 10mm radius inclusions). Finally, we created depth variation phantoms moving the 10 mm radius inclusion to a depth of 30 mm and then 35 mm. The phantoms, while not comprehensive in nature, are designed to test the method in the presence of typical potential variations in hematoma behavior.

4.2. Experimental phantoms

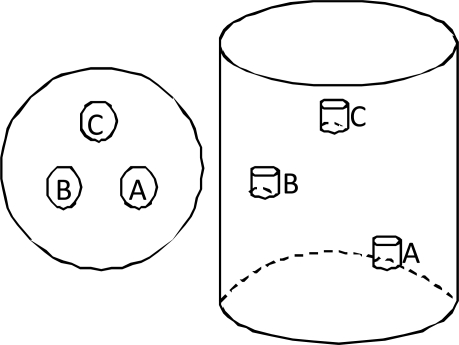
Many types of optical phantoms for NIR studies have been considered over the years. Good review papers have been written on the subject, for example [31]. In this work we have chosen to use resin phantoms, which allow us flexibility of shape for later studies in head models while maintaining experimental consistency. They will further allow us to create “dynamic” (blob in/blob out) phantoms without the potential confounding issues of refractive index mismatches, as were noted when using mixed material phantoms in [27]. We have used two phantoms in this work, a homogenous “null” phantom and a phantom with three blobs situated at different heights in the phantom; both phantoms are cylindrical with a diameter of 70 mm. The blobs are at heights of 50, 75, and 100 mm and are distributed at 120 degrees to each other, centered at a radius of 17.5 mm. The blobs are 10 mm in height and 8 mm in diameter. The geometry of this phantom is illustrated in Fig. 5 below.

Fig. 5.

The geometrical layout of the blobs in the cylindrical phantom. The blobs are located at 120 degrees to each other, centered at 17.5 mm from the center of the phantom at planes of 50, 75, and 100 mm.

The optical properties of the phantoms are the following:

• 1. Homogenous phantom
  • a. µ_a = 0.01 ± 0.002 mm⁻¹
  • b. µ_s′ = 1.0 ± 0.02 mm⁻¹
• 2. Heterogeneous phantom
  • a. Background
    • i. µ_a = 0.01 ± 0.002 mm⁻¹
    • ii. µ_s′ = 0.85 ± 0.1 mm⁻¹
  • b. Blob A
    • i. µ_a = background
    • ii. µ_s′ = 10x background
  • c. Blob B
    • i. µ_a = 5x background
    • ii. µ_s′ = 5x background
  • d. Blob C
    • i. µ_a = 10x background
    • ii. µ_s′ = background

Full descriptions of these phantoms can be found in [32] and [33]. The phantoms were supplied on loan from UCL and are available for study from there.

5. Results

5.1. Theoretical model

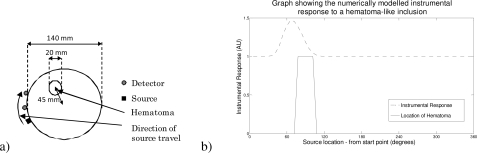
In Fig. 6 we illustrate the effect of examining the difference (ratio of measures) between a source and two detectors as they are translated around the basic spherical numerical phantom. The presented data are normalized to remove meshing artifacts (as we translate the source, the unstructured mesh alters slightly in shape causing variations in the signal, which confound the visualization of the actual data). As these fluctuations are not relevant to the instrumental design, which will rely solely on measured data with no modeling involved, they have been removed for clarity. The graph (Fig. 6b) illustrates the intensity difference (ratio) between two fibers with separations of 20 and 40 mm from the source.

Fig. 6.

A graph illustrating how the hematoma detector would be capable of detecting a hematological event in the dural/subarachnoid region of the head. a) Illustrates the geometry and the source detector configuration with direction of travel, b) shows the intensity ratio as the source detector combination moves along the indicated trajectory.

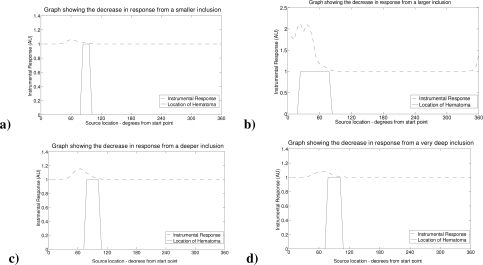
In Fig. 7 we illustrate the effect of changing the location and size of the hematoma inclusion, as described in the numerical phantoms section. In the instance of depth change it is important to note we have not adjusted the separation of the source detector pairs to accommodate the depth change.

Fig. 7.

A set of graphs illustrating how the model can be used to identify the device’s ability to discriminate and detect hematomas based on size: a) smaller—50% size; b) larger—two radially aligned touching spheres of the same size, and on depth: c) at an extra 5 mm depth; d) at a further 5 mm depth.

5.2. Experimental Results

Here we present the results collected from the two phantoms used. We first present data collected on the phantom containing the inclusions. Then as a validation study we show data from the “null” or homogeneous phantom.

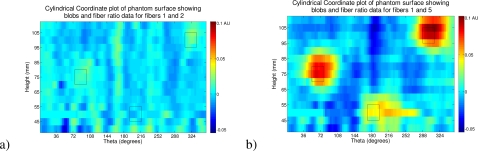
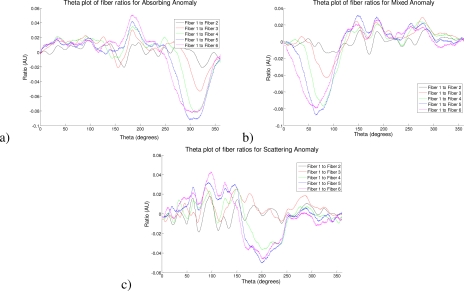
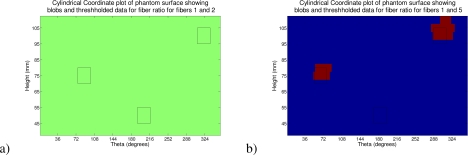
In Fig. 8 we demonstrate the intensity ratio data for fiber 1 (Source Detector separation: 8.816 mm) to each of fibers 2 (Source Detector separation: 17.632 mm) and 5 (Source Detector separation: 44.08 mm). These fiber separations roughly compare a maximum sensitivity depth of around 4.4 mm to depths of 8.8 mm and 22 mm; these approximations are based on the case of an infinite half space as given in [34]. It is difficult to be precise in the absence of analytic models for the cylindrical case; however, the approximation is accurate enough to ascertain that fibers 1 and 2 do not penetrate to the depth of the hematoma and fiber 5. The figure shows surface plots of the data described in height on the cylinder and the angular location θ for the two separation pairs; these and all following surface intensity ratio plots have been plotted on the same color scale for clarity. The blob locations are illustrated by black outlines on the surface. We have used a zero centered ratio and, for the images, we used the negative of the data to provide a color scale where a high value represents a positive inclusion. Note: the theta location of the inclusions is shifted in each case as, for each image, we have set theta 0 to be the angular location of the mid-point of the source and the “far” detector (fiber 2 or 5) at the start of the scan. In Fig. 9 we plot the ratio at the height of each anomaly in the cylinder for all fiber pairs to fiber 1. Here the theta is corrected to the source location. In Table 1 we give the peak contrast for each detector pair and anomaly. In Fig. 10 we illustrate the detection of the two absorbing anomalies in the image by using a threshold similar to the principle of the hematoma detector (the threshold level was chosen at −0.07 AU). Here again we show a surface map in height and θ and have located the blobs with outlines as shown previously.

Fig. 8.

A visualization of the intensity ratio data on the surface of the cylinder, position given by height in mm and degrees from a nominal point based on source to far fiber detector midpoint. Here showing the data with the blob outlines projected to the surface, from a) fibers 1 and 2 and b) fibers 1 and 5.

Fig. 9.

A plot of the intensity ratio data on the surface of the cylinder, position given in degrees from a nominal point based on source position. Here showing the data ratios from fiber 1 to all other fibers at the level, for a) the absorbing anomaly, b) the mixed anomaly, and c) the scattering anomaly.

Table 1. A table giving the peak ratios for each anomaly and each fiber pair.

Fiber Pair	Absorbing Anomaly	Mixed Anomaly	Scattering Anomaly
Fiber 1 to fiber 2	−0.026	−0.0147	−0.0201
Fiber 1 to fiber 3	−0.0607	−0.0424	−0.0050
Fiber 1 to fiber 4	−0.936	−0.0757	−0.0423
Fiber 1 to fiber 5	−1.1023	−0.0866	−0.0557
Fiber 1 to fiber 6	−0.994	−0.0786	−0.0407

Fig. 10.

A visualization of the thresholded intensity ratio data on the surface of the cylinder, position given by height in mm and degrees from a nominal point based on source to far fiber detector midpoint. Here showing the data with the blob outlines projected to the surface from a) fibers 1 and 2 and b) fibers 1 and 5

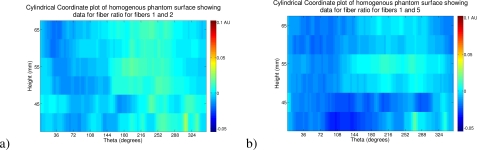
For the purposes of a control experiment we demonstrate the same imaging procedure on the homogeneous phantom. Figure 11 shows the intensity ratio data for the homogeneous phantom using the same fiber pairs and the same color scale as that given in Fig. 8.

Fig. 11.

A visualization of the intensity ratio data on the surface of the cylinder, position given by height in mm and degrees from a nominal point based on source to far fiber detector midpoint. Here showing the data on the homogeneous phantom (color-scale matched to heterogeneous data) from a) fibers 1 and 2 and b) fibers 1 and 5.

6. Discussion

Our initial simulation results were aimed at demonstrating the viability of the concept of using motion as a signal from a theoretical point of view. It is clear from Fig. 5 that an absorbing inclusion (such as a pool of blood or hematoma) can easily be detected if we move a single source with two detectors, at the properly chosen separations from the source, past it. This point is illustrated more clearly in Fig. 6 (c and d) where we vary the depth of the inclusion and change our sensitivity to it. We further illustrate how the size of the inclusion will affect the data as shown in Fig. 6 (a and b). These factors will be further studied in future work based on evaluating the sensitivity and specificity of the device using data obtained from databases of CT scans of hematoma subjects.

Based on the success of the simulations we went on to show a proof of concept device. Here, by using a more sophisticated instrument than needed, we were able to acquire data of a quantitative nature on a tissue-like phantom. Figure 7 clearly demonstrates how the device picks up different anomalies in the tissue-like phantom with differing contrasts. These differing contrasts clearly show the importance of choosing the fiber separations correctly as the anomalies are only detected when the correct source detector separations are used, as expected. In this case we have chosen fibers 1 and 5. The data in Fig. 8, where we show plots of the data at the level of each anomaly in the phantom, clearly illustrate the choice of this fiber pair as the most sensitive for this depth. Further, if we examine the data in Table 1, we can see that by subtracting out the scattering effect from the mixed anomaly (half the peak value) and then halving the left over absorption effect in the mixed anomaly we find the ratio of the absorbing effect to be 0.574 of the absorbing anomaly. If we consider that the mixed anomaly has half the absorption of the pure absorbing anomaly, this is a very close quantitative value to the absorption contrast and is skewed upwards as the removal of the scattering effect does not compensate for the increased absorption caused by the increased scatter. Figure 9 goes on to show how by selecting an appropriate (quantitative) threshold for our contrast we may obtain very accurate localization of the absorption inclusions in a map of the surface. The detection technique shown here is suitable for non-expert use as no numerical methods are used and no decisions concerning algorithms or regularization parameters are required.

Finally as a control to illustrate the absence of false positives we showed data in Fig. 10 from a homogeneous phantom. Here, as we plot the data on the same color scale as the original heterogeneous maps, it is entirely clear that no inclusions were detected.

One open question is the choice of optical contrast parameters. In this study we have chosen an existing phantom that suited our needs. The background properties can be considered as tissue like. The absorbing anomaly at a factor of 10x background is reasonable as it can be estimated that total blood consists of 2 mM concentration of hemoglobin and there is ~3% blood content in brain tissue [2,24], which corresponds to 60 µM hemoglobin. In the case of a hematoma, 100% blood is present, which corresponds to the 2mM concentration. Hence, the absorption ratio increase could be considered as much as 33 fold as blood is the strongest absorber in the NIR range; while this ratio may not represent a precise contrast, we consider a factor of 10, therefore, to be reasonable.

We have demonstrated, then, both in theory and with a proof of concept device that motion can be used as a signal for NIR imaging. We have shown that such a device can be used to locate structural absorption anomalies such as would occur in a hematoma in the dural region. From existing work on functional imaging we know that diode based systems [35] are capable of providing light penetration into brain tissue to the depth required for such imaging. Therefore, we have demonstrated that a handheld hematoma device based upon this technique can be realized potentially filling the gap in triage assessment of the possibility of hematoma. An interesting aside was that the strong scattering inclusion was not detected with the given thresholding. This suggests that the scattering changes that can be reasonably expected in tissue are unlikely to affect the device’s imaging capacity—this result implies a good specificity for the device, but will require further investigation.

7. Conclusion

In this work we have presented a novel approach to NIR imaging to allow the detection of both unilateral and bilateral hematomas. We have demonstrated the novel idea of using a moving NIR device to detect structural changes in the dural region. This approach introduces a new paradigm for diffuse optical imaging, which has previously relied on static imaging approaches, considering motion as noise.

We have shown with numerical modeling that such a device is theoretically possible. Further, we illustrated that such models can be used to effectively determine the ability of such an instrument to detect hematomas and categorize sensitivity and specificity.

Finally we have demonstrated, using a simple experimental set-up, that we can effectively detect inclusions in a tissue-like phantom. These inclusions are detected accurately in terms of localization (based on the use of motion trackers) and with good quantitative assessment of inclusions. No false positives were detected in the control phantom (null test).

Future work will involve building a statistical model of hematomas based on existing CT data. This approach will allow us to optimize the design of a device for the detection of both unilateral and bilateral hematomas.