Abstract
The endothelial glycocalyx layer is a ~2 µm thick glycosaminoglycan rich pericellular matrix expressed on the luminal surface of vascular endothelial cells, which has implications in vessel mechanics and mechanotransduction. Despite its role in vascular physiology, no direct measurement has of yet been made of vessel glycocalyx material properties. Vaterite microviscometry is a laser tweezers based microrheological method, which has been previously utilized to measure the viscosity of linear and complex fluids under flow. This form of microrheology has until now relied on complete recollection of the forward scattered light. Here we present a novel method to extend vaterite microviscometry to relatively thick samples. We validate our method and its assumptions and measure the apparent viscosity as a function of distance from the vascular endothelium. We observe a differential response in conditions designed to preserve the EGL in comparison to those designed to collapse it.
OCIS codes: (140.7010) Laser trapping, (160.1435) Biomaterials, (170.4520) Optical confinement and manipulation
1. Introduction
Mechanical inputs in the form of surface shear stresses have a profound impact on the development, morphology [1], homeostasis, and pathology [2] of the vascular endothelium. Fluid shear stresses derived from blood flow are transduced by endothelial cells (ECs) to biochemical signals in a process central to their overall role in vascular physiology. ECs possess known molecular force sensors at their basolateral surface, cell-cell adhesions, and at the cell plasma membrane [2]. However, ECs express an often overlooked glycosaminoglycan (GAG) rich pericellular matrix, known as the endothelial glycocalyx layer (EGL), on their luminal surface in contact with blood flow [3,4]. Overlooking the EGL is in part understandable, as it is notoriously difficult to image. In situ imaging methods typically rely on exclusion [5]. There is good reason to believe that the EGL is mechanically significant [6,7], plays a role in distributing forces to the possible force sensors [8], or that it in fact acts as a mechano-sensitive structure itself [4,9].
The biochemical composition of the EGL is well known. It is comprised primarily of free GAGs, proteoglycans, and glycoproteins [4]. Heparin sulfate comprises the bulk of EGL GAG content [10] and is typically found bound to syndecan-1, −2, and −4 [11,12]. The balance of EGL GAG content consists of condroitin sulfate [10], which is typically bound to syndecan-1 and hyaluronic acid (HA) [4,13]. HA is the highest molecular weight EGL GAG, ranging from 200 kDa to 2 MDa [14]. HA is thought to contribute greatly to EGL material properties as it is long enough to form an entangled network [15,16]. HA is binds to the cell surface receptor CD44 and also associates with chondroitin sulfate side chains [4,17]. Syndecan [18] molecules as well as CD44 [19] have cytoplasmic tails which associate with the actin cytoskeleton. This association may provide a mechanism to distribute fluid shear stresses from the luminal side to mechano-sensitive structures at other locations with-in the cell [8].
Despite the depth with which we understand the biochemical make-up of the EGL, surprisingly little is known about its material properties. As a first approach, Nijenhuis et. al. used passive michrorheology to measure the broadband shear modulus of HA solutions [16] and cocktails with other EGL GAGs [15]. Damiano’s group has used micro-particle image velocimetry to map the fluid flow profile in venules [7], arterioles [6], and in vitro collagen channels [20] to measure the hydrodynamic effect of the EGL. In these studies, particles are not observed close to the endothelial layer and EGL thickness is estimated by extrapolation of the measured flow profile to zero. Several mathematical models have been developed to estimate EGL material properties based on its composition, structure, and experimental observation [21–24]. However, direct measurement of flow mediated EGL material properties has remained elusive.
Here we use microrheology to directly measure the EGL. Microrheology is a set of tools and techniques designed to measure microscale material properties of soft materials such as the EGL. In one form of laser tweezers based microrheology pioneered in the lab of Dr. Halina Rubinsztein-Dunlop, small spherical vaterite crystals are optically rotated to probe local apparent viscosity in purely viscous and viscoelastic systems [25,26]. Vaterite is a birefringent form of crystalline CaCO3. It can however, be synthesized in the laboratory with a simple precipitation reaction. The resulting spherical vaterite particles are on the order of 1-10 µm in diameter and can be manipulated with optical tweezers. A trapped vaterite microsphere orients itself in the electric field such that it can be rotated with circularly polarized light. The applied torque can be accurately measured optically. When compared to the viscous drag torque for a rotating spherical particle in a Newtonian fluid, the apparent viscosity can be accurately determined [26]. Importantly, this form of microrheology applies continuous flow to the material, which is essential to measuring the material properties and hydrodynamic relevance of the EGL. However, published methods for measuring the angular momentum transfer require recollection of all the trapping light [26–28]. This has limited vaterite based microviscometry (VMV) to relatively thin samples. Here we present a method in which changes in apparent viscosity are detected by a serial calibration protocol, without the need for complete recollection of the forward scattered light. In our method we first measure trap stiffness and culture media viscosity from the linear displacement of silica beads far from a boundary. We then measure viscosity near to the vessel wall by first determining vaterite rotation rate and thus applied optical torque far from the wall. We apply this technique to the ex vivo porcine femoral artery, where we show a differential response in luminal apparent viscosity as a function of radial distance from the vessel wall in a system designed to preserve the EGL as compared to a system designed to collapse it.
2. Materials and methods
2.1. Experimental setup
All measurements were carried out using a custom built optical trapping and detection system as described previously [29], modified to apply and measure optical torque. Briefly, the trap is developed using a randomly polarized 1064 nm fiber laser (IPG Photonics, Oxford, MA). The beam passes through a calcite polarizer (105:1) and quarter wave plate to generate circular polarization, and expanded to fill the back aperture of the microscope objective. The forward scattered light is collected by the microscope condenser and the back focal plane of the microscope objective is imaged onto a quadrant photo diode (New Focus, Irvine, CA) for position detection. A glass coverslip was placed in front of the quadrant photo diode at a 45 degree angle to partially reflect the S-polarized component of forward scattered light. As the vaterite microsphere rotates, the S-polarized component will be modulated as detected by a photodiode (ThorLabs, Newton, NJ), which measures vaterite microsphere rotational orientation [26].
2.2. Calibration of trap stiffness and measurement of viscosity
The positional power spectral density of an optically trapped dielectric particle fluctuating in purely viscous media takes the form of a Lorentzian [30,31]:
| (1) |
where denotes the plateau value, f denotes frequency, and denotes the corner frequency. The corner frequency is expressed as:
| (2) |
whereis the trap stiffness and γ is the drag coefficient. For a spherical particle, the drag coefficient is simply for a bead of radius r in a Newtonian fluid of viscosity η. Thus, for a particle of known radius we can simply determine the trap stiffness from a measurement obtained in a purely viscous fluid of known viscosity [30–32]. On the other hand, once we have determined the trap stiffness, the same process yields a measurement of viscosity, provided the new fluid is of sufficiently similar index of refraction and the calibration and experimental measurements are conducted at the same temperature [33]. We will take advantage of this relationship in our serial calibration approach to VMV.
2.3. Passive microrheology (PMR)
At equilibrium, the imaginary part of the complex material response function is related to the power spectral density of probe particle position through the fluctuation-dissipation theorem. Provided the measurement is obtained with sufficiently high sampling frequency and duration, the real component can be recovered using the Kramer’s-Kronig integral [34], evaluated as serial discrete cosine and sine transforms [16,34,35]. Evaluation of the real component allows us to correct for the effect of the trap. The complex shear modulus is then determined using the Generalized Stokes Einstein Relationship [34].
2.4. Vaterite microsphere production
Vaterite microspheres were synthesized via a precipitation reaction [27] and stabilized [36] as previously described. One hundred µL of vaterite microsphere stock solution was washed 2X and resuspended in 100 µL of Millipore water for each experiment. Both stabilized and non-stabilized vaterite microspheres tends to bind electrostatically to glass surfaces, making optical manipulation difficult. We coated our glass bottom dishes (MatTek, Ashland, MA) with bovine serum albumin (BSA) by pre incubation with a 10% BSA solution in phosphate buffered saline at room temperature for ~30 minutes prior to the experiment to prevent this interaction. We note that BSA alone is unable to rescue a collapsed glycocalyx [37]. Furthermore, coating the glass or the vaterite microspheres themselves are equally effective in preventing the electrostatic binding (data not shown).
2.5. Tissue collection
Yucatan mini pigs of either sex (n = 3), weighing 30 kg, were initially sedated with ketamine, 20 mg/Kg and xylazine, 2 mg/Kg. Animals were intubated and then mechanically ventilated (Seimens Elema, Solna, Sweden) at a rate of 10 mL/Kg/hour and placed under general anesthesia (2.5% isoflurane). The animals had been used for a protease inhibition study under protocol: 2006-2674. At the conclusion of these studies, but prior to animal sacrifice, we administered heparin (300 units/Kg, IV), which we allowed to circulate for 90 seconds, and immediately administered intravenous euthasol, 10 mL. Following euthasol administration, 2.5 cm of femoral artery was collected. The excised tissue was immediately placed in modified KREBS-Henseleit buffer [38], placed on ice and transported from UCI Medical Center to UCI Main Campus. The cold tissue was then cut into rings of roughly 1 mm in thickness using a pair of sterilized safety razor blades. The rings were placed into incubation medium (EBM-2 + 10% FBS + 5 units/mL Pen/Strep) and allowed to recover for at least 2 hours at 37 ˚C and 5% CO2.
2.6. Data collection
A femoral artery ring was placed in a number zero BSA coated glass bottom dish and held in place with a weight. The dish was filled with either “EGL collapsing” media (Modified KREBS-Henseleit buffer + 1% BSA) or “EGL preserving” media (incubation medium). Samples were placed on the microscope stage within a XY piezo insert (Physik Instrumente, Karlsruhe, Germany) and kept warm (24.6° C) with an objective warmer (Warner Instruments, Hamden, CT). Five μL of the vaterite microsphere solution were added and a single vaterite microsphere was selected which was both round in appearance and able to rotate in the trap without noticeable wobble. The vaterite microsphere was moved to a location at least 20 µm from the vessel endothelium, which typically was more than 50 µm above the glass surface. Photodiode output was recorded at 10 kHz for one second and transformed by fast Fourier transform to determine the rotational frequency. Measurements were repeated five times. The microsphere was then stepped towards the wall in 0.5 µm steps using the piezo insert, until the microsphere was displaced from the trap after contacting the vessel wall. For each position, the gap thickness was measured as the shortest distance between the vessel wall and the surface of the microsphere. Next, 1 µm diameter silica beads (Bangs Laboratories, Fishers, IN) were pipetted into the vessel lumen and a single silica bead was trapped hundreds of microns away from the vessel wall and at least 5 µm above the cover glass. Silica bead fluctuations were recorded by sampling QPD signals at 100 kHz for 60 seconds. The viscosity was then determined by solving Eq. (2) after computing by fitting a Lorentzian function to the microsphere position power spectrum. In “solid boundary” experiments, the femoral artery ring was replaced by a 0.5 inch diameter, number 1.5 glass cover slip placed in water at room temperature. VMV data acquisition was carried out as described above.
2.7. Posterior calibration
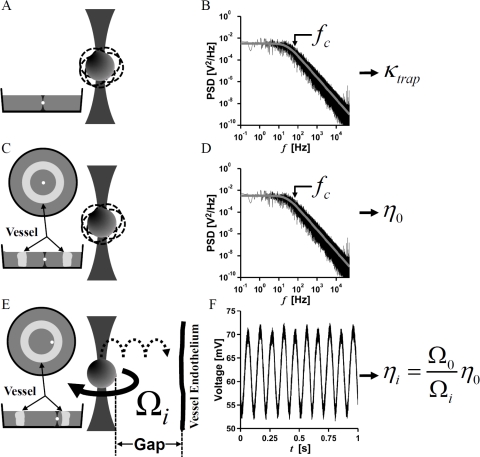
Our approach to VMV near to a thick sample such as a vessel slice is to solve for apparent viscosity near the vessel by comparing the rotational rate to that measured far from the vessel. A schematic of our approach is shown in Fig. 1 . The local viscosity of fluid surrounding a vaterite microsphere rotating at far from a boundary is given by [26,27]:
| (3) |
whereis the difference in input vs. output circular polarization, P is the laser power, ω is the frequency of the trapping light, and is the rotational frequency of the vaterite microsphere. It is assumed that input polarization is known, all the trapping light is recollected, the fluid is continuous on the length scale of the microsphere and boundary effects are insignificant. This condition is satisfied far from the vessel wall. Consider a microsphere rotating near to, or within the EGL at rotational rate If measurements are made on the same microsphere far from the wall, but at the same laser wavelength, polarization and power, then we can normalize the equation for viscosity at position ‘i’ by Eq. (3):
Fig. 1.
Schematic of experimental approach. Laser trap stiffness, is first measured by trapping a particle of known diameter in water (A), and then determining the corner frequency from a Lorentzian fit to the power spectral density of particle fluctuations (B). is related to the corner frequency by Eq. (2). The procedure is repeated in the center of an excised vessel slice (C), where the corner frequency of the power spectral density (D) is used to determine the viscosity,of the culture media by Eq. (2). The apparent viscosity, as a function of gap thickness is determined by optically measuring the rotation rate of a vaterite particle rotating under constant optical torque at various distances from the vessel wall (E). For each gap thickness, is calculated by measuring vaterite particle rotation rate and Eq. (5) (F).
| (4) |
Thus, the apparent viscosity
| (5) |
is simply a function of and vaterite microsphere rotation rate. Since can be determined from fluctuation analysis of silica beads (Fig. 1 C) far from the wall using Eqs. 1 and 2 and vaterite microsphere rotation rate (Fig. 1 F) can be determined without the use of a high numerical aperture condenser, we can extend VMV to relatively thick samples. This will hold for culture medium that is linear across observable frequencies.
3. Results
3.1. VMV in water near a solid boundary
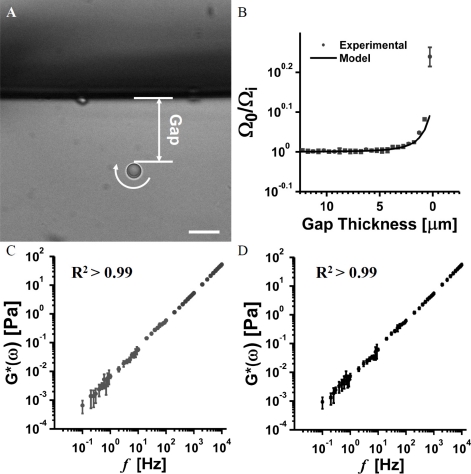
To validate our method, we first measured the apparent viscosity at each position as a function of gap thickness by VMV with a 4.5 µm vaterite microsphere rotating at 6.4 Hz approaching a solid boundary comprising a glass wall (Fig. 2 A ). The ratio remains near unity until the surface of the microsphere was approximately 3 µm from the boundary (Fig. 2 B). In Fig. 2 B, the data is fit to the model presented by Leach et. al. [39] for a sphere rotating about an axis perpendicular to surface normal of a nearby solid boundary (residual = 0.0791). Important to our method, both culture media preparations behave as linearly viscous materials (R2 > 0.99) with cP and cP (95% confidence interval) across observable frequencies as assessed by PMR (Figs. 2 C and D).
Fig. 2.
Validating VMV near a glass boundary and linearity of our culture media. (A) A 4.5 µm vaterite microsphere rotating at 6.4 Hz in water at room temperature near a solid boundary comprising a glass wall. The gap thickness is measured as shown. Scale bar is 10 µm (B) Experimental data and fit of relative rotation rates as a function of gap thickness. The residual of fit is 0.0791, mostly due the point closest to the boundary. Note the fine scale on the vertical axis. (C) PMR measurement in EGL collapsing media. (D) PMR measurement in EGL preserving media. PMR confirms linearity of the culture media across observed frequencies.
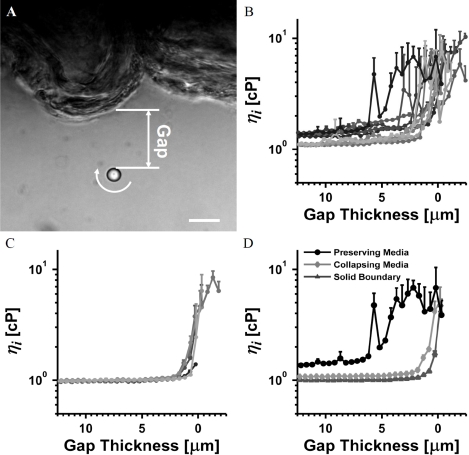
3.2. VMV in excised vessel slices
VMV was performed in excised vessels (Fig. 3 A ) cultured in media known to preserve or collapse the EGL [4,37]. As seen in Fig. 3 A, a vessel slice buckles when removed from an intact vessel due to tissue prestress [40]. Using Eq. (5), was measured by vaterite microspheres approaching the vessel wall in media known to preserve EGL structure [4,37] (Fig. 3 B). Viscosity was determined to be spatially heterogeneous and significantly greater than that of the media far from the vessel wall or that in Fig. 2 B for a solid glass boundary. In contrast, spatial variation in viscosity was confined to a region closer to the wall for vessel slices cultured in media chosen to collapse the EGL (Fig. 3 C), as expected. To highlight role of the EGL in modulating viscosity, sample curves from each condition are plotted together in Fig. 3 D.
Fig. 3.
VMV of the EGL in an excised porcine femoral artery. (A) A 4.7 µm vaterite microsphere rotating at 6.0 Hz in EGL preserving media near the endothelium of an excised vessel slice. The gap thickness is measured as shown. Scale bar is 10 µm. (B) Apparent viscosity, measured in an excised vessel slice cultured in EGL preserving media (C) Apparent viscosity, measured in an excised vessel slice cultured in EGL collapsing media. (D) Representative data for vessel experiments in EGL preserving and collapsing media, as well as the solid glass boundary experiment in water highlight role of the EGL in modulating local apparent viscosity.
4. Discussion
Much interest has been expressed towards measuring the material properties of the EGL [15,16], as it may play key roles in regulating blood flow and vessel reactivity [4]. Mimetic solutions have been previously measured by passive rheology [15,16], a powerful method that reports broad spectrum measures of shear modulus. However PMR and oscillatory active microrheology methods do not set up continuous flow, and will likely report different material properties than VMV since the EGL is comprised of an entangled meshwork of long fibrous components [4,16], which may rearrange themselves under flow. Typically biological materials exhibit nonlinear material properties in which strain [29,41,42] and strain rate [15,16,43] modulate elastic and viscous moduli. As such, it is expected that the EGL will behave differently when probed by an oscillating microsphere as compared to a continuously rotating one.
VMV has been demonstrated to measure small volumes of fluid, both linear [27] and non-linear [25,26], through continuous rotation of a vaterite microsphere under constant optical torque. Our group has long sought a method for extending VMV to the direct measurement of EGL hydrodynamic effects [6,7] in arteries, in which collection of all the forward scattered light is not feasible and multiple scattering within the thick tissue will randomize polarization independent of vaterite microsphere-material interactions, thus affecting our measurement of optical torque. Important to our method, measurement of S polarization by partial reflection off the glass coverslip maintains sufficient signal to noise to extract rotational position of the vaterite microsphere (Fig. 1 F).
In our approach to VMV, the rotational position is recorded as described, but the applied optical torque is not measured directly. Instead, we take advantage of the relatively large vessel lumen to measure the applied torque in situ. We use passive fluctuation analysis (Fig. 1 B and D) to first characterize the media, and then calculate the applied torque from measured vaterite microsphere rotation rates (Fig. 1 F). We maintain a constant laser power and assume torque is not modulated significantly as we move the vaterite microsphere towards the EGL. Critical to our method is the assumption of linearity with respect to the viscous behavior of the culture media, which we validated using PMR as shown in Figs. 2 C and D. Since the viscosity of the media is frequency independent, changes in microsphere rotation frequency can be attributed to changes in the microenvironment. Therefore, modulation of apparent viscosity shown in Figs. 3 B - D must be a result of either a boundary condition or the presence of the EGL, which is notoriously difficult to image [3,4], but can be ‘felt’ by the rotating microsphere.
Since the shape of the vessel wall is not easily determined, and more so for the EGL, models for extracting material properties from VMV will not be exact. However, much can be gained from understanding the differential apparent viscosity under varying physiological conditions. By rotating a microsphere towards a glass boundary (Figs. 2 A and B), we established a baseline against which we compare vessel measurements. Our solid glass boundary data was well described and validated by the Leach model, and consistent with previously reported VMV results [39]. When a rotating vaterite microsphere approaches a collapsed EGL, resembles that observed in the solid boundary experiments until the microsphere is just against the vessel wall (Figs. 3 B and C). Deviation from the solid boundary condition in data near the wall may be attributed to vessel geometry and the presence of a collapsed EGL. For the first time, we have observed the viscous properties of the intact arterial EGL as shown in Figs. 3 B and D. As compared to both the solid boundary and the collapsed EGL experiment, the intact EGL modulates viscosity far from the cell plasma membrane, with increasing by 3X at a gap thickness of 6 µm. In situ exclusion [5] and imaging [44] experiments suggest the EGL thickness ranges from 0.4 to 4.5 µm, but do not report a measure of its effect on hydrodynamics. Interestingly our vaterite microspheres are similar in size to red blood cells and report hydrodynamic effects 6 µm from the solid cell boundary, beyond the limits of the EGL as reported in dye exclusion experiments. Our application of VMV opens the door to quantitatively analyze the role of the EGL in determining near wall hemodynamics, the distribution of shear stresses on the endothelial lining, and vascular mechano-sensing. With the development of our posterior calibration methods, we can now proceed to integrate VMV with either dye exclusion or fluorescently labeled HA binding protein measures of EGL geometry to quantitatively model EGL properties.
Acknowledgments
The authors thank Dr. Halina Rubinsztein-Dunlop for assistance in developing vaterite microviscometry protocols, Linda McCarthy, Claire Robertson consulting in tissue culture and Jian Zhou consulting in vessel slice mounting. Support for this research was provided by the National Science Foundation (DMR-0805164) and the National Institutes of Health (P41- RR001192 and R01-HL085339).
References and links
- 1.Davies P. F., “Flow-mediated endothelial mechanotransduction,” Physiol. Rev. 75(3), 519–560 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chien S., “Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell,” Am. J. Physiol. Heart Circ. Physiol. 292(3), H1209–H1224 (2007). 10.1152/ajpheart.01047.2006 [DOI] [PubMed] [Google Scholar]
- 3.Reitsma S., Slaaf D. W., Vink H., van Zandvoort M. A. M. J., oude Egbrink M. G. A., “The endothelial glycocalyx: composition, functions, and visualization,” Pflugers Arch. 454(3), 345–359 (2007). 10.1007/s00424-007-0212-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weinbaum S., Tarbell J. M., Damiano E. R., “The structure and function of the endothelial glycocalyx layer,” Annu. Rev. Biomed. Eng. 9(1), 121–167 (2007). 10.1146/annurev.bioeng.9.060906.151959 [DOI] [PubMed] [Google Scholar]
- 5.Vink H., Duling B. R., “Identification of distinct luminal domains for macromolecules, erythrocytes, and leukocytes within mammalian capillaries,” Circ. Res. 79(3), 581–589 (1996). [DOI] [PubMed] [Google Scholar]
- 6.Savery M. D., Damiano E. R., “The endothelial glycocalyx is hydrodynamically relevant in arterioles throughout the cardiac cycle,” Biophys. J. 95(3), 1439–1447 (2008). 10.1529/biophysj.108.128975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Smith M. L., Long D. S., Damiano E. R., Ley K., “Near-wall micro-PIV reveals a hydrodynamically relevant endothelial surface layer in venules in vivo,” Biophys. J. 85(1), 637–645 (2003). 10.1016/S0006-3495(03)74507-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thi M. M., Tarbell J. M., Weinbaum S., Spray D. C., “The role of the glycocalyx in reorganization of the actin cytoskeleton under fluid shear stress: a “bumper-car” model,” Proc. Natl. Acad. Sci. U.S.A. 101(47), 16483–16488 (2004). 10.1073/pnas.0407474101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tarbell J. M., Pahakis M. Y., “Mechanotransduction and the glycocalyx,” J. Intern. Med. 259(4), 339–350 (2006). 10.1111/j.1365-2796.2006.01620.x [DOI] [PubMed] [Google Scholar]
- 10.Oohira A., Wight T. N., Bornstein P., “Sulfated proteoglycans synthesized by vascular endothelial cells in culture,” J. Biol. Chem. 258(3), 2014–2021 (1983). [PubMed] [Google Scholar]
- 11.Halden Y., Rek A., Atzenhofer W., Szilak L., Wabnig A., Kungl A. J., “Interleukin-8 binds to syndecan-2 on human endothelial cells,” Biochem. J. 377(2), 533–538 (2004). 10.1042/BJ20030729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rosenberg R. D., Shworak N. W., Liu J., Schwartz J. J., Zhang L., “Heparan sulfate proteoglycans of the cardiovascular system. Specific structures emerge but how is synthesis regulated?” J. Clin. Invest. 99(9), 2062–2070 (1997). 10.1172/JCI119377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kokenyesi R., Bernfield M., “Core protein structure and sequence determine the site and presence of heparan sulfate and chondroitin sulfate on syndecan-1,” J. Biol. Chem. 269(16), 12304–12309 (1994). [PubMed] [Google Scholar]
- 14.Itano N., Sawai T., Yoshida M., Lenas P., Yamada Y., Imagawa M., Shinomura T., Hamaguchi M., Yoshida Y., Ohnuki Y., Miyauchi S., Spicer A. P., McDonald J. A., Kimata K., “Three isoforms of mammalian hyaluronan synthases have distinct enzymatic properties,” J. Biol. Chem. 274(35), 25085–25092 (1999). 10.1074/jbc.274.35.25085 [DOI] [PubMed] [Google Scholar]
- 15.Nijenhuis N., Mizuno D., Spaan J. A., Schmidt C. F., “Viscoelastic response of a model endothelial glycocalyx,” Phys. Biol. 6(2), 025014 (2009). 10.1088/1478-3975/6/2/025014 [DOI] [PubMed] [Google Scholar]
- 16.Nijenhuis N., Mizuno D., Schmidt C. F., Vink H., Spaan J. A. E., “Microrheology of hyaluronan solutions: implications for the endothelial glycocalyx,” Biomacromolecules 9(9), 2390–2398 (2008). 10.1021/bm800381z [DOI] [PubMed] [Google Scholar]
- 17.Henry C. B. S., Duling B. R., “Permeation of the luminal capillary glycocalyx is determined by hyaluronan,” Am. J. Physiol. 277(2 Pt 2), H508–H514 (1999). [DOI] [PubMed] [Google Scholar]
- 18.Yoneda A., Couchman J. R., “Regulation of cytoskeletal organization by syndecan transmembrane proteoglycans,” Matrix Biol. 22(1), 25–33 (2003). 10.1016/S0945-053X(03)00010-6 [DOI] [PubMed] [Google Scholar]
- 19.Jensen P. V., Larsson L. I., “Actin microdomains on endothelial cells: association with CD44, ERM proteins, and signaling molecules during quiescence and wound healing,” Histochem. Cell Biol. 121(5), 361–369 (2004). 10.1007/s00418-004-0648-2 [DOI] [PubMed] [Google Scholar]
- 20.Potter D. R., Damiano E. R., “The hydrodynamically relevant endothelial cell glycocalyx observed in vivo is absent in vitro,” Circ. Res. 102(7), 770–776 (2008). 10.1161/CIRCRESAHA.107.160226 [DOI] [PubMed] [Google Scholar]
- 21.Damiano E. R., Stace T. M., “A mechano-electrochemical model of radial deformation of the capillary glycocalyx,” Biophys. J. 82(3), 1153–1175 (2002). 10.1016/S0006-3495(02)75474-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Han Y., Weinbaum S., Spaan J. A. E., Vink H., “Large-deformation analysis of the elastic recoil of fibre layers in a brinkman medium with application to the endothelial glycocalyx,” J. Fluid Mech. 554(-1), 217–235 (2006). 10.1017/S0022112005007779 [DOI] [Google Scholar]
- 23.Secomb T. W., Hsu R., Pries A. R., “Motion of red blood cells in a capillary with an endothelial surface layer: effect of flow velocity,” Am. J. Physiol. Heart Circ. Physiol. 281(2), H629–H636 (2001). [DOI] [PubMed] [Google Scholar]
- 24.Weinbaum S., Zhang X., Han Y., Vink H., Cowin S. C., “Mechanotransduction and flow across the endothelial glycocalyx,” Proc. Natl. Acad. Sci. U.S.A. 100(13), 7988–7995 (2003). 10.1073/pnas.1332808100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Knoner G., Parkin S., Heckenberg N. R., Rubinsztein-Dunlop H., “Characterization of optically driven fluid stress fields with optical tweezers,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72(3), 031507 (2005). 10.1103/PhysRevE.72.031507 [DOI] [PubMed] [Google Scholar]
- 26.S. J. W. Parkin, G. G. Knoener, T. A. Nieminen, N. R. Heckenberg, and H. Rubinsztein-Dunlop, “A constant torque micro-viscometer,” in Nanomanipulation with Light (SPIE, San Jose, CA, USA, 2005), pp. 59–65. [Google Scholar]
- 27.Bishop A. I., Nieminen T. A., Heckenberg N. R., Rubinsztein-Dunlop H., “Optical microrheology using rotating laser-trapped particles,” Phys. Rev. Lett. 92(19), 198104 (2004). 10.1103/PhysRevLett.92.198104 [DOI] [PubMed] [Google Scholar]
- 28.Nieminen T. A., Heckenberg N. R., Rubinsztein-dunlop H., “Optical measurement of microscopic torques,” J. Mod. Opt. 48, 405–413 (2001). [Google Scholar]
- 29.Kotlarchyk M. A., Shreim S. G., Alvarez-Elizondo M. B., Estrada L. C., Singh R., Valdevit L., Kniazeva E., Gratton E., Putnam A. J., Botvinick E. L., “Concentration independent modulation of local micromechanics in a fibrin gel,” PLoS ONE 6(5), e20201 (2011). 10.1371/journal.pone.0020201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Allersma M. W., Gittes F., deCastro M. J., Stewart R. J., Schmidt C. F., “Two-dimensional tracking of ncd motility by back focal plane interferometry,” Biophys. J. 74(2), 1074–1085 (1998). 10.1016/S0006-3495(98)74031-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Svoboda K., Block S. M., “Biological applications of optical forces,” Annu. Rev. Biophys. Biomol. Struct. 23(1), 247–285 (1994). 10.1146/annurev.bb.23.060194.001335 [DOI] [PubMed] [Google Scholar]
- 32.Schnurr B., Gittes F., MacKintosh F. C., Schmidt C. F., “Determining microscopic viscoelasticity in flexible and semiflexible polymer networks from thermal fluctuations,” Macromolecules 30(25), 7781–7792 (1997). 10.1021/ma970555n [DOI] [Google Scholar]
- 33.Peterman E. J. G., Gittes F., Schmidt C. F., “Laser-induced heating in optical traps,” Biophys. J. 84(2), 1308–1316 (2003). 10.1016/S0006-3495(03)74946-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mizuno D., Head D. A., MacKintosh F. C., Schmidt C. F., “Active and passive microrheology in equilibrium and nonequilibrium systems,” Macromolecules 41(19), 7194–7202 (2008). 10.1021/ma801218z [DOI] [Google Scholar]
- 35.Gittes F., Schnurr B., Olmsted P. D., MacKintosh F. C., Schmidt C. F., “Microscopic viscoelasticity: Shear moduli of soft materials determined from thermal fluctuations,” Phys. Rev. Lett. 79(17), 3286–3289 (1997). 10.1103/PhysRevLett.79.3286 [DOI] [Google Scholar]
- 36.Vogel R., Persson M., Feng C., Parkin S. J., Nieminen T. A., Wood B., Heckenberg N. R., Rubinsztein-Dunlop H., “Synthesis and surface modification of birefringent vaterite microspheres,” Langmuir 25(19), 11672–11679 (2009). 10.1021/la901532x [DOI] [PubMed] [Google Scholar]
- 37.Adamson R. H., Clough G., “Plasma proteins modify the endothelial cell glycocalyx of frog mesenteric microvessels,” J. Physiol. 445, 473–486 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mochizuki S., Vink H., Hiramatsu O., Kajita T., Shigeto F., Spaan J. A. E., Kajiya F., “Role of hyaluronic acid glycosaminoglycans in shear-induced endothelium-derived nitric oxide release,” Am. J. Physiol. Heart Circ. Physiol. 285(2), H722–H726 (2003). [DOI] [PubMed] [Google Scholar]
- 39.Leach J., Mushfique H., Keen S., Di Leonardo R., Ruocco G., Cooper J. M., Padgett M. J., “Comparison of Faxén’s correction for a microsphere translating or rotating near a surface,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 79(2), 026301 (2009). 10.1103/PhysRevE.79.026301 [DOI] [PubMed] [Google Scholar]
- 40.Fung Y. C., “What are the residual stresses doing in our blood vessels?” Ann. Biomed. Eng. 19(3), 237–249 (1991). 10.1007/BF02584301 [DOI] [PubMed] [Google Scholar]
- 41.Brown A. E. X., Litvinov R. I., Discher D. E., Purohit P. K., Weisel J. W., “Multiscale mechanics of fibrin polymer: gel stretching with protein unfolding and loss of water,” Science 325(5941), 741–744 (2009). 10.1126/science.1172484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Winer J. P., Oake S., Janmey P. A., “Non-linear elasticity of extracellular matrices enables contractile cells to communicate local position and orientation,” PLoS ONE 4(7), e6382 (2009). 10.1371/journal.pone.0006382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Errill E. W., “Rheology of blood,” Physiol. Rev. 49(4), 863–888 (1969). [DOI] [PubMed] [Google Scholar]
- 44.Megens R. T., Reitsma S., Schiffers P. H., Hilgers R. H., De Mey J. G., Slaaf D. W., oude Egbrink M. G., van Zandvoort M. A., “Two-photon microscopy of vital murine elastic and muscular arteries,” J. Vasc. Res. 44(2), 87–98 (2007). 10.1159/000098259 [DOI] [PubMed] [Google Scholar]