Abstract
Gentamicin is commonly used in the management of neonatal infections. Development of adaptive resistance is typical for aminoglycosides and reduces the antibacterial effect. There is, however, a lack of understanding of how this phenomenon influences the effect of different dosing schedules. The aim was to develop a pharmacokinetic-pharmacodynamic (PKPD) model that describes the time course of the bactericidal activity of gentamicin and its adaptive resistance and to investigate different dosing schedules in preterm and term newborn infants based on the developed model. In vitro time-kill curve experiments were conducted on a strain of Escherichia coli (MIC of 2 mg/liter). The gentamicin exposure was either constant (0.125 to 16 mg/liter) or dynamic (simulated concentration-time profiles in a kinetic system with peak concentrations of 2.0, 3.9, 7.8, and 16 mg/liter given as single doses or as repeated doses every 6, 12, or 24 h). Semimechanistic PKPD models were fitted to the bacterial counts in the NONMEM (nonlinear mixed effects modeling) program. A model with compartments for growing and resting bacteria, with a function allowing the maximal bacterial killing of gentamicin to reduce with exposure, characterized both the fast bactericidal effect and the adaptive resistance. Despite a lower peak concentration, preterm neonates were predicted to have a higher bacterial killing effect than term neonates for the same per-kg dose because of gentamicin's longer half-life. The model supported an extended dosing interval of gentamicin in preterm neonates, and for all neonates, dosing intervals of 36 to 48 h were as effective as a 24-h dosing interval for the same total dose.
INTRODUCTION
Bacterial infections with Escherichia coli is common in both preterm and term newborn infants (31, 40), and gentamicin has traditionally been used as standard treatment for confirmed Gram-negative infections and also used empirically in suspected sepsis (37). The approach to dosing in newborns has been suggested to be based on their body weight, gestational age (GA), and postnatal age as these characteristics reflect the pharmacokinetics (PK) in this population (43). A three-compartment PK model of gentamicin disposition in preterm and term newborn infants was recently described based on a prospective study (35).
Gentamicin is an antibiotic with a concentration-dependent bacterial killing effect, and based on studies in vitro and in patients, it has been suggested that it is important to achieve a ratio of peak plasma concentration to MIC (Cmax/MIC) higher than 8 to 10 (12, 25, 30). Nephrotoxicity, a well-known side effect, has been suggested to be related to trough levels above 1 to 2 mg/liter (6, 9, 13). In order to increase the peak concentrations and allow for lower trough concentrations, the administration of gentamicin for adults has changed from three-times-daily dosing to an extended dosing interval of 24 h (33). In newborn infants dosing intervals of 24, 36, or 48 h with an increased daily dose are frequently used (11, 26, 33, 38). However, irrespective of the dosing there seems to be a need for therapeutic drug monitoring of gentamicin in this population (16, 17, 20, 39). The changed practice to extended dosing intervals of gentamicin has also been based on gentamicin's postantibiotic effect and the presence of adaptive or phenotypic resistance (3).
Adaptive resistance of gentamicin is a pharmacodynamic (PD) process that is characterized by a reversible refractoriness to the bactericidal action that has been demonstrated by in vitro and in vivo studies (4, 5, 14, 15, 44). The resistance emerges already at the initiation of therapy, is enhanced by higher exposures, and is augmented by consecutive doses if they are administered before the bacteria return to their susceptible stage (10). The time to full recovery of the susceptibility is longer for the higher doses (4). However, there is limited understanding of how the emergence of adaptive resistance (AR) is influenced by different dosing regimens.
PKPD models developed based on in vitro data may be used to predict bacterial killing following different dosing schedules. The adaptive resistance observed for Pseudomonas aeruginosa and Acinetobacter baumannii exposed to constant gentamicin concentrations has been modeled as an increase in 50% effective concentration (EC50) with time and drug concentration (41). However, this model predicts a continuous development of resistance as it is dependent on time, prohibiting the bacteria from reverting to the initial susceptibility when gentamicin exposure diminishes. In addition, the model does not consider the coexistence of sensitive and resting bacteria with different susceptibilities to antibacterial agents (21). While other PKPD models have this capability (36), they lack the capability to predict adaptive resistance without increasing the model complexity.
The aim of this work was to develop a predictive PKPD model that characterizes the bactericidal activities of a range of gentamicin exposures, both static and dynamic, and thereby to consider the development of adaptive resistance. This PKPD model was linked to a previously developed PK model in preterm and term newborn infants (35) to make predictions of the effectiveness of different gentamicin dosing schedules.
MATERIALS AND METHODS
Bacteria and media.
The bacteria used in all experiments were E. coli ATCC (American Type Culture Collection) 25922, and bacteria were grown on blood agar plates (Columbia agar base with 5% horse blood; Acumedia Manufactures Inc., Baltimore, MD). Six hours prior to the time-kill curve experiments, the bacteria were incubated in Mueller-Hinton (MH) broth (Difco) supplemented with Ca2+ and Mg2 at 35°C, resulting in an inoculum of approximately 109 CFU/ml.
Antibiotics.
Gentamicin (gentamicin sulfate salt) was obtained from Sigma-Aldrich (Schnelldorf, Germany). Stock solutions were prepared before each experiment by dissolving the antibiotic in sterile distilled water to a concentration of 10,000 to 12,000 mg/liter. The stock solution was diluted in MH broth to the desired concentrations. The MIC (2 mg/liter) was determined by using the macrodilution method, according to the guidelines of the Clinical and Laboratory Standards Institute (formerly NCCLS). Genetic resistance can be identified as an increase in MIC, but as adaptive resistance is reversible and dependent on drug concentration, MIC determinations that measure the susceptibility after an additional 16 to 20 h of drug exposure will not reflect the degree of adaptive resistance at the sampling time point. In a selection of experiments, samples were taken to check for possible drug degradation and to ascertain that the antibiotic concentration decreased as intended in the dynamic experiments, i.e., mimicking the concentration-time profile in newborns. The gentamicin concentrations were analyzed by fluorescence polarization immunoassay (TDx; Abbot Laboratories, Chicago, IL).
Time-kill curve experiments.
Two types of in vitro time-kill curve experiments were conducted: experiments with constant (static) gentamicin concentrations and experiments with dynamic gentamicin concentration-time profiles with a decline in drug concentration mimicking the kinetics of gentamicin in newborn infants. In both types of experiments, incubations were performed at 35°C, and samples were taken frequently, diluted in series, and cultivated on two to four blood agar plates. The blood agar plates were incubated at 35°C, and the numbers of colonies were counted manually after 18 to 24 h. For each concentration, the time-kill curve experiment was conducted in at least duplicates at different occasions. The limit of detection (LOD) was 10 CFU/ml.
Static time-kill curve experiments.
All static experiments were performed in 10-ml glass tubes with 4 ml of MH broth to which bacteria were added to obtain an initial inoculum of approximately 5 × 105 CFU/ml. Gentamicin was added to the bacterial cultures to achieve concentrations of 0.125, 0.25, 0.5, 1, 2, 4, and 16 mg/liter. All tubes were placed in sand to reduce temperature fluctuations. Samples were taken predose and at 1, 2, 3, 4, 6, 9, 12, and 24 h after the start of the experiments in order to follow the bacterial count. A growth control experiment, where no antibiotic was added to the tube, was conducted for each day of experiment. A second set of experiments with constant antibiotic concentrations was performed in order to study the inoculum effect. In these experiments the start inocula were prepared as described above, but the bacteria were allowed to grow for an additional 12 h, resulting in a bacterial count of approximately 109 CFU/ml, before gentamicin was added. The gentamicin concentrations used in these experiments were 1, 2, 4, and 16 mg/liter.
Dynamic time-kill curve experiments.
Experiments with dynamic concentration-time profiles were conducted in an in vitro kinetic system as described previously (29). The system consisted of an open-bottom glass flask with a magnetic stirrer for homogeneous mixing. The flask was attached to a bottom part but separated by two filters that functioned to maintain the bacteria in the flask. A pump (P-500; Pharmacia Biotech, Uppsala, Sweden) was connected to the bottom part, and this device pumped medium out from the flask to a sink vessel. The flask has two arms; in one of the arms there was a silicone membrane for repeated sampling, and the other arm was used to transport fresh medium to the flask to dilute the drug concentration.
The in vitro kinetic system was used to simulate a two-compartment concentration-time profile corresponding to the neonatal kinetics by application of two different flow rates. The flow rates were calculated based on typical PK parameter values in a preterm newborn infant of 1 kg that were obtained from an interim analysis of an ongoing clinical study at the neonatal ward at the University Children's Hospital, Uppsala, Sweden. From predicted concentration-time profiles, two rate constants were obtained: 0.33 h−1 for the first phase and 0.037 h−1 for the second phase, with corresponding flow rates in the in vitro kinetic system of 37 and 4 liters/h. The concentration-time profiles studied were those predicted to be obtained following gentamicin doses of 1, 2, 4, and 8 mg/kg as single or repeated doses in this population. The corresponding peak concentrations obtained in the system were 2.0, 3.9, 7.8, and 16 mg/liter, respectively. The 2-mg/kg dose (Cmax of 3.9 mg/liter) was studied with a 6- and 12-hourly dosing interval, and the 4- and 8-mg/kg doses (Cmax of 7.8 and 16 mg/liter, respectively) were studied with a 24-hourly dosing interval.
The flask was filled with 110 ml of sterile MH broth, and E. coli was added to the flask to obtain a start inoculum of 5 × 105 CFU/ml. Gentamicin was added to achieve the desired start concentrations described above. The pumps were initially set at 37 liters/h to mimic the first phase of drug decline. Four hours after the dose, the flow rate was changed to 4 liters/h to mimic the second phase of the pharmacokinetic profile. The change of the flow rate was repeated with subsequent dosing of gentamicin. Samples were taken predose and at 1, 2, 3, 4, and 6 h after the start of the experiments and thereafter continued with a frequency dependent on the respective dosing schedules. Each experiment was performed in duplicates or triplicates. For experiments where there were ambiguous results, e.g., regrowth of bacteria versus no regrowth, additional experiments were performed. This occurred for the experiments with a Cmax of 16 mg/liter every 24 h, where eventually two experiments showed bacterial counts below the LOD at the end of the experiment while in four experiments regrowth had occurred. Bacterial counts from all experiments were included in the modeling.
Semimechanistic PKPD model building.
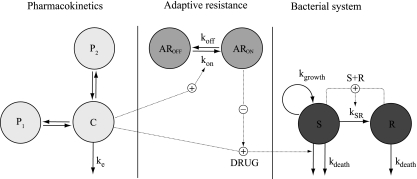
A previously developed semimechanistic model for antibiotics (36) formed the basis and was expanded to evaluate different functions describing the adaptive resistance development (Fig. 1). The model has compartments for drug-susceptible, growing bacteria (S) and insusceptible, resting bacteria (R) with first-order rate constants for growth (kgrowth) and natural death (kdeath). The relationship in the absence of antibiotics can be described by the equations below:
| (1) |
| (2) |
All bacteria were here assumed to be in the growing stage (S) at the start of the experiments. The bacteria transfer into a resting stage (R), with the rate constant kSR, when the total bacterial content in the system increases. Eventually, the bacterial count approaches a stationary phase where the total bacterial population is no longer increasing. In the resting stage, there is no bacterial growth, but the bacteria are assumed to have the same natural death rate (kdeath) as bacteria in the growing stage. In the current model, kdeath was fixed to 0.179 h−1, the value obtained in the previous study (36), as there was limited information on this parameter in these experiments and fixing the parameter stabilized the model.
Fig 1.
Schematic illustration of the final PKPD model. The bacteria are either in a proliferating and drug-susceptible compartment (S) or in a resting and drug-insusceptible compartment (R). The bacteria multiply with a first-order rate constant in the susceptible compartment (kgrowth), and the bacteria in both compartments are affected by a first-order natural death rate (kdeath). The total bacterial content in the system (S + R) stimulates the transfer from the proliferating stage into the resting stage (kSR) when numbers of bacteria are above an estimated number. The central compartment, with a first-order elimination rate (ke), was driving the killing of the bacteria. The PD model included a binding model with a rate constant for development (kon) of adaptive resistance (AR), which was stimulated by the gentamicin concentration and a rate constant for return to susceptibility (koff). The degree of AR resulted in a reduction of the maximum bacterial killing of gentamicin (Emax). In the dynamic in vitro experiments and in model development, the PK model was a two-compartment model with one peripheral compartment (P1), while in the predictions a three-compartment model with two peripheral compartments (P1 and P2) was applied.
The transfer rate constant kSR was set to be equal to a proportionality constant times the total number of bacteria in the system (S + R). The maximum number of bacteria in the stationary phase (Bmax) is derived from the difference between the rate constant of growth (kgrowth) and the rate constant of death (kdeath), divided by this proportionality constant. As in the previous model, it was assumed that there was no transfer from the resting to the proliferating bacterial stage (kRS = 0) as there was minimal improvement in the model fit when the rate constant kRS was estimated. To be able to predict the pronounced bacterial killing observed following high gentamicin exposures, kSR was here set to be zero at low bacterial counts, and the transfer from the sensitive stage into the resting stage occurred only when the total bacterial content in the system exceeded an estimated breakpoint value (BP).
The drug effect on bacterial killing (DRUG; equation 3) and on the adaptive resistance (AR) (equation 4) was incorporated into equation 1 as described in equation 5. The drug affected only the bacteria in the growing susceptible stage (S).
| (3) |
| (4) |
| (5) |
The influence of gentamicin in killing the bacteria was best described by a simple Emax model as Emax models were significantly better than linear models, and there was no improvement in the fit when γ was allowed to be estimated and to be different from 1. Emax(0) represents the maximal achievable rate constant of bacterial killing when no adaptive resistance has developed while EC50 is the antibiotic concentration that results in 50% of Emax(0).
The presence of gentamicin-initiated adaptive resistance development was in the final model described as a binding function (1), where the degree of binding resulted in a reduction of Emax from its initial value [Emax(0)] (equation 4 and Fig. 1). At the start of the experiments the amount in the compartment representing the adaptive resistance in the “off” state (AROFF) was set to 1, and the amount in the compartment describing the degree of adaptive resistance in the “on” state (ARON) was zero. The gentamicin concentration was driving the amount to transfer from AROFF to ARON, and kon and koff describe the rate of development and reversal of adaptive resistance, respectively (equations 6 and 7). The inhibition of Emax was determined by the fraction of the amount in ARON, and AR50 describes the estimated value of ARON when Emax is reduced by 50% (equation 4).
| (6) |
| (7) |
Several other different models for adaptive resistance were also evaluated: a function where EC50 of gentamicin at the initiation of the experiment [EC50(0)] increases with time (t) and gentamicin concentration (C), according to the equation EC50 = EC50(0)·(1 − e−kCt) (41); a turnover model (18) where increased gentamicin concentrations increased the production of a hypothetical variable that influenced EC50; and a model including an additional compartment with growing, insusceptible bacteria and where the gentamicin concentration was driving the rate of bacteria transferring from the susceptible compartment to this compartment of adaptively resistant bacteria.
Although there was a fast killing, a time delay might exist between the addition of a drug and bacterial killing, and to account for this, several models were assessed including an effect compartment and lag time and transit compartments.
As there was no observed degradation of gentamicin in these experiments, the rate constant of drug elimination (Fig. 1, ke) was set to 0 for the static experiments. For the data derived in the dynamic experiments, ke values were set to the values of 0.33 and 0.037 h−1 for the two phases, according to the simulated elimination rates in the kinetic system as described above.
Data analysis.
All bacterial count data were transformed into natural logarithms prior to data analysis and were fitted simultaneously. All plates with detectable numbers of bacteria were included, and hence there was generally more than one observation per sampling time point and experiment included in the analysis. In order to avoid the bias that can occur due to correlations between replicate samples, the residual error was estimated as two components: one consistent difference common for all replicates at the same time point and experiment (residual error [RE]) and one replicate-specific difference (replicate RE [RRE]) (23). For time points where all dilutions had bacterial counts below the LOD, the probability for the observation to be below the LOD was estimated using the M3 method for handling data below the LOD (2, 7).
The mean tendencies in the population, i.e., the typical parameter values, were estimated along with random effects described by the residual errors. Interexperimental variability was not estimated. Model performance was assessed by evaluation of diagnostic plots and the objective function value (OFV). In order to discriminate between nested models, the difference in OFVs (−2 log likelihood) was used. The more complex model was selected when the reduction in OFV was at least 10.83 (P value of <0.001 for 1 degree of freedom). The model was also evaluated by performing visual predictive checks (VPC) (24) with stratification on the type of experiments and on the concentration of gentamicin used. A total of 1,000 replicates were simulated by using the original data set as a template. Log-likelihood profiling was utilized to obtain standard errors of the parameters.
Predictions of dosing schedules.
Gentamicin concentration-time profiles and E. coli counts were predicted based on the final model for four typical newborn infants with gestational ages (GA) of 25, 29, 34, and 40 weeks and birth weights (WT) of 778, 1,200, 2,710, and 3,500 g, respectively. The typical ages and weights were selected based on the same gentamicin study from which the three-compartment PK model was chosen to drive the bacterial killing in the predictions (35). A starting inoculum of 4.83 × 105 CFU/ml, the average value of all starting inocula in the experiments, was applied in all predictions. The treatments were assumed to start on the day of birth and included doses of 2 to 7 mg/kg administered at dosing intervals ranging between 8 and 48 h as 5-min infusions.
Software.
The data were analyzed using the Laplacian method and ADVAN9 within the population analysis software NONMEM (nonlinear mixed effects modeling), versions VI and VII (8). NONMEM was also used to predict concentration-versus-time and bacterial count-versus-time profiles. The Xpose program (version 4) (22) and R (version 2.10 [www.r-project.org]) were used for data set review and graphical evaluation. Simulations and calculations for VPC and execution of log-likelihood profiling were performed using Perl speaks NONMEM (PsN) (28).
RESULTS
Time-kill curve experiments.
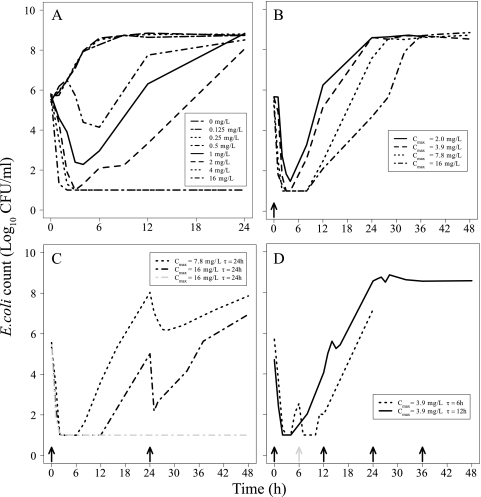
From 48 static experiments and 25 dynamic experiments, there were a total of 1,695 data points (where 168 data time points entered in the data set were below the LOD) in the data analysis. Time-kill curves for typical experiments are shown in Fig. 2. The bacteria exposed to no gentamicin or low concentrations of gentamicin were initially growing exponentially, but at high inocula the growth rate reduced to approach a maximum bacterial count of approximately 109 CFU/ml. In the static experiments (Fig. 2A) regrowth occurred for concentrations of 0.5, 1, and 2 mg/liter while the bacterial count remained below the LOD during the 24 h of incubation following exposures to concentrations of 4 and 16 mg/liter. In the experiments where the bacteria were grown for 12 h before the addition of the antibiotic, an antibacterial effect was seen only for the highest concentration used, i.e., 16 mg/liter. In all dynamic experiments with single doses administered at time zero (Fig. 2B), regrowth occurred. There was consistently a limited bacterial killing effect with subsequent doses of the same size, indicating development of resistance (Fig. 2C and D).
Fig 2.
Typical time-kill curves for E. coli exposed to gentamicin. (A) Static time-kill curve experiments with concentrations ranging between 0 and 16 mg/liter. (B) Dynamic time-kill curve experiments with four single doses (Cmax of 2.0, 3.9, 7.8, or 16 mg/liter). (C) Dynamic time-kill curve experiments with repeated dosing (Cmax of 7.8 or 16 mg/liter) administered at 24-h intervals. (D) Dynamic time-kill curve experiments with repeated dosing (Cmax = 3.9 mg/liter) with a single second dose at 6 h or at 12 h interval. In panel C, some experiments with a Cmax of 16 mg/liter showed bacterial regrowth at approximately 12 h (black dash-dotted line) while others had bacterial counts that stayed below limit of detection throughout the experiment (gray dash-dotted line). Arrows indicate the times of dose administration. Gray arrow in panel D indicates the second dose at 6 h. Bacterial counts below limit of detection are plotted as 10 CFU/ml.
Semimechanistic PKPD model.
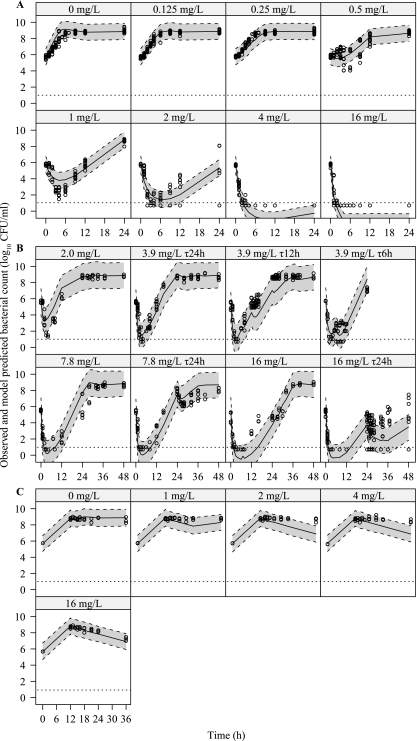
As expected, the original semimechanistic PKPD model (36) could not describe the gentamicin data well due to the development of adaptive resistance, and the model was therefore further expanded. The final model described in Fig. 1 characterized the observed adaptive resistance development by the binding function (1), and as indicated by the VPC, the model described the observed data well for both static and dynamic experiments (Fig. 3A and B). For the experiments where the bacteria were allowed to grow for 12 h prior to addition of gentamicin (Fig. 3C), the model overpredicted the antibacterial effect when the bacteria were exposed to gentamicin concentrations of 2 and 4 mg/liter.
Fig 3.
Visual predictive checks for the final model with observed bacterial counts (o), as well as the median (solid line) and the 80% prediction interval (dashed line) of the simulated data. (A) Growth controls and experiments with static gentamicin concentrations. (B) Dynamic experiments using single and repeated dosing regimens (for 3.9 mg/liter every six hours, only one additional dose was administered). (C) Experiments with static gentamicin concentrations added after a 12-h period of bacterial growth.
The parameter estimates of the final model were all estimated with acceptable precision (Table 1). Gentamicin had a fast bactericidal effect, with a maximum killing rate constant [Emax(0)] of 51 h−1 and an EC50 of 9.85 mg/liter. The growth rate constant was estimated at 2.00 h−1. The rate constant for the development of adaptive resistance in the presence of gentamicin (kon) was estimated at 0.0426 liters mg−1 h−1 while there was limited information in the data on the half-life for the bacteria to return to the susceptible state after adaptive resistance developed (ln 2/koff). This parameter was therefore fixed to 50 h as lower half-lives resulted in an increased OFV. The estimated value of AR50 indicated that the maximum Emax inhibition by the adaptive resistance mechanism was 90% as the maximum amount possible in ARON is 1 [1/(1 + 0.113)]. Experiments performed in the system with dynamic gentamicin concentrations were estimated to have a 66% higher residual error than those performed with static concentrations (ΔOFV of 66 units for separate REs for static and dynamic experiments).
Table 1.
Population parameter estimates for the final model
| Parameter | Explanation | Estimate for parameter (95% CI)a |
|---|---|---|
| kgrowth (h−1) | Rate constant of bacterial growth | 2.00 (1.89–2.27) |
| kdeath(h−1) | Rate constant of natural bacterial death | 0.179 (fix) |
| BP (CFU/ml) | Breakpoint, the lowest total no. of bacteria required for the transfer rate constant from the sensitive (S) to the resting (R) compartment being >0 | 2.09 × 106 (1.01 × 106–3.32 × 106) |
| Bmax (CFU/ml) | Bacterial count in the stationary phase | 8.26 × 108 (6.18 × 108–11.10 × 108) |
| Emax(0) (h−1) | Maximal achievable kill rate constant by gentamicin | 51.0 (44.6–61.6) |
| EC50 (mg/liter) | The antibiotic concn that produces 50% of Emax | 9.93 (8.45–12.1) |
| AR50 | The relative amt in compartment for adaptive resistance needed to reduce Emax by 50% | 0.113 (0.0983–0.146) |
| kon (liters mg−1 h−1) | Rate constant for the development of adaptive resistance in the presence of gentamicin | 0.0426 (0.0376–0.0478) |
| koff (h−1) | Rate constant for the bacteria to return to the susceptible state after developing adaptive resistance | 0.0139 (fix) |
| REstatic | Residual error (on ln scale) for static experiments | 1.69 (1.52–1.83) |
| REdynamic | Residual error (on ln scale) for dynamic experiments | 2.80 (2.56–2.98) |
| RRE | Replicate residual error (on ln scale) | 0.618 (0.59–0.649) |
The 95% confidence intervals (CI) were obtained from log-likelihood profiling. “fix” indicates that the value was fixed in the estimation.
Alternative models could not fit the data as well. When the adaptive resistance was modeled as a time- and concentration-dependent EC50, the OFV was 169 units higher, and the diagnostic plots indicated a lack of fit at the later time points. The model with a third bacterial compartment with adaptively resistant bacteria had an OFV that was 53 units higher than when the binding function was applied.
Model predictions.
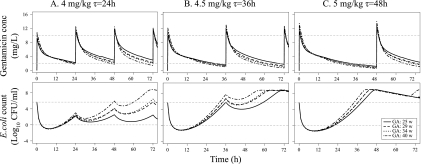
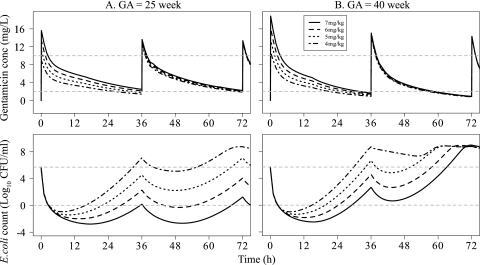
In Fig. 4, the time courses of gentamicin concentrations and bacterial counts following several commonly used dosing schedules in neonates were predicted. The higher initial doses produced more bacterial killing in all typical newborn infants during the first 24 h. In the extreme preterm newborn infant gentamicin achieved lower peak concentrations than in the more mature infants but nevertheless had a higher overall bacterial killing effect because of the lower clearance and consequently larger area under the concentration-time curve (AUC). The model predicted, however, regrowth of the bacteria for all three dosing schedules. For 4 mg/kg every 24 h, the bacterial count reached the initial starting inoculum (5 × 105 CFU/ml) at 48 h for a typical full-term newborn. For 4.5 mg/kg every 36 h and 5 mg/kg every 48 h, the starting inocula were reached already at 32 to 39 h for both preterm and term neonates.
Fig 4.
Model predictions of gentamicin concentration (top) and E. coli count (bottom) for four typical newborn infants at various GAs for three commonly used dosing schedules in neonates. Gray dotted lines represent gentamicin concentrations of 2 and 10 mg/liter (top) or a bacterial count of 4.83 × 105 CFU/ml (starting inoculum) and 1 CFU/ml (bottom). w, weeks.
Predictions using different initial doses of 4 to 7 mg/kg for the extreme preterm (GA of 25 weeks) and term (GA of 40 weeks) newborn infants (Fig. 5) showed that there are only minor differences in bacterial killing between the different dose levels during the first 6 hours. However, at 36 h the predicted difference in bacterial counts was several log10 units for the highest and lowest doses investigated. At all dose levels and in both groups of newborn infants, the adaptive resistance was obvious as administration of a second dose of 5 mg/kg at 36 h produced less bacterial killing than the initial doses. The second dose produced similar magnitudes of bacterial killing (approximately 2 log10 CFU/ml) for all initial doses of 4 to 7 mg/kg in both term and preterm newborn infants, indicating no clear difference in the degree of adaptive resistance for these dose levels.
Fig 5.
Model predictions of gentamicin concentration (top) and E. coli count (bottom) for different initial doses (4, 5, 6, and 7 mg/kg) and subsequent dosing of 5 mg/kg every 36 h starting at 36 h. Predictions are shown for an extreme preterm newborn infant at a GA of 25 weeks and a term newborn infant at a GA of 40 weeks. Gray dotted lines represent gentamicin concentrations of 2 and 10 mg/liter (top) or a bacterial count of 4.83 × 105 CFU/ml (starting inocula) and 1 CFU/ml (bottom).
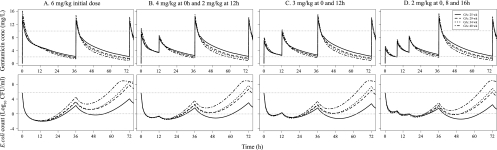
There seemed to be no major advantage of a fractionated schedule over 36 h, as illustrated when a single dose of 6 mg/kg was compared to fractionated schedules with the same total dose, i.e., when the AUC from 0 to 36 h (AUC0-36) was the same for all regimens (Fig. 6). The highest initial bacterial killing (8 log10 reduction in CFU/ml) was predicted for the single dose, but the time for the bacterial count to reach the initial starting inoculum was slightly longer for the fractionated schedules.
Fig 6.
Model predictions of gentamicin concentrations (top) and E. coli counts (bottom) for different schedules of gentamicin with a total dose of 6 mg/kg for the first 36 h followed by 5 mg/kg every 36 h. Gray dotted lines represent gentamicin concentrations of 2 and 10 mg/liter (top) or bacterial counts of 4.83 × 105 CFU/ml (starting inocula count) and 1 CFU/ml (bottom).
Given that trough gentamicin concentrations should be <2 mg/liter to reduce the risk for nephrotoxicity (Table 2), the highest possible dose for the typical extreme preterm newborn infant would be 6 mg/kg for a 36 h interval, while a dose of 7 mg/kg with a 36-h interval would be possible in the typical term newborn infant. For an extreme preterm newborn infant, the dosing interval would need to be longer than 24 h to reach trough levels of <2 mg/liter unless the dose is reduced to less than 4 mg/kg. For the typical extreme preterm newborn infant, none of the evaluated doses resulted in concentrations of <1 mg/liter within 36 h. The typical term newborn infant, however, is predicted to achieve concentrations of <1 mg/liter for both the 4-mg/kg and 5-mg/kg doses for a 36-h interval.
Table 2.
Predictions of the duration that gentamicin concentration is below the target trough level for different initial doses within the first 36 h
| Initial dose (mg/kg) | Duration (h) of the indicated gentamicin concn in:a |
|||
|---|---|---|---|---|
| Extreme preterm newborn infant |
Term newborn infant |
|||
| <2 mg/liter | <1 mg/iter | <2 mg/liter | <1 mg/liter | |
| 7 | NA | NA | 3.5 | NA |
| 6 | 0.1 | NA | 7.6 | NA |
| 5 | 4.8 | NA | 11.3 | 1 |
| 4 | 11.5 | NA | 16.4 | 4.5 |
Predictions are for an extreme preterm newborn infant with a GA of 25 weeks and a term newborn infant with a GA of 40 weeks. NA, not achieved.
DISCUSSION
A semimechanistic PKPD model that incorporates the adaptive resistance of gentamicin was developed that could well characterize the observed time courses of bacterial killing for a wide range of concentration-time profiles. In the developed model, gentamicin was killing the bacteria upon introduction into the infectious environment at a maximum rate determined by Emax. Simultaneously, the drug triggered the development of adaptive resistance, resulting in a graded reduction of the Emax value and thereby a reduced capacity to kill the bacteria. When gentamicin diminishes, there is a reduction of the degree of adaptive resistance and thereby a graded return of Emax to its initial level. The antibacterial effect of subsequent administration of gentamicin will depend on the fraction predicted in the adaptive resistance stage. Mechanistically, the MexXY efflux pump has been demonstrated to be rapidly overproduced in the presence of aminoglycosides and to interact with the OprM component to actively export gentamicin (19). In the absence of drug, the activation of MexXY expression is turned down, leading to a gradual return of susceptibility.
The estimated half-life of the development of the adaptive resistance in the current study was concentration dependent and was estimated at 16, 4, and 1 h for constant concentrations of 1, 4, and 16 mg/liter, respectively. The half-life of return to susceptibility was fixed at 50 h as there was limited information on this value in the current data and as 50 h was the lowest value that did not result in a decreased model fit. The emergence and reversibility of adaptive resistance of gentamicin have also previously been studied experimentally in an in vitro time-kill study (4) where Pseudomonas aeruginosa was exposed to gentamicin at initial peak concentrations of 2.5, 8, and 25 mg/liter In that study, full recovery of drug susceptibility occurred at approximately 36 to 44 h. The apparent slower return to full susceptibility in the present study may be due to the differences in type of bacteria or experimental design. A full characterization of the rate of return to the susceptible stage would require a wide range of additional experiments. We regard the initial therapy to be the most important part to characterize.
Predictions from the developed PKPD model showed that adaptive resistance needs to be considered when proposing dosing regimens of gentamicin as there was a reduced bacterial killing effect of subsequent doses (Fig. 4 and 5). Depending on the degree and time course of adaptive resistance development, different dose-fractionation schedules may result in different degrees of bacterial killing (Fig. 6). The single dose had the best initial bacterial kill but a somewhat faster return to the starting bacterial inoculum. With respect to initial bacterial killing, resistance development, and risk of toxicity (i.e., trough concentration of >2 mg/liter), there was no obvious benefit of dose fractionation of gentamicin.
The predictions for three commonly used dosing regimens in newborn infants (Fig. 4) suggested that the dose of 4 mg/kg every 24 h is the most effective of these schedules for the term newborn infant as the bacteria stayed below the starting inoculum for the longest time. However, for the extended-dose intervals, higher doses should be considered as the bacterial killing effect increased as the loading dose increased (Fig. 5). An initial aggressive front-loading was suggested earlier based on outcomes in adult patients with nosocomial pneumonia (25), and as lingering bacteria may mutate and cause further problems, it may be better to aim for a high bacterial killing rate at first dose.
In previous dosing suggestions for gentamicin (35), it was assumed that the clinically used peak target concentration of 8 to 10 mg/liter needs to be reached, and a standard gentamicin dosage of 4 mg/kg was regarded as being suboptimal in preterm neonates. With the developed PKPD model, we could show that even though the peak concentration was lower in the extreme preterm newborn infant, the bacterial killing was higher than in the term newborn infant. This indicates the importance of the total drug exposure (AUC), rather than the peak concentration, as the driver for the bacterial killing in this patient population (Fig. 4) (34). However, a 24-h dosing interval with trough concentrations of <2 mg/liter is not achievable in the extreme preterm infant, and an extended dosing interval (36 to 48 h) is therefore justified (35, 42). A meta-analysis of 16 controlled trials, with 14 trials on gentamicin, evaluating the extended dosing interval (24 h in term and 36 to 48 h in preterm infants) compared to the traditional dosing interval (8 to 12 h for term and 12 to 24 h for preterm infants) showed that the former is safe and effective (32). The concentration-toxicity relationship was not studied here, but most doses, except for the 7 mg/kg in the extreme preterm newborn infants, achieved a trough level of <2 mg/liter at 36 h. Another limitation of the dosage evaluations performed here is that between-subject variability in PK and PD was not considered.
One weakness of the current and other PKPD models is that they always predict regrowth upon drug removal as the bacteria cannot be totally eradicated. The presence of the immune system in vivo, depending on the maturity and status, will play an important role in killing lingering bacteria. The simulations in this study would reflect a worst-case scenario with a very poor immune defense. It should also be noted that in clinical practice, gentamicin is often combined with beta-lactam antibiotics, resulting in a possibly more efficient eradication of the infection (27).
In summary, a semimechanistic PKPD model with a binding function to describe the emergence of adaptive resistance of gentamicin observed in time-kill curve experiments in vitro was developed. For the sizes and ages of preterm newborn infants investigated, the PKPD model showed that even with lower peak gentamicin concentrations, the overall higher drug exposure resulted in higher bacterial killing than in the term newborn infant. There was no obvious advantage of fractionated dosing schedules, but the predictions from the PKPD model suggest that it would be of interest to clinically evaluate an extended dosing interval (>24 h) in the extreme preterm infants. This study supports the idea that adaptive resistance of gentamicin plays a role in the efficacy of gentamicin and will affect the choice of optimal dosage. The developed semimechanistic model could thereby be a valuable tool in the development of treatment regimens and be used to design clinical studies evaluating suggested dosing regimens.
ACKNOWLEDGMENTS
We acknowledge Nurcan Akkurt and Juliana Larsson for data generation and technical assistance.
Ami Mohamed was supported by a grant from the Ministry of Health Malaysia and the Swedish Cancer Society. Lena Friberg was partly supported by the Swedish Foundation for Strategic Research.
We have no conflicts of interest related to the content of this study.
Footnotes
Published ahead of print 28 October 2011
REFERENCES
- 1. Abelo A, Andersson M, Holmberg AA, Karlsson MO. 2006. Application of a combined effect compartment and binding model for gastric acid inhibition of AR-HO47108: a potassium competitive acid blocker, and its active metabolite AR-HO47116 in the dog. Eur. J. Pharm. Sci. 29:91–101 [DOI] [PubMed] [Google Scholar]
- 2. Ahn JE, Karlsson MO, Dunne A, Ludden TM. 2008. Likelihood based approaches to handling data below the quantification limit using NONMEM VI. J. Pharmacokinet Pharmacodyn. 35:401–421 [DOI] [PubMed] [Google Scholar]
- 3. Barclay ML, Begg EJ. 2001. Aminoglycoside adaptive resistance: importance for effective dosage regimens. Drugs 61:713–721 [DOI] [PubMed] [Google Scholar]
- 4. Barclay ML, Begg EJ, Chambers ST. 1992. Adaptive resistance following single doses of gentamicin in a dynamic in vitro model. Antimicrob. Agents Chemother. 36:1951–1957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Barclay ML, Begg EJ, Chambers ST, Peddie BA. 1996. The effect of aminoglycoside-induced adaptive resistance on the antibacterial activity of other antibiotics against Pseudomonas aeruginosa in vitro. J. Antimicrob. Chemother. 38:853–858 [DOI] [PubMed] [Google Scholar]
- 6. Barclay ML, Duffull SB, Begg EJ, Buttimore RC. 1995. Experience of once-daily aminoglycoside dosing using a target area under the concentration-time curve. Aust. N Z J. Med. 25:230–235 [DOI] [PubMed] [Google Scholar]
- 7. Beal SL. 2001. Ways to fit a PK model with some data below the quantification limit. J. Pharmacokinet Pharmacodyn. 28:481–504 [DOI] [PubMed] [Google Scholar]
- 8. Beal SL, Sheiner LB, Boeckmann AJ. 1989. –2006. NONMEM users guide. Icon Development Solutions, Ellicott City, MD [Google Scholar]
- 9. Beaubien AR, et al. 1991. Evidence that amikacin ototoxicity is related to total perilymph area under the concentration-time curve regardless of concentration. Antimicrob. Agents Chemother. 35:1070–1074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Begg EJ, Peddie BA, Chambers ST, Boswell DR. 1992. Comparison of gentamicin dosing regimens using an in-vitro model. J. Antimicrob. Chemother. 29:427–433 [DOI] [PubMed] [Google Scholar]
- 11. Begg EJ, et al. 2009. Eight years' experience of an extended-interval dosing protocol for gentamicin in neonates. J. Antimicrob. Chemother. 63:1043–1049 [DOI] [PubMed] [Google Scholar]
- 12. Blaser J, Stone BB, Groner MC, Zinner SH. 1987. Comparative study with enoxacin and netilmicin in a pharmacodynamic model to determine importance of ratio of antibiotic peak concentration to MIC for bactericidal activity and emergence of resistance. Antimicrob. Agents Chemother. 31:1054–1060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Dahlgren JG, Anderson ET, Hewitt WL. 1975. Gentamicin blood levels: a guide to nephrotoxicity. Antimicrob. Agents Chemother. 8:58–62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Daikos GL, Jackson GG, Lolans VT, Livermore DM. 1990. Adaptive resistance to aminoglycoside antibiotics from first-exposure down-regulation. J. Infect. Dis. 162:414–420 [DOI] [PubMed] [Google Scholar]
- 15. Daikos GL, Lolans VT, Jackson GG. 1991. First-exposure adaptive resistance to aminoglycoside antibiotics in vivo with meaning for optimal clinical use. Antimicrob. Agents Chemother. 35:117–123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Darmstadt GL, et al. 2007. Determination of extended-interval gentamicin dosing for neonatal patients in developing countries. Pediatr. Infect. Dis. J. 26:501–507 [DOI] [PubMed] [Google Scholar]
- 17. Darmstadt GL, Miller-Bell M, Batra M, Law P, Law K. 2008. Extended-interval dosing of gentamicin for treatment of neonatal sepsis in developed and developing countries. J. Health Popul. Nutr. 26:163–182 [PMC free article] [PubMed] [Google Scholar]
- 18. Dayneka NL, Garg V, Jusko WJ. 1993. Comparison of four basic models of indirect pharmacodynamic responses. J. Pharmacokinet Biopharm. 21:457–478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Hocquet D, et al. 2003. MexXY-OprM efflux pump is necessary for a adaptive resistance of Pseudomonas aeruginosa to aminoglycosides. Antimicrob. Agents Chemother. 47:1371–1375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Hossain MM, et al. 2009. Simplified dosing of gentamicin for treatment of sepsis in Bangladeshi neonates. J. Health Popul. Nutr. 27:640–645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Joers A, Kaldalu N, Tenson T. 2010. The frequency of persisters in Escherichia coli reflects the kinetics of awakening from dormancy. J. Bacteriol. 192:3379–3384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Jonsson EN, Karlsson MO. 1999. Xpose—an S-PLUS-based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Comput. Methods Programs Biomed. 58:51–64 [DOI] [PubMed] [Google Scholar]
- 23. Karlsson MO, Beal SL, Sheiner LB. 1995. Three new residual error models for population PK/PD analyses. J. Pharmacokinet Biopharm. 23:651–672 [DOI] [PubMed] [Google Scholar]
- 24. Karlsson MO, Holford N. 2008. A tutorial on visual predictive checks, abstr 1434. Abstr. Annu. Meet. Popul. Approach Group Eur., Marseille, France, 18 to 20 June 2008. http://www.page-meeting.org/?abstract=1434 [Google Scholar]
- 25. Kashuba AD, Nafziger AN, Drusano GL, Bertino JS., Jr 1999. Optimizing aminoglycoside therapy for nosocomial pneumonia caused by Gram-negative bacteria. Antimicrob. Agents Chemother. 43:623–629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Lanao JM, et al. 2004. Pharmacokinetic basis for the use of extended interval dosage regimens of gentamicin in neonates. J. Antimicrob. Chemother. 54:193–198 [DOI] [PubMed] [Google Scholar]
- 27. Leibovici L, Paul M. 2007. Aminoglycoside/beta-lactam combinations in clinical practice. J. Antimicrob. Chemother. 60:911–912 [DOI] [PubMed] [Google Scholar]
- 28. Lindbom L, Pihlgren P, Jonsson EN. 2005. PsN-Toolkit—a collection of computer intensive statistical methods for non-linear mixed effect modeling using NONMEM. Comput. Methods Programs Biomed. 79:241–257 [DOI] [PubMed] [Google Scholar]
- 29. Lowdin E, Odenholt I, Bengtsson S, Cars O. 1996. Pharmacodynamic effects of sub-MICs of benzylpenicillin against Streptococcus pyogenes in a newly developed in vitro kinetic model. Antimicrob. Agents Chemother. 40:2478–2482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Moore RD, Lietman PS, Smith CR. 1987. Clinical response to aminoglycoside therapy: importance of the ratio of peak concentration to minimal inhibitory concentration. J. Infect. Dis. 155:93–99 [DOI] [PubMed] [Google Scholar]
- 31. Muller-Pebody B, et al. 2011. Empirical treatment of neonatal sepsis: are the current guidelines adequate? Arch. Dis. Child Fetal Neonatal Ed. 96:F4–F8 [DOI] [PubMed] [Google Scholar]
- 32. Nestaas E, Bangstad HJ, Sandvik L, Wathne KO. 2005. Aminoglycoside extended interval dosing in neonates is safe and effective: a meta-analysis. Arch. Dis. Child Fetal Neonatal Ed. 90:F294–F300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Nicolau DP, et al. 1995. Experience with a once-daily aminoglycoside program administered to 2,184 adult patients. Antimicrob. Agents Chemother. 39:650–655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Nielsen EI, Cars O, Friberg LE. 2011. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: a step toward model-based dose optimization. Antimicrob. Agents Chemother. 55:4619–4630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Nielsen EI, Sandstrom M, Honore PH, Ewald U, Friberg LE. 2009. Developmental pharmacokinetics of gentamicin in preterm and term neonates: population modelling of a prospective study. Clin. Pharmacokinet. 48:253–263 [DOI] [PubMed] [Google Scholar]
- 36. Nielsen EI, et al. 2007. Semimechanistic pharmacokinetic/pharmacodynamic model for assessment of activity of antibacterial agents from time-kill curve experiments. Antimicrob. Agents Chemother. 51:128–136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Pacifici GM. 2010. Clinical pharmacokinetics of penicillins, cephalosporins and aminoglycosides in the neonate: a review. Pharmaceuticals 3:2568–2591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Rao SC, Ahmed M, Hagan R. 2006. One dose per day compared to multiple doses per day of gentamicin for treatment of suspected or proven sepsis in neonates. Cochrane Database Syst. Rev. 2006:CD005091. [DOI] [PubMed] [Google Scholar]
- 39. Rocha MJ, Almeida AM, Falcao AC, Caramona MM. 2007. Performance of gentamicin population kinetic parameters in Portuguese neonates. Pharm. World Sci. 29:104–108 [DOI] [PubMed] [Google Scholar]
- 40. Sherlock R. 2009. Neonatal sepsis and septic shock: Current trends in epidemiology and management. J. Pediatr. Infect. Dis. 4:153–159 [Google Scholar]
- 41. Tam VH, et al. 2008. Pharmacodynamic modeling of aminoglycosides against Pseudomonas aeruginosa and Acinetobacter baumannii: identifying dosing regimens to suppress resistance development. Antimicrob. Agents Chemother. 52:3987–3993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Thingvoll ES, Guillet R, Caserta M, Dicenzo R. 2008. Observational trial of a 48-hour gentamicin dosing regimen derived from Monte Carlo simulations in infants born at less than 28 weeks' gestation. J. Pediatr. 153:530–534 [DOI] [PubMed] [Google Scholar]
- 43. Touw DJ, Westerman EM, Sprij AJ. 2009. Therapeutic drug monitoring of aminoglycosides in neonates. Clin. Pharmacokinet. 48:71–88 [DOI] [PubMed] [Google Scholar]
- 44. Xiong YQ, et al. 1997. Adaptive resistance of Pseudomonas aeruginosa induced by aminoglycosides and killing kinetics in a rabbit endocarditis model. Antimicrob. Agents Chemother. 41:823–826 [DOI] [PMC free article] [PubMed] [Google Scholar]