Abstract
The present study investigated the pharmacokinetic/pharmacodynamic (PK/PD) relationships of a prototype biotin carboxylase (BC) inhibitor, PD-0162819, against Haemophilus influenzae 3113 in static concentration time-kill (SCTK) and one-compartment chemostat in vitro infection models. H. influenzae 3113 was exposed to PD-0162819 concentrations of 0.5 to 16× the MIC (MIC = 0.125 μg/ml) and area-under-the-curve (AUC)/MIC ratios of 1 to 1,100 in SCTK and chemostat experiments, respectively. Serial samples were collected over 24 h. For efficacy driver analysis, a sigmoid maximum-effect (Emax) model was fitted to the relationship between bacterial density changes over 24 h and corresponding PK/PD indices. A semimechanistic PK/PD model describing the time course of bacterial growth and death was developed. The AUC/MIC ratio best explained efficacy (r2 = 0.95) compared to the peak drug concentration (Cmax)/MIC ratio (r2 = 0.76) and time above the MIC (T>MIC) (r2 = 0.88). Static effects and 99.9% killing were achieved at AUC/MIC values of 500 and 600, respectively. For time course analysis, the net bacterial growth rate constant, maximum bacterial density, and maximum kill rate constant were similar in SCTK and chemostat studies, but PD-0162819 was more potent in SCTK than in the chemostat (50% effective concentration [EC50] = 0.046 versus 0.34 μg/ml). In conclusion, basic PK/PD relationships for PD-0162819 were established using in vitro dynamic systems. Although the bacterial growth parameters and maximum drug effects were similar in SCTK and the chemostat system, PD-0162819 appeared to be more potent in SCTK, illustrating the importance of understanding the differences in preclinical models. Additional studies are needed to determine the in vivo relevance of these results.
INTRODUCTION
Steadily increasing bacterial resistance to existing antibiotics continues to be a major public health concern (3, 8). Because most new antibacterial agents represent chemical modifications of existing chemical classes of antibacterial agents (5), it is suspected that the limited options of chemically distinct antibiotics have led to extensive drug resistance among bacterial pathogens. Therefore, it is of the utmost importance to identify novel, safe, and effective antibacterial agents that work through unique antibacterial biological mechanisms. The discovery of a new chemical class of antibacterial compounds, the pyridopyrimidines, targeting bacterial biotin carboxylase (BC), was recently reported (14, 15) and offers the potential that this novel chemical class, targeting a unique antibacterial mechanism, can be developed into drugs effective against multidrug-resistant bacteria.
Compared to the development of drugs from an existing chemical class, the discovery of a novel class of compounds presents extra challenges (1, 5). The translation of pharmacokinetic/pharmacodynamic (PK/PD) relationships between animal infection models and human patients has been well established for several existing chemical classes across a variety of indications (1), but for novel chemical classes, PK/PD relationships, and the translation of these relationships between in vitro systems, animals, and humans, are not known. Moreover, the physicochemical and pharmacokinetic properties of compounds at early stages of the drug discovery process are often not optimized for extensive concentration-response testing in animal models (21). Thus, as an alternative, in vitro infection models offer a rapid and resource-sparing method to determine PK/PD relationships. Building and applying mathematical PK/PD models that quantitatively describe the time course of bacterial replication/death and drug effects enables the construction of a more efficient drug discovery process. Furthermore, these quantitative PK/PD relationships derived from in vitro data can inform future in vivo testing as to optimal dose selection and dosing intervals and thereby reduce the resources necessary to perform adequate in vivo experiments. They can also provide the framework for understanding knowledge gaps and for determining optimal drug properties (e.g., pharmacokinetics) required for a successful drug candidate (6, 7, 9).
The present study investigated the PK/PD relationships of a prototype BC inhibitor, PD-0162819, against Haemophilus influenzae 3113 in static concentration time-kill (SCTK) and one-compartment chemostat in vitro infection models. The objectives of this study were to (i) establish a basic understanding of concentration-response relationships in vitro for a prototype BC inhibitor and (ii) use in vitro and mathematical modeling tools to guide the drug discovery program by understanding the translation among in vitro infection models.
MATERIALS AND METHODS
Compound, microorganism, and susceptibility studies.
PD-0162819 was synthesized by Pfizer chemists (14). Broth microdilution susceptibility testing was performed using a BioMek FX robotic workstation (Beckman-Coulter, Fullerton, CA). A β-lactamase-producing clinical isolate of H. influenzae, H. influenzae 3113, was tested using Haemophilus Test Medium (HTM) (PML Microbiologicals, Wilsonville, OR) and incubated at 35°C in an ambient atmosphere as described by the Clinical and Laboratory Standards Institute (CLSI) (17).
SCTK experiments.
In vitro SCTK testing was performed following CLSI methodology (17). Specifically, testing was carried out in 10 ml of HTM and incubated at 35°C with a 5% CO2 atmosphere. PD-0162819 concentrations ranged from 0.06 to 2 μg/ml (0.5 to 16× MIC; MIC = 0.125 μg/ml) and were determined by liquid chromatography-tandem mass spectrometry (LC–MS-MS) to remain constant during the course of the experiment. Serial medium samples (100 μl/sample) were collected at time (t) = 0, 2, 4, 6, and 24 h. Postexposure MIC testing was performed, and changes in MICs were not observed.
One-compartment chemostat infection model.
In vitro dynamic concentration studies were performed using a one-compartment chemostat system as previously described (12, 23). The chemostat system consisted of a 250-ml glass chamber with ports for the addition and removal of test media via polyethylene tubes connected to peristaltic pumps, injection of drug solution, and removal of medium samples. Single-dose and dose fractionation experiments were performed. Prior to each experiment, colonies from an overnight growth of H. influenzae 3113 on chocolate agar were added to the HTM as necessary to obtain a suspension of 108 CFU/ml. To produce a starting inoculum of ∼106 CFU/ml, 2.5 ml of this suspension was added to each flask. A drug stock solution of PD-0162819 was prepared at the start of each experiment, and this solution was diluted with saline so that a dosing volume of 0.5 ml was added to each flask via bolus dosing. To increase the solubility of PD-0162819, 3% sulfobutyl ether–β-cyclodextrin was added to the dosing solution. Because PD-0162819 is projected to have a short half-life in vivo (data not shown), the pump rates for all chemostat experiments were set to achieve a drug elimination half-life of 4 h. A dose escalation study was performed to determine the efficacious exposure range using an area under the concentration-time curve over 24 h divided by the MIC (AUC/MIC ratio) of 1 to 1,100 (MIC = 0.125 μg/ml). To determine the efficacy driver, a dose fractionation study was performed using exposures corresponding to the 20% effective dose (ED20), ED50, and ED80 from the dose escalation study divided into 1 time/day (dosed at t = 0 h), 2 times/day (t = 0 and 12 h), or 3 times/day (t = 0, 6, and 12 h) dosing regimens. Medium samples were collected at 0, 0.5, 1, 2, 4, 6, 12, and 24 h after dosing for analysis of drug concentrations and determination of bacterial densities. Postexposure MIC testing was performed, and changes in MICs were not observed.
Determination of bacterial density.
Medium samples were washed with saline to remove any drug carryover. Samples were then reconstituted and diluted 10-fold, and 100 μl of diluted and undiluted samples was plated onto chocolate agar. After 24 h of incubation, CFU (CFU/ml) were counted and corrected for dilution. Because an undiluted 100-μl sample was used for determining bacterial density in samples with low bacterial counts, the limit of detection was 10 CFU/ml.
Drug concentration analysis.
Medium samples were stored at −20°C until analysis. A freeze-thaw study conducted during method development indicated that PD-0162819 was stable at −20°C for >4 weeks and that <5% degradation occurred after repeated freeze-thaw cycles. The samples were thawed at room temperature, spiked with 200 μl of the internal standard (200 ng/ml of PF-01135527 in acetonitrile), and vortexed for 1 min. Following centrifugation at 5,000 rpm for 5 min, 3 μl of the supernatants was injected into a validated LC–MS-MS system. A Varian Polaris C-18-A column (50 by 2.0 mm) was employed and run under ambient reversed-phase conditions. The mobile phases were 100% water with 0.1% formic acid (A) and 100% acetonitrile with 0.1% formic acid (B). The gradient was programmed with a flow rate of 250 μl/min starting at 10% mobile phase B to reach 70% mobile phase B in 1.5 min and 90% mobile phase B in an additional 1 min. At the end of the program, the analytical column was reequilibrated with 10% mobile phase B for 1 min. The total cycle time for the assay was 3.6 min/sample. Molecular ion precursor-product transitions of 393.7→298.1 and 382→271.1 were used for PD-0162819 and the internal standard, respectively, in multiple-reaction monitoring (MRM) mode. Data acquisition, integration of peak areas, regression analysis, and sample quantification were performed using the standard quantitative-analysis package of Analyst 1.4 (Applied Biosystems, Foster City, CA). A 12-point standard curve consisting of PD-0162819 concentrations ranging from 5 to 10,000 ng/ml was used to quantify PD-0162819 concentrations in samples. Where appropriate, medium samples were diluted for analysis. The lower limit of quantitation (LLOQ) was 5 ng/ml. Using standards of known concentration, accuracy was determined to be ±20%, and intraday and interday precision was ±20%.
Endpoint efficacy driver analysis.
Data collected using the one-compartment chemostat system was used to determine the efficacy driver. The change of bacterial density over 24 h (Δlog CFU/ml) was calculated and plotted against corresponding endpoint PK/PD parameters (the AUC/MIC ratio, the maximum concentration of drug in serum divided by the MIC [Cmax/MIC ratio], and time above MIC [T>MIC]). The observed drug concentration data were used to calculate the pharmacokinetic parameters. A sigmoid Emax model was fitted to the relationship between Δlog CFU/ml and corresponding PK/PD indices. This model was used to determine the endpoint PK/PD index that best explained efficacy and the magnitude of each parameter to achieve bacterial killing ranging from 0-log-unit to ≥3-log-unit killing.
Time course PK/PD data analysis.
SCTK and chemostat PK/PD data were modeled via a two-step process using NONMEM version V (GloboMax LLC, Ellicott City, MD). Based on a study to assess the chemical and metabolic stability of PD-0162819 in HTM, drug concentrations were determined by LC–MS-MS to be constant throughout the course of the SCTK studies. Less than 5% degradation occurred over 24 h at 35°C. A population pharmacokinetic one-compartment open model with first-order elimination (kelim) and proportional error was used to fit the drug concentration-time profiles. The population pharmacokinetic model incorporated interindividual (i.e., interflask) variability of clearance (CL) and volume of distribution (Vd) to describe the observed drug concentration data in each flask. The pharmacokinetic parameters were then fixed in the PK/PD model, and the bacterial density time course profiles were modeled using a modified net effect mathematical model that is outlined in Fig. 1. Similar mathematical models have been previously described (e.g., see references 2, 10, 13, 16, 18, 20, and 22). In this model, changes in drug concentrations over time were described using equation 1:
| (1) |
where Cm is the PD-0162819 concentration in HTM. kelim is the first-order drug elimination rate constant, which is determined by the pump rate of the chemostat system. kelim can also be represented as CL/Vd. kelim was 0 h−1 in SCTK because the drug was not flushed out of the system. In the chemostat, kelim was approximately 0.17 h−1 to achieve a drug half-life of approximately 4 h. For chemostat data, kelim was estimated using the previously described population pharmacokinetic model.
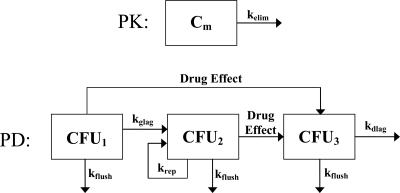
Fig 1.
Schematic representation of the mathematical PK/PD model. The total bacterial density (CFUtotal) is the combination of nonreplicating (CFU1), replicating (CFU2), and damaged (CFU3) cells. Bacterial replication eventually results in bacterial counts reaching a stationary phase, which is determined by the total number of bacteria in the system (Nmax). The replication rate (krep) is modified as bacterial counts increase {krep × [(Nmax − CFUtotal)/Nmax]} and, ultimately, achieves a stationary phase. The maximum drug effect (kkill), the drug concentration associated with 50% of the maximum effect (EC50), the drug concentration in the medium (Cm), and the Hill coefficient (γ) determine the magnitude of the drug effect [kkill × Cmγ/(Cmγ + EC50γ)]. Rate constants associated with a growth lag (kglag), a death lag (kdlag), and flushing of bacteria out of the in vitro system (kflush) are also included in the model. See Materials and Methods for equations and a more complete description of the model.
The bacterial population was hypothesized to be composed of three bacterial populations of nonreplicating, replicating, and damaged bacterial cells. To model the time course of bacterial density, equations 2 to 5 were applied:
| (2) |
| (3) |
| (4) |
| (5) |
where, as illustrated in Fig. 1, CFU1, CFU2, and CFU3 represent the densities of nonreplicating, replicating, and damaged bacterial cells, respectively. CFUtotal is the sum of all bacterial cells in the system. For the drug effect, kkill is the rate constant for maximal bacterial killing, the EC50 is the drug concentration at which 50% of maximal killing occurs, and γ is the Hill coefficient corresponding to the degree of sigmoidicity of the concentration-response curve. For the replication rate, krep is the net growth rate constant and Nmax is the maximum number of bacteria in the in vitro system. As CFUtotal approaches Nmax, the total bacterial population reaches a stationary phase and was observed as a plateau of the bacterial density-time profile. Where appropriate, a bacterial-growth lag rate constant (kglag) and a bacterial-death lag rate constant (kdlag) were incorporated into the model to describe lags in bacterial growth and death. For the dynamic chemostat data, kflush is the rate constant associated with flushing HTM, bacteria, and drug out of the in vitro system. Because HTM, bacteria, and drug were flushed out of the system at a rate determined by the pump rate, kflush has the same magnitude as kelim. For modeling SCTK data, kflush was excluded from the model because HTM, bacteria, and drug were not flushed out of the system. Best-fit parameters of the PK/PD model were obtained using first-order conditional estimation, and the goodness of fit of the models to the experimental data was assessed by visual inspection of observed versus predicted plots, the coefficient of determination, evaluation of weighted residuals (versus time and concentration), and comparison of objective function values for nested models.
RESULTS
SCTK of PD-0162819 against H. influenzae 3113.
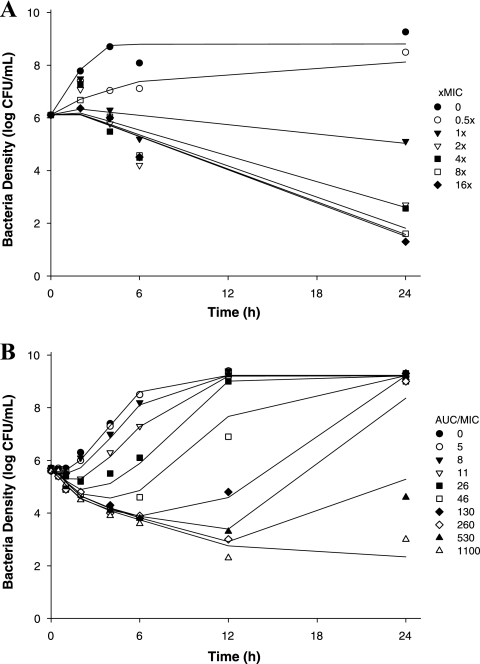
PD-0162819 demonstrated concentration-dependent killing, achieving 3-log-unit killing after 6 h. PD-0162819 was bactericidal at concentrations of ≥2× the MIC. The PK/PD model (Fig. 1) adequately described the observed bacterial density data (r2 = 0.91). Observed data and model-predicted fits to the data are shown in Fig. 2A. The maximum bacterial net growth rate constant in this system was 2.04 ± 0.14 h−1, and the death lag rate constant was 1.91 ± 0.20 h−1. A growth lag rate constant was not estimated due to the absence of data between 0 and 2 h. The maximum number of bacteria in the system was estimated to be 108.80 ± 0.15 CFU/ml. The maximum drug effect (kkill) was 2.53 ± 0.14 h−1, and the EC50 of PD-0162819 against H. influenzae 3113 was estimated to be 0.0456 ± 0.0043 μg/ml. Model parameter estimates and 90% confidence intervals are shown in Table 1.
Fig 2.
PK/PD modeling of PD-0162819 against H. influenzae 3113 in SCTK (A) and the chemostat system (B). The symbols represent observed data. The lines represent model predictions.
Table 1.
PK/PD modeling results of the time course effects of PD-0162819 against H. influenzae 3113 in SCTK and chemostat systems
| Parameter | Unit | Value |
|
|---|---|---|---|
| Static concentration time-killa | Dynamic concentration time-killa | ||
| krep | h−1 | 2.04 ± 0.14 (1.8–2.3) | 1.80 ± 0.10 (1.6–2.0) |
| Nmax | CFU/ml | 108.80 ± 0.15 (108.6–109.0) | 109.28 ± 0.04 (109.2–109.3) |
| kkill | h−1 | 2.53 ± 0.14 (2.3–2.8) | 2.02 ± 0.11 (1.8–2.2) |
| EC50 | μg/ml | 0.0456 ± 0.0043 (0.039–0.053) | 0.340 ± 0.041 (0.27–0.41) |
| γ | 1.80 ± 0.15 (1.6–2.1) | 1.88 ± 0.42 (1.2–2.6) | |
| kglag | h−1 | 0.171 ± 0.065 (0.07–0.28) | |
| kdlag | h−1 | 1.91 ± 0.20 (1.6–2.2) | 3.06 ± 1.10 (1.2–4.9) |
| r2 | 0.91 | 0.98 | |
NONMEM estimate ± standard error (90% confidence intervals are shown in parentheses).
Dynamic concentration time-kill study in chemostat.
The PK/PD model outlined in Fig. 1 adequately described the observed time course of bacterial density data (r2 = 0.98). Observed data and model-predicted fits to the pharmacodynamic data are shown in Fig. 2B. The maximum bacterial net growth rate constant in this system was 1.80 ± 0.10 h−1, and the death lag rate constant was 3.06 ± 1.10 h−1. A growth lag was observed over the first hour of the experiment, and the growth lag rate constant was estimated to be 0.171 ± 0.065 h−1. The maximum number of bacteria in the system was estimated to be 109.28 ± 0.04 CFU/ml. The maximum drug effect (kkill) was 2.02 ± 0.11 h−1, and the EC50 of PD-0162819 against H. influenzae 3113 was estimated to be 0.340 ± 0.041 μg/ml. Model parameter estimates and 90% confidence intervals are shown in Table 1.
Efficacy driver analysis in chemostat.
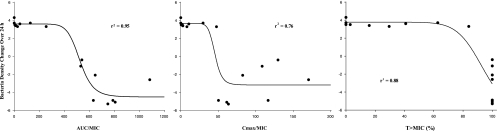
The one-compartment chemostat system was used to determine the efficacy driver of PD-0162819 against H. influenzae 3113. Although all three PK/PD indices exhibited relationships with efficacy (Fig. 3), the AUC/MIC ratio was the best predictor of antibacterial efficacy (r2 = 0.95) compared to the Cmax/MIC ratio (r2 = 0.76) and T>MIC (r2 = 0.88). A static effect over 24 h was achieved at an AUC/MIC value of 500. An AUC/MIC magnitude of 600 was required to achieve 3-log-unit killing (i.e., 99.9% killing) against H. influenzae 3113.
Fig 3.
Efficacy driver analysis of PD-0162819 against H. influenzae 3113 in the chemostat system. The circles represent observed data, and the lines represent model-predicted values.
DISCUSSION
The data and modeling presented in this report represent initial studies to characterize the PK/PD relationships of PD-0162819, a prototype BC inhibitor. Using two different in vitro infection systems and mathematical modeling tools, a basic understanding of endpoint efficacy driver and time course concentration-response relationships was established for this novel compound, which works through a unique mechanism of action. The results of this study indicate there is a significant need to understand the quantitative translation of these data from in vitro systems to in vivo systems and, ultimately, to humans.
In this study, both endpoint efficacy drivers and time course PK/PD relationships were evaluated. Typically, endpoint efficacy driver approaches have been utilized for understanding antibacterial PK/PD (4). However, endpoint data often minimize the importance of the time course of drug effects. Endpoint efficacy driver studies typically assess the change in bacterial densities between t = 0 h and t = 24 h, which essentially ignores the time course of drug effects over the 24-h period. By understanding the drug effects of the entire time course of the experiment, a more thorough understanding of PK/PD relationships can be achieved. Even so, endpoint efficacy driver analyses are traditionally used for developing an understanding of PK/PD relationships for antibacterial agents. Thus, this study was designed to enable analysis of both the endpoint efficacy driver and time course concentration-response relationships.
Efficacy driver analysis results indicate that all three PK/PD indices exhibit some trend with efficacy. However, based on visual inspection of the plots and the coefficient of determination, the AUC/MIC ratio appears to be a better predictor of efficacy than the Cmax/MIC ratio and T>MIC. Although T>MIC exhibits a strong coefficient of determination, it is not likely that T>MIC is a good predictor of efficacy due to the observed variation of approximately 5 log units of bacterial killing among the different dosing regimens that achieved 100% T>MIC.
The mathematical model presented in Fig. 1 is the most parsimonious model that was fitted to the observed data. It is similar to previously published models (2, 10, 13, 16, 18, 20, 22), but the basic structure of the model is most similar to the net effect model (2). Comparisons of the different mathematical models showed that potency estimates produced by the various mathematical models were similar (analysis not shown). An additional compartment was added to the basic net effect model to more accurately describe the apparent growth lag phase over the first hour of the chemostat experiments but was not incorporated for SCTK data due to lack of data in this early phase. This growth lag phase is hypothesized to be the result of nonreplicating cells during the initial stages of the experiments. After this early phase, the cells are assumed to begin replicating. In addition, an extra compartment was added to describe the apparent death lag, hypothesized to be caused by damaged cells, that was more obvious in SCTK experiments. Because bacterial death was delayed relative to drug concentrations, application of a transit compartment model was useful for describing this observation (19). This model assumes that bacterial cells are damaged by the drug, lower their proliferation rates, and eventually die. In addition, because bacteria were constantly being flushed out of the chemostat system, a parameter (kflush) was added to the model to account for this. Without this parameter, the potency would have been overestimated. This parameter was not needed when modeling the SCTK data because bacteria were not flushed from the SCTK system.
Even though H. influenzae 3113 replication rates were similar in the two infection systems, PD-0162819 was ∼7 times more potent in SCTK than in the chemostat system. Differences in experimental conditions between the two study designs can account for this finding. In the chemostat system, nutrients are replenished via fresh media, while drug, wastes, and old media are being removed from the system. This differs from the SCTK design, where less optimal growth conditions exist (i.e., nutrients are fixed and used up during the course of the experiment). Because the chemostat system provides more optimal bacterial growth conditions than SCTK, it is not surprising that PD-0162819 appears less potent in the chemostat.
Rebound of bacterial counts over the course of the experiment was not observed in SCTK studies. Although collecting more extensive samples between 6 and 24 h would allow a more definitive determination of potential resistance development in SCTK studies, the lack of resistant subpopulations was supported by the low frequency of resistance (∼1 resistant cell in >108 cells) (14), which is well above the starting inoculum of 106 CFU/ml used in these studies. Thus, the observed experimental data did not warrant the inclusion of additional “subpopulations” of resistant bacteria in the mathematical model, which have been incorporated into previously published models (e.g., 2, 13, 20, 22). In addition, the pyridopyrimidine inhibitors are the only antibacterial agents known to target BC, and therefore, no preexisting clinical resistance is expected. Although rebound was observed in the chemostat studies, this rebound was likely caused by reductions in drug concentrations over the course of the experiments and not by the emergence of resistant bacterial subpopulations.
Although this study focused on in vitro PK/PD relationships, simply understanding the in vitro PK/PD of a compound is not sufficient. To be useful, the in vivo relevance, and ultimately the clinical relevance, of in vitro relationships need to be determined. In addition, only one bacterial isolate was tested in this study. The AUC/MIC exposure targets presented in this report will likely be modified when additional clinical isolates are taken into consideration (11). At this point, the results of this study have been used to guide the discovery project team in the process of synthesizing a more optimal compound. Attempts to optimize the molecule have included improving the physicochemical properties, potency, pharmacokinetics, and other parameters.
In conclusion, mathematical modeling of data generated in in vitro infection systems was successfully employed to evaluate the PK/PD relationships of a novel BC inhibitor early in the drug discovery program. Although H. influenzae 3113 replication rates were similar in the two systems, PD-0162819 was ∼7 times more potent in SCTK than in the chemostat system, illustrating the importance of understanding differences in preclinical models when making decisions about drug exposures required for efficacy. Thus, the results of this study indicate that PK/PD relationships need to be interpreted with respect to the system in which the data are generated. Different in vitro and in vivo systems are likely to produce different results, which underscores the importance of understanding the quantitative translation of these systems to humans. The relevance of this modeling approach can be enhanced by translating this approach to in vivo systems. Thus, additional studies with additional strains of bacteria are required to determine the in vivo relevance of these results.
Footnotes
Published ahead of print 10 October 2011
REFERENCES
- 1. Ambrose PG, et al. 2007. Pharmacokinetics-pharmacodynamics of antimicrobial therapy: it's not just for mice anymore. Clin. Infect. Dis. 44:79–86 [DOI] [PubMed] [Google Scholar]
- 2. Campion JJ, McNamara PJ, Evans ME. 2005. Pharmacodynamic modeling of ciprofloxacin resistance in Staphylococcus aureus. Antimicrob. Agents Chemother. 49:209–219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Charles PGP, Grayson ML. 2004. The dearth of new antibiotic development: Why we should be worried and what we can do about it. Med. J. Australia 181:549–553 [DOI] [PubMed] [Google Scholar]
- 4. Craig WA. 1998. Pharmacokinetic/pharmacodynamic parameters: rationale for antibacterial dosing of mice and men. Clin. Infect. Dis. 26:1–10 [DOI] [PubMed] [Google Scholar]
- 5. Fernandes P. 2006. Antibacterial discovery and development: the failure of success? Nat. Biotechnol. 24:1497–1503 [DOI] [PubMed] [Google Scholar]
- 6. Gabrielsson J, Green AR, Van der Graaf PH. 2010. Optimising in vivo pharmacology studies: practical PKPD considerations. J. Pharmacol. Toxicol. Methods 61:146–156 [DOI] [PubMed] [Google Scholar]
- 7. Gabrielsson J, Green AR. 2009. Quantitative pharmacology or pharmacokinetic-pharmacodynamic integration should be a vital component in integrative pharmacology. J. Pharmacol. Exp. Ther. 331:767–774 [DOI] [PubMed] [Google Scholar]
- 8. Levy SB, Marshall B. 2004. Antibacterial resistance worldwide: causes, challenges and responses. Nat. Med. 10:S122–S129 [DOI] [PubMed] [Google Scholar]
- 9. Liu KK, et al. 2010. Design and synthesis of orally-active and selective azaindane 5HT2c agonist for the treatment of obesity. Bioorg. Med. Chem. Lett. 20:266–271 [DOI] [PubMed] [Google Scholar]
- 10. Liu P, Rand KH, Obermann B, Derendorf H. 2005. Pharmacokinetic-pharmacodynamic modeling of antibacterial activity of cefpodoxime and cefixime in in vitro kinetic models. Int. J. Antimicrob. Agents 25:120–129 [DOI] [PubMed] [Google Scholar]
- 11. MacGowan AP, Reynolds R, Noel AR, Bowker KE. 2009. Bacterial strain-to-strain variation in pharmacodynamic index magnitude, a hitherto unconsidered factor in establishing antibiotic clinical breakpoints. Antimicrob. Agents Chemother. 53:5181–5184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. McGrath B, Lamp KC, Rybak MJ. 1993. Pharmacodynamic effects of extended dosing intervals of imipenem alone and in combination with amikacin against Pseudomonas aeruginosa in an in vitro model. Antimicrob. Agents Chemother. 37:1931–1937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Meagher AK, Forrest A, Dalhoff A, Stass H, Schentag JJ. 2004. Novel pharmacokinetic-pharmacodynamic model for prediction of outcomes with an extended-release formulation of ciprofloxacin. Antimicrob. Agents Chemother. 48:2061–2068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Miller JR, et al. 2009. A class of selective antibacterials derived from a protein kinase inhibitor pharmacophore. Proc. Natl. Acad. Sci. U. S. A. 106:1737–1742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Mochalkin I, et al. 2009. Discovery of antibacterial biotin carboxylase inhibitors by virtual screening and fragment-based approaches. ACS Chem. Biol. 4:473–483 [DOI] [PubMed] [Google Scholar]
- 16. Mouton JW, Vinks AA. 2005. Pharmacokinetic/pharmacodynamic modeling of antibacterials in vitro and in vivo using bacterial growth and kill kinetics. Clin. Pharmacokinet. 44:201–210 [DOI] [PubMed] [Google Scholar]
- 17. National Committee for Clinical Laboratory Standards 1999. Methods for determining bactericidal activity of antimicrobial agents. Approved guideline M26-A. National Committee for Clinical Laboratory Standards, Wayne, PA [Google Scholar]
- 18. Schaper KJ, Schubert S, Dalhoff A. 2005. Kinetics and quantification of antibacterial effects of beta-lactams, macrolides, and quinolones against gram-positive and gram-negative RTI pathogens. Infection 33(Suppl. 2):3–14 [DOI] [PubMed] [Google Scholar]
- 19. Simeoni M, et al. 2004. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 64:1094–1101 [DOI] [PubMed] [Google Scholar]
- 20. Tam VH, Schilling AN, Poole K, Nikolaou M. 2007. Mathematical modeling response of Pseudomonas aeruginosa to meropenem. J. Antimicrob. Chemother. 60:1302–1309 [DOI] [PubMed] [Google Scholar]
- 21. van de Waterbeemd H. 2009. Improving compound quality through in vitro and in silico physicochemical profiling. Chem. Biodivers. 6:1760–1766 [DOI] [PubMed] [Google Scholar]
- 22. Yano Y, Oguma T, Nagata H, Sasaki S. 1998. Application of logistic growth model to pharmacodynamic analysis of in vitro bactericidal kinetics. J. Pharm. Sci. 87:1177–1183 [DOI] [PubMed] [Google Scholar]
- 23. Zinner SH, Dudley M, Blaser J. 1986. In vitro models for the study of combination antibiotic therapy in neutropenic patients. Am. J. Med. 80:156–160 [DOI] [PubMed] [Google Scholar]