Effect of intersubject variability of extrathoracic morphometry, lung airways dimensions and respiratory parameters on particle deposition

Abstract

Objective

The structure of extrathoracic passages, variability of tracheobronchial (TB) airways and alveolar dimensions and individual variations of breathing pattern exhibit significant intersubject variations, which affect extrathoracic deposition and, in further consequence, the fraction of inhaled particles actually reaching the thoracic region. The present study was conducted to quantify the intersubject variability of lung deposition fractions caused by the fluctuations in these three major sources of intersubject variability.

Methods

To quantify intersubject variability of extrathoracic, thoracic and total deposition fractions (TDF), different combinations of the three sources of variability were simulated to identify the most important factors. Deposition fractions of inhaled particles were computed by the stochastic airway generation model IDEAL. The dimensions of the respiratory airways were scaled in proportion to age and height of the subject to calculate TDFs.

Results

The variability of deposition fractions increased with the stepwise addition of influencing factors and the resulting standard deviations ranged up to 30%. While some combinations enhanced the effects of individual factors on deposition by up to 40%, others seemed to compensate each other with only a minor effect on deposition.

Conclusion

The present study attempts to quantify experimentally observed intersubject variability of regional deposition fractions caused by individual variations of nasal and oral geometry, lung airway dimensions and breathing patterns in healthy lungs, serving as a baseline for subsequent calculations for diseased lungs, e.g. asthma, COPD, and emphysema, which may further increase intersubject variabilities of medically relevant depositions.

Introduction

The extrathoracic (ET) region (nasal and oral passages, pharynx and larynx) of the human respiratory tract serves as an important first stage filter for inhaled particulates entering the thoracic region (tracheobronchial and pulmonary regions), i.e. the lungs per se, of the human respiratory tract. For medical aerosol administration and measurements of aerosol deposition in the human lung, consideration of particle deposition in the extrathoracic region is of utmost importance as it eventually determines the fraction of inhaled particles actually entering the lungs.

Due to the complex morphometry of the ET region and the resulting intersubject variability, it is presently not possible to derive specific analytical models for the estimation of deposition efficiencies, although very promising results have been obtained by computational fluid dynamics (CFD) (1)-(4). Thus the modeling approach currently taken is to develop semi-empirical deposition equations for nasal and oral deposition by fitting available experimental data as functions of physical deposition parameters. However, the complexity of the extrathoracic region, which depends on gender, age and health condition, results in different experimental deposition efficiencies and hence in different deposition equations.

Since experimental data from in-vivo studies have revealed significant intersubject variations, particularly for high nasal/oral deposition efficiencies (5), various authors attempted to explain these differences by the specific geometry of nasal and oral airway passages in these volunteers (6)-(9). For example, Cheng (10) proposed an average shape factor (S_f) and a minimum cross sectional area (A_min) to predict the variability of in-vivo nasal deposition in the diffusion and the inertial impaction regime respectively. For the calculation of the intersubject variability in oral airways in the impaction regime, Cheng (10) approximated the Stokes number as a function of an equivalent diameter (d) while Grgic et al. (11) approximated it as a function of the mouth-throat volume (V) and centerline path length (L). Garcia et al. (12) developed an alternative approach to find inter-individual variability in nasal filtration as a function of nasal cavity geometry by relating it to the trans-nasal pressure drop. Since the range of the morphometric parameter values were also reported in these studies, they can be used to predict intersubject variability of ET deposition.

In a previous study, Hofmann et al. (13),(14) investigated the effect of intersubject variability of airway dimensions in the thoracic region on total deposition fractions (TDF). Since TDF may be significantly affected by ET deposition, the intersubject variability of the ET region has been correlated in the present study to the intersubject variability of the thoracic region. This correlation is based on the observation that the dimensions of the trachea are closely related to the head region rather than to the lungs (6). Hence the geometric parameters of the ET regions are related to the randomly selected lung structure by the scaling factor (SF) (6), which is defined as the ratio of the tracheal diameters in a reference adult to that given subject. In vivo measurements of nasal and oral deposition efficiencies were commonly carried under well defined breathing conditions. For normal breathing, however, significant intersubject variations of tidal volume (V_T), breathing frequency (f) and functional residual capacity (FRC) could be observed (15),(16). Therefore, in addition to the intersubject variability of the nasal and oral geometry, the variability of the breathing pattern and lung scaling through FRC will also contribute to the overall predicted intersubject variability of ET and TDF.

Thus the primary objectives of the present study are (i) to quantify intersubject variations of nasal and oral deposition efficiencies for inhalation and exhalation based on semi-empirical equations as well as from ET morphometric parameters; (ii) to evaluate their effects generational deposition (inhalation plus exhalation); (iii) to evaluate intersubject variations produced by the SF, with and without lung airway scaling, (iv) to compare intersubject variations produced by the SF, lung airway dimensions and with those caused by the variability of the respiratory parameters.

Methods

Assuming that the differences between several semi-empirical ET deposition equations based on human volunteers and ET-casts can be attributed primarily to intersubject variations of nasal and oral geometries, ET deposition was computed by inserting different semi-empirical deposition equations (Appendix) into the deposition model.

To analyze the intersubject variability caused by nasal and oral morphometric parameters, nasal airway dimensions measured by Cheng et al. (17) in 10 adult male subjects (Table 1) and a set of mean oral diameters obtained from seven mouth-throat geometries defined by Grgic et al.(11) (Table 2) were used. For ultrafine particles (≤ 0.2 µm), diffusion is the dominant deposition mechanism and hence the nasal deposition efficiency is expressed as a function of the diffusion coefficient (D) and flow rate (Q) by fitting equation , where S_f , is the average shape factor of the nasal turbinate region(10). For large particles (> 0.2 µm), impaction is the dominant deposition mechanism and the nasal deposition efficiency is calculated by as a function of the aerodynamic diameter (d_a) and flow rate (Q) by fitting equation E_n = 1 – exp(–110 Stk), the where dimensionless Stokes number () depends on the nasal cross sectional area A_min (10).

Table 1. Nasal airway dimensions S_f and A_min in 10 subjects (17).

Subjects†	A	B	C	D	E	F	G	H	I	J	Mean±SD
Sf	2.90	2.76	2.62	2.60	2.45	2.56	2.42	2.29	2.38	2.09	2.51±0.23
Amin (cm2)	2.28	1.65	2.42	2.21	1.87	3.10	3.10	2.06	1.54	2.37	2.1±0.52
Height (m)	1.92	1.85	1.78	1.73	1.70	1.83	1.67	1.91	1.65	1.85	1.79±0.10

^†The subjects include mixed ethnicity males and females aged 24-58 years with heights of 1.65-1.93m.

Table 2. Oral airway mean diameters of seven realistic mouth throat models† based on MRI scans (13).

Model	Idealized ‡	S1a§	S1b§	S2	S4	S5a§	S5b§	S3	Mean±SD
dmean	2.1	1.8	1.5	2.5	2.4	2.6	2.8	2.0	2.21±0.43

^†The model includes Caucasian male and female subjects aged 23-43 years; ^‡Subject representing average geometry of actual subjects; ^§Model with intrasubject geometric configurations.

For oral deposition in the diffusion region no correlation between oral geometry and deposition efficiency has yet been found. However, in the inertial impaction regime, the deposition efficiency was calculated as function of the aerodynamic diameter (d_a) and the air flow velocity (U) by fitting equation E₀ = 1 – exp(–19.2 Stk), where Stk is the dimensionless Stokes number (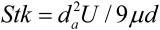). This Stokes number depends on the characteristic length which is assumed to be the equivalent diameter of the average cross sectional area of the oropharyngeal region (10) (Table 2). Since coefficients for expiratory deposition are not significantly different from inspiratory deposition (10), the same equation was used in this paper for extrathoracic deposition calculations.

To model the effects of individual anatomical dimensions of extrathoracic and thoracic airway relative to an adult reference man, ICRP (6) proposes the application of the scaling factor SF. This factor also relates the extrathoracic geometry to the tracheal diameter i.e. SF = 1.65/d_o, where d_o is the diameter of the trachea in units of centimeters. Tracheal diameters can either be randomly selected from a defined tracheal diameter distribution or can be directly related to the height of a subject by the allometric equation d_o = 1.324(H)–0.80, where H is measured in units of meter. This equation was obtained by fitting published data on the relationship between subject height and tracheal diameter (18). This SF is incorporated into the modified ICRP equations 1a-4a (Appendix) to determine their effect on particle deposition.

Significant intersubject variability due to different respiratory parameters, such as functional residual capacity (FRC), tidal volume (V_T) and breathing frequency (f), was found in 25 male and female subjects (15),(16). Airway dimensions, i.e. lengths and diameters of bronchial and acinar airways were scaled in proportion to the third root of the individual functional residual capacity (FRC) (6), where FRC is calculated as a function of age (A), height (H) and gender of a given subject. For example, FRC = 2.24H + 0.009A – 1.09 for males and FRC = 2.24H + 0.001A–1 for females.

Deposition fractions of inhaled particles were computed by the stochastic airway generation model IDEAL (Inhalation, Deposition and Exhalation of Aerosols in the Lung), originally developed by Hofmann and Koblinger (19) and Koblinger and Hofmann (20), but revised many times in the years thereafter (13),(16),(19),(21),(22),(23). Formulated mathematically as a Langrangian random pathway model, airway dimensions are randomly selected by parameter probability density functions and correlations among several of these parameters, which were derived from measured morphometric data (24),(25). The paths of individual inhaled particles through the random airway geometry are simulated by Monte Carlo methods. The diffusion deposition efficiency in bronchial airways was calculated by the deposition equations proposed by Ingham (26) for laminar flow and by Cohen and Asgharian (27) for developing flow. For sedimentation, the equations of Yeh and Schum (28) and for impaction Zhang et al.(29) were used (Appendix).

Results

Deposition fractions for unit density monodisperse particles in the size range of 1 nm to 10 µm were computed for sitting and light exercise breathing conditions. Flow rates for sitting and light exercise conditions are assumed to be 18 and 50 L min⁻¹ respectively (8). Furthermore, uniform breathing with equal inspiration and expiration and zero breath hold time was considered. These input data were used to obtain nasal, oral and TDF for all subjects.

Effect of variable ET geometry on deposition

Nasal breathing

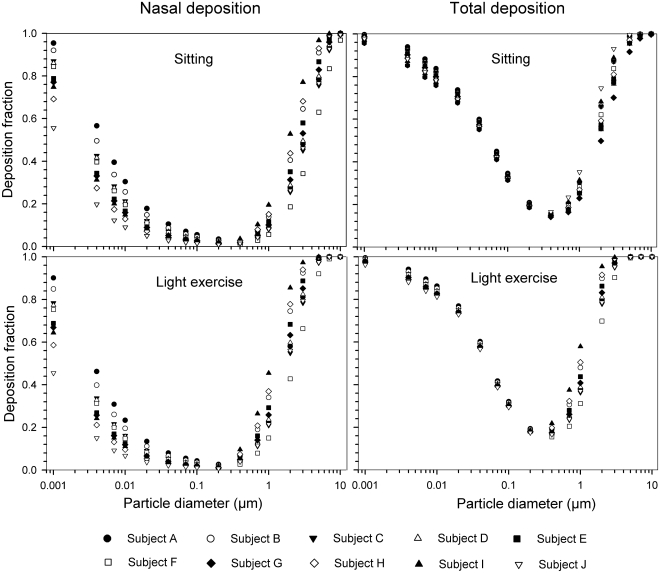
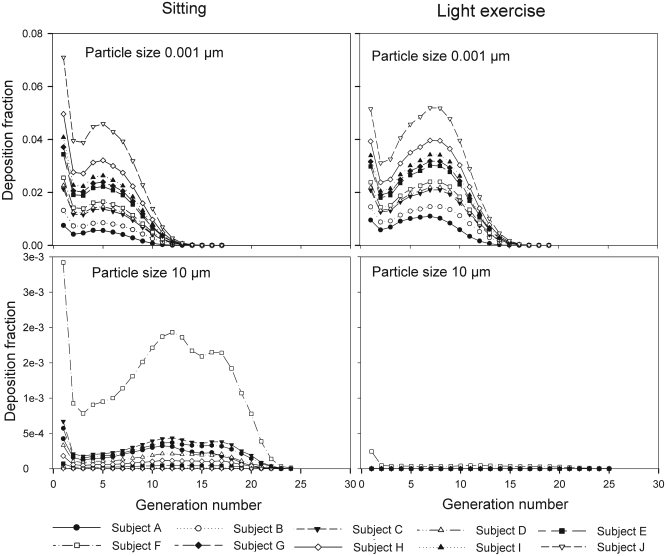
The simulated effects of intersubject variability in nasal airways dimensions and its effect on nasal and total deposition are presented in Fig 1. In these simulations intersubject variations of the nasal deposition are determined primarily by corresponding fluctuations of S_f , and A_min. Simulations revealed that deposition increases proportionally with increase in S_f in the diffusion dominant regime and with decrease in A^min in the impaction regime. In the diffusion regime, nasal deposition efficiency decreases with increase in particle size and with decrease in flow rate. In the impaction regime it increases distinctly with increase in particle size and flow rate (Tables 3-6). But TDF increases with a growing flow rate in both regimes except for the intermediate particle size range (0.07–0.2 µm).

Fig 1. Intersubject variability of particle deposition caused by different nasal geometries in 10 subjects under sitting (18 Lmin⁻¹) and light exerc-ise (50 Lmin⁻¹) breathing conditions.

Table 3. Summary of nasal deposition fractions in 10 different subjects under sitting breathing conditions using different deposition equations.

Particle diameter (µm)	Cheng(10) equation†	Other equations‡	ICRP equation without lung scaling	ICRP equation with lung scaling§	ICRP equation with different breathing patterns§
0.001	0.80±0.23	0.91±0.14	0.87±0.005	0.88±0.009	0.88±0.018
0.01	0.30±0.13	0.23±0.12	0.22±0.004	0.22±0.007	0.22±0.012
0.1	0.05±0.02	0.06±0.13	0.04±0.001	0.04±0.002	0.04±0.002
1	0.09±0.08	0.12±0.05	0.17±0.07	0.17±0.07	0.2±0.09
5	0.78±0.20	0.74±0.11	0.78±0.08	0.79±0.08	0.82±0.08
10	0.99±0.02	0.93±0.13	0.92±0.03	0.93±0.03	0.94±.03

^†see equation 9 in the Appendix; ^‡other equations include average deposition fraction obtained from ICRP (6) , NCRP (31), Cheng (10), Martonen et al. (2), Asgharian et al. (30); ^§see equations 1a and 3a in the Appendix.

Table 6. Summary of thoracic deposition fraction in 10 different subjects under oral and sitting breathing conditions using different equations.

Particle diameter (µm)	Cheng equation†	Other equations‡	ICRP equation without lung scaling	ICRP equation with lung scaling§	ICRP equation with different breathing patterns§
0.001	-	0.24±0.02	0.34±0.001	0.32±0.003	0.31±0.011
0.01	-	0.65±0.04	0.65±0.001	0.64±0.057	0.63±0.06
0.1	-	0.30±0.02	0.30±0.0001	0.29±0.056	0.26±.092
1	0.18±0.01	0.17±0.01	0.17±0.001	0.17±0.044	0.15±0.068
5	0.57±0.08	0.56±0.024	0.53±0.025	0.52±0.079	0.48±0.059
10	0.49±0.09	0.40±0.04	0.31±0.015	0.31±0.025	0.27±.022

^†se equation 10 in appendix; ^‡other equations include average deposition fraction obtained from ICRP (6), NCRP (31) and Cheng (10); ^§see equations 2a and 4a in appendix.

Oral breathing

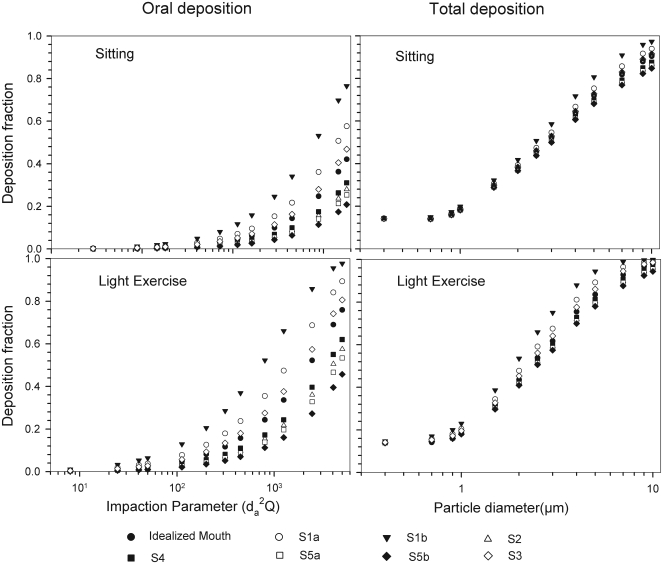
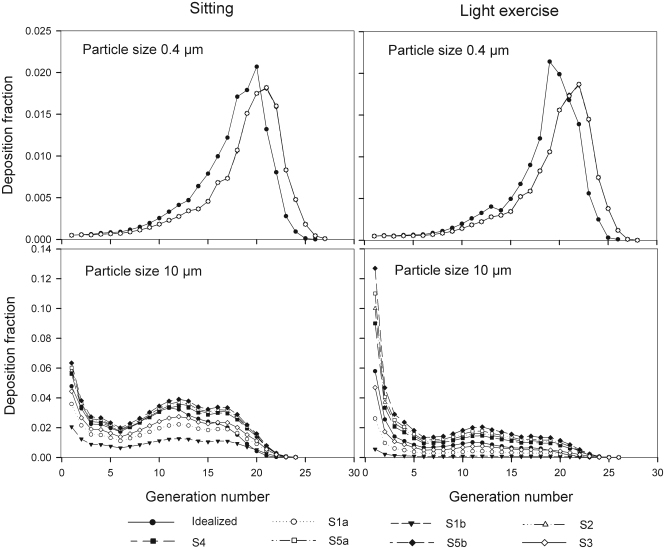
The intersubject variations of the oral deposition are determined by corresponding fluctuations of oral equivalent diameter d. The simulations in the impaction regime revealed that deposition is high for small values of a given d (Fig 2). Deposition efficiency increases with rising particle size and flow rate. For different subjects, a large variability in oral deposition was observed. Higher values of deposition efficiencies are observed with oral breathing in the thoracic region as compared to nasal breathing.

Fig 2. Intersubject variability of particle deposition caused by different oral geometries in 7 subjects (impaction regime only) under sitting and light exercise breathing conditions.

Intersubject variability caused by different semi-empirical deposition equations

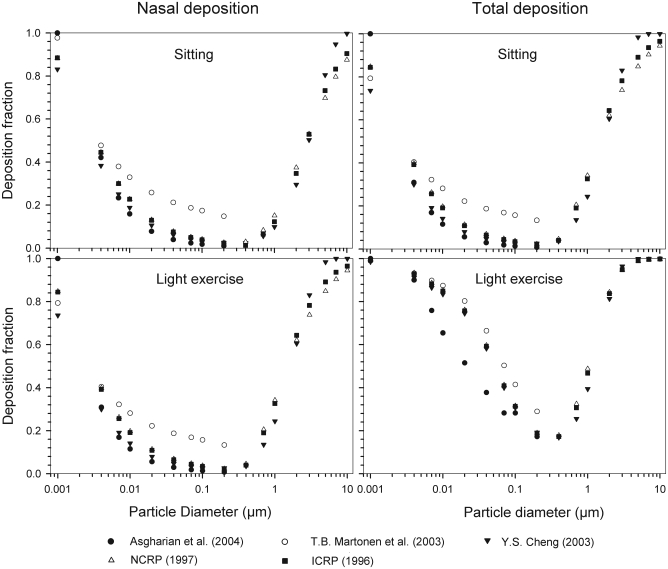
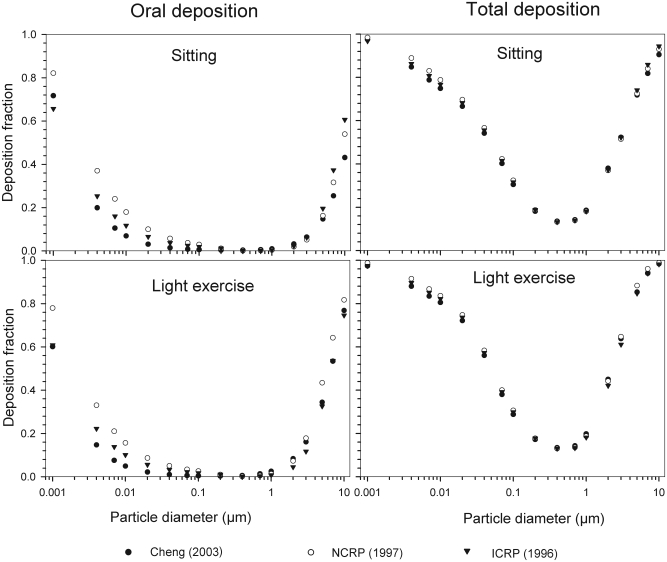
Semi-empirical nasal and oral deposition equations were used in this study assuming that these equations primarily reflect intersubject variations, provided that identical breathing conditions and aerosol data are used. Figs 3–4 exhibit deposition efficiencies in nasal and oral airways and consequently in TDF using these equations. For nasal deposition, Asgharian (30) and Martonen et al. (2) have derived equations for fine particles size ≤ 2 µm only. The equation derived by Martonen et al. (2) produces comparatively higher deposition fractions, possibly due to the consideration of 70% turbulent flow compared to 30% laminar flow (Appendix). The deposition fraction derived from NCRP (31) and ICRP (6) yield quite similar results in the diffusion regime as compared to impaction regime where NCRP equations give somewhat lower deposition fractions. This is most likely due to the lower value of the coefficient derived for the impaction parameter.

Fig 3. Variability of particle deposition during nasal breathing caused by use of different semi-empirical deposition equations under sitting and light exercise breathing conditions.

Fig 4. Variability of particle deposition during oral breathing caused by different semi-empirical deposition equations under sitting and light exercise breathing conditions.

Table 4. Summary of thoracic deposition fraction in 10 different subjects under sitting nasal breathing condition using different deposition equations.

Particle diameter (µm)	Cheng(10) equation†	Other equations‡	ICRP equation without lung scaling	ICRP equation with lung scaling§	ICRP equation with different breathing patterns§
0.001	0.18±0.02	0.08±0.012	0.12±0.001	0.11±0.001	0.11±0.004
0.01	0.54±0.05	0.57±0.05	0.61±0.002	0.59±0.014	0.57±0.05
0.1	0.30±0.02	0.29±0.11	0.29±0.0001	0.29±0.055	0.26±0.09
1	0.19±0.07	0.17±0.05	0.16±0.06	0.16±0.076	0.14±0.07
5	0.18±0.05	0.21±0.03	0.17±0.021	0.17±0.024	0.14±0.02
10	0.01±0.002	0.06±0.013	0.06±0.003	0.06±0.004	0.05±0.004

^†see equation 9 in the Appendix; ^‡other equations include average deposition fraction obtained from ICRP(6), NCRP(31), Cheng(10), Martonen et al.(2), Asgharian et al. (30); ^§see equations 1a and 3a in the Appendix.

Table 5. Summary of oral deposition fraction in 7 different subjects under sitting breathing conditions using different deposition equations.

Particle diameter (µm)	Cheng equation†	Other equations‡	ICRP equation without lung scaling	ICRP equation with lung scaling§	ICRP equation with different breathing patterns§
0.001	-	0.73±0.166	0.64±0.008	0.65±0.014	0.65±0.025
0.01	-	0.12±0.11	0.12±0.002	0.12±0.009	0.12±0.007
0.1	-	0.02±0.02	0.02±0.0001	0.019±0.001	0.019±0.001
1	0.01±.013	0.005±.007	0.004±0.001	0.004±0.001	0.005±0.002
5	0.15±0.19	0.17±0.05	0.22±0.057	0.22±0.046	0.26±0.091
10	0.41±0.38	0.53±0.18	0.64±0.076	0.64±0.061	0.68±0.099

^†see equation 10 in appendix; ^‡other equations include average deposition fraction obtained from ICRP (6), NCRP(31) and Cheng(10); ^§see equations 2a and 4a in Appendix.

Generational deposition fraction

Nasal breathing

The generational deposition fractions are significantly different for all 10 subjects for 1nm and 10 µm sized particles up to generation 15 (Fig 5). The deposition fractions for 1 nm particles exhibit two maxima, the first in generation 1 and the second around generation 5. The later is shifted to about generation 7–8 under light exercise breathing conditions. The generational deposition fractions for intermediate particle diameter do not show much variability in all 10 subjects. For 10 µm sized particles, very low deposition fractions up to generation 23 can be observed.

Fig 5. Generational deposition fractions during nasal breathing under sitting and light exercise breathing conditions.

Oral breathing

The generational deposition fractions for 0.4 µm sized particle in airway generations do not show much variability for all 5 subjects except for an idealized mouth (Fig 6). The highest deposition fraction is about 2% in generation 20 for both breathing conditions. The deposition fractions for 10 µm sized particle exhibit variability in each generation up to generation 24. For light exercise breathing conditions, deposition fractions are highest in the first generation and gradually decrease in subsequent generations.

Fig 6. Generational deposition fractions during oral breathing under sitting and light exercise breathing conditions.

Intersubject variability caused by SF and lung airway scaling

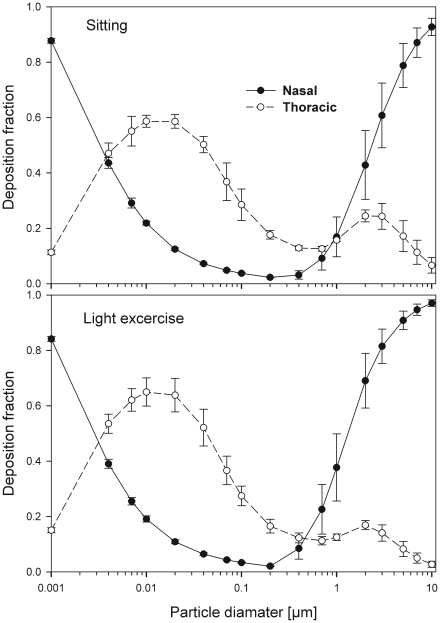
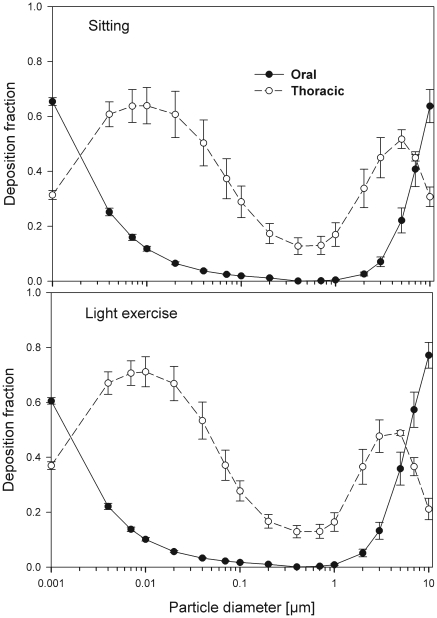
The effect of the correlation between SF and the scaling of the lung dimensions using the ICRP equations for nasal and thoracic deposition are shown in Figs 7 and 8 (mean values and standard deviations) for both nasal and oral breathing respectively. Significant variability in thoracic deposition can be observed during both sitting and light exercise breathing conditions. Comparison of deposition fractions with lung scaling shows a higher variability as compared to simulations without lung scaling (Tables 3–6).

Fig 7. Nasal and thoracic deposition fractions (mean ± SD) caused by the SF and the variability of the lung airway dimensions during nasal breathing.

Fig 8. Oral and thoracic deposition fractions (mean ± SD) caused by the SF and the variability of the lung airway dimensions during oral breathing.

Intersubject variability caused by SF, lung airway scaling and different breathing patterns

Fig 9 shows intersubject variability of particle deposition due to SF, different breathing patterns and lung scaling in 25 male and female subjects. The mean values and standard deviation for age and height of the subjects used in this study were 25 ± 3.35 yr and 1.74 ± 0.1 m respectively. The mean values and standard deviations for breathing parameters were 3220 ± 605 mL for FRC, 670 ± 138 mL for V_T, 15.6 ± 4.43 min⁻¹ for f, and 21 ± 7 L min⁻¹ for the flow rate. Residence times of aerosols in the lungs and hence their deposition probabilities by diffusion or sedimentation are controlled by three parameters: FRC, V_T, and f. At present no definite correlation between these parameters could be found. However, using a fixed value of the FRC and an increased tidal volume enhances the flow rate and thus an increase in ET as well as thoracic deposition can be observed. This increase in both deposition fractions are affected inversely with a decrease in breathing frequency of the same subject. If individual breathing patterns are considered, a smaller variability in the diffusion regime is found for the ET region, while a 3–4 times higher variability can be observed for thoracic deposition (Tables 3–6). In the impaction regime, the variability in the ET region is higher than that for thoracic deposition.

Fig 9. Variability of particle deposition caused by the SF, lung airway scaling and the variability of the breathing patterns.

Comparison of intersubject variability based on the Coefficient of Variation (CV)

The coefficient of variation is defined as the ratio of the standard deviation to the mean value of the deposition fraction. A comparative overview of the variability of deposition in ET and TDF in terms of CV for sitting breathing conditions is shown in Fig 10. Incorporation of geometric parameters tends to increase the CV. The maximum values of CV during nasal and oral breathing are 0.75 and 1.41, respectively. For thoracic deposition, the maximum value of CV is 0.26 and 0.12 for nasal and oral breathing conditions respectively. Larger values of CV are observed in the diffusion regime when different formulas for nasal breathing are employed while they decrease in the impaction regime. This larger variability when using different deposition formulas seems to be related to causes other than intersubject variability.

Fig 10. Comparison of deposition fractions expressed by the coefficient of variation (CV) using different semi-empirical deposition equations and conditions.

Without lung scaling, lower variability is observed in the diffusion regime as compared to the impaction regime for both ET and TDF. In the impaction regime, lung scaling according to age and height yields a CV value up to 0.23 for TDF as compared to 0.01 for oral breathing without lung scaling. For nasal breathing, the observed CV values were 0.23 and 0.19 with and without lung scaling, respectively.

Intersubject variability for different subjects caused by SF, lung scaling and consideration of different breathing patterns produces the highest values of CV, e.g. 0.3 and 0.42 for TDF in nasal and oral breathing, respectively. The larger values of CV when considering SF, lung scaling and individual breathing pattern shows that variation in deposition increases with the consideration of individual physical and breathing parameters.

Discussion

Effect of variable ET geometry on deposition

The use of different anatomical data affects nasal, oral and thoracic deposition and seems to be major controlling factors for the experimentally observed intersubject variability in ET airways. Larger values of S_f are a measure of larger complexity, which increases turbulences and results in secondary flows which in turn increase particle deposition. On the other hand, smaller values of A_min, which is variable during the breathing cycle, impede air flow, and hence increase deposition. At very low and high flow rates, the deposition efficiencies for 1 nm and 10 µm particles approach 100% in nasal airways. Deposition of ultrafine particles increases with the diffusion coefficient and with longer residence times in the airways. Hence, low flow rates and smaller particle diameters produce higher deposition efficiencies in the diffusion regime. For oral breathing in the impaction regime, smaller values of d and higher flow rates cause higher deposition efficiencies. The higher oral deposition efficiency in the impaction regime is caused by increased turbulences in the narrow parts of the oral passage.

Generational deposition efficiencies

For nasal breathing the deposition fraction for 1 nm particles in the first generation are high relative to the following generations. This is due to turbulent flow caused by the complex geometry of the ET region. However, after passing through the trachea, the flow becomes smooth and deposition fraction decreases up to generation 5 to 8, depending upon the flow rate. Similar behavior of deposition can be observed for 10 µm size particles with the highest deposition in generation 10 (Fig 5). Deposition fractions of large particles within the thoracic region are higher for oral breathing as compared to nasal breathing due to the lower oral filtration efficiency.

The variability of deposition efficiencies in different generations also affects TDF. The relative variability in thoracic deposition tends to be high for low thoracic deposition and low for high thoracic deposition as the case of 1 nm and 10 µm particles (Figs 5–6). This effect of relative variability in ET and thoracic region is consistent with the findings of Borgström et al.(32) In the diffusion regime, a higher flow rate decreases deposition in the ET region but increases it in thoracic region. In the impaction regime, ET as well as thoracic deposition rise with an increase in flow rate, similar to the results obtained by Wang et al.(5) Finally, large intersubject variability can be observed in TDF for oral breathing as compared to nasal breathing (Figs 2 and 4).

Intersubject variability caused by SF and lung airway scaling

The values of the scaling factor SF are inversely proportional to the tracheal diameter or height of the subject. In the diffusion deposition regime, ET deposition efficiency is higher for lower values of SF, but exhibit the opposite behavior in the impaction regime. This highlights the fact that at younger ages (< 20 years) diffusion deposition is higher as compared to older ages, while an opposed trend can be observed in the impaction regime.

Scaling of the lung airways, approximated by FRC variations is not the only factor affecting deposition fractions but must be considered in combination with the breathing pattern of a given subject. Under sitting nasal breathing conditions and keeping all breathing parameters constant, for each 5 cm rise of the height of the subject, a 1 to7% decrease in TDF is observed in the impaction regime. For oral breathing conditions this decrease amount to 1 to 9%. In females relative to male subjects of the same age group, TDF increases by 2 to 5% due to lower FRC values. In diffusion regime, the effect of FRC variations on TDF is negligible.

Intersubject variability caused by SF, lung airway scaling and different breathing patterns

Intersubject variability for particle deposition tends to increase by up to 40% among the subjects if a third factor i.e. the breathing pattern of the subjects is combined with the other two factors i.e. SF and lung airways scaling, as discussed in the previous section. In some cases different breathing parameters produce compensatory effects; in others they enhance effects on particle deposition. Deposition fractions increase with diminishing breathing frequency when V_T is kept constant in both the diffusion and impaction regimes. If both parameters, i.e. V_T and breathing frequency, are increased or decreased simultaneously, they compensate each other and no significant effect on particle deposition is observed. In subjects with similar FRC and V_T during nasal breathing, each increase in breathing time of 3 to 5 seconds, increase TDF up to 35% in diffusion regime and up to 30% in the impaction regime. During oral breathing, corresponding increases are 35% and 42%. For subjects with similar FRC and breathing times during nasal breathing leads to increases TDF up to 11% in the diffusion regime and up to 17% in the impaction regime for each 100 ml rise in V_T. During oral breathing, corresponding increases are up to 15% and 14%. These results show that an increase in flow rate, either as a result of shorter breathing time or by higher tidal volumes affects TDF differently regardless of nasal or oral breathing. The contribution of ET deposition to TDF increases for higher tidal volume, where as the contribution of thoracic deposition to TDF increases with rising breathing times. This relatively high contribution of ET deposition in TDF with higher tidal volumes is due to the related increase in airways dimensions which consequently causes a lower thoracic deposition. On the other hand an increase in residence time without any change in airways dimensions results in higher deposition fraction in the thoracic region. The results predicted for both the TDF and the thoracic deposition are in accordance with the experimental results obtained by Kim et al. (33)-(37).

Conclusion

The variability in deposition fraction increases with the addition of influencing factors and the resulting standard deviations ranged up to 30%. The present calculations reveal that the range of the experimentally observed ET deposition efficiencies can be approximated by corresponding fluctuations of the S_f, A_min and d values. However in the absence of detailed nasal and oral geometric data, the use of scaling factor SF also provides a reasonable approximation of the intersubject variability of resulting deposition fractions. The variations of the breathing patterns partly caused by the above mentioned parameters and bronchial airway scaling, tend to increase the related variations in deposition fractions among the subjects by up to 40%. Hence, for individual dosimetric values, the effect of inter-subject variability in ET region must be considered. More reliable results for ET and total deposition can be obtained with a more precise determination of nasal or oral geometry, scaling of lung dimensions and considering the individual breathing habits of the subjects.

The parameter variations and resulting variations simulated in the present study refer to healthy lungs. The results obtained for healthy lung will serve as a baseline for future calculations for diseased lungs, which will further increase intersubject variability.

APPENDIX

1. Semi-empirical deposition equations for the extrathoracic (ET) region:

1.1.Equations recommended by ICRP(6)

For fine particles < 0.2 µm equations 1 and 2 were proposed by Swift et al. (38) to calculate the deposition efficiencies for nasal and oral passages during inhalation.

[1]

with scaling factor (SF)

[1a]

[2]

with SF

[2a]

where D (cm² s⁻¹) is the diffusion coefficient and Q (ml s⁻¹) is the flow rate.

For particles ≥ 0.2 µm the equation 3 and 4 were derived by Rudolf et al. (39) and Stahlhofen et al. (40) to determine the deposition efficiencies for nasal and oral passages during inhalation.

[3]

with SF

[3a]

[4]

with SF

[4a]

where V_T (ml) is the tidal volume and d_a (µm) is the particle aerodynamic diameter.

Since differences between inhalation and exhalation are relatively small (about 10%), it is recommended to use equations 1-4 and 1a-4a for both inhalation and exhalation.

1.2.Equations recommended by NCRP(31)

For fine particles < 0.2 µm NCRP(31) adopted the following formulas (equations 5-6) based on a turbulent diffusion model proposed by Cheng et al.(41) in which the deposition efficiency can be expressed as a function of the diffusion coefficient D(cm² s⁻¹) and the flow rate Q (L min⁻¹).

[5]

The values of constant a for nasal N and oral O inhalation (i) and exhalation (e) are given as follows:

N_i: a=12.8; N_e: a=15.0; O_i: a=10.3; O_e: a=8.51

For particles ≥ 0.2 µm the following formulas obtained by Yeh et al.,(42) by fitting of a logistic function to the summarized data of Yu et.al.(43) are used.

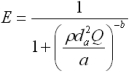[6]

where ρ (g cm⁻³) is the particle density and d_a (µm) is the aerodynamic diameter. The coefficients a and b are experimentally derived parameters for inhalation and exhalation for both oral and nasal breathing:

N_i: a=4600 & b=0.94; N_e: a=2300 & b=1.01; O_i: a=30,000 & b=1.37; O_e: a=30,000 & b=1.37

1.3.Equation formulated by Martonen et al. (2)

The mathematical model of Martonen et al.(2) describes diffusion deposition efficiency in the human ET region by Equation 7. This model combines the effect of turbulent and laminar flows where 70% turbulent and 30 % laminar flow contribution provided the best fit to the experimental data for both nasal inhalation and exhalation.

[7]

where the term Δ = πDL / 4Q is a dimensionless diffusion parameter (L is the airway path length in units of centimetres) and is the Schmidt number (ν is the kinematic viscosity in units of (m²s⁻¹).

1.4.Equationsproposed by Cheng (10)

Cheng(10) proposed equations 8 and 9 for regional nasal and oral deposition efficiencies in adult humans for both inhalation and exhalation.

[8]

[9]

where and Q (L min⁻¹) is the flow rate.

1.5.Equation derived by Asgharian et al. (20)

For nasal breathing (inhalation and exhalation), Asgharian et al. (29) fitted equation 10 for nano particles deposition accounting both axial diffusion and dispersion.

[10]

where Q (L min⁻¹) is flow rate.

1.6.Equation presened by Grgic et al.(11)

Grgic et al. (11) measured deposition in realistic mouth throat geometries taken from seven subjects by MRI scans. The empirical function (equation 11) that predicts the mouth throat deposition is given by:

[11]

where 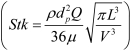and 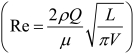are Stokes and Reynolds numbers respectively which depend on mouth-throat volume (V)and the centre line path length (L) (11).

2. Semi-empirical deposition equations implemented into the IDEAL code for the bronchial and the pulmonary region

2.1.Deposition by diffusion

2.1.1. For laminar flow

Ingham (26) derived the following equation for the deposition efficiency in the human airways for laminar flow conditions:

[12]

where flow rate is given in ml s⁻¹.

2.1.2. For developing flow

For a replica cast of the upper bronchial airways Cohen and Asgharian(27) derived the following empirical equation for the diffusion deposition efficiency (η_D) of particles for turbulent flow conditions due to the branching of bronchial airways:

[13]

2.2. Deposition by Sedimentation

The deposition efficiency for sedimentation (P_s) in cylindrical tubes was suggested by Yeh and Schum(28)

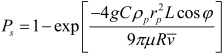[14]

where g is the acceleration of gravity, φ is the gravity angle relative to the horizontal line, i.e. perpendicular to the direction of gravity, ρ_p is the density of the particle, C is the Cunningham slip correction factor, r_p is the particle radius, and µ is the viscosity of the fluid.

2.3. Deposition by Impaction

Zhang et al.(29) derived following deposition equation cylindrical tubes by impaction:

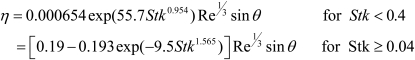[15]

for parabolic flow and

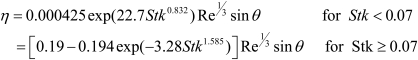[16]

for a uniform inflow, where θ is bend or branching angle measured in degrees.