Abstract
Quantifying ear-canal sound level in forward pressure has been suggested as a more accurate and practical alternative to sound pressure level (SPL) calibrations used in clinical settings. The mathematical isolation of forward (and reverse) pressure requires defining the Thévenin-equivalent impedance and pressure of the sound source and characteristic impedance of the load; however, the extent to which inaccuracies in characterizing the source and/or load impact forward pressure level (FPL) calibrations has not been specifically evaluated. This study examined how commercially available probe tips and estimates of characteristic impedance impact the calculation of forward and reverse pressure in a number of test cavities with dimensions chosen to reflect human ear-canal dimensions. Results demonstrate that FPL calibration, which has already been shown to be more accurate than in situ SPL calibration, can be improved particularly around standing-wave null frequencies by refining estimates of characteristic impedance. Better estimates allow FPL to be accurately calculated at least through 10 kHz using a variety of probe tips in test cavities of different sizes, suggesting that FPL calibration can be performed in ear canals of all sizes. Additionally, FPL calibration appears a reasonable option when quantifying the levels of extended high-frequency (10–18 kHz) stimuli.
INTRODUCTION
Two options for quantifying sound in human ear canals are (1) measurements of sound pressure level (SPL) in an acoustic coupler or ear simulator and (2) measurements of SPL in situ. As currently performed in clinical practice, both options can result in substantial differences between assumed and actual sound levels (e.g., Voss et al., 2000a,b; Voss and Herrmann, 2005; Siegel, 1994; Siegel and Hirohata, 1994; Dreisbach and Siegel, 2001). These differences arise primarily from variability in ear-canal impedance across individuals and from the variability in SPL along the length of the ear canal. Errors in quantifying stimulation levels used during audiometric testing and in verifying hearing-aid output have the potential to translate into diagnostic and treatment errors. While errors can be detrimental to all patients, there is particular concern about the impact of errors on diagnosing and treating/managing hearing impairments in children.
Recently, calculating in situ forward pressure level (FPL) has been suggested as a more accurate way to quantify sound in the ear canal [see Scheperle et al. (2008) and Withnell et al. (2009) for detailed descriptions of the derivation]. Briefly, forward pressure is the wave component of the measured pressure that propagates away from the sound source, and FPL is the level of the forward pressure expressed in dB re 20 μPa rms. The backwards traveling reflected wave components, which contribute to total SPL, are not included in FPL. Quantifying sound in FPL has the advantage of taking into account subject-specific ear-canal properties while avoiding measurement errors due to phase interactions between forward and reverse wave propagation in the ear canal. Additionally, in situ FPL calibration is performed using the sound pressure level (SPL) measured at a microphone distant from the eardrum, making it non-invasive. A previous study validated the calculation of FPL through 10 kHz in a single test cavity representative of an average adult ear canal (Lewis et al., 2009); however, the characteristic impedance of the test cavity was equal to the estimate used to calculate FPL, making the test condition relatively ideal. The purpose of this study was to examine the accuracy with which FPL can be calculated in less ideal, more realistic situations representative of those encountered when using the procedure across a range of human ear-canal sizes, including pediatric sizes. Additionally, the frequency range under consideration was extended to 18 kHz due to increasing interest in hearing above 10 kHz and the need for accurate stimulus calibration at higher frequencies.
Several investigators have tested whether the theoretical advantages of quantifying ear-canal sound level in FPL are apparent empirically using distortion product otoacoustic emissions (DPOAE) or behavioral thresholds as outcome measures (DPOAEs: Scheperle et al., 2008; Burke et al., 2010; Rogers et al., 2010; Kirby et al., 2011. Behavioral Thresholds: Withnell et al., 2009; McCreery et al., 2009; Lewis et al., 2009). Regarding DPOAEs, response magnitudes can be affected by as much as 20 dB when stimuli calibrated in SPL are adjusted for standing-wave nulls (Siegel and Hirohata, 1994; Dreisbach and Siegel, 2001). Because the frequency location of the largest standing-wave calibration errors depends upon the position of the reference microphone in the ear canal (e.g., Stinson, 1985; Dirks and Kincaid, 1987; Chan and Geisler, 1990; Siegel, 1994), DPOAE levels at a single frequency are expected to be less variable with repeated measurements using FPL calibration rather than with SPL calibration. Additionally, DPOAE test performance and threshold prediction are expected to improve when responses are obtained with stimuli calibrated in FPL.
Scheperle et al. (2008) demonstrated that within subject test/retest reliability of DPOAEs improved when stimuli were calibrated in FPL, as predicted. However, studies comparing the effects of calibration method on DPOAE test performance and threshold prediction in subjects with hearing sensitivities ranging from normal to severe hearing loss have been less conclusive about the clinical benefits of FPL calibration. Burke et al. (2010) found essentially no improvements in test performance when using FPL calibration. One exception was improved test performance at 8 kHz; however, this frequency also showed low sensitivity and specificity. Similarly, Rogers et al. (2010) failed to demonstrate that FPL calibration improved threshold predictions. In contrast, Kirby et al. (2011) found a significant improvement in test performance when FPL calibration was used; however, the calibration method was paired with optimized stimulus levels, and the sources of improvement could not be examined independently.
One proposed explanation for the lack of significant improvements with FPL calibration (Burke et al., 2010; Rogers et al., 2010) was that limiting the investigation to discrete frequencies may have reduced the number of times standing-wave nulls negatively affected SPL calibration, and the large number of subjects (N = 155) would have minimized the benefits of FPL calibration due to averaging. However, Richmond et al. (2011) re-examined the data and found the strongest evidence of standing-wave nulls at 4 kHz across subjects. These findings indicate that a lack of standing-wave effects on SPL calibration could not account for the general lack of improvements seen with FPL calibration. Additionally, Richmond et al. (2011) demonstrated that improvements in test performance at 8 kHz could not be attributed to detrimental standing-wave effects on SPL calibration at that frequency.
The findings from studies comparing behavioral thresholds expressed as in situ FPL or SPL have been more consistently positive (Withnell et al., 2009; McCreery et al., 2009; Lewis et al., 2009). A pattern observed across these studies is that thresholds expressed in dB SPL tend to show “notches,” or better thresholds than expected, at standing-wave null frequencies. Thresholds expressed in dB FPL at these same frequencies tend to be higher and more similar to adjacent thresholds. These results suggest that FPL was not influenced by standing-wave pressure minima and that FPL thresholds were more indicative of hearing sensitivity than thresholds expressed in SPL.
While all of the above-mentioned studies demonstrate that results referenced to FPL are no worse than results referenced to in situ SPL, and at times are better, the improvements observed with FPL calibration were less than expected. The inconsistency of empirical benefits demonstrated with FPL calibration warrants further investigation, specifically with respect to the accuracy of the FPL calibration process itself. To date, there has only been one study attempting to directly verify the derivation of FPL. Lewis et al. (2009) calculated forward and reverse pressure ( and , respectively) in a hard-walled test cavity after obtaining the Thévenin-equivalent characteristics for a sound source coupled to subject earmolds. Forward and reverse pressure magnitudes were summed, forming a third measurement termed integrated pressure. Because phase is not taken into consideration, integrated pressure level (IPL) is expected to equal the SPL at the terminal end of a uniform tube (SPLterminal) for frequencies where the assumption of one-dimensional plane-wave propagation is valid. Therefore, differences between IPL and SPLterminal would suggest errors in the calculation of the magnitude of and/or . Lewis et al. (2009) found good agreement between IPL and SPLterminal in an ideal load, with differences ≤2 dB across 0.25–10 kHz. While these findings suggest that the procedures and mathematical calculations used to obtain FPL are valid, ear canals are not ideal loads.
An important variable used in the calculation of FPL that has not been emphasized in previous studies is characteristic impedance (). Characteristic impedance can be defined as the impedance of an infinitely long uniform tube. Because an infinite tube is unterminated, its impedance is completely resistive. A completely resistive quantity is not frequency dependent and can be expressed as a single value. In uniform cylinders,
| (1) |
where ρ is density of air, c is the speed of sound, and A is cross-sectional area. The relationships between and and are shown in the following equations:
| (2) |
and
| (3) |
where is load pressure (i.e., total sound pressure), and is load impedance, which is determined by both resistive and reactive elements. Both and are frequency-specific. The relationships between FPL, RPL and SPL are thus constrained by two extreme conditions. As approaches infinity (i.e., a completely reflective termination), the ratio approaches zero, and and are each exactly one-half of the total pressure. In contrast, when and are equal, will be equal to the total pressure in the tube and will be 0.
In uniform cavities, may be determined using the relationship described in Eq. 1; however, of human ears must be estimated. With the exception of Withnell et al. (2009), all other FPL studies to date have used the characteristic impedance associated with an 8.0-mm uniform diameter tube as the estimate for all subjects. While this diameter estimate might be reasonable for average adult ears, adult ear canals range in size (e.g., Stinson and Lawton, 1989). Additionally, the ear canals of infants and young children are significantly smaller than adult ear canals (e.g., Keefe et al., 1993). Withnell et al. (2009) used the size of the probe tip (coupled to an Etymtic Research 10C probe assembly) to estimate ear-canal cross-sectional area, which provided a more subject-specific estimate of . While this method takes into account some of the variability across subjects, a single probe tip can fit into a number of ear-canal sizes. Also, within a single subject, cross-sectional area varies along the length of the ear canal, and an estimate of area at the location of the probe may not be the best estimate for determining characteristic impedance. Finally, the results of Withnell et al. (2009) do not show improvements over other comparable studies using a single estimate of for all subjects (McCreery et al., 2009; Lewis et al., 2009). While it may be that a gross estimate is sufficient to accurately calculate FPL, this issue deserves further investigation. It is of interest to determine what effect, if any, a single estimate of has on the derivation of FPL in order to determine whether FPL was reasonably calculated in previous studies and whether a different estimate would be required for pediatric ears.
Recently, Rasetshwane and Neely (2011b) describe a method of estimating characteristic impedance in non-uniform cavities, using time-domain reflectance (TDR) to optimize the estimate. In the frequency domain, reflectance (R) is related to load and characteristic impedance by
| (4) |
and TDR is found by taking the real part of the inverse Fourier transform of R after applying a frequency-domain window to eliminate ringing in the time domain. The best estimate of is derived by iteratively adjusting the value of to minimize the corresponding TDR at a time zero. This approach to estimating exploits its relation to surge impedance and is consistent with reflectance having the property of being strictly causal (i.e., zero both for t < 0 and at t = 0). Rasetshwane and Neely (2011b) tested estimates of characteristic impedance obtained as described above by working backwards to the calculation of area (inverse solution), and their results were in good agreement with actual tube dimensions. Additionally, the inverse solution was used to evaluate estimates of characteristic impedance in a number of human ears, and the findings were generally consistent with data on ear-canal dimensions reported in earlier studies.
The main purpose of the present study was to further examine the use of FPL for in situ calibration by evaluating its accuracy in predicting SPL at the terminal end of a tube. While human data were not gathered for this study, practical concerns related to using FPL calibration in human ears, and specifically in pediatric ears, motivated the specific questions. For example, calculating FPL first requires characterizing the source and load. Coupling sound sources to pediatric ears requires different probe-tip sizes and styles than mature ears, which may impact the source calibration. Additionally, the characteristic impedance of pediatric ears is different than adult ears. It is unknown how errors in the characterization of either the source or the load will impact the mathematical decomposition of SPL into forward and reverse components. Specifically, the study addressed the following questions:
-
1.
Does the choice of probe tip affect the source calibration, and is there an impact on the calculation of FPL?
-
2.
Using the characteristic impedance of an 8-mm tube as an estimate, how is the calculation of FPL affected in test cavities of various sizes, and what are the implications for results of previous studies investigating the benefits of FPL calibration and for future applications of FPL calibration?
-
3.
Using the TDR procedure suggested by Rasetshwane and Neely (2011b), can an accurate estimate of characteristic impedance be obtained for test cavities of various sizes, and how do these estimates impact the calculation of FPL?
-
4.
Can FPL be calculated accurately at frequencies >10 kHz?
These questions were addressed by comparing FPL errors for various probe-tip styles, cavity diameters, cavity lengths, and estimates of characteristic impedance.
METHODS
Custom MATLAB software (MathWorks® version 7.8.0 R2009a) along with the audio utility Playrec (Humphrey, 2008) was used for presenting stimuli and recording responses. Playback and recording were made using a 24-bit soundcard (Lynx L22, Sound Technology) and a rate of 44.1 kHz. The output signal was routed through a stereo power amplifier (ADCOM, GFA-5002) and presented via ER-2 (Etymtic Research) loudspeakers coupled to an ER-10B+ probe assembly. The external loudspeaker tubing of the ER-2 phones (standard length, 25.7 cm) was cut to 2.7 cm to increase high-frequency output; internal tubing length was left unchanged. This physical modification alters the flat frequency response below 10 kHz, but this study did not require constant output across frequency. Source and load calibrations were performed using an ER-10B+ microphone. To verify the decomposition of total pressure into forward and reverse components at the plane of the ER-10B+ probe, the simultaneous response of an ER-7 C probe tube microphone at the terminal end of each test cavity was obtained. Both microphones were calibrated through 18 kHz to ensure that comparison of IPL (calculated from response of the ER-10B+) and terminal SPL (determined by the ER-7C) would not be confounded by inherent differences in microphone sensitivity, specifically above 10 kHz (Siegel, 2007; Rasetshwane and Neely, 2011a).
Probe tip coupling options
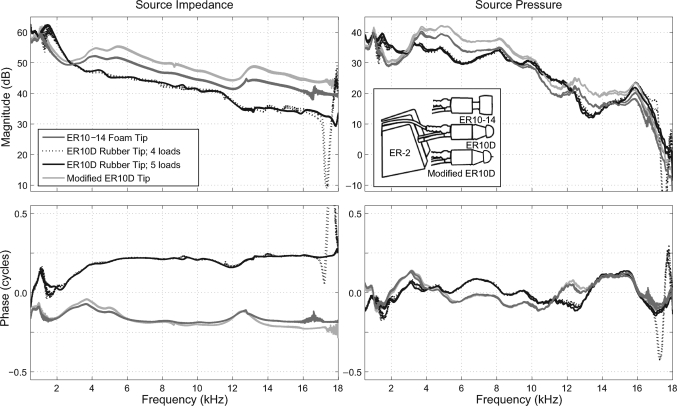
Two types of tips are commercially available for coupling the ER-10B+ probe assembly to the ear. The ER10-14 is a 13-mm vinyl (PVC) foam tip that can be compressed to fit a large number of adult ear canals; however, a pediatric version of this type of tip is not available. The ER10D tips are made from a rubber material (styrene block copolymer) and come in 13 sizes, including sizes for infant ears. When the ER10D tips are coupled to the probe assembly, the inlet to the microphone is recessed from the edge of the tip, creating an additional resonant cavity anterior to the microphone inlet. A modified version of the ER10D tip was created by cutting approximately 2.5 mm from the back edge. This modification allowed the microphone inlet and tip edge to align, resulting in a protrusion of the metal loudspeaker tubes beyond the edge of the tip by 1–1.5 mm. A schematic of the three tips (ER10-14, ER10D and modified ER10D) is displayed as an inset in Fig. 1.
Figure 1.
Schematic of probe tips. Panels: Source characteristics as a function of frequency. Similar characteristics were observed using the ER10-14 (dark gray) and modified ER10D (light gray) tips. The dotted black lines are the source characteristics obtained with the ER10D tip using four acoustic loads with overlapping resonant peaks at 17.5 kHz (see Fig. 2), and the solid black lines are the source characteristics obtained with the same tip using five acoustic loads with non-overlapping resonant peaks.
Acoustic loads: Test cavities
Three sets of brass tubes were used to verify the calculations of FPL (and RPL), with five tubes in each set (see Table TABLE I.). Given the dependence between area and characteristic impedance [Eq. 1], it would not be unreasonable to expect the accuracy of FPL (and RPL) calculations to vary with the diameter of the acoustic load if the estimate of characteristic impedance is not load-specific. It is uncertain whether accuracy will change with length of the acoustic cavity, but because length and diameter of human ear canals typically co-vary and because effective length is also dependent upon probe insertion depth, the length dimension was examined as well.
Table 1.
Test cavity dimensions. Three sets of cavities were used in this study. The first column describes the cavity set with equal lengths and varying diameters. The second column describes the cavity set with equal diameters and varying lengths. The third column describes the cavity set with diameters and lengths chosen to co-vary in a manner similar to the human ear canal (Keefe et al., 1993).
| 36-mm length (diameters in mm) | 8-mm diameter (lengths in mm) | Diameter/length (mm) |
|---|---|---|
| 6.4 | 16.8 | 6.4/17.8 |
| 7.2 | 17.8 | 7.2/20.4 |
| 8.0 | 20.4 | 8.0/21.3 |
| 8.8 | 22.0 | 8.8/22.0 |
| 9.6 | 24.0 | 9.6/22.7 |
Tubes with diameters ranging between 6.4 and 9.6 mm were purchased from a local hardware store. These diameters are within the range of mean ear-canal diameters reported by Keefe et al. (1993) for infants and adults. Cavity sets one and two varied in either the length or diameter dimension. A constant tube length of 36 mm, which is 1 standard deviation above the mean adult ear-canal length reported by Westwood and Bamford (1992), was used when investigating the effects of diameter. A diameter of 8.0 mm was used when investigating the effects of length. The third set of test cavities varied in both the length and diameter dimensions. The tubes were cut to lengths such that the diameter and length of each tube approximated realistic dimensions of human ear canals (Keefe et al., 1993).
Calibration
Stimulus
Source and load impedance and pressure were obtained across 0.25–18 kHz using a wideband-chirp stimulus. In addition to shortening the loudspeaker tubing as described previously, the electrical chirp was created with high-frequency emphasis, which increased loudspeaker voltage drive by approximately 12 dB at 18 kHz to compensate for loudspeaker roll-off.
Source calibration
Thévenin-equivalent characteristics of the ER-10B+ probe assembly were determined (Møeller, 1960; Rabinowitz, 1981; Allen, 1986; Keefe et al., 1992) using four known acoustic loads (8.0-mm i.d.; 30 -, 40 -, 50 -, and 70-mm lengths). As an alternative to cutting brass tubes to specific lengths and attaching them to a plate (e.g., see Fig. 4 in McCreery et al., 2009), a single brass tube (8.0-mm i.d.; 350-mm total length) was used. The ER-10B+ probe was inserted into one end of the brass tube, and a steel rod (8.0-mm diameter; 350-mm total length) was manually inserted into the opposite end by the amount necessary to result in the desired cavity length. This design allows the sound source to remain stationary throughout the calibration procedure and allows the investigator to choose any number and combination of lengths for the source calibration. A separate source calibration was performed for each type of probe tip (ER10-14, ER10D, modified ER10D) and repeated every day of data collection (Burke et al., 2010). The calibrations assumed room temperature (25 °C) since subsequent load calibrations were being performed in test cavities.
One way to estimate the accuracy of the source calibration is to use the source characteristics to predict the pressure or impedance of a known acoustic load (Keefe et al., 1992). Comparing the predicted with the measured pressure or expected impedance values allows both quantitative (pressure) and qualitative (impedance) assessments of the source calibration. While load (calibration cavity) pressure is initially measured and used to calculate the Thévenin-equivalent source pressure and impedance ( and ), the mathematical relationship amongst source and load impedances and pressures allows load pressure to be predicted () from the previously determined source parameters and the known load impedance. In equation form,
| (5) |
where is the known impedance of the calibration cavity. Calculating the predicted load pressure allows the validity of the source calibration to be assessed as a normalized sum-of-squares error term:
| (6) |
The squared differences between the measured () and predicted () cavity pressure are summed both across the frequency range of interest (0.25–18 kHz in the present study) and across the calibration cavities. The software used in previous FPL studies (EMAV, Neely and Liu, 1994) and in the current study scales the dimensionless error term by a multiplier of 10 000 such that a typical, well-performed calibration has a source-calibration error of about 1.0 following an iterative fitting procedure. When errors are ≤1.0, calculated load impedance is generally in good agreement with actual load impedance (qualitative assessment). Several studies have used an error criterion of ≤1.0 for the source calibration to be considered acceptable (e.g., Scheperle et al., 2008; Burke et al., 2010; Rogers et al., 2010); however, other studies have used a more lax criterion and still observed agreement between calculated and actual load impedance (e.g., McCreery et al., 2009; Lewis et al., 2009).
Load calibration
The terminal end of each tube was attached with mounting putty to a flat metal plate. An ER7-14 C probe tube was inserted sleeve-first into a 1.9-mm opening in the center of the plate. The ER7-14 C probe-tube (0.58-mm i.d.) was visually centered when attaching the tube to the plate. Load impedance was determined for each test cavity using the calibrated ER-10B+ probe assembly at the cavity entrance.
Three values for characteristic impedance were used to derive FPL and RPL. The first value, , was the characteristic impedance of an 8.0-mm diameter tube (81.55 acoustic ohms). Since the majority of previous studies investigating FPL used this value for all subjects, it was of interest to examine how much the calculation of FPL is affected when actual of the test cavity deviates from 81.55 acoustic ohms. The second value, , was defined as the characteristic impedance which would minimize reflectance at time zero (Rasetshwane and Neely, 2011b). The third value, , was the actual characteristic impedance of the test cavity [Eq. 1]. This third condition is the most ideal, and the results for this condition were expected to be similar to the results of Lewis et al. (2009), showing ≤2 dB differences between IPL and SPL at the terminal end of the tube through 10 kHz. A summary of these three impedance values is given in Table TABLE II.. The corrections necessary to convert total pressure at the plane of the ER-10B+ probe into forward and reverse components [derived from Eqs. 2, 3] were determined using the source characteristics associated with each of the three probe tips (which affected the calculation of ) and using each of the three values for characteristic impedance: , , and .
Table 2.
Comparison of characteristic impedance estimates according to cavity diameter. The far right column displays expected quarter-wave null frequencies in the transverse direction.
| Diameter (mm) | / | / | λ/4 frequency (kHz) | |||
|---|---|---|---|---|---|---|
| 6.4 | 81.55 | 0.64 | 127.42 | 1.01 | 128.43 | 13.4 |
| 7.2 | 81.55 | 0.81 | 100.68 | 1.00 | 100.36 | 11.9 |
| 8.0 | 81.55 | 1.00 | 81.55 | 0.99 | 80.42 | 10.7 |
| 8.8 | 81.55 | 1.21 | 67.40 | 0.96 | 64.81 | 9.7 |
| 9.6 | 81.55 | 1.44 | 56.63 | 0.95 | 53.85 | 8.9 |
| Meana | 0.24 | 0.02 | ||||
| St. Dev.a | 0.17 | 0.02 |
Means and standard deviations were calculated using: /. These values are reported in text as percents.
Verification
Test conditions varied along three parameters: probe tip, characteristic impedance estimate, and test-cavity size. A unique stimulus was created for each test condition using the appropriate FPL corrections, with the intent of presenting a stimulus with a flat frequency response at the terminal end of the tube. The FPL corrections in the frequency domain were inverted and converted into an impulse response, resulting in an “FPL-shaped click.” The peak of the electrical click stimulus was scaled to 0.1 for all conditions, so that a constant peak voltage drive was delivered to each tube. Five hundred clicks were presented via one channel of the ER-10B+ probe assembly, and simultaneous responses of the ER-10B+ (entrance) and ER-7C (terminal end) microphones were obtained. Using the corrections obtained for the specific test condition, IPL was derived from the ER-10B+ microphone response at the tube entrance (IPLentrance). Integrated pressure level was then subtracted from the SPL at the terminal end of the cavity (SPLterminal). Deviations from 0 were considered to reflect errors in the calculation of FPL (and/or RPL).
One potential issue with this method of verification is that at higher frequencies, SPL at the terminal end may be affected by transverse wave propagation. Variable pressure along the surface of the terminal end could result in differences between SPLterminal and IPLentrance that are unrelated to FPL or RPL calculation errors. The largest cavity diameter used in this study (9.6 mm) has a corresponding λ/4 null at 8.9 kHz, and the smallest cavity diameter used in this study (6.4 mm) has a corresponding λ/4 null at 13.4 kHz (see Table TABLE II. for corresponding λ/4-null frequencies for all diameters). This implies that our verification procedure may be problematic at high frequencies, and particularly above 13.4 kHz where transverse wave propagation may affect SPL measured at the terminal end of all of the test cavities. Since extending the frequency range to 18 kHz did not require much additional effort, and since cavity diameter was systematically varied, it was of interest to examine the differences between SPLterminal and IPLentrance through the extended high-frequency range, even in light of the potential difficulties with interpreting the findings.
Experiments
Experiment one: Effects of probe tip
The first experiment was designed to assess the effects of probe tip on the calculation of source impedance and pressure, and ultimately on the calculation of FPL. The source was calibrated with each tip as described, and IPLentrance was calculated in the five acoustic loads comprising cavity set three (variable lengths and diameters), using .
Experiment two: Effects of characteristic impedance estimates
The modified ER10D tip was used for this experiment. The first part of the experiment aimed to quantify the effects of using a single value () as the estimated characteristic impedance on the calculation of FPL. IPLentrance was calculated in cavity sets one (variable diameters, and therefore, mismatched characteristic impedances) and two (variable lengths). The second part of this experiment was designed to examine whether estimating characteristic impedance from load impedance () was more accurate than using . For each test cavity in set one, IPLentrance was first calculated using , and then again using , which represented the most ideal condition. Data from the first portion of the experiment, obtained using to calculate IPLentrance in the test cavity set one, were also used for comparison.
RESULTS
While frequency is typically viewed on a logarithmic axis, a linear frequency axis was chosen for all figures in order to allow a more detailed examination of how source and load calibrations and differences between SPLterminal and IPLentrance behave beyond 10 kHz.
Experiment one: Effects of probe tip
Source calibration
Source impedance and pressure obtained for each of the three probe tips are compared in Fig. 1. There are two sets of values plotted for the ER10D probe tip, which is explained below. Because the probe tip is part of the Thévenin-equivalent source, it is not unreasonable to expect to see some differences in the source characteristics obtained with the different tips. The tips are not only different shapes (flat termination versus a rounded termination), but they are also different materials (foam versus rubber), and simply observing differences among the tips does not necessarily imply problems. However, source-calibration errors were <0.1 when the modified ER10D and ER-14 C tips were used. In contrast, source calibrations with the ER10D tip always resulted in errors >1.0, even when calculated and expected load impedance were in reasonable agreement (see Fig. 2 for example).
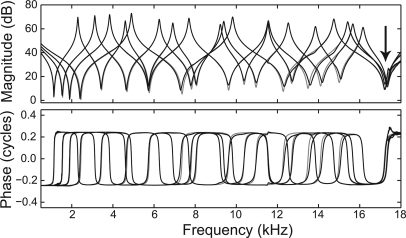
Figure 2.
Load impedance magnitude (top) and phase (bottom) for the four cavity lengths (30, 40, 50, and 70 mm) used during source calibration with ER10D tip. Gray lines are the expected values (Keefe et al., 1992), and black lines are the calculated values for each tube. Impedance magnitude notches correspond to resonant peaks; the pair of lines with the lowest frequency notch corresponds to the longest tube length. The arrow at 17.5 kHz highlights the overlapping resonance at this frequency for all four cavity lengths. Low impedance at this frequency for all cavities caused errors in the calculation of source impedance and pressure around this frequency range (Fig. 1). This situation illustrates the importance of choosing cavity lengths with minimal overlap in resonant peak frequencies.
Previous studies have documented variability in repeated source characteristics when a single type of probe tip is used (Scheperle et al., 2008; Burke et al., 2010), and the differences between the ER10-14 and the modified ER10D tips are within this range of variability, suggesting that the tips themselves did not have much of an effect on the source characteristics. In contrast, the pattern of source impedance and pressure across frequency is distinct for the ER10D tip. One of the most apparent differences is a notch around 17.5 kHz in the magnitudes and a corresponding spike in the phase when using the ER10D tip (ER10D-4 loads, Fig. 1). Further investigation revealed that all four cavity lengths used for the source calibration had resonant notches (dips in load impedance magnitude and zero phase) near 17.5 kHz (Fig. 2). While the same nominal cavity lengths were used for all three probe tips, differences in probe insertion depth (and effective cavity length) resulted in overlapping resonant notches at 17.5 kHz only for the ER10D tip. Source calibration was repeated for the ER10D tip using five cavity lengths (18.5, 25.6, 40, 54.3, and 83 mm) which avoided the complete overlap of resonances at any one frequency across cavities. Large deviations in source characteristics at 17.5 kHz disappeared (ER10D-5 loads, Fig. 1); however, source characteristics remained distinct from the other two tips, and the source-calibration errors remained >1.0 (4.68 and 3.70 for left and right channels, respectively). Subsequent measurements obtained with the ER10D probe tip used the ER10D-5cav source characteristics.
Verification of FPL and RPL
For each type of probe tip, the calculations of FPL and RPL were verified in the set of test cavities with variable lengths and diameters (Table TABLE I., column 3). Five sets of differences between SPLterminal and IPLentrance (one set per test cavity) were obtained for the ER10D and modified ER10D tips, but only four sets were obtained for the ER10-14 tip because it could not be compressed enough to fit into the 6.4-mm diameter tube. Figures 34 display differences between SPLterminal and IPLentrance across frequency. An ideal calculation would be expected to result in differences of 0 dB. Figure 3 separates the data by test cavity in order to examine possible effects of transverse wave propagation on SPLterminal. Dashed vertical lines mark the quarter-wave null frequency corresponding to the diameter of the test cavity. Figure 4 combines the data across test cavities.
Figure 3.
Comparison of differences between SPLterminal and IPLentrance across frequency for the three probe tips. Ideal characteristic impedance () was used for the calculation of IPLentrance. Each panel displays results from a single test cavity. Diameter of the test cavity is indicated in the top left corner. The dashed vertical line marks the quarter-wave null frequency associated with the diameter of the test cavity.
Figure 4.
Comparison of differences (top) and absolute differences (bottom) between SPLterminal and IPLentrance across frequency for the three probe tips, collapsed across test cavities. For each probe tip, the shaded area encloses the minimum and maximum SPL-IPL differences across the test cavities. Differences between SPLterminal and IPLentrance are the smallest at frequencies below 4 kHz for all three probe tips. Below 10 kHz, differences are ≤2.5 dB. Above 14 kHz, differences are the largest for the standard ER10D tip (black shading).
One trend observed in these two figures is that the differences between SPLterminal and IPLentrance tend to increase with increasing frequency; however, there is no specific pattern observed relative to the positions of the vertical lines (Fig. 3). Since the effects of transverse wave propagation on SPLterminal would be approximately the same for all probe tips, it appears that the effects of transverse wave propagation were small relative to the differences among the probe tips. Another pattern observed in Figs. 34 (top) is that differences between SPLterminal and IPLentrance for the modified ER10D and the ER10-14 tips tend to be in the positive direction, indicating that IPLentrance was lower than the SPLterminal. In other words, IPL under-estimated the actual SPL at the terminal end of the test cavity. The opposite pattern is seen when the ER10D tip was used; differences tend to be negative, meaning that IPLentrance was larger than SPLterminal.
Because differences between SPLterminal and IPLentrance are considered problematic regardless of direction, absolute differences are displayed in the bottom panel of Fig. 4 to make the comparison across frequency and tips clearer. Below 10 kHz, the differences are < 2.5 dB for all tips, which is similar to the findings of Lewis et al. (2009) when using earmolds and a test cavity with an 8.0-mm diameter. Above 10 kHz, differences approach 5 dB for the modified ER10D and ER10-14 foam tips, and exceed 8 dB for the ER10D tip. Differences between SPLterminal and IPLentrance with the ER10D tip are larger than differences with the other two tips only above 14 kHz. The modified ER10D tip was used for experiment two due to the increased errors above 14 kHz with the standard tip and the poor fit of the ER10-14 tip in smallest and largest test cavities.
Experiment two: Effects of characteristic impedance
Table TABLE II. lists the characteristic impedance values used in this study according to tube diameter, as well as the differences between estimates ( and ) and actual () characteristic impedance for each tube. The differences are expressed as ratios so that values close to 1.0 indicate a good estimate. Since does not change, it is not surprising to see the ratios between and depart from a value of 1.0 as cavity diameter departs from 8.0 mm. In contrast, the ratios between and are close to 1.0 for all cavity diameters.
Another way to compare the ratios is to examine the differences between estimated and actual characteristic impedance expressed as a percent of the actual. On average, is only 2% different than , and the largest difference is 5% for the 9.6-mm test cavity. For comparison, the average difference between and is 24%, and the largest difference is 44% for the 9.6-mm test cavity. It is clear from these values that is a better estimate of than . The next question to answer is how good of an estimate is required for accurate calculations of FPL.
Characteristic impedance estimate: 8-mm diameter
For each test cavity (sets one and two) differences between SPLterminal and IPLentrance calculated using are displayed in the bottom panels of Fig. 5. The top panels display SPL at the cavity entrance for reference. Standing-wave null patterns seen in the entrance SPL are consistent with the fact that cavity set one had equivalent lengths (left panels) and cavity set two had variable lengths (right panels). An effect of cavity diameter can be seen from difference data (bottom left panel). Differences systematically increase as cavity diameter deviates from 8.0 mm, exceeding 5 dB. Stated another way, as actual characteristic impedance () of the test cavity deviates from (Table TABLE II.), errors in the calculation of FPL and RPL increase. Of particular interest is that differences between SPLterminal and IPLentrance are the largest at frequencies corresponding to standing-wave nulls. One potential concern is that FPL and RPL calculation errors are simply a result of low stimulus levels (poor signal-to-noise ratios) at null frequencies; however, this interpretation is unlikely given that differences are not systematically elevated at null frequencies when cavity length is varied (bottom right panel). While differences between SPLterminal and IPLentrance are greater than zero when cavity length is varied, the magnitude of the differences is the same regardless of cavity length, and the pattern of increased errors at null frequencies is eliminated. These results indicate that the length dimension does not impact the accuracy of calculating FPL. Alternatively, an inaccurate estimate of characteristic impedance does affect the calculation of FPL, especially at frequency regions surrounding standing-wave nulls. These findings demonstrate that it is inappropriate to use as the estimate of characteristic impedance irrespective of the dimensions of the acoustic load.
Figure 5.
Effects of using a single characteristic impedance estimate to calculate FPL in test cavities with various lengths and diameters. (top) SPL at the test cavity entrance. (bottom) Differences between SPLterminal and IPLentrance when was used to calculate IPLentrance. The y-scale is different for top and bottom panels. (left) Test cavities with equal lengths but variable diameters (Table TABLE I., column 1). Differences between SPLterminal and IPLentrance systematically increase around null frequencies, and the differences become greater as actual characteristic impedances deviate further from the estimate used (Table TABLE II., column 3). (right) Test cavities with equal diameters and variable lengths (Table TABLE I., column 2). Differences between SPLterminal and IPLentrance do not systematically change as a function of tube length.
Characteristic impedance estimate: Calculated from load impedance
For each test cavity (set one) IPLentrance was calculated using and . The effects of characteristic impedance on the calculation of FPL (and RPL) are shown in Fig. 6 as differences between SPLterminal and IPLentrance. Shaded regions encompass minimum and maximum differences across test cavities. Differences obtained using (Fig. 5, bottom left panel) are re-plotted for comparison.
Figure 6.
Comparison of differences between SPLterminal and IPLentrance resulting from different values of characteristic impedance (, , and ). Each characteristic impedance value was used to determine FPL and RPL of the set of test cavities with equal lengths and variable diameters (Table TABLE I., column 1). Shaded areas enclose the minimum and maximum of differences between SPLterminal and IPLentrance across test cavities obtained for each characteristic impedance condition. When cavity-specific characteristic impedance was used ( or ), errors did not systematically increase with cavity diameter and were generally below 2.5 dB through 10 kHz and below 4 dB through 18 kHz.
Figure 6 reveals that differences between SPLterminal and IPLentrance for are smaller than those obtained using , as would be expected solely based on the finding that values of were more similar to (Table TABLE II.). More importantly, the differences between SPLterminal and IPLentrance were reduced to the same degree as differences obtained using . For these two conditions ( and ), the differences between SPLterminal and IPLentrance range from approximately −1 to +4 dB across the frequency range. These data suggest that, at least for uniform tubes, characteristic impedance can be accurately estimated without knowledge of cavity dimensions using the method developed by Rasetshwane and Neely (2011b). Assuming that this method can be accurately extended to non-uniform tubes, such as ear canals, it should result in an improvement of FPL accuracy.
DISCUSSION
Lewis et al. (2009) verified the calculation of FPL through 10 kHz in a single, ideal test cavity. This study expanded upon these findings by extending the frequency range to 18 kHz, and by examining the influence of different probe tips, cavity lengths, cavity diameters, and characteristic impedance estimates on FPL calculation.
Implications for past FPL studies
The results from this study show that FPL can be affected by non-ideal estimates of characteristic impedance (Figs. 56), which suggests that results from previous studies may have been impacted by less-than-ideal calculations of FPL, specifically at standing-wave null frequencies. Given that SPL calibration errors can approach 20 dB at null frequencies (Siegel, 1994; Siegel and Hirohata, 1994; Dreisbach and Siegel, 2001), it is not surprising that some benefits of using FPL for in situ calibration have been shown in previous studies (e.g., Scheperle et al., 2008; McCreery et al., 2009; Lewis et al., 2009; Withnell et al., 2009). However, the fact that differences between SPLterminal and IPLentrance approached 8 dB at null frequencies might explain why the benefits of FPL calibration were not always apparent (e.g., Burke et al., 2010; Rogers et al., 2010).
Implications for future use of FPL calibration
The results from this study indicate that, at least in uniform, cylindrical tubes, more accurate calculations of FPL can be obtained with appropriate estimates of characteristic impedance. Characteristic impedance can be estimated without knowledge of ear-canal dimensions using the method developed by Rasetshwane and Neely (2011b), and calculating characteristic impedance in this manner does not increase test time appreciably because it is determined using the values already needed to convert SPL into FPL. Based on these findings, it is recommended that estimating characteristic impedance through the optimization of TDR be integrated into FPL calibration routines. Accurate estimates of characteristic impedance are particularly important when considering performing FPL calibrations in pediatric ears or surgically modified ear canals. When characteristic impedance was accurately estimated, differences between SPLterminal and IPLentrance were small, even in the smallest test cavity in the set (6.4 mm), and it is expected that the procedure would work in even smaller cavities (presumably the case for ear canals of infants younger than 6 months; Keefe et al., 1993).
This study also demonstrated that pediatric tips currently available for the ER-10B+ can be used to calculate FPL accurately across the standard frequency range. An unanticipated finding resulting from the comparison of source characteristics across tip types was that lengths of the acoustic loads used to determine source impedance and pressure need to be chosen with minimal overlap among resonant notches in the frequency range of interest, which is an essential consideration whenever FPL calibration is implemented. When this criterion was met and an appropriate characteristic impedance value was used ( or ), differences between SPLterminal and IPLentrance were ≤2.5 dB for frequencies below 10 kHz regardless of tip. These results are similar to the findings of Lewis et al. (2009), who demonstrated differences ≤2 dB when using a subject’s earmold attached to the sound source.
With specific regard to frequencies above 10 kHz, the present study showed that differences between SPLterminal and IPLentrance increased with frequency. From this experiment, it is not possible to determine whether the differences reflect errors in the calculation of FPL and/or RPL at high frequencies, or if the differences reflect sub-optimal test conditions for the verification procedure. For example, for each test condition one of the brass tubes was attached to the terminal plate with putty. While care was taken to ensure a complete seal, the tubes were attached and detached from the plate a number of times throughout data collection. Additionally, while small, the ER7C-14 probe tube inserted at the center of the plate (including during the measurements used to calculate FPL and RPL corrections), may have reduced the reflectance of the terminating surface. The location of the probe tube across the terminating surface may have also been an issue at frequencies >9 kHz due to possible transverse wave propagation in the tube, which may explain why differences increased with frequency.
Despite these problems, it is still worthwhile to consider using FPL to quantify extended high-frequency sound levels. The more invasive procedure of placing a probe microphone near the tympanic membrane is inadequate for extended high-frequency calibrations due to the oblique orientation and multi-modal vibration pattern of the tympanic membrane (Khanna and Stinson, 1985). Even if the differences between SPLterminal and IPLentrance at frequencies >10 kHz were reflecting errors in the calculation of FPL, calibration errors <10 dB may still be preferable to standing–wave null errors up to 20 dB. However, if FPL calibrations are desired for frequencies beyond 10 kHz, the probe tip (or earmold) used to couple the source to the ear canal should be evaluated to ensure sufficiently low errors in a test cavity over the frequency range of their intended use.
Pressure vs. Power Calibration
There is some debate as to whether the cochlea acts as a pressure or power detector (e.g., Rosowski et al., 1986 and Puria et al., 1997), which is relevant to consider when deciding if stimulation levels should be referenced in terms of power or pressure. Recently, Keefe and Schairer (2011) proposed specifying in situ sound level of the stimulus in terms of absorbed power. Similar to FPL calibration, absorbed power eliminates the influence of longitudinal standing waves and can be determined noninvasively. The difference between specifying level with respect to absorbed power versus forward pressure is that the effectiveness of middle-ear transfer is taken into account with the power reference. It is debatable as to whether middle-ear status should be taken into consideration when calibrating stimulus level; however, in either case (absorbed-power or FPL) characteristic impedance of the load must be defined. The findings from this study emphasize the importance of an accurate estimate of characteristic impedance for the calculation of FPL, and it is reasonable to assume that absorbed-power calculations require a similar accuracy.
CONCLUSIONS
The results presented here demonstrate that FPL calibration can be improved by using accurate estimates of characteristic impedance, which are obtainable from measurements of load impedance and do not require cavity dimensions to be known (Rasetshwane and Neely, 2011b). While human data were not collected in this study, these results add support to the recommendation to consider in situ FPL calibration in humans, including infants and young children. Forward pressure level can be accurately calculated at least through 10 kHz for a variety of probe tips (this study) and earmolds (Lewis et al., 2009), and relatively accurately through 18 kHz, although more careful attention to the choice of probe tip is necessary. It remains to be seen whether improving the estimate of characteristic impedance will improve empirical benefits of FPL calibration in human ears and whether quantifying in situ sound in FPL should be implemented into routine clinical practice.
ACKNOWLEDGMENTS
This work was supported by Grant IRG-77-004-31 from the American Cancer Society, administered through the Holden Comprehensive Cancer Center at the University of Iowa and a 2010 Clinical Research Grant from the American Speech-Language-Hearing Foundation. The first author was supported by an NIH training grant (T32-D0073666). The authors thank James Lewis for helpful insights throughout data collection/analysis and individuals at AAS 2011 and the reviewers for their comments and suggestions.
References
- Allen, J. B. (1986). “Measurement of eardrum acoustic impedance,” in Peripheral Auditory Mechanisms, edited by Allen J. B., J. L., Hall, Hubbard A., Neely S. T., and Tubis A. (Springer-Verlag, New York: ), pp. 44–51. [Google Scholar]
- Burke, S. R., Rogers, A. R., Neely, S. T., Kopun, J. G., Tan, H., and Gorga, M. P. (2010). “Influence of calibration method on distortion-product otoacoustic emission measurements: I. test performance,” Ear Hear. 31(4), 533–545. 10.1097/AUD.0b013e3181d86b3d [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan, J. C. K., and Geisler, C. D. (1990). “Estimation of eardrum acoustic pressure and of ear canal length from remote points in the canal,” J. Acoust. Soc. Am. 87, 1237–1247. 10.1121/1.398799 [DOI] [PubMed] [Google Scholar]
- Dirks, D. D., and Kincaid, G. E. (1987). “Basic acoustic considerations of ear canal probe measurements,” Ear Hear. 8, 60S–67S. 10.1097/00003446-198710001-00002 [DOI] [PubMed] [Google Scholar]
- Dreisbach, L. E., and Siegel, J. H. (2001). “Distortion-product otoacoustic emissions measured at high frequencies in humans,” J. Acoust. Soc. Am. 110(5), 2456–2469. 10.1121/1.1406497 [DOI] [PubMed] [Google Scholar]
- Humphrey, R. (2008). Playrec (Version 2.1.0) [software], retrieved from http://www.playrec.co.uk/index.php (Last viewed June 2, 2011).
- Keefe, D. H., Bulen, J. C., Hoberg Arehart, K., and Burns, E. M. (1993). “Ear-canal impedance and reflection coefficient in human infants and adults,” J. Acoust. Soc. Am. 94(5), 2617–2638. 10.1121/1.407347 [DOI] [PubMed] [Google Scholar]
- Keefe, D. H., Ling, R., and Bulen, J. C. (1992). “Method to measure acoustic impedance and reflections coefficient,” J. Acoust. Soc. Am. 91, 470–485. 10.1121/1.402733 [DOI] [PubMed] [Google Scholar]
- Keefe, D. H., and Schairer, K. S. (2011). “Specification of absorbed-sound power in the ear canal: Application to suppression of stimulus frequency otoacoustic emissions,” J. Acoust. Soc. Am. 129(2), 779–791. 10.1121/1.3531796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanna, S. M., and Stinson, M. R., (1985). “Specification of the acoustical input to the ear at high frequencies,” J. Acoust. Soc. Am. 77(2), 577–589. 10.1121/1.391876 [DOI] [PubMed] [Google Scholar]
- Kirby, B. J., Kopun, J. G., Tan, H., Neely, S. T., and Gorga, M. P. (2011). “Do ‘optimal’’ conditions improve distortion product otoacoustic emission test performance?” Ear Hear. 32(2), 230–237. 10.1097/AUD.0b013e3181fa5da2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis, J. D., McCreery, R. W., Neely, S. T., and Stelmachowicz, P. G. (2009). “Comparison of in situ calibration methods for quantifying input to the middle ear,” J. Acoust. Soc. Am. 126(6), 3114–3124. 10.1121/1.3243310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCreery, R. W., Pittman, A., Lewis, J., Neely, S. T., and Stelmachowicz, P. G. (2009). “Use of forward pressure level to minimize the influence of acoustic standing waves during probe-microphone hearing-aid verification,” J. Acoust. Soc. Am. 126(1), 15–24. 10.1121/1.3143142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Møller, A. R. (1960). “Improved technique for detailed measurements of the middle ear impedance,” J. Acoust. Soc. Am. 32(2), 250–257. 10.1121/1.1908029 [DOI] [Google Scholar]
- Neely, S. T., and Liu, Z. (1994). “EMAV: Otoacoustic emission averager,” Technical Memo No. 17, Boys Town National Research Hospital, Omaha, NE.
- Puria, S., Peake, W. T., and Rosowski, J. J. (1997). “Sound-pressure measurements in the cochlear vestibule of human-cadaver ears,” J. Acoust. Soc. Am. 101, 2754–2770. 10.1121/1.418563 [DOI] [PubMed] [Google Scholar]
- Rabinowitz, W. M. (1981). “Measurement of the acoustic input immittance of the human ear,” J. Acoust. Soc. Am. 70, 12–22. 10.1121/1.386953 [DOI] [PubMed] [Google Scholar]
- Rasetshwane, D. M., and Neely, S. T. (2011a). “Calibration of otoacoustic emission probe microphones,” J. Acoustic. Soc. Am. 130, EL238–EL243. 10.1121/1.3632047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasetshwane, D. M., and Neely, S. T. (2011b). “Inverse solution of ear-canal shape from reflectance,” J. Acoust. Soc. Am. 130(6), 3873–3881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richmond, S. A., Kopun, J. G., Neely, S. T., Tan, H., and Gorga, M. P. (2011). “Distribution of standing-wave errors in real-ear sound-level measurements,” J. Acoust. Soc. Am. 129(5), 3134–3140. 10.1121/1.3569726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers, A. R., Burke, S. R., Kopun, J. G., Tan, H. Neely, S. T., and Gorga, M. P. (2010). “Influence of calibration method on distortion-product otoacoustic emission measurements: II. Threshold prediction,” Ear Hear. 31(4), 546–554. 10.1097/AUD.0b013e3181d86b59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosowski, J. J., Carney, L. H., Lynch, T. J., III, and Peake, W.T. (1986). “The effectiveness of external and middle ears in coupling acoustic power into the cochlea,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A., Neely S. T., and Tubix A. (Springer-Verlag, New York: ), pp. 3–12. [Google Scholar]
- Scheperle, R. A., Neely, S. T., Kopun, J. G., and Gorga, M. P. (2008). “Influence of in situ, sound-level calibration on distortion-product otoacoustic emission variability,” J. Acoust. Soc. Am. 124(1), 288–300. 10.1121/1.2931953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, J. H. (1994). “Ear-canal standing waves and high-frequency sound calibration using otoacoustic emission probes,” J. Acoust. Soc. Am. 95(5), 2589–2597. 10.1121/1.409829 [DOI] [Google Scholar]
- Siegel, J. H., and Hirohata, E. T. (1994). “Sound calibration and distortion product otoacoustic emissions at high frequencies,” Hear. Res. 80, 146–152. 10.1016/0378-5955(94)90106-6 [DOI] [PubMed] [Google Scholar]
- Siegel, J. H. (2007). “Calibrating Otoacoustic emission probes,” in Otoacoustic Emissions: Clinical Applications, 3rd ed., edited by Robinette M. S. and Glattke T. J. (Thieme, New York: ), Chap. 15, pp. 403–427. [Google Scholar]
- Stinson, M. R. (1985). “The spatial distribution of sound pressure within scaled replicas of the human ear canal,” J. Acoust. Soc. Am. 75(5), 1596–1602. 10.1121/1.392797 [DOI] [PubMed] [Google Scholar]
- Stinson, M. R., and Lawton, B. W. (1989). “Specification of the geometry of the human ear canal for the prediction of sound-pressure level distribution,” J. Acoust. Soc. Am. 85(6), 2492–2503. 10.1121/1.397744 [DOI] [PubMed] [Google Scholar]
- Voss, S. E., Rosowski, J. J., Merchant, S. N., Thornton, A. R., Shera, C. A., and Peake, W. T. (2000). “Middle ear pathology can affect the ear-canal sound pressure generated by audiologic earphones,” 21(4), 265–274. [DOI] [PubMed]
- Voss, S. E., Rosowski, J. J., Shera, C. A., and Peake, W. T. (2000). “Acoustic mechanisms that determine the ear-canal sound pressures generated by earphones,” J. Acoust. Soc. Am. 107(3), 1548–1565. 10.1121/1.428440 [DOI] [PubMed] [Google Scholar]
- Voss, S. E., and Herrmann, B. S. (2005). “How does the sound pressure generated by circumaural, supra-aural, and insert earphones differ for adult and infant ears?” Ear Hear. 26(6), 636–650. 10.1097/01.aud.0000189717.83661.57 [DOI] [PubMed] [Google Scholar]
- Westwood, G. F. S., and Bamford, J. M. (1992). “Probe-tube microphone measurements with very young infants,” Br. J. Audiol. 26, 43–151. 10.3109/03005369209079032 [DOI] [PubMed] [Google Scholar]
- Withnell, R. H., Jeng, P. S., Waldvogel, K., Morgenstein, K., and Allen, J. B. (2009). “An in situ calibration for hearing thresholds,” J. Acoust. Soc. Am. 125(3), 1605–1611. 10.1121/1.3075551 [DOI] [PubMed] [Google Scholar]