Statistical bias in the assessment of binaural benefit relative to the better ear

Abstract

The comparison of measured binaural performance with the better of two monaural measures (one from each ear) may lead to underestimated binaural benefit due to statistical sampling bias that favors the monaural condition. The mathematical basis of such bias is reviewed and applied to speech reception thresholds measured in 32 bilateral cochlear implant (CI) users for coincident and spatially separated speech and noise. It is shown that the bias increases with test-retest variation and is maximal for uncorrelated samples of identical underlying performance in each ear. When measured differences between ears were assumed to reflect actual underlying performance differences, the bias averaged across the CI users was about 0.2 dB for coincident target and noise, and 0.1 dB for spatially separated conditions. An upper-bound estimate of the bias, based on the assumption that both ears have the same underlying performance and observed differences were due to test-retest variation, was about 0.7 dB regardless of noise location. To the extent that the test-retest variation in these data is comparable to other studies, the results indicate that binaural benefits in bilateral cochlear implant users are not substantially underestimated (on for average) when binaural performance is compared with the better ear in each listening configuration.

INTRODUCTION

Over the past decade or so bilateral cochlear implantation has experienced a steady increase in clinical uptake. It is generally assumed that the provision of bilateral devices will restore at least some of the benefits available to normal hearing listeners with two ears, particularly in relation to speech understanding in noise and localization abilities.

The assessment of speech intelligibility in noise has been a key focus in a considerable number of studies with adult bilateral cochlear implantees (e.g., Schön et al., 1999; van Hoesel and Clark, 1999; Gantz et al., 2002; Müller et al., 2002; Schön et al., 2002; Stark et al., 2002; Tyler et al., 2002; van Hoesel et al., 2002; Au et al., 2003; van Hoesel and Tyler, 2003; Dormann and Dahlstrom, 2004; Laszig et al., 2004; Schleich et al., 2004; Ramsden et al., 2005; Senn et al., 2005; Litovsky et al., 2006, 2009; Ricketts et al., 2006; Tyler et al., 2006, 2007; Buss et al., 2008;Chan et al., 2008;Dunn et al., 2008; Zeitler et al., 2008; Eapen et al., 2009; Laske et al., 2009; Loizou et al., 2009; Koch et al., 2009; Mosnier et al., 2009). Despite variation in methodology and materials, it is generally the case that the largest speech intelligibility benefit from having two implants derives from the monaural effect of the headshadow at each ear, which allows the listener to attend the ear with the better signal-to-noise ratio (SNR) when target and interferers are spatially separated. For target speech presented to the front of the listener and noise at 90 degrees to the right or left, for example, the monaural improvement in performance is on the order of 5 dB in terms of 50%-correct speech reception thresholds (SRTs) when the noise source is contralateral rather than ipsilateral to the implant. While a unilateral implant user will benefit from the headshadow only when the noise source is contralateral to the implant user, a bilateral implant may do so when the SNR is higher at either ear.1 That advantage however does not require the use of both ears together, and therefore does not reflect binaural processing per se in the auditory system. Two measures of benefit that are usually assumed to result from the use of both ears together are the diotic benefit for collocated speech and noise, and the “squelch” benefit that is obtained when adding the ear with a poorer SNR for spatially separated speech and noise. Both are generally small in implant users, typically on the order of one dB in terms of SRTs, although there is some variation across studies and subjects. Some of that variability arises from the use of different monaural reference conditions (e.g., the better ear, first implanted ear, or average of the two sides). When a fixed ear is used as the monaural reference condition (such as the first implanted ear) or if results are averaged across ears or listeners before calculating the benefit, some of the assumed “binaural benefit” may actually be due to attending an added ear with better performance (van Hoesel, 2011) so that the true binaural benefit will be overestimated. A conservative estimate of the binaural benefit that must be attributed to the use of both ears is obtained by comparing binaural performance with the better monaural result for each listener and spatial configuration.

A potential drawback when choosing the better ear as reference, however, is that the benefit may be underestimated for statistical reasons. Measured performance for any specific listener and listening condition fluctuates due to test-retest variability around a presumed underlying performance average. Such variability will be influenced for example by listener attention and, for speech tests, variations in sentence difficulty. It can readily vary across listeners and, particularly for asymmetric performance, also across ears. By sampling monaural performance twice (once for the left ear and once for the right ear) and retaining only the better of the two samples, there is an increased likelihood of obtaining a higher monaural score (due to test-retest variability) compared to the single binaural measure. By analogy, consider rolling an unbiased dice twice and preserving only the higher of the two outcomes. On average, that procedure leads to a higher score than for single dice rolls. For the case where both ears have identical underlying monaural performance, measured performance with either ear alone can be considered as a sample from a normal distribution with a mean equal to the true performance and variance that reflects the test-retest variation of the measurement. When single samples are randomly drawn from such a distribution, the expected value (mean) corresponds to the true performance. In contrast, if the distribution is sampled twice (once for each ear) and only the maximum of the two samples is preserved, the probability density function of the maximum is skewed to the right relative to the single sample distribution, and a higher mean is obtained. When the maximum of the two monaural measurements is used to estimate better ear performance, it therefore provides a biased estimate of that performance.

Such bias may influence measures of benefit when fitting bilateral hearing aids or cochlear implants, because overestimation of the better monaural performance leads to underestimation of the binaural benefit. It is incurred not only in speech measures, but any measure where binaural performance is compared with the better of the two monaural measurements. It has been noted in relation to bilateral hearing aid use, for example by Byrne and Dillon (1979) and Day et al. (1988). The approach adopted by the latter authors was to measure monaural performance in either the left or right ear twice, and subtract the mean from the better of those two measurements. It was assumed that same amount of bias was inherent in selecting the better of two different ears, and the “true better ear performance” was determined by subtracting the monaurally determined bias from the performance with the better ear. In that approach, the bias was assumed to be unaffected by performance asymmetry between ears. However, the influence of asymmetry is clearly demonstrated by considering the case where one ear always performs better than the other. For such a listener, selection of the better ear is equivalent to selecting a fixed ear, so that no bias is imparted. Note that the dependence of the bias on asymmetry means that measuring the binaural performance twice, and comparing the better of the two binaural outcomes with the better monaural outcome is not a good way to ameliorate the effect of bias because the binaural measure effectively has zero asymmetry, so that it is more affected by bias than the better monaural measure and in that case the binaural benefit will be overestimated. The effect of asymmetry in selecting the better ear is incorporated in the approach adopted by Byrne and Dillon (1979), who modeled the performance in the two ears as independent normal distributions with equal variance but potentially different means, and calculated the increased expectation that arises when a single sample is selected and the largest is preserved. In the present work, the approach by Byrne and Dillon (1979) is extended to allow different standard deviations for each ear, as well as non-zero correlation between measures in the two ears. In addition, rather than assume that the sampled data accurately reflect the performance difference between ears, an upper-bound estimate of the bias is provided that assumes both ears have the same underlying performance and the sampled difference is entirely due to test-retest variation. When measured performance differs little between ears in comparison to the test-retest variation, the upper-bound estimate may be more appropriate, whereas for larger differences between ears it is increasingly likely that the upper bound overestimates actual bias.

The approach described was applied to speech intelligibility data collected previously (Litovsky et al., 2006; Litovsky et al., 2009) from 32 bilateral cochlear implant users. Estimates of the bias were used to determine how much binaural benefits were underestimated when the better ear was selected as the monaural reference condition, both for collocated and spatially separated target speech and interfering noise sources.

METHODS

Bias calculation

Bias in the present context is described as the difference between the underlying performance with the better ear, and the estimate of that value obtained (on average) by selecting the better ear score. When better performance corresponds to higher test scores, mathematically the bias corresponds to the difference between the expected value of the maximum of two random variables, and the larger of the two expected values obtained for each variable alone. When better performance corresponds to lower values, such as for SRTs, the bias is the difference between the expected value of the minimum of two random variables, and the lesser of the two expected values for each variable alone. Representing left and right ear performance measurements in a single listener as samples from normally distributed variables X₁ and X_2, with underlying means µ₁ and µ_2, and standard deviations σ₁ and σ₂, respectively, the expected value of the maximum of (X₁, X₂) is described by (e.g., Nadarajah and Kotz, 2008):

$${\mathrm{E}(\max (\mathrm{X}}_1{\mathrm{,}\mathrm{X}}_2))={\mu }_1·\Phi (({\mu }_1-{\mu }_2)/\theta )+{\mu }_2·\Phi (({\mu }_2-{\mu }_1)/\theta )+\theta ·\phi (({\mu }_1-{\mu }_2)/\theta )$$ (1a)

and the expected value of the minimum of (X₁, X₂) is given by

$$\begin{array}{c}\multicolumn{1}{c}{{\mathrm{E}(\min (\mathrm{X}}_1{\mathrm{,}\mathrm{X}}_2))={\mu }_1·\Phi (({\mu }_2-{\mu }_1)/\theta )+{\mu }_2·\Phi (({\mu }_1-{\mu }_2)/\theta )-\theta ·\phi (({\mu }_2-{\mu }_1)/\theta ),}\end{array}$$ (1b)

where Φ is the cumulative distribution function (cdf) of the standard normal distribution, φ is the probability distribution function (pdf) of the standard normal distribution, θ is given by

$$\theta =\sqrt{{\sigma }_1^2+{\sigma }_2^2-2\rho {\sigma }_1{\sigma }_2}$$ (2)

and ρ is the correlation coefficient between X₁ and X_2. The correlation conveys the extent to which the sampled values from X1 and X2 covary, and is high when the deviation from the true performance in the two ears is determined by a common factor. High correlation decreases the effective variance of the joint pdf [Eq. 2] and therefore reduces the bias, whereas low correlation (independent X1 and X2) leads to maximal bias values. Consideration of the case for independent X₁ and X₂, therefore, provides a more liberal estimate of the bias. For the independent case ρ = 0 so that Eq. 2 becomes

$$\theta =\sqrt{{\sigma }_1^2+{\sigma }_2^2}.$$ (3)

In the special case when X₁ and X₂ have identical distributions with ${\mu }_1$ = ${\mu }_2$ = μ, and σ₁ = σ₂ = σ, and noting that $\phi (0)$ = $1/\sqrt{2\pi }$, Eqs. 1a, 1b become

$${\mathrm{E}(\max (\mathrm{X}}_1{\mathrm{,}\mathrm{X}}_2))=\mu +\sigma /\sqrt{\pi },$$ (4a)

$${\mathrm{E}(\min (\mathrm{X}}_1{\mathrm{,}\mathrm{X}}_2))=\mu -\sigma /\sqrt{\pi }.$$ (4b)

In other words, for two independent samples drawn from the same distribution, selecting the greater of the two produces a value that on average is $\sigma /\sqrt{\pi }$ above the underlying distribution mean E(X). Similarly, by selecting the smaller of the two produces a value that on average is $\sigma /\sqrt{\pi }$ below the underlying distribution mean. In either case the magnitude of the bias is $\sigma /\sqrt{\pi }$.

If it is assumed that the observed difference in performance between the two ears is due to true differences (i.e., underlying distribution means) rather than measurement noise, the bias is described by Eq. 1a, 1b. As can be seen from that equation, larger differences in performance lead to smaller effects of bias. In the extreme case where the same ear is always the better ear (non-overlapping distributions) no bias is imparted. When the difference between means is large in relation to the standard deviations, Eq. 1a, 1b becomes

$${\mathrm{E}(\max (\mathrm{X}}_1{\mathrm{,}\mathrm{X}}_2))\approx \max ({\mu }_1,{\mu }_2),$$ (5a)

$${\mathrm{E}(\min (\mathrm{X}}_1{\mathrm{,}\mathrm{X}}_2))\approx \min ({\mu }_1,{\mu }_2).$$ (5b)

When the results from left and right ears are determined from small numbers of measurements in each listener, and the variance in the monaural data is comparable to (or exceeds) the difference between ears, it may be unreasonable to assume the difference in monaural means accurately reflects underlying performance asymmetry. In that case, it may be preferable to estimate an upper bound for the bias (${\mathrm{bias}}_{\max }$) that is based on sampling a single underlying distribution twice. Setting the variance of that hypothetical distribution equal to the root-mean-squared average of the left and right ear variances, that upper bound is given by

$${\mathrm{bias}}_{\max }=\sqrt{({\sigma }_L^2+{\sigma }_R^2)\mathrm{/}2\pi }.$$ (6)

Assessment of bias in bilateral CI users

The effect of bias associated with selecting the better ear as the monaural reference condition was assessed using speech intelligibility data collected in relation to two previous reports (Litovsky et al., 2006; Litovsky et al., 2009). The subject pool under consideration comprised listeners with a broad age range at implantation, and also a wide range of durations of severe to profound degree of hearing loss. Etiology of the hearing loss was for most subjects reported as “unknown.” Individual sentence-list data from all subjects were re-analyzed in the present study to determine measures of benefit and bias. Speech intelligibility was measured using the BKB-SIN (BKB-Speech In Noise) test (Etymotic Research Inc., 2005). Tests were conducted with target sentences always presented directly to the front of the listener at 65 dB SPL and babble noise either also to the front (S₀N₀), or in alternative test-blocks, from 90 degrees to the left (S₀N₋₉₀) or right (S₀N₉₀). Levels were verified using a sound level meter (A-weighted) positioned at the head in absentia. Each sentence list consisted of eight to ten sentences presented at SNRs that decreased progressively from +21 (very easy) to −6 (extremely difficult) in 3 dB steps. For each list a speech reception threshold (SRT), representing the SNR for 50%-correct responses, was estimated by scoring the total number of correctly reported target words over the range of nine SNRs (Killion et al., 2004). For each monaural listening condition, as well as the binaural condition, four repeat SRTs were obtained. The procedure was repeated for all three noise positions, requiring in total 36 SRTs from each listener. Left, right and binaural listening tests, and the order of noise positions was randomized across listeners. Prior to all speech tests, left and right-ear processor sensitivity controls were adjusted so that sounds originating directly in front of the listener gave rise to percepts that were lateralized approximately in the medial plane and were equally loud in both ears. Those levels were subsequently used for all three noise positions. Data from 41 listeners were initially reviewed. However, because the BKB-SIN test cannot measure SRTs in excess of 21 dB, listeners who showed a floor effect for any list measurement were excluded from the formal data analysis, resulting in a total of 32 subjects from whom results are reported. All subjects were native English speaking adults with post-lingual deafness, and had received Nucleus 24 Contour implants in each ear, either simultaneously or no more than 1 month apart. They all routinely used bilateral body-worn or ear-level speech processors, programmed with the widely used clinical sound coding strategies Spectral PEAK (SPEAK), advanced combination encoder (ACE) or continuous interleaved sampling (CIS). Testing was conducted for each subject using the clinically fitted processors. IRB approval and informed consent was obtained from all participants. Subjects received no additional training prior to measurement of the SRTs.

Because the SRT is expressed as a signal to noise ratio, better performance corresponds to lower values, and the bias for each subject and spatial configuration was calculated as

$${\mathrm{bias}\mathrm{=}\mathrm{E}(\min (\mathrm{SRT}}_{\mathrm{L}}{\mathrm{,}\mathrm{SRT}}_{\mathrm{R}}))-{\min (\mathrm{SRT}}_{\mathrm{L}}{\mathrm{,}\mathrm{SRT}}_{\mathrm{R}})$$ (7)

where E(min(SRT_L, SRT_R)) is the expected value of the minimum function described by Eq. 1b, and min(SRT_L, SRT_R) is the mean SRT for the ear with better measured performance. In addition, upper-bound estimates of the bias were determined for each subject and spatial configuration according to Eq. 6.

The test-retest variation expected for a single list score was estimated for each listener, for each ear and spatial configuration, from the four repeat SRT measures. That value was subsequently divided by two (the square root of the number of SRTs) to determine the test-retest variation for the average of four lists, corresponding to the value of σ used in Eq. 1b and Eq. 6 to estimate the bias for each listener.

RESULTS

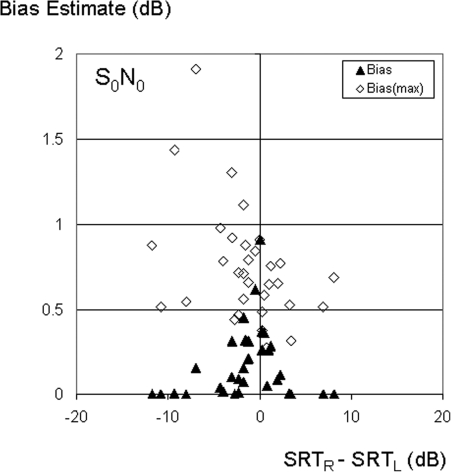
Figure 1 shows bias estimates inherent in selecting the better ear when speech and noise were both presented from directly in front of the listener (S₀N₀). Bias is plotted as a function of the observed asymmetry in mean left-and right-ear SRTs. The filled symbols describe estimated values of bias calculated according to Eq. 7. In that case the dependence of bias on left-right performance symmetry is clearly shown by the higher values when the difference in performance between ears is close to 0 dB. Averaged across subjects, the bias is only about 0.2 dB, but in a small number of subjects with a well matched performance between ears, it ranges between 0.5 and almost 1 dB. The open symbols show the estimated values for the upper bound (bias_max) described by Eq. 6. Because that value is independent of the difference in means, there is no systematic dependence on interaural SRT differences. Averaged across subjects, bias_max is about 0.7 dB, and ranges across subjects from about 0.3 dB to almost 2 dB. Data pairs for individual subjects, describing bias (closed symbols) and bias_max (open symbols), are aligned along the abscissa. The two values converge when the difference in measured performance between ears is small. The considerable variation in bias_max across subjects reflects differences in test-retest variation. Estimated standard deviations for the monaural four-list averaged SRT scores ranged across listeners from as little as 0.25 dB, to as much as 4.5 dB. A regression analysis showed that test-retest variation was not correlated between ears in these subjects (F(1,31) = 0.05, p = 0.8). These outcomes suggest that nominal values of test-retest variability are unlikely to be good predictors for individual subject outcomes when limited testing is conducted, as is usually the case for speech perception measures with cochlear implant users. For reference, the nominal critical difference for a four-list averaged SRT described by the test manufacturer corresponds to a standard deviation of about 1.6 dB, which is in approximate agreement with the average standard deviation of 1.3 dB found for the listeners in this study.

Figure 1.

Estimates of bias according to Eq. 7 (filled symbols), and upper-bound estimates (open symbols) according to Eq. 6, as a function of the difference between right and left ear SRTs, for target speech and noise both to the front (S₀N₀). Data are from 32 subjects who showed no floor effects for any of the listening conditions at all three noise positions.

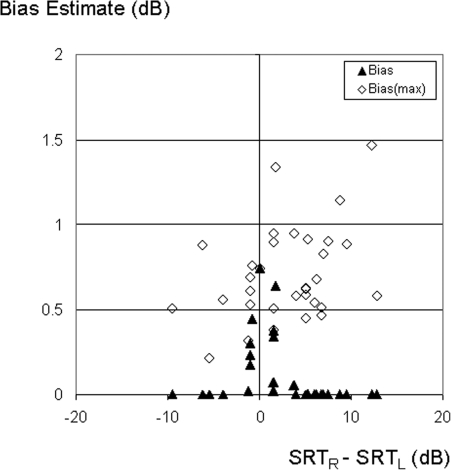
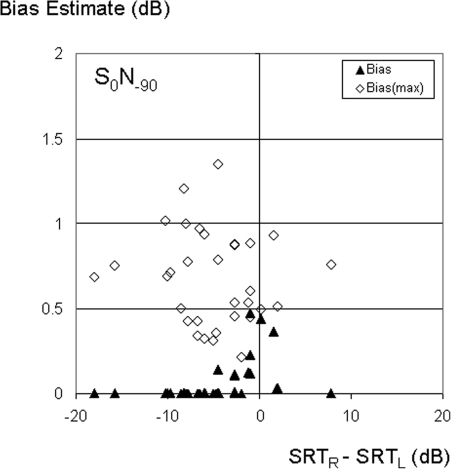
Figures 23 show similar plots of bias for N₉₀ and N_-90 noise positions respectively. For the N₉₀ configuration (Fig. 2), the distribution of data points is shifted to the right compared to the S₀N₀ condition (Fig. 1) because the left ear SRT is reduced by the headshadow. Similarly, the distribution is shifted to the left when noise was on the left (Fig. 3). In both cases, there were fewer listeners with similar left and right ear performance than for the S₀N₀ condition. For example, the number of subjects that showed (R-L) SNRs within a +/−3 dB range decreased from almost two thirds (19 out of 32) for the N₀ condition, to just over one third with noise to either side (11 subjects for N_-90, and 12 for N₉₀). Averaged across subjects, the estimated bias was significantly smaller [paired t-test, t(31) = 1.4, p = 0.02] for N₋₉₀ (0.07 dB) than N₀ (0.18 dB), but the difference between N₀ and N₉₀ (0.11 dB) was not significant [t(31) = 1.4, p = 0.17]. For a small number of subjects with a well matched performance across ears despite the mismatch in SNR for either N₋₉₀ or N₉₀ conditions, the estimated bias again approached or exceeded 0.5 dB. Because the upper-bound estimate of bias [Eq. 6] assumes the data are noisy samples of identical performance in the two ears, it ignores the mean performance differences between ears that arise for different noise positions. Accordingly, subject-averaged estimates of bias_max (open symbols) were around 0.7 dB for both N₋₉₀ and N₉₀ conditions, as was the case for the N₀ condition. Averaged across subjects and ears, the four-list test-retest variance was about 1.2−1.3 dB (depending on noise position). Using a root-mean-square average across ears [see Eq. 6] before averaging across subjects had only a small effect on those values (increase from 1.23 to 1.26 averaged across the three noise positions). Accordingly, the use of the average test-retest variation in Eq. 6 results in a bias_max estimate that closely matches the value obtained when variance in each ear is explicitly incorporated for each listener. Although bias_max was not dependent on noise position, its use as an estimate of actual bias is only reasonable when performance is similar in the two ears. Using a +/−3 dB criterion, the number of listeners for whom that was the case was about twice as small for N₋₉₀ or N_90, compared to the N₀ condition. As for the N₀ condition, individual subject results for N₋₉₀ and N₉₀ showed considerable variation in bias_max ranging from about 0.2 to 1.5 dB. However, the correlation of individual subject bias_max estimates across the three noise conditions was not significant, which suggests that subject specific sources of test-retest variation were not consistent.

Figure 2.

Estimates of bias according to Eq. 7 (filled symbols), and upper-bound estimates (open symbols) according to Eq. 6, as a function of the difference between right and left ear SRTs, for target speech to the front and noise located 90 degrees to the right (S₀N₉₀).

Figure 3.

Estimates of bias according to Eq. 7 (filled symbols), and upper-bound estimates (open symbols) according to Eq. 6, as a function of the difference between right and left ear SRTs, for target speech to the front and noise located 90 degrees to the left (S₀N₋₉₀).

Averaged across the 32 subjects who showed no floor effects, the binaural benefits calculated relative to the better ear were 0 dB (standard deviation [s.d.] = 2.4 dB) for the diotic N₀ condition, 1.0 dB for N₋₉₀ (s.d. 2.2 dB), and 0.8 dB for N₉₀ (s.d. 3.0 dB).

CONCLUSION AND DISCUSSION

The results from these bilateral CI users show that, if it is assumed that measured performance reflects true differences between ears, the effect of bias [according to Eq. 7] was on average very small: about 0.2 dB for N₀ and about half that value for N₉₀ and N₋₉₀ conditions. Using the subject averaged standard deviation and interaural performance difference for each noise configuration in these data, the method of Byrne and Dillon (1979, Table I) produces smaller bias estimates that are less than 0.05 dB for all three noise positions. For subjects with very similar performance in both ears for any specific noise position, larger bias estimates between 0.5 and 1 dB were obtained using the present approach. When it was assumed that differences between ears for all listeners were entirely due to test-retest variation, the subject-averaged upper-bound estimate of bias [Eq. 6] was about 0.7 dB for all three noise conditions. The use of the mean rather than RMS averaged variance between ears in Eq. 6 produced essentially the same upper-bound estimate, and is equivalent to using the approach of Byrne and Dillon (1979) with zero interaural performance difference. The upper bound may be the preferred estimator when measured performance is similar in the two ears relative to the test-retest variation. For the N₀ condition about two thirds of the listeners showed matched performance between ears within +/−3 dB. For N₋₉₀ and N₉₀ conditions that fraction decreased to only one third, in accordance with the increased performance asymmetry between ears due to the headshadow. Accordingly, although the upper bound is independent of noise position, it will less often be an appropriate estimator for the N₋₉₀ and N₉₀ conditions, than for N₀.

The estimates described above are based on the assumption that the deviations from true performance in the two ears were uncorrelated. While the validity of that assumption will have been ameliorated through the use of randomized test conditions partial correlation may have remained. However, as discussed in Sec. 2A, higher correlation leads to reduced bias. Recalculation of the bias according to Eq. 7, but assuming unity rather than zero correlation, reduced the subject-averaged bias estimate from 0.2 to 0 dB. The range in bias values thus calculated across subjects was also much smaller when assuming unity correlation: only three of 32 subjects showed bias in excess of 0.1 dB for the N₀ condition, and just a single subject for the N₉₀ and N₋₉₀ conditions. Upper-bound estimates of the bias for all three noise positions were reduced from 0.7 dB for zero correlation, to 0.5 dB for unity correlation. The further reduction in bias that results when the assumption of zero correlation is relaxed strengthens the conclusion that the effect of bias was small in these listeners.

To the extent that the test-retest variation in the present study is comparable to that in other studies, the results indicate that binaural benefits in bilateral cochlear implant users are not substantially underestimated (on average) when binaural performance is compared to the better monaural result in each listening configuration. Averaged across the 32 listeners who showed no floor effects, the diotic S₀N₀ benefit was 0 dB and the binaural benefit in spatially separated conditions was about 1 dB, when referred to the better monaural result in each condition. Those results are in good agreement with a recent review of the bilateral CI literature (van Hoesel, 2011) in which binaural benefits were recalculated relative to better ear outcomes for a large number of studies. On average, the binaural SRT benefit in that review was found to be slightly smaller than 1 dB for S₀N₀ presentation, and slightly greater than 1 dB for spatially separated speech and noise. Although the small effect of bias found in the present paper may be considered substantial relative to a 1 dB benefit, in absolute terms the binaural benefit remains small even when adjusted for bias. The increase in bias when performance becomes more similar in the two ears may account in part for why the diotic benefit in bilateral cochlear implant studies to date appears marginally smaller than for spatially separated speech and noise. The results support the use of the better monaural result as reference condition to assess binaural benefits, which in contrast to other reference conditions avoids overestimated binaural benefit due to better ear contributions.