Image analysis tools and emerging algorithms for expression proteomics

Abstract

Since their origins in academic endeavours in the 1970s, computational analysis tools have matured into a number of established commercial packages that underpin research in expression proteomics. In this paper we describe the image analysis pipeline for the established 2-D Gel Electrophoresis (2-DE) technique of protein separation, and by first covering signal analysis for Mass Spectrometry (MS), we also explain the current image analysis workflow for the emerging high-throughput ‘shotgun’ proteomics platform of Liquid Chromatography coupled to MS (LC/MS). The bioinformatics challenges for both methods are illustrated and compared, whilst existing commercial and academic packages and their workflows are described from both a user’s and a technical perspective. Attention is given to the importance of sound statistical treatment of the resultant quantifications in the search for differential expression. Despite wide availability of proteomics software, a number of challenges have yet to be overcome regarding algorithm accuracy, objectivity and automation, generally due to deterministic spot-centric approaches that discard information early in the pipeline, propagating errors. We review recent advances in signal and image analysis algorithms in 2-DE, MS, LC/MS and Imaging MS. Particular attention is given to wavelet techniques, automated image-based alignment and differential analysis in 2-DE, Bayesian peak mixture models and functional mixed modelling in MS, and group-wise consensus alignment methods for LC/MS.

1 Introduction

In the post-genomic era, the search for disease associated protein changes and protein biomarkers is reliant on good experimental design and the power to drive high throughput, robust, and reproducible quantitative platforms. Accurate quantification, using either traditional 2-DE techniques or more recent label-free LC/MS approaches, is currently largely dependent on semi-automated signal and image analysis tools where speed, objectivity, and sound statistics are key factors [1].

2-DE, which has been employed for protein separation since 1975 [2, 3], enables the separation of complex mixtures of proteins on a polyacrylamide gel according to charge or isoelectric point (pI) in the first dimension and molecular weight (M_r) in the second dimension. Proteins are visualised by pre-labelling the sample prior to 2-DE or by subsequently staining the gel, thus delivering a map of intact proteins characteristic for that particular cell or tissue type. Once the gels have been converted to digital images, informatics tools are responsible for background subtraction, spot modelling and matching, data transformation and normalization, and statistical analysis for quantification of protein spot volumes across gel images [4]. The search for differential expression under significant biological variability has driven researchers to replicate their experiments more and more, but current informatics tools tend to decrease in performance as more gels are added to the analysis [5]. Emerging algorithms are consequently seeking to model and fuse the data directly in the image domain, therefore avoiding isolated decisions too early in the pipeline.

The alternative ‘shotgun proteomics’ workflow of LC/MS is more recent [6, 7], but its promise of automation has realised a number of software tools in a short period of time. In LC/MS, proteins are first digested and then separated in an LC column, usually by their hydrophobicity. Multiple LC stages are possible. The eluting solvent is then directly interfaced with MS at regular intervals through ESI [8], though offline approaches using MALDI have also been demonstrated [9]. With the use of ESI and MS/MS, a small time-limited number of intense peaks in each mass spectrum may be subjected to CID for subsequent identification. In effect, the output of an LC/MS run can be visualised and analysed as an image, with RT in the first dimension, m/z in the second dimension, and acquired MS/MS spectra (if any) annotated as points. LC/MS imaging tools essentially follow the 2-DE workflow except that: m/z is far more reproducible than RT; each peptide is likely to appear multiple times with different charge states (especially with ESI); and in high-resolution MS the isotopic distribution of each peptide resolves into multiple spots. The relative simplicity of 1-D LC alignment (compared to 2-DE), and the rise in importance of RT as a discriminant for protein identification, has led to emerging algorithms for the group-wise alignment of LC/MS datasets and therefore the derivation of normalised (group-average) retention times.

Imaging in proteomics is mainly used for the purpose of comparison, that is, for differential display and analysis. At a lower level, 2-D gel and LC/MS images both require data quality control since the presence of contaminants, among others, is readily spotted in such images. The main difference between 2-DE and LC/MS images lies in the expression/transcription of underlying experimental data. A 2-D gel is a physical object whereby proteins are fixed at set coordinates, the image of which is digitised for analysis. The image is therefore a direct/exact reflection of the underlying experimental data. In contrast, LC/MS, as the juxtaposition of two techniques, does not produce a physical object but two types of spectral data that are plotted and visualised as a two-dimensional image. Consequently, an LC/MS image is a conceptual construction representing the underlying experimental data. This distinction bears multiple cascading consequences. To begin with, the origin of noise and the sources of variability are different. As a result, detection and alignment procedures do not stumble on the same obstacles. An obvious example would be the possible need to rotate a gel image with respect to another when the placement of the gel prior to scanning is slightly at an angle. This operation is pointless in the case of LC/MS given the absence of image capture. Secondly, the meaning of image resolution also differs. In the case of electrophoresis, the scanning of a 2-D gel is usually guided by recommendations of software developers to achieve a reasonably faithful capture. But ultimately, the image resolution is bounded by the power of separation of the gel. The quality of polyacrylamide, the choice of solvent or that of staining can be factored in to account for the overall quality of the final 2-D gel. This information is however difficult to quantify and to relate to image resolution. In the case of LC/MS, image resolution is directly linked to the resolution of the instrument. LC coupled to a FT-ICR device will yield much clearer images than those generated from TOF data.

While image analysis and protein identification are the crucial final steps in biological interpretation of comparative proteomic studies, these approaches must first be considered at the experimental design stage to ensure the scale of the analysis is manageable, cost effective, and productive. In this review, we firstly address the current challenges in 2-DE image analysis before moving onto characterisation of the MS signal and then the issues in extending the analysis to the LC dimension. The 2-DE image analysis pipeline is then described from both the user and technical perspectives, using some current tools as examples, before we survey promising data driven algorithms including image-based alignment and differential analysis. To open the discussion on LC/MS methodology, we present peak detection, desiostoping and functional analysis from the perspective of recent advancements in MS, and particular SELDI MS [10], a MALDI technique augmented with a target providing biochemical affinity to a protein subset. SELDI has recently seen an explosion of research in these areas due to its relevance to high-throughput clinical screening. Some of these techniques provide full posterior distributions of statistical uncertainty, whilst others are robust to multiple sources of systematic bias and variation, and therefore are of significant interest to the 2-DE and LC/MS image analysis communities. After this, we review current tools and emerging methods for LC/MS image analysis, highlighting the work towards unbiased group-wise alignment of LC/MS data. Finally, we briefly cover the downstream statistical and results visualisation issues that both 2-DE and LC/MS methods share.

1.1 Challenges for image analysis in 2-DE

Whilst initially the resolution of 2-DE looks substantial, there are a number of issues that confound reliable analysis [4], contributing to significant software-induced variance [11] and therefore requiring substantial manual intervention with existing packages [5]. Issues include:

Artifacts and co-migration

Due to the large number of proteins captured in a single separation, it is highly probable that some will have similar pI and M_r values and therefore co-migrate. If the gel is stained to saturation, the merged spots may not be distinguishable. Spots tend to have symmetric Gaussian distribution in pI, though, if saturated, the diffusion model is a better fit [12]. However, there are often heavy tails in the M_r dimension and particular proteins can also cause streaks and smears. The gel edges, cracks, fingerprints and other contaminants can also be present and must be removed before analysis.

Intensity inhomogeneity

The dynamic range of detection depends on the stain/label used. For example, silver stain has a limited dynamic range with poor stoichiometry, whilst fluorescent labels have a dynamic range of 10³ and detection limit 0.1 ng. However, recent approaches to obtain time-lapse acquisitions of silver stain exposure [13, 14] have increased dynamic range by up to two orders of magnitude [14]. Nevertheless, the dynamic range of proteins in cells and body fluids is far greater than even the most sensitive radiolabelling technique. Instrument noise from the scanner becomes a factor when quantifying the weakest expression. Furthermore, quantification reliability is reduced due to variation in stain exposure, sample loading and protein losses during processing, which in addition can vary across the gel surface [15]. There is also a significant smoothly varying background signal due to the stain/label binding to non-protein elements.

Geometric distortion

Variations in gel casting and polymerisation of the poly-acrylamide net, buffer and electric field all contribute to irrepressible geometrical deformation between experiments, thus inhibiting the deduction of matching spots. Amongst many other minor factors, fixing the gel may cause it to shrink and swell unevenly during staining. Whilst there has been some work on modelling gel migration [16], in practice this has not led to specialised transformation models due to the range and scales of distortion present. One exception to this is due to current leakage, which causes a characteristic frown in the spot pattern [17].

The DIGE protocol [18] was invented to allow up to three samples to be run on the same gel, each labelled with a cyanine dye that fluoresces at a different wavelength. Whilst there is consequently only marginal geometric disparity between these samples, typical experiments use multiple gels and therefore the correspondence issue remains. Another advantage of DIGE is that if a pooled standard is used as one of the samples, it can be used as a per-spot correction factor to normalise protein abundances between gels. Since a recent study showed a loss of sensitivity with three multiplexed dyes compared to two [19], a number of laboratories now run each DIGE gel with only a single sample against a normalisation channel.

1.2 Challenges for signal analysis in MS

Whilst m/z measurements are considerably more reliable than RTs, the ionisation source may generate specific problems. With MALDI and SELDI, the sample is mixed with a matrix, which aids desorption and ionisation when hit with a short laser pulse, whereas with ESI, analyte solution in a metal capillary is subjected to a high voltage that forms an aerosol of charged particles. The matrix in MALDI instruments can cause mass drift, but with ESI sources, variation between runs is less apparent. The MS signal is, however, affected by a number of noise sources and systematic contaminants [9, 20], including:

Distribution of m/z

In TOF devices, the ions are subject to an accelerating voltage and then drift down a flight tube until they hit the detector. The flight time recorded by the detector has a quadratic relationship with m/z. Due to random initial velocities, detector quantisation, variable trajectories and continual mutual repulsion during flight, the spread of arrival times for specific peaks is approximately Gaussian but with a stronger falling edge and with greater spread as arrival time increases. If the detector is a time-to-digital convertor (most today are analogue-to-digital type), a ‘dead-time effect’ is evident, which causes strong peaks to partially mask subsequent arrivals [21]. In more advanced instruments, the accelerating voltage may be delayed to provide optimal resolution at a specific m/z. TOF MS may also increase resolution by employing one or more reflectrons which attempt to bring the ions back into focus [22]. With FT-ICR systems, ions are injected into a cyclotron and resonate in a strong magnetic field. This induces a current on metal detector plates, which captures the frequencies of oscillation of all ions simultaneously. A Fourier transformation of this data gives very high-resolution m/z values with residual spread approximated by the Lorentz distribution. A similar class of device, the Orbitrap, operates without a magnetic field by trapping the ions electrostatically in orbit around a central electrode [23].

Instrument noise and bias

Johnson thermal noise or ‘dark current’ is present, which can be approximated by white (distributed evenly over the frequency spectrum) Gaussian noise with a constant baseline. The nature of discrete ion counting in the detector also suggests a Poisson ‘shot noise’ component [24]. Furthermore, through power spectral density analysis, elements of ‘pink’ noise (proportional to the reciprocal of the frequency) are visible as well as periodic signals caused by interference from within the instrument, the power supply and surrounding equipment [25]. In TOF equipment, noise is ‘heteroscedastic’, which means that variance differs at different points in the spectrum (in fact it appears to reduce as flight time increases). In FT-ICR spectra, the ion count is much greater and therefore suffers far less from stochastic variability. In general, however, ion count does not remain constant between spectra and so some form of normalisation is required.

Isotope distribution and charge states

The average isotope envelope of an unknown peptide with known m/z can be determined through multinomial expansion of the natural distributions of C, H, N, O and S in each amino acid [26], together with all expected amino acid configurations obtained from a proteomics database [27]. The distribution is heavily skewed to the right for low m/z, and approaches Gaussian distribution as m/z rises. In high-resolution equipment, each isotope forms a separate peak at approximately 1 Da intervals, whereas in low-resolution MS the distribution affects the shape of a single peak. With ESI in particular, peptides are present in a number of charge states dependent on their length due to the number of exposed protonation sites. Since MS measures the mass to charge ratio, there is a deterministic reduction in m/z and narrowing of the m/z interval between isotopes as the charge state increases. The intensity distribution of the charge state envelope for a peptide, however, has thus far only been empirically modelled and is believed to depend on the number and accessibility of the protonation sites [28].

Chemical baseline and biological variation

Each mass spectrum is corrupted with a baseline composed of contaminants and fragmentation caused by various collisions. In high-resolution MS, the singly charged baseline is clearly periodic every 1 Da [29]. In MALDI, matrix molecules contribute to an increased baseline in the low m/z range, which eventually decays exponentially. Each species of peptide has a different ionisation efficiency and hence a different abundance/intensity relationship. Towards the goal of absolute quantification [30] and the revitalisation of PMF protein identification [31], correlations between ionisation efficiency and amino acid sequence have recently been investigated.

As has been illustrated, these signal characteristics have been extensively studied in MS, with recent studies seeking to understand the consequences of the technical issues listed above. For example, Coombes et al. [32, 33] and then Dijkstra et al. [20] provide from first principles simulators for delayed extraction MALDI/SELDI TOF MS in order to explore the nature of the separation. In these simulations, an exponential baseline function is modelled and the peaks are generated based on the stochastic isotopic distribution of peptides.

1.3 Challenges for image analysis in LC/MS

The deformation of spots in 2-D gels mainly stems from the gel surface and the staining procedure, whereas the deformation of peaks in LC/MS images originates from the chromatogram. The variability in RT, which can be severely non-linear, is chiefly caused by packing, contamination and degradation of the mobile phase due to its finite lifespan and fluctuations in pressure and temperature in and between runs [34]. Chromatogram peaks are susceptible to this distortion, and therefore have been typically modelled by EMGs, which allow skew to either the front or tail [35]. Occasionally, the elution order of peptides with similar RTs swap between runs. If multidimensional LC separation is performed, the other dimension is typically a small number of discrete fractions. RT variation inside and between these low-resolution fractions provides a severe and currently unsolved processing problem. Also, if some ions are selected for MS/MS, there could be dropouts in the LC signal whilst the second MS stage takes place. Regarding the chemical baseline, whilst it is periodic in 1 Da intervals in the MS dimension, in the LC dimension it has been shown to vary smoothly [36].

As well described in [37], there are basically three strategies for measuring protein expression via LC/MS: spectral counting, label-free quantification and isotope-labelling. Spectral counting uses LC/MS/MS data to provide a semi-quantitative measure of abundance through sampling statistics such as the number of identifications for each protein [38]; The latter two methods involve LC/MS imaging: The label-free approach solely relies on the study of isotopic patterns between elution profiles; Isotope-labelling with SILAC or iTRAQ [39], on the other hand, ensures that distinct isotopes are co-present in the same spectrum and therefore may be easier to detect, but the interpretation of weak signals remains quite misleading. The isotopes also increase spectrum crowding and LC alignment is still necessary as multiple replicates are often essential. For both approaches, it is clear that the modelling and matching of peaks is a decisive step that justifies the emphasis on this subject in this review.

In general, signal generation has been less extensively studied in LC (and 2-DE) than in MS. However, recently Schulz-Trieglaff et al. [40] simulated a whole ESI LC/MS experiment including: virtual peptide digestion; prediction of RT, ionising efficiency and charge distribution for each peptide; and an EMG peak shape in the LC dimension. These computer models give increasingly objective data for comparison of competing algorithmic techniques.

2 Image analysis in 2-DE

The first stage in any computational analysis of 2-D gels is the acquisition of digital images from the stain or label signal. Three categories of capture device are available [41]. The least expensive offerings are typically flatbed scanners. A CCD is mechanically swept under the gel to record light transmitted through or reflected from the gel. The SNR is limited, since the device must be small, and further degradation can result from the ‘image stitching’ required to reconstruct the full image. Utilising a larger fixed CCD camera at a much greater focal distance results in much improved SNR of 10⁴ [42]. Furthermore, different filters can be employed to capture a number of labelling methods, such as fluorescent, chemiluminescent and radioactive. Disadvantages stem from the use of a single fixed focus camera: Vignette and barrel distortion must be compensated for and the overall resolution is limited to that of the sensor. The third category of capture device is the laser scanner, where an excitation beam is passed over each point in the gel through mechanical scanning or optical deflection. The wavelength of the laser must be matched to that of the desired fluorescent label (or fluorescent backboard used to image visible light stains), whilst PMTs are used to amplify the resulting signal for detection. This leads to excellent resolution and dynamic range up to 10⁵ [42].

Whilst sometimes overlooked, correct scanner preparation and calibration is vital for the discovery of statistically meaningful results. This ensures dynamic range is maximised without saturation and with minimal noise [43, 44]. Fixed CCD-camera systems require post-processing to remove geometric and light-field lens distortion, whilst flatbed scanners normalise inconsistencies due to image stitching during acquisition. On some devices use of a calibration wedge is needed to ensure linearity of response. Individual experiments may also benefit from employing a first pass analysis or use of a protein concentration wedge, since signal response often depends on sample type e.g. Back et al. [45] established optimal PMT voltage by evaluating saturation levels on two randomly selected gels. A suitable protocol for laser scanning is given by Levänen and Wheelock [43].

Once the gels are captured, they are typically saved in TIFF format or preferably in the native format of the scanner, e.g. GEL or IMG, since they often preserve a greater dynamic range and avoid incompatibilities between different implementations of the TIFF ‘standard’. Furthermore, manipulation in generic image editing packages should generally be avoided, as vital metadata may be silently lost [41].

2.1 Image analysis workflow

Image analysis is often viewed as a major bottleneck in proteomics, where the time spent on analysis is largely down to user variability. Most commercially available gel base analysis platforms are now designed to encourage minimal user intervention in the interest of reproducibility, although this varies according to the package. A comprehensive list of current commercial 2-DE packages and their features is given in [46]. Several reports evaluating 2-DE software platforms have been published [5, 47–49]. The workflow for 2-D gel analysis varies according to the package, and is largely dependent on whether spot matching is performed after spot detection, or whether gel alignment is performed prior to consensus spot detection, as shown in Supplementary Material Figure 1. In the instance of three leading commercial 2-DE packages and one web-based service, the basic workflows are described below.

DeCyder (GE Healthcare)

The DeCyder workflow is immediately apparent to the user in the main window, which systematically displays icons for the batch processor, image loader, Difference In-gel Analysis, Biological Variation Analysis, and the XML Toolbox (Supplementary Material Figure 2a). Images can be uploaded via the Image Loader, or in the case of large experiments via the batch processor, and the experimental setup is defined at this stage of the analysis. The Differential In-gel Analysis module automatically performs spot detection, background subtraction, in-gel normalisation, and calculates protein spot ratios for quantification. In addition, artifact removal is an option based on spot slope, area, peak height and volume. The Biological Variation Analysis module performs gel-to-gel matching of spots, allowing for comparisons across multiple gels. The user interface is divided into four views including the 1) image view, 2) 3D View of selected spots, 3) Graph view displaying the standardised log abundance across groups, and 4) Table view as displayed in Supplementary Material Figure 2b. Spot matching and landmarking is performed in the Match Table Mode and is user defined; it can therefore be a lengthy process depending on the scale of the experiment and user variability. Spot editing (split and merge) is also performed at this stage. Statistical analysis is typically performed in Protein Table Mode and includes the Students t-test, ANOVA, fold change calculation, and FDR adjustment. The aim of FDR is to achieve an acceptable ratio of true and false positives, where an FDR rate of 5% means that on average 5% of changes identified as significant would be expected to have arisen from type one errors [50]. Finally, the Extended Data Analysis package enables the user to perform multivariate statistical analysis and includes tools such as PCA (Supplementary Material Figure 2c), hierarchical clustering analysis (Supplementary Material Figure 2d), and discriminant analysis.

Melanie (Genebio) and ImageMaster 2D Platinum (GE Healthcare)

Melanie 2D gel analysis software (also sold under the name ImageMaster 2D Platinum by GE Healthcare) was one of the first 2-DE gel analysis platform created for analysing gel images and has been in development for over two decades. The software includes a viewer that can display an unlimited number of images simultaneously. Though Melanie is licensed, the viewer is freely downloadable (http://www.expasy.org/melanie/2DImageAnalysisViewer.html). This viewer shares functionalities with the full version of the software, however, spots and matches cannot be created nor edited, gel images cannot be rotated, cropped nor flipped and reports cannot be saved.

A single analysis workflow is followed in gel studies, both for conventional 2D electrophoresis and DIGE gels (Supplementary Material Figure 3a). It is divided into 3 steps: In the Import & Control step the images can be edited (rotated, flipped, cropped, and inverted) or calibrated to remove image-scanning variations. The contrast settings and colour palettes can also be adjusted at any time. In the Organize & Process step, selected gels are subsequently inserted into a project, by simple drag and drop, for spot detection and matching. Gels can be hierarchically organized (DIGE, biological group, replicate, etc.) for easier matching and comparison as in Supplementary Material Figure 3a. In last step Analyze & Review, Melanie offers a wide range of statistical reports containing e.g. standard t-Test, ANOVA statistics to extract relevant proteins (Supplementary Material Figure 3b). Therefore each protein can be annotated and linked with information contained in an external database either on the web or in a LIMS. At each step, Melanie allows users to display, manipulate, and annotate gel images. Images can be reorganized at convenience to optimise space and visibility in accordance with personal preferences. Melanie offers fully dynamic tables, histograms, plots, and 3-D views in which both content and selection are continuously updated to stay up-to-date.

Progenesis Same Spots (Nonlinear Dynamics)

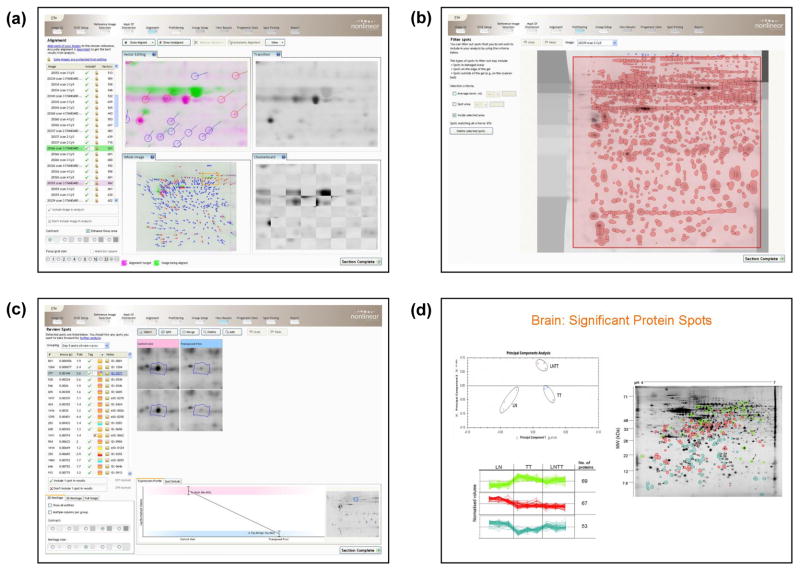
The Progenesis Same Spots work flow is streamlined via the tool bar at the top of the analysis screen which displays tabs for image QC, DIGE setup, reference image selection, mask of disinterest, alignment, prefiltering, group setup, view results, Progenesis stats, spot picking and report (Figure 1). Following addition of the gel images in the experiment setup, the Image QC step examines images and provides feedback and recommendations for the user. QC checks can include image format and compression, level of saturation, and dynamic range etc. while image manipulation tools include rotate, flip, invert, and crop functions. Once the experimental setup is complete, the user selects the reference gel and area of interest. The user is then free to proceed to the image Alignment stage whereby alignment vectors are put in place to improve gel-to-gel matching. Visual tools such as alignment overlay colours, spot transitions before and after alignment, grids, and checkerboards are provided to guide the user during the alignment process as illustrated in Figure 1a. On completion of alignment, image prefiltering is made available to the user where spots may be excluded from selected or poor regions within in the gel images (Figure 1b). For the SameSpots analysis the software automatically carries out spot detection, imposes a same spot outline across the experiment and carries out background subtraction, normalisation, and spot matching across gel images. Within the Group Setup tab, images can then be grouped according to experiment structure, with the ability to set up multiple experimental groupings eg. male vs female, control vs treated etc. Automatic statistical testing by ANOVA is performed, and significant spots are ranked by p-value and fold change in the View Results tab. Colour coded spot tags can also be applied at this stage to assist with data exploration (Figure 1c). In addition, spot editing (split, merge, delete, and add) can be preformed, where the statistics and tables are automatically updated. Finally, advanced statistical analysis and data interpretation in Progenesis Stats includes q-values for FDR, power analysis, PCA, and clustering of co-regulated spots (Figure 1d).

Figure 1.

Progenesis SameSpots user interface. The workflow is streamlined via the tool bar at the top of the analysis screen including Image QC, DIGE setup, reference image selection, mask of disinterest, alignment, prefiltering, group setup, view results, Progenesis Stats, spot picking, and report. (a) Illustrates vector editing in the alignment mode, where alignment vectors are positioned between the current image (green) and a chosen reference image (magenta). (b) Displays image prefiltering in which poor regions of the gel may be excluded from the analysis. (c) In view results mode, significant spots have been ranked according to ANOVA and colour coded tags have been applied to facilitate with data exploration. (d) PCA analysis of differentially expressed spots where the 2-D gels are clustered into one of three groups, and groups of co-regulated protein spots are clustered according to expression profile.

REDFIN Solo and Analysis Center (Ludesi)

Ludesi take a different approach to other vendors by offering their analysis package REDFIN as a free download but charging for the analysis results on a per-gel basis. They offer two workflows and a free tool for assessing analysis performance, including that of other 2-DE packages. Gel IQ (http://www.ludesi.com/free-tools/geliq/) provides a framework for rating spot detection and matching performance by selecting a random sample of spot segmentations and matches for the user to rate visually for correctness. From this a single ‘Combined Correctness’ is derived as the spot correctness multiplied by the pair-wise match correctness.

In the first analysis workflow, REDFIN Solo, the user drives a consensus-based spot-detection based approach using the software in standalone mode. Initial warping proceeds by defining a reference gel and a region of interest for all the other gels to be aligned to. Inaccuracies at this stage can be fixed by tweaking with some local landmarks or setting a handful of landmarks globally and rerunning the auto-warp function. The aligned images are then subjected to fusion, which outputs a composite image with infrequent expression up-weighted. A spots step then detects a user-selected number of spots on the composite image and a borders step adds spot outlines of a user-selectable size. Once the user has visually verified these stages and is content, payment is made and the results of differential expression analysis become available.

In the second workflow, centralised analysis is performed by uploading gels and downloading results from the Ludesi Analysis Center. This workflow uses a more conventional spot detection and matching approach but, unlike other approaches that require selection of a reference gel, all gels are pair-wise matched to each other. Moreover, use of specialised in-house group-centric software and standardised working procedures help to normalise away subjective inter-user variability typically associated with standalone analyses. To attain the best results, the aforementioned Combined Correctness metric is repeatedly applied and optimised. Two service offerings are available, which depend on the level of manual expert examination desired.

Algorithm pipeline

The algorithmic details of most commercial packages are necessarily closed-source. For a conventional image analysis workflow we are able to piece together a representative pipeline from a number of academic publications of the last 20 years, though this necessarily excludes a number of modern commercial algorithms for which no details have been published.

The first step is to pre-process the gels to remove systematic artifacts. In order to correct for inhomogeneous background, methods based on mathematical morphology or smooth polynomial surface fitting are often used. To suppress instrument noise from the scanning device, a number of filtering techniques are available [51]. The next step is to explicitly detect protein spots whilst remaining robust to lingering artifacts. This involves an initial segmentation with a watershed transform, where the spots are viewed as depressions in a landscape, which is slowly flooded. Where the flooded regions meet, watersheds are drawn. Parametric spot mixture modelling then separates co-migrating spots. This involves fitting a 2-D Gaussian to each watershed. More specialised parametric models have been proposed that model saturation [12] and learn from training data with statistical point distribution models [52]. If a single modelled spot does not explain the intensities in the watershed, a ‘greedy’ approach is often used which iteratively subtracts the fitted spot and fits a further spot to the residual [53]. In heavily saturated regions gradient information cannot be used and thus a linear programming solution with elliptical elements has been proposed [54].

Point pattern matching is employed to match spots between gels whilst coping with the range of nonlinear geometric distortion present. Due to errors in the spot detection phase as well as true differential expression, these methods also need be robust to significant numbers of outliers. A wide selection of point pattern matching methods have been developed, but only a few perform an explicit warp [55, 56], whilst the others implicitly cope with deformation by allowing the distance between neighbouring spots to lie within an error range. The fundamental issue with feature-based approaches is combinational explosion due to mapping each arc (drawn between two points) in the reference point pattern to every arc in the sample point pattern, in order to test all possible match orientations. Reduction of this complexity is typically performed by heuristically removing implausible arcs from the test set [54]. Subsequently, a matrix of spot quantifications for each spot across all gels is produced. This matrix can be interrogated with univariate statistical tests or multivariate data mining techniques to discern which protein spots are differentially expressed across treatment groups.

For further detail on the feature-based image analysis pipeline, please refer to the reviews in [4, 44].

2.2 Emerging techniques

The conventional analysis pipeline essentially consists of a series of deterministic data-reduction steps. Since uncertainty due to noise and artifacts confound the source images, errors are inevitable and are propagated (and therefore amplified) from one step to the next. Two strategies to mitigate this problem are:

• Avoid throwing away information by data transformation rather than data reduction. Typically this involves performing alignment and differential expression analysis directly in the image domain.

• Or at each step, output a distribution of probable results reflecting the uncertainty associated with the processing. This would involve statistical derivation of the posterior distribution associated with the data reduction model, which at present is typically estimated with computationally expensive sampling methods. Because of the computation demands, these Bayesian methods have emerged primarily for one-dimensional processing of MS data, and shall be discussed further in Section 3.2.

Wavelet-based analysis

In proteomics, the pre-processing step most associated with the data transformation strategy is ‘wavelet denoising’. The DWT decomposes a 1-D signal into two signals half the length, one containing fine details (high frequencies) and the other underlying structure (low frequencies), with the nature of the extracted fine details being determined by the design of the wavelet. The low frequency signal is recursively decomposed to generate a set of signals of increasing scale, each representing the contribution of that scale of detail (frequency) to the original signal. Unlike the Fourier transform, however, the spatial location of each contribution is preserved. As shown in Figure 2, for 2D images a separable extension to the algorithm decomposes an image into four images at each scale, containing horizontal details, vertical details, (mixed) diagonal details and underlying structure.

Figure 2.

A single iteration of a decimated 2-D wavelet transform with a 6-tap Daubechies wavelet on a 2-D gel region. The image is decomposed into low frequency structure (top-left), horizontal high frequency details (top-right), vertical details (bottom-left), and details from both diagonals (bottom-right). For the detail components, black represents negative values and white positive values. The diagonal detail component is scaled up by 100, which illustrates the wavelet transform’s relative insensitivity to these orientations.

The assumption behind wavelet denoising is that protein signal is structured and therefore can be parsimoniously approximated by a small number of contributions at each scale, whereas the noise is white and therefore spread evenly over all scales. To this end, while conventional noise reduction tends to blur the true signal, wavelet de-noising adaptively sets to zero only those areas of the wavelet decomposition that do not have a strong contribution to the overall signal. The choice of threshold is vital to balance sensitivity against specificity. Originally, the best approach used in proteomics [51, 57] was found to be the ‘BayesThresh’ procedure, which is based on the ratio between the estimated noise variance and variance of the wavelet signal set. A later paper [58] advocated use of the UDWT (where the signals are not halved in length during decomposition) because sub-sampling in the standard DWT could cause significantly different decompositions dependent on just a small translation in the input image. The UDWT provides more reliable and accurate denoising but at the expense of greater computational cost.

As illustrated in Figure 2, a general criticism of the 2-D wavelet transform is the bias towards horizontal and vertical details, with a lack of separation of diagonal features. This results in artifacts, which can be overcome by using alternative transforms such as ‘contourlets’, which specifically capture details at many different orientations [59].

Note that variance stabilisation is typically performed on quantified spot volumes [50, 60, 61], but the spot modelling and image alignment algorithms described herein invariably test closeness of fit assuming white Gaussian noise. Therefore, techniques that do not explicitly consider a mean-variance dependence would benefit from pre-transformation of pixel values. Another general method of noise reduction is to borrow strength across a set of biological replicates. By the central limit theorem, averaging n gels (pixel by pixel) will result in a mean (‘master’) gel with noise reduced by a factor of √n. Whilst other image fusion methods have been proposed that maximise the number of spots in the master gel [62, 63], statistically weak spots are artificially amplified so there is a risk of an increased false positives rate. Morris et al. [58] show that simple background correction and peak detection after wavelet denoising on the mean gel gives results with greater validity and more reliable quantifications than commercial packages, including Progenesis SameSpots [64]. In order to compute the mean gel, the set of gels must be pre-aligned in the image domain, either by SameS-pots or a more automatic method. As shall be explained, however, automatic gel alignment is not trivial.

Image-based alignment

As well as underpinning consensus spot detection, a further benefit of aligning images rather than matching spots lies in the multitude of other reproducible features that can guide the alignment, such as background, smears and streaks. The method is termed ‘image registration’ in the medical imaging field, and over a last few years a number of automatic techniques have appeared for 2-DE that fit into a classical image registration framework [60]:

• A ‘transformation’ (warping) is defined which maps each point in a ‘reference’ image to a point in a ‘sample’ image. The transformation usually only has a few degrees of freedom (parameters) which restricts the range of admissible mappings to adhere to some favourable properties (e.g. continuity).

• Since the transformation does not generally map a pixel in the reference image directly onto a pixel in the sample image, a ‘resampler’ must be defined to estimate the intensity of that point in the sample image.

• A ‘similarity measure’ quantifies the match between the reference image and the transformed, resampled sample image. The similarity measure typically only compares the intensities of corresponding pixels between images.

• A ‘reguliser’ adds a penalty term to the similarity measure to penalise unrealistic transformations e.g. based on the smoothness of the transform. Well-behaved transformations require less regulisation, whereas the presence of noise and artifacts necessitates using more.

• Manually defined landmark spots can be incorporated through another penalty term, which decreases as corresponding landmarks become nearer each other.

• An ‘optimiser’ is used to find the set of transformation parameters which maximises the similarity measure. Typically a ‘root finding’ technique is employed, which, from an initial starting point, iteratively re-estimates the transformation parameters and moves to that point if the similarity is increased.

• The optimiser is only guaranteed to find a maximum near the starting estimate, which may not be the global maximum since all protein spots are homogeneous and therefore will match reasonably well with each other. To remove local maxima in the similarity function, a ‘multi-resolution approach’ is often taken, which finds an approximate alignment on coarse images first, and iteratively improves the estimate on more and more detailed images.

• Overly flexible transformations can become unrealistic, and therefore can also cause local maxima. By using a ‘hierarchical model’, a basic transformation with a limited number of parameters is initially used. The number of parameters and therefore the flexibility is then iteratively increased.

• A ‘coupling’ strategy is devised, which defines which detail level in the multi-resolution approach is paired with which level in the transformation hierarchy.

Veeser et al. [65] presented the first fully image-based registration technique for 2-DE in 2001, called MIR. They employ a multi-resolution pyramid, where the images are doubled in size at each iteration, and a hierarchy of piecewise bilinear mappings, each generated by sub-division of the last. Cross-correlation is used as the similarity measure, which is invariant to a global linear change in intensity between images, and a quasi-Newtonian optimiser provides fast convergence based on derivation of the partial derivatives of the similarity measure with respect to the transformation parameters. In a comparison between MIR and the now discontinued Z3 package [66], MIR scored better 29 out of 30 times under expert quantification of spot mismatches. Subsequently, Gustaffson et al. [17] presented a similar approach but added a preceding step to parametrically de-warp the characteristic ‘frown’ exhibited when a gel exhibits current leakage problems, and provided a favourable comparison with PDQuest (Bio-Rad).

Despite the good performance, it was noted MIR suffered some robustness issues in areas with local spatial bias and regarding the irregularity of the transformation. To solve this, Sorzano et al. [67, 62] replaced the transformation with a more realistically smooth hierarchical piecewise cubic B-spline model, adding regularisation to constrain local expansion and rotation of the warp. For difficult gels, they also added the option of specifying landmarks to aid the registration. The RAIN algorithm of Dowsey et al. [68] further improved alignment robustness and accuracy by compensating for spatial inhomogeneities between gels, as shown in Figure 3. During concurrent registration with a hierarchical piecewise cubic B-spline transformation (Figure 3c), a similar cubic B-spline surface was fitted to the multiplicative change in intensity between the images (representing regional differences in stain/label exposure) and a residual surface was fitted to additive changes to compensate for artifacts present solely on one image. Other novel features of RAIN include: Weighting pixel intensity by the Jacobian (determinant of the first derivatives of the warp with respect to x and y axes) to ensure protein volume in warped spots remains constant; Variance stabilisation of the image intensities prior to registration; And a parallel implementation on a consumer graphics processing unit [69]. As illustrated for large sets of gels from the HUPO Brain Proteome Project, RAIN provides significant improvement in accuracy and robustness compared to MIR [70].

Figure 3.

The first four scales of multi-resolution image-based 2-D gel alignment, as illustrated with the RAIN algorithm [68, 70]. (a) Two overlaid gels, one in magenta, one in green, showing the range of geometric deformations and intensity inhomogeneities between them. (b) The top row shows the multi-resolution pyramid for the two gels, with variance-stabilised pixel intensities. The middle and bottom rows show respectively the regionally varying multiplicative and addition spatial bias between the two gels, as modelled with hierarchical piecewise cubic B-splines. (c) The first four scales of alignment with RAIN (there are 7 in total). At each scale, finer and finer deformations are accounted for with a hierarchical piecewise cubic B-spline transformation. Elements reproduced from [68] with author permission under the Creative Commons Attribution-Non-Commercial license.

A number of other techniques have also appeared around this time, which have interesting aspects although do not provide comparative validation with existing techniques:

Some authors have introduced techniques based on implicit transformations [71–74], where each pixel has its own displacement vector and realistic mappings are based solely on constraints or regularisation. Worz and Rohr [71] introduced a physics model based on the Navier equation to regularise the elastic energy so that a stretch along one axis will cause an equal compression along the other. Landmarks are also incorporated and their alignment is also subject to elastic forces through analytical solutions of the Navier equation. Rogers et al. [55] propose a spot-matching approach but based on a multi-resolution framework with an implicitly smooth transformation and geometric hashing utilising pixel intensities. Their method is designed to robustly handle false positive spots detected by basic peak finding, and therefore is suitable for alignment before more advanced consensus spot modelling. Woodward et al. [73] demonstrated the applicability of an alternative multi-resolution approach using the complex wavelet transform. This transform additionally separates each scale into intensity and sub-location (‘phase’) components, and, similar to contourlets, decompositions are provided along six different orientations. For each scale, intensity-invariant displacement vectors can be calculated based on the phase difference at each orientation between corresponding pixels in the two images. For 2-DE, these displacement vectors must be denoised and regularised to portray realistic deformation between the gels, with a small number of iterations required to generate close alignments.

All the techniques described above use a fixed coupling between the image and transformation scales - at each stage the image detail and transformation flexibility is increased by a factor of two. Wensch et al. [75] propose holding back the change in either the image or transformation scale at each stage and assess the change in registration accuracy on many permutations of these decision chains on a set of training gels. Further registrations can then utilise the learnt coupling strategy.

Image-based differential analysis

The fundamental advantage of image-based differential analysis is that no spot model is required, since we seek only systematic differences in pixel intensities between sets of images. With a spot-based approach, parametric models must be assigned even in complex merged areas where there may be little evidence for specifying a concrete or even probable number of constituents [54]. Moreover, if a greedy method were used which fitted a single spot to the complex region [52], a change in a co-migrated spot would only be detected if it were significant compared to the total spot volume of the complex region as a whole. With the image-based approach, differential expression can be found even if the spot in question has no characteristic peak or boundary. In this setting univariate testing of pixel intensities is sub-optimal since the strong co-dependencies between pixels from the same spot would be ignored.

Daszykowski et al. [57] and Færgestad et al. [76] introduced the use of supervised PLSR methods on 2-DE pixel data. PLSR aims to identify the underlying factor or factors (linear combinations of pixels) that have the maximum covariance with one or a linear combination of dependent variables. In these proteomic studies, a single dependent variable either models the treatment group e.g. −1 for control, +1 for sample [57], or the time-point in a time course experiment [76]. Cross-validation ensures that the model is fitted to the data rather than noise by computing permutations of the PLSR with each image left out and then gauging how close the computed factors can predict the missing image. For each pixel, a statistical test is then performed on its regression coefficient to assess its significance to the model [76]. Since PLSR is a linear method, the images must be background subtracted to remove a significant source of non-linearity, and non-spot pixels also removed to improve the power [57, 77].

Subsequently, Safavi et al. [78] applied ICA to pixel data, in which the observed images are modelled as an unknown set of non-orthogonal factors and where each image has an unknown linear mixture of these factors. ICA methods are a specialised form of unsupervised ‘blind source separation’ where the factors are separated based solely on their statistical independence. In an experiment with two random effects (male/female and treatment/control), Safavi et al. show that the univariate ANOVA technique with FDR correction is very sensitive to the FDR derived p-value, whereas ICA is able to identify and separate differential expression into the correct factors without any p-value threshold. Furthermore, analysis in the wavelet domain with de-noised data gives robustness to slight image misalignments. However, they also note that the main limitation of the employed ICA methods is the need to pre-specify the number of factors: Too few factors cause overfitting, whilst too many lead to effects being split between multiple factors. Furthermore, posterior distributions and therefore confidence levels for each pixel are not offered, though ICA methods with this ability are emerging [79].

ICA represents a powerful unsupervised technique, and has also been applied to MS data [80]. In [81] and Section 3.2, similarly powerful supervised techniques are discussed further in relation to MS biomarker discovery.

Alignment-based differential analysis

With experiments now involving multiple replicates per treatment group, is may be possible to detect local regions in the alignment transfomation, or their proxies the spot locations, that systematically differ between treatment groups due to post-translational modifications or other systematic changes in pI or M_r. This task, called ‘morphometry’, is greatly confounded by the range and scales of uninteresting deformation inherent inside each treatment group, causing significant covariances that again must be handled by multivariate techniques. Rodríguez-Piñeiro et al. [82] have demonstrated a proof-of-concept approach using Relative Warps Analysis, a geometric mophometrics technique that fits TPS transformations to a set of landmarks. A TPS provides a closed form solution of the smoothest warp that perfectly matches a set of landmarks. By adding a smoothing regularisation to this formulation, a range of maximum permissible deformations can be simulated. In [82], PCA is performed on the landmark displacements derived from the set of these TPS warps, and the derived factors tested to find significant differences between treatment groups.

The similar approach of ‘deformation-based morphometry’, based on direct analysis of the transformation parameters rather than the landmark positions, has widespread use in neuroimaging. In this field, brain images are non-linearly registered to each other using methods similar to alignment in 2-DE. Subsequently, the transformation parameters are analysed to track tumour growth or assess population variance of the cortical folds [83].

3 Signal analysis in MS

Since LC/MS is fundamentally a collection of mass spectra, we review recent progress in analysis of protein or peptide MS data as well as describing how these have influenced or could influence the analysis of LC/MS datasets.

MS is fundamentally automated, so the raw data can be directly interfaced into the signal analysis pipeline without any user interaction. Likewise, data format issues between MS instruments and processing pipelines are exposed and discussed elsewhere [84] so that further explanations are not warranted. Suffice to say, efforts invested in standardisation positively influence software development since most tools accept standard formats like mzML [85].

Opinion is divided as to the complexity of a priori modelling suitable for peak detection in MS. On the one hand, generalised assumptions about the true signal give reasonable confidence that those assumptions will not be violated. On the other hand, more specialised prior models may lead to greater sensitivity but also to erroneous results for datasets where the models fail to hold. The starting point is typically removal of the chemical noise baseline [86]. Then, with high-resolution MS, simplified peak detection has typically been followed by complex peak-based deisotoping routines [87] and charge envelopes for each peptide, whereas in low-resolution MS only the charge envelope is established. A number of heuristic methods have been developed to pattern match with the averagine distribution. A typical greedy approach [88] is to iteratively examine the most intense peak in the dataset, determine the charge state from the frequency of neighbouring peaks, and then fit the averagine distribution with the identified charge state to it.

For further information on conventional MS informatics, please see [89, 90] for an overview. For a comprehensive review of conventional baseline subtraction, peak detection and peak-based deisotoping/decharging methods, see Hilario et al. [81].

3.1 Emerging techniques

The rising popularity of SELDI has pushed forward the need for statistical peak modelling to extract maximal information from low-resolution spectrometers with increased noise and overlapping peaks [91]. Compared with 2-DE, the reduced size and complexity of MS datasets has enabled researchers to increase model complexity, including the statistical handling of uncertainty and the indication of ambiguity in the final result through an error (‘posterior’) distribution.

Wavelet-based peak detection

The most generalised approach to peak modelling is based on wavelet denoising. This methd was introduced for peak detection by denoising followed by identification of local maxima with SNR above a pre-described threshold [92–94]. Morris et al. [32] then applied the technique on the point-wise averaged ‘mean spectrum’ from a set of replicate spectra to increase the sensitivity further. Chen et al. [95] alternatively fuse the spectra by detecting peaks on each spectrum separately but combine the results with KDE: For each detected peak, a normal distribution with mean equal to that peak’s m/z is added to a synthetic spectrum, with the local maxima becoming the consensus peak list. A denoising threshold can also be found automatically from this synthetic spectrum in an ad-hoc manner through iterative refinement: The volume of the baseline, which represents noise-influenced peak detections, is balanced with the volume of the consensus peaks. Whilst the denoising threshold used in these papers was estimated over the full spectrum, Kwon et al. [96] have suggested approximating the dependence of noise variance on m/z by a collection of segments of constant variance, trading off the number of segments with the accuracy of variance estimation within each segment.

Wavelet methods can also be used to detect peaks directly. At each scale the underlying trends from larger scales are no longer present, so no prior denoising or baseline subtraction is required. Moreover, shoulder peaks engulfed in larger peaks can be detected even if they do not have a local minimum. Randolph and Yasui [97, 98] performed the UDWT on a set of spectra and obtain consensus peaks by detecting local maxima on the sum of responses over the set at each scale. On these results, McLerran et al. [99] used robust regression to determine the periodic peak pattern that represents chemical noise.

If one is willing to make assumptions about peak shape then a wavelet can be designed to respond to peak-specific patterns in the signal. In these methods the CWT is used, in which the decomposition is neither decimated nor restricted to scales of a power of 2. Lange et al. [100] proposed use of the ‘Mexican hat’ wavelet, which for each particular scale is sensitive to Gaussian peaks of a particular width. By splitting the mass spectrum up into small regions and finding the location and scale of the maximum wavelet response within each section, they obtain the amplitude and width of each detected peak. Conversely, Du et al. [101] performed the CWT on the whole mass spectrum at a large number of scales and place the output into a response matrix, with m/z and scale on the horizontal and vertical axes respectively. Peaks form ‘ridges’ in the response matrix, which are local maxima visible at a number of consecutive scales, starting from the finest, that can be connected together to form a curve. The largest response is present at the scale which best matches the width of the peak, and the ridge tends to end soon after. In this method, ridges are deemed peaks if they are of sufficient length and their derived width and SNR are reasonable.

Zhang et al. [102, 103] note that, at large scales, long ridges can represent peak mixtures, whilst at smaller scales multiple ridges represent components of those mixtures. They decompose the response matrix into a collection of ‘ridge trees’, recursively splitting the longest ridges and connecting them to the ends of the shorter ridges if they are both bounded on the same side by a shared local minimum. Each tree root represents a single detected peak or peak mixture, and if the tree contains branches, each further level of the tree represents a set of candidate peaks for that mixture with increasing cardinality. Each ridge segment is then reduced into statistics describing peak position, width, SNR and the probability it is a true peak given Gaussian noise, based on the distribution of responses in the segment but correcting for the influence of sibling peaks. Determination of the most likely candidate set for each tree is based on agreement over the set of mass spectra through a trade-off between peak probability and either consensus peak width for each m/z [102] or consensus peak pattern where peaks are matched between spectra through KDE [103]. The algorithm iteratively refines the peak detection result and consensus agreement until neither is improved. Comparative evaluation in [103] showed significantly improved sensitivity and FDR compared to the UDWT denoising approach [93] and the method of Du et al. [101].

Hussong et al. [104] have presented an interesting application of the CWT for signal-based deisotoping and decharging in high-resolution MS. They designed a family of isotope wavelets parameterised by mass and charge that are sensitive to the averagine isotope pattern. In this method the CWT is applied only at scales relating to each possible charge state. The wavelet responds to each peak in the isotope envelope resulting in a characteristic pattern of local maxima and minima in the output centred on the monoisotopic peak. The patterns are coalesced to determine a score value for each m/z from which local maxima are extracted. If the same maximum occurs at multiple scales, the charge state with greatest score is chosen.

Another attractive application of wavelet analysis is for improved generation of the mass spectra themselves. SELDI/MALDI spectra are composed of multiple sub-spectra generated from single shots of the desorbing/ionizing laser fired at different locations in the sample. Skold et al. [105] recognised that simple averaging of the sub-spectra is suboptimal due to their disparate nature, and provide a heteroscedastic linear regression to pool the spectra and calculate the pooled variance. Meuleman et al. [106] used the CWT peak detector on each sub-spectrum and aggregate the results, annotating each peak with the confidence level of its detection over the sub-spectra.

Bayesian peak modelling

Parametric peak modelling represents a method with more specialised assumptions. In this area, Gaussian fitting has been a popular method for some time [107]. For example, to reduce bias in TOF peak measurements in ESI and MALDI respectively, Strittmatter et al. [108] and Kempka et al. [109] fitted a mixture of two Gaussians to each peak, where the second was smaller and offset to simulate the skewed falling edge.

Peak modelling provides accurate quantification of overlapping peaks whereas methods based solely on peak height over-estimate the true relative protein abundance [110]. In complex regions, the proportion of signal at each m/z value assigned to each peak can be found with ‘finite mixture modelling’ of parametric peak models. Lange et al. [100] fitted a mixture of asymmetric Lorentz distributions to the output of their wavelet peak detector using a standard non-linear optimiser. Dijkstra et al. [110] employed the EM algorithm, which is perhaps the most widely used in the literature for statistically sound finite mixture modelling. They separate a mixture of SELDI peaks with ‘log-normal’ distribution (Gaussian with logarithmic skew), a baseline composed of uniform and exponentially decreasing distributions, and Gaussian noise. The EM iterates between two steps: The expectation step, where the expected proportions of the mixture elements (‘latent variables’) are calculated, given the current peak/baseline parameter estimates; And the maximisation step, where the peak/baseline parameters are updated to maximise the model likelihood (fit) to the signal, given the mixture proportions. Peak locations are initialised by a standard peak detection method, and a single peak width and skew that increases as m/z increases is estimated for the whole dataset. Initial peaks that do not converge to a realistic shape are automatically down-weighted as artifacts.

Whilst EM is a statistical technique that considers uncertainty through an explicit noise model and a distribution of values for the latent variables, it only outputs point estimates of the most likely peak parameters. In order to gauge ambiguity and uncertainly in the derived peak parameters, the posterior distribution must be calculated. However, calculation of the posterior probability requires normalisation by the sum of every possible outcome, which is a large multidimensional integration with an intractable analytical solution. It can, however, be approximated through MC random sampling, but in this case independent sampling from such a complex distribution is also difficult. The MCMC methods alleviate this problem by modelling the posterior distribution as the limiting equilibrium distribution of a MC, which is a stochastic graph of states augmented with transition probabilities that depend only on the state transitioning from. In the most basic form of MCMC, each state represents a parameter which is updated in turn through random sampling from a much simpler conditional distribution of itself given all other parameters remain fixed. The parameters may go through a large number of updates before the MCMC model reflects the posterior distribution (‘burn-in’), followed by even more to reliably estimate the distribution itself.

Despite the heavy computation, a handful of MCMC methods have recently appeared for finite mixture modelling of SELDI MS data. For instance, Handley et al. [111, 112] use the twin-Gaussian peak model and generate the joint posterior distribution for Gaussian noise variance, peak locations, peak heights and a single peak width that increases proportionally with m/z. A Strauss process prior on the peak locations penalises peaks that begin to close in onto the same location. The method takes 563.5 minutes to quantify consensus peaks in 144 mass spectra, though cluster computing can be used to significantly reduce this time.

To seed these approaches, peak locations must be initialised by a preceding peak detection stage. To separate an unknown number of merged peaks, methods similar to 2-DE spot splitting have been employed. For example, a greedy method iteratively fits and subtracts the most intense peak [113]. However, this approach is inaccurate since it will always start by fitting the largest possible peak to the mixture even if a mixture of smaller peaks would be more likely. To exploit the ability of true mixture modelling to separate an unknown number of coalesced peaks with no clear maxima, the MCMC approach has been extended with reversible jumps [114, 115]. In RJ-MCMC, extra states are added to the MC so that peaks can be randomly created, destroyed, merged or split during each iteration. Since the posterior distribution is therefore estimated for each number of peaks modelled, the algorithm can determine the number of peaks that give the optimal configuration.

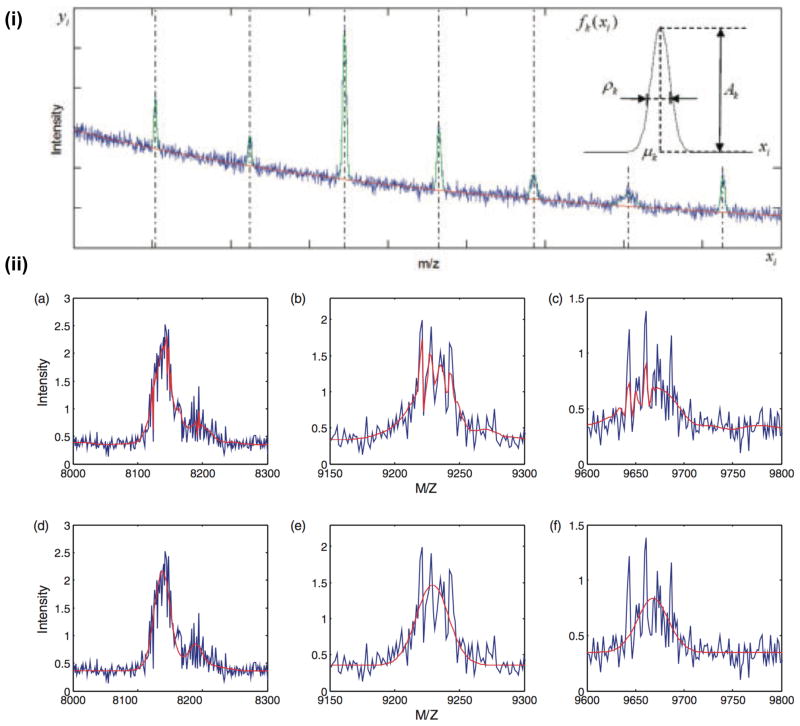
As shown in Figure 4, Wang et al. [114] use a Gaussian peak model and polynomial baseline to model SELDI MS data. For computational practicality and to support a heteroscedastic noise variance with respect to m/z, they split the mass spectrum into regions and process each independently. They compared their technique against a wavelet denoising approach [93], showing a significant increase in sensitivity coupled with a massive reduction in the FDR. Guindani et al. [116] described a technique for two sets of MALDI spectra in which they employ mixtures of Beta distributions for both the peak model and the baseline (with a large standard deviation specified a priori). Peak position and width is allowed to deviate between spectra, but each spectrum shares the same number of peaks and in each set relative protein abundance is assumed to stay constant. Clyde et al. [115] provided further specialised modelling, representing peaks as Lorentz distributions and the baseline as a combination of constant and exponentially decreasing components. They pay particular attention to the noise assumption, employing a Gamma noise distribution for non-negativity and linear mean-variance dependence. Moreover, unknown parameters are assigned specific prior models, including the noise variance, proportion of mean-variance, rate of fall of the baseline, and peak detection limit. Prior distributions for the number of peaks (negative binomial), peak abundances (truncated Gamma) and peak resolution (hierarchical log-normal distribution to allow for moderate variation over the spectrum) are jointly modelled as a Lévy random field, which guarantees non-negative peaks and allows for efficient RJ-MCMC sampling. After an EM phase estimates a set of initial peak locations, they describe the requirement for 2 million iterations of RJ-MCMC burn-in, followed by 1,000 more to sample the posterior distribution.

Figure 4.

The RJ-MCMC mixture modelling approach of Wang et al. [114] for SELDI MS (i) Example instance of the generative model. The red curve indicates the baseline and green curves indicate peak functions. The mixture with added noise is shown in blue. (ii) (a–c) Regions of a spectrum (in blue) denoised with the UDWT (in red). Simple peak detection on the output will lead to false positives. (d–e) Result of the RJ-MCMC mixture modelling (in red) on the same data. Reproduced from [114] with author permission under the Creative Commons Attribution-Non-Commercial license.

Signal-based differential analysis

There have been a number of recent reviews on classification and related dimensionality reduction [117] and feature selection [118] techniques, which have become a significant growth area in proteomics research [119]. This has been driven by the goal of automated clinical detection of early disease processes [120, 121] through patterns of protein biomarkers [122] and their relationship with other ‘omics data [123]. Comprehensive coverage and critique of data mining methods applied to MS data is presented in Hilario et al. [81]. Given a set of two or more treatment groups, the multivariate methods presented learn to classify each sample into the correct group based on correlated features in its mass spectrum. The authors particularly emphasis strategies that ensure the resultant discriminatory pattern is both generalisable (does not overfit the data by finding discriminants purely in noise) and stable (reproducible given unavoidable variation in data collection over time).

Unless it is possible for proteomics experiment design to be simplified and self-contained, there will typically be a number of confounding systematic biases (‘fixed effects’) such as the blocking of runs over different days, and the mixing of sources of statistical variation (‘random effects’) such as combining technical and biological replicates. Since most data mining techniques make more simplified assumptions about variation in the data, it is vital to first correct for these factors in order to realise the maximum potential of data mining. Furthermore, if a suitable algorithm could analyse the interrelationships, then mixed effects could be intentionally studied, e.g. consideration of samples from multiple physiological sites and strata of the population.

Techniques that consider linear fixed and random effects are termed ‘linear mixed models’. Two-stage hierarchical linear mixed models have been applied to 2-D DIGE spot lists for normalisation of protein-specific dye effects [124, 125]. For SELDI MS, Handley [112] combined parametric mixture modelling with a two-level linear mixed model. The twin-Gaussian peak model was employed and the intensity of each pre-detected peak was given separate fixed effects for each treatment group and separate random effects for each spectrum. The random effects were modelled as multivariate Gaussians, thus allowing heteroscedasticity, and peak locations were refined during the algorithm. Though the optimal peak width parameter is found through MCMC, only point estimates for the fixed effects and random effects covariance matrix were generated. The result is a mean intensity for each peak in each treatment group with spectrum-dependent random effects compensated for.

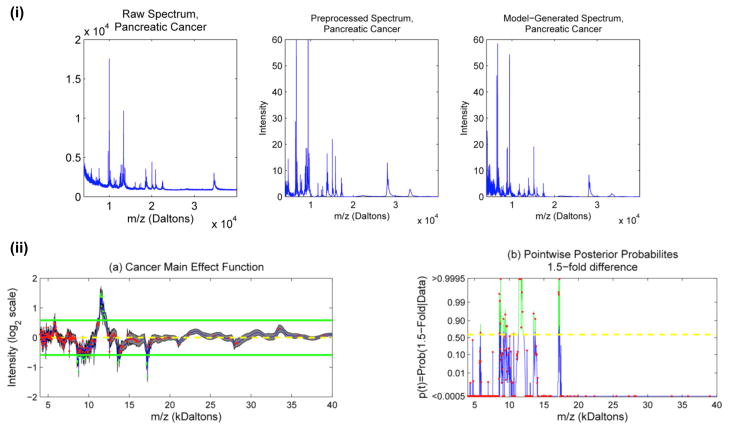
As has been noted in Section 2.2, subtle differential expression may be missed due to the problem of modelling multiple merged peaks. Morris et al. [126, 127] advocate the general assumptions of wavelet modelling by treating each mass spectrum as a function, and through MCMC are able to generate full posterior distributions of differential expression accounting for general user-defined design matrices of nonpara-metric fixed and random effects on a per-experiment basis, such as the systematic technical and biological factors cited above. Their WFMM approach requires prior calibration, normalisation, denoising and baseline subtraction to remove excess variation from these non-linear effects, and the spectra log-transformed to stabilise variance. The set of mass spectra are then modelled in the DWT domain as the sum of a set of unknown functions factored by the fixed effect design matrix, and two sets of independent Gaussian random processes with unknown covariance matrices, one factored by the random effects design matrix and the other modelling residual error in each spectrum. These random process priors on DWT data allow heteroscedasticity both spatially and at different scales, whilst the fixed effects use an adaptive sparsity promoting prior to promote sharp peak-like signals, illustrated in Figure 5i. The result is a posterior distribution of functions for each factor, as shown in Figure 5ii. Given a desired false discovery rate and minimum effect size (e.g. 1.5-fold), the method then flags sets of m/z in the spectra for differential expression based on each factor, while compensating for the other factors. The authors also note that, if an extra factor is added to the model giving equal weighting to each spectrum, the resulting function is a mixed effect-compensated mean spectrum that can be used for improved consensus peak detection. Algorithm performance has been optimised in [128] so that a 256-spectrum analysis with 5 fixed effects takes a total of 3 hours and 8 minutes of processing time on a single processor, with shorter times possible if parallel computing is used.

Figure 5.

The fixed and random effect WFMM approach of Morris et al. [127] on MALDI TOF data. Blood serum of 139 pancreatic cancer patients and 117 healthy controls were collected, fractionated and processed with a WFMM. The spectra were collected in 4 blocks spread over several months, so a fixed effect was modelled for each of the 4 blocks as well as the cancer/control main effect. (i) A raw spectrum from a pancreatic cancer patient (left) and its corresponding denoised, baseline corrected and normalised version (middle). After processing with the WFMM, a randomly drawn spectrum from the posterior predictive distribution is shown (right), illustrating that the algorithm is capable of modelling the peaky data. (ii) (a) Posterior mean and 95% point-wise posterior credible bands for cancer main effect. The horizontal lines indicate 1.5-fold differences, and dots indicate peaks detected with the mean spectrum [32]. (b) Pointwise posterior probabilities of 1.5-fold differences. The dots indicate detected peaks, and the dotted lines indicate the threshold for flagging a location as significant, controlling the expected Bayesian FDR to be less than 0.1. Reproduced from [127] with author and publisher (Wiley-Blackwell) permission.

4 Image analysis in LC/MS

Two recent reviews detail the range of tools and explain issues associated with LC/MS imaging [37, 129]. The software lists provided in these reviews are still up-to-date and are not repeated here. However, the bulky size of the raw data (several hundred gigabytes for a few dozen LC/MS runs) remains a motivation for reflecting on a new compaction format. To this end, by exploiting the redundancies in LC/MS data, Miguel et al. [130] have attained a lossless compression ratio of 25:1 and 75:1 for near-lossless (where each measurement lies within an error bound). For comparison, 2-D gel images are less redundant, with lossless compression limited to 4:1 and near-lossless to 9:1 [131].

4.1 Image analysis workflow

Due to the high-throughput nature of LC/MS, a proportion of the recent flood of academic LC/MS packages are batch-processing pipelines without any interactive user interface. Most 2-DE software is implemented to reduce user editing but complete automation always comes at a cost. LC/MS image editing is of course rather painful and somehow impracticable, but a timely solicitation of a user for checking weak but potentially interesting signals or for validating borderline cases or outliers remains a relevant feature for guaranteeing quality analysis.

Two of the tools described in Section 2.1 on 2-DE workflow have sister packages tailored to LC/MS analysis: Decyder MS (GE Healthcare) and Progenesis LC-MS (Nonlinear Dynamics). Moreover, a number of other packages are available for performing these functions, a selection of which was compared from a users perspective in [132]. Regarding performance, six popular peak detection [40] and six feature-based alignment algorithms [133] have recently been assessed by OpenMS initiative participants. The peak detection test used synthetic data generated from their LC/MS simulation engine [40], whereas real data with ground-truth warps from MS/MS identifications were used to for the alignment tests.

Below we describe the workflows of MSight, SuperHIRN and Progenesis LC/MS and discuss the typical algorithm pipeline.

MSight

MSight runs under Windows and targets users with little background in computer science. Other popular software as listed in [37, 129] is more suited to high-throughput environments.

MSight is designed to perform several functions starting with data display. For example, a single spectrum can be displayed in a 1-D view along with a flat 2-D view or a 3-D landscape view (Figure 6a). Data can be shown at various resolutions without information loss, since for each desired zoom factor, the image is recalculated on the fly for an optimal display of the data given the available window size.

Figure 6.

The MSight workflow. (a) The 3-D view highlights aid quality control of the input data and results. The alignment procedure is based on the use of landmarks to compensate for differences in elution time or migration distance. Small letters a to e are potential landmarks. (b) Thus, the peak detection algorithm looks for areas of high intensity peaks to delineate their shapes. The deisotoping step then looks for the monoisotopic peaks of the same molecule, links them together (dashed lines connect isotopes) and determines ion charge states.

Data from various experiments or experimental conditions can be compared simultaneously in various ‘manual’ modes (side-by-side, one over the others, with transparency) while an alignment procedure based on the use of landmarks to compensate differences in elution time or migration distance performs automatic comparison. The user annotates landmarks at the level of individual pixels. The typical workflow to achieve comparison of MS runs is to create a match set, detect and deisotope the peaks, and then match the MS runs. As illustrated in Figure 6b, the peak detection algorithm looks for areas of high intensity peaks to delineate their shapes. The deisotoping step then looks for the monoisotopic peaks of the same molecule, links them together (dashed lines connect isotopes) and determines ion charge states. Finally, statistical analysis is undertaken to identify peptides with significant group variation.

SuperHirn

The typical computational tasks involved in LC/MS data analysis are also provided by SuperHirn [134], including detection of peptide features in the mass spectra and alignment of samples by correcting for shifts in retention time and normalisation of the data. SuperHirn contains some compulsory modules, which include these critical steps, and some other optional modules. The compulsory modules generate a file containing a normalised MasterMap, i.e. the MS feature profiles. A MasterMap can be subsequently exploited either by any quantitation tool that calculates the ratios of the matched peptides and defines those differentially expressed, or by launching more modules within SuperHirn to cluster profiles and determine trends in proteins. For example, [135] shows the use of MasterMaps for analysing changes in protein complexes and finding specific partners in interaction networks.

To cluster profiles, SuperHirn uses the k-means clustering method to group all constructed feature profiles. The starting k cluster centres are randomly chosen from the input feature profiles and the clustering cycle is repeated until all cluster centres reach convergence or a maximal number of iterations (e.g. 500) are achieved. Each finished cluster is stored and subsequently used for targeted profiling analysis. At the end of each step, SuperHirn produces a text file that can be easily read by end-users and scripting programs.

In [40], running times of SuperHirn are shown to be significantly shorter than most other software on a series of datasets.

Progenesis LC/MS (Nonlinear Dynamics)

The user interface look and feel, as well as several components of the workflow for Progenesis LC/MS, are essentially similar to that for Progenesis SameSpots described in Section 2.1 (in particular the statistics modules are the same – ANOVA, power calculation, q-value, PCA, hierarchical clustering). The workflow is divided via tabs at the top of interface into LC/MS data import, reference run selection, licensing, alignment, filtering, group setup, view results, Progenesis stats, peptide search, peptide filter, protein view, and report.

The import of raw data files into the program automatically initiates a peak modelling step using a wavelet-based approach. Each of the LC-MS runs is then aligned in the retention time dimension to a user selected run in a pair-wise fashion. The placement of alignment vectors is automated but the user can supplement this alignment by manually placing vectors based on the inspection of the overlaid images from the run being aligned and the reference run. A non-linear alignment is then calculated based on the automated and user-placed vectors. A common set of peptide features is determined with respect to isotopic distribution, charge state and elution profile, and abundances are calculated as the sum of the peak areas for each isotope in the envelope with an ensuing normalisation step. At this stage the MS/MS spectra from all of the runs included in the analysis can be exported in a single peak list file which is queried against an appropriate protein database with one of a number of compatible search tools (i.e. Mascot, Sequest, Phenyx, PLGS). The resulting peptide spectrum matches are imported into Progenesis where the peptide identities are mapped on to the peptide feature set. Finally, the peptide identities and abundance data are rolled up to the protein level and summary statistics are calculated.

Algorithm Pipeline

In the case of the conventional LC/MS image analysis pipeline, the large size of the raw data files imposes intermediary steps involving data reduction that are key to the quality of results. This aspect is detailed in [129]. Indeed, data can be processed raw or in a reduced form prior to alignment and this may lead to different outcomes. Filtering operations mainly exploit the time dimension at different stages of the work-flow in the various existing tools. In fact, the independence of the two dimensions allows a separate treatment of the two sets of values.

Peak and isotope distribution detection may involve an initial focus on m/z values. Then, findings are validated while taking advantage of the redundancy provided by RT measurements. For instance, this strategy is implemented in SuperHirn [134]. The sequential processing of raw data is a form of reduction. In contrast, some tools are designed to postpone reduction to a later stage, as is the case in MSight [136], where both dimensions are considered for peak detection. These packages borrow elements of the 2-DE workflow directly. For example, in MapQuant [137], baseline subtraction, noise suppression, watershed segmentation and parametric peak detection has been shown to provide 1000-fold linearity in quantification.

As in 2-DE, alignment techniques for LC/MS are split between peak pattern matching approaches and those that use the full signal. Unlike 2-DE, the signal-based approaches actually originated earlier, through the field of speech processing and then chromatography, and have only recently incorporated information from the MS dimension. Conversely, pattern matching approaches have naturally exploited the MS peak pattern, and are typically favoured in established packages. A representative approach would first find the closest match between the reference and sample point sets using a robust linear regression, before iteratively adding nonlinear flexibility to the LC warp [34, 133]. If a number of MS/MS readings are taken during LC/MS acquisition, confidently identified ions can be matched between runs and therefore used as landmarks for alignment [138, 139].

Despite the significant variability in RT between runs, the use of RT as a discriminant for protein identification was recognised early on. This was initially exploited in the AMT tag approach [140, 141], which reinforces identifications found from comprehensive LC/MS/MS if peptides are found in approximately the same location in subsequent LC/MS runs. In a similar fashion, data-dependent MS/MS identifications performed during a set of LC/MS runs can be propagated to every run in the set. In order to establish databases of representative RTs with minimal variance and bias in their measurement, consensus alignment techniques have been advocated. Conversely, in 2-DE the derivation of representative spot positions has so far received only minor interest [131, 63]. The typical approach is to perform alignment within the whole set of runs, and then compute average RTs for each peptide post-hoc. However, the number of spectrum pairs to align and the final merging of the individual spectra (as in MSight) as opposed to the progressive integration of data to construct a consensus alignment (as in SIEVE, Thermo Scientific) are two of the key choices that underlie the management of variability and computational complexity.

For further information, see [142] for an overview of the all the computational aspects, while a thorough review of LC/MS alignment with emphasis on feature-based-approach is provided by Vandenbogaert et al. in [34].

4.2 Emerging techniques

We can identify two core themes that are emerging in LC/MS informatics. Firstly, some emerging MS peak detection methods described in Section 3.1 have recently been extended to also explicitly model the peak surface in the LC dimension, thus providing for a more discriminatory segmentation. For example, during the greedy method of parametric peak modelling, Gröpl et al. [143] have iteratively fitted a Gaussian-smoothed isotope distribution to the MS dimension whilst simultaneously fitting an EMG to the LC dimension. Schulz-Trieglaff et al. [144] have also employed this technique, but instead apply it to the output response of the isotope wavelet of Hussong et al. [104]. More recently, the CWT method of Du et al. [101] has also been demonstrated as applicable to this task [145].

Feature-based groupwise alignment

The second theme is that of group-wise chromatogram alignment. The aforementioned 2-DE and LC/MS alignment techniques all operate on pairs, therefore requiring the user to specify a representative reference image to align the rest of the images to, or perform exhaustive pair-wise alignment followed by post-hoc computation of a consensus transformation. This post-hoc RT normalisation has a significant disadvantage compared to methods that simultaneously align sets of LC/MS maps in a ‘group-wise’ manner. Group-wise alignment can borrow strength across samples to determine outliers that would otherwise affect alignment accuracy (whether unexpected differential expression, localised artifacts or whole runs), whereas each alignment in a pairwise strategy has no way of identifying these outliers. Moreover, whilst quality assurance procedures could either discard poor runs before pair-wise alignment or poor alignments prior to RT normalisation, they cannot easily correct alignments with localised areas of distorted geometry due to missing peaks or artifacts. For these reasons, advancements in the medical imaging literature are now considering aligning full sets of images together simultaneously [146] as well as generation of a consensus frame of reference that averages out the deformations. While there has been limited research in group-wise alignment in 2-DE [147], there has been more development along these lines in LC/MS.

The feature-based approach to group-wise alignment typically follows a combined regression and clustering strategy, where each cluster ideally contains one peak from each peak list and each cluster centroid represents a matched peak with normalised m/z and RT. Conventional clustering approaches only consider random perturbations of the features, but peak RTs are systematically biased with high covariance. To mitigate this issue, Smith et al. [148] use KDE while representing peaks as Gaussians with large variance in the LC dimension to model RT uncertainty. Clusters are identified as each local maximum in every 0.25 m/z interval of this Gaussian mixture. Confident peak matches (those clusters with approximately one peak per sample) are then used to generate piece-wise polynomial alignments through robust LOWESS regression. The clustering is then repeated on the newly aligned datasets, and the process iterates until no new matches are found. More recently, Łuksza et al. [149] replaced the KDE approach with an EM Gaussian mixture model, seeded by hierarchical clustering. To reduce the computational burden, peaks are grouped spatially within each LC/MS run. The fit of each mixture component determines the clustering of the runs in each group.

Fischer et al. [150, 151] aligned data-driven LC/MS/MS by considering only the identified peptides as landmarks and therefore avoid the clustering step. Instead, they develop the regression step as a Canonical Correlation Analysis (CCA), which finds a linear projection (smooth piecewise warp) onto the consensus time axis such that the correlation between two landmark lists is maximised. They extend CCA by: Considering multiple landmark lists through maximisation of pair-wise correlations; Using regularisation to smooth the warp, which is adapted to each run through cross-validation; Constraining the warp to not change direction and to adapt to the local landmark proximity through the use of hyperbolic tangent splines. The consensus alignment is iteratively refined until convergence by updating each pair-wise alignment whilst keeping the other pair-wise alignments fixed.

Wang et al. [152] provided a combined alignment and consensus peak detection algorithm by determining the optimal peak set from a ‘peptide library’ built from either an AMT database or an initial comprehensive peak detection and deisotoping stage on all the runs [98]. Systematic RT misalignments are first corrected in a pair-wise manner by iteratively performing linear and smoothing-spline robust regression on peaks sharing similar m/z values. Each mass spectrum is then modelled as a mixture of peptide isotope envelopes from the library that lie within a suitable RT range, plus Gaussian noise. The authors hypothesise that finding the minimal set of peptides that fit this model for the whole set of LC/MS runs is equivalent to matching peaks, since unmatched peaks add to library size without significantly improving fit. Consequently, they iteratively reduce the size of the library by regressing all the peptide envelopes against all the spectra using a sparse regression technique that promotes grouping, followed by merging features that cluster in the resulting coefficients.

Signal-based group-wise alignment

Recently a group-wise signal-based algorithm called CPM was proposed by Listgarten et al. [153], in which a number of raw LC/MS datasets are aligned together into a consensus reference frame. To appreciate the methodology, it is necessary to briefly review the pair-wise signal-based LC alignment algorithms from which it is based [154].

Since 1-D alignment is an order of magnitude less complex than 2-D alignment, signal-based LC approaches have traditionally relied upon the brute-force consideration of a set of possible alignments. In DTW, a 2-D image is created with the x and y-axes representing position in the first and second chromatograms respectively, whilst at each pixel a similarity measure scores the similarity between the mass spectra in the two chromatograms at those positions. Different similarity measures have been proposed, originally simple intensity difference [155], then correlation coefficient [156–158], square of the normalized dot-product [159] and hybrid approaches that assess the closeness of the two peak sets [160]. The warp is established by finding the path between the bottom-left and top-right corners with the greatest sum of similarities, which can be performed efficiently using dynamic programming. Since paths can follow only orthogonal or diagonal directions, it is beneficial to smooth the warp post-hoc and penalise unrealistic paths [156, 159]. To reduce computation, two-stage multi-resolution approaches have been proposed [158, 159].

The related technique of COW employs an explicit piece-wise linear transform. The correlation between reference and warped sample chromatogram segments is precomputed for a plausible range of alignments, with an optimal path through the search space established through dynamic programming [161]. To incorporate an MS dimension, Christin et al. [162] determined up to 30 discriminating m/z values per segment to use in the correlation calculation. A hybrid COW approach has also appeared [163], which calculates the likelihood of observing similar m/z and RTs between peaks detected in the mass spectra of the reference and warped segments. This method can also be used to propagate LC/MS/MS identifications to LC/MS datasets in the AMT approach by normalising each identification by the probability of its occurrence.

In its current form, group-wise DTW/COW is intractable due to the exponential increase in the search space as more dimensions are added. The aforementioned CPM borrows some ideas from the DTW whilst providing tractable group-wise alignment in a fundamentally stochastic setting. In the CPM, an unknown ‘template’ is defined, representing the noise-free consensus chromatogram. Each observed chromatogram is modelled as a Markov chain, where each state represents a time-point in the template and state transitions allow a distribution of plausible RT deformations by probabilistically allowing states to be skipped. Since the template cannot be observed directly, a HMM is employed to link the observed and template total ion currents through a Gaussian noise ‘emission’ variance. The CPM is therefore a HMM technique with an additional set of unknown parameters (the template chromatogram) that affect the emission probabilities. The EM algorithm is used to learn the consensus template as well as each observed chromatogram’s emission variance and state transition probabilities. Note that the HMM state space encapsulates a posterior deformation distribution (albeit discretised) that could be used in downstream statistical testing, even though the EM algorithm itself only establishes point-estimates for the template and other parameters. If desired, the maximum likelihood alignment can be determined through dynamic programming on the state space, since the transition probabilities represent the statistical equivalent of the search space in DTW and COW.

In the original technique [153], each time-point state was also split into a number of scale states to model a time-variant multiplicative change in intensity between the observed signal and the template, and the transition probabilities were modelled as multinomial distributions encouraging smooth changes in scaling and RT deformation. In a follow-up paper [164], information from the MS dimension was added by splitting each time-point state into 4 bins, each modelling the total current in one quarter of the spectrum (more bins were shown to provide diminishing returns). To avoid the resulting increase in state space, the time-variant scaling states were removed (and therefore generation of their posterior distribution), replaced by estimation of a piece-wise linear mapping. The CPM later [165] offered an alternative MCMC approach to generate full posterior distributions for all unknowns and, to explicitly account for differences between treatment groups, a hierarchical template was added. This consisted of a parent template containing similarities between treatment groups and children templates carrying only the impulse-like differences. Whilst the learned model could then be used for differential inference directly on the child templates, with regards to LC/MS its main purpose was robust alignment since no information from the MS dimensions was integrated.

5 Interpreting results

5.1 General statistical analysis

In addition to image processing, several factors must be taken into consideration in order to generate statistically and biologically meaningful results. These factors are essential when considering both 2-DE and LC/MS data and include data normalization, transformation, univariate and multivariate statistical testing, multiple testing and FDR control, and power analysis. As statistical analysis for proteomic data has become more sophisticated over the years, commercially available analysis platforms have struggled to keep up with demand, where only a handful have succeeded. In general, the statistical workflow in commercial packages can be summarized as follows [166]:

Normalisation

This is intended to correct for variation or a uniform bias that may arise due to experimental procedure, rather than from biological variation. Experimental variation factors can range from scanner settings, to sample quantity, labelling yield, protein digestion efficiency, isotope impurities etc. To correct for these systematic errors, a global normalisation factor is usually applied, which can be based on a measured sample median or mean, a reference standard, or LOWESS regression [167]. For DIGE and other multiplexed approaches, the normalisation reference is fixed within each multiplex, e.g. the internal standard (usually Cy2) in DIGE. Normalisation is essential to derive a change in protein abundance with biological significance, and is applied automatically in commercially available platforms.

Transformation (Variance Stabilisation)

As statistical testing relies on data that fits a normal distribution, analysis is typically performed on the log of the normalised volume. Log transformation approximately removes distributional skew in the biological data and improves the normal distribution approximation i.e. to obtain valid p-values. Log transformation of the data has the advantage of representing increases and decreases in expression as positive and negative values, making for easy interpretation of changes in abundance when viewed graphically. Like normalization, transformation of data is the default setting in commercially available analysis platforms. However, log transformation does not model baseline instrumental noise, and so unreliable results have been noted for weakly expressed proteins [168]. Variance stablisation is discussed in more detail in [60].

Statistical testing for differential expression

Traditional statistical testing is typically employed, where the t-test is used to identify significant changes in expression between two population means, and ANOVA is applied when several population groups are compared. These tests are conducted one protein at a time and the threshold for significance is typically set at 1% (p = 0.01) or 5% (p = 0.05). In addition to univariate testing, some up-to-date commercially available software packages offer multivariate algorithms such as principle component analysis (PCA) and hierarchical clustering (dendrograms). Multivariate algorithms enable researchers to group protein data into subsets and visualise clusters of proteins that exhibit similar patterns of expression changes. Overall, these tools help the biologist to identify outliers, interpret complex proteomic data that has many variables, and consider important clusters of co-regulated proteins that would otherwise go unnoticed.

Multiple testing

Both univariate and multivariate statistical approaches are commonly used in the analysis of scientific data and are generally considered robust. However, in the case of proteomic data where a single test is required per protein, 1 in every 20 tests (5%) will occur by chance alone at p < 0.05. Where 1000’s of proteins are tested, the issue of accumulating false positives is known as the multiple testing problem. This can be controlled for using the Bonferroni correction, which is considered overly stringent for proteomic data [169]. Alternatively, the FDR correction by Benjamini and Hochberg [170] can be applied. Storey and Tibshirani [171] further developed the correction, defining a q-value as the converse of a p-value. That is, p is the probability of seeing the data given there are no true differences, whereas q is the probability that there are no true differences given the data, and is therefore inherently Bayesian. Thus, the q-value of an individual hypothesis test is the minimum FDR at which the test may be called significant (i.e. where the p-value of a test is the minimum false positive rate that is incurred when calling that test significant). The q-value calculation is typically considered as suitable for proteomic data.

Power analysis

The power of a statistical test is the probability that the test will not fail to detect a significant change when there is one. In proteomics, power analysis estimates the optimal sample size required to detect ‘true’ positives or significant changes in protein expression when they exist. Power analysis is usually carried out a priory to determine the number of replicates required to achieve adequate power, where a power of >80% is considered acceptable by statisticians. The usefulness of a post hoc power analysis is controversial, although it may be used as a guide to increase replicates until a certain power is achieved.

FDR q-value calculation and power analysis have recently been added the statistical package in Progenesis Same Spots (Nonlinear Dynamics). For further information on statistics in proteomics, tutorials and reviews of the methodology are found in [46, 172].

5.2 Visualisation

Together, signal/image analysis and robust statistical testing procedures convert the enormous amount of raw data generated by a proteomics experiment into a rich, but still significantly large, set of quantifications and differential expression candidates. An expert operator must then verify the output data by crosschecking the results generated at each stage of the pipeline (registration, segmentation, quantification and identification). Even as algorithms become more accurate and automated, this step will nevertheless always be essential since problems in sample preparation, experiment design and implementation are often only revealed by user scrutiny as computer algorithms lack the expert domain knowledge to identify them. It is therefore widely acknowledged [132] that an integrated global visualisation of the data and results is a significant benefit to results interpretation.

Differential display through overlays (e.g. magenta/green), illustration of LC/MS datasets as ‘virtual gels’ and annotation of identified spots are now commonplace. For example, Jones et al. [173] annotate each 2-DE spot with a graphical representation of the parts of the protein sequence that were matched successfully in the MS database search. Replacing each digitised spot with a glyph such as a circle or sphere can be used to visualise metrics such as spot volume and confidence of differential expression. In recent research, glyph diameter has been used to represent a single parameter [174], and more recently, two parameters have been represented simultaneously through sphere diameter and colour [175]. In 3D, the height and colour of cones on a plane has been used to display peptide fold change [176].

3D topographical visualisations of the digitised gel or LC/MS map are particularly pertinent. With LC/MS, the challenge is to allow real-time interactive exploration of the landscape despite the size and complexity of the dataset. To this end, Corral and Pfister [177] transform the data into a set of hierarchical rectilinear grids so that only the coarse level of detail is cached in graphics memory if the user is zoomed out, whilst only a section of the map at high detail is required if the user is zoomed in. Their streaming graphics hardware-based implementation runs at 130 frames per second. Recently, Linsen et al. [178] presented a similar method based on a wavelet decomposition that ensures each peak’s height is preserved at all scales. They also incorporate differential display as well as integrated visualisation of multi-step LC by colour-coding the peaks from different fractions.

Imaging Mass Spectrometry

Visualisations are becoming ever more paramount due to the wealth of spatially localised data generated by the emerging technique of IMS [179]. In IMS, a whole tissue section is analysed, with a distinct spectrum captured at each point on a regular grid [180]. The spectra are typically pre-processed as in standard MS [181], and software such as ClinproTools (Bruker Daltronics) [182] or Biomap (Novartis) [183] is then employed to reconstruct the spectra into a set of 2D images, one for each desired m/z, thus enabling visualisation of spatial expression changes across the tissue section.

It is possible to further improve capability through simple landmark registration by fusing the functional IMS data with an optical acquisition of the tissue section and also any histology stains performed. Crecelius et al. [184] perform this in 3D by analysing multiple parallel tissue slices of a whole mouse brain and fusing the IMS with a surface reconstruction from the optical images. Sinha et al. [185] then showed that rigid 3D registration with a mutual information similarity measure could be used to fuse the optical image stack with pre-acquired MRI volumes. This opens up the possibility of integrated visualisation encompassing any combination of suitable modalities.

Unless the protein(s) of interest are known in advance, exploratory visualisation and analysis can also be significantly aided by eliminating uninteresting signal. With ‘digital staining’, the whole dataset is summarised into a small set of factor images that capture linear combinations of spectrum m/z channels that vary the most between pixels. This aims to delineate the most important functional changes across the tissue section. The task was first tackled with PCA, first for SIMS data and later for MALDI [186]. Since factors are not orthogonal in practice, ICA [80] would be preferred. However, Hanselmann et al. [187] argue PLSA is even more suitable as it ensures peak component weights are non-negative, therefore providing a probability distribution over the spectrum for each factor. Furthermore, they use a statistical model selection scheme that estimates the optimal number of factors underlying the data, which would otherwise have to be selected through prior histological knowledge. If required, a clustering [186] or classification [188] step can also be performed on the factor images to produce a single segmentation of the tissue section into a number of ‘tissue classes’. These methods often do not currently consider the spatial location of each pixel and therefore the results can be noisy, so in [188] a smoothing step is performed post-hoc.

The techniques discussed above generate only linear factors, and differential analysis between datasets is not likely to be accurate since the same factorisation will not be generated on each dataset. The field of Fluorescence Lifetime Imaging generates similar data with similar issues to IM, for which Fixed Reference IsoMap has recently been proposed [189]. IsoMap is a technique that embeds each spectrum into a low dimensionality space in a way that ensures the distance between spectra is proportional to their similarity. Since distance in this respect is ‘geodesic’ rather than Euclidian (computed over the ‘manifold’ represented by the shortest path though the graph of nearest neighbours), the factors are inherently nonlinear. By selecting a training set that best represents variability within all the tissue samples, new samples are embedded into a reference coordinate system such that local similarities are preserved.

6 Discussion

We have reached a juncture where proteomics is capable of playing a vital role in the elucidation of biomarkers for routine, clinical screening of disease states long before the onset of physical manifestations. The diversity and dynamic range of natural biological variation, however, deeply confounds the problem. To this end, it is essential that the informatics tools underpin the science through holistic statistical consideration of all the modes of variation, to provide a sound and fully automated pipeline for high-throughput differential analysis and set the stage for generalised and stable classification. Such a framework is essential for discovering statistically sound yet practical biomarker patterns for the development of a predictive, personalised and preventative approach to medicine. In this review, we have presented the current landscape for expression proteomics tools in 2-DE, and described the rapid recent sculpturing of an alternative landscape in LC/MS. At present, both techniques are complementary [190], but the promise of full automation in LC/MS is encouraging, as long as issues with reproducibility, coverage and expense can be overcome.

The emerging algorithms presented in this review demonstrate two strategies to mitigate the propagation of errors inherent in the conventional approach. Either data reduction must be discarded in favour of data transformation, or data reduction must be accompanied by error distributions representing uncertainty in the data. Ideally, both strategies would be combined, as in the WFMM approach of Morris et al. [126]. Without these strategies, the conventional pipeline produces discrete errors in the spot detection and matching phases, which leads to missing values in the resulting spot quantification lists. Since missing values can also be caused by differential expression, setting them all to 0 or ignoring them completely adds significant bias to the results. Statistical methods have been developed [191] to adaptively estimate the best imputation values based on error rates within each gel and within each protein, but post-hoc correction will never be optimal.

We have presented LC/MS methods that show group-wise alignment as a capable technique for improving the robustness and accuracy of consensus RT determination. The integration of domains corresponding to the same RT for the same peptide is an interesting lead for improving alignment, which could well have the same benefits for 2-DE. Image-based group-wise alignment often implies diffeomorphic, inverse consistent mappings (registering image A to image B gives the same result as B to A), which necessarily are smooth and bijective (cannot fold over [151]) and have a smooth inverse. In medical imaging research, diffeomorphic fluid flow transformations allow for realistic deformations of even considerable magnitude [192], and are an interesting topic for application in proteomics.

The image-based approach to alignment and differential expression analysis has improved the throughput and effectiveness of 2-DE. Multi-resolution image registration and physics-based transformation models contribute to robust automated analysis, whilst the software has evolved towards focusing and detecting regions of common quantification. This trend could soon be followed in LC/MS imaging. In LC/MS, current research into feature-based and signal-based alignment is equally popular, with feature-based and signal-based approaches favoured for application in high and low-resolution MS respectively. The signal-based approaches have their roots in DTW, which is still evident with the group-wise CPM approach of Listgarten et al. [164]. Since these approaches perform brute-force exhaustive search over a set of plausible alignments, they are unable to harness a physics-based transformation model due to the exponential increase in search space size with each additional unknown parameter. Conversely, the 2-DE image registration approaches realise their efficiency by considering only the most likely path to optimum alignment without statistical consideration of uncertainty, relying instead on regularisation to avoid errors with disparate images or in regions with no guiding information. Whilst a simple registration approach has been proposed for LC [193], it does not rival the modelling complexities of the 2-DE methods and therefore cannot provide a guide to the effectiveness of signal-based registration techniques in LC/MS [194]. We therefore anticipate that the 2-DE and LC/MS alignment approaches will ‘meet in the middle’ at some point in the future.

The advent of Bayesian peak mixture models and functional mixed modelling in MS has brought a number of significant gains complementary to data mining techniques [81], including increased reliability and precision of expression quantification and differential analysis, and the output of full posterior distributions for downstream statistical testing. These methods have been developed for MS due to the widespread promise of clinical SELDI MS and the relatively small dataset size (compared to 2-DE, LC/MS and IMS), which offsets the computational complexity. Recent research to separate overlapped spots in 2-DE has led to a genetic algorithm for mixtures of diffusion model spots [195] but the most visually promising results lie in the RJ-MCMC approach of Yoon et al. [196]. Nevertheless, both techniques restrict processing to watersheds or small regions of the gel. A Bayesian mixture modelling approach has also recently been proposed for high-resolution LC/MS spot modelling. Strubel et al. [197] define each MS peak to be a sum of multiple Gaussians representing three charge states and three isotopes, with corresponding averagine abundances, whilst a single Gaussian is used in the LC dimension. One caveat is that, since their framework is based on the LOCCANDIA lab-on-a-chip system for detecting multi-protein disease markers [198], the number and approximate positions of peaks in the LC/MS datasets is assumed known. More recently, Morris et al. [199] have demonstrated an extension of their WFMM method for modelling image data like 2-DE and LC/MS without significantly increasing complexity. Initial results from this study suggest that this image-based modelling approach may be able to find differential expression for co-migrating proteins that are not visually detectable as independent spots, and thus are missed by spot-based analysis algorithms. We envisage that multivariate data mining algorithms can also be applied in a similar manner.

An alternative technique that has received only modest attention in proteomics for separating complex spot mixtures is the ‘image deconvolution’ restoration approach [200]. The premise of this method is that the signal or image is blurred with a ‘point-spread function’ as well as corrupted with noise. The image deconvolution procedure attempts to find the inverse of this highly ill-conditioned problem. It has a wide range of established applications ranging from astronomical imaging to wide-field and confocal microscopy. For 2-DE, LC/MS and IMS, the problem would suggest an underlying model which assumes that the uncorrupted signal has perfectly sharp spots that are blurred to give the various shapes of spot seen in practice [55]. In 2002, Mohammad-Djafari et al. [201] instigated the first mention of image deconvolution for MS, providing a review of deconvolution techniques but only demonstrating the approach on synthetic spectra. More recently, Malyarenko et al. [202] confirmed some resolution enhancement by using a nonlinear combination of linear filters matched to the inverse of a peak model with Gaussian leading edge and Lorentz trailing edge. They also present an approach to account for the varying peak width in TOF MS with a quadratic fit [203]. Nevertheless, it is recognised that non-iterative approaches can only approximate the inverse with an unfavourable trade-off between noise amplification and poor reconstruction of edges [200]. In order to become pervasive, image deconvolution therefore requires an iterative Bayesian methodology with prior knowledge of the underlying signal, statistical modelling of the noise model and a precise varying point-spread function [204].

The widespread acceptance of MCMC Bayesian methodology, and the RJ-MCMC approach in particular, is reliant on management of the computational complexity. One possible alternative approach is to adopt a Variational Bayes formulation [205, 204], which approximates the intractable integral in the posterior by a number of simpler independent distributions, rather than going to the expense of random sampling. The procedure is a generalisation of the EM algorithm that iteratively updates the unknown parameters in each distribution to provide a closer and closer fit to the true posterior distribution. Whilst the fundamental approach is still an active and growing area of research, the computational benefits make this method promising for both 2-DE and LC/MS image analysis. Another option is to employ parallel computing technologies through workstation clusters, as in [131, 128], or harness modern Graphics Processing Units (GPU) that, as of today, can add up to 4 teraflops of power to a single workstation. To give researchers convenient access to this high-throughput computing resource, a collection of programming languages, frameworks and libraries have been released for scientific computation on GPUs [69]. So far, their use in proteomics applications [68, 206] has demonstrated up to 200× speedup compared to conventional workstation processors [206].

Abbreviations

AMT

Accurate Mass and Time

CCA

Canonical Correlation Analysis

CCD

Charge-Coupled Device

COW

Correlation Optimised Warping

CPM

Continuous Profile Model

CWT

Continuous Wavelet Transform

DTW

Dynamic Time Warping

DWT

Discrete Wavelet Transform

EM

Expectation Maximisation

EMG

Exponentially-Modified Gaussian

FDR

False Discovery Rate

GPU

Graphics Processing Unit

HMM

Hidden Markov Model

ICA

Independent Components Analysis

IMS

Imaging Mass Spectrometry

KDE

Kernel Density Estimation

LIMS

Laboratory Information Management System

LOCCANDIA

Lab-On-Chip based protein profiling for CANcer DIAgnosis

LOWESS

Locally Weighted Scatterplot Smoothing

MC

Markov Chain

MCMC

Monte Carlo Markov Chain

MIR

Multi-resolution Image Registration

PMT

Photo-Multiplier Tube

PLSA

Probabilistic Latent Semantic Analysis

PLSR

Partial Least Squares Regression

QC

Quality Control

RAIN

Robust Automated Image Normalisation

RJ

Reversible Jump

RT

Retention Time

SIMS

Secondary Ion Mass Spectrometry

SNR

Signal to Noise Ratio

TPS

Thin-Plate Spline

UDWT

Undecimated Discrete Wavelet Transform

WFMM

Wavelet Functional Mixed Models