Cellular self-organization by autocatalytic alignment feedback

Abstract

Myoblasts aggregate, differentiate and fuse to form skeletal muscle during both embryogenesis and tissue regeneration. For proper muscle function, long-range self-organization of myoblasts is required to create organized muscle architecture globally aligned to neighboring tissue. However, how the cells process geometric information over distances considerably longer than individual cells to self-organize into well-ordered, aligned and multinucleated myofibers remains a central question in developmental biology and regenerative medicine. Using plasma lithography micropatterning to create spatial cues for cell guidance, we show a physical mechanism by which orientation information can propagate for a long distance from a geometric boundary to guide development of muscle tissue. This long-range alignment occurs only in differentiating myoblasts, but not in non-fusing myoblasts perturbed by microfluidic disturbances or other non-fusing cell types. Computational cellular automata analysis of the spatiotemporal evolution of the self-organization process reveals that myogenic fusion in conjunction with rotational inertia functions in a self-reinforcing manner to enhance long-range propagation of alignment information. With this autocatalytic alignment feedback, well-ordered alignment of muscle could reinforce existing orientations and help promote proper arrangement with neighboring tissue and overall organization. Such physical self-enhancement might represent a fundamental mechanism for long-range pattern formation during tissue morphogenesis.

Introduction

Myoblasts differentiate from single cells into multinucleated muscle fibers during the course of myogenesis. This self-organization process is spatiotemporally regulated and involves multiple steps including proliferation, specification, alignment, fusion and myofibrillogenesis (Yaffe and Feldman, 1965). During this process, myoblasts must modify spatial cellular arrangement over distances considerably longer than an individual cell without a central coordinator or a blueprint to proceed from a disordered state of individual, undifferentiated cells into well-ordered, aligned and multinucleated myotubes (Blanchard et al., 2009; Bryson-Richardson and Currie, 2008; Nelson, 2009). Many details of how such information is physically coordinated over a long distance remain unknown and represent fundamental questions in cell biology. Understanding the physical aspects of the myogenic self-organization process will also have profound impacts on various myogenic diseases and regeneration processes. For example, abnormalities of muscle fibers and myofibril structures due to genetic and environmental factors are the underlying causes of various myopathies, including centronuclear myopathy (Jungbluth et al., 2008) and muscular dystrophy (Kanagawa and Toda, 2006). Physical factors in the microenvironment, such as tissue stiffening caused by muscular dystrophy, are also known to influence the result of satellite cell regeneration (Scime et al., 2009). Moreover, the ability to manipulate the tissue morphogenic process will enable the creation of microengineered tissue constructs and novel disease models.

Tissue morphogenic processes are generally regulated by a combination of numerous physicochemical factors, such as morphogens, cell–cell contacts, microenvironments and cell mechanics (Elsdale and Wasoff, 1976; Garfinkel et al., 2004; Green and Davidson, 2007; Gregor et al., 2010; Keller, 2002; Krauss et al., 2005; Lecuit and Lenne, 2007; Nakao and Mikhailov, 2010; Ruiz and Chen, 2008; Technau et al., 2000; Turing, 1952). Nevertheless, relatively little is known about the roles of physical factors in the regulation of the tissue morphogenic process. For instance, an unsolved aspect of the development process that is known to regulate cellular self-organization during tissue generation is the positional information at physical boundaries. Despite the fact that regulation through positional information at boundaries has been seen in vivo to influence myogenic developmental processes such as axis formation, initiation of myogenesis and alignment of reintroduced mesenchymal stem cells to existing muscle tissue (Cossu et al., 1996; Green et al., 2004; Rowton et al., 2007; Shake et al., 2002), the details of how physical boundaries guide tissue organization remain unclear. By contrast, myoblasts aggregate, differentiate, and fuse over time, and their physical size and properties evolve during the differentiation process (Engler et al., 2004b; Stya and Axelrod, 1983). The effects of these physical changes of the cells on the organization of myotubes during myogenesis have not been thoroughly investigated.

With the advent of microfluidics and micropatterning techniques, systematic manipulation of various physical and biochemical factors can be achieved in controlled microenvironments with high spatiotemporal resolution (Kim et al., 2009; Nelson et al., 2006; Wong et al., 2008). For example, topographical and chemical cues have been demonstrated to guide the alignment of cardiac or skeletal muscles (Charest et al., 2007; Feinberg et al., 2007). However, most of these studies focus on guiding cell alignment with local cues instead of exploring the inherent self-organization ability of myoblasts. To understand the effects of global geometric cues and differentiation-induced changes of the myoblasts in the long-range alignment of myotubes, we have developed a biomechanical framework combining micropatterning, microfluidics and cellular automata modeling techniques (Junkin et al., 2011; Junkin et al., 2009; Junkin and Wong, 2011). This allows us to systematically perturb the environmental factors and cell–cell interactions for elucidating the regulatory processes in myogenic self-organization. Here, we demonstrate a physical mechanism by which alignment information from a geometric boundary can propagate over long distances to guide the organization of muscle tissue. Understanding the details of how muscle tissue forms from individual cells will have important implications for future developmental biology, regenerative medicine and systems theory (Mahmud et al., 2009; Parrish and Edelstein-Keshet, 1999; Zheng et al., 2006).

Results

Geometric constraints guide alignment of myotubes during myogenesis

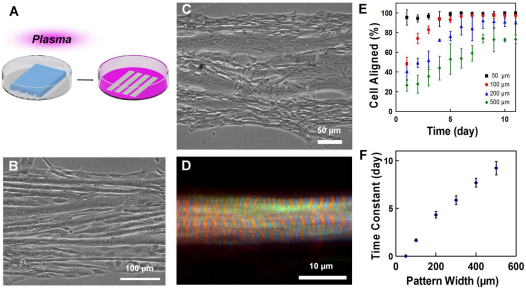
To investigate the myogenic self-organization process within a geometric context, we studied the organization of myoblasts constrained in microscale patterns. The micropatterning was achieved by plasma lithography, which produces spatial cues on polystyrene substrates by means of selective exposure of the surface to plasma treatment (Fig. 1A; supplementary material Fig. S1). The self-organization of C2C12 mouse myoblasts (Fig. 1B) and primary chick skeletal myoblasts (Fig. 1C) were studied on line patterns created on polystyrene Petri dishes. Most differentiated myotubes aligned in parallel with the line patterns despite the large distance of the cells from the geometric boundaries. Additionally, we observed instances where myoblasts that differentiated on the plasma lithography-patterned lines possessed characteristics of functional myotubes, including the presence of well-developed sarcomeres (Fig. 1D), and the ability to spontaneously twitch after 4–5 days of differentiation (supplementary material Movie 1). During the alignment process, myoblasts near the boundary of the line pattern were observed to first elongate and align to the boundary, and myoblasts adjacent to an elongated myoblast then polarized along the same direction (supplementary material Fig. S2). Quantitative measurement of the cell alignment angle at different locations from the boundary confirms these observations (supplementary material Fig. S3). As a result, the alignment information appeared to propagate from the boundary to neighboring cells and the myoblasts self-organized into myotubes that aligned in parallel with the line patterns. These results suggest myoblasts can use geometric cues for guiding the self-organization process.

Fig. 1.

Self-organization of myoblasts and geometric alignment of myotubes on plasma patterned substrates. (A) Plasma lithography to create chemical patterns for guiding cell alignment. Areas exposed to plasma (pink) present surface functional groups that facilitate cell adhesion, whereas areas shielded by PDMS (blue structure) prevent cell adhesion. (B) C2C12 mouse myoblasts, and (C) primary chick myoblasts guided on line patterns form linear, aligned myotubes parallel to the boundaries. (D) Sarcomeres in patterned primary chicken skeletal muscle fibers. F-actin is labeled by phalloidin (green), Z-discs by α-actinin (blue) and M-line by titin T114 (red). (E) The temporal evolution of myoblasts aligned to the line patterns with different widths. (F) Time constants of myoblast alignment on different pattern widths. Error bars in E and F are s.d. and s.e. of the mean, respectively.

In the experiment, the presence of well-developed sarcomeres (Fig. 1D) and spontaneous twitching of myoblasts were observed after 4–5 days of differentiation (supplementary material Movie 1). Quantification of twitching and sarcomere formation, nevertheless, was not undertaken systematically because the dynamic alignment process was the focus of the current study. The patterns that were used in our experiments consisted of alignment cues connected to unpatterned areas that also possessed cells. The presence or absence of neighboring cells could potentially influence the development process. As a comparison, we additionally cultured myocytes on isolated patterns of finite length, not surrounded by masses of unpatterned cells at the ends. These cells also displayed alignment to patterns and fusion. This suggests that the alignment and fusion processes observed in this study are not sensitive to the cells connected in the unpatterned regions. However, we do not rule out the possibility that the cells in the unpatterned areas might influence the twitching behavior and sarcomere development. Another factor that has been reported to be relevant to sarcomere development is adhesion (Engler et al., 2004a; Griffen et al., 2004; Sen et al., 2011). In our experiments, cell adhesion to patterned substrates was not investigated during the alignment process, although we observed that alignment as guided by patterns did not differ between different cell layers, when present.

Length-scale dependence of the alignment process

To systematically investigate the alignment process, line patterns from 50 μm to 500 μm in width were created to test the length-scale dependence of the alignment process. The myoblasts generally aligned to the line patterns for all widths (Fig. 1E). For pattern widths that were 50 μm or smaller, most of the cells aligned with the line patterns immediately after cell seeding. For larger patterns, the portion of cells that aligned to the line patterns increased gradually over time towards a steady state value. The extent of alignment was found to be influenced by pattern size because wider patterns tended to not align as well over time. Examination of the temporal evolution of the alignment angles revealed that the time constant of the process increased linearly with the width of the line patterns (Fig. 1F). The fraction of multinucleated cells was also examined and was found to be similar for all pattern widths examined (~70%). These observations further support the idea that the physical boundary guides the alignment of the myoblasts and the orientation information can propagate from the geometric boundary to guide the alignment of myotubes.

Long-range alignment of myoblasts in semi-infinite domains

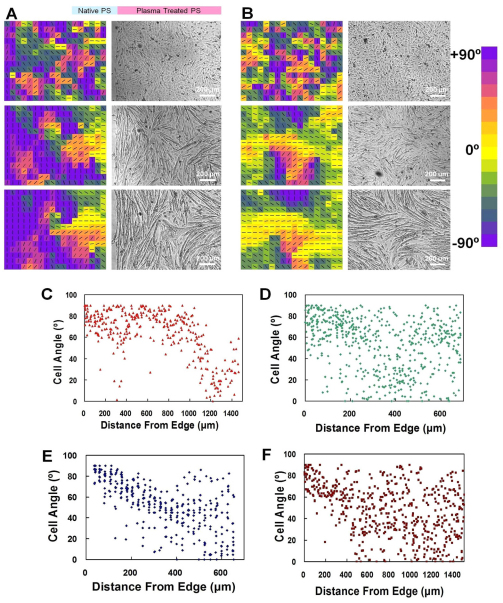
The dependence of the alignment process was further studied in a semi-infinite domain created by plasma lithography (Fig. 2A). This consisted of creating a large (millimeters in size) hydrophobic area with straight edges surrounded by a larger hydrophilic area. The result was compared with that from cells grown on homogeneously plasma-treated substrates (Fig. 2B). The myoblasts, in both cases, self-organized into aligned domains: groups of myotubes aligned in similar directions over the course of myotube formation (~1 week). Myoblasts cultured on homogeneous substrates developed into multiple aligned domains without preference to the orientation of each domain, similarly to polycrystalline materials. The dimension of the alignment domains could be over 600 μm. By contrast, myotubes that formed near a pattern edge became well aligned along the boundary, and the distance away from the edge where alignment was preserved was taken as an estimate of the length scale that the geometric cue propagated (Fig. 2C). Cell angles remained aligned to the orientation of the geometric boundary for a distance approximately 1000±250 μm before alignment started to decay and become randomized. Alignment of myoblasts far away from the boundary (i.e. ⪢1000 μm) resembled the behavior of cells on homogeneous substrates, which form multiple aligned domains in random directions. Other cell types, such as fibroblasts, are also known to self-organize into multiple alignment domains by contact guidance (Edelstein-Keshet and Ermentrout, 1990; Nubler-Jung, 1987), and so experiments were also performed using 3T3 mouse embryonic fibroblasts. When 3T3 fibroblasts were grown on the semi-infinite domain, the alignment angle, however, decayed rapidly away from the edge in approximately 200 μm (Fig. 2D), and did not show the long-range propagation of orientation information observed in differentiating myoblasts. To study the underlying mechanisms responsible for the long-range propagation of orientation information, the alignment experiments were performed inside a microfluidic channel to perturb any possible morphogen gradient created in the extracellular space (supplementary material Fig. S4). Initially, fresh differentiation medium was continuously perfused into the microchannel. Under this condition, the alignment relative to the boundary decayed rapidly (Fig. 2E), similarly to the alignment of 3T3 fibroblasts. It should be noted that the myoblasts did not fuse, owing to the removal self-generated growth factors required for initiating the fusion process (Florini et al., 1991). Interestingly, re-circulating the culture medium resumed cell fusion and the long-range alignment of myotubes (data not shown). This suggests that morphogen gradients in the extracellular space are unlikely to be responsible for the long-range propagation of the alignment information because the continuous fluid flow should disrupt the formation of a morphogen gradient. In addition, shear stress does not have an observable influence on the long-range alignment process because when re-circulating of the culture medium was carried out, the extended alignment was present. Myoblasts were also grown in medium that lacked sufficient calcium, which inhibits fusion of myoblasts (Knudsen and Horwitz, 1977). Without calcium, cell fusion and long-range propagation were again not observed, and the alignment behavior resembled that of fibroblasts (Fig. 2F).

Fig. 2.

Spatiotemporal evolution of cell alignment in semi-infinite domains. (A,B) Myoblast alignment near an interface (A) and on a homogeneous surface (B) at days 1 (top), 4 (middle) and 8 (bottom). Color maps of alignment angle (left) and the corresponding micrographs of cells (right). (C–F) Representative measurements for propagation of geometric orientation information with fusing myoblasts (C), 3T3 fibroblasts (D), myoblasts inside a microchannel, which was supplied with fresh differentiation medium to block fusion (E), and myoblasts in medium without calcium to block fusion (F). PS, polystyrene.

In our experiments, myoblasts that differentiated on homogeneous substrates could self-organize into multiple alignment domains (Fig. 2B). This suggests that the alignment of myoblasts does not require local cues and is probably an inherent self-organizing property of myoblasts. However, the long-range alignment of myoblasts cannot be fully explained by the contact guidance mechanism, which was observed in fibroblasts (Edelstein-Keshet and Ermentrout, 1990; Nubler-Jung, 1987). Unlike the long-range (~1000 μm) alignment of differentiating myoblasts, the alignment of 3T3 fibroblasts decayed and randomized within a short distance (approximately 200 μm) from the geometric boundary (Fig. 2D). Cell densities were also measured and found to be similar in all experiments (data not shown). Additionally, significant layering of myocytes on top of each other was not observed, as reported in other studies (Griffen et al., 2004; Sen et al., 2011). Additional or alternative mechanisms, therefore, are required to explain the long-range alignment of myoblasts. Because the surface that the cells contacted was uniform, the long-range alignment of myotubes observed was different from that previously reported because of local topographic (Charest et al., 2007) or chemical signals (Feinberg et al., 2007), which provide short-range alignment cues on the dimension of a cell to guide the alignment. Interestingly, the long-range alignment only occurs for differentiating myoblasts that can be fused into myotubes in the experiments. Rapid decay of the alignment angle from boundaries was observed for all non-fusing cells such as 3T3 fibroblasts and myoblasts that are perturbed by microfluidic disturbance or low calcium medium (Fig. 2D–F).

Long-range propagation of alignment information

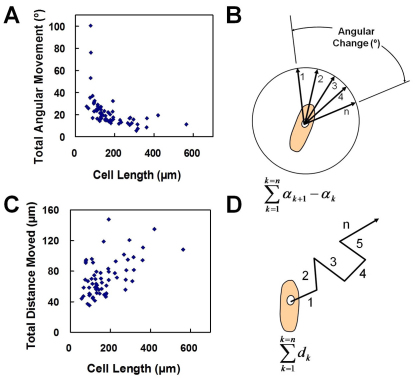
Our data suggest that the long-range propagation of alignment information only occurs with differentiating myoblasts that can fuse into myotubes. However, it is unclear how myoblast fusion can affect the long-range alignment of myotubes. To investigate the roles of myoblast fusion in the alignment process, we measured the physical properties of differentiating myoblasts (Fig. 3). In particular, live images at various stages of the fusion process were captured to evaluate rotational and linear motions and their dependence upon fusion. The angular motion decreased rapidly with the size of the cells (Fig. 3A,B). In other words, the rotational inertia – the resistance of the cell to rotate – increased with the cell size. However, the displacement of myoblasts showed only weak correlation with cell size (Fig. 3C,D). Other measurements of linear motion, including the ratio of distance traveled parallel and perpendicular to the interface, and velocity data, also did not show any correlation with cell length or to position relative to pattern edge (data not shown). Because rotational inertia changed with the size of cells, the ability of differentiating myoblasts to adjust relative to surrounding cells decreased during the differentiation process. We therefore hypothesized that rotational inertia could serve as a mechanism for the enhanced propagation of orientation information (Meinhardt, 1982).

Fig. 3.

Dependence of motion on cell fusion. (A,B) Total angular movement in relation to cell length. (C,D) Measurement of total distance moved in relation to cell length. Measurements record motion taking place between successive image capture intervals and were recorded after 7 days of fusion.

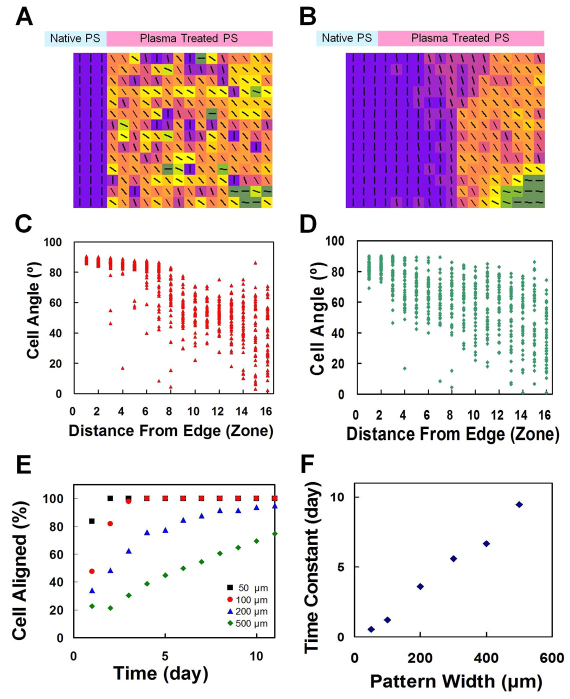
To test the possibility that myogenic fusion in conjunction with rotational inertia functions in a self-reinforcing manner to enhance long-range propagation of orientation information, a cellular automata model was developed to evaluate the alignment of myoblasts under geometric constraints resembling the experimental conditions (Ermentrout and Edelstein-Keshet, 1993). In the cellular automata model, each cell, which is surrounded by a grid of 5×5 neighboring cells, was subjected to a decision on whether or not to align. Alignment would proceed if most of the surrounding cells were aligned to a high degree, and partial alignment was executed if a lesser number of cells were aligned (supplementary material Fig. S5). The increase in rotational inertia due to cell fusion was incorporated into the model because aligned cells, similarly to a long cell having the same angle over its whole length, are less likely to rapidly rotate. Using the cellular automata model, the propagation of the alignment information from the boundary can be observed (Fig. 4A,B, and supplementary material Movie 2) and closely resembled the experimental observation (Fig. 2A). The model was able to capture the spatial distribution of the self-organization process with a geometric boundary (compare Fig. 2C,D and Fig. 4C,D). Furthermore, the model successfully described the formation of multiple alignment domains observed in homogeneous substrates (supplementary material Movie 4; Fig. 2B). For non-fusing cells, only short-range alignment could be observed in the numerical study (supplementary material Movie 3) similarly to our experiments (Fig. 2D–F). We have also applied the model to describe the length scale dependences and time constants of myoblast alignment to line patterns of different widths (Fig. 4E,F). The portions of cells that are aligned to the line patterns gradually increase toward steady state values, with time constants linearly increasing with the pattern width. Despite the simplicity of the model, the numerical data are in excellent agreement with our experiment results (Fig. 1E,F). These data indicate that the cellular automata model successfully describes the spatiotemporal distribution of myogenic self-organization providing a model to understand the self-organization process.

Fig. 4.

Cellular automata modeling of autocatalytic alignment feedback during myogenic self-organization. (A,B) Myoblast alignment calculated using the cellular automata model at days 1 and 8. (C,D) Propagation of geometric orientation information of fusing cells (C) and non-fusing cells (D) estimated using the model. (E) Simulation of alignment on line patterns with different widths. (F) Time constants of myotube alignment on different pattern widths.

Discussion

In this study, we observed that orientation information can propagate for a long distance from a geometric boundary during myogenic self-organization. This long-range alignment process can be understood within a biomechanical context. In particular, examining the temporal evolution of the cellular automata model revealed that myogenic fusion in conjunction with rotational inertia can serve as an autocatalytic mechanism to enhance long-range propagation of orientation information. During the alignment process, cells near the geometric boundary first align as a result of contact guidance (Brock et al., 2003; Edelstein-Keshet and Ermentrout, 1990) (Fig. 2A; supplementary material Fig. S2 and Movie 2). Cells near aligned cells tend to align with the elongated cells and polarized cells fuse with each other, which increases the rotational inertia of the cells. Then, the increase in rotational inertia further facilitates the alignment and fusion of nearby cells. The rotational inertia functions in an autocatalytic, or self-enhancing, manner to propagate the alignment information from the boundary. In fact, the increase in the size of aligned domains during differentiation was observed consistently in our experiment where myoblasts were fused with and without geometric guidance (Fig. 2A,B). For non-fusing cells, the rotational inertia does not increase autocatalytically. Therefore, the cells are more likely to align in random directions as a result of the small rotational inertia and the alignment information from the boundary can only propagate for a short distance, as shown in both experiments and numerical simulation (Fig. 2D–F and Fig. 4D). In addition to non-fusing fibroblasts, microfluidic perturbation and medium with low calcium, which prevented myoblasts fusion, were applied to modulate the rotational inertia of myoblasts in our experiment, and both conditions demonstrated only short-range alignment, which is consistent with our model. Collectively, the fusion of myoblasts in conjunction with the increase in rotational inertia provides a physical mechanism for the long-range alignment observed only in differentiating myoblasts.

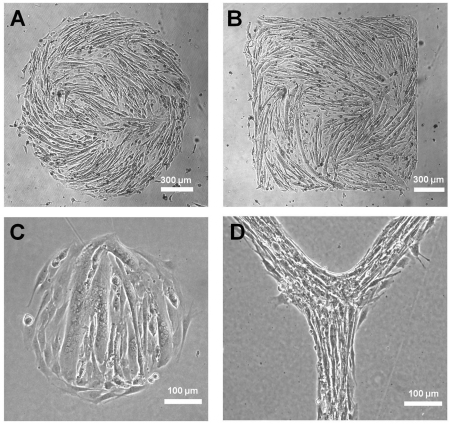
A major finding in this study is that myoblasts propagate global geometric alignment cues by local autocatalytic alignment feedback towards the regulation of long-range myotube architecture. The interplays between autocatalytic alignment feedback and geometric cues were therefore investigated by means of creating arbitrary shapes for myoblast differentiation (Fig. 5). Myotubes formed on large patterns show the ability of myoblasts to follow geometric cues in the microenvironment, as seen by curved myotubes formed as a result of juxtaposed geometric cues (Fig. 5A). The limit of geometric guidance can be seen by patterns with sharp corners, and small radii of curvature where myotubes are not able to completely follow the pattern and sharp edges become smoothed out when myotubes form (Fig. 5B,C). The overall tendency for myotube alignment and domain growth, however, is apparent, and autocatalytic alignment feedback favors not only production of well-ordered structures but also correction of local misalignment to ensure that globally well-aligned structures needed for proper tissue function are achieved. This can be seen in myoblasts differentiating on Y-shape patterns, in which multiple segments of muscle can connect smoothly (Fig. 5D). This is likely to have an important role during embryogenesis where muscle does not form in isolation but in conjunction with neighboring tissues whose structure could provide the spatial cue to provoke alignment feedback (Cossu et al., 1996; Green et al., 2004; Rowton et al., 2007; Shake et al., 2002; Yaffe and Feldman, 1965). Well-ordered alignment of striated muscle could then reinforce existing axes and orientations and help to promote proper development of neighboring tissue and overall organization.

Fig. 5.

Effect of myogenic differentiation on geometrical patterns for investigating the relationship between spatial cues and alignment feedback. (A–D) Phase-contrast images of myotubes formed on circular (A,C), square (B) and Y-shaped (D) patterns of different sizes.

Autocatalysis, or self-enhancement, is a hallmark in pattern formation where initial inputs become amplified by the action of individual cells to produce higher-order structure (Ermentrout and Edelstein-Keshet, 1993; Meinhardt, 1982). Most established autocatalytic factors in tissue morphogenesis, such as morphogens and surface receptors, are biochemical in nature. Our results suggest that physical factors can also be used in cellular self-organization, such as the autocatalytic alignment feedback mechanism observed in myoblast differentiation. Physical autocatalytic feedback is then probably involved in guiding the formation of other types of tissue, because adhesion and boundaries are crucial parts of many morphogenic processes.

Materials and Methods

Plasma lithography

Patterns used to guide cell attachment were generated using 3D polydimethylsiloxane (PDMS) molds (Dow Corning Sylgard 184) placed in conformal contact with polymer surfaces to selectively shield the substrates from the effects of air exposure (Junkin et al., 2011; Junkin et al., 2009; Junkin and Wong, 2011; Keyes et al., 2008). The patterning was done at room temperature in a plasma chamber (PDC-001, Harrick Plasma) at 150 Pa, with a radio frequency power of 29.6 W for 10 minutes. Selective exposure to the plasma results in a cell-sensitive chemical pattern that guides cellular attachment and movement. 3D molds were made using replica molding from photolithographically patterned masters. After plasma patterning, the surfaces were placed under UV for 10 minutes before cell seeding.

Cell culture and primary cell preparation

Cell lines, CRL-1772 mouse myoblast (C2C12) and ATCC CRL-1658 mouse embryo fibroblasts (3T3) were obtained from the American Type Culture Collection (ATCC). C2C12 cells were used from passage 3–10. Differentiation of C2C12 cells was induced upon reaching a confluence of 80–90% by switching to a medium with 5% horse serum that was exchanged every other day. Calcium-free culture and differentiation media were identical to normal medium except for the use of calcium and magnesium-free DMEM and the addition of 270 μM ethylene glycol tetraacetic acid (EGTA) (Neff et al., 1984). All cell lines were maintained under standard conditions and media formulations per ATCC guidelines unless otherwise specified. Primary cells comprising embryonic chick skeletal myoblasts were maintained and isolated as originally described (Almenar-Queralt et al., 1999; Gregorio and Fowler, 1995) and were cultured in DMEM (Invitrogen) supplemented with 10% ‘selected’ FBS (Sigma), 4% chick embryo extract and 1% antibiotics and antimycotics.

Immunostaining

C2C12 cells were stained with Alexa Fluor 555 Phalloidin (Invitrogen) to label actin, FITC-conjugated anti-vinculin (Sigma) to label focal adhesions and sealed with ProLong Gold Antifade Reagent (Invitrogen) containing 4′,6-diamidino-2-phenylindole (DAPI; Invitrogen) to label nuclei. Alternatively cell membranes were stained with CellMask Orange (Invitrogen). Primary cells were stained with primary antibodies including monoclonal anti-α-actinin (Sigma) to mark the Z-disc, polyclonal anti-titin T114 (Invitrogen) to mark the M-line and Alexa-Fluor-488-conjugated Phalloidin for F-actin. Secondary antibodies consisted of Alexa-Fluor-350-conjugated goat anti-mouse IgG (Invitrogen), and Texas-Red-conjugated donkey anti-rabbit IgG (Invitrogen). Coverslips for primary cells were mounted onto slides with Aqua Poly/Mount (Polysciences).

Imaging

Phase-contrast images of cells were captured on an inverted Nikon TE2000-U microscope using a SPOT camera from Diagnostic Instruments (model 2.2.1). Fluorescence images were captured on a Leica inverted DMI4000 B microscope using a Cooke SensiCamQE. Continuous, live-cell images were recorded using a custom fabricated live-cell apparatus consisting of a microscope stage incubator (AmScope Model TCS-100) to which a plastic enclosure was added. Normal atmospheric conditions were maintained by placing water trays to maintain humidity and by supplying 5% CO₂ passed through a 0.3 μm in-line filter at a slight overpressure to the chamber. Continuous imaging was conducted using either a Nikon TE2000-U or a Nikon Diaphot microscope with an Imaging Source DMK41AU02 camera. Cells were visually identified with phase-contrast microscopy by determining cell size and border, and examining morphology in contrast-enhanced images. Movement of cells was analyzed using a custom ImageJ macro that tracked a line drawn over the long axis of each cell. Position data was then exported for analysis and data including length, endpoints, angle and center point of each cell was followed sequentially over time. Alignment angle was measured relative to pattern direction with either 90° or 180° corresponding to the direction of the guidance cue. Time constants for alignment data were extracted from angle measurements by best fit of data to a first-order system. Multinucleation of cells was assessed by counting number of nuclei inside cells with multiple nuclei and comparing with total number of nuclei present.

Cellular automata modeling

Mathematical modeling was carried out using a MATLAB cellular automata program that was created to model cell alignment based upon relationships between a small neighborhood of cells. The program examines angles of cells in a 5×5 grid and places cells into groups of 10°bins. The number of cells in each bin is counted and if ten or more cells fall into the same angle bin then the cell at the center of the grid assumes the average angle of those ten (or greater) aligned cells. Otherwise, if between eight and nine cells fall into the same angle bin then the central cell assumes the average of the angle of the aligned block of cells and its current cellular angle. Otherwise, if any bin of cells has less than eight cells in it, then the cell at the center of the 5×5 grid assumes an 8:1 weighted average of its own alignment (8) and the average alignment of the cells with the greatest number in their alignment bin (1). This is then repeated for every cell in the array once per time step and cellular angle is mapped to a color and displayed. The algorithm for non-fusing cells is for alignment to neighboring cells without a decision based upon fusion or a high degree of alignment. During each time step, the central cell assumes a 2:1 weighted average of the largest aligned bin of cells (2), and the value of the central cell (1). During all steps of the algorithms, a small random angular change is either added or subtracted to the cell being analyzed.