Modeling the relative relationship of transcription factor binding and histone modifications to gene expression levels in mouse embryonic stem cells

Abstract

Transcription factor (TF) binding and histone modification (HM) are important for the precise control of gene expression. Hence, we constructed statistical models to relate these to gene expression levels in mouse embryonic stem cells. While both TF binding and HMs are highly ‘predictive’ of gene expression levels (in a statistical, but perhaps not strictly mechanistic, sense), we find they show distinct differences in the spatial patterning of their predictive strength: TF binding achieved the highest predictive power in a small DNA region centered at the transcription start sites of genes, while the HMs exhibited high predictive powers across a wide region around genes. Intriguingly, our results suggest that TF binding and HMs are redundant in strict statistical sense for predicting gene expression. We also show that our TF and HM models are cell line specific; specifically, TF binding and HM are more predictive of gene expression in the same cell line, and the differential gene expression between cell lines is predictable by differential HMs. Finally, we found that the models trained solely on protein-coding genes are predictive of expression levels of microRNAs, suggesting that their regulation by TFs and HMs may share a similar mechanism to that for protein-coding genes.

INTRODUCTION

Precise regulation of gene expression at specific times and spatial locations is fundamental to many biological processes. At the transcriptional level, gene expression is mainly regulated by transcription factors (TFs) (1) and histone modifications (HMs) (2,3). TFs activate or repress the initiation of gene transcription though binding to specific DNA sequences in promoters or enhancers. They could also affect gene expression by recruiting chromatin-modifying enzymes to induce chromatin structure changes (4,5). HMs regulate gene transcription by (1) modulating local chromatin structure and thereby changing the accessibility of TFs (2) directly recruiting transcriptional activators or repressors (4). In high eukaryotic organisms such as mice, several thousand of TFs act cooperatively to form a complex regulatory network, engaging in precise gene expression regulation (6). Meanwhile, an increasing number of HM types have been identified (7) and are thought to function individually or in combination to constitute a ‘histone code’ (8,9).

Predictive models have been constructed in previous studies to understand the relationship between gene expression and TF associated features, such as the occurrences of TF-binding sites (TFBSs) from computational analysis or experiments (10–12). These features have been used as inputs to predict gene expression patterns (12,13) or infer activities of TFs (14). However, these models accounted for only a small fraction of variation in gene expression due to high false positive rate of TFBS prediction or low quality of the experimental data (10,11). On the other hand, the effects of HMs on gene expression have been explored by high-throughput experiments. For example, H3K4me3 has been shown to be associated with active promoters in different species (3,15–17). More recently, two studies have shown that a large fraction of variations in gene expression could be explained by TF-binding signals (18) or HMs (19) from ChIP-seq experiments. Both of the two studies applied a linear model, but the former used a data set in mouse embryonic stem cells (ESC) and the latter was in human CD4⁺ T cells. Although the two studies have provided important information on gene expression by TFs and HMs, they did not answer the following questions: (i) do TFs and HMs provide complementary information or are they redundant for gene expression prediction? (ii) do signals of TF binding or HMs have different predictive power at different positions, e.g. upstream versus downstream of the transcription start site (TSS)? (iii) can the models be used to predict differential gene expression between two different conditions or tissues if the HM data are available for both? and (iv) can the models be extended to predict expression levels of non-protein-coding genes such as microRNAs (miRNAs)?

To answer these questions, we use the ChIP-seq data for 12 TFs and 7 HMs in mouse ESC cells, which provide TF binding profiles and HM patterns across the whole genome, respectively. We divide the DNA regions around TSS and TTS (transcription terminal site) into small bins of 100 bp, and for each bin we apply the support vector regression (SVR) method to predict gene expression based on the TF-binding signals (the TF model), HMs (the HM model) or a combination of TF and HMs (the TF + HM model). This strategy enables us to explore the spatial effect of TF binding and HMs on gene expression regulation. We also investigate the redundancy of the TFs and the HMs by gradually increasing the number of predictors in the models. Moreover, we examined the specificity of the TF and the HM models and the capability of the HM model for predicting differential gene expression between ESC and NPC (neural progenitor cell) using differential HMs as predictors. Finally, we investigate the effectiveness of the models for miRNA expression prediction. Here, we would focus our analysis on the mouse ESC data set, for it provides us with matched TF binding, HM as well as gene expression data. However, the statistical framework and the models introduced in this work can be generally applied to other datasets and species. With the accelerated accumulation of genome-wide data from the projects such as ENCODE and modENCODE, the models are expected to be refined and provide new insight on gene expression regulation.

MATERIALS AND METHODS

Expression data of protein coding and miRNAs genes

Gene expression data is available from two data sources measured by using RNA-seq and microarray techniques, respectively. We downloaded the mapped RNA-seq reads for mouse ESC and EB cells from http://grimmond.imb.uq.edu.au/mESEB.html (20). The expression levels for all mouse RefSeq genes were calculated according to the RPKM definition (21). Microarray data for mouse ESC, Mouse Embryonic Fibroblast (MEF) and NPC cells were downloaded from the NCBI Gene expression Omnibus (GEO) database under the accession designation GSE8024 (17). Based on the data, we calculated the expression levels (log intensities) of 17 560 RefSeq genes. Expression levels for 382 mouse miRNAs in ESC, MEF and NPC cells were quantified by using short RNA-sequencing experiments, which were downloaded from (22).

TF-binding data and HM data

The binding data for 12 mouse TFs in ESC by ChIP-seq experiments were downloaded from NCBI GEO under the accession designation GSE11431 (23). The ChIP-seq data for HMs in mouse ESC (seven HMs) and NPC (six HMs) cells were available from two data sources. The data for H3K4me1 and H3K4me2 were from (24) and the data for H3K4me3, H3K9me3, H3K20me3, H3K27me3 and H3K36me3 were from (17), both downloaded from ftp://ftp.broad.mit.edu/pub/papers/chipseq/.

Separating DNA regions into bins

To understand the spatial effect of TF binding or HM on gene expression, we separated the DNA regions around the TSS and TTS (−4 to ∼4 kb) of all RefSeq genes into small bins, each of 100 bp in size. This resulted in 80 bins centered at TSS (40 upstream bins and 40 downstream bins) and 80 bins centered at TTS (40 upstream bins and 40 downstream bins) for each gene. Based on the ChIP-seq data for a TF or a HM, we have calculated the coverage of each nucleotide (number of reads that cover a nucleotide) in the genome. To calculate the signal of TF binding or HM, we averaged the coverage of the 100 nt in each of the 160 bins. The above procedure resulted in a TF-binding data matrix and a histone modification data matrix for each bin. The matrix contains the TF-binding signals or histone modifications for all RefSeq genes in a corresponding bin. In addition, to capture the histone modification or TF-binding signals in the transcribed regions, we calculated the average signal of each feature in the exonic regions of genes. The annotation for 24 874 mouse RefSeq genes was downloaded from the UCSC Genome Browser at http://genome.ucsc.edu/, which provided the positions of the TSS and TTS of genes.

Calculation of signal profiles and correlation patterns

For a TF or a histone mark, we calculated its signal in each of the 160 bins for all RefSeq genes, which was then averaged across all genes to obtain the signal profile of the TF or the histone mark in the 160 bins. This resulted in a vector with 160 elements for each TF or HM, displaying its relative signal in DNA regions around the TSS and TTS. For visualization, the signal profiles were further normalized against the maximum value in these 160 bins. After normalization, the signal profiles always have a maximum value of one. The correlation pattern was obtained by correlating signal of a TF or a histone mark with gene expression levels in each of the bins. Spearman correlation coefficient was used to obtain a robust estimation of the relation between gene expression and TF/HM signals.

SVR models for predicting gene expression

The data matrix of TF binding or HMs was used to predict expression levels of genes quantified by RNA-seq or microarrays using a supervised machine learning method, SVR (25). In practice, we use the R package ‘e1071’ to implement the algorithm and choose the non-linear radial basis kernel. Cross-validation was used to estimate the prediction accuracy of SVR model. Data (predictors and expression) were divided into a training data set and a testing data set. Specifically, we randomly selected 10% of genes (approximately 2000) as the training data and used the remaining as the testing data. The SVR model was trained in the training data and subsequently applied to the testing data. We then calculated the Pearson correlation coefficient (PCC) (26) between the predicted expression values and experimental measured levels in the testing data. This procedure was repeated 10 times and the average PCC was computed to represent the prediction accuracy of the model. The square of PCC (R², coefficient of determination) indicates the proportion of variation of the gene expression levels that has been explained by the model (27).

We estimated our models by using the cross-validation method. We trained the model based on 2000 randomly selected genes and then applied it to predicting the expression levels of the remaining genes (approximately 20 000). The prediction accuracy was finally measured as the correlation (PCC) between the predicted values and the experimental values averaged from 20 cross-validations. The significance (P-value) for a PCC = r was calculated using Fisher Z transformation method: where Z′ follows a normal distribution with standard error of 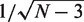(N ≈ 20 000 is the number of genes) (28). We also calculated the Spearman correlation coefficients between the predicted and experimental expression levels, which usually gave rise to a similar value as the PCC.

SVR models for predicting differential gene expression

The SVR method was also applied to predict the differential expression of genes in ESC versus NPC cells (log ratios). For this purpose, we calculate the signal difference of six HMs between the two cell lines and use them as the predictors. In this analysis, we used gene expression data measured by microarrays, since the microarray data, but not the RNA-seq data, was available for both ESC and NPC cell lines. The predictive model for differential expression prediction (NPC versus ESC) is only available for HM data, as the TF-binding data is only available for the ESC cell.

Two-layer SVR models

The two-layer model is to combine the signals of all features (TF or HM) in all the 160 bins. In the first layer, we predicted expression levels in each of the bins based on all the features in each individual bin. Then the expression levels predicted by each bin are combined in the second layer to make a final prediction. To be consistent, we applied the SVR method to both layers; however, the other machine learning approaches can also be used. More flexibly, the model can be designed in an alternative manner: first predicts expression levels using individual feature across all the bins in the first layer, and then integrates predictions by all the features in the second layer. Our results indicate that the first design achieved a more accurate prediction based on both TF-binding data and HM data.

Redundancy between individual TFs and HMs

Redundancy analysis is performed to investigate the minimum number of features that are required to achieve relatively high prediction accuracy. Using the TF model as the example, we constructed all the possible models by choosing m out of the 12 TFs as predictors (m = 1, 2, … , 12), resulting in a total of 4095 models [C (12,1)+ C (12,2)+… + C (12,12)]. The prediction accuracies of all these models were estimated by cross-validation.

Predicting expression levels of miRNAs

We downloaded the annotation of 400 mouse miRNAs from the miRBASE database (29). For most miRNAs, the annotation provides no information about the TSSs. Instead, only the start and end positions of the corresponding pre-miRNAs (∼100 nt in length) are available. For each miRNA, we calculated the numbers of reads covering each nucleotide and averaged them as the signal for a TF or a HM. The resulted TF-binding signals or HM signals were input into the SVR model trained solely on the protein-coding data. Specifically, the model was trained on the expression data of protein-coding genes from RNA-seq and TF-binding data in Bin 40 (0-bp upstream of TSS) for the TF model or HM data in Bin 46 (600-bp downstream of TSS) for the HM model, which are the best predictive bin for TF model and HM model, respectively, according to protein-coding gene results. The trained SVR regression model was used to predict miRNA expression levels.

We validated the predicted values of miRNAs by comparing with their expression levels from small RNA-Seq experiments (22), which provided expression levels of miRNA in mouse ESC, MEF and NPC cells. Based on the experiment results, we divide the miRNAs into highly expressed (H group, more than 100 reads) and lowly expressed (L group, 0 reads) miRNA groups in each of the three cell types. We compared the predicted expression levels of the E group miRNAs with those of the NE group miRNAs using the t-test to examine the effectiveness of our model. We used different threshold setting to determine highly and lowly expressed miRNA groups, which all resulted in similar results.

Classification of mouse promoter based on CpG content

We calculated the normalized CpG content in the DNA regions surrounding the TSS (from −1500-bp upstream to 1500-bp downstream) of mouse RefSeq genes using the method described in Saxonov et al. (30). The normalized CpG contents for all promoters showed a bimodal distribution. We therefore set the cutoff value to 0.32, which best separated the two peaks in the distribution. Promoters with a normalized CpG content ≥3.2 were classified as high CpG content promoters (HCPs), and the remaining promoters were classified as low CpG content promoters (LCPs). Accordingly, the mouse RefSeq genes were grouped into HCP genes and LCP genes.

Gene ontology analysis

GO analysis was performed using the DAVID functional annotation tool at http://david.abcc.ncifcrf.gov (31). Given a gene set, the tool identifies the over- or under-represented gene categories prefunded by the Gene Ontology project (http://www.geneontology.org) (32). A P-value cut-off of 0.01 was used in the analysis.

RESULTS

Correlation patterns of TFs and HMs with gene expression

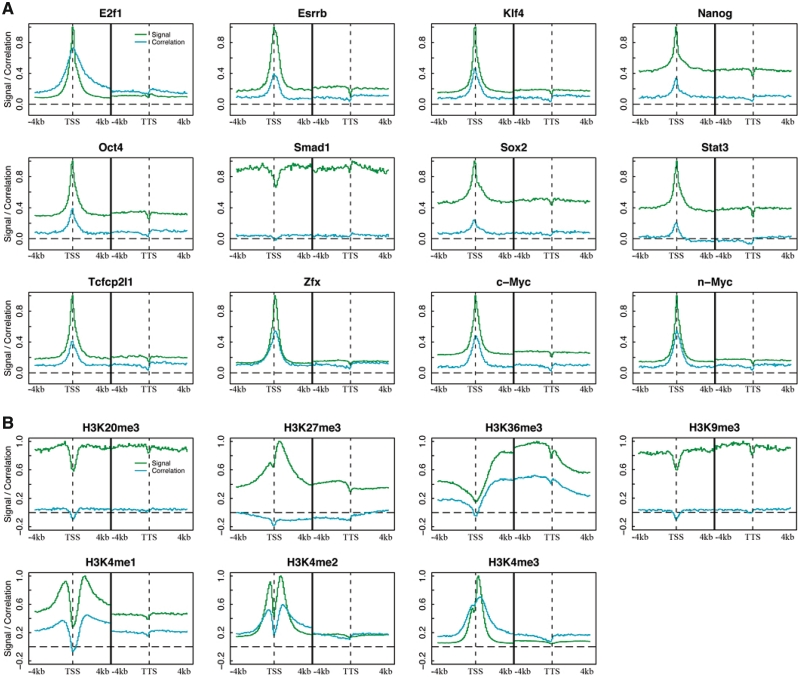
The strength of TF binding (18) and HMs (19) has been shown to be correlated with gene expression levels. However, the spatial effect of TF binding and HMs on gene expression has not been systematically explored. To address this issue, we use the mouse ESC as a model to investigate signal profiles of 12 TFs (E2f1, Esrrb, Klf4, Nanog, Oct4, Stat3, Smad1, Sox2, Tcfcp2l1, Zfx, c-Myc and n-Myc) (23) and seven histone marks (H3K4me1, H3K4me2, H3K4me3, H3K9me3, H3K20me3, H3K27me3 and H3K36me3) (17,24) as well as their correlation pattern with gene expression. In our analysis, DNA regions (−4 to ∼4 kb) around the TSS and TTS of all mouse RefSeq genes were separated into small bins, each of 100 bp in size. ChIP-Seq was used to quantify TF-binding signals and HMs across the whole genome. Expression levels for all genes were measured by RNA-seq (20) and represented as RPKM, the number of reads per kilobase of exon region per million mapped reads (21). For a TF or a histone mark, we calculated its signal in each of the 160 bins for all RefSeq genes, which was then averaged across all genes to obtain the signal profile of the TF or the histone mark in the 160 bins (See ‘Materials and Methods’ section for detail). Correlation pattern was obtained by correlating signal of a TF or a histone mark with gene expression levels in each of the bins. Signal profiles demonstrate the distribution of TF-binding signals or HM signals around gene loci, while correlation patterns display their positional contributions to influencing gene expression levels.

Figure 1A and B show the signal profiles (green) and correlation patterns (cyan) of the 12 TFs and 7 histone marks in ESC. With the exception of Smad1, signal profiles of all TFs are similar to one another, exhibiting a peak at the TSS. The signals of all these TFs are positively correlated with gene expression levels. More interestingly, correlation patterns are highly consistent with the corresponding signal profiles, suggesting that as a whole the DNA regions with stronger-binding signals contribute more to gene expression regulation. Smad1 shows no enriched signal in the vicinity of TSS, indicating that its binding might not be restricted to the promoter regions. In fact, we examined the binding peaks of Smad1, and found that only 3% are within ±1 kb and >86% are 5-kb away from the TSS of any gene. This is very different from the distribution of the binding peaks of E2f1, c-Myc and n-Myc, which associate extensively with promoter regions (33), e.g. >65% of the binding sites of c-Myc are within ±1 kb of TSS (Supplementary Figure S1).

Figure 1.

Signal distribution and correlation pattern of TFs (A) and histone marks (B) around TSS and TTS. DNA regions around TSS and TTS (−4 to ∼4 kb) of genes were divided into100-nt bins. Signal distribution (green curves) was calculated by averaging signal across all genes in each bin. Correlation pattern (cyan curves) was obtained by correlating signal with expression levels across all genes. The black line at the center of each plot separates TSS and TTS regions.

Histone marks, in contrast with TFs, vary dramatically with one another in their signal profiles and correlation patterns (Figure 1B). H3K4me1, H3K4me2 and H3K4me3 exhibit strong signals around TSS, which is consistent with their function as marks for active promoters. Signals from H3K27me3 and H3K36me3 cover the whole transcribed region (34). The former mainly function in 5′-UTR and the latter shows stronger signal in 3′-UTR, which is also consistent with previous studies (35). In contrast, signals from H3K20me3 and H3K9me3 show no significant differences between transcribed and inter-genic regions. It is also notable that almost all these HMs, exhibit relatively lower signals at the TSS than in the nearby region, presumably due to the low occupation of nucleosomes around TSS (36). On the other hand, similar to the results for TFs, the contribution of HMs to gene expression regulation is also dependent on the strength of their signals as indicated by the consistency between their signal profiles and correlation patterns. Moreover, as shown by their correlation patterns, H3K4me1, H3K4me2, H3K4me3, H3K36me3 function in general as positive marks, whereas H3K27me3 acts mainly as a negative mark. There is no obvious correlation between gene expression levels and the signals for H3K20me3 or H3K9me3.

As described above, many TFs and HM are individually correlated with gene expression levels. We thus ask: how good can the TF signals and/or HM signals predict gene expression levels in a combinatorial manner? In the next three sections, we describe the machine learning models using the predictors of TFs, HMs and a combination of them, respectively.

TF binding is predictive of gene expression levels

To investigate the power of TFs for predicting gene expression in a combinatorial manner, we applied the supervised machine learning method, called SVR, to each of the 160 bins. In each bin the signals (mean coverage of the 100 bp in the bin) for these 12 TFs were taken as inputs (predictors) to predict gene expression levels [log(RPKM)] measured by RNA-seq experiments. We estimated the prediction accuracy of each bin using the cross-validation. Specifically, the model trained from a training data set was applied to predict expression levels of genes in an independent testing data set. Prediction accuracy was calculated as the PCC between the predicted and the experimental measured expression levels, or alternatively as the R² (i.e. coefficient of determination) which can be interpreted as the proportion of the variation in gene expression that can be accounted for by the model (27).

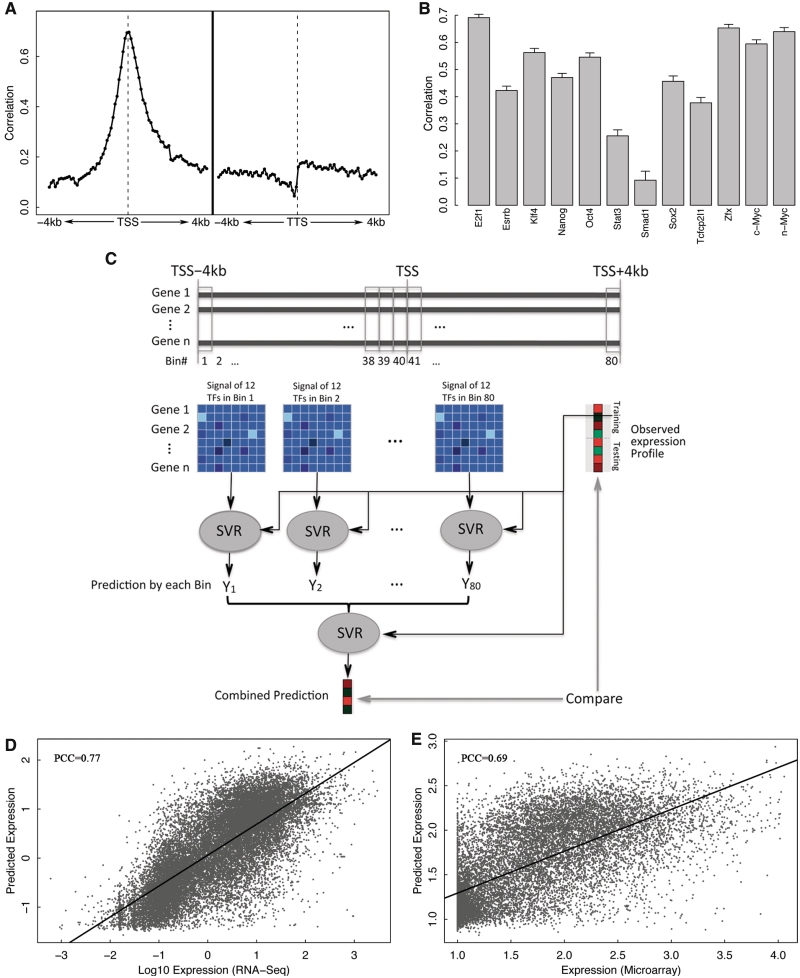
Figure 2A shows the prediction accuracy of all the 160 bins centered at TSS or TTS. As shown, the highest predictive power (PCC = 0.71) was achieved at the TSS, which individually accounts for ∼50% of the variation of gene expression (Supplementary Figure S2). Predictive power decays quickly with an increase of distance from the TSS. As shown, TF-binding signals >2 kb away from the TSS provide very limited contributions to gene expression levels. Our results also indicate that DNA regions downstream of the TSS contribute as much or more to the control of gene expression levels than the upstream DNA regions. Although there are many TFBSs in distal regions (Supplementary Figure S1), overall the distal sites might contribute less to gene expression levels than those in promoter regions.

Figure 2.

TF model for gene expression prediction in ESC. (A) Prediction accuracy of each of 160 bins around TSS or TTS (−4 to 4 kb). In each bin, expression levels are predicted using SVR based on binding signal of 12 TFs. (B) Individual predictive power of the 12 TFs. For each TF, expression levels are predicted using SVR based on signal in all bins. (C) A two-layer TF model. Expression levels are first predicted using TF-binding signals in 80 bins and then the predicted values are integrated in the second layer to make final predictions. SVR method is applied in both layers. (D) Prediction results of the two-layer model for RNA-Seq expression data. (E) Prediction results of the two-layer model for microarray expression data.

To examine the relative importance of each TF for gene expression regulation, we constructed a model for each TF using its signals in the 160 bins as predictors, and estimated their individual prediction accuracy by cross-validation. As shown in Figure 2B, among the 12 TFs E2f1 has the highest and Smad1 has the lowest power for gene expression prediction. The TFs with high predictive powers, including E2f1, n-Myc, c-Myc and Zfx, tend to have binding peaks associated with promoter regions. Conversely, TFs with relatively lower predictive powers, e.g. Smad1and Stat3, are more likely to bind DNA regions distant from the TSS (Supplementary Figure S1). From the statistical point of view, the expression levels of genes are largely determined by promoter-associated TFs such as E2f1. The dominance of E2f1 for expression prediction might be explained by the fact that it binds a large number of promoters. Specifically, there are 10 932 genes that contain at least one binding peaks of E2f1 in their promoter region (from −1000-bp upstream to 500-bp downstream of the TSS), much more than the other TFs (e.g. the second most targeted TF, Zfx, binds only 6511 genes, see Supplementary Table S1).

In order to integrate the binding signals of all TFs at different locations, we designed a two-layer model for gene expression prediction. In the first layer, signals of all the 12 TFs were combined to make predictions of expression separately at each bin. The predicted expression levels by distinct bins (80 bins centered at TSS) were then combined in the second layer to make the final prediction (Figure 2C). For both layers the SVR algorithm was utilized. When applied to RNA-seq data, the model achieved a correlation of 0.77 (R² = 0.59) between predicted and real expression levels according to our cross-validation results, which is significantly higher than the accuracy from any bin individually (Figure 2D). When the average TF-binding signals in the exonic regions were also integrated into the two-layer model, the prediction accuracy was further improved to 0.78. Instead of combining TFs first, an alternative two-layer model is to first combine signals of different TFs in all bins followed by the integration of predictions based on each of the TFs (Supplementary Figure S3). It turned out that the second model has lower prediction accuracy, with a correlation of 0.75 (R² = 0.55). Other than these two-layer models, we also examined a simple model that uses the maximum signal of each TF across all the 160 bins as predictors. The maximum signal-based model achieves a comparable prediction accuracy to the two-layer model shown in Figure 2C, implying that the regulation of a TF to its target can be best represented by the maximum signal around the gene loci. The maximum signal-based model is sensitive to noise and signal from nearby genes or intronic regions (e.g. intronic miRNAs). When applied to a more compact genome such as C. elegans, it resulted in much worse prediction accuracy (PCC = 0.58) than the two-layer model (PCC = 0.75). In addition, we examined the predictive power of a one-layer model that used the TF features in all of the 160 bins (12 × 160 predictors). The model gave rise to similar prediction accuracy (PCC = 0.75) and it required considerably more computation time for training the model due to the large number of parameters. A TF can activate the transcription of some of its target genes while, at the same time, also represses the transcription of others. In Ouyang et al. (18), this issue was overcome by applying regression model to the principle component vectors (TFPCs) extracted by PCA analysis. The same strategy can also be applied to our models. For instance, we examined the SVR model based on TFPCs from the maximum signal of the TF-binding data, which, however, did not improve the prediction accuracy (Supplementary Figure S4). Thus, in this work, we mainly focus on the two-layer model and utilize the maximum signal-based model only when the computation is too intensive (e.g. redundancy analysis).

We also applied the two-layer model to predict gene expression measured by microarrays. As shown in Figure 2E, the prediction accuracy for microarray data is much less than that for RNA-seq data with a correlation of 0.69 (R² = 0.48). The relatively lower performance in microarray data is largely due to its insensitivity to genes with low expression (Supplementary Figure S5).

HMs are predictive of gene expression levels

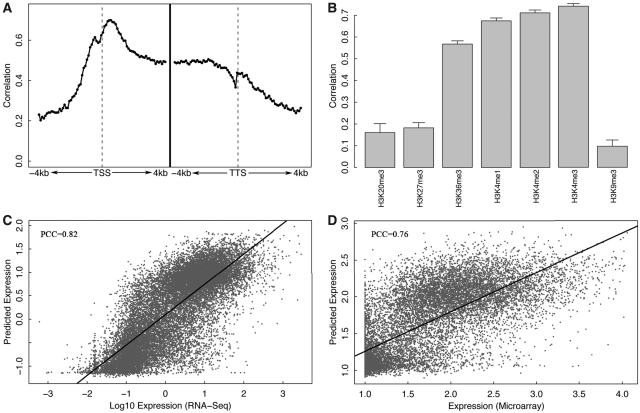
We next examined the relationship between gene expression and HMs. In keeping with the process for TFs, we combined the seven histone marks (as predictors for the SVR model) in each of the 160 bins using the SVR model to predict gene expression levels. The prediction accuracies of these bins were displayed in Figure 3A. In comparison with the profile of the TF models (Figure 2A), the HM models are highly predictive to expression across the whole of the transcribed regions and extend to upstream of the TSS and downstream of the TTS (Figure 3A). The highest predictive bins are within the transcribed region immediately downstream of the TSS. The substantial difference in the pattern of predictive powers between the TF models and the HM models results from the fact that most TFs mainly function at the TSS region whereas distinct HMs function at different locations for gene expression regulation (34,37).

Figure 3.

HM model for gene expression prediction in ESC. (A) Prediction accuracy of each of 160 bins around TSS or TTS −4 to 4 kb). In each bin, expression levels are predicted using SVR based on signal of seven HMs. (B) Individual predictive power of the seven HMs. For each HM, expression levels are predicted using SVR based on signal in all bins. (C) Prediction results of the two-layer HM model for RNA-Seq expression data. (D) Prediction results of the two-layer HM model for microarray expression data. The prediction powers of H3K36me3, H3K4me1, H3K4me2 and H3K4me3 are significantly higher than those of H3K20me3, H3K27me3 and H3K9me3 (P < 0.001, t-test).

We also estimated the individual predictive power of each of the seven HMs. As shown in Figure 3B, H3K4me1, H3K4me2, H3K4me3 and H3K36me3 are highly predictive of gene expression, while H3K9me3, H3K20me3 and H3K27me3 only show low predictive powers. It is not surprising to see the low predictive power of H3K9me3 and H3K20me3, since their signal profiles are invariant around the gene loci and have no significant correlation with gene expression (Figure 1B). The low predictive power of H3K27me3, however, is to some extent out of expectation considering that its signal profile shows a strong peak right after the TSS and is considerably anti-correlated with gene expression (maximum PCC < −0.2).

To integrate the HM signals in different bins, we applied a two-layer predictive model similar to the one shown in Figure 2C for TF. In this model, the signals in all the 160 bins are considered, instead of using only the 80 bins around TSS as in the TF model, since the HM signal contribute to expression prediction across the who gene loci as shown in Figure 3A. The predictive power of the two-layer model for HMs (HM model) is a little higher than that of the two-layer model for the 12 TFs (TF model). When applied to RNA-seq data, the HM model achieves a correlation of 0.82 (R² = 0.67) between the predicted and the real expression levels (Figure 3C). When applied to microarray expression data, the HM model obtains a correlation of 0.76 (R² = 0.58) (Figure 3D), which is consistent with the results by the TF model and again indicates the lower sensitivity of the microarray relative to RNA-seq for detecting low expression genes. When the average HM signals in the exonic regions were also integrated into the two-layer model, the prediction accuracy could be further improved to 0.84 (RNA-seq model).

TFs and HMs are redundant for predicting gene expression levels

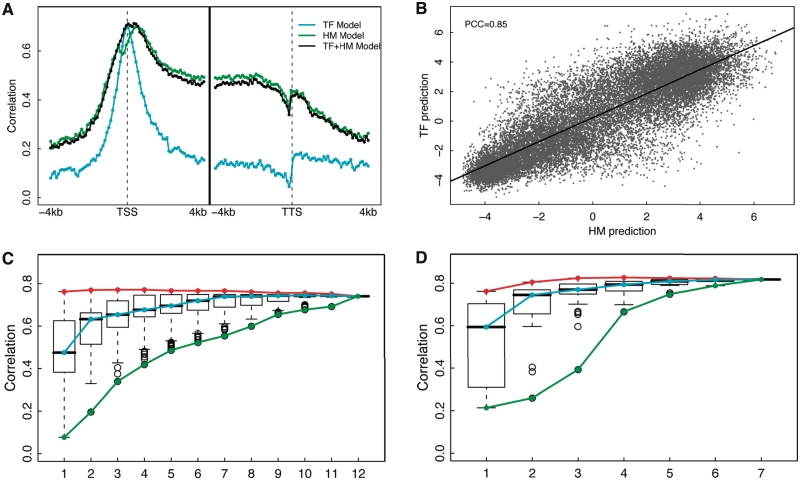
As shown above, both the TF-based models (TF models) and the HM-based models (HM models) are highly predictive of gene expression. We then ask: can the combination of TF signals and the HM signals further improve the predictive power? How many factors or histone marks are needed for the two models to achieve high prediction accuracy? To answer these questions, we examined the prediction accuracies of the 160 bins, for which SVR was implemented using the 12 TFs and the 7 HMs as predictors. As shown in Figure 4A, the TF+HM models only obtain prediction accuracy similar to that of the HM models or the TF models across all bins, suggesting that the TF binding signal and HM signal are generally redundant for gene expression prediction. The redundancy between them might be partially explained by the correlation between the TF-binding signals and HM signals (Supplementary Figure S6).

Figure 4.

Redundancy of the TF and the HM models in ESC. (A) The prediction accuracy of three models: the TF model, the HM model and a combined TF+HM model, in each of the 160 bins. (B) Consistency between TF model predictions and HM model predictions. The predicted expression values were based on the two-layer TF model (y-axis) and the two-layer model (x-axis). (C) Distribution of prediction accuracies of all m-TF models with m taken from 1 to 12. (D) Distribution of prediction accuracies of all m-HM models with m taken from 1 to 7. The maximum, the median and the minimum prediction accuracy for m-TF (C) or m-HM (D) models are connected by the red, cyan and green curves, respectively. In (C) and (D), the maximum signals for TF binding or HMs across the 160 bins were used as the predictors.

Again, we applied a two-layer model to make an overall prediction. The model is similar to the two-layer TF model described in Figure 2C, but integrates the signals of the 12 TFs in the 80 bins around TSS and the 7 HMs in all the 160 bins. This two-layer TF+HM model achieves similar prediction accuracy as the two-layer HM model (PCC = 0.85, R² = 0.72), again indicating the high redundancy between TF binding and HM signals (Supplementary Figure S7). To further investigate their redundancy, we examined whether the HM model was able to predict expressions that had not been captured by the TF model. Specifically, we first applied the TF model, and calculated the difference between the predicted and real expression levels of genes (expression residuals). The expression residuals represent the expression levels that have not been explained by the TF model. Then we applied the HM model to predict the expression residues. If the HM model provides additional predictive capability to the TF model, we would expect to predict the expression residuals accurately. However, our results show that the HM model is poorly predictive of the expression residuals (i.e. there is no correlation between the predicted values and the expression residues in cross-validation) from the TF model. Similarly, the TF model is not able to predict the expression residuals from the HM model either, suggesting that HMs do not provide additional information to TFs and vice versa. Moreover, the prediction results by the TF model and the HM model are fairly consistent with each other (PCC = 0.85) as shown in Figure 4B. All these results further support that the idea that the TF models and the HM models are statistically redundant for predicting gene expression. We identified a subset of genes that are predicted differentially by the TF and the HM models. Gene Ontology analysis was performed and no gene set was found to be significantly enriched in these genes. Although the overall prediction performance was not improved by combining TF binding and HM signals, the TF+HM model tended to achieve more accurate predictions (i.e. smaller difference between predicted values and real expression levels) than the TF or HM model alone.

We next explored the redundancy among the 12 TFs in the TF model and the redundancy among the 7 HMs in the HM model in terms of gene expression prediction. Using the TF model as our example, we constructed the predictive models based on all possible combinations of TFs by choosing m out of the 12 TFs (m = 1, 2, … , 12), which resulted in a total of 4095 models. To simplify the calculation, the maximum signals of TFs in the 160 bins were used as the predictors. The results were slightly different from those obtained by the two-layer model described in Figure 2A, but the tendency of the prediction accuracy to change with factor numbers was similar between the two models. We calculated the predictive accuracies of these 4095 models by using cross-validation. Figure 4C shows the distributions of the accuracies for models based on various numbers of TFs (denoted as m-TF model).

The cyan curve and the red curve mark, respectively, the median and the best prediction accuracy of the one-TF, two-TF and until 12-TF models. As shown, although models with more factors are generally more predictive (cyan curve), there is no significant improvement for the maximum prediction accuracy of the m-TF models (red curve). In fact, the one-TF using E2f1 as the predictor resulted in a correlation of 0.76 (R² = 0.58) between predicted and real expression levels, which is just a slightly lower than the best prediction achieved by the four-TF model with predictors E2f1, Zfx, c-Myc and n-Myc (PCC = 0.77, R² = 0.60). These results indicate the high redundancy among these 12 TFs for expression prediction. In addition, the best of the m-TF models (m = 1, 2,…,12) always includes the factor E2f1, indicating that it contributes mostly to statistical prediction of gene expression levels. It has been shown that Oct4, Sox2, C-Myc and Klf4 are sufficient for reprogramming fibroblasts to induce pluripotent stem cells, which are functionally similar to ES cells (38–40). The model using these four TFs as predictors, however, results in prediction accuracy only close to the average of all the four-TF models (PCC = 0.67, R² = 0.45).

Similarly, HMs are also highly redundant for gene expression prediction. As shown in Figure 4D, the maximum prediction accuracies achieved by models with two or more HMs are approximately similar (red curve), indicating gene expression levels can be predicted by using only two HMs. This redundancy has been shown in Karlic et al. based on linear predictive models in human CD4⁺ T cells (19). The best model is from the four-HM models with predictors H3K4me2, H3K27me3, H3K36me3 and H3K4me3 (PCC = 0.83), which account for >68% of the variation of gene expression (R² = 0.68).

The above analysis is based on all mouse RefSeq protein-coding genes, which potentially has the following two caveats: (i) for genes with multiple transcripts, we might mix up TF binding or HM signals from different transcripts; (ii) a gene might contain TF binding or HM signals from nearby genes (≤4 kb). To overcome these problems, we identified 6609 non-overlapping mouse ResSeq genes that have only single transcript and ≥8-kb away from any other genes. We repeated the above analysis in these non-overlapping genes and obtained consistent results (Supplementary Figure S8).

Predicting expression levels for genes with HCP and LCP

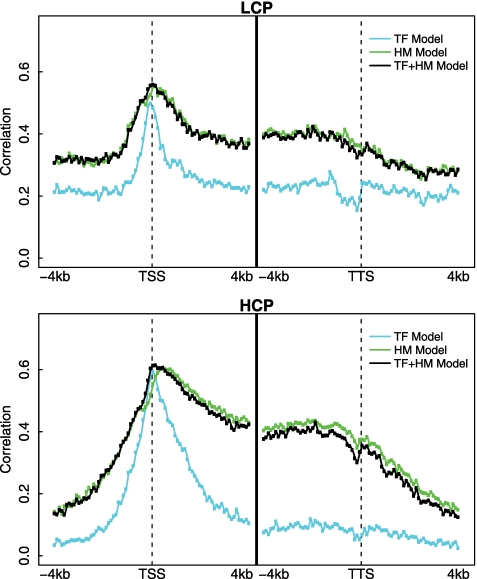
It has been shown previously in human that promoters could be distinguished into two classes with HCP and LCP (30). These two classes of promoters are differentially marked by HMs and might be regulated by different mechanisms (17). Using the method proposed in (30), we calculated the normalized CpG content for all mouse RefSeq genes. As in human, the normalized CpG content of mouse promoters also follows a bimodal distribution, based on which we identified 8505 LCP and 15 712 HCP genes (Supplementary Figure S9A). The HCP genes are more likely to be highly expressed than the LCP genes (Supplementary Figure S9B).

We applied our models to the LCP genes and the HCP genes separately and examined their predictive powers. As shown in Figure 5, the spatial patterns of predictive power are similar to cases where the models are applied to all genes (Figure 4A), though the values are consistently lower. Nevertheless, the models perform better in the HCP group than in the LCP group. These results were further confirmed by using our two-layer models. As described above, when applied to all genes, the two-layer TF, HM and TF+HM models achieved prediction accuracy of PCC = 0.77, PCC = 0.82 and PCC = 0.85, respectively. But for the LCP group, the accuracy was PCC = 0.63, PCC = 0.73 and PCC = 0.74; for the HCP group the accuracy was PCC = 0.70, PCC = 0.77 and PCC = 0.77. We examined the power of each individual TF or HM for predicting the expression levels of the LCP genes and the HCP genes, and found that different modifications are important in these two groups (Supplementary Figure S10). These results suggest that the expression of the LCP genes and the HCP genes might be regulated by different mechanisms.

Figure 5.

Predicting the expression level of genes with LCP and HCP promoters.

To further investigate the regulatory difference between genes, we selected 1000 most easily predicted and 1000 hardest to predict genes according to their residuals (the difference between the predicted and the real values): the former genes were more accurately predicted than the latter ones by the two-layer HM model. We examined the HM signals in TSS regions of the two gene sets, and found that some histone marks, e.g. H3K36me3, showed different patterns (Supplementary Figure S11).

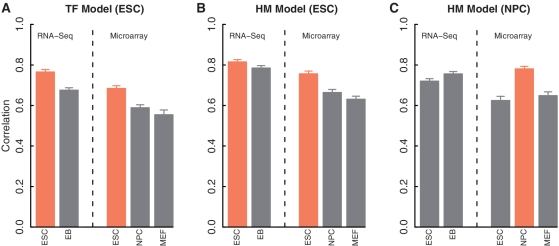
TF and HM models are cell line specific

TF binding and HMs are dynamical processes that depend on tissues, cell lines or conditions. We investigated the cell line specificity of the TF models and the HM models. If the model is cell line specific, we would expect to obtain the best prediction accuracy when matched TF binding and gene expression data (i.e. from the same cell line) are used. For the TF model, we applied the two-layer model to the TF-binding data in ESC to predict gene expression levels measured by RNA-seq in ESC and in EB (Embryoid Body) cell lines, as well as by microarrays in ESC, NPC (Neural Progenitor Cell) and MEF cell lines. As shown in Figure 6 (left panel), the TF model based on TF-binding data in ESC predicts more accurately for gene expression levels in the same cell line, indicating that the TF model is cell line specific. For instance, the correlation between the expression levels predicted by the TF model (using TF-binding data in ESC) and the RNA-seq expression levels is 0.77 (R² = 0.59) in ESC, significantly >0.68 (R² = 0.46) in EB.

Figure 6.

Cell line specificity of the TF and the HM models. (A) TF models based on TF-binding data in ESC for predicting expression levels from RNA-Seq in ESC and EB, and from microarrays in ESC, NPC and MEF. (B) Similar to the Left, but for HM models. (C) Similar to the Middle, but the HM models are based on HMs in NPC. For all models, the prediction accuracies are estimated from the cross-validation results of 100 re-sampled data sets. The cell line matched models are highlighted in yellow color. In all groups, the predictions are more accurate for the matched cell line (yellow bars) than for the others (gray bars) (P < 0.001) according to t-test.

The HM model is also cell line specific. The HM data is available for two cell lines, ESC and NPC. As shown in Figure 6 (the middle and the right panels), the HM model based on ESC or NPC always shows the highest predictive power for expression levels in the corresponding cell lines, no matter RNA-seq or microarray is used for measuring gene expression. It also should be noted that the predictability of the TF model or the HM model for expression levels in a distinct cell line is largely due to similarity in expression levels in these cell lines, e.g. the correlation of the expression profiles in ESC and EB by RNA-seq is 0.95 (PCC).

Differential HMs are predictive of differential expression of genes between cell lines

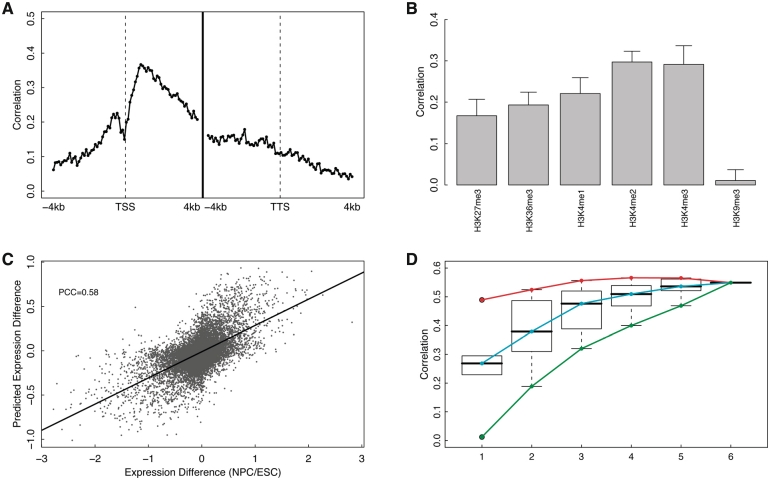
Motivated by the fact that HMs are cell line specific, we next investigated the possibility of predicting differential gene expression based on differential HMs between cell lines. The signal profiles of six HMs, H3K4me1, H3K4me2, H3K4me3, H3K9me3, H3K27me3 and H3K36me3, are available for the cell line ESC and NPC. We calculated the difference of these six HMs between NPC and ESC, and utilized them to predict the differential expression [log₂(NPC/ESC)]. A corresponding TF model has not been examined since the binding profiles of those 12 TFs are available only in mESC.

Using individual bins separately, the spatial pattern of prediction accuracies for differential expression across 160 bins is shown in Figure 7A. Interestingly, the pattern exhibits a peak in the DNA region right after TSS, which resembles the spatial pattern of the TF model (Figure 2A), rather than the HM model (Figure 3A). In other words, the predictive power of the HM model in differential expression is much lower in the 3′ of transcribed region, which is in strong contrast with the HM model for expression level prediction. Regarding to the relative importance of the six histone marks for predicting differential gene expression, as shown in Figure 7B, the differences in H3K4me3, H3K4me2 and H3K4me1 are most important, whereas the contribution of H3K9me3 is more or less neglectable.

Figure 7.

HM model for predicting differential gene expression in NPC versus ESC. (A) Prediction accuracy of each of 160 bins around TSS or TTS (−4 to 4 kb). In each bin, log ratios of gene expression for NPC/ESC are predicted using SVR based on signal differences of six HMs between the two cell lines. (B) Individual predictive power of the six HMs. For each HM, expression levels are predicted using SVR based on difference of the modification in all bins. (C) Prediction results of the two-layer HM model that combines differential signals of the six HMs in all of the 160 bins. (D) Distribution of prediction accuracies of all m-HM models with m taken from 1 to 6. The maximum, the median and the minimum prediction accuracy for the m-HM models are connected by the red, cyan and green curves, respectively.

We further built up the two-layer model that combined the differential signal of these six HMs in the 160 bins (similar to the one shown in Figure 2C). The model predicted the differential expression log₂(NPC/ESC) fairly well, with a correlation of 0.58 between the predicted and the experimental determined log ratios (Figure 7C). In short, the differential expression is more challenging than expression level for prediction: the HM data-based model explains ∼68% of the variation of expression levels in ESC, but only 34% of variation of the differential expression, log₂(NPC/ESC).

To address whether differential histone signals are redundant in predicting differential gene expression, we examined the predictive powers of all the possible models (63 models) by choosing m (m = 1, 2, … , 6) predictors out of the six differential HMs between NPC and ESC (Figure 7D). Again, to simplify the calculation the maximum difference of a HM in the 160 bins is used as the input for the SVR models. Generally, the prediction accuracy increases by including more HMs in the model, but gradually the improvement become less substantial. In fact, the highest prediction accuracy is achieved when four HMs (H3K4me2, H3K4me3, H3K27me3 and H3K36me3) are used. These results indicate that individual HMs are to some extent redundant for predicting gene expression, as well as predicting differential expression between cell lines.

TF and HM Models are predictive of miRNA expression levels

All the analysis described above is for protein-coding genes. Can signals for TF binding or HMs predict the expression levels of miRNA genes? To answer this question, we downloaded the annotation of all mouse miRNAs from the miRBase (29), which in most cases provided the start position and end position of the corresponding pre-miRNAs (∼100 nt). We predicted the expression levels of all mouse miRNAs using the SVR model trained solely on the protein-coding data (see ‘Materials and Methods’ section for details). Unlike the protein-coding genes, the DNA regions corresponding to pre-miRNAs are narrow and need not to be divided into bins. We therefore simply used the TF binding signal or HM signal within the pre-miRNA regions as predictors.

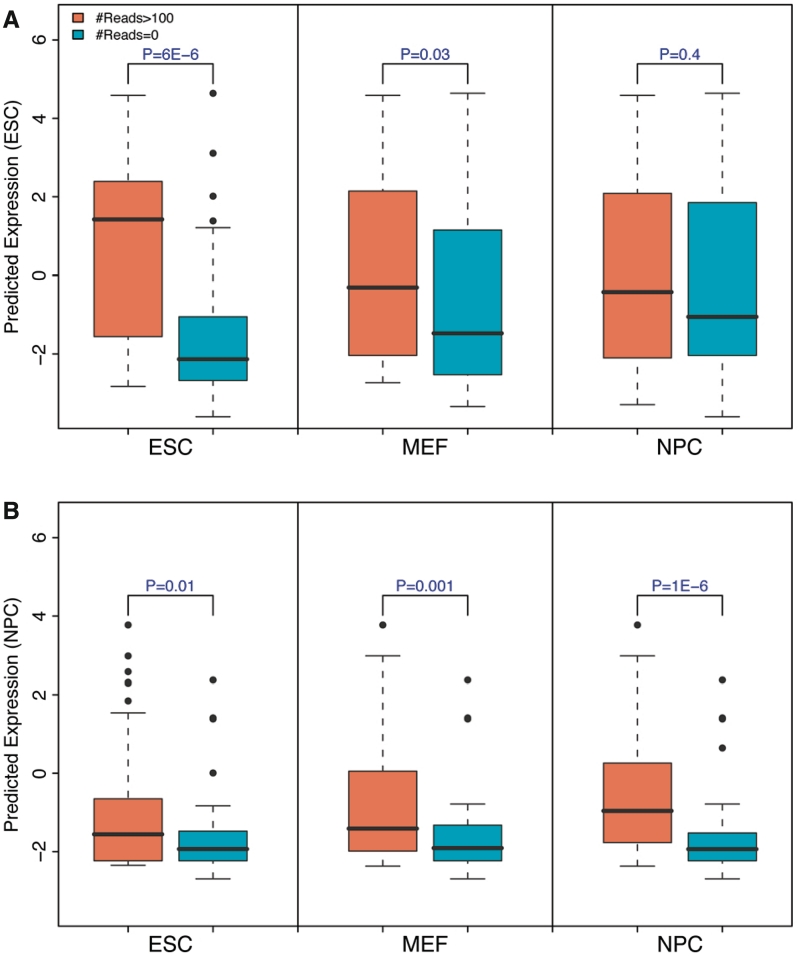
To validate our predictions, we used data from the small-RNA sequencing experiment performed by Marson et al. (22), which provided expression levels of miRNA in mouse ESC, MEF and NPC cells. First of all, using the data, we classified highly expressed (H group) and lowly expressed (L group) miRNA groups in each of the three cell types. We then examined the predicted expression values for miRNAs in these groups. As shown in Figure 8A, using the HM profiles in ESC, the HM correctly distinguishes the two miRNA groups: the H group is predicted to have significantly higher levels than the L group (P = 6E – 6, t-test). The H group and L group for MEF and NPC, however, shows no significant difference in their expression levels, indicating that the HM model is cell line specific. Similarly, the miRNA expression levels predicted based on HM data in NPC best distinguish the H group from the L group for NPC, but not for MEF and ESC (Figure 8B). Therefore, the HM model trained solely on protein-coding data can predict miRNA expression in a cell line specific manner. This suggests that protein-coding and miRNA genes may share a similar mechanism of transcriptional regulation by HMs. In mouse, >50% miRNAs reside in known genes, e.g. in the intronic regions, and their expression might be affected by the promoters of the hosts. To overcome this problem, we repeated the analysis using a subset of miRNAs that were not overlapping with any other genes, and obtained very consistent results (Supplementary Figure S12).

Figure 8.

The HM model is predictive of miRNAs expression with cell line specificity. (A) Distribution of predicted miRNAs expression levels for highly and lowly expressed miRNAs in ESC (left), MEF (middle) and NPC (right). The model is trained on data for protein-coding genes in ESC. (B) Similar to (A), but the model is trained on data in NPC. High and low miRNA groups are determined based on small RNA sequencing data.

On the other hand, the TF model failed to predict expression levels of miRNAs. It might be the case that TF signals are predictive of miRNA expression only around the TSS region, as demonstrated in Figure 2A for coding gene expression. As the pre-miRNA DNA regions were in general distant (>1 kb) from the actual TSS of miRNAs (i.e. the TSS of pri-miRNAs), the TF-binding signals corresponding to the pre-miRNA regions contribute little to transcriptional regulation and are not able to predict gene expression levels with high accuracy. Nevertheless, we found evidence that TF signals contribute to the expression of miRNAs. Using computationally predicted promoter regions for mouse miRNAs (22), we calculated the signals of the 12 TFs and the 7 HMs in these promoter regions and utilized them to predict miRNA expression levels in mouse ESC cells. Again, using models trained solely on data sets for protein-coding genes, we found that both TF signals and HM signals in promoter regions can distinguish highly and lowly expressed miRNAs (Supplementary Figures S13 and S14).

Comparison with other statistical models

In this article, we selected the SVR-based models for predicting gene expression. We have also examined the models based on linear regression method, for which we kept the main statistical framework but replaced the SVR with the linear regression method. The SVR-based models, unlike the linear regression model, do not assume a linear relationship between expression and signals for TF-binding/HM. Our results indicated that the SVR-based model achieved higher prediction accuracy than the linear regression based ones. Specifically, when the linear regression-based TF models and HM models were used in each of the 160 bins, the maximum predictive power was 0.6 (Bin 41) and 0.66 (Bin 45), respectively, significantly lower than the SVR-based models—0.71 for the TF model and 0.72 for the HM model (Supplementary Figure S15). In addition, we compared the two-layer SVR model with previous approaches, including the ones introduced in (18, 19). The prediction accuracies of different approaches were summarized in Supplementary Table S2.

DISCUSSION

In this work, we have quantified the relative contribution of TFs and HMs for gene expression regulation. Two recent studies also explored the predictive power of TF binding (18) and HMs (19) for gene expression levels. Our analysis improved these two studies in the following aspects. First, by dividing the DNA regions around TSS and TTS into small bins, we were able to investigate the spatial effect of transcriptional regulation by TFs and histone marks. Second, we compared the relative contributions of TFs and HMs and examined their combined contribution to gene expression regulation based on data from the same cell line. Third, we have shown that both the TF and the HM models were cell line specific and that differential HMs were predictive of differential gene expression between cell lines. Fourth, instead of a linear model, we applied the SVR method, which does not assume a linear relationship between gene expression and signals for TF binding or HMs.

Both TFs and HMs are important for gene expression regulation. TFs are involved in initiation of transcription by promoting (as an activator) or blocking (as a repressor) the recruitment of RNA polymerase. The precise roles of HMs, though highly correlated with gene expression, are still under debate about its precise roles: are they causal or a consequence of active/repressive transcription? If HMs act as causal regulators like TFs, we would expect them to provide information that is additional to that provided by TFs. That is, we should be able to obtain more accurate predictive power for gene expression by combining the TF binding and HM features than by using TF or HM model alone. However, the TF+HM model shows no improvement for gene expression prediction, which suggests that HMs might not provide additional information. In addition to the mouse ESC data set, we also examined the redundancy of the two models in two other data sets: worm early embryo data set and human K562 data set. The former contains data for 6 TFs and 13 HMs provided by the modENCODE project (41). The latter contains data for 23 TFs and 10 HMs from the ENCODE project (42). Both data sets confirm the result that TF binding and HMs are redundant for statistical prediction of gene expression (Supplementary Figures S16 and S17). With more and more data sets coming out, it would be interesting to examine this problem in other species or in more tissues/cell lines.

Besides the redundancy between TFs and histone marks, we observe that individual TFs and HMs are statistically redundant. This suggests that a small subset of TFs or histone marks dominates the prediction of gene expression levels. On the other hand, it should be noted that the redundancy only exists with regard to gene expression prediction. Essentially, distinct TFs or HM types play very different roles during transcriptional regulation. For example, both H3K4me3 and H3K36me3 act as marks for active genes, the former mainly occurs in the promoter regions facilitating the initiation of transcription, whereas the latter functions mainly in the transcribed regions involved in transcriptional elongation. As shown in Supplementary Figure S18, the predictive powers of individual histone marks or TFs are different in different genomic positions. In exonic regions, H3K36me3 achieves the highest predictive accuracy, while in TSS proximal regions H3K4me3 achieves the highest predictive accuracy. The redundancy between TFs and histone marks also imply that either (i) a causal relationship, namely, TFs function as regulators for gene transcription whereas HMs are simply the subsequent readout; or (ii) a coordinated way for affecting gene expression. Previous studies have demonstrated the recruitment of chromatin modifier by TFs (43) and vice versa (44). From the gene expression prediction perspective, our results suggest an information redundancy between them.

Our results indicate that TFs and histone marks account for at least 67% of variation of gene expression in mouse ESC cells. Interestingly, ∼60% of variation can be explained by only 12 TFs, and in particular, E2f1 alone accounts for ∼50% of variation. These results are somehow unexpected, considering the facts that there are approximately 2000 TFs in mouse genome and that TFs regulate gene expression in a highly combinatorial fashion. This apparent confliction might be explained by the following reasons. First, some of the TFs, e.g. E2f1 and c-Myc, mainly bind the promoter regions and function like general TFs (e.g. TATA-binding protein). These factors are dominant for gene expression prediction in the models. Second, the combinatorial effect of different TFs might be reflected in their binding profiles, which can be captured by ChIP-Seq. For instance, if a gene is regulated two TFs synergistically, we might observe a strong binding peak for either TF. This also explains that the binding profiles of TFs are highly correlated (Supplementary Figure S6) and that the existence of hot regions of TF binding (41).

Similar to the TF and the HM models, we also constructed a model based on the ChIP-Seq data for RNA Pol II. The Pol II model explains only 36% of variation of gene expression (R = 0.6), which is much lower than those explained by the TF and the HM models. This indicates that TFs and HMs might regulate not only the recruiting but also the extension of RNA Pol II. As such, the binding of TFs and the signal of HMs are more informative for predicting gene expression levels than Pol II binding. In addition, despite the importance of distal regulation (e.g. by enhancers), our results suggest that the expression levels of genes are mainly determined by the regulatory signals around the genic regions. The additional variation of gene expression that is contributed by the distal regulation should be <33%.

Although the HMs are redundant for predicting the overall gene expression, there might exist different gene groups that are regulated by HMs in different ways. As we have shown genes with low and high CpG content in their promoters might have different regulatory mechanisms. Moreover, Pekowska et al. (45) demonstrated that genes could be divided into different classes based on the H3K4me2 profiles around their TSS. We repeated their analysis using the mouse ESC H3K4me2 data and obtained very similar results. As shown in Supplementary Figure S19, genes with distinct H3K4me2 profiles showed different expression levels, and were presumably subject to different regulatory mechanisms. Moreover, other than the high/low CpG genes, there are other potential gene categories, e.g. marked by different HM patterns (46). The two-layer models we described here can be combined with those classification methods to detect new gene categories and investigate their regulatory mechanisms.

To measure the association strength of a TF to a gene, Ouyang et al. (18) calculated the weighted sum of intensities of all binding peaks of the TF. In our analysis, we simply used the average intensities of all nucleotides within a DNA region, e.g. a 100-nt bin. In principle, the peak-based method ignores noise from non-peak regions and can potentially achieve better prediction results. As a consequence, when applied to the same data set our model explains ∼60% of variation of gene expression whereas Ouyang et al.’s model explains ∼64%. In spite of this, we did not apply the peak-based method because it is not valid for HM data. The HM profiles usually show very broad peaks across the genome and therefore association strength of a HM to genes cannot be quantified by the peak-based method. To make a fair comparison of the TF and the HM models and to facilitate the combination of TF binding and HM features into the same model, we applied our simple measurement at the cost of a little prediction accuracy.

Though TF model and HM model could independently explain 60% and 67% of variations in gene expression respectively, we do not claim that HMs could statistically explain gene expression better than TF binding profiles. Indeed, our analysis includes only a small subset of HMs and TFs. Moreover, the usage of average bin intensity as a feature may introduce a boundary effect and weaken the predictive power of TF-binding profiles. This is because the sharp peaks exhibited in TF profiles might be split and assigned to two nearby bins. In fact, using a peak-based method which does not suffer from such boundary effects, Ouyang et al. found that TFs could explain ∼64% of variation. Nevertheless, peak-based methods could not be easily applied to HM signals as their profiles usually show very broad peaks across the genome. Thus despite a slightly decrease in prediction accuracy, using the average bin intensities as features allow us to compare the positional dependence of prediction power in both TF and HM models, which is not addressed in Ouyang et al.

In summary, we have shown that the signals of TF binding and HMs are predictive of gene expression in mouse ESC cells. The TF model shows highest predictive power in a small DNA region centered at the genes’ TSS. In contrast, the HM model exhibits high predictive power in a wide region from TSS to TTS, with the highest power achieved in the transcribed region close to TSS. The two models are largely redundant as indicated by the fact that a more integrated model combining TFs and HMs does not further improve prediction accuracy. Both the TF model and the HM model are cell line specific. Related to this, the HM model based on differential HMs accurately predicts the differential expression of genes in ESC versus NPC. Moreover, the models trained solely on data for protein-coding genes are predictive of expression levels of miRNAs, suggesting that their regulation by TFs and histone marks may share a similar mechanism.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health; the AL Williams Professorship funds. Funding for open access charge: NIH.

Conflict of interest statement. None declared.