Abstract
Current methodology in real-time Polymerase chain reaction (PCR) analysis performs well provided PCR efficiency remains constant over reactions. Yet, small changes in efficiency can lead to large quantification errors. Particularly in biological samples, the possible presence of inhibitors forms a challenge. We present a new approach to single reaction efficiency calculation, called Full Process Kinetics-PCR (FPK-PCR). It combines a kinetically more realistic model with flexible adaptation to the full range of data. By reconstructing the entire chain of cycle efficiencies, rather than restricting the focus on a ‘window of application’, one extracts additional information and loses a level of arbitrariness. The maximal efficiency estimates returned by the model are comparable in accuracy and precision to both the golden standard of serial dilution and other single reaction efficiency methods. The cycle-to-cycle changes in efficiency, as described by the FPK-PCR procedure, stay considerably closer to the data than those from other S-shaped models. The assessment of individual cycle efficiencies returns more information than other single efficiency methods. It allows in-depth interpretation of real-time PCR data and reconstruction of the fluorescence data, providing quality control. Finally, by implementing a global efficiency model, reproducibility is improved as the selection of a window of application is avoided.
INTRODUCTION
The polymerase chain reaction (PCR) is an elegant technique in which as little as a single DNA molecule can be specifically amplified to detectable levels. The advent of fluorescent dyes made it possible to monitor this amplification process in real time, allowing relative quantification of the initial amount of template DNA. Due to its unprecedented accuracy and sensitivity, real-time PCR has gained widespread application in the biomedical field, becoming one of the most generally used techniques in modern molecular biology [for a review see (1)].
Since its inception, little has changed in the way real-time PCR data are typically used. Most laboratories use the so called ‘fit point’ method in which a fixed fluorescence threshold is chosen whose intersection with the baseline subtracted fluorescence yields the Cq value (quantification cycle, the fractional cycle in which the fluorescence signal reaches the chosen threshold). This approach performs adequately as long as the threshold is placed within the ‘exponential phase’ of the reaction [where PCR efficiency (E) is presumed constant] and as long as little or no difference in PCR efficiency exists between reactions. PCR efficiency is defined as the fold change in the amount of amplicons after each cycle of amplification.
From a theoretical point of view E should be constant and maximal (i.e. E = 2) over the entire reaction as the enzyme duplicates the target sequences during each cycle of amplification. However, two phenomena counteract this assumption. First, the efficiency is not constant but declines over the course of the reaction due to consumption of reagents and build up of reaction products (2). Second, the efficiency may not be maximal due to the presence of so called PCR inhibitors (3) which limit reaction efficiency.
While it is generally acknowledged that the assumption of constant PCR efficiency may be frequently violated, it is less well recognized that small differences in reaction efficiency can lead to considerable quantification errors (4). The shift in Cq values induced by inhibition (inhibited reactions reach the threshold later than uninhibited reactions) causes an underestimation of the initial amount of target copies. Due to the logarithmic nature of the Cq value, even relatively small shifts produce a significant underestimation of the number of initial target sequences.
Bias introduced by a difference in efficiency between two samples is problematic for relative and absolute quantification alike. When investigating gene expression or quantifying sample content, differences in PCR efficiency between samples before and after treatment, or between a sample and standard, introduce bias that may skew the conclusions of an assay. Ideally each single reaction analysis should therefore return two values: a Cq value as a measure of the number of initial target copies and an E estimate as a reference for inter-reaction comparability.
Especially in samples, the possible presence of coextracted inhibitors (3,5) complicates data analysis. Knowledge of the individual reaction efficiencies may be used to compensate for such effects (6,7,8) or to simply remove reactions with aberrant efficiency from the analysis. But classical inhibition assays [e.g. the golden standard of serial dilution (9) or inclusion of internal controls (10,11)] demand additional analysis and/or costs. Therefore, their routine application can become cumbersome when large numbers of reactions are involved (e.g. PCR arrays).
Another point of concern is baseline subtraction: this step in the analysis work flow is commonly regarded as trivial and details on how baseline subtraction was performed are often omitted in the literature. But the choice of baseline subtraction method has a profound impact on the data, as is shown in (12,13) where the authors demonstrate that baseline error will lead to error in the observed efficiency value. Yet, due to the complex nature of the origin of base fluorescence a comprehensive baseline model is currently infeasible.
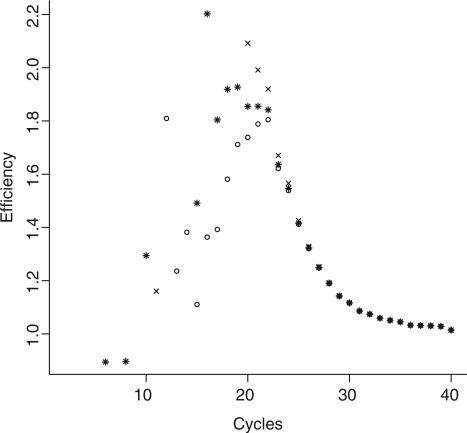
The majority of single reaction efficiency estimation methods fit an exponential curve to a select region of the data (the exponential phase) where efficiency is presumed constant and near maximal (6,7,13–15). However, theoretical models predict a constant amplification rate during the initial cycles of the reaction followed by a precipitous decrease in cycle efficiency when the consumption of reagents and the build up of reaction products reaches critical values (16–20). This seriously questions the existence of a true exponential phase in the data: by the time the increase in fluorescence due to amplification becomes distinguishable from the baseline, efficiency is probably no longer constant. Otherwise put: true exponential amplification may only happen early on in the reaction when amplicon numbers are too low to yield fluorescence levels which are readily distinguishable from the base fluorescence. Hence, the fluorescence measurements may not contain a recognizable phase of exponential increase (see Figure 2 and ‘Results and Discussion’ section for further motivation).
Figure 2.
Fold changes in baseline subtracted fluorescence per cycle 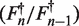 for a single PCR reaction (soybean, le1 target, approximately 103600 initial copies) using the flat baseline model (open circle), the slanted baseline model (cross symbol) and the baseline protocol proposed by (12) (asterisk, carried out by the LinReg PCR program v12.11). Neither model displays an extended phase of true constant efficiency. Note the differences in cycle efficiency between the models during the ‘exponential phase’ (centered around cycle 21).
for a single PCR reaction (soybean, le1 target, approximately 103600 initial copies) using the flat baseline model (open circle), the slanted baseline model (cross symbol) and the baseline protocol proposed by (12) (asterisk, carried out by the LinReg PCR program v12.11). Neither model displays an extended phase of true constant efficiency. Note the differences in cycle efficiency between the models during the ‘exponential phase’ (centered around cycle 21).
We present a new model for cycle-to-cycle behavior of reaction efficiency, called Full Process Kinetics-PCR (FPK-PCR), and demonstrate its application in PCR analysis. This approach uses as many data points of the reaction as possible and, as a consequence, no ‘window of application’ has to be chosen, adding to the robustness of the method. Fitting a bilinear model to the data reveals the individual cycle efficiency values. The latter allows reconstruction of the fluorescence readings. The model has been tested on soybean (Glycine max) event GTS-40-3-2 (Roundup Ready Soybean) genomic DNA extracts. Its performance is compared to other single reaction efficiency estimation methods and the method's capacity to distinguish inhibited from uninhibited reactions is discussed. An R-file implementing the presented method and three datasets are provided as Supplementary Data.
MATERIALS AND METHODS
DNA samples
Genetically modified Glycine max event GTS-40-3-2 (Roundup Ready Soybean) was grown in house using a growth chamber and standard conditions (25°C, 16 h/8 h day/night regime, 80% humidity, 20 000 lux). Genomic DNA was isolated using a CTAB based method (21) (all chemicals were obtained from Merck or Acros organics). All DNA extracts were quantified spectrophotometrically (Biorad Smartspec plus).
The inhibited datasets were created by adding either isopropanol (Merck) or tannic acid (Agros organics), which are known PCR inhibitors (5,22–24), to the sample DNA. The inhibitors were subsequently co-diluted with the DNA. In the case of isopropanol, its final concentration in each of the sample dilutions were: 2.5, 0.5, 0.1, 0.02 and 0.004% (v/v), respectively. In the case of tannic acid the amounts present per reaction were 5, 1, 0.2, 0.04 and 0.08 ng, respectively.
PCR reactions
All PCR reactions were performed in 25 μl using primers targeted against the soybean Lectin endogene [Le1, Forward: 5′-AACCggTAgCgTTgCCAg-3′; Reverse: 5′-AgCCCATCTgCAAgCCTTT-3′; product: 81 bp (25)] and the event specific plant-transgene border [Forward: 5′-CgCAATgATggCATTTgTAgg-3′; Reverse: 5′-TTTCATTCAAAATAAgATCATACATACAggTTA-3′; product: 94 bp (25)]. SYBRgreen mastermix (Diagenode) was used with primers at a final concentration of 260 nM. All reactions were amplified in 96-well plates using either a ABI7300 or Biorad IQ5. Hardware platforms were not mixed within a single dataset. A single protocol was used for all reactions: 10 min 95°C, 40–70 × (15 s 95°C, 1 min 60°C).
For the calibration and validation of the presented method a total of five serial dilution datasets were generated: three from individual DNA extractions and two after addition of an inhibitor to an existing extract. Each dataset consists of a five point serial dilution series with a high number of repeats per dilution point (ranging from 18 to 36, depending on the dataset). All dilution series start at approximately 100 000 target copies and use 5-fold dilution (initial target copies per reaction: S1 ≈100 000, S2 ≈20 000, S3 ≈4000, S4 ≈800 and S5 ≈160). The raw data (i.e. background subtracted, not baseline corrected) were exported from the thermocycler's software for further analysis.
For the confirmation of the effect of isopropanol on amplicon fluorescence in SYBR-chemistry an additional dataset was generated using the isopropanol dilution series and a FAM-TAMRA' labeled probe (5′-FAM-TTCgCCgCTTCCTTCAACTTCACCT-TAMRA-3′) in combination with the abovementioned Le1 primers. These reactions were run using six repeats per dilution point.
Serial dilution-based efficiency estimation
Initial template copy numbers were calculated from the amount of DNA engaged per reaction using haploid genome weights (26). Cq values were calculated as the position of the first positive maximum of the second derivative of a five parameter logistic model (5PLM) (27):
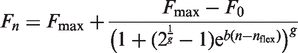 |
(1) |
where n is the cycle number, F0 is the base fluorescence value, Fmax is the maximal fluorescence value which defines the plateau of the reaction, nflex is the inflection point of the curve. Parameter b is the ‘growth rate’ and affects the slope of the curve at nflex whereas g determines the asymptote where maximum growth occurs.
Linear regression between the log of the initial copy numbers and the threshold cycles yields a slope from which the reaction efficiency is calculated using Equation 2, where base is the base of the logarithm used on the initial copy numbers. Standard errors for these efficiencies were obtained by fixed-x bootstrapping (28) (100 bootstraps using 3 replicates per dilution point).
| (2) |
Baseline subtraction
Here, the term ‘background’ refers to the fluorescence read from an empty plate and accounts for the auto-fluorescence of the plate material. The term ‘baseline’, or ‘base fluorescence’, refers to the auto-fluorescence value of the reaction mix (DNA and reagents) as opposed to the fluorescence generated by the PCR products. It is common practice to estimate the baseline from the so called ‘ground phase’ of the reaction, during which measurable fluorescence increase due to DNA amplification is assumed to be negligible. All baseline calculations were performed manually in R after data export from the thermocycler software.
Baseline subtraction was performed according to two methods: one is referred to as ‘flat’, the other as ‘slanted’. The flat baseline calculation assumes a constant level of base fluorescence with normal measurement error (i.e. an identical baseline value for all cycles), and its value is calculated as the arithmetic mean of the ground phase. The slanted baseline model uses a variable level of base fluorescence: linear least squares regression is performed on the ground phase and the linear model predictions are seen as individual base fluorescence values for each cycle in the reaction.
For either model, the baseline values are subtracted from the fluorescence reading of their respective cycles. Throughout the text baseline subtracted fluorescence values will be indicated with a † (e.g.  ).
).
Exponential fit
Several approaches to determine the exponential phase of the PCR reaction have been described (6,12–14,29). For use in a comparative analysis with FPK-PCR approach, three protocols to select the exponential phase of the reaction have been adopted from the literature. By separating the selection protocol for the exponential phase from the baseline subtraction models and recombining them, a broad array of approaches is created which include the combinations used in (13,29). The protocols that were adopted are: (I) fixed fluorescence limits: the exponential phase is situated between fixed instances of baseline subtracted fluorescence units (FU) (see Equation 3); (II) the exponential phase is situated between the point where the fluorescence signal exceeds the baseline plus its standard error and the first positive second derivative maximum of a four parameter logistic model fitted to the data [as is used in (13), see Equation 4]; (III) the exponential phase is defined as a 10-fold fluorescence range around a midpoint (M) where the amplification rate is assumed accurately determinable [as is used in (29), see Equation 5].
In Equations 4 and 5 σnoise is the standard error of the baseline, in Equation 4 nflex and b are parameters from the four parametric logistic model (see Equation 6).
| (3) |
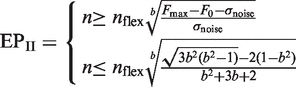 |
(4) |
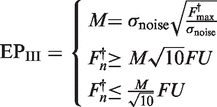 |
(5) |
The four parametric logistic model (4PLM) is given by:
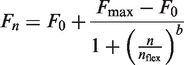 |
(6) |
where n is the cycle number, F0 is the base fluorescence value, Fmax is the maximal fluorescence value which defines the plateau of the reaction, nflex is the inflection point of the curve and b describes the slope of the curve at nflex.
Linear regression of efficiency
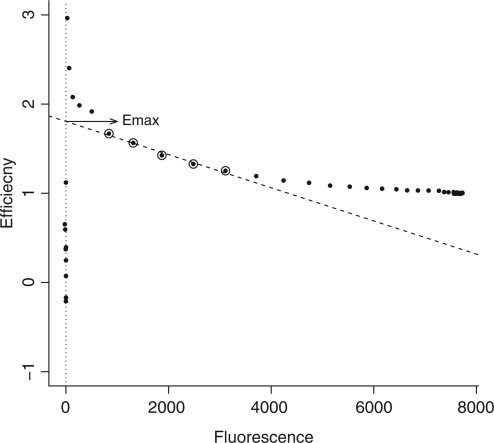
The linear regression of efficiency (LRE) analysis approach does not assume a pure exponential character of PCR and is also included in the comparative analysis of the FPK-PCR approach. LRE uses sigmoid modeling of the reaction's fluorescence increase (19). Linear regression of the cycle efficiency 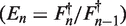 versus the cycle fluorescence (
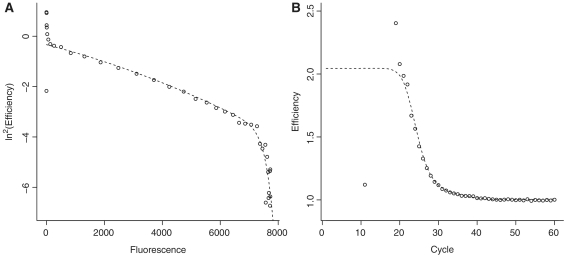
versus the cycle fluorescence ( ) is applied to a limited portion of the data in order to estimate the initial reaction efficiency as is illustrated in Figure 1. See (19) for details on the approach.
) is applied to a limited portion of the data in order to estimate the initial reaction efficiency as is illustrated in Figure 1. See (19) for details on the approach.
Figure 1.
The Linear Regression of Efficiency (LRE) approach. Cycle efficiency is regressed against cycle fluorescence. The window of application for the linear regression is designated by circles. The y-intercept of the regression line then yields the maximal efficiency estimate (Emax).
Data processing
All calculations and curve fitting were done using R version 2.9.2 (30). The raw data were exported from the thermocycler and imported into R. All non-linear curve fitting was performed in R using the nls function with the exception of the variable efficiency model for which one dimensional optimization (optimize function) was used on the model's residual sum of squares. The five parameter logistic function (1) was fitted using the Levenberg–Marquardt algorithm (31,32) available through the package ‘minpack.lm’ version 1.1-5. The algorithms used for this publication are available as additional material and can be inspected for more detail on the exact methods used.
RESULTS AND DISCUSSION
Efficiency analysis methods
Several methods for individual reaction efficiency estimation are available throughout the literature. Three main types of approaches can be distinguished: (I) those which use the assumption of constant efficiency: these approaches are characterized by the selection of an ‘exponential phase’, during which the efficiency is supposed constant, and the subsequent application of an exponential fit to the selected phase either directly (13,14) or after logarithmic transformation (6,12,29); (II) those that assume that the efficiency varies throughout the reaction and use a model of efficiency decline to obtain a measure of its initial (maximal) value (19,33); (III) those that model the PCR reaction as a stochastic branching process (34–37) in which the efficiency is viewed as the probability that a molecule will be duplicated after one cycle of amplification.
This last category will not be discussed since their nature is fundamentally different from the other two and since, to our knowledge, none of these methods is at present routinely applied in real-time PCR data analysis.
A critical point in the first category of methods is the assumption of constant efficiency. Figure 2 displays the cycle efficiency (En) for a real time PCR reaction targeting the soybean Le1 gene (approximately 103 600 initial copies) and illustrates that under neither of the three baseline models considered the data contain an extended phase of true constant efficiency.
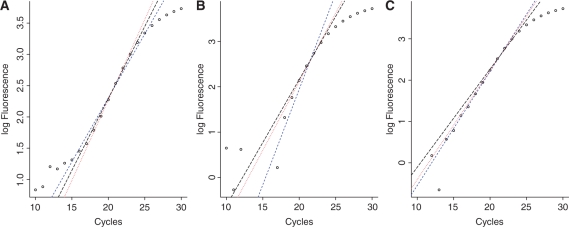
Theoretical models of efficiency (16–18,20) predict an initially maximal plateau followed by a decline as reagents are consumed and reaction products build up. This phase of maximal efficiency, whose length is dependent on the initial number of targets, is considered to be drawing to an end by the time enough amplicons are generated to yield measurable amounts of fluorescence. Thus the contributions in fluorescence from the cycles during which the efficiency is maximal are indistinguishable from the base fluorescence. This explains the absence of an initial plateau of maximal efficiency in Figure 2. Consequently it is nearly impossible to find a window of application in which the assumption of constant efficiency is valid. This results in considerable differences in efficiency estimates obtained from slightly different windows of application when using a purely exponential fit (see Figure 3 and Table 1).
Figure 3.
Linear regression of the log transformed baseline subtracted fluorescence data for a single PCR reaction (soybean, le1 target approximately 103 600 initial copies) using three different approaches to determine the exponential phase [short dashed (blue), dotted (red) and long dashed (black) lines representing Equations 3, 4 and 5, respectively]. In (A) the flat baseline model was used, in (B) the slanted model was used, in (C) the baseline protocol proposed by (12) was used (carried out by the LinReg PCR program v12.11).
Table 1.
Average efficiency estimates (±standard error)
| S1 | S2 | S3 | S4 | S5 | ||
|---|---|---|---|---|---|---|
| EPI | Flat | 1.901 ± 0.181 | 1.806 ± 0.135 | 1.785 ± 0.062 | 1.837 ± 0.078 | 1.708 ± 0.042 |
| Slanted | 2.300 ± 0.232 | 2.068 ± 0.123 | 2.211 ± 0.130 | 2.099 ± 0.086 | 2.099 ± 0.079 | |
| EPII | Flat | 1.840 ± 0.037 | 1.820 ± 0.042 | 1.854 ± 0.013 | 1.823 ± 0.008 | 1.818 ± 0.025 |
| Slanted | 1.896 ± 0.046 | 1.901 ± 0.024 | 1.935 ± 0.022 | 1.890 ± 0.026 | 1.892 ± 0.022 | |
| EPIII | Flat | 1.873 ± 0.085 | 1.873 ± 0.072 | 1.891 ± 0.034 | 1.894 ± 0.043 | 1.837 ± 0.029 |
| Slanted | 1.948 ± 0.066 | 1.944 ± 0.040 | 1.972 ± 0.036 | 1.958 ± 0.039 | 1.912 ± 0.019 | |
| LRE | Flat | 1.881 ± 0.010 | 1.857 ± 0.046 | 1.886 ± 0.007 | 1.861 ± 0.009 | 1.864 ± 0.020 |
| Slanted | 1.910 ± 0.030 | 1.871 ± 0.022 | 1.906 ± 0.012 | 1.874 ± 0.019 | 1.883 ± 0.022 | |
| FPK | Flat | 1.972 ± 0.029 | 1.985 ± 0.075 | 1.969 ± 0.012 | 1.948 ± 0.013 | 1.942 ± 0.020 |
| Slanted | 2.028 ± 0.044 | 2.015 ± 0.020 | 2.009 ± 0.017 | 1.976 ± 0.021 | 1.986 ± 0.016 |
Comparison of the average PCR efficiency (±standard error) for the soybean le1 target at five different concentrations and using five efficiency calculation approaches: three ‘exponential fit’ methods (EPI, EPII and EPIII. See Equations 3–5, respectively), LRE and FPK. Note that the true value is assumed to be 2.
The number of initial target copies for S1–S5 can be found in ‘Materials and Methods’ section under ‘PCR reactions’.
Several techniques have been introduced to increase robustness of the efficiency estimate. In (13) iterative regression is presented, which uses a weighed average of the efficiencies obtained from every possible window within the exponential phase. In (12) the exponential phase is determined as the cycle range that yields an efficiency estimate with the least variation among replicate reactions. Although these practices improve the classical approach, they are still based on the assumption of a prolonged cycle range with constant efficiency.
Methods in the second category acknowledge the changing nature of the reaction efficiency and model the changes in efficiency throughout the reaction to estimate the initial efficiency value. Yet, all of these methods still confine their analysis to a specific window of application rather than using the whole set of data.
Limited reaction efficiency models (i.e. not valid for the entire reaction) require a window of application, which ultimately affects the robustness of the efficiency estimate: defining a valid window often is difficult and data at its extremities are likely to fit the model less well. As a result, it is not uncommon that only about 10% of the available data are used to fit such efficiency models (19,29).
FPK-PCR approach
The FPK-PCR approach relies on two conditions for more accurate and realistic efficiency modeling in PCR analysis: (A) a data condition, which is the analysis of the complete reaction profile instead of focusing on a limited window of application, and (B) a methodology condition, which is the use of an efficiency model valid for the entire reaction. This ‘full process kinetics’ approach to PCR analysis provides a comprehensive model that correctly shapes reaction fluorescence by means of its underlying cycle-to-cycle efficiency changes.
The term ‘complete reaction profile’ not only refers to the use of as much of the available data as possible, but more importantly to the fact that the true plateau of the reaction should be attained (where the efficiency has reached its minimum) before the last cycle of amplification. For reasons detailed in the following sections, having access to data from several cycles of the plateau phase is of paramount importance. Reactions with low initial target copy numbers may not reach the plateau after 40 or 45 cycles and it may take up to 60 cycles for amplification to reach a full stop.
At the base of the FPK-PCR approach presented in this article lies the general equation of PCR kinetics:
 |
(7) |
where Fn is the total fluorescence of cycle n as opposed to Fn,0, its respective base fluorescence value, α is the fluorescence emitted by a single amplicon, i0 is the initial amount of target copies and Ej is the reaction efficiency of cycle j. The FPK-PCR approach aims at total elucidation of the PCR process and ultimately yields efficiency values for each cycle as well as an estimate of the amount of initial target copies.
The outline of the approach can be summarized as follows: in a first step the baseline (Fn,0) is estimated from the data. Next, the reaction efficiency model is constructed by regressing the double log of the cycle efficiencies and their respective baseline subtracted fluorescence values. In a third and final step the initial target fluorescence (α · i0) is found by fitting the general PCR kinetics model to the fluorescence data.
Kinetic demarcation
A first problem one encounters when processing real-time PCR data is how to divide the data in the different reaction phases: separating the ground phase from the rest of the data and discriminating the different phases of efficiency decline (see the ‘FPK-PCR efficiency model’ section). Here, a technique based on the accumulation of fluorescence is used.
Since (I) fluorescence is assumed to be proportional with amplicon build up, since (II) amplicon build up is proportional to reagent consumption and since (III) amplicon build up and reagent consumption are considered the main driving forces behind efficiency decline it follows that the percentual increase in fluorescence (e.g. 5% of total fluorescence increase) can be used as kinetic milestones for demarcating the different phases the reaction goes through.
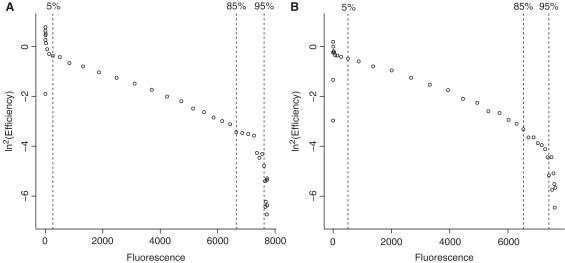
The end of the ground phase was empirically observed to lie around the 5% fluorescence increase mark. This may be considered a somewhat conservative limit, but the FPK-PCR approach has the advantage of using a large number of data points when fitting the model, making the certainty of excluding all ground phase contamination preferable to the possible salvation of an extra data point. Hence the presented method benefits from a more extended ground phase, whereas for other methods this protocol may ‘consume’ too much of the available data. The transition between the two phases of efficiency decline was empirically found to be situated between 85% and 95% of total fluorescence increase. Its location was not affected by either initial target concentration or inhibition. For an illustration of the application of the kinetic demarcations see Figure 4.
Figure 4.
The double log of the reaction efficiency is plotted against the fluorescence values for two soybean reactions with le1 target: in (A) approximately 103 600 initial targets were used and in (B) approximately 150 initial targets. Both panels demonstrate the application of the kinetic demarcations: data on the left hand side of the 5% line are considered to be part of the ‘ground phase’ of the reaction, the phase change is situated between the 85% and the 95% lines.
Using the five parametric logistic model (1) it can be shown that, for any value p between zero and one, the fractional cycle in which the reaction reaches p times the total fluorescence increase is given by:
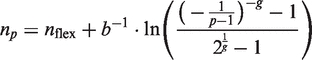 |
(8) |
The drawback of this approach is that it relies heavily on the condition that the amplification profile is complete: the maximal fluorescence (plateau) should be reached before the end of the reaction or should be correctly extrapolated by the five parametric logistic model when this is not the case. The latter condition is discussed later in this text.
Baseline estimation
Since background fluorescence is largely hardware specific its subtraction is in most cases auto-performed by the thermocycler software (as was the case here).
In this publication the influence of the baseline noise on the data is considered insignificant once amplicon-specific fluorescence reaches 5% of its total increase. The cycles preceding that point are considered part of the ground phase. However, not all of these cycles qualify for baseline calculation: the last cycles of the ground phase contain significant amounts of fluorescence originating from amplification products.
To avoid bias by inclusion of such cycles, the baseline calculation window is shortened to the point where amplicon specific fluorescence is 100 times less: i.e. 6.64 (log2 100) cycles before the 5% increase mark. Hence, the last seven cycles of the ground phase are discarded during baseline calculation, as are the first three to avoid the inclusion of high noise data.
Two baseline models have been considered in this study: one is ‘flat’ (assuming an identical baseline value for each cycle), the other is ‘slanted’ (individual baseline values for each cycle based on linear regression of the initial reaction cycles). The absence of a sound theoretical base for either model is problematic in light of their extensive influence on the efficiency estimate (see Table 1), an influence that is not limited to a single analysis method but affects all approaches. Baseline subtraction is a ‘universal’ problem in the field of real-time PCR and the many elements that contribute to the base fluorescence level (unbound SYBR green, DNA background of the target sequences, primers, etc.), their cycle-to-cycle changes and their mutual interactions form a very complex topic. The current level of their understanding may not form enough ground for the development of an algorithm suitable for accurate baseline determination (12,13). As a consequence, one must rely on the observations from early cycles in order to estimate base fluorescence behavior.
Due to the complex nature of the cycle-to-cycle efficiency changes it was decided to refrain from using the data's log-profile as a means of optimizing the baseline (12). The latter technique may be the only model to achieve cycles of constant efficiency in the data, but this is not surprising since the method uses an iterative algorithm that maximizes the linear character of the log-transformed exponential phase thus imprinting its assumption on the data. Also, the window obtained is in most cases only 2–3 cycles long (see Figure 2 for an example), while the method assumes the efficiency to be constant over a much larger number of cycles.
Instead, careful consideration of the various options served to select the model that is least likely to introduce systematic error. For the FPK-PCR approach, the flat baseline model was found to return a lower efficiency estimate with each decrease in number of initial target copies (an average efficiency difference of about 10% between S1 and S5 over various datasets). This effect was less pronounced for other efficiency estimation techniques. The slanted baseline model on the other hand appears stable with regard to initial target copy number and, as reaction efficiency is presumed to be independent of the initial target concentration, is thus considered preferable. A second effect of the use of a slanted baseline appears to be a systematically higher estimation of reaction efficiency compared to the flat model (see Table 1). However, it is its stability over a large range of initial copy numbers that drives our choice to use it in combination with the FPK-PCR approach.
Note that of the three definitions of the range of exponential cycles tested, the first (EPI) has a considerably larger standard error than the others (EPII and EPIII, see Table 1). This may indicate that ‘rigid’ limits are less suitable to define the cycle range with the highest amount of exponential character than reaction specific ranges. Other tables in the text mention only one approach of ‘exponential fit’, i.e. EPII with slanted baseline model, as it yields somewhat smaller standard errors than the EPIII approach.
FPK-PCR efficiency model
As outlined in the introduction, the profile of the cycle efficiency is expected to consist of an initial phase of constant and maximal efficiency followed by a decrease toward a terminal asymptote of minimal efficiency, resulting in an overall inverse S-shape. The Gompertz equation (38) is not only capable of taking this form, it also allows for a convenient estimation from the data (i.e. regressing the double logarithm of En). Rather than describing the efficiency in function of the cycle number, the efficiency is expressed in function of the cycle fluorescence (39). The particular instance of the Gompertz family of biological growth curves used in this publication is given by Equation 9 where 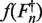 represents a function of
represents a function of  .
.
| (9) |
After double logarithmic transformation of the cycle efficiency (calculated as the fold increase in baseline subtracted cycle efficiency), its relation to the respective fluorescence values can be made apparent. Figure 4 shows two examples of the double log of the reaction efficiency plotted against fluorescence values (i0 ≅ 103 600 and i0 ≅ 150). The data on the left hand side of the dotted line are considered part of the ‘ground phase’ of the reaction, where insufficient amplicons have accumulated to generate measurable fluorescence, and do not reflect the efficiency profile. The remaining data can be described as an efficiency decline in two phases: an initial phase of gentle decline that is almost linear in relation to the fluorescence increase and a final phase of steep decline where the amplification rate rapidly decreases as fluorescence approaches its plateau.
For the high copy number reaction the initial decline phase is nearly linear. However, in case of low initial target copies the non-linear character of the first phase increases, adding to the complexity of the cycle efficiency profile. A function that can adequately describe this type of behavior is given by (10). The latter is an adaptation of the general bilinear model presented in (40) that allows for curvature during the initial phase of efficiency decline.
| (10) |
The complete model takes six parameters: three ‘slopes’ (a1 and a2 which together describe the curve of the first phase and a3 describing the slope of the second phase), a constant (χ) for shifting along the vertical axis, a parameter (η) for adjusting the abruptness of transition between the two phases and a constant (Fc) corresponding to the horizontal (x-axis) position of the phase-change.
A major advantage of the general bilinear model is that it incorporates linear models that can be used separately on the linear portions of the parameter-space with a direct connection to them (40). The model parameters thus can be calculated in several steps: first the parameters of the first phase (a1 and a2) are found by fitting a linear model (quadratic curve) to the data between the end of the ground phase and the 85% fluorescence mark of the reaction (as calculated from a five parameter logistic model using (8) with P = 0.85). The value of χ follows from the intercept of the first phase's linear model. In a following step the slope of the second phase is found by fitting a linear model to the data between the 95% fluorescence mark and the end of the reaction. When fitting the linear models to both phases, the horizontal distances (i.e. the fluorescene residuals) are minimized rather than the vertical distance [i.e. the log2(En) residuals] although the manner of plotting the data may suggest the reverse. Indeed, minimizing the fluorescence residuals is the more logical procedure since cycle efficiencies are themselves calculated from the fluorescence measurements. In a last step both η and Fc are given initial values (−0.5 and the intersection of both linear models, respectively) which are subsequently optimized in order to minimize the residual sum of squares of the bilinear model.
Figure 5 demonstrates the fit of this model to a representative reaction using both a double logarithmic plot as well as a more standard efficiency versus cycle plot.
Figure 5.
FPK-PCR model fitted efficiency to a single soybean reaction with le1 target at approximately 103 600 initial copies. (A) displays the bilinear model fit (ln2En plotted versus  ) whereas (B) plots the untransformed efficiencies, calculated from the bilinear model, against their respective cycles (En versus n).
) whereas (B) plots the untransformed efficiencies, calculated from the bilinear model, against their respective cycles (En versus n).
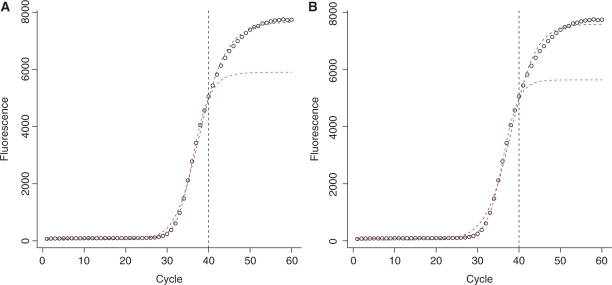
Currently, many standard PCR protocols use 40 or 45 cycles of amplification which may not be sufficient for reactions with low amounts of initial target copies to reach the plateau phase, certainly when inhibition is involved. Such ‘truncated’ datasets do not include the second phase of efficiency decline thus preventing application of the bilinear model. However, an efficiency estimate can still be obtained by fitting a quadratic curve to the available data.
To decide whether a dataset is truncated or not, a basic decision criterion is used: the 95% fluorescence mark of the reaction is calculated using Equation 8, if this point is reached anywhere during the last four cycles of the reaction (n95 ≥ ntotal − 4) the dataset is considered truncated since there are not enough datapoints (three or less) to reliably fit the second phase.
As a result of the inability of the five parameter logistic model to correctly extrapolate the plateau (as explained in section ‘Evaluation of the model fit’ and Figure 8) the 95% mark will nearly always fall before the end of the reaction. This is no hindrance for the identification of truncation, but it prevents this approach from distinguishing between ‘early’ and ‘late’ truncations: it does not allow to estimate how far from the true end of the reaction (i.e. full stop of amplification) the truncation occurs. As a consequence the algorithm assumes at least 95% of the total fluorescence is reached and ignores data between the presumed 85% fluorescence mark and the end of the reaction during the quadratic fit. Thus, results for a single phase fit may vary depending on where the truncation appears. In the authors' experience, 60 cycles of amplification are sufficient to accommodate the entire range of initial target copies. Even though inhibited reactions may not reach the plateau phase after 60 cycles, sufficient data points from the first phase of efficiency decline should have accumulated to obtain an acceptable estimate of maximal efficiency.
Figure 8.
Illustration of the effect of truncated data on two empirical model fits. In (A) the Four parameter logistic model is used. In (B) the Sigmoid model is used. In both cases the blue line represents the fit to the full reaction profile (60 cycles), whereas the red line represents the fit to the truncated dataset (40 cycles). Data truncation affects all model parameters both for the 4PLM (parameters: nflex = 36.3, F0 = 86.0, Fmax = 5817 and b = −17.7 for the 40 cycle fit; nflex = 38.1, F0 = 52.4, Fmax = 7633 and b = −12.2 for the 60 cycle fit) and for the sigmoid model (parameters: nflex = 36.2, F0 = 83.1, Fmax = 5553 and k = 1.93 for the 40 cycle fit; nflex = 38.1, F0 = 29.7, Fmax = 7561 and k = 3.05 for the 60 cycle fit). Note that in case of truncation the plateau is placed directly after the truncation, hence the cycle in which 95% of the total fluorescence is reached, is found within the available cycle range.
Initial target input estimation
Since the model yields efficiency values for every cycle, α and i0 are the last unknown quantities in the general equation of PCR kinetics (7). Estimating both separately is not feasible without the physical determination of single amplicon fluorescence, but an estimate of their product (α · i0) can be calculated. Since the amplification profile is determined by the cumulative product of the cycle efficiencies, α · i0 can be viewed as a ‘scaling factor’ which can be estimated by minimizing the residual sum of squares:
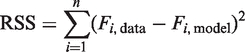 |
(11) |
where Fi,model represents the fluorescence values obtained by combining the baseline and the cycle efficiency model into the general kinetics Equation (7).
Throughout this study it was observed that in certain cases the fluorescence level of the plateau phase tends to decline after several cycles of stability. This phenomenon is observed in the raw fluorescence data and thus is not caused by baseline subtraction. The origin of this effect is at present unknown. However, it violates the assumptions of the FPK-PCR model and is especially troublesome since the efficiency is expressed as a function of cycle fluorescence. As a consequence the model returns increasing efficiency values as the plateau progresses resulting in a suboptimal fit and biased α · i0 values. As a means to remove this artifact the raw fluorescence plateau is ‘flattened’ prior to baseline subtraction (i.e. any cycle beyond the maximal fluorescence which has a lower value is replaced by the maximum) resulting in a noticeably smaller residual sum of squares and better α and i0 estimates.
Evaluation of the model fit
There are two ‘fits’ of the FPK-PCR model to be considered: the fit of the efficiency model to the cycle efficiency values calculated from the data on the one hand and the fit to the raw reaction fluorescence on the other hand. Both should be scrutinized because, as is demonstrated below, a good fit to fluorescence data does not guarantee a good fit to the underlying pattern of efficiencies.
Efficiency fit
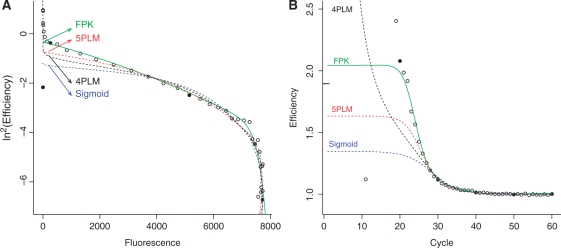
Figure 6 illustrates how the kinetic aspect of the FPK-PCR model compares to those of a number of S-shaped models used in the field of real-time PCR analysis. Both figures contain the same soybean reaction data (Le1 target, approximately 103 600 initial copies) plotted in two different ways (ln2En versus Fn and En versus n). The FPK-PCR model approximates the data more closely than the other models. The largest differences between the models are situated in the initial stages of the reaction and to a lesser degree during the phase transition of the double log plot.
Figure 6.
Comparison of the FPK-PCR efficiency model to other models used in the field of real-time PCR analysis. The different models are: the four parameter logistic model (4PLM, see Equation 6), the five parameter logistic model (5PLM, see Equation 1 and the sigmoid model [Sigmoid, as used in (19)]. Both panels (A) and (B) represent the cycle efficiency of the same reaction (soybean Le1 target, approximately 103 600 initial copies) once after double log transform, plotted against the cycle fluorescence (A), and once untransformed, plotted against the cycle number (B). In the latter panel, the mark on the right hand side of the vertical axis represents the efficiency estimate returned by the golden standard of serial dilution. To improve comparison between both panels cycles 10, 20, 30, and so on, have been marked with solid dots.
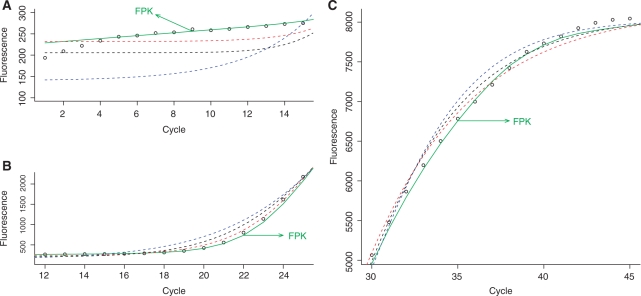
Figure 6B further illustrates the differences in initial efficiency between the different models. Despite their magnitude these differences are not apparent from a standard fluorescence versus cycle plot: due to the infinitesimal nature of the early fluorescence increase and the scale needed to accommodate the total fluorescence increase they remain hidden in the ground phase. This is illustrated by Figure 7: in panel A the reaction ground phase is shown on a proper scale illustrating the differences between the models, whereas in panel B the scaling has to accommodate a larger increase in fluorescence, effectively hiding the initial differences between the models.
Figure 7.
Detailed comparison of the FPK-PCR efficiency model and other models fitted to a single PCR reaction (soybean Le1 target, approximately 103 600 initial copies). Fluorescence measurements are plotted versus their respective cycle number in three plots each containing a subset of the reaction data. In (A) cycles 1–15 are shown, illustrating the ground phase of the reaction. In (B) cycles 12–25 are shown, illustrating fluorescence emergence from the ground phase. In (C) cycles 30–45 are shown, detailing the gradual decrease in fluorescence growth and the onset of the plateau phase.
The lesser kinetic performance of the logistic and sigmoid models is not entirely surprising due to their ‘empirical’ nature. They were originally adopted to real-time PCR based on their S-shaped profile and goodness of fit to fluorescence data, while the underlying mechanisms of amplification were not considered.
Despite their differences all models, with the exception of the 4PLM, indicate an initial phase of constant efficiency. This is in accordance with several papers (17,18,41). For the highest target concentration (approximately 100 000 copies) the efficiency remains constant during the first 18 cycles (a decline of less then 1% efficiency as calculated by the FPK-PCR approach). The subsequent cycles are characterized by a dramatic acceleration in the decrease of efficiency: by cycle 23 E has dropped by >30% (an average E23 of 1.69 compared to the initial average Emax of 2.03). When comparing these results with the ‘exponential phase’ selected by the exponential fit methods (cycles 17.25 to 22.23, averaged over all selection protocols and all repeats) it is obvious that the assumption of constant efficiency is not supported by the data. The exponential phase is therefore not log-linear but remains slightly curved and is only optically straight. While the effect of this curvature on Cq values calculated by the fit point method is likely negligible, the consequences for single reaction efficiency calculation methods that heavily rely on the assumption of constant efficiency may be considerably larger.
Fluorescence fit
Table 2 lists the average relative residual sum of squares for the different model fits to the fluorescence data (expressed as a percentage of the residual sum of squares of a linear model applied to the same data). The model that approximates the data most closely is the 5PLM, followed by the FPK-PCR model. The explanation for the somewhat lesser fit of the FPK-PCR model should be sought in the fact that the 5PLM is a purely empirical model that was not designed to be kinetically realistic whereas the FPK-PCR approach tries to merge both aspects. The fact that the FPK-PCR model fits the data more closely than the sigmoid and four parametric logistic model confirms that fluorescence fitting and kinetic realism are not mutually exclusive.
Table 2.
Residual sum of squares for a number of models applied to real-time PCR in percentage
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| 4PLM | 0.60 | 0.53 | 0.53 | 0.62 | 0.56 |
| Sigmoid | 1.47 | 1.36 | 1.28 | 1.30 | 1.07 |
| 5PLM | 0.31 | 0.17 | 0.09 | 0.05 | 0.03 |
| FPK | 0.30 | 0.42 | 0.31 | 0.42 | 0.21 |
Residual sum of squares (RSS) for four models applied to real-time PCR, expressed as a percentage of the residual sum of squares of a linear model (F = a · n + b) applied to the same data. Values displayed are the relative RSS values obtained on the separate reactions (soybean, le1 target), averaged per dilution point. ‘4PLM’ and ‘5PLM’ stand for Four and Five Parameter Logistic Model, respectively, ‘Sigmoid’ stands for Sigmoid model and ‘FPK’ represents the FPK-PCR approach.
The largest residuals of the FPK-PCR approach are situated near the end of the reaction. This has two main reasons: first, the phase transition is somewhat difficult to fit and the model has problems reaching a complete stop of amplification (i.e. E = 1). Due to its double exponential nature there remains some residual amplification during the plateau phase, often not more than about 1 ppm which is enough to increase fluorescence. Second, error accumulates throughout the model fit. This is a natural consequence of the way the FPK-PCR model is conceived: the cumulative product amplifies the individual cycle-efficiency errors preventing them from canceling each other out.
For truncated datasets the goodness of fit depends on where the truncation falls: limited availability of data negatively influences the model fit. But truncated datasets also influence the fitting of empirical models: due to the nature of the least squares method, the value of the terminal asymptote (plateau) is not correctly extrapolated. Instead, the plateau value is adjusted to maximize the fit to the available data. This affects all model parameters to a certain degree (see Figure 8). One should thus proceed with caution when basing estimations on any model fitted to an incomplete reaction profile.
As mentioned earlier, the amplification profile is determined by the cycle efficiencies, whereas initial target fluorescence scales the profile to the data. The relatively close fit of the FPK-PCR model thus provides further support for the accuracy of the cycle efficiency model.
Model Interpretation
The two ‘fits’ (efficiency and fluorescence) also represent two levels of model interpretation: the general PCR kinetics equation on the one hand, which acts as a supra structure and offers straightforward information, and the bilinear (efficiency) model on the other hand which has a more complicated structure and offers greater detail on the internal changes in amplification rate.
At the first level, the initial target fluorescence (α · i0) provides a relative measure of the initial target copy number whereas the chain of individual cycle efficiencies (En) provides information on the reaction efficiency.
At the second level, the bilinear model χ is related to the initial reaction efficiency (Emax). Parameter Fc represents the point of rather sudden decrease of amplification (fluorescence instance where the transition between the two decline phases happens). Finally η together with the slopes (a1, a2 and a3) represent the main kinetic shape parameters.
Evaluation of efficiency estimates
In order to compare the output of the FPK-PCR method to other single reaction efficiency methods, the maximal efficiency initially obtained by the reaction will be used as final model output. The evaluation of the model performance will be carried out on two levels: its ability to detect inhibited reactions on the one hand and the accuracy and robustness of the efficiency estimates on the other hand. To that end several single reaction efficiency estimation methods as well as the golden standard of serial dilution are compared using both an inhibition free dataset as well as inhibited datasets (Table 3 summarizes the data by means of their Cq values).
Table 3.
Overall comparison of the results obtained on soybean data
| Cq | Edilution | Eexponential | ELRE | EFPK | |
|---|---|---|---|---|---|
| Glycine max | |||||
| S1 | 22.75 ± 0.13 | 1.862 ± 0.016 | 1.896 ± 0.046 | 1.910 ± 0.030 | 2.028 ± 0.044 |
| S2 | 25.30 ± 0.11 | 1.901 ± 0.024 | 1.871 ± 0.022 | 2.015 ± 0.020 | |
| S3 | 27.67 ± 0.06 | 1.935 ± 0.022 | 1.906 ± 0.012 | 2.009 ± 0.017 | |
| S4 | 30.27 ± 0.11 | 1.890 ± 0.026 | 1.874 ± 0.019 | 1.976 ± 0.021 | |
| S5 | 33.21 ± 0.21 | 1.892 ± 0.022 | 1.883 ± 0.022 | 1.986 ± 0.016 | |
| Glycine max + Isopropanol | |||||
| S1 | 26.20 ± 0.46 | 2.003 ± 0.029 | 1.426 ± 0.047 | 1.592 ± 0.031 | 1.611 ± 0.025 |
| S2 | 26.02 ± 0.12 | 1.725 ± 0.069 | 1.815 ± 0.066 | 1.960 ± 0.095 | |
| S3 | 28.56 ± 0.09 | 1.755 ± 0.043 | 1.857 ± 0.024 | 1.975 ± 0.022 | |
| S4 | 30.56 ± 0.13 | 1.757 ± 0.035 | 1.869 ± 0.015 | 2.011 ± 0.015 | |
| S5 | 33.08 ± 0.22 | 1.775 ± 0.028 | 1.862 ± 0.046 | 1.987 ± 0.030 | |
| Glycine max + tannic acid | |||||
| S1 | 25.57 ± 0.39 | 1.928 ± 0.025 | 1.431 ± 0.027 | 1.719 ± 0.018 | 1.834 ± 0.015 |
| S2 | 25.50 ± 0.06 | 1.558 ± 0.039 | 1.862 ± 0.042 | 1.974 ± 0.044 | |
| S3 | 27.78 ± 0.05 | 1.587 ± 0.041 | 1.821 ± 0.013 | 1.998 ± 0.022 | |
| S4 | 30.51 ± 0.25 | 1.565 ± 0.029 | 1.830 ± 0.039 | 1.979 ± 0.027 | |
| S5 | 32.76 ± 0.18 | 1.560 ± 0.047 | 1.835 ± 0.026 | 1.980 ± 0.014 |
Overall comparison of different efficiency estimation methods: Edilution, serial dilution; Eexponential, exponential fit; ELRE, linear regression of efficiency; EFPK, full process kinetics PCR. All reactions targeted soybean Le1 at various concentrations with and without inhibitors. The values displayed represent averages ± standard error. For Edilution the first dilution point (S1) was omitted from analysis in the inhibited dilution series. All standard errors were obtained using available replicates per dilution point, with the exception of the dilution estimate for which a bootstrap method was used. Cq values were calculated as the position of the first positive maximum of the second derivative of a five parameter logistic model (1). The number of initial target copies for S1–S5 can be found in ‘Materials and Methods’ section under ‘PCR reactions’.
The inhibited datasets contain either isopropanol or tannic acid [known reaction inhibitors (5,22–24)] which were codiluted with the DNA as explained under ‘Materials and Methods’ section. All tested approaches identify the first dilution point of the inhibited datasets as having a significantly lower efficiency (see Table 3). This confirms the expectations since only the first dilutions contain inhibitors above their inhibitory concentration (1% (v/v) for isopropanol (42); for tannic acid no data were found, but inhibitory concentration is presumed to be in the 0.1 ng/μl range). The other dilutions contain progressively lower concentrations and should not suffer from significant inhibition. Indeed the serial dilution, LRE and FPK-PCR approaches return E estimates close to their respective results for the uninhibited dataset. The results for the exponential fit approach, on the other hand, while consistent within each dataset, exhibit a large between-dataset variation.
All efficiency estimation methods tested have a comparable standard deviation which is constant over the entire dilution series but may slightly increase in the presence of inhibitors (see Table 3). The size of the maximal efficiency estimates differs somewhat between methods (averages over all non-inhibited reactions: Edilution=1.895, Eexponential=1.899, ELRE=1.944, EFPK=2.016), with the variable efficiency methods (i.e. LRE and FPK-PCR) returning higher estimates than the exponential fit method. Concerning the efficiency values that are larger than two it should be noted that the theoretical maximum always falls within the margins of error. Such cases are a result of normal measurement error and the efficiency of these reactions should be considered near, or at, the theoretical maximum. The FPK-PCR method has no embedded constraints that limit the maximal efficiency estimate. On this account it is in line with the other methods, which may also report efficiencies higher than 2, although they rarely do. This may be due to the inclusion of cycles with submaximal efficiency in the latter's window of application.
The repeatability between datasets (when ignoring S1 for the inhibited series) is best for the LRE and FPK-PCR approaches, and less stable for the exponential fit and dilution assay. The latter may be due to its sensitivity to dilution errors. Overall we can conclude that the FPK-PCR method returns efficiency estimates that are comparable in both accuracy and repeatability to other methods, but has the advantage of yielding a complete cycle efficiency chain that is able to accurately reconstruct the fluorescence values.
The symmetric distribution of efficiency values returned by the FPK-PCR model (see Figure 9) is in line with previous findings (12), and supports the notion that the between reaction variability in efficiency values is due to limited precision of the individual data (statistical error) as opposed to actual kinetic differences between reactions (43,44). One should therefore assume equal efficiencies unless one suspects otherwise, in which case a t-test or Grubbs-test [as recommended by ISO (45)] should be used to decide the faith of the suspect reaction(s) (provided sufficient replicates are available).
Figure 9.
Box and whisker plots for the results of the FPK-PCR approach on three soybean (le1 target) datasets: uninhibited (blue), containing tannic acid (orange) and containing isopropanol (red). For each dataset 5 initial target concentrations are shown, each dilution point contains approximately the same number of target copies for each dataset. (A) contains the efficiency estimates (Emax), (B) contains the initial target fluorescence estimates (α · i0).
Apart from the efficiency, the FPK-PCR model provides an estimate of the number of initial target copies as well (see Table 4). As these estimates are the product of the target copy number and the fluorescence value of a single amplicon their use is limited to relative comparisons between reactions with the same target (or methods with identical target fluorescence). Yet, the uninhibited dilution series displays in α · i0 values about 2-fold higher compared to the inhibited series. However, within each series the values are linearly decreasing in accordance with the initial target copy number, indicating that i0 is correctly estimated by the model. The difference thus follows from variation in the single amplicon fluorescence (α). Indeed the observed fluorescence plateau displays similar trend between the different datasets (on average 8660FU, 4440FU and 2430FU for the uninhibited, isopropanol and tannic acid data, respectively). Since SYBRgreen is typically used at subsaturating concentrations this may account for the observed differences.
Table 4.
Summary of the initial target estimates
| Glycine max | + Isopropanol | + Tannic Acid | |
|---|---|---|---|
| α · i0 values | |||
| S1 | 1.4E-04 ± 4.6E-05 | 1.2E-03 ± 2.7E-04 | 4.9E-05 ± 1.8E-05 |
| S2 | 2.8E-05 ± 6.0E-06 | 1.4E-05 ± 5.3E-06 | 9.7E-06 ± 3.7E-06 |
| S3 | 5.9E-06 ± 1.2E-06 | 2.7E-06 ± 7.2E-07 | 1.5E-06 ± 3.5E-07 |
| S4 | 1.4E-06 ± 3.7E-07 | 3.9E-07 ± 8.1E-08 | 3.1E-07 ± 1.1E-07 |
| S5 | 1.5E-07 ± 5.0E-08 | 1.1E-07 ± 4.8E-08 | 6.7E-08 ± 2.3E-08 |
| Dilution factors based on Cq values | |||
| S1–S2 | 6.0 | 0.9 | 1.0 |
| S2–S3 | 5.3 | 5.6 | 4.7 |
| S3–S4 | 6.1 | 3.9 | 6.7 |
| S4-S5 | 7.4 | 5.8 | 4.6 |
| Dilution factors based on α · i0 values | |||
| S1–S2 | 5.0 | 80 | 5.1 |
| S2–S3 | 4.6 | 5.2 | 6.3 |
| S3–S4 | 4.1 | 7.1 | 4.9 |
| S4–S5 | 9.3 | 3.4 | 4.7 |
Summary of the initial target estimates (average±standard error) and dilution factors (average) for both the uninhibited and inhibited datasets (all soybean, Le1 target). The Cq based dilution factors are calculated as 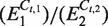 , whereas the α · i0-based dilution factors are the ratios between subsequent initial target estimates. The number of initial target copies for S1–S5 can be found in ‘Materials and Methods’ section under ‘PCR reactions’.
, whereas the α · i0-based dilution factors are the ratios between subsequent initial target estimates. The number of initial target copies for S1–S5 can be found in ‘Materials and Methods’ section under ‘PCR reactions’.
The dilution factors calculated from the α · i0 values are comparable to those calculated from the Cq values, with the exception of the S1 estimate for the isopropanol inhibited dataset, which is over 10 times too large (see Table 4 and Figure 9b). The explanation for this artifact lies in the fact that the calculation of dilution factors from the initial fluorescence estimates assumes that the amplicon fluorescence is not affected by the presence of an inhibitor: a number of observations indicate that isopropanol does interfere with binding between DNA and dye. First there is a shift in the PCR product's melting temperature (Tm) of about 2°C in isopropanol inhibited reactions (data not shown). This suggests the inhibitor is interfering with the DNA rather than with the polymerase. Second, this artifact can be ‘cured’ by switching to probe-based chemistry (resulting in a dilution factor of 4.1, ES1 = 1.59 and 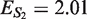 ).
).
Tannic acid, on the other hand, has been previously described as a polymerase inhibitor (24) and indeed did not influence the Tm of the PCR product. The dilution factors calculated from tannic acid inhibited reactions are comparable to their non-inhibited counterparts (see figure 9), showing that the initial target fluorescence estimates are not hindered by a lack of reaction efficiency when the assumption of constant amplicon fluorescence is not violated. This illustrates that the initial target fluorescence estimates provided by the FPK-PCR approach are a useful tool in overcoming the difficulties caused by inhibition and provides further proof for the accuracy of the FPK-PCR cycle efficiency estimates.
CONCLUSION
The FPK-PCR model provides a kinetically more realistic approach to analyze real-time PCR data. By reconstructing the chain of cycle efficiencies the amplification steps underlying the fluorescence increases are revealed, readily giving access to the internal efficiency behavior. The maximal efficiency estimates returned by the FPK-PCR approach are comparable in both accuracy and repeatability to the golden standard of serial dilution, and to other single reaction efficiency methods. The cycle efficiency changes as described by the FPK-PCR procedure are considerably closer to the actual data than those for other S-shaped models (Figure 6).
The general equation of PCR kinetics provides a solid supra structure with intuitive parameter interpretation. Furthermore, the underlying efficiency model, which details the different phases of the amplification process, opens a second, more advanced, level of interpretation.
The FPK-PCR approach demonstrates that by implementing a global efficiency model the use of a restricted window of application is unnecessary. One thus enhances reproducibility by avoiding an ad hoc selection of data. Furthermore, knowledge of the individual cycle efficiencies allows reconstructing the fluorescence data. This provides quality control over the efficiency estimate since unrealistic efficiency estimates will produce an inadequate overall fit.
Future opportunities for FPK-PCR analysis hold the development of more accurate whole reaction efficiency models. In this light, the role of baseline subtraction in the field of real-time PCR should not be minimized given its profound impact on the efficiency estimate. Further improvements to real-time PCR analysis should therefore encompass the development of a sound baseline model. In conclusion, the presented FPK-PCR approach holds the potential to make single reaction analysis a powerful tool for future widespread application.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
IAP research network grant (nr. P6/03) of the Belgian government (Belgian Science Policy in part). Funding for open access charge: Scientific Institute of Public Health J. Wytsmanstreet 14 B-1050 Brussels, Belgium.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
The authors would like to thank the GMOlab section of the institute of Public health in Brussels, Belgium and Nancy Roosens in particular for their support during the research and development that lead to this publication. We acknowledge the support of Ghent University (Multidisciplinary Research Partnership “Bioinformatics: from nucleotides to networks”).
REFERENCES
- 1.Kubista M, Andrade JM, Bengtsson M, Forootan A, Jonak J, Lind K, Sindelka R, Sjoback R, Sjogreen B, Strombom L, et al. The real-time polymerase chain reaction. Mol. Aspects Med. 2006;27:95–125. doi: 10.1016/j.mam.2005.12.007. [DOI] [PubMed] [Google Scholar]
- 2.Kainz P. The pcr plateau phase - towards an understanding of its limitations. Biochim Biophys. Acta. 2007;1494:23–27. doi: 10.1016/s0167-4781(00)00200-1. [DOI] [PubMed] [Google Scholar]
- 3.Bessetti J. An introduction to pcr inhibitors. Profiles in DNA. 2007;10:9–10. [Google Scholar]
- 4.Bar T, Stahlberg A, Muszta A, Kubista M. Kinetic outlier detection (kod) in real-time PCR. Nucleic Acids Res. 2003;31:e105. doi: 10.1093/nar/gng106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Demeke T, Jenkins GR. Influence of DNA extraction methods, PCR inhibitors and quantification methods on real-time PCR assay of biotechnology-derived traits. Anal. Bioanal. Chem. 2009;396:1977–1990. doi: 10.1007/s00216-009-3150-9. [DOI] [PubMed] [Google Scholar]
- 6.Ramakers C, Ruijter JM, Deprez RH, Moorman AF. Assumption-free analysis of quantitative real-time polymerase chain reaction (PCR) data. Neurosci. Lett. 2003;339:62–66. doi: 10.1016/s0304-3940(02)01423-4. [DOI] [PubMed] [Google Scholar]
- 7.Liu W, Saint DA. A new quantitative method of real time reverse transcription polymerase chain reaction assay based on simulation of polymerase chain reaction kinetics. Anal. Biochem. 2002;302:52–59. doi: 10.1006/abio.2001.5530. [DOI] [PubMed] [Google Scholar]
- 8.Meijerink J, Mandigers C, van de Locht L, Tonnissen E, Goodsaid F, Raemaekers J. A novel method to compensate for different amplification efficiencies between patient DNA samples in quantitative real-time pcr. J. Mol. Diagn. 2001;3:55–61. doi: 10.1016/S1525-1578(10)60652-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wilson IG. Inhibition and facilitation of nucleic acid amplification. Appl. Environ. Microbiol. 1997;63:3741–3751. doi: 10.1128/aem.63.10.3741-3751.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nolan T, Hands RE, Ogunkolade W, Bustin SA. Spud: a quantitative PCR assay for the detection of inhibitors in nucleic acid preparations. Anal. Biochem. 2006;351:308–310. doi: 10.1016/j.ab.2006.01.051. [DOI] [PubMed] [Google Scholar]
- 11.Swango KL, Timken MD, Date Chong M, Buoncristiani MR. A quantitative PCR assay for the assessment of DNA degradation in forensic samples. Forensic Sci. Int. 2006;158:14–26. doi: 10.1016/j.forsciint.2005.04.034. [DOI] [PubMed] [Google Scholar]
- 12.Ruijter JM, Ramakers C, Hoogaars WM, Karlen Y, Bakker O, van den Hoff MJ, Moorman AF. Amplification efficiency: linking baseline and bias in the analysis of quantitative pcr data. Nucleic Acids Res. 2009;37:e45. doi: 10.1093/nar/gkp045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhao S, Fernald RD. Comprehensive algorithm for quantitative real-time polymerase chain reaction. J. Comput. Biol. 2005;12:1047–1064. doi: 10.1089/cmb.2005.12.1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tichopad A, Dilger M, Schwarz G, Pfaffl MW. Standardized determination of real-time PCR efficiency from a single reaction set-up. Nucleic Acids Res. 2003;31:e122. doi: 10.1093/nar/gng122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rutledge RG, Stewart D. Critical evaluation of methods used to determine amplification efficiency refutes the exponential character of real-time PCR. BMC Mol. Biol. 2008;9:96. doi: 10.1186/1471-2199-9-96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schnell S, Mendoza C. Enzymological considerations for a theoretical description of the quantitative competitive polymerase chain reaction (qc-PCR) J. Theor. Biol. 1997;184:433–440. doi: 10.1006/jtbi.1996.0283. [DOI] [PubMed] [Google Scholar]
- 17.Mehra S, Hu WS. A kinetic model of quantitative real-time polymerase chain reaction. Biotechnol. Bioeng. 2005;91:848–860. doi: 10.1002/bit.20555. [DOI] [PubMed] [Google Scholar]
- 18.Gevertz JL, Dunn SM, Roth CM. Mathematical model of real-time PCR kinetics. Biotechnol. Bioeng. 2005;92:346–355. doi: 10.1002/bit.20617. [DOI] [PubMed] [Google Scholar]
- 19.Rutledge RG, Stewart D. A kinetic-based sigmoidal model for the polymerase chain reaction and its application to high-capacity absolute quantitative real-time PCR. BMC Biotechnol. 2008;8:47. doi: 10.1186/1472-6750-8-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Garlick M, Powell J, Eyre D, Robbins T. Mathematically modeling pcr: an asymptotic approximation with potential for optimization. Math. Biosci. Eng. 2010;7:363–384. doi: 10.3934/mbe.2010.7.363. [DOI] [PubMed] [Google Scholar]
- 21.Barbau-Piednoir E, Lievens A, Mbongolo-Mbella G, Roosens N, Sneyers M, Leunda-Casi A, Van den Bulcke M. SYBR® green qPCR screening methods for the presence of 35s promoter and nos terminator elements in food and feed products. Eur. Food Res. Technol. 2010;230:383–393. [Google Scholar]
- 22.Kontanis EJ, Reed FA. Evaluation of real-time PCR amplification efficiencies to detect PCR inhibitors. J. Forensic Sci. 2006;51:795–804. doi: 10.1111/j.1556-4029.2006.00182.x. [DOI] [PubMed] [Google Scholar]
- 23.Sisti D, Guescini M, Rocchi MB, Tibollo P, D'Atri M, Stocchi V. Shape based kinetic outlier detection in real-time PCR. BMC Bioinformatics. 2010;11:186. doi: 10.1186/1471-2105-11-186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Opel KL, Chung D, McCord BR. A study of PCR inhibition mechanisms using real time PCR. J. Forensic Sci. 2010;55:25–33. doi: 10.1111/j.1556-4029.2009.01245.x. [DOI] [PubMed] [Google Scholar]
- 25.Terry CF, Shanahan DJ, Ballam LD, Harris N, McDowell DG, Parkes HC. Real-time detection of genetically modified soya using lightcycler and ABI 7700 platforms with taqman, scorpion, and SYBR green I chemistries. J. AOAC Int. 2002;85:938–944. [PubMed] [Google Scholar]
- 26.Arumuganathan K, Earle ED. Nuclear dna content of some important plant species. Plant Mol. Biol. Reporter. 1991;9:211–215. [Google Scholar]
- 27.Richards FJ. A flexible growth function for empirical use. J. Exp. Bot. 1959;10:290–301. [Google Scholar]
- 28.Fox J. An R and S-PLUS Companion to Applied Regression. Thousand Oaks California: Sage Publications; 2002. [Google Scholar]
- 29.Peirson SN, Butler JN, Foster RG. Experimental validation of novel and conventional approaches to quantitative real-time PCR data analysis. Nucleic Acids Res. 2003;31:e73. doi: 10.1093/nar/gng073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. R Development Core Team. (2009) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- 31.Levenberg K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944;2:164–168. [Google Scholar]
- 32.Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963;11:431–441. [Google Scholar]
- 33.Batsch A, Noetel A, Fork C, Urban A, Lazic D, Lucas T, Pietsch J, Lazar A, Schomig E, Grundemann D. Simultaneous fitting of real-time PCR data with efficiency of amplification modeled as gaussian function of target fluorescence. BMC Bioinformatics. 2008;9:95. doi: 10.1186/1471-2105-9-95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jagers P, Klebaner F. Random variation and concentration effects in PCR. J. Theor. Biol. 2003;224:299–304. doi: 10.1016/s0022-5193(03)00166-8. [DOI] [PubMed] [Google Scholar]
- 35.Schnell S, Mendoza C. Theoretical description of the polymerase chain reaction. J. Theor. Biol. 1997;188:313–318. doi: 10.1006/jtbi.1997.0473. [DOI] [PubMed] [Google Scholar]
- 36.Lalam N. Estimation of the reaction efficiency in polymerase chain reaction. J. Theor. Biol. 2006;242:947–953. doi: 10.1016/j.jtbi.2006.06.001. [DOI] [PubMed] [Google Scholar]
- 37.Lalam N. Statistical inference for quantitative polymerase chain reaction using a hidden Markov model: a bayesian approach. Stat. Appl. Genet. Mol. Biol. 2007;6 doi: 10.2202/1544-6115.1253. Article10. [DOI] [PubMed] [Google Scholar]
- 38.Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of dermining the value of life contingencies. Philos. Trans. Roy. Soc. London. 1825;115:513–585. doi: 10.1098/rstb.2014.0379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Alvarez MJ, Vila-Ortiz GJ, Salibe MC, Podhajcer OL, Pitossi FJ. Model based analysis of real-time PCR data from DNA binding dye protocols. BMC Bioinformatics. 2007;8:85. doi: 10.1186/1471-2105-8-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Buchwald P. A general bilinear model to describe growth or decline time profiles. Math. Biosci. 2007;205:108–136. doi: 10.1016/j.mbs.2006.08.013. [DOI] [PubMed] [Google Scholar]
- 41.Platts AE, Johnson GD, Linnemann AK, Krawetz SA. Real-time PCR quantification using a variable reaction efficiency model. Anal. Biochem. 2008;380:315–322. doi: 10.1016/j.ab.2008.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Peist R, Honsel D, Twieling G, Löffert D. PCR inhibitors in plant DNA preparations. Qiagen news. 2001;3:7–9. [Google Scholar]
- 43.Cikos S, Bukovska A, Koppel J. Relative quantification of mRNA: comparison of methods currently used for real-time PCR data analysis. BMC Mol. Biol. 2007;8:113. doi: 10.1186/1471-2199-8-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nordgard O, Kvaloy JT, Farmen RK, Heikkila R. Error propagation in relative real-time reverse transcription polymerase chain reaction quantification models: the balance between accuracy and precision. Anal. Biochem. 2006;356:182–193. doi: 10.1016/j.ab.2006.06.020. [DOI] [PubMed] [Google Scholar]
- 45. International Organisation for Standardization. (1994) Accuracy (trueness and precision) of measurement methods and results. [Google Scholar]