Abstract
In the cat or primate primary visual cortex (V1), normal vision corresponds to a state where neural excitation patterns are driven by external visual stimuli. A spectacular failure mode of V1 occurs when such patterns are overwhelmed by spontaneously generated spatially self-organized patterns of neural excitation. These are experienced as geometric visual hallucinations. The problem of identifying the mechanisms by which V1 avoids this failure is made acute by recent advances in the statistical mechanics of pattern formation, which suggest that the hallucinatory state should be very robust. Here, we report how incorporating physiologically realistic long-range connections between inhibitory neurons changes the behavior of a model of V1. We find that the sparsity of long-range inhibition in V1 plays a previously unrecognized but key functional role in preserving the normal vision state. Surprisingly, it also contributes to the observed regularity of geometric visual hallucinations. Our results provide an explanation for the observed sparsity of long-range inhibition in V1—this generic architectural feature is an evolutionary adaptation that tunes V1 to the normal vision state. In addition, it has been shown that exactly the same long-range connections play a key role in the development of orientation preference maps. Thus V1’s most striking long-range features—patchy excitatory connections and sparse inhibitory connections—are strongly constrained by two requirements: the need for the visual state to be robust and the developmental requirements of the orientational preference map.
Keywords: evolution, fluctuations
The primary visual cortex, V1, represents external stimuli as patterns of neural excitation. In the normal state, patterns of excitation on V1 are driven by sensory stimuli generated in the retina mapped to V1 from the visual field by the retinocortical map (1, 2). Patterns seen as visual hallucinations arise in exceptional circumstances when external stimuli are overwhelmed by internally generated spontaneous patterns of neural excitation. This situation occurs when the circuit parameters governing the dynamics of V1 are changed, for example, through the influence of psychotropic drugs that may act in part through effectively weakening cortical inhibition (3). The mechanism governing spontaneous pattern formation has been shown in previous studies to be closely related to that of diffusion driven pattern formation in chemical and other biological systems, known as the Turing mechanism (4–6). Compelling evidence for this mechanism has been provided by previous studies that have shown that precisely the four basic classes of geometric visual hallucinations (or form constants) and no others, commonly reported by subjects (7), follow directly from the Turing mechanism and spontaneous symmetry breaking of the basic approximate symmetries of V1 associated with translation and orientation preference (6). Here we show that V1 is specially configured to avoid the formation of visual hallucinations and remain stable under typical operating conditions in the visual state. Together with recent reports of developmental plasticity in V1 (8), and the apparent universality of the self-organizing principles behind the structure of its orientation columns (9), our results imply strong constraints on the key features and evolution of its global architecture at intermediate length scales.
We analyze and compare two classes of model for the spatiotemporal dynamics of neural excitation in V1. The first model is subject to network connections that are similar to the real V1 network, whereas the second model represents a family of a priori physiologically plausible alternative network structures. We show that the alternative network structures substantially degrade normal visual function, thereby illuminating the functional advantages of the network structure actually realized in V1. Similar approaches have been successfully applied to other robust phenomena in biology, such as embryonic pattern formation (10), bistable genetic switching (11), and the generation of temporal oscillations of gene expression (12). In these cases, the requirement that the network dynamics robustly preserve some function under variation of parameters or noise led naturally to the elucidation of key features such as the coupling of positive and negative feedback loops to generate robust oscillations in the level of gene expression (12). We will show that the requirement that V1 activation be primarily driven by external sensory stimuli strongly constrains the topology of its connections by allowing only sparse long-range inhibition. This feature of V1 is well-established empirically (13), but has not yet been explained. In other parts of the cortex where the function is presumably different, there is some evidence that sparse long-range connections do exist that provide some lateral disinhibition (14, 15). By combining this requirement with the recent experimental confirmation of calculations that predict that long-range interactions between V1 neurons are essential for stabilizing the development of orientational preference maps (9), we obtain sufficient constraints on V1 network structure to strongly constrain the character of its long-range connections.
Geometric visual hallucinations arise through a variant of the Turing mechanism for pattern formation (4). In V1, spatial patterns arise when the range of local excitatory to inhibitory connections (E–I) is sufficiently longer than the range of excitatory to excitatory (E–E) connections. Thus when there is a local burst of excitation, the longer-ranged connections to inhibitory neurons contain the burst. Fluctuations of activity are then confined over some characteristic length scale, leading to spatial pattern formation. The difference in length scale of E–E connections versus E–I connections results in an effective “Mexican hat” potential if inhibitory neurons are integrated out, exactly as required for the successful development of a stable orientation preference map (9).
Model
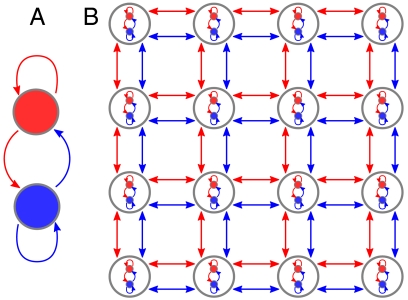
We model each local hypercolumn using the most general possible wiring, consistent with the physiological separation of excitatory and inhibitory neurons. Alternatively, the local structure can be viewed as many copies of a simplified version of the Douglas–Martin canonical microcircuit (16). This microcircuit is shown schematically in Fig. 1A.
Fig. 1.
(A) Simplified Douglas–Martin microcircuit. The blue circle corresponds to inhibitory neurons, and the red circle to excitatory neurons. Similarly, excitatory connections are shown as red arrows from their source and inhibitory connections as blue arrows. Inputs to the microcircuit vary and are not shown. (B) Simplified representation of patchy connections between hypercolumns in V1. Each hypercolumn is represented by a circle, with both E–E and E–I connections between hypercolumns indicated by red arrows.
We now introduce a model of V1 as a two-dimensional lattice of canonical microcircuits. To capture the lattice structure, we distinguish two length scales. The first length scale is local and is the one on which canonical microcircuits, each of which has a width of approximately 100 µm, interact with their neighbors. We model this local scale as comprising all the approximate 10 microcircuits in one V1 hypercolumn (1). Based on neuroanatomical data, our model includes excitatory and inhibitory connections between all microcircuits within a hypercolumn (17).
The second length scale is longer ranged. On this length scale, hypercolumns are coupled together by patchy excitatory connections. These connections have a range of approximately 4 mm with axonal arbors every 1 mm or so (18). Thus they are between hypercolumns. If we take the lattice spacing between individual microcircuits to be L mm, then the spacing between hypercolumns is 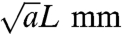 where a is the number of microcircuits per hypercolumn. Thus the connections between differing lattice sites support a mixture of both local and nonlocal or lattice scale excitation and inhibition. These couplings are as shown in Fig. 1. For even longer-ranged connections, which would provide a third length scale, the best evidence to date (19) suggests that they are small world (20). However, in this paper, we do not consider their effects. The model presented here is a special case of that introduced to analyze the formation of geometric visual hallucinations (6). As we note later, it is also closely related to a model of the cortex introduced to study the development of stable orientation preference maps (9, 21).
where a is the number of microcircuits per hypercolumn. Thus the connections between differing lattice sites support a mixture of both local and nonlocal or lattice scale excitation and inhibition. These couplings are as shown in Fig. 1. For even longer-ranged connections, which would provide a third length scale, the best evidence to date (19) suggests that they are small world (20). However, in this paper, we do not consider their effects. The model presented here is a special case of that introduced to analyze the formation of geometric visual hallucinations (6). As we note later, it is also closely related to a model of the cortex introduced to study the development of stable orientation preference maps (9, 21).
These assumptions yield variants of the Wilson–Cowan equations (22) for local density of neural excitation of excitatory (φ) and inhibitory (ψ) neurons (see SI Text). On length scales much greater than the lattice scale, the Wilson–Cowan equations reduce to the partial differential equations
| [1] |
with currents given by
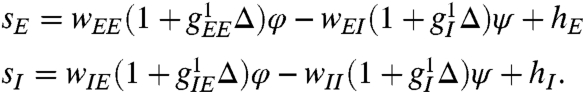 |
[2] |
The functions fI and fE are sigmoidal and capture the saturating response of neurons to external stimuli. The symbol Δ represents the continuous Laplacian in two dimensions. The matrix W captures the local synaptic interactions as in Fig. 1A; for example, wIE denotes the synaptic weight of E–I connections. The parameters 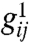 are effective length scales of the indicated connections, and we take gEI = gII = gI. For the purposes of this study of spontaneous pattern formation, external stimuli h are set to zero. Although most of the key conclusions of the present work are analytical, typical simulation parameters are wEE = 1.3 with all other w = 1, αI = αE = 0.1. The lattice scale spacing is taken in units of
are effective length scales of the indicated connections, and we take gEI = gII = gI. For the purposes of this study of spontaneous pattern formation, external stimuli h are set to zero. Although most of the key conclusions of the present work are analytical, typical simulation parameters are wEE = 1.3 with all other w = 1, αI = αE = 0.1. The lattice scale spacing is taken in units of 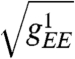 . Previously cited neuroanatomical data (13) indicates that
. Previously cited neuroanatomical data (13) indicates that 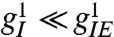 .
.
Results
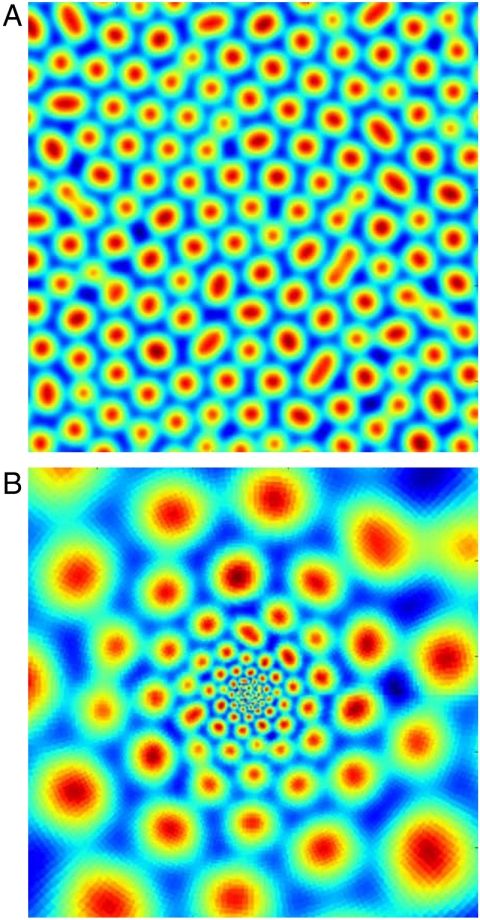
Provided couplings that promote excitation, such as wEE, are sufficiently large compared to relaxation and inhibitory couplings, Eq. Eq. 1 with lattice scale effects neglected (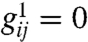 ), support a stable fixed point at nonzero excitation levels of both excitatory and inhibitory neurons. When such effects are restored, normal vision corresponds to a stable homogeneous steady state. Failure of normal vision to geometric visual hallucinations occurs when the homogeneous steady state becomes unstable to spatially inhomogeneous perturbations, leading to regular pattern formation (see Fig. 2A).
), support a stable fixed point at nonzero excitation levels of both excitatory and inhibitory neurons. When such effects are restored, normal vision corresponds to a stable homogeneous steady state. Failure of normal vision to geometric visual hallucinations occurs when the homogeneous steady state becomes unstable to spatially inhomogeneous perturbations, leading to regular pattern formation (see Fig. 2A).
Fig. 2.
(A) Turing pattern of neural excitation in visual cortex coordinates. (B) The same pattern represented in visual field coordinates (i.e., in the coordinates that a patient undergoing geometric visual hallucinations would see). The logarithmic map between visual field and V1 is responsible for the dramatic logarithmic spiral structure of the hallucination. Although the image shown here is from computation, its qualitative features are very similar to those reported by patients (7). Figure generated with the parameters indicated in the text plus 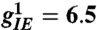 ,
, 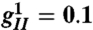 with all other
with all other 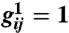 .
.
The exotic spiral structure of hallucinations reported by patients (7) and shown in Fig. 2B arises from regular pattern formation through the retinotopic map. The retinotopic map transforms coordinates of excitation on V1 into visual field coordinates through an approximate logarithmic conformal map, as demonstrated experimentally in ref. 2. When regular patterns are subjected to a logarithmic conformal map, they are transformed into logarithmic spiral patterns, implying that regular pattern formation on V1 results in the logarithmic spiral patterns observed in geometric visual hallucinations (5).
In the full model above, with 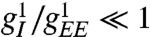 as physiologically motivated, geometric hallucinations occur when
as physiologically motivated, geometric hallucinations occur when
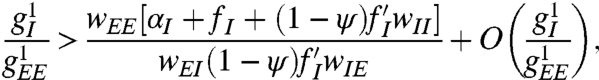 |
[3] |
where all functions, derivatives, and concentrations of firing inhibitory neurons are evaluated at the homogeneous fixed point (see SI Text). Such conditions may possibly be achieved through the effects of hallucinogenic drugs (5, 7).
How would V1 behave if extensive lattice scale I–I connections were present? This extensive lattice scale inhibition means that inhibitory activity in one microcircuit suppresses inhibition in distant microcircuits, leading to more excitatory activity in the distant site: I–I connections tend to enhance negatively correlated fluctuations in activity. We introduce such connections by relaxing the requirement that 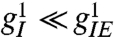 . Linear stability analysis shows that a sufficient condition for the normal visual state to be unstable to spontaneous spatial order is
. Linear stability analysis shows that a sufficient condition for the normal visual state to be unstable to spontaneous spatial order is
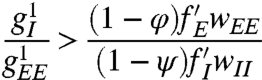 |
[4] |
(see ref. 23). The right-hand side of the above inequality is typically less than one for reasonable parameters. Because, in the absence of fine tuning, the existence of extensive lattice scale I–I connections requires the left-hand side of inequality 4 to be O(1) or greater (to avoid dangling axons between hypercolumns), we can conclude that the requirement that V1 represent visual stimuli through patterns of excitation is incompatible with such I–I connections. Only with fine tuning could such I–I connections be constructed so as to not generate spontaneous spatial order. Because changing conditions in the brain make such fine tuning impossible, the organization of V1 for robust visual function requires that lattice scale I–I connections be sparse. Experimental support for this statement is provided by data on the connections made by a special class of inhibitory cells called large basket cells (LBC), which have long axons and so can provide lattice scale inhibition (14): A recent count (13) of the number of lattice scale inhibitory synapses found on V1 LBC indicates that such connections are sparse compared with the number of lattice scale excitatory synapses found on such neurons and on V1 pyramidal neurons.
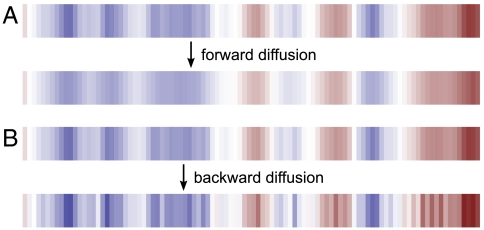
The spatial structures that occur in the presence of extensive lattice scale I–I coupling differ from those observed in geometric visual hallucinations and contrast with the usual scenario by which a single characteristic length scale emerges from a pattern-forming process. In such a case, the homogeneous steady state is typically unstable for some bounded region of wave vectors greater than zero. Surprisingly, in the case of lattice scale I–I connections, the instability occurs for all spatial frequencies greater than some threshold, so that the long wavelength approximation breaks down (see SI Text). These effects originate in the suppressive nature of inhibition, captured in the negative sign of the Laplacian for inhibitory connections in Eq. 2. Laplacian operators with positive signs are associated with signals from excitatory neurons. When the long-range connections are primarily from excitatory neurons, the overall sign of the Laplacian is positive, and the dynamics are those associated with normal diffusion: spatial smoothing if primarily excitatory neurons are excited at long ranges, and Turing patterns if primarily inhibitory neurons are excited at long ranges. When the long-range connections primarily are associated with inhibitory neurons, the overall sign of the Laplacian is negative, leading to reverse diffusion. Reverse, or backward diffusion, has exactly the opposite effect of normal diffusion. Where normal diffusion leads to smoothing of excitations, reverse diffusion leads to clumping of excitations at ever shorter length scales (see Fig. 3). These dynamics rely on the unusual spatial distribution of I–I connections. When an inhibitory neuron fires, connected inhibitory neurons at distant lattice sites become less active, allowing excitatory neurons at that site to become more active. Meanwhile, the level of excitation at the original lattice site may be maintained by local feedbacks with excitatory neurons. Close to each of these sites, excitatory activity is suppressed via short range I–E or E–I connections, unless E–E connectivity is strong enough to counteract the overall effect. This local feedback leads to increasingly incoherent local excitations, with activity patterns nearby lattice sites less strongly correlated. If the long-range connections in the network are dominated by I–I connections, then increasingly localized clumping of excitations results.
Fig. 3.
Schematic representation of how long-range inhibition leads to instability in strips of visual cortex. An excess of excitatory over inhibitory activity is indicated in red and the converse in blue. A illustrates dynamics with normal visual cortex architecture, where long-range inhibition is forbidden. These dynamics are analogous to normal diffusion. The upper row shows an initial distribution of activity and the lower row shows the evolution of this distribution at a later time. The spatial distribution of activity is smoothed. B illustrates dynamics with added long-range inhibition, whose dynamics are analogous to backward diffusion. The upper row shows the same initial distribution of activity, and the lower row shows the evolution of this distribution at a later time. Under reverse diffusion, the spatial distribution of activity becomes less smooth, leading to short length scale spatial structures.
Recent theoretical studies of Turing patterns in reaction-diffusion systems have shown that intrinsic and extrinsic noise enhances the stability of Turing patterns (24–26) through an extension of the quasi-cycle mechanism of McKane and Newman (27, 28). If such results were to hold for pattern formation in V1, achieving robust visual function would be very difficult. We have investigated the effects of noise on the dynamics of our model of V1 and found that, when lattice scale I–I connections are sparse, noise does not enlarge the set of parameters that support patterns. However, when extensive lattice scale I–I coupling is introduced, fluctuation-induced “quasi-patterns” incompatible with normal visual function are generated (see SI Text). A further functional role of forbidding such connections may then be avoidance of quasi-pattern generation. We also note that the Turing patterns that do occur in our model of the visual cortex with realistic connectivity are deterministic and highly regular. This behavior is in contrast to most Turing systems, where quasi-patterns dominate and substantial fluctuations in the patterning are expected (24–26). However, it was shown in ref. 29 that Turing patterns generated by noise can be pinned to an underlying lattice provided by the lattice scale patchy E–E connections described earlier. The lack of extensive lattice scale inhibitory connections contributes to the stability of such a pinning, and helps to explain, for example, why subjects report seeing geometric visual hallucinations that are highly regular (7).
It should be noted that, although the model we present in Eqs. 1 and 2 is highly simplified, the results are based only on the elementary features of the bifurcation structure of the model. It is well known that the bifurcation structure of models in statistical mechanics and dynamical systems is sensitive to only primitive, detail-independent considerations such as symmetry, fluctuations, range of interaction, and spatial dimension (30, 31). Thus it can be expected that the results will be largely unchanged in more detailed models of V1, which include other standard formulations, such as integrodifferential equations (5) and versions where the lattice structure is explicitly considered.
Discussion
Results on the development of the orientational preference map (9, 21) can be combined with our work to constrain the evolution of several of the basic features of the network anatomy of V1. In refs. 9 and 21, it was shown that, for the orientational preference map of V1 to develop correctly, a lattice scale Mexican hat interaction is required—i.e., short-range amplification and long-range suppression. To achieve this in a two-population excitatory-inhibitory model, either long-range inhibition or long-range E–I connections must dominate long-range activation of excitatory neurons. Because our work suggests that extensive lattice scale inhibitory connections are detrimental for normal vision, the only network structure that is consistent with both of these results must have only sparse lattice scale inhibitory connections, and the lattice scale E–I connections must have greater effective range than the lattice scale E–E connections. However, to avoid hallucinations, the lattice scale E–I range must not greatly exceed the local E–E range. These V1 circuit properties apply to both the avoidance of hallucinations in normal vision and to the development of orientation preference maps. In fact, both connectivity properties deal with exactly the same problem: breaking the symmetry of translation and orientation preference.
In summary, in V1 the lattice scale network’s most elementary features—patchy excitatory connections and sparse inhibitory connections—are completely constrained by two considerations: the need for the visual state to be robust and the developmental requirements of the orientational preference map.
Supplementary Material
Acknowledgments.
This work was partially supported by National Science Foundation Grant NSF-EF-0526747. Additional funding for T.C.B. was provided through a Drickamer fellowship from the University of Illinois Department of Physics.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1118672109/-/DCSupplemental.
References
- 1.Hubel DH, Wiesel TN. Uniformity of monkey striate cortex: A parallel relationship between field size, scatter and magnification factor. J Comp Neurol. 1974;158:295–306. doi: 10.1002/cne.901580305. [DOI] [PubMed] [Google Scholar]
- 2.Tootell RBH, Silverman MS, Switkes E, De Valois RL. Deoxyglucose analysis of retinotopic organization in primate striate cortex. Science. 1982;218:902–904. doi: 10.1126/science.7134981. [DOI] [PubMed] [Google Scholar]
- 3.Passie T, Halpern J, Stichtenoth D, Emrich H, Hintzen A. The pharmacology of lysergic acid diethylamide: A review. CNS Neurosci Ther. 2008;14:295–314. doi: 10.1111/j.1755-5949.2008.00059.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Turing AM. The chemical basis of morphogenesis. Philos Trans R Soc B Biol Sci. 1952;237:37–72. [Google Scholar]
- 5.Ermentrout GB, Cowan JD. A mathematical theory of visual hallucination patterns. Biol Cybern. 1979;34:137–150. doi: 10.1007/BF00336965. [DOI] [PubMed] [Google Scholar]
- 6.Bressloff PC, Cowan JD, Golubitsky M, Thomas PJ, Wiener MC. Geometric visual hallucinations, euclidean symmetry and the functional architecture of striate cortex. Phil Trans R Soc Lond. 2001;356:299–330. doi: 10.1098/rstb.2000.0769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kluver H. Mescal and Mechanisms of Hallucinations. Chicago: Univ Chicago Press; 1966. [Google Scholar]
- 8.Keil W, Schmidt K, Löwel S, Kaschube M. Reorganization of columnar architecture in the growing visual cortex. Proc Natl Acad Sci USA. 2010;107:12293–12298. doi: 10.1073/pnas.0913020107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kaschube M, et al. Universality in the evolution of orientation columns in the visual cortex. Science. 2010;330:1113–1116. doi: 10.1126/science.1194869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Eldar A, et al. Robustness of the BMP morphogen gradient in Drosophila embryonic patterning. Nature. 2002;419:304–308. doi: 10.1038/nature01061. [DOI] [PubMed] [Google Scholar]
- 11.Gardner T, Cantor C, Collins J. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 12.Tsai T, et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321(5885):126–129. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stepanyants A, Martinez LM, Ferecskó AS, Kisvárday Z. The fractions of short- and long-range connections in the visual cortex. Proc Natl Acad Sci USA. 2009;106:3555–3560. doi: 10.1073/pnas.0810390106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Markham H, et al. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci. 2004;5:793–807. doi: 10.1038/nrn1519. [DOI] [PubMed] [Google Scholar]
- 15.Kisvardy ZF, Beaulieu C, Eysel UT. Network of GABAergic large basket cells in cat visual cortex (area 18): Implication for lateral disinhibition. J Comp Neurol. 1993;327:398–415. doi: 10.1002/cne.903270307. [DOI] [PubMed] [Google Scholar]
- 16.Douglas RJ, Martin KAC. A functional microcircuit for cat visual cortex. J Physiol. 1991;440:735–769. doi: 10.1113/jphysiol.1991.sp018733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bressloff PC, Cowan JD. An amplitude equation approach to contextual effects in visual cortex. Neural Comput. 2002;14:493–525. doi: 10.1162/089976602317250870. [DOI] [PubMed] [Google Scholar]
- 18.Gilbert CD, Wiesel TN. Clustered intrinsic connections in cat visual cortex. J Neurosci. 1983;3:1116–1133. doi: 10.1523/JNEUROSCI.03-05-01116.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bullmore E, Sporns O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- 20.Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 21.Wolf F. Symmetry, multistability, and long-range interactions in brain development. Phys Rev Lett. 2005;95:208701. doi: 10.1103/PhysRevLett.95.208701. [DOI] [PubMed] [Google Scholar]
- 22.Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12:1–22. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ermentrout GB, Cowan JD. Secondary bifurcation in neuronal nets. SIAM J Appl Math. 1980:323–340. [Google Scholar]
- 24.Butler T, Goldenfeld N. Robust ecological pattern formation induced by demographic noise. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80:030902. doi: 10.1103/PhysRevE.80.030902. [DOI] [PubMed] [Google Scholar]
- 25.Butler T, Goldenfeld N. Fluctuation-driven Turing patterns. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84:011112. doi: 10.1103/PhysRevE.84.011112. [DOI] [PubMed] [Google Scholar]
- 26.Biancalani T, Fanelli D, Di Patti F. Stochastic Turing patterns in the Brusselator model. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;81:046215. doi: 10.1103/PhysRevE.81.046215. [DOI] [PubMed] [Google Scholar]
- 27.McKane AJ, Newman T. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys Rev Lett. 2005;94:218102. doi: 10.1103/PhysRevLett.94.218102. [DOI] [PubMed] [Google Scholar]
- 28.Wallace E, Benayoun M, van Drongelen W, Cowan JD. Emergent oscillations in networks of stochastic spiking neurons. PLoS One. 2011;6 doi: 10.1371/journal.pone.0014804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Baker TI, Cowan JD. Spontaneous pattern formation and pinning in the primary visual cortex. J Physiol Paris. 2009;103:52–68. doi: 10.1016/j.jphysparis.2009.05.011. [DOI] [PubMed] [Google Scholar]
- 30.Cross M, Hohenberg P. Pattern formation outside of equilibrium. Rev Mod Phys. 1993;65:851–1112. [Google Scholar]
- 31.Goldenfeld ND. Lectures on Phase Transitions and the Renormalisation Group. Boulder, CO: Westview; 1992. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.