Exploring the Surface Sensitivity of ToF-SIMS by Measuring the Implantation and Sampling Depths of Bi_n and C₆₀ Ions in Organic Films

Abstract

The surface sensitivity of Bi_n^q+ (n = 1, 3, 5, q = 1, 2) and C₆₀^q+ (q = 1, 2) primary ions in static time-of-flight secondary ion mass spectrometry (ToF-SIMS) experiments were investigated for molecular trehalose and polymeric tetraglyme organic films. Parameters related to surface sensitivity (impact crater depth, implantation depth, and molecular escape depths) were measured. Under static ToF-SIMS conditions (primary ion doses of 1 × 10¹² ions/cm²), the 25 keV Bi₁⁺ primary ions were the most surface sensitive with a molecular escape depth of 1.8 nm for protein films with tetraglyme overlayers, but they had the deepest implantation depth (~18 and 26 nm in trehalose and tetraglyme films, respectively). The 20 keV C₆₀⁺⁺ primary ions were the second most surface sensitive with a slightly larger molecular escape depth of 2.3 nm. The most important factor that determined the surface sensitivity of the primary ion was its impact crater depth, or the amount of surface erosion. The most surface sensitive primary ions, Bi₁⁺ and C₆₀⁺⁺, created impact craters with depths of 0.3 and 1.0 nm, respectively, in tetraglyme films. In contrast, Bi₅⁺⁺ primary ions created impact craters with a depth of 1.8 nm in tetraglyme films and were the least surface sensitive with a molecular escape depth of 4.7 nm.

1. Introduction

Time-of-flight secondary ion mass spectrometry (ToF-SIMS) is a powerful surface analysis technique that has found increasing use in the fields of medicine and molecular biology for purposes such as protein film characterization,^1–12 molecular depth profiling,^13–17 and single cell imaging.^18–22 The ToF-SIMS technique has recently benefited from the development of cluster ion sources such as Au_n⁺ (n = 1–5),²³ Bi_n^q+ (n = 1–7, q = 1 and 2),²⁴ C₆₀^q+ probes (q = 1–3),^{25, 26} and large Ar clusters.^27–29 These cluster ion sources have been shown to provide enhanced secondary ion yields, especially for high mass fragments. Since large secondary ion fragments sputtered from organic samples contain molecular information about the sample surface, the use of cluster primary ions provide a more detailed sample chemistry than their monoatomic counterparts. Cluster ions typically leave less residual chemical damage due to their lower implantation depths and higher sputter yields.^30–33 For these reasons, there has been a significant increase in the use of cluster ion sources in recent years for applications where high yields of high mass molecular fragments are needed,³⁴ and most notably in depth profiling applications to map the distribution of specific chemistries within a matrix to create 3D images of organic and biological samples.³⁵

Molecular dynamic (MD) simulations and collision cascade theories have provided insight into the energy deposition process during primary ion bombardment.^{30, 33, 36–39} Of particular interest are the implantation and probing depths of the different primary ion species. Depending on the primary cluster size (nuclearity) and on the target properties (e.g., stopping power), the depth range where the primary ions deposit their energy in the sample can vary significantly. This will, in turn, affect properties such as the sputtered volume per ion impact and the surface sensitivity. For example, MD simulations comparing the bombardment of 15 keV Ga⁺ and C₆₀⁺ into Ag substrates showed that these ions are implanted 7 and 2 nm, respectively.⁴⁰ However, 80% of the atoms sputtered by Ga⁺ originated from the first layer of the Ag substrate, while 80% of the atoms sputtered by C₆₀⁺ came from the first 3 layers.⁴⁰. These differences observed between the Ga⁺ and C₆₀⁺ ions can be attributed to different sputtering mechanisms for monoatomic and cluster ions. For monoatomic primary ions and inorganic samples, the ejection of secondary species results from a single linear collision cascade in which low-energy recoil atoms cause the ejection of secondary species from the uppermost layers.⁴¹ This implies that only a small fraction of the primary ion incident energy is deposited in the uppermost layer of the sample. In contrast, the simultaneous impact of the atoms in a C₆₀ cluster ion induces a collective motion near the impact zone that results in the ejection of a large amount of material.^{25, 40, 42} As most of the ejected fragments typically originate from the impact crater, the C₆₀ implantation depth is typically similar to the impact crater depth.^{30, 38, 43} Therefore, the smaller ejected volume and the low energy of the recoil atoms in inorganic targets make Ga⁺ more surface sensitive (lower sampling depth) in the static ToF-SIMS mode despite its deep implantation depth. Applying the same reasoning to organic samples, the ejection of molecular fragments from monoatomic primary ion impact should primarily occur from the low-energy recoil atoms created by the deep implantation of the primary ions in the sample. Also the hindered transport of fragments from the sub-surface region to the surface by the limited size of the monoatomic impact crater diameter will provide high surface sensitivity in the static mode.

MD simulations have also been performed with water ice substrates, comparing Au₃⁺ and C₆₀⁺ cluster ions at the same incident energy to emphasize the effect of cluster nuclearity (number of constituents) on implantation depth and sputter yield.^{44, 45} Those studies reported a general increase in the implantation depth and sputter yield for both sources as the incident energy increased from 5 – 40 keV. At the same energies, the implantation depth of Au₃⁺ was significantly larger, but its sputter yield was at least 2x lower than that of C₆₀⁺. This suggests that Au₃⁺ deposits its energy along its implantation path in a manner similar to that of the monoatomic Ga⁺ ion discussed earlier, with only fragments created near the surface having sufficient energy to be ejected. However, as the C₆₀⁺ impact crater is larger in diameter than the Au₃⁺ impact crater, C₆₀⁺ with its low implantation depth can provide better surface sensitivity than Au₃⁺ in molecular solids such as water ice, in spite of its larger sputter yield.

The characterization of implantation depths and molecular surface sensitivities has not been well-studied experimentally for organic and biological systems. Thus, there is a need to experimentally determine these parameters so that biological ToF-SIMS experiments, such as probing the conformation and orientation of proteins on surfaces, can be optimized to obtain the maximum information about the sample. Surface sensitivities have been studied previously for organic films. However, the experiments were limited to the observation of metal substrate atoms ejected through a layer of cadmium stearate LB layers,⁴⁶ thiolate,⁴⁷ water ice,³² and through multilayers of alternate polyelectrolyte films.⁴⁸ For applications of ToF-SIMS in biology and organic systems, an understanding of the ejection pathway of high mass molecular fragments is required.

To elucidate the surface sensitivity of monoatomic and cluster primary ions, the impact crater depth, implantation depth, and secondary ion escape depths in polymer and sugar films were measured for Bi_n^q+ (n = 1, 3, and 5, q = 1 and 2) and C₆₀⁺⁺ primary ions. The analysis of these organic films is a first step towards determining these parameters in biological samples such as cells and tissues. Atomic force microscopy (AFM) was used to measure the impact crater depth of the primary ions in the organic films. C₆₀ single beam depth profiling of the organic films implanted with 10¹² Bi_n^q+ ions per cm² was used to measured the Bi primary ion implantation depths. The sputtered depth scales (i.e., the z-scales) for the implantation studies were calibrated using AFM. For the determination of surface sensitivity, mica substrates covered first with a monolayer of adsorbed bovine serum albumin were then covered with 1.2 to 53.8 nm thick polymeric tetraglyme overlayers. By monitoring the intensity of the protein molecular fragments as a function of polymer overlayer thickness, the surface sensitivity of each primary ion could be determined. Both polymeric tetraglyme and molecular trehalose films have been shown to be well suited for model studies due to uniform film coverage, low roughness, high sputtering yield, and reproducibility.^{13, 16, 17}

2. Experimental

2.1. Sample preparation

Bovine serum albumin (BSA, A-2153) was purchased from Sigma (St. Louis, MO), reconstituted into buffer at 1 mg/mL. Protein adsorption was performed at 37 °C for 2 hrs in CPBSz buffer (0.11 M NaCl, 0.01 M sodium citrate, 0.01 M NaH2PO4, 0.02% NaN3, pH = 7.4)⁴⁹ onto freshly cleaved mica substrates (SPI Supplies, West Chester, PA) at a concentration of 100 μg/mL. After the adsorption was terminated by dilution displacement with buffer, the samples were rinsed twice in stirred CPBSz buffer to remove loosely bound protein and three times in deionized water to remove buffer salts, all in separate beakers for one minute each. The samples were then dried under a stream of nitrogen and stored under nitrogen until further analysis.

A 10 cm silicon wafer (Silicon Valley Microelectronics, CA) was cut into 1 × 1 cm² square pieces using a Kuliche & Soffa 780 dicing saw with a 15 μm diamond impregnated blade (Willow Grove, PA). Distilled water was used to wash away any dicing dust. Silicon pieces were then soaked in 5% hydrofluoric acid (Aldrich Chemical Co.) for five minutes to remove the native oxide layer.

2.2. Film deposition

Tetraglyme overlayers were deposited onto protein films as well as bare silicon pieces by radio frequency glow discharge (RFGD). The films on the bare silicon pieces were used to determine their thicknesses by AFM. The capacitively coupled, external electrode RFGD deposition system has been described in detail elsewhere.⁵⁰ The tetraglyme monomer was degassed by three cycles of liquid nitrogen freezing and thawing. The monomer was first preheated to 90 °C to evaporate water molecules from the liquid, then vaporized by heating at 105 – 110 °C and introduced into the reactor through a flow valve at a rate of 1.55 sccm at 350 mTorr. The RFGD was maintained at 10 W for 2 to 10 minutes to create layers approximately 1 to 50 nm thick. The flow valve was shut immediately after stopping the RFGD to prevent monomer deposition. The samples were removed from the reactor and used without any modification or soaking.

Trehalose (Aldrich Chemical Co., Milwaukee, WI) thin films were prepared by casting 150 μL of 0.5 M solution onto 1 × 1 cm² silicon substrates and spinning at 6000 R.P.M. for 20 seconds. This yielded films with a thickness of ~150 nm. The AFM determined root mean square roughness of the cast trehalose film was < 0.7 nm (measured over several 400 μm² areas across the sample surface).

2.3. Atomic Force Microscopy (AFM)

The thickness of the dried protein film was measured using a tip-scratch method. Using a Dimension 3100 AFM (Veeco Metrology, Santa Barbara, CA) equipped with an NPS tip (0.6 N/m force constant) and operated in contact mode in air, a 500 × 500 nm² area on the sample was scratched at a force setpoint of 4 V to remove the protein overlayer. At 4 V, no scratching of the mica substrate occurred. The setpoint was then decreased to 0 V and the scan area was increased during analysis to 2 × 2 μm² to obtain an image of the protein film with the crater. Three craters were formed in various locations of the sample to calculate the average thickness.

The tetraglyme and trehalose film thicknesses were measured by first gently scratching the film with a clean razor blade (Ted Pella Inc.) and then using AFM to measure the step height between the film surface and the silicon substrate. A scan size of 50 × 50 μm² ensured that the flat part of the film was measured. The AFM was equipped with a 315 kHz, 42 N/m PointProbe Plus silicon tip (Nanosensors, Neuchâtel, Switzerland) and operated in the intermittent contact mode in air for the film thickness measurements. At least three locations on the sample were scanned to determine the average thickness.

2.4. Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS)

ToF-SIMS experiments were performed using an ION-TOF TOF.SIMS 5–100 (IONTOF GmbH, Münster, Germany) equipped with a 25 kV Bi_n^q+ source (n = 1, 3, and 5, q = 1 and 2) and a 10 kV C₆₀^q+ source (q = 1–2). Primary ions from both sources struck the sample surface at an incident angle of 45°. For the impact crater depth study, both Bi and C₆₀ ions were rastered over a 100 × 100 μm² area (128 × 128 pixels) with dose densities ranging from 1 to 5 × 10¹² ions/cm². For the implantation depth study, Bi ions were rastered over a 100 × 100 μm² area at a dose density of 1 × 10¹² ions/cm². The implanted region was then depth profiled with 10 keV C₆₀⁺ in the single-beam mode, switching between high-current bunched analysis mode (25 × 25 μm²) and direct-current, sputter mode (500 × 500 μm²) using a batch job written in-house. The analysis raster size of 25 × 25 μm² was experimentally determined to yield the best depth resolution.¹⁶ For the molecular escape depth study, the analysis beam settings of a 100 × 100 μm² raster area and a primary ion dose of 10¹² ions/cm² were used. Prior to each analysis, target currents were measured in a Faraday cup and were adjusted so that the total secondary ion count rate at the sample surface would not exceed 200 × 10³ counts/second to prevent detector saturation. Typical Faraday cup currents of the high-current bunched ions were 0.5 pA for Bi₁⁺, 0.08 pA for Bi₃⁺, 0.05 pA for C₆₀⁺ and 0.015 pA for C₆₀⁺⁺. The direct current C₆₀⁺ sputter beam had a current of 0.7 nA and its dose was kept constant for all runs at 2.5 × 10¹² ions/cm² per etching cycle. The mass resolutions (m/Δm) at m/z 70 were >7000 (Bi_n^q+), ~2400 (C₆₀⁺) and ~4100 (C₆₀⁺⁺).

3. Results and discussion

Similar to how surface sensitivities in AES and XPS are measured by terms such as the effective attenuation length (EAL), inelastic mean free path (IMFP), information depth (ID), and mean escape depth (MED),⁵¹ the surface sensitivities in ToF-SIMS can also be measured using similar terms. One measure of ToF-SIMS surface sensitivity is the escape depth, expressed as the average depth normal to the surface from which secondary ions escape into vacuum. This is the information depth from which atomic and molecular secondary ions are detected, and is an important parameter which can, for example, guide the use of appropriate primary ion species for elucidating the orientation of molecules ⁵². The second measure of surface sensitivity is the implantation depth of the primary ion normal to the sample surface, which depends on its incident angle and kinetic energy, as well as its nuclearity (i.e., clusters) and rate of energy loss due to collisions in the sample. The implantation depth provides a measurement of the depth of atomic mixing beneath the sample surface, which can be related to the achievable depth resolution during dual-beam depth profiling. The implantation depth is related to the actual penetration depth of the ion through the sample by the following equation:

$$\text{implantation}\text{depth}=\text{penetration}\text{depth}\times cos\theta$$ (Equation 1)

where θ is the angle of the incident beam relative to the sample normal. The third measure of surface sensitivity is the depth of sample erosion (i.e., impact crater depth) incurred by primary ion bombardment. Since ToF-SIMS is a destructive technique, the rate of sample erosion is important for interpreting spectra of thin films or small molecules. These terms collectively give a measure of the surface sensitivity of ToF-SIMS, and are investigated in this study.

3.1. Impact crater depths of Bi_n^q+ and C₆₀^q+ ions in organic films

The primary ion dose used in static ToF-SIMS studies of organic and biological samples typically vary from 1 × 10¹¹ to 1 × 10¹³ ions/cm², with values at the higher end of this range often used to increase signal intensity. This study uses ion doses in this range so that the results and conclusions will be useful for others using similar samples, instruments, and primary ion species. The surface erosion results will be discussed first, since they directly affect the results of implantation depth and molecular escape depth studies.

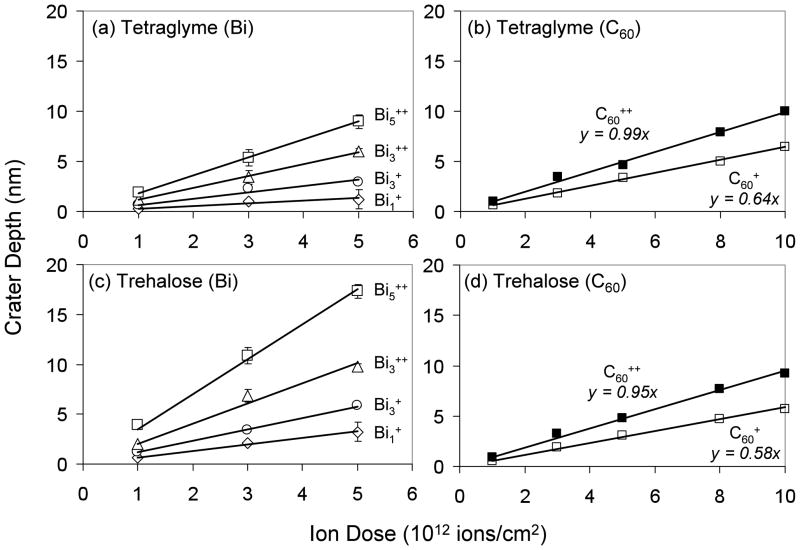
Figure 1 shows the depth of craters formed by Bi_n^q+ and C₆₀^q+ as a function of primary ion dose for both tetraglyme and trehalose films. The linear increase with increasing dose suggests that the sputter rates for these primary ions remain approximately constant over the range of ion doses examined. More importantly, they show that there is significant sample erosion even at 1 × 10¹² ions/cm², and the amount of erosion is seen to increase with increasing incident energy and cluster size. For example, bombardment of the tetraglyme film with 1 × 10¹² ions/cm² of 25 keV Bi₁⁺, 25keV Bi₃⁺, 50 keV Bi₃⁺⁺ and 50 keV Bi₅⁺⁺ resulted in the formation of 0.3, 0.7, 1.2, and 1.8 nm deep craters, respectively (Table 1). When the sample was changed to trehalose, the crater depths increased roughly two-fold to 0.7, 1.2, 2.1, and 3.7 nm for the same ion dose density. The difference in crater depths between the two samples could be due to their different densities and/or cohesive energies. RFGD deposited tetraglyme is a low-density, plasma-polymerized film with a complex network of crosslinks^53–56, whereas trehalose is a molecular solid with no intra-molecular covalent bonding. A higher sputter yield should be seen from samples with weaker cohesive energies, and this is what was observed. In addition, the amount of energy deposited per nanometer into the sample is influenced by the density of the sample. For example, a MD simulated bombardment of a 15 keV Ga⁺ ion into a Ag substrate required 11 nm to stop the ion, but a solid benzene film required 21 nm to stop a Au⁺ ion having just 5 keV of energy ³⁷. The larger impact crater depths and sputtered volumes from Bi ions (see Table 1) observed for the higher-density, molecular trehalose films relative to the lower-density, polymerized tetraglyme films are consistent with the MD results.

Figure 1.

AFM measured impact crater depth as a function of ion dose for (a) tetraglyme bombarded by Bi ions, (b) tetraglyme bombarded by C₆₀ ions, (c) trehalose bombarded by Bi ions, (d) trehalose bombarded by C₆₀. Average depths and errors were calculated from measurements made on 2 craters. The raster area was 100 × 100 μm². At 1 × 10¹² ions/cm², only the Bi₃⁺⁺ and Bi₅⁺⁺ craters were deep enough to be measured. Depths for Bi₁⁺ and Bi₃⁺ were estimated by interpolation through the origin.

Table 1.

Sputter yields of Bi_n^q+ and C₆₀^q+ at an ion dose of 1 × 10¹² ions/cm² for tetraglyme and trehalose films.

	Bi1+ (25 keV)	Bi3+ (25 keV)	Bi3++ (50 keV)	Bi5++ (50 keV)	C60+ (10 keV)	C60++ (20 keV)
Total Sputtered Depth (nm)
Tetraglyme	0.3 ± 0.1	0.7 ± 0.1	1.2 ± 0.1	1.8 ± 0.1	0.6 ± 0.1	1.0 ± 0.1
Trehalose	0.7 ± 0.1	1.2 ± 0.1	2.1 ± 0.2	3.7 ± 0.2	0.6 ± 0.1	0.9 ± 0.1
Sputtered Yield Volume (nm3/ion)
Tetraglyme	28 ± 5	66 ± 10	117 ± 2	183 ± 7	64 ± 2	101 ± 9
Trehalose	67 ± 3	115 ± 1	209 ± 17	366 ± 22	60 ± 3	98 ± 7

In contrast, the results for C₆₀ ion bombardment did not follow this relationship; it was seen to produce similar impact crater depths for both tetraglyme and trehalose films. For an ion source such as C₆₀ with a high efficiency value (i.e., ratio of damage removal relative to damage generation) ⁵⁷, its implantation depth must be similar to its impact crater depth. Since a C₆₀ ion deposits all of its energy in the upper few layers of the sample because of its low kinetic energy per constituent, its implantation depths will be similar for materials with small differences in densities. Comparisons of sputter yields and sputter yield volumes of tetraglyme and trehalose from literature show that these values are rather similar for the two materials ^{13, 16, 58}.

3.2. Implantation depths of Bi_n^q+ ions in organic films

The implantation depth was determined experimentally using a two-step process: First, 1 × 10¹² Bi_n^q+ ions/cm² were implanted into the organic films and then the implanted area was depth profiled in the single-beam mode using C₆₀ ions. Since neither the film nor the analysis and etching ion beams contain bismuth, any bismuth intensity observed in the depth profiles can be attributed to implanted bismuth. These depth profiles of implanted bismuth in both tetraglyme and trehalose films show a Gaussian distribution (see Supporting Information, Figure S-1), with implantation range and trailing edge straggle increasing with incident energy per atom. Also, the area under the curve was seen to increase with the number of atoms, as expected. Unfortunately, the implantation depth of C₆₀ ions could not be determined using a similar experiment since the carbon atoms in the fullerene projectiles could not be differentiated from carbon atoms in the organic films.

A Gaussian curve was fit to the data, and the average implantation depth was defined as the depth at the peak maximum of the response function. Since Bi_n^q+ bombardment at 1 × 10¹² ions/cm² was observed to cause surface erosion (see Table 1), the average implantation depth was corrected by subtracting half of the mean sputter depth at this ion dose. This is because the primary ion craters have a depth of 0 nm of sputtered depth at 0 ions/cm², and a finite depth at 1 × 10¹² ions/cm². The relationship of impact crater depth with time is assumed to be linear (see Figure 1). Thus, the impact crater depth averaged over the time required to reach an ion dose of 1 × 10¹² ions/cm² corresponds to 1/2 of the impact crater depth at this ion dose.

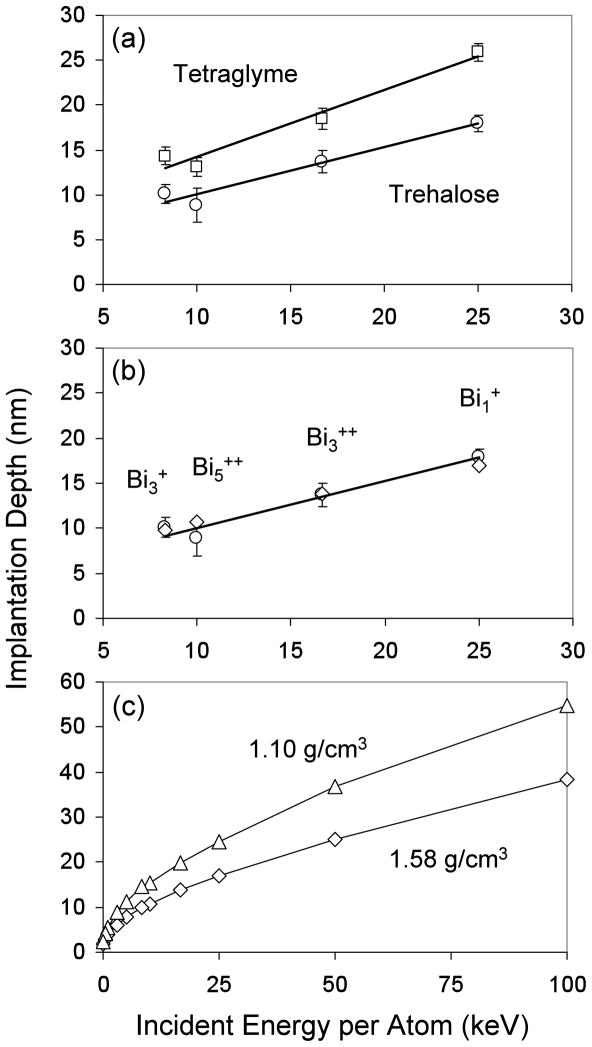
Figure 2(a) shows the corrected implantation depth as a function of kinetic energy per bismuth atom for both tetraglyme and trehalose films. For a given primary ion species, bismuth is implanted deeper into tetraglyme than into trehalose (see Table 2). Bismuth implantation depths also increase linearly with increasing energy per constituent atom in the primary ion species. The fact that this linear relationship applies to Bi⁺ as well as the Bi₃⁺, Bi₃⁺⁺ and Bi₅⁺⁺ cluster ions suggests that the cluster ions break up upon impact and behave as single atoms during implantation. This argument is supported by MD simulations that predict that polyatomic projectiles dissociate into individual atoms upon impact, with each atom taking an equal fraction of the total energy.⁴⁵ In addition, the SRIM algorithm (Stopping and Range of Ions in Matter^{59, 60}) was used to estimate the implantation depth of single Bi atoms into model targets with a molecular composition (C₁₂H₂₂O₁₁) and density (1.58 g/cm³) matched to that of trehalose. The results in Figure 2(b) show the SRIM calculated implantation depths are in good agreement with the experimentally determined implantation depths. Since the Monte Carlo algorithm in SRIM calculates trajectories for monoatomic ions, the fact that a theoretical Bi₁⁺ ion with an energy of 16.7 keV has the same implantation depth as the experimental Bi₃⁺⁺ ion at 50 keV, for example, also supports the claim that clusters dissociate upon impact with each atom bearing an equal portion of the total energy as it travels through the solid. Overall, the good agreement between the experimental and calculated implantation depths for Bi_n^q+ ions suggests that SRIM can be used to accurately predict the implantation range of monoatomic and small cluster ions in simple organic systems with uniform compositions and densities. However, further studies are needed to determine how large of a primary cluster ion can be modeled using a monoatomic ion. This is because Figure 2(b) shows that for Bi₅⁺⁺ there is a ~1.5nm difference between in the experimental and simulated implantation depth, with the experimental value being smaller.

Figure 2.

(a) The average bismuth implantation depths in tetraglyme (□) and trehalose (○) films. (b) The experimental implantation depths of Bi_n^q+ ions in trehalose (○) compared with theoretical values (⋄) obtained using the SRIM algorithm. (c) SRIM calculations comparing Bi⁺ implantation in a C₁₀H₂₂O₅ solid with a density of 1.10 g/cm³ (▵), and in a C₁₂H₂₂O₁₁ solid with a density of 1.58 g/cm³ (⋄).

Table 2.

Average bismuth implantation depths (nm) of Bi_n^q+ ions in tetraglyme and trehalose films at an ion dose of 1 × 10¹² ions/cm². These values have been corrected by the amount of surface erosion.

	Bi1+ (25 keV)	Bi3+ (25 keV)	Bi3++ (50 keV)	Bi5++ (50 keV)
Tetraglyme	25.9 ± 6.4	14.3 ± 5.3	18.5 ± 6.8	13.1 ± 5.0
Trehalose	17.9 ± 6.9	10.1 ± 5.4	13.7 ± 6.2	8.8 ± 6.4

As discussed above, the target density is a good indicator of the implantation depth. In Figure 2(c) the SRIM algorithm was used to plot the implantation depths of variable-energy bismuth ions through two solids of different densities. Since the density of RFGD deposited tetraglyme film was not known, SRIM calculations were performed on a target having the same atomic composition as tetraglyme (C₁₀H₂₂O₅), but with varying densities. This density was then adjusted until the SRIM calculated implantation depths matched the experiment implantation depths. The film density that provided the best match between the SRIM calculations and the experimental tetraglyme film results was 1.10 g/cm³. Since other sample properties such as degree of cross-linking can also affect the implantation depth, the density value obtained by matching the SRIM calculations to the experimental results should be considered an “effective” density.

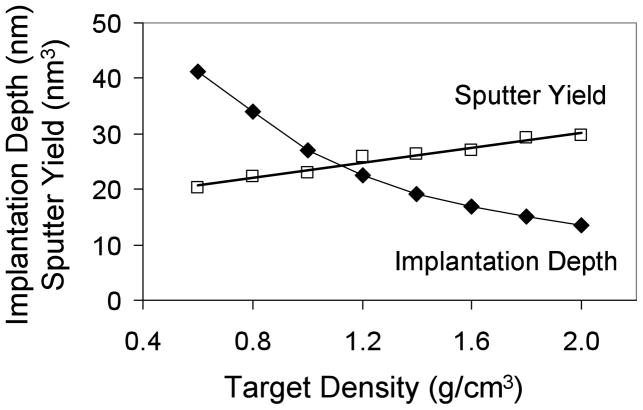
For the two solids, a negative correlation was seen between implantation depth and sputter depth. For example as shown in Tables 1 and 2, 25 keV Bi₁⁺ had implantation depths of 25.9 (tetraglyme) and 17.9 nm (trehalose), but their corresponding impact crater depths were 0.3 (tetraglyme) and 0.7 nm (trehalose). In essence, the implantation depth had decreased ~30% but the impact crater depth had increased ~130% going from tetraglyme (1.10 g/cm³) to a trehalose film (1.58 g/cm³). As mentioned previously, the major reason for this observed difference in impact crater depth is likely due to the higher density solid hindering the penetration of the primary ion into the sample and causing a larger fraction of its energy to be deposited closer to the surface. This would result in a decreased implantation depth and an increased impact crater depth with increasing target density. This is supported by SRIM calculations in Figure 3, which shows that sputter yield (i.e., impact crater depth) and implantation depth are negatively correlated for a simulated Bi₁⁺ ion at 25 keV, and that even small changes in density can significantly affect both parameters. For example, a 0.5 g/cm³ increase in film density resulted in a ~30% decrease in implantation depth, and a ~80% increase in sputter yield volume. The sputter yield differences between experiment and simulation most likely stems from differences in intrinsic sample properties such as cohesive energy or extent of polymer crosslinking density.

Figure 3.

Simulated bismuth implantation depths (nm) and sputter yields (nm³) for a 25 keV monoatomic Bi₁⁺ particle bombarding a target with the same atomic composition as tetraglyme (C₁₀H₂₂O₅), but with different densities. The cohesive energy parameters were not changed. The experimentally determined density of tetraglyme was 1.10 g/cm³.

3.3. Atomic and molecular secondary ion escape depths from bombardment of organic films with Bi_n^q+ and C₆₀⁺⁺ primary ions

The surface sensitivities of secondary ions emitted by Bi_n^q+ and C₆₀⁺⁺ primary ions were investigated by observing both the atomic and molecular escape depths of the secondary ions from a protein layer through a tetraglyme overlayer. In general, shallower secondary ion escape depths would indicate a more surface sensitive primary ion. The sample was made by first adsorbing BSA onto a mica surface and then using RFGD to deposit a tetraglyme film over the protein monolayer. The attenuation of the protein and substrate signals as a function of tetraglyme overlayer thickness was studied. Since nitrogen is unique to the protein monolayer and potassium is unique to the mica substrate, it is possible to determine the atomic and molecular secondary ion escape depths as a function of primary ion species. This assumes complete overlayer coverage with uniform thickness. The nitrogen containing fragments CH₄N⁺ (m/z 30) and C₄H₈N⁺ (m/z 70) were chosen to represent the protein signal while K⁺ (m/z 39) was chosen to represent the substrate signal. The intensities of the selected peaks were monitored for different samples with overlayers ranging in thickness from 1.2 to 53.8 nm. Signal attenuation followed an approximate exponential decay curve of the form:

$$I=B+(I_0-B)exp(-d/\lambda )$$ (Equation 2)

for all primary ion species used (see Supporting Information, Figure S-2). I is the protein or substrate signal intensity associated with the tetraglyme thickness d, B is the baseline intensity of the protein or substrate signal, I₀ is the initial protein or substrate intensity, and λ is the decay parameter. The initial protein intensities were measured from a BSA monolayer on mica without a tetraglyme overlayer. The initial substrate intensities were measured from mica sample without either a protein or tetraglyme overlayer. A least squares best fit line was drawn, but due to matrix effects and variation in ether content and crosslinking density of the plasma deposited polymer overlayers, the decay curve only approximated an exponential decay curve. Therefore, the escape depth of the secondary ions was determined as the thickness where its intensity was 3 standard deviations from the baseline intensity. At 3 standard deviations, there is 99.7% confidence that the intensity is above the baseline. For this study, 10 keV C₆₀⁺ was not used since the mass resolution (m/Δm) at m/z 70 was below 1500, which made it difficult to differentiate the protein peak from the large tetraglyme peak at this same nominal mass.

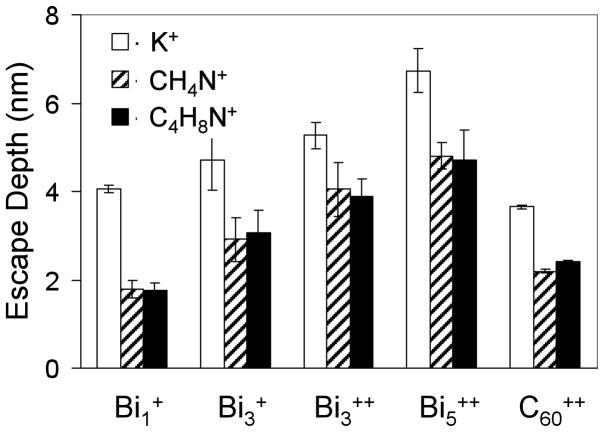
Figure 4 compares the escape depths of K⁺, CH₄N⁺, and C₄H₈N⁺ secondary ions through a tetraglyme overlayer when bombarded by Bi_n^q+ and C₆₀⁺⁺ primary ions. Similar to the implantation depth measurements (Figure 2), the escape depths were corrected by subtracting half the mean sputter depth. Numerous MD studies discuss the extreme surface sensitivity of C₆₀,^{25, 33, 36, 37, 61} which agree with the results presented here. The sampling depth of C₆₀⁺⁺ was 2.3 nm for molecules and 3.7 nm for atoms. SRIM calculations predict a 0.333 keV carbon atom (from the breakup of 20 keV C₆₀⁺⁺) would be implanted ~2.7 nm into a substrate with an atomic composition identical to tetraglyme and a density of 1.10 g/cm³. Thus, the C₆₀⁺⁺ SRIM calculations and experimental results are in good agreement. SRIM calculations suggest 10 keV C₆₀⁺ would be more surface sensitive than 20 keV C₆₀⁺⁺, as the predicted implantation depth for a 0.167 keV carbon (from the breakup of 10 keV C₆₀⁺) would be ~1.8 nm.

Figure 4.

The escape depths of K⁺, CH₄N⁺, and C₄H₈N⁺ ions for the five primary ions. Singly charged bismuth species had incident energies of 25 keV, doubly charged species had 50 keV, and C₆₀⁺⁺ had an energy of 20 keV.

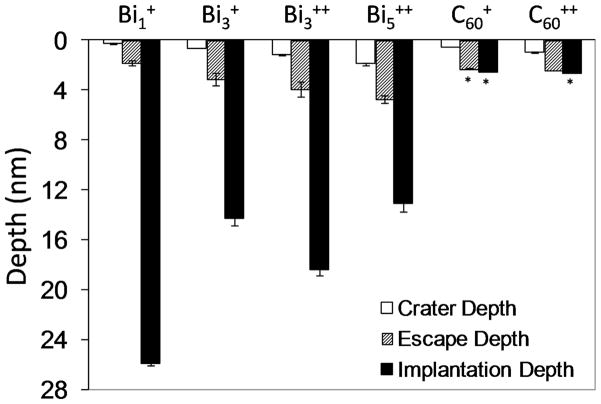
In the static mode 25 keV Bi₁⁺ primary ions have similar surface sensitivities to 20 keV C₆₀⁺⁺ primary ions. However, the surface sensitivity decreased as bismuth energy and cluster size increased. This seems counterintuitive since increased cluster size reduces the energy per atom and confines the deposition of energy nearer to the surface, which should make the primary ion source more surface sensitive. However, the bismuth atoms are more massive and their clusters have significantly fewer atoms than C₆₀. This suggests the bismuth clusters have a different way of depositing energy compared to C₆₀ clusters. The graph in Figure 5 shows there is a direct correlation between impact crater depth and escape depth, which suggests that the surface sensitivity is related to the impact crater depth of the primary ion rather than its implantation depth. A large crater cross-section allows the escape of molecules from further beneath the surface. Since sputter depth is directly related to energy and cluster size, larger clusters will cause molecules from deeper into the sample to escape, and monoatomic ions will create small craters that limit the escape of molecules to the topmost surface. MD simulations of monoatomic ions show that they create a small impact crater at the surface, penetrate deep into the sample while depositing their energy along their entire path.^{25, 40, 62} The energy deposited from monoatomic ions below the surface region fragments the sample and contributes to vertical mixing, but few secondary ion have sufficient energy to travel through material above them and into vacuum. Consequently, larger clusters such Bi₃ and Bi₅ that create larger impact craters facilitate the escape of secondary ions from deeper in the sample. Also, clusters release more energy closer to the surface, increasing the number of fragments that have sufficient energy to escape. It is interesting to see how Bi₁⁺ with an implantation depth of 26 nm is seen to be the most surface sensitive with a molecular escape depth of 1.8 nm, while Bi₅⁺⁺ is the least surface sensitive with an escape depth of 4.8 nm. This is because in the static mode, Bi₁⁺ had an impact crater depth of 0.3 nm compared to the 1.9 nm impact crater depth for Bi₅⁺⁺.

Figure 5.

(a) The impact crater depths, escape depths, and implantation depths (nm) of Bi_n^q+ and C₆₀⁺⁺ primary ions in a tetraglyme film. The escape depths are for the C₄H₈N⁺ (m/z 70) molecule. Asterisk (*) denotes a simulated value.

The escape depths of K⁺ ions (atomic) were slightly higher than those of CH₄N⁺ and C₄H₈N⁺ ions (molecular). Since atomic secondary ions typically have larger kinetic energies and smaller sizes than molecular secondary ions, it was expected that K⁺ would have a larger escape depth than CH₄N⁺ or C₄H₈N⁺. The results from this study are consistent with the smaller and more energetic atomic secondary ions being less hindered as they pass through the crater and are ejected into the vacuum. However for the organic films used in this study, the escape of atomic and molecular ions both requires the physical removal of the overlayer. It is interesting to compare the current results with a previous study that examined the escape depths of Ag⁺ ions from a silver substrate beneath a water ice overlayer.³² For Au⁺, Au₂⁺, and Au₃⁺ at incident energies of 25 keV, Au⁺ was observed to display the deepest atomic escape depth. The interpretation was that since water ice in UHV has no significant cohesive energy between the molecules, the collision of the primary ion most likely led to sublimation, which in essence swept away the overlayer. Thus, with water ice overlayers the primary ion species with the deepest implantation depth (i.e., the monoatomic ion) was the least surface sensitive. The fact that Bi monoatomic ion was most surface sensitive for polymerized tetraglyme films show the importance of film properties such as cohesive energy on the impact crater dimensions and resulting surface sensitivity.

4. Conclusion

The objective of this study was to investigate the surface sensitivities of secondary ions produced by Bi₁⁺, Bi₃⁺, Bi₃⁺⁺, Bi₅⁺⁺, and C₆₀⁺⁺ primary ions. The quantities examined include the primary ion impact crater and implantation depths, as well as the ion escape depths. Due to limitations in mass resolution, the surface sensitivity of C₆₀⁺ could not be determined. Results using RFGD deposited tetraglyme films and spin cast trehalose films showed that for bismuth ions accelerated at 25 kV, the impact crater depth increased for larger clusters and higher incident kinetic energy, and varied linearly with ion dose density. In addition, the impact crater depth was deeper in trehalose films compared to tetraglyme films, likely because the higher density of the trehalose film resulted in the primary ions depositing more energy in the near surface regions. Similar trends were seen for C₆₀ ions; impact crater depth increased with incident kinetic energy and it varied linearly with ion dose. However, the same C₆₀ incident energy resulted in similar impact crater depths in both organic films. This observation was attributed to the unique sputtering mechanism of C₆₀, where nearly all the impact energy is deposited in the near surface region for both the trehalose and tetraglyme films.

The implantation depth of the bismuth primary ions varied linearly with energy per constituent atom, consistent with the dissociation of the bismuth cluster ions upon impact. In addition, the comparison of the results from the tetraglyme and trehalose films revealed that density affects the transport of energetic ions through the solid as well as their sputter yields.

The escape depths of atoms and molecules were not proportional to the implantation depth of the primary ion, but were found to correlate with the impact crater depth. The results showed for the two organic films investigated that under static ToF-SIMS conditions the Bi₁⁺ and C₆₀⁺⁺ primary ions produced secondary ions that were the most surface sensitive. The observed C₄H₈N⁺ (m/z 70) secondary ion escape depths were 1.8 nm (Bi₁⁺) and 2.4 nm (C₆₀⁺⁺). The corresponding impact crater depths at primary ion doses of 1 × 10¹² ions/cm² were 0.3 and 1.0 nm, respectively. The primary ion with the largest sputter depth, Bi₅⁺⁺, was the least surface sensitive with a molecular secondary ion escape depth of ~5 nm. This study suggests that the surface sensitivity is largely dependent on the amount of surface erosion caused by the primary ion source. Thus, sample properties such cohesive energy and density that can influence the amount of surface erosion will also influence the surface sensitivity of the ion source.

Table 3.

Escape depths of substrate (K⁺) and protein (CH₄N⁺ and C₄H₈N⁺) secondary ions through a RFGD deposited tetraglyme overlayer for Bi_n^q+ and C₆₀⁺⁺ primary ions.

	Bi1+ (25 keV)	Bi3+ (25 keV)	Bi3++ (50 keV)	Bi5++ (50 keV)	C60++ (20 keV)
K+ (m/z 39)	4.1 ± 0.1	4.7 ± 0.7	5.3 ± 0.3	6.7 ± 0.5	3.7 ± 0.1
CH4N+ (m/z 30)	1.8 ± 0.2	2.9 ± 0.5	4.0 ± 0.6	4.8 ± 0.3	2.2 ± 0.1
C4H8N+ (m/z 70)	1.8 ± 0.2	3.1 ± 0.5	3.9 ± 0.4	4.7 ± 0.7	2.4 ± 0.1