Abstract
We studied static prehension of a horizontally oriented object. Specific hypotheses were explored addressing such issues as the sharing patterns of the total moment of force across the digits, presence of mechanically unnecessary digit forces, and trade-off between multi-digit synergies at the two levels of the assumed control hierarchy. Within the assumed hierarchy, at the upper level, the task is shared between the thumb and virtual finger (an imagined finger producing a wrench equal to the sum of the wrenches of individual fingers). At the lower level, action of the virtual finger is shared among the four actual fingers. The subjects held statically a horizontally oriented handle instrumented with six-component force/torque sensors with different loads and torques acting about the long axis of the handle. The thumb acted from above while the four fingers supported the weight of the object. When the external torque was zero, the thumb produced mechanically unnecessary force of about 2.8 N, which did not depend on the external load magnitude. When the external torque was not zero, tangential forces produced over 80% of the total moment of force. The normal forces by the middle and ring fingers produced consistent moments against the external torque, while the normal forces of the index and little fingers did not. Force and moment variables at both hierarchical levels were stabilized by co-varied across trials adjustments of forces/moments produced by individual digits with the exception of the normal force analyzed at the lower level of the hierarchy. There was a trade-off between synergy indices computed at the two levels of the hierarchy for the three components of the total force vector, but not for the moment of force components. Overall, the results have shown that task mechanics are only one factor that defines forces produced by individual digits. Other factors, such as loading sensory receptors may lead to mechanically unnecessary forces. There seems to be no single rule (for example, ensuring similar safety margin values) that would describe sharing of the normal and tangential forces and be valid across tasks. Fingers that are traditionally viewed as less accurate (e.g., the ring finger) may perform more consistently in certain tasks. The observations of the trade-off between the synergy indices computed at two levels for the force variables but not for the moment of force variables suggest that the degree of redundancy (the number of excessive elemental variables) at the higher level is an important factor.
Keywords: prehension, hand, synergy, safety margin
Introduction
Many studies of five-digit static prehension used vertically oriented objects with the external torque either zero or acting in the grasp plane defined as the plane containing the centers of all the individul digit force sensors (reviewed in Zatsiorsky and Latash 2008). Several studies of tripod grasping (thumb and two fingers) and pinch grasping (thumb and index finger) explored the human prehension in three dimensions (Kinoshita et al. 1997; Burstedt et al. 1999; Baud-Bovy and Soechting 2001; Gentilucci et al. 2003). To our knowledge, only Shim and colleagues (2005a,b) studied the mechanics and multi-digit synergies involved in five-digit prehensile tasks with the external torque acting not within the grasp plane but orthogonal to that plane. In those studies, synergies were defined as co-varied adjustments of elemental variables (forces produced by individual digits) (reviewed in Latash et al. 2007; Latash and Zatsiorsky 2009).
In everyday life grasped objects are frequently oriented non-vertically, and external torques are not confined to the grasp plane. We selected to study prehension of a horizontally oriented handle with external torque acting about the long axis of the handle because such a configuration allows addressing a number of underexplored issues related to the control of prehension.
If the external torque is zero, the top digit (in our experiment, it was always the thumb) does not have to produce normal force. It has been documented, however, that mechanically unnecessary normal forces are produced by the thumb in such conditions (Pataky et al. 2004a). In that study, the external load was kept constant and the external torque was zero. We explored the dependence of such forces on the load and torque magnitude. We expected qualitatively different behaviors in the zero-torque and non-zero-torque conditions because, when the external torque in not zero, normal force of the thumb could be used to balance portion of the external torque and hence may be expected to scale with it.
We defined safety margin as the proportion of normal force above the level required to prevent slippage given the friction coefficient (for more details see Methods). Several researchers suggested that safety margins may be defined by the neural controller for individual digits separately, given local friction conditions (Burstedt et al. 1997, 1999; Quaney and Cole 2004). On the other hand, synergic adjustments in all digit forces to local changes in friction have been reported (Aoki et al. 2007). When friction conditions are common across the fingers, safety margin values are similar (Pataky et al. 2004b). We tested the hypothesis that the sharing patterns of the normal force and of the tangential force would be similar across the fingers reflecting similar safety margin values (similar friction coefficients were assumed across the digits).
Total moment of force in our experiment was produced by both tangential and normal digit forces (for the horizontal bar orientation, the tangential forces of the thumb and fingers had to act in opposite directions and cancel each other). We explored sharing of the total moment of force across the digits and between the contributions of the normal and tangential forces. Earlier studies of static prehension of a vertically oriented handle have suggested that the contributions of normal and tangential forces to the total moment of force are nearly equal (Zatsiorsky et al. 2002, 2003b). A more recent study, however, has suggested that total moment sharing may be task specific (Sun et al. 2011).
Sharing of the total moment of force across the four fingers is another potentially important issue. In an earlier study, it has been suggested that the “central” fingers (middle and ring) are mostly load-bearing while the “lateral” fingers (index and little) are moment-producing (Zatsiorsky et al. 2002). This was interpreted as reflecting the larger mechanical advantage of the “lateral” fingers during grasping of a vertically oriented handle. When the handle is horizontal, this argument is no longer valid: The moment arms are about the same for all finger forces. We tested the hypothesis on the different roles of the “lateral” and “central” finger pairs by comparing, across the fingers, the sharing of the total moment and the contributions of the normal and tangential forces to the total moment of force within each digit.
Finally, we quantified synergy indices at the two levels of a hypothetical control hierarchy (Arbib et al. 1985). At the upper (VF-TH; virtual finger and thumb) level, the task is assumed to be shared between the thumb and a virtual finger (VF, an imagined finger with the mechanical action equal to that of the four fingers combined). At the lower (IF; individual finger) level the action of the VF is shared among the four fingers. Synergy indices were computed to reflect the amount of co-variation among elemental variables produced by digits that helped reduce variance of their combined action. Earlier studies (Gorniak et al. 2007, 2009) documented a trade-off between the synergy indices computed at the two levels: High indices at the upper level were associated with low indices at the lower level. However, the trade-off was not absolute. While holding a vertically oriented handle, the trade-off was pronounced for the normal force, but not for the tangential force and not for the total moment of force. We explored this trade-off for all three components of the force vector and all three components of the moment vector.
Methods
Subjects
Nine right-handed young adult volunteers served as subjects in this study. Average data of the participants were (mean ± standard deviation): 27 ± 3 years of age, 1.73 ± 0.11 m in height, 70.7 ± 11.8 kg in mass, 18.1 ± 0.9 cm for hand length, 9.2 ± 1.6 cm for hand width. Hand length was measured as the distance from the tip of the distal phalanx of the middle finger to the distal wrist crease with the wrist in a neutral pose. Hand width was defined as the distance between the lateral aspects of the metacarpophalangeal joints of the index and little fingers. All subjects had no history of neuropathy or trauma to the upper limbs. None of the subjects had a history of long-term involvement in hand or finger activities such as playing musical instruments. All subjects gave informed consent according to the procedures approved by the Office for Research Protections of the Pennsylvania State University.
Apparatus
Five six-component force/torque sensors (model Nano 17-R; ATI Industrial Automation, Apex, NC, USA) were used to measure the forces and moments of force produced by the tips of individual digits. These sensors were attached to an aluminum handle. In some trials, an aluminum beam (25.5 × 0.6 × 1.2 cm) was affixed to the handle to attach loads and create non-zero external torques (Figure 1A). The local x-, y-, and z-axes of each sensor were, respectively, parallel to the global X- (horizontal axis in a sagittal plane), Y- (horizontal axis in a frontal plane), and Z-axes (vertical). The centers of the sensors were aligned along the Y-axis. The centers of adjacent sensors for the fingers were spaced 3 cm apart. The center of the thumb sensor was positioned at the mid-point between the sensors for the middle and ring fingers. The grip width, the shortest distance between the contact surfaces of the thumb and finger sensors, was 6.25 cm. The centers of the five sensors were within one plane – the grasp plane. Sandpaper (320 grit, as in the study by Savescu et al. 2008) was placed on the contact surface of each sensor to provide high friction.
Figure 1.
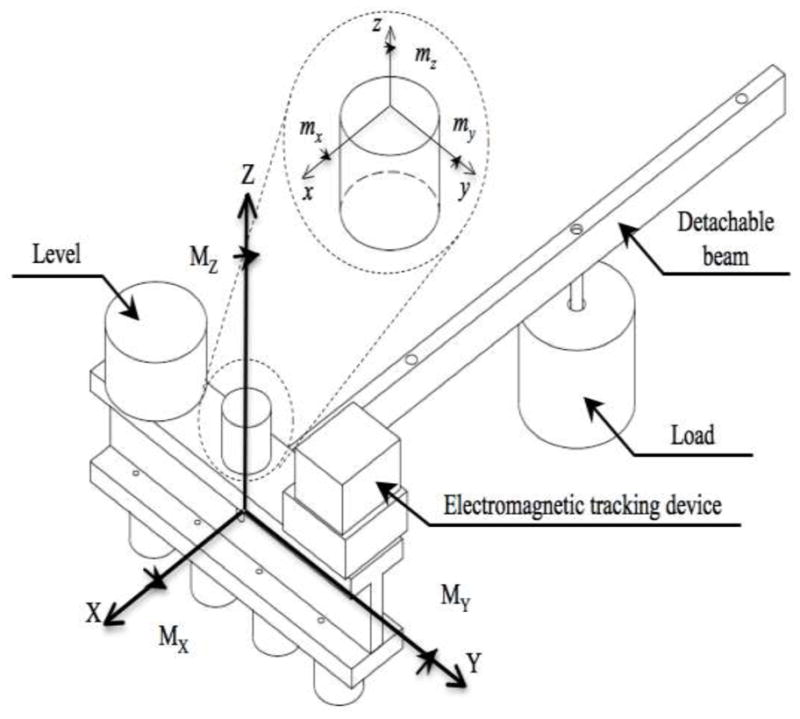
The handle and subject position during experiment. (A) Digit sensors were attached to an aluminum handle, and a load could be attached at different points along a rigid, light-weight rod. An electromagnetic tracking device and a bubble level were attached to the handle. MX, MY, and MZ are the global moments with respect to the global X-, Y-, Z-axes; mx, my, and mz are the local moment with respect to the local x-, y-, and z-axes on each sensor. (B) The position of the subject. The subject maintained the handle horizontal by monitoring the orientation angles around the X- and Y-axes shown on the computer screen.
A 6-component (3 position and 3 orientation components) electromagnetic tracking device (Polhemus LIBERTY, Colchester, VT, USA) was affixed to the top of the handle on a wooded base (2.5 × 2.5 × 1.2 cm.). During the procedures, the distortion indicator of the tracking system remained in steady green indicating that the magnetic system was working undistorted by the experiment setup.
The mass of the handle with the sensors was 0.35 kg. External loads with the mass 0.1, 0.2, and 0.3 kg could be attached to the handle or to the beam using a threaded rod (Figure 1A). Affixing a load to the handle between the middle and ring finger sensors produced an external load without generating external torque. Attaching loads to the three different locations on the beam created both external load and torque about the Y-axis.
A desktop computer with a 19” monitor and customized software (LabVIEW 9.0, National Instruments, Austin, TX, USA) was used to acquire data and to render visual feedback on the handle orientation. Thirty analog signals from the force/torque sensors were conditioned, amplified, and digitized with a 16-bit data acquisition card (NI PCI-6225, National Instruments, Austin, TX, USA) installed in the computer, while the signals from the magnetic device were sent to the computer using a USB 2.0 interface. All data were collected at the sampling frequency of 100 Hz.
Procedure
Two sets of tasks, static-hold and hold-lift tasks, were used. For the zero external torque conditions, the aluminum beam was detached and three weights (0.1, 0.2, and 0.3 kg) were attached directly to the handle. The fourth condition was without any additional load (0 kg). In conditions with non-zero external torque, each of the three loads could be attached at each of the three locations (0.08, 0.16, and 0.24 m away from the grasp plane). The static-hold task consisted of all four zero torque conditions and four conditions with external torques (0.2 kg × 0.16 m, 0.2 kg × 0.24 m, 0.3 kg × 0.16 m, and 0.3 kg × 0.24 m.) The hold-lift task included the remaining five non-zero-torque conditions. The combinations were selected to achieve three objectives. First, in zero-torque conditions, the external load effect could be tested. Second, the static-hold task and the static-hold phase of the hold-lift task composed a balanced design to test both torque and load effects. Third, the hold-lift task allowed investigating the effects of the rotational moment of inertia (not reported in the current paper).
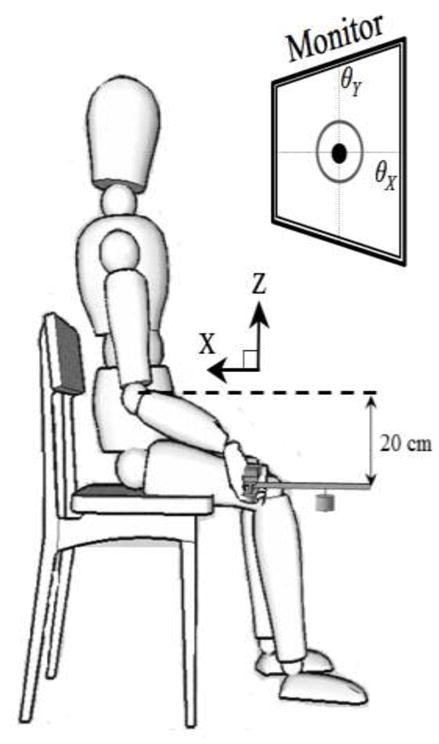
Two trials were performed for each static-hold condition, while twenty trials were conducted for each hold-lift condition. In the hold-lift task, the instruction for the first 3 s (the static phase) was the same as in the static-hold task. After 3 s, the subjects would hear a sound signal generated by the data collection software and lifted the handle in a self-paced manner to a target located 20 cm higher than the initial position with an elbow flexion movement as quickly as possible. Once reaching the target height, the subjects held the handle statically until the end of the trial. In this manuscript we do not describe the lifting action. So, we analyzed only the static phase of all the trials. In the hold-lift task, this phase was selected to be sufficiently far from the lifting phase to avoid any possible contamination of the data by preparation to perform the action. The instructions for the steady-state phases of both tasks were identical: to keep the object horizontal and steady.
The position of the wrist was about 20 cm lower than the elbow level determined when the subject sat on a chair with the upper arm naturally hanging down (the elbow extended, Figure 1B). During the trials, the subjects held the handle by placing individual digit tips on the contact surfaces of each sensor, the forearm supinated and the wrist slightly hyperextended to keep the handle horizontal. The subjects released the handle after each trial, and the handle was held by the experimenter.
Subjects were instructed to grasp the handle and to maintain it horizontal by watching a cursor on the computer screen showing the orientation of the handle about the X- and Y-axes. The horizontal and vertical axes on the screen corresponded to the orientation of the handle about the X- and Y-axes, respectively. A target circle was displayed on the screen representing 0° of both angles, and the radius of the circle corresponded to 2° deviations. The data recording procedure started when the subjects reported that they were holding the handle as instructed. The data were collected for 6 s. After the data collection stopped, the experimenter held the handle and the subjects released it.
A minimum 20-s rest interval was given to the subjects between trials, and a 5-min break was given between conditions. The order of conditions was pseudo-randomized, and the total duration of the experiment was about 1.5 h.
Data Analysis
The data were processed off-line using customized MATLAB software (MathWorks Inc., Natick, MA, USA.) The force, position, and orientation data were low-pass filtered at 30 Hz using a 2nd order, zero-lag Butterworth filter. The data were averaged over the middle 3-s period in each trial.
Center of Pressure
The center of pressure (COP) coordinates were calculated as , where m is the local moment of force recorded by the sensor, F is the digit force, subscripts x and y denote local coordinates, X, Y, and Z stand for global coordinates, and superscript j represents digits (j = {TH, I, M, R, and L} referring to the thumb, index, middle, ring, and little fingers, respectively). The values of COP were used to compute the lever arms of digit forces to determine the moment of force exerted by individual digits. Net moments acting on the handle were calculated with respect to the geometric center of the handle (X = Y = Z = 0.)
Model
During static-hold phases, we assume that the handle was in static equilibrium. Hence, the forces and torques acting on the handle had to satisfy the following six constraints.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where j = {th, i, m, r, l}; w is the total weight of the object; T is the external torque; m is a local moment of force; M is a moment of force and F is a digit force; d is the distance along Z-axis from the center of the handle to the contact surface of a sensor; subscripts X, Y, and Z show the direction of a vector; superscripts t and n denote tangential and normal forces. Note that infinitely many different force and moment configurations could satisfy the task constraints. Therefore, there is a need for a selection rule for force/moment production.
All analyses were done at two levels of the assumed hierarchy (Arbib et al. 1985): At the VF–TH level and IF level (see Introduction). The VF normal force ( ), tangential force ( ), and moment of force (MVF ) were computed by summing up the normal forces, tangential forces, and moments of force of individual fingers, respectively. The center of pressure of virtual finger (COPVF) was calculated as: , where d is the lever arm equal to the half of the grip width. At the IF level, each mechanical variable was shared across the four fingers. The sharing of each variable across the fingers was defined as a proportion of the total VF value of that variable , where k = {I, M, R, and L}, and i stands for Fn, Ft, and M.
The total moment of force (MTOT) was computed as the sum of the moments produced by the five digits. The moment of force produced by each digit was viewed as the sum of the moments generated by the normal and tangential forces. Thus, MTOT was decomposed into ten summands (i.e., moments produced by the normal and tangential forces by each of the five digits). Sharing of was computed as , where j = {TH, I, M, R, and L}, i denotes the direction of force inducing the moment (i = n or t).
Safety Margin
The safety margin has been defined as the proportion of normal force above the threshold for slippage (Johansson and Westling 1984; Burstedt et al. 1999; Pataky et al. 2004b) as:
| (7) |
where μs is the coefficient of static friction between the finger pad and the contact interface of the object. The maximum value for SM is one when no tangential force (Ft) is exerted on the object and the minimum value for SM is zero when just sufficient normal force (Fn) is exerted on the object to prevent slippage. The coefficient of friction between the skin and an object changes with the magnitude of normal force; we used the equation , where Fn is the normal force, and reflects Young’s modulus of the skin and average dimension of the adhesive contact (Seo et al. 2009). The method used to estimate the coefficient α was to fit the Savescu et al. (2008) data using the log-log regression. The fitted equation was μ = 1.44 (Fn)−0.293. Since the power is similar to the original equation, the fitted equation was adopted to estimate the friction coefficient. Fisher transformation was applied to the SM values before using parametric statistics.
Analysis of multi-digit synergies
We used a definition of a multi-digit synergy as co-variation (across trials) among variables produced by individual digits (elemental variables) that reduces variance of (stabilizes) their combined mechanical effect. At the VF–TH level, the output of the VF and thumb are viewed as elemental variables that produce mechanical action on the handle. At the IF level, the outputs of each individual finger within the VF are elemental variables that produce the output of the VF. So, at the IF level, the elemental variables included the normal and tangential forces of individual fingers ( and ; k = I, M, R, and L), and the moments produced by the fingers (Mk). At the VF–TH level, the elemental variables were , MVF, and MTH.
The indices of co-variation of elemental variables were computed at each of the two levels, VF–TH and IF, across the trials for each condition and each subject separately. Each index, ΔV, was computed as the difference between the sum of the variances of elemental variables [ΣVar(EV)] and the variance of the total output of these elemental variables [Var(ΣEV)] normalized by ΣVar(EV) to allow comparisons across conditions and subjects:
| (8) |
Specifically, six indices were computed:
| (9) |
| (10) |
where i stands for Fn, Ft, and M.
Positive values of ΔV reflect predominantly negative co-variation among forces (or moments of force) produced by either the thumb and VF (equation 9) or by the individual fingers (equation 10). We interpret ΔV > 0 as sign of a force (or moment of force) stabilizing synergy (Shim et al. 2005a; Gorniak et al. 2009). Large positive ΔV values correspond to larger amounts of negative co-variation, thus a stronger synergy. A result of ΔV = 0 implies independent variation of digit forces, and correspondingly the absence of a synergy, while ΔV < 0 may be interpreted as co-variation of elemental variables destabilizing their combined output. By computation, ΔVs have lower bounds of −1 at the VF-TH level and −3 at the IF level. Fisher transformation was applied to these values before using parametric statistics.
Statistics
The descriptive statistics are presented in the text and figures as means and standard errors. Repeated-measures analyses of variance (ANOVAs) were conducted using SPSS software (SPSS 19, IBM, Somers, NY, USA) on the force, moment of force, , and safety margin values (after Fisher transformation) with the factors: Load (four levels for zero external torque conditions and three levels for the non-zero torque conditions), and Moment-Arm (three levels). A three-way multivariate analysis of variance (MANOVA) was performed on the force sharing pattern with the factors: Load (three levels), Moment-Arm (three levels), and Force-Direction (two levels, tangential and normal). A two-way MANOVA was conducted on ΔV with the factors: Load (three levels) and Moment-Arm (three levels). Tukey’s pair-wise contrasts with the Bonferroni corrections were used to explore significant effects. Data on safety margin and ΔV were subjected to Fisher transformation; non-transformed data are also shown in figures.
Results
Task Mechanics
Normal Forces
When the external torque was zero, there were no changes in the normal force produced by the thumb with external load. On average, . The load was supported by the four fingers (virtual finger, VF); hence, the normal force of the scaled with external load as dictated by mechanics: .
When the external torque was not zero, the normal forces of the VF and thumb formed a couple that produced a portion of the total moment of force. As a result, both and scaled with the external load and its lever arm (Figure 2). Two-way ANOVAs with the factors Moment-Arm (3 levels) and Load (3 levels) on the normal forces of VF and thumb showed significant effects for both variables [F(2, 16) > 98.262; P < 0.001] with a significant interaction [F(4, 32) > 18.67; P < 0.001]. The interaction reflected an increase in the effect of Moment-Arm for larger loads.
Figure 2.
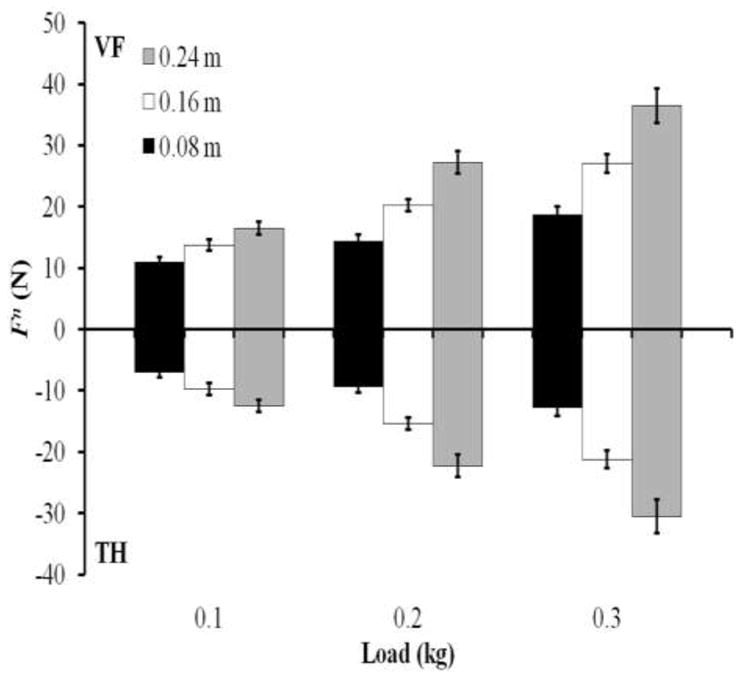
Normal forces (Fn) of the thumb (TH) and vitual finger (VF) exerted on the handle under different load conditions (0.1, 0.2, and 0.3 kg) and different lever arms (black bars: 0.08 m; white bars: 0.16 m; gray bars: 0.24 m). The averaged data across trials and subjects are presented with standard error bars. Both VF and thumb normal forces scaled with the load and lever arm.
The pattern of sharing the total VF normal force among the individual fingers was, on average, [I, M, R, L] = [28.0 ± 0.5%, 28.4 ± 0.6%, 24.7 ± 0.4%, 18.9 ± 0.6%]. It was similar across all conditions with non-zero external torque. This pattern produced a non-zero supination moment that was balanced by the moments produced by the tangential forces and thumb force such that the total moment was close to zero.
Tangential Forces
The tangential forces in the medio-lateral direction were low and showed no consistent changes across conditions. Therefore, they are not presented here.
In contrast, the tangential forces in the anterior-posterior direction (X-axis) formed a couple that produced the other component of the total moment of force. The lever arm of the tangential forces was constant, defined by the width of the handle. The magnitude of these forces produced by the thumb and VF, and , scaled with both external load magnitude and lever arm (Figure 3). Two–way ANOVAs, Moment-Arm × Load showed main effects of both factors for both variables [F(2, 16) > 651.917; P < 0.001] as well as a significant interaction [F(4, 32) > 116.598; P < 0.001].
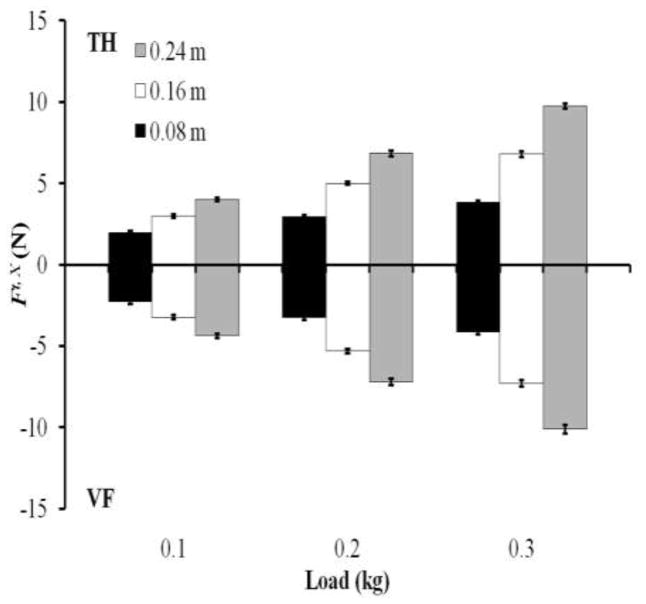
Figure 3.
Tangential forces (Ft,X) in the anterior-posterior direction (X-axis) by the thumb an VF under different loads (0.1, 0.2, and 0.3 kg) and lever arms (0.08, 0.16, and 0.24 m). Averaged data across trials and subjects are presented with standard error bars. The tangential forces of VF and thumb formed a force couple acting against the external torque. Magnitudes of both VF and thumb tangential forces scaled with the external load and its lever arm.
The sharing pattern of the VF tangential force across the individual fingers remained almost unchanged across all conditions with external torque: [I, M, R, L] = [35.3 ± 0.9 %, 21.5 ± 1.6 %, 14.1 ± 1.1 %, 29.2 ± 1.2 %]. This pattern was significantly different from that of the VF normal force. In particular, the shares of the “central” fingers (M and R) were smaller for as compared to , while the shares of the “lateral” fingers (I and L) were higher for . A three-way MANOVA Moment-Arm × Load × Direction supported the observation by showing main effect of force Direction [F(1, 144) > 15.365; P < 0.001] (Figure 4).
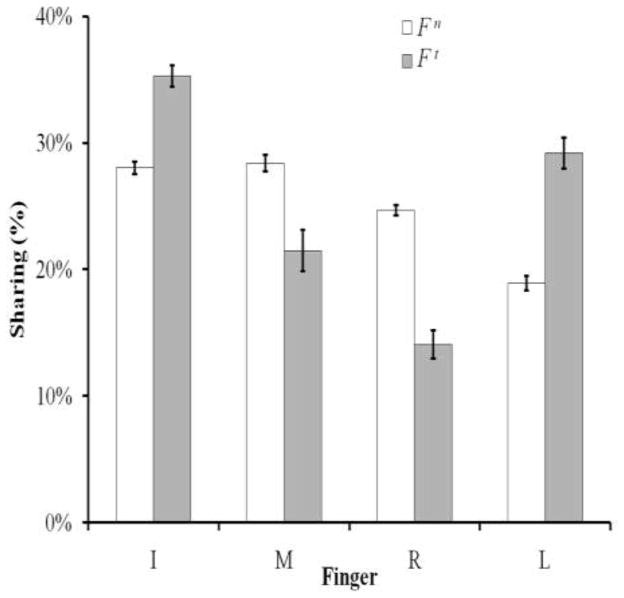
Figure 4.
The sharing patterns of the VF tangential (gray bars) and normal (white bars) forces across the individual fingers. The averaged data across trials, subjects, and conditions are presented with standard error bars. Note that the shares of the “central” fingers (M and R) were smaller for the VF tangential force as compared to the normal force. I, M, R, and L stand for the index, middle, ring, and little fingers, respectively.
Moments of Force
The total moment of force (MTOT) about the Y axis produced by the hand may be viewed as the sum of the moments produced by the thumb and VF, MTH and MVF. It may also be viewed as the sum of moments produced by the normal and by the tangential forces, Mn and Mt. MTOT was shared nearly equally between MTH and MVF; on average, the MVF share was slightly higher, 51.1 ± 0.7 %. Note that the tangential forces of the VF and thumb in the X direction formed a couple while the normal forces could potentially produce different contributions to MTOT. The magnitudes of MTH and MVF changed with the external load magnitude and lever arm as illustrated in Figure 5. Two–way ANOVAs, Moment-Arm × Load showed main effects of both factors for both MTH and MVF [F(2, 16) > 1075.750; P < 0.001] with a significant interaction [F > 185.752; P < 0.001]. Sharing of MVF across the moments produced by the four fingers was consistent across conditions: [I, M, R, L] = [26.6 ± 0.8 %, 28.9 ± 1.7 %, 19.4 ± 1.2 %, 25.2 ± 1.2 %].
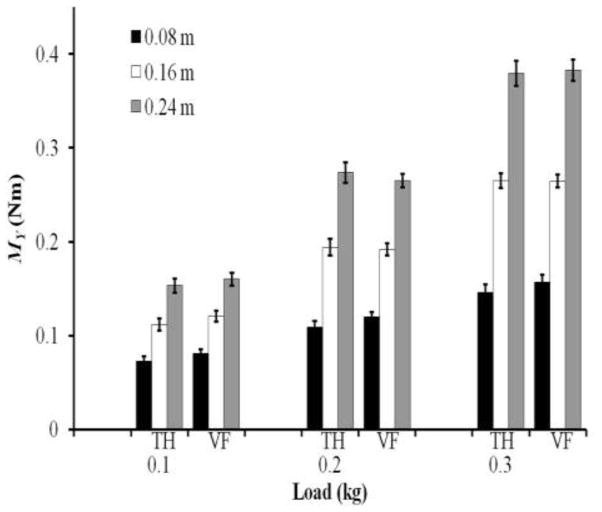
Figure 5.
The moments about the Y-axis (MY) generated by the VF and thumb under different loads (0.1, 0.2, and 0.3 kg) and lever arms (0.08, 0.16, and 0.24 m). The averaged data across trials and subjects are presented with standard error bars. Note that the total moment against external torque was shared nearly equally between moments exerted by VF and thumb.
Most of MTOT was produced by the tangential forces as illustrated in Figure 6. This was true for each of the five digits. Across all conditions with non-zero external torque, Mt contributed, on average, 83.6 ± 0.9% of MTOT. Note that the “lateral” fingers (I and L) produced higher Mt, while their normal forces produced, on average, close to zero moments of force. The moments produced by the normal forces of the thumb and “medial” fingers (M and R) were always in the direction against the external torque.
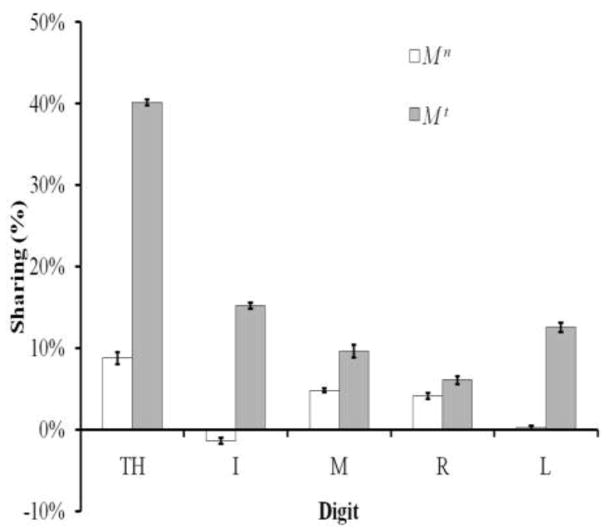
Figure 6.
The sharing of total moment about the Y-axis (MY) between the moments generated by normal (Mn – white bars) and tangential (Mt – gray bars) forces by all five digits. The averaged data across trials, subjects, and conditions are presented with standard error bars. Most of the total MY was produced by the tangential forces. Note that the “lateral” fingers (I - index and L - little) produced higher Mt, while their Mn, on average, was close to zero.
While the lever arm of the tangential forces was always constant, the lever arm of the normal forces could change. Figure 7 shows the changes in the anterior-posterior coordinate of the center of pressure (COPX) with the external load magnitude and lever arm. COPX showed an increase with both load magnitude and lever arm only for the thumb. Two–way ANOVAs, Moment-Arm × Load, showed main effects of both factors for without an interaction. No significant effects on were observed.
Figure 7.
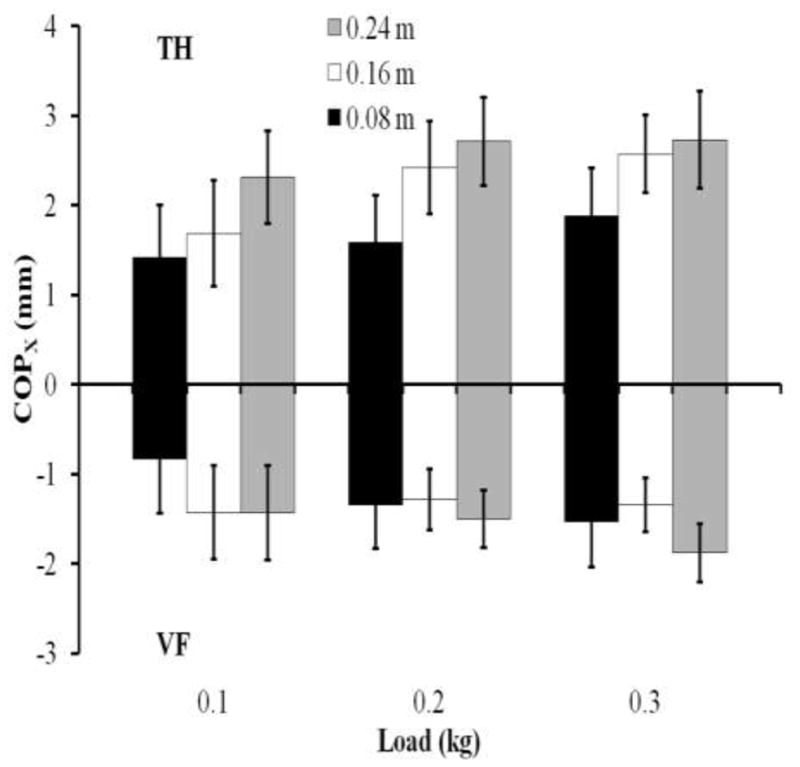
The changes in the anterior-posterior coordinate (X-axis) of the center of pressure (COPX) with the external load (0.1, 0.2, and 0.3 kg) and lever arm (0.08, 0.16, and 0.24 m) for the thumb and VF. The averaged data across trials and subjects are presented with standard error bars. Only for the thumb, COPX showed an increase with both load magnitude and lever arm.
Thumb Safety Margin
In the absence of external torque, neither VF nor the thumb had to produce tangential force. Hence, in conditions with zero external torque, safety margin (SM) values were very high. In particular, on average, SM for the thumb was 0.94; after Fisher transformation, average SMZ was 1.51 ± 0.09.
When there was a non-zero external torque, the digits produced non-zero tangential forces. Figure 8 shows SM values for the thumb across the conditions; SM dropped with both load magnitude and lever arm. Two–way ANOVA, Moment-Arm × Load, on SMZ for the thumb showed main effects of both factors [F(2, 16) > 41.236; P < 0.001].
Figure 8.
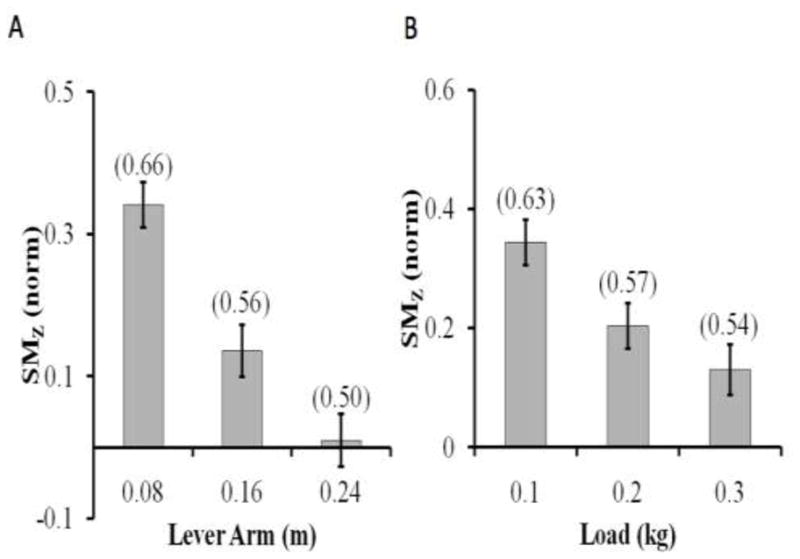
The safety margin (SM) values of the thumb across trial conditions. (A) The SM values across lever arms (0.08, 0.16, and 0.24 m). (B) The SM values across external load magnitudes (0.1, 0.2, and 0.3 kg). The bars show SM values after Fisher transformation (averaged across subjects with standard error bars), while the values in parentheses refer to data before Fisher transformation. SM values dropped with both lever arm and load magnitude.
Multi-Digit Synergies
Indices of co-variation of elemental variables (those produced by individual digits) were computed across trials at the two levels of the assumed hierarchy, VF-TH and IF (see Methods). Figure 9 shows averaged across subjects ΔV indices for all six components of the force and moment of force vectors across lever arms (panels A and C) and loads (panels B and D). Note that at both levels (VF–TH and IF), the indices are predominantly positive corresponding to negative co-variation of elemental variables. Changes in the load magnitude and lever arm had only minor effects on ΔV. Two–way MANOVA on ΔV values after Fisher transformation (ΔVZ), Moment-Arm × Load, across all six mechanical variables confirmed only effects of Moment-Arm for MY and MZ and Load for MY [F(2, 72) > 3.298; P < 0.05].
Figure 9.
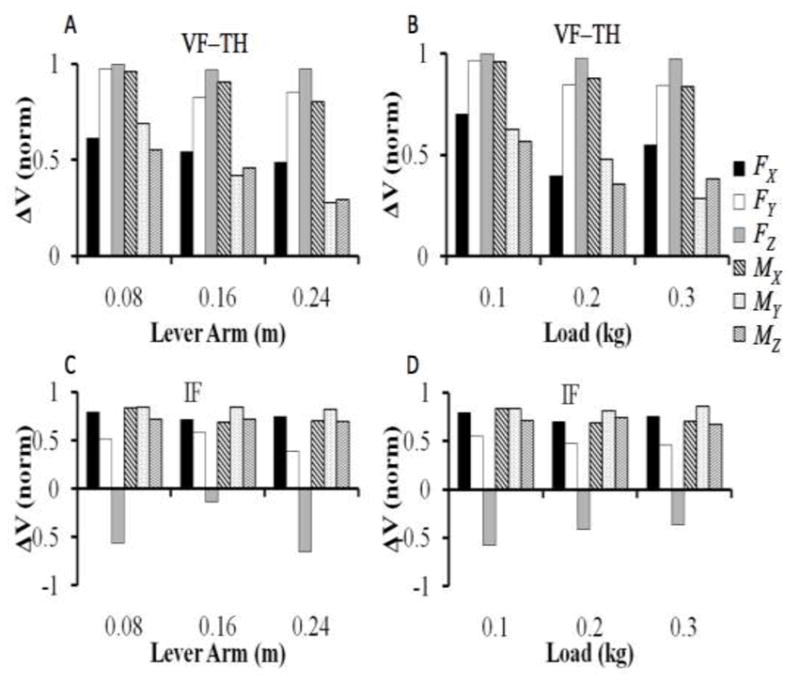
Indices of co-variation of elemental variables (ΔV) averaged across subjects for all six component of the force and moment of force vectors. (A) and (C) show ΔV across lever arms at the VF-TH and IF level, respectively. (B) and (D) show ΔV across external loads at the VF-TH and IF level, respectively. Note that ΔV are predominantly positive at both levels (with the exception of Fn at the IF level), and changes in the lever arm and load magnitude had only minor effects on ΔV.
All three force components showed highly positive ΔV indices at the VF-TH level; the highest ΔV magnitudes were observed for the normal force component (FZ). In contrast, only the two tangential force components showed high ΔV indices at the IF level, while this index for the normal force was close to zero or even negative.
Figure 10A illustrates the relations between ΔV values after Fisher transformation (ΔVZ) computed at the two levels of analysis across individual subjects for the three force components. Note a strong trade-off between the ΔV indices at the VF-TH and IF levels across the three force components: Higher index values at one level corresponded to lower values at the other level.
Figure 10.
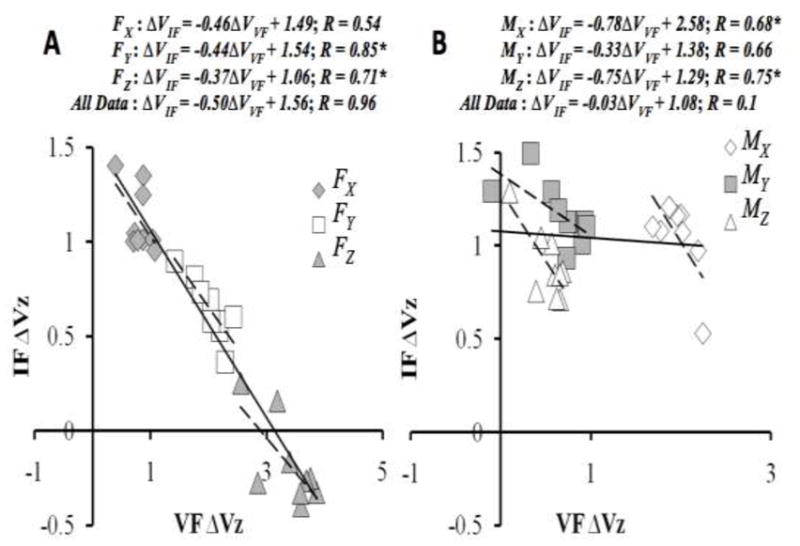
The relations between indices values after Fisher transformation (ΔVZ) averaged across subjects and trial conditions at the VF and IF levels for (A) the three force components and (B) the three moment of force components. Note that there was a strong negative relation between the ΔVZ at the VF-TH and IF levels across the force variables, but not across the moment of force variables. Linear regression equations are shown with correlation coefficients; * - p < 0.05.
Among the three moment components, only MX showed consistently positive ΔV values at the VF-TH level, while the values for MY and MZ were low. Note that the external torque acted in the Y direction; nevertheless, there were only weak signs of MY stabilization by covaried adjustments of and . At the IF level, all three moment of force components showed similarly high ΔV indices. As illustrated in Figure 10B, there were modest negative correlations between the indices of moment of force stabilization at the two levels, VF-TH and IF and no signs of a trade-off between the two levels across the three moment variables.
Discussion
Four issues were addressed in the described experiments. First, when the external torque was zero, the thumb produced a non-zero normal force, which was not mechanically necessary (cf. Pataky et al. 2004a); this force did not depend on magnitude of the external load. When the external torque was not zero, the normal force of the thumb scaled with both load magnitude and its moment arm.
Second, in our study the tangential forces contributed over 80% to the total moment of force. This result is different from the earlier reports on nearly equal contributions of the normal and tangential forces to the total moment of force (Zatsiorsky et al. 2003b), and results of a recent study showing that the normal forces contribute much more to the total moment of force adjustments (Sun et al. 2011). We observed a major difference among the moments of force produced by the normal forces of individual fingers. The middle (M) and ring (R) fingers produced consistent moments of the normal force acting against the external torque, while the index (I) and little (L) fingers, on average, produced close to zero moment of the normal force.
Third, we observed different patterns of sharing of the normal and tangential forces among the four fingers. This finding is opposite to that reported by Pataky et al. (2004b) who observed highly correlated sharing patterns for the normal and tangential forces. Assuming no differences in the friction coefficients among the fingers, this result suggests that there was no single rule defining safety margin values for the individual fingers.
Finally, we observed a trade-off between synergy indices computed at the higher (VF-TH) and lower (IF) levels of the assumed hierarchy (cf. Gorniak et al. 2007, 2009). This tradeoff was, however, found only for the three force variables, not for the three moment of force variables. Further, we discuss implications of these findings for the mechanics of holding a horizontally oriented object and associated multi-digit synergies.
Mechanically necessary and unnecessary thumb forces
The mechanics of holding the handle in the zero-torque and non-zero-torque conditions were quite different. In the zero-torque condition, only the weight of the load had to be supported by the normal forces of the fingers. No tangential forces were necessary, and the thumb did not have to produce any force. Nevertheless, when the external torque was zero, the thumb produced a non-zero normal force, which did not depend on magnitude of the external load (cf. Pataky et al. 2004a). The magnitude of this force was rather high compared to typical magnitudes of the tangential force the thumb produced. As a result, the safety margin was extremely high, close to its ceiling value of 1.0. We may conclude, therefore, that the purpose of producing the normal force by the thumb was not solely related to ensuring sufficient friction (cf. Johansson and Westling 1984). Since the magnitude of this force did not depend on the magnitude of the external load, the magnitude of the thumb normal force may be viewed as a default value. This force could load the pressure sensitive receptors and play a role in the sensory function of the thumb (cf. Ducic et al. 2006). It could also be related to ensuring stability of the handle in cases of its unexpected perturbations, which did not happen in our experiments but may be common in everyday tasks.
When the external torque was not zero, the normal force of the thumb played two roles. First, it provided enough friction to allow generating the tangential forces, which contributed most of the total moment of force produced by the thumb (Figure 6). Second, shifts of the thumb COP allowed the normal force to contribute to the moment of force against the external torque. Note that COPX shifts for the thumb scaled significantly with both external load and its lever arm (Figure 7). The fact that the percentage of total moment of force produced by the thumb tangential force did not change across conditions suggests that there is a simple rule defining the thumb normal force magnitude as a result of fixed sharing among three components: , where the superscripts d, M, and SM stand for the fractions of the normal force related to the default value, moment of force production, and ensuring adequate safety margin, respectively.
Moment of force sharing
In the non-zero-torque conditions, the thumb and VF shared the total moment of force nearly equally (cf. Zatsiorsky et al. 2002; Shim et al. 2003). The contributions of the tangential forces of the two digits to the moment of force were expected to be equal because of the necessity to keep the total tangential force zero (one of the constraints of statics) and the equal lever arm of the two forces; in other words, they formed a couple (see Figure 11A). The contributions of the normal forces could be substantially unequal because the VF normal force was much higher than the thumb normal force due to the requirement to hold the additional load. However, since the tangential forces contributed over 80% to the total moment of force, the unequal contributions of the normal forces did not play a major role.
Figure 11.
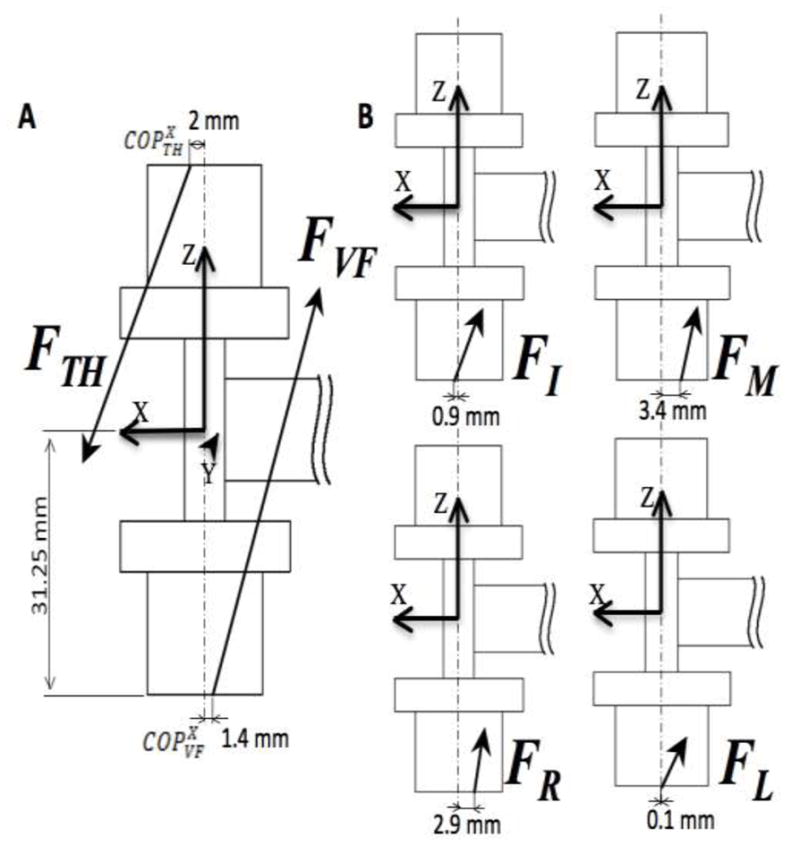
An illustration of the sagittal view of the handle with the force vectors and COPX of each digit at (A) the VF–TH level and at (B) the IF level. The averaged data across trials, subjects, and conditions are illustrated. The aluminum beam to which the external load attached is truncated. The subscripts (TH, VF, I, M, R, and L) refer to the thumb, virtual finger, index, middle, ring, and little fingers, respectively.
To our knowledge, this is the first study to document much higher proportion of the total moment of force produced by tangential forces. In earlier studies with holding a vertically oriented handle, the share of the total moment produced by the normal forces was either 50% or much higher (Zatsiorsky et al. 2002; Sun et al. 2011). As illustrated in Figure 11, this could be due to the unequal moment arms that were higher for the tangential forces and were limited for the normal forces by the displacement of the center of pressure of individual digits.
Different roles of fingers in moment of force production
At the level of individual fingers comprising the VF, sharing of the VF normal force was similar to the results of previous studies of pressing and prehension (Li et al. 1998; Zatsiorsky et al. 2003a,b) and considerably different from the reported patterns of the sharing of the VF tangential force (Zatsiorsky et al. 2003; Pataky et al. 2004b). This finding is opposite to that reported by Pataky et al. (2004b) who observed highly correlated sharing patterns for the normal and tangential forces. Assuming that safety margin is an important variable that the central nervous system tries to keep at a certain magnitude (an assumption present in many of the cited studies), using a single safety margin has an advantage of fewer variables to be specified by the controller. The different sharing patterns of the normal and tangential forces suggest that there was no single rule that would define similar safety margin values across the fingers (note that this result hinges on the assumed similar friction coefficients across the digits, which makes it tentative). This result is in line with the idea that safety margins could be adjusted locally for individual fingers (Burstedt et al. 1997, 1999; Quaney and Cole 2004; although see Aoki et al. 2007). In the cited papers, local friction conditions were manipulated. In our case, the different safety margins could be due to the difference in the role of the fingers in normal and tangential force production.
In earlier studies, it has been suggested that the M and R fingers play a major role in supporting the weight of the object, while the I and L fingers play a major role in producing rotational effort (Zatsiorsky et al. 2002, 2003b; Shim et al. 2003). All those studies used a vertically oriented handle. As a result, in those studies, the lever arms for the normal forces of the I and L fingers were much larger than for the M and R fingers (with respect to rotation about the transverse axis of the handle). In contrast, in our experiment, a horizontally oriented handle was used and it put all four fingers in equal mechanical conditions for resisting the external torque (applied with respect to the longitudinal axis). All four fingers used primarily tangential forces to produce moments of force. However, there was a major difference among the moments of force produced by the normal forces: The M and R fingers produced consistent moments of the normal force acting against the external torque, while the I and L fingers, on average, produced close to zero moment of the normal force. In other words, the M and R fingers showed better control of the COPX coordinate that allowed their normal forces to produce moments in the required direction (Figure 11B).
This is not a trivial result. Most studies have reported that the I finger is the one with most accurately controlled force, while the R finger is typically viewed as less independent from other fingers and less accurate in force production (Li et al. 1998; Zatsiorsky et al. 2000; Gorniak et al. 2008). It allows offering a hypothesis that all the fingers are specialized to perform specific task components. There are no accurate fingers and sloppy fingers, indices of performance are task dependent. This conclusion is similar in spirit to the hypothesis offered by Wang and Sainburg (2007) that the left hand is not a “bad right hand” but is better in aspects of everyday performance.
The relatively higher shares of the normal force in the MR finger pair may be related to the fact that their normal forces had two functions, ensuring sufficient friction for the production of the tangential forces and the generation of the moment of force. The normal force of the IL finger pair played only the former role and, hence, showed relatively smaller magnitudes.
The role of individual fingers in static prehensile tasks depends on the finger configuration and on direction of the external torque. In an earlier study by Shim et al. (2005), only 10% of the total torque was supported by the moments produced by the tangential forces of the four fingers. In our case, this value was close to 40%; since about the same amount was produced by the thumb tangential force, the total contribution of the tangential forces to moment production was 80%. Note that in the Shim et al. study, the handle was held vertically and the external torque acted about an axis orthogonal to the handle long axis. As a result, tangential forces of the radial (IM) and ulnar (RL) fingers had to act in opposite directions to produce a net moment of the VF. In our case, all fingers produced tangential forces in the same direction to counteract the external moment acting about the long axis of the handle.
Prehension synergies in a hierarchical system
We defined synergies as co-varied adjustments in elemental variables that help reduce variance of their combined output (reviewed in Latash et al. 2007; Zatsiorsky and Latash 2008). At the VF-TH level, the elemental variables were forces and moments of force produced by the thumb, while at the IF level, these were forces and moments of force produced by individual fingers. At both levels and for all six components of the force and moment of force vectors, we found high synergy indices suggesting that all these variables were stabilized (in a sense of reduced variance) by co-varied adjustments of corresponding elemental variables. This was true even for variables with the average magnitudes very close to zero, such as MY and FY. One notable exception was provided by the analysis of synergies stabilizing normal force at the IF level; the synergy index for this analysis was consistently negative, in stark contrast to the highly positive values for the analysis at the VF-TH level (similar to results reported by Gorniak et al. 2009).
Several earlier studies documented lack of stabilization of normal force at the lower level of a two-level hierarchy for both two-hand pressing tasks and prehensile tasks (Gorniak et al. 2007a,b; 2009). One interpretation of this finding has been offered related to the method of computation of the synergy index. Total variance at the level of elemental variables may be viewed as consisting of two components, “good” variance (VGOOD, that does not affect variance of their combined output) and “bad” variance (VBAD, that does). At the higher level of the hierarchy (the VF-TH level), large amounts of VGOOD increase the synergy index. On the other hand, large VGOOD means that variance of both thumb and VF outputs is high. At the lower level of the hierarchy, where co-variation of finger forces is expected to reduce variance of the VF output, the VF force variance is VBAD and, as such, brings the synergy index down. It is possible to have strong synergies at both levels (as shown in experiments for synergies stabilizing tangential force, Gorniak et al. 2009; Sun et al. 2011). For performance variables that represent the sums of elemental variables (such as and ), this requires:
| (11) |
where the superscripts refer to level of analysis.
In our study, there was a negative correlation between synergy indices computed at the two levels across the three force variables (and for two of those variables analyzed separately), and no such correlation for synergy indices computed across the three moment of force variables (although two individual moment of force components showed significant negative correlations between the two ΔV indices). This was true independently of the sign of the synergy indices.
The following interpretation can be offered for this result. For all the force variables, at the VF-TH level, the number of elemental variables was always two; so, there was only one way of organizing co-variation at that level stabilizing the total action of the hand. All the moment variables got contributions from at least two components produced by each digit. For example, the moment acting against the external load was produced by contributions from both the normal and tangential forces of both the thumb and VF. This increase in the number of elemental variables allows numerous ways of stabilizing total moment of force (cf. Zhang et al. 2008). In particular, the magnitudes of forces produced by the thumb and VF may not co-vary at all while the overall synergy is provided by co-variation between the contributions of the normal and tangential forces within each digit. The availability of such a strategy invalidates the earlier analysis (see inequalities 11). It emphasized that availability of additional degrees-of-freedom may allow organizing synergies at two levels within a two-level (multi-level) hierarchy. The issue of the organization of synergies within a hierarchical system has been discussed in a recent target article (Latash 2010) and associated commentaries; this issue is central in the attempts to link the idea of synergic control to the referent configuration hypothesis of motor control (Feldman et al. 2007).
Concluding Remarks
We would like to reiterate the main lessons from the described series of experiments. First, the results have shown that task mechanical constraints are only one component that defines forces produced by individual digits. This conclusion is in line with a number of earlier studies (Flanagan and Wing 1993, 1995; McIsaac et al. 2009; reviewed in Schieber and Santello 2004). Other factors, such as loading sensory receptors may lead to mechanically unnecessary forces. In particular, the default magnitude of the thumb normal force supports this conclusion.
Second, fingers show a lot of independence in the production of normal and tangential forces (each individual finger can control the normal and tangential force generated by it independently). There seems to be no single rule (for example, ensuring similar safety margin values) that would be valid across tasks. This is illustrated by the different sharing patterns of the normal and tangential forces across the four fingers. One has to be careful in generalizing conclusions of studies with specific tasks.
Third, we do not have “good fingers” and “bad fingers”. Individual fingers are specialized for their typical roles in everyday tasks; compared to other fingers, each finger may show better performance indices in some laboratory tasks, while its performance may be worse in other tasks. Likely, there are good evolutionary reasons why we do not have four index fingers in each hand. This conclusion is supported by the more consistent performance of the ring finger in the control of the COP of its force as compared to the index finger. This pattern of performance may well reflect an optimization principle that remains unknown.
Fourth, we are only starting to understand the complexity of the neural organization of multi-digit synergies in a hierarchal system. The observations of the trade-off between the synergy indices computed at the two levels for the force variables but not for the moment of force variables suggest that the degree of redundancy (the number of excess elemental variables) at the higher level of the hierarchy may allow the controller to facilitate synergies at both levels of the hierarchy.
Acknowledgments
The study was supported in part by NIH grants AG-018751, NS-035032, and AR-048563.
References
- Aoki T, Latash ML, Zatsiorsky VM. Adjustments to local friction in multi-finger prehension. J Motor Behav. 2007;39:276–290. doi: 10.3200/JMBR.39.4.276-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbib MA, Iberall T, Lyons D. Coordinated control programs for movements of the hand. In: Goodwin AW, Darian-Smith I, editors. Hand Function and the Neocortex. Berlin: Springer Verlag; 1985. pp. 111–129. [Google Scholar]
- Baud-Bovy G, Soechting JF. Two virtual fingers in the control of the tripod grasp. J Neurophysiol l. 2001;86:604–615. doi: 10.1152/jn.2001.86.2.604. [DOI] [PubMed] [Google Scholar]
- Burstedt MK, Edin BB, Johansson RS. Coordination of fingertip forces during human manipulation can emerge from independent neural networks controlling each engaged digit. Exp Brain Res. 1997;117:67–79. doi: 10.1007/s002210050200. [DOI] [PubMed] [Google Scholar]
- Burstedt MK, Flanagan JR, Johansson RS. Control of grasp stability in humans under different frictional conditions during multidigit manipulation. J Neurophysiol. 1999;82:2393–2405. doi: 10.1152/jn.1999.82.5.2393. [DOI] [PubMed] [Google Scholar]
- Ducic I, Dellon AL, Bogue DP. Radial sensory neurotization of the thumb and index finger for prehension after proximal median and ulnar nerve injuries. J Reconstr Microsurg. 2006;22:73–78. doi: 10.1055/s-2006-932500. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Goussev V, Sangole A, Levin MF. Threshold position control and the principle of minimal interaction in motor actions. Prog Brain Res. 2007;165:267–281. doi: 10.1016/S0079-6123(06)65017-6. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Wing AM. Modulation of grasp force with load force during point-to-point arm movements. Exp Brain Res. 1993;95:131–143. doi: 10.1007/BF00229662. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Wing AM. The stability of precision grasp forces during cyclic arm movements with a hand-held load. Exp Brain Res. 1995;105:455–464. doi: 10.1007/BF00233045. [DOI] [PubMed] [Google Scholar]
- Gentilucci M, Caselli L, Secchi C. Finger control in the tripod grasp. Exp Brain Res. 2003;149:351–360. doi: 10.1007/s00221-002-1359-3. [DOI] [PubMed] [Google Scholar]
- Gorniak S, Zatsiorsky VM, Latash ML. Hierarchies of synergies: An example of the two-hand, multi-finger tasks. Exp Brain Res. 2007a;179:167–180. doi: 10.1007/s00221-006-0777-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak S, Zatsiorsky VM, Latash ML. Emerging and disappearing synergies in a hierarchically controlled system. Exp Brain Res. 2007b;183:259–270. doi: 10.1007/s00221-007-1042-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Zatsiorsky VM, Latash ML. Hierarchical control of static prehension: II. Multi-digit synergies. Exp Brain Res. 2009;194:1–15. doi: 10.1007/s00221-008-1663-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Duarte M, Latash ML. Do synergies improve accuracy? A study of speed-accuracy trade-offs during finger force production. Motor Control. 2008;12:151–172. doi: 10.1123/mcj.12.2.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson RS, Westling G. Roles of glabrous skin receptors and sensorimotor memory in automatic control of precision grip when lifting rougher or more slippery objects. Exp Brain Res. 1984;56:550–564. doi: 10.1007/BF00237997. [DOI] [PubMed] [Google Scholar]
- Kinoshita H, Backstrom L, Flanagan JR, Johansson RS. Tangential torque effects on the control of grasp forces when holding objects with a precision grip. J Neurophysiol. 1997;78:1619–1630. doi: 10.1152/jn.1997.78.3.1619. [DOI] [PubMed] [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Zatsiorsky VM. Multi-finger prehension: Control of a redundant motor system. Adv Exp Med Biol. 2009;629:597–618. doi: 10.1007/978-0-387-77064-2_32. [DOI] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM. Force sharing among fingers as a model of the redundancy problem. Exp Brain Res. 1998;119:276–286. doi: 10.1007/s002210050343. [DOI] [PubMed] [Google Scholar]
- McIsaac TL, Santello M, Johnston JA, Zhang W, Gordon AM. Task-specific modulation of multi-digit forces to object texture. Exp Brain Res. 2009;94:79–90. doi: 10.1007/s00221-008-1671-7. [DOI] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during non-vertical grasping. I. Experimental observations. Biol Cybern. 2004a;91:148–158. doi: 10.1007/s00422-004-0505-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Tangential load sharing among fingers during prehension. Ergonomics. 2004b;47:876–889. doi: 10.1080/00140130410001670381. [DOI] [PubMed] [Google Scholar]
- Quaney BM, Cole KJ. Distributing vertical forces between the digits during gripping and lifting: the effects of rotating the hand versus rotating the object. Exp Brain Res. 2004;155:145–155. doi: 10.1007/s00221-003-1711-2. [DOI] [PubMed] [Google Scholar]
- Savescu AV, Latash ML, Zatsiorsky VM. A technique to determine friction at the fingertips. J Appl Biomech. 2008;24:43–50. doi: 10.1123/jab.24.1.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schieber MH, Santello M. Hand function: peripheral and central constraints on performance. J Appl Physiol. 2004;96:2293–2300. doi: 10.1152/japplphysiol.01063.2003. [DOI] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ, Drinkaus P. A comparison of two methods of measuring static coefficient of friction at low normal forces: a pilot study. Ergonomics. 2009;52:121–135. doi: 10.1080/00140130802238622. [DOI] [PubMed] [Google Scholar]
- Shim JK, Latash ML, Zatsiorsky VM. Prehension synergies in three dimensions. J Neurophysiol. 2005a;93:766–776. doi: 10.1152/jn.00764.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim JK, Latash ML, Zatsiorsky VM. Prehension synergies: trial-to-trial variability and principle of superposition during static prehension in three dimensions. J Neurophysiol. 2005b;93:3649–3658. doi: 10.1152/jn.01262.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y, Zatsiorsky VM, Latash ML. Prehension of half-full and half-empty glasses: Time and history effects on multi-digit coordination. Exp Brain Res. 2011;209:571–585. doi: 10.1007/s00221-011-2590-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. The dominant and nondominant arms are specialized for stabilizing different features of task performance. Exp Brain Res. 2007;178:565–570. doi: 10.1007/s00221-007-0936-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Prehension synergies: Effects of object geometry and prescribed torques. Exp Brain Res. 2003a;148:77–87. doi: 10.1007/s00221-002-1278-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Finger force vectors in multi-finger prehension. J Biomech. 2003b;36:1745–1749. doi: 10.1016/s0021-9290(03)00062-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multi-finger prehension: Biomechanics and Control. Part I. Biomechanics. Biol Cybern. 2002;87:50–57. doi: 10.1007/s00422-002-0321-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Enslaving effects in multi-finger force production. Exp Brain Res. 2000;131:187–195. doi: 10.1007/s002219900261. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Multi-finger prehension: An overview. J Motor Behav. 2008;40:446–476. doi: 10.3200/JMBR.40.5.446-476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Scholz JP, Zatsiorsky VM, Latash ML. What do synergies do? Effects of secondary constraints on multi-digit synergies in accurate force-production tasks. J Neurophysiol. 2008;99:500–513. doi: 10.1152/jn.01029.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]