Feature-based classifiers for somatic mutation detection in tumour–normal paired sequencing data

Abstract

Motivation: The study of cancer genomes now routinely involves using next-generation sequencing technology (NGS) to profile tumours for single nucleotide variant (SNV) somatic mutations. However, surprisingly few published bioinformatics methods exist for the specific purpose of identifying somatic mutations from NGS data and existing tools are often inaccurate, yielding intolerably high false prediction rates. As such, the computational problem of accurately inferring somatic mutations from paired tumour/normal NGS data remains an unsolved challenge.

Results: We present the comparison of four standard supervised machine learning algorithms for the purpose of somatic SNV prediction in tumour/normal NGS experiments. To evaluate these approaches (random forest, Bayesian additive regression tree, support vector machine and logistic regression), we constructed 106 features representing 3369 candidate somatic SNVs from 48 breast cancer genomes, originally predicted with naive methods and subsequently revalidated to establish ground truth labels. We trained the classifiers on this data (consisting of 1015 true somatic mutations and 2354 non-somatic mutation positions) and conducted a rigorous evaluation of these methods using a cross-validation framework and hold-out test NGS data from both exome capture and whole genome shotgun platforms. All learning algorithms employing predictive discriminative approaches with feature selection improved the predictive accuracy over standard approaches by statistically significant margins. In addition, using unsupervised clustering of the ground truth ‘false positive’ predictions, we noted several distinct classes and present evidence suggesting non-overlapping sources of technical artefacts illuminating important directions for future study.

Availability: Software called MutationSeq and datasets are available from http://compbio.bccrc.ca.

Contact: saparicio@bccrc.ca

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The genome-wide search for functionally important somatic mutations in cancer by emergent, cost-effective next-generation sequencing (NGS) technology has begun to revolutionize our understanding of tumour biology. The discovery of diagnostic mutations (Shah et al., 2009a), new cancer genes (ARID1A (Wiegand et al., 2010), PBRM1 (Varela et al., 2011), PPP2R1A (McConechy et al., 2011), IDH1 (Yan et al., 2009), EZH2 (Morin et al., 2010)), insights into tumour evolution and progression (Ding et al., 2010; Shah et al., 2009b) and definitions of mutational landscapes in tumour types [CLL (Puente et al., 2011), myeloma (Chapman et al., 2011), lymphoma (Morin et al., 2011)] among many others, provide important examples of the power and potential of NGS in furthering our knowledge of cancer biology.

Using NGS to interrogate cancers for somatic mutations usually involves sequencing tumour DNA and DNA derived from non-malignant (or normal) tissue (often blood) from the same patient. Consequently, cancer-focused NGS experiments differ considerably in experimental design from the study of Mendelian disorders or normal human variation. In cancer studies, sequence reads from the two matched samples are aligned to a reference human genome, and lists of predicted variants using single nucleotide variant (SNV) callers [e.g. Samtools (Li et al., 2009a), SOAPsnp (Li et al., 2009b), VarScan (Koboldt et al., 2009), SNVMix (Goya et al., 2010), GATK (McKenna et al., 2010), VipR (Altmann et al., 2011)] are compared in the tumour and normal data. Using naive approaches, those variants appearing in the tumour, but not the normal sample would be considered putative somatic mutations and provide the investigator with a list of candidates to follow up for functional impact and clinical relevance. Unfortunately, such naive approaches often result in false predictions and we suggest herein that the problem of computational identification of somatic mutations from NGS data derived from tumour and matched normal DNA remains an unsolved challenge. As a result, labour intensive and often costly validation experiments are still required to confirm the presence of predicted somatic mutations for both research purposes and clinical interpretation.

Although some false predictions may be due to under-sampled alleles, most can be attributed to detectable artefacts that we argue can be leveraged in principled inference techniques to improve computational predictions. Many different approaches to the problem of SNV discovery from NGS have been implemented. Model-based methods such as SNVMix and SOAPsnp aim to probabilistically model the allelic distributions present in the data and infer the most likely genotype from allelic counts. These methods avoid imposing ad hoc depth-based thresholds on allelic distributions, but their accompanying software packages do not explicitly handle known sources of technical artefacts and they must rely on pre- or post-processing of the data to produce reliable predictions. Examples of features that can indicate artefacts include strand bias induced by polymerase chain reaction (PCR) duplicates from the sequencer whereby all variant reads are sequenced in the same orientation (Chapman et al., 2011), mapping quality (how well each read aligns to its stated position), base quality (the signal to noise ratio of the base call) and average distance of mismatched bases to the end of the read, among many others (Section 2). Many of these features are readily available from aligned data in packages such as GATK and Samtools and it is generally accepted that applying filters on these quality metrics is necessary to remove false signals. Some software tools such as VarScan, Samtools and GATK aim to leverage these features in their SNV prediction routines; however, they are often guided by heuristics, whereby somewhat arbitrary decision boundaries are implemented.

We propose that training feature-based classifiers using robust classification methods from the machine learning literature will better optimize the contribution of each feature to the discrimination of true and false positive somatic mutation predictions. Fitting such classifiers to large sets of ground truth data should allow us to discriminate classes of false positives that may be predicted for different reasons, enabling a more thorough understanding of NGS machine, alignment and biology-related artefacts that are informed by data. We suggest that features that best identify somatic mutations will differ in importance in the normal data compared with the tumour data, and so integrated analysis of the tumour and normal data will yield better results than independent treatment of the two datasets. To our knowledge, this notion is currently not considered in any published somatic mutation detection method. Finally, flexible feature-based classifiers that can use any number of features can combine features from different software packages and therefore leverage newly discovered discriminative features to continually improve somatic mutation prediction accuracy as the bioinformatics literature and methodology matures.

In this article, we study the use of discriminative, feature-based classifiers and investigate computational features from aligned tumour and normal data that can best separate somatic SNVs from non-somatic SNVs. We implemented four standard machine learning algorithms: random forest, Bayesian additive regression tree, support vector machine and logistic regression, and compared their performance to each other and to standard methods for somatic mutation prediction. We trained the classifiers on a set of 106 features computed from tumour and normal data on a set of ~3400 ground truth positions from 48 primary breast cancer genomes sequenced with exome capture technology, while simultaneously estimating the importance of features. Classifiers were evaluated in a cross-validation scheme using robust quantitative accuracy measurements of sensitivity and specificity on labelled training data, and on independent held-out test data derived from four additional cases sequenced with a different technology. We show that principled, feature-based classifiers significantly improve somatic mutation prediction in both sensitivity and specificity over standard approaches such as Samtools and GATK. Finally, using discriminative features, we show how false positive (wild-type) positions can be segregated into several distinct types of systematic artefacts that contribute to false positive predictions.

2 METHODS

Supplementary Figure S1 shows the workflow of the feature-based classifier for somatic mutation prediction. We used supervised machine learning methods fit to validated, ground truth training data originally predicted using naive methods (see below for details). Using deep sequencing to validate predictions, we define positions as somatic mutations where the variant was found in the tumour but not the normal, germline variants where the variant was found in the tumour and the normal or wild-types (no variants found in either the tumour or the normal, i.e. false positive predictions). The germline and wild-type positions are classed as non-somatic positions so that binary classifiers can be used. Features are constructed for each SNV in the training data using the exome capture bamfiles from the tumour and normal alignments. As explained below, we use features available in Samtools, GATK and a set of features we have defined ourselves. These features along with their somatic/non-somatic labels are the inputs to train classifiers. Given test bamfiles, we construct features for each candidate site, and apply the trained classifier to predict the probability of somatic mutation for each site.

2.1 Feature construction

We formalize the somatic mutation prediction problem as a classification problem. Each candidate mutation site of the genome is represented by a feature vector x with 106 feature components {x₁,…, x₁₀₆}. The problem is to predict the label y of the feature represented site. y is defined as ‘1’ if the site is a somatic mutation, and ‘0’ otherwise. Below we first define each component of the feature vector in detail, and then compare different models to predict y given x.

Features x₁ to x₂₀ are constructed from the normal data and their definitions are given in Table 1. This table is based on the table in http://samtools.sourceforge.net/mpileup.shtml. Features x₂₁ to x₄₀ have the same definitions but are constructed from the tumour. Features x₄₁ to x₆₀ are constructed from the normal data and their definitions are given in Table 2. These features are constructed based on GATK. Features x₆₁ to x₈₀ have the same definitions but are constructed from the tumour. We show in Section 3.3 how simultaneous treatment of the tumour and normal data allow the classifiers to differentially weight corresponding features so as to emphasize tumour-specific and normal-specific features that best discriminate between real and false predictions.

Table 1.

The definitions of features x₁ to x₂₀

(1) Number of reads covering or bridging the site	(11) Sum of squares of reference mapping qualities
(2) Number of reference Q13 bases on the forward strand	(12) Sum of non-reference mapping qualities
(3) Number of reference Q13 bases on the reverse strand	(13) Sum of squares of non-reference mapping qualities
(4) Number of non-reference Q13 bases on the forward strand	(14) Sum of tail distances for reference bases
(5) Number of non-reference Q13 bases on the reverse strand	(15) Sum of squares of tail distance for reference bases
(6) Sum of reference base qualities	(16) Sum of tail distances for non-reference bases
(7) Sum of squares of reference base qualities	(17) Sum of squares of tail distance for non-reference bases
(8) Sum of non-reference base qualities	(18) P(D∣Gi=aa), phred−scaled, i.e. x is transformed to −10log(x)
(9) Sum of squares of non-reference base qualities	(19) maxGi≠aa(P(D∣Gi)), phred-scaled
(10) Sum of reference mapping qualities	(20) ∑Gi≠aa (P(D∣Gi)), phred-scaled

Q13 means base quality bigger or equal to Phred score 13; D represents the three dimensional vector (depth, number of reference bases and number of non-reference bases) at the current site; G_i∈{aa, ab, bb} means the genotype at site i, where a, b∈{A, C, T, G} and a is the reference allele and b is the non-reference allele. These features are constructed from Samtools.

Table 2.

The definitions of features x₄₁ to x₆₀

(41) QUAL: phred-scaled probability of the call given data	(51) QD: variant confidence/unfiltered depth
(42) Allele count for non-ref allele in genotypes	(52) SB: strand bias (the variation being seen on only the forward or only the reverse strand)
(43) AF: allele frequency for each non-ref allele	(53) SumGLbyD
(44) Total number of alleles in called genotypes	(54) Allelic depths for the ref-allele
(45) Total (unfiltered) depth over all samples	(55) Allelic depths for the non-ref allele
(46) Fraction of reads containing spanning deletions	(56) DP: read depth (only filtered reads used for calling)
(47) HRun: largest contiguous homopolymer run of variant allele in either direction	(57) GQ: genotype quality computed based on the genotype likelihood
(48) HaplotypeScore: estimate the probability that the reads at this locus are coming from no more than 2 local haplotypes	(58) P(D∣Gi=aa), phred-scaled
(49) MQ: root mean square mapping quality	(59) P(D∣Gi=ab), phred-scaled
(50) MQ0: total number of reads with mapping quality zero	(60) P(D∣Gi=bb), phred-scaled

These features are constructed from GATK.

To account for variance in depth across the data, features that scale with depth (e.g. feature x₂ to x₁₇) are first normalized by dividing by the depth. In addition to Samtools and GATK, we added several features that we noticed may contribute to systematic errors. For example, in Meacham et al. (2011a,b), the authors found that GGT sequences are often erroneously sequenced as GGG. To capture this artefact, we computed the difference between the sum of the base qualities of the current site and the next site, the sum of the square of the base qualities of the current site and the next site, for both normal and tumour. These features are defined as features x₈₁₋₈₄. In addition, the reference base, the alternative base of the normal as well the alternative base of the tumour are included as features x₈₅₋₉₅ (by dummy representation of categorical variables). In addition, to combine strand bias effects from the tumour and normal data, we define feature x₉₆ and feature x₉₇ to estimate the strand bias from the pooled normal and tumour data.

To boost weak signals such as rare somatic mutations that may be under-sampled or represent a mutation occurring in a small proportion of cells in the tumour, and to decrease the influence of germline polymorphism, another nine features are introduced. The definitions of these features are given in Table 3. Note in the table, F_i means the normalized version of the i-th feature (dividing by the depth feature). All features are standardized to have zero mean and unit variance prior to training and testing.

Table 3.

The definitions of x₉₈ to x₁₀₆

(98) Forward strand non-reference base ratio F24/F4	(103) Sum of squares of non-reference mapping quality ratio F33/F13
(99) Reverse strand non-reference base ratio F25/F5	(104) Sum of non-reference tail distance ratio F36/F16
(100) Sum of non-reference base quality ratio F28/F8	(105) Sum of squares of non-reference tail distance ratio F37/F17
(101) Sum of squares of non-reference base quality ratio F29/F9	(106) Non-reference allele depth ratio F75/F55
(102) Sum of non-reference mapping quality ratio F32/F12

These features are used to boost weak mutation signals in the tumour and decrease the influence of germline polymorphism. In this table, F_i means the normalized version of the i-th feature.

2.2 Models

After constructing the feature value vector x for each candidate somatic position, the problem is to find a discriminative function f(x), which optimally separates the true somatic positions from false somatic positions. In so doing, we wished to simultaneously learn the features that best discriminate the two classes. Numerous tools have been developed to solve this problem in the statistics and machine learning community. Here we compare four methods: random forests (Hastie et al., 2009), Bayesian additive regression tree (Chipman et al., 2010), support vector machines and logistic regression. These methods (described below) differ in their underlying methodology and generally represent broad classes of classifiers present in the machine learning literature. We set out to compare performance of the different approaches in the specific context of predicting somatic mutations from NGS data. (Note that additional material on all methods, including approaches for hyperparameter settings, is presented in the Supplementary Material.)

2.2.1 Random forests

Random forests (RF) are tree-based methods for classification and regression analysis. Given a training dataset, a classification tree g is grown by repeatedly splitting the feature vector into disjoint pieces {R_m}_m=1^M. The splitting rules are typically based on a single component of the whole feature vector and are of the form {x≤s} versus {x>s}, where s is a real number determined in training. After the classification tree is grown (a series of s are determined), given a test feature vector x, if it is in piece R_m, the probability of its label y can be estimated as

where k∈{0, 1} in our case, θ is all the parameters of the splitting rules, N_m is the number of training sites in piece R_m, x_j is a training site, y_j is its label and I(.) is the indicator function. RF makes a prediction based on an ensemble of B trees {g_b}_b=1^B, i.e. the mode of B trees

where g_b=k means that tree g_b's prediction is k. Specifically, B bootstrap samples (random sampling with replacement) are drawn from the training data, and a tree is grown on each bootstrap sample. To reduce the dependence of the B trees, p features out of all the features (106 for our case) are chosen at each node when a tree is grown.

2.2.2 Bayesian additive regression tree

The Bayesian additive regression tree (BART) model is based on regression trees. The regression tree is grown by repeatedly splitting the feature vector into disjoint pieces {R_m}_m=1^M. The problem is to predict a continuous output z given an input feature vector x. Given a test feature vector x, if it is in piece R_m, the distribution of z can be modelled by

where 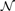(z∣μ_m, σ²) is a Gaussian distribution with mean μ_m and standard deviation σ. μ_m is the mean of dependent variables of the training sites in region R_m,

As for RFs, BART models the output z using the sum of B trees, so

where g_b is the output of the b-th tree. For binary classification, e.g. to classify a site i as somatic (y_i=1) or non-somatic (y_i=0), the class probability is defined as:

where Φ(.) is the standard Gaussian cumulative distribution function, as opposed to the majority vote used by RFs.

The BART model differentiates from RF because BART is a fully Bayesian model. All the parameters are given priors and use Markov-Chain Monte-Carlo sampling for inference.

2.2.3 Support vector machine

The support vector machine (SVM) classifier finds a linear discriminative function of the the form

where Φ is a basis function which maps x from 106 dimension to a higher dimension. Note f(x) is a linear function of Φ(x) but may be a non-linear function of x.

The SVM assumes that the optimal discriminative function is the one which leaves the largest possible margin on both sides of the feature space. For SVM, the importance of each feature is estimated by backward elimination.

2.2.4 L1 regularized logistic regression

The logistic regression (Logit) method models the probability of y given the feature vector x, representing candidate mutation site, as

where w=(w₁,…, w_D) is the weight for each feature, D=106 is the dimensionality of each feature vector and the function 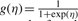is the logistic link function. The parameter vector w and w₀ can be found by maximum likelihood estimation.

Here we put a prior p(w) on the weight of the logit model, and do maximum a posterior estimation (MAP) of the parameter w. We focus on the factorized Laplace prior

Given N i.i.d. validated mutation sites (x_i, y_i)_i=1^N, we can estimate w by minimizing the following negative log posterior

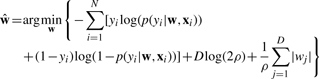The Laplace prior introduces a penalty term 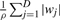to the negative log-likelihood function. Since the L₁ norm is defined as ‖w‖₁≔∑_j=1^D|w_j|, the above logistic regression model with Laplace prior on the weights is called L₁ regularized (penalized) logistic regression model. The L₁ regularized logistic regression model has the property of shrinking the weights of irrelevant features to zero.

2.3 Datasets

We used two independent datasets to train and test the performance of the models for somatic mutation prediction. The first dataset (exome capture data) consists of 48 triple negative breast cancer Agilent SureSelect v1 exome capture tumour/normal pairs sequenced using the Illumina genome analyzer as 76 bp pair-end reads. These data were generated as part of a large-scale sequencing project (Shah et al., manuscript in preparation) whereby 3369 variants were predicted using only allelic counts and liberal thresholds. Follow-up re-sequencing experiments achieving ~6000× coverage for the targeted positions revalidated 1015 somatic mutations, 471 germline and 1883 wild-type (false positive) positions. The exome capture data are subdivided into two groups consisting of non-overlapping positions:

• SeqVal1 (somatic:775 germline:101 wild−type: 487, total: 1363)

• SeqVal2 (somatic:269, germline:428, wild−type: 1410, total: 2107)

SeqVal1 positions were obtained by aligning the reads to the whole human genome, while SeqVal2 positions were obtained by aligning the reads to a reference limited to the targeted human exons. SeqVal2 was considerably noisier due to misalignments. (Note that 101 positions overlapped in the two datasets therefore we removed redundant sites from the combined dataset.)

The second dataset (whole genome shotgun data) is from four whole human genome tumour/normal pairs sequenced using the Life Technologies SOLiD system as 25–50 bp pair-end reads. These data were aligned to the human genome by using the BioScope aligner. Ground truth for these samples was obtained from orthogonal exome capture experiments followed by targeted resequencing on the same DNA samples resulting in 113 somatic mutations, 57 germline mutations and 337 wild-types. We deliberately held these positions out of the training data so as to have a completely independent test set for evaluation.

2.4 Experimental design

For each of the four classifiers, we used the exome capture data for classifier training, and tested on the whole genome shotgun data. For training, we used the following procedure. Since each of the models accepts hyper-parameters, we applied a 10-fold cross-validation analysis on a range of hyper-parameters (Supplementary Materials) to approximate the optimal settings. We applied the resulting settings on all of the exome capture data in the final training step. We obtained a set of discriminative features using ensemble feature selection (Abeel et al., 2010) after training using 40 bootstrap samples and finally computed a feature set aggregated from these 40 samples for each classifier. To test the robustness of each classifier to the input set of features, we trained each classifier using each of the other classifiers' feature sets, producing 4×4=16 results, which were then assessed using sensitivity, specificity and accuracy metrics.

To compare our classification methods to standard approaches for SNV detection, we used two popular methods: Samtools v1.16 and GATK v1.0.5543M. Samtools mpileup and bcftools were run independently on the tumour and normal bamfiles to produce SNV calls at the 3369 positions in the exome capture data. Those SNVs present in the tumour list, but not the normal were considered somatic mutations, otherwise they were considered non-somatic. For GATK, we used the UnifiedGenotyper tool in a similar fashion to classify the positions in the exome capture data. We also compared the results after removing small indel-induced artefacts using GATKs local realignment and base quality recalibration tool. We then compared all methods using accuracy and receiver operator characteristic curves (ROCs).

3 RESULTS

3.1 Classifiers outperform standard approaches

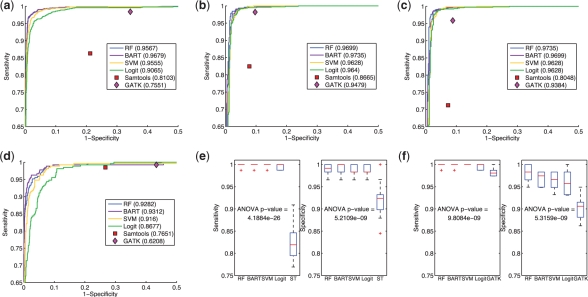
To visually investigate the discriminative ability of the features, we used principal component analysis (PCA) to project the 106 dimensional space to a 3D space. Supplementary Figure S2 shows that somatic mutations were reasonably separated from non-somatic mutations, suggesting that accurate classifiers could potentially be learned from the set of features we chose to examine. Comparison of accuracy on the combined dataset SeqVal1+2 of the different classifiers, Samtools bcftools and GATK's UnifiedGenotyper (Fig. 1a, Supplementary Table S1) showed that BART was most accurate (0.9679) followed by RF (0.9567), SVM (0.9555) and Logit (0.9065). All classifiers were better than Samtools (0.8103) and GATK (0.7551). We next evaluated the contribution of specificity to the accuracy results using a high fixed sensitivity of 0.99 to establish a probability threshold for each of the classifiers. Specificity at this threshold was 0.9584, 0.9422, 0.9405 and 0.8704 for BART, RF, SVM and Logit, respectively, suggesting that Logit had less discriminative power than the other classifiers. The comparative sensitivity and specificity breakdown for Samtools was 0.8631 and 0.7876, and for GATK it was 0.9842 and 0.6563. Thus, Samtools had more balanced misclassifications, whereas GATK was very sensitive but with a lower specificity than the other methods.

Fig. 1.

(a) Accuracy results from cross-validation experiments on all the exome capture data (SeqVal1+2). All classifiers showed better results than Samtools and GATK's prediction results in terms of ROC comparison. The numbers in parentheses are the prediction accuracy by fixing the sensitivity at 0.99, except for Samtools and GATK's prediction results because their outputs are deterministic. (b) Accuracy results from cross-validation experiments on the exome capture data of SeqVal1. (c) Accuracy results from cross-validation experiments on the exome capture data of SeqVal1 after GATK's local realignment around indels and base quality recalibration. (d) Accuracy results from cross-validation experiments on the exome capture data of SeqVal2. (e) Comparison of classifiers and Samtools's (ST) performance at the specificity and sensitivity level given by Samtools. (f) Comparison of classifiers and GATK's performance at the specificity and sensitivity level given by GATK.

Similar patterns were observed for independent analysis of SeqVal1 (Fig. 1b, Supplementary Table S2), although results for GATK (sensitivity: 0.9819, specificity: 0.9031) and Samtools (sensitivity: 0.8245, specificity: 0.9218) were better than for the SeqVal1+2 results. We also tested whether local realignment reads around insertions and deletions and base quality re-calibration (post-alignment processing tools in the GATK package) improved results. The classifier results were nearly identical to those shown in Figure 1b for SeqVal1 (Fig. 1c). However, while results for Samtools and GATK both showed an improvement in specificity, there was a substantial reduction in sensitivity (Fig. 1c, Supplementary Tables S2 and S3). We also assessed results on SeqVal2 independently (Fig. 1d, Supplementary Table S4) and found that accuracy was highest for BART (0.9312) followed by RF (0.9282), SVM (0.9160), Logit (0.8677), Samtools (0.7651) and GATK (0.6208). All methods were worse on this dataset than on SeqVal1, although the difference for the classifiers was more moderate than the other methods. The markedly worse performance of Samtools and GATK for this dataset was mainly due to considerably decreased specificity; this dataset was generated from constrained alignments to exons that likely induce many false alignments, thus the classifier methods may be more robust to artefacts introduced by misalignments.

Finally, we assessed the statistical significance of the observed differences between methods using the best performing results for Samtools and GATK (SeqVal1). For each cross-validation fold, we fixed sensitivity according to the Samtools results and computed the specificity of the other methods. We then compared the specificity distributions of the methods over all folds using a one-way ANOVA test. Similarly, we evaluated sensitivity distributions by fixing specificity. A similar procedure was then applied to the GATK results. The classifiers were not statistically different from each other in any comparison. However, all classifiers were statistically significantly higher in specificity and sensitivity (ANOVA, P<0.00001) than Samtools and GATK (Supplementary Table S5).

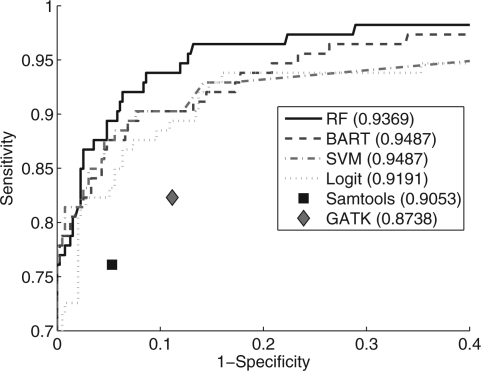
To test the generalization performance of the trained classifiers, we applied them to the test data: four cases with whole genome shotgun sequencing from tumour and normal DNA on the SOLiD platform. Despite being trained on exome data, the classifiers performed extremely well and recapitulated the results seen in the cross-validation experiments (Fig. 2). The accuracy for the classifiers was 0.9487, 0.9487, 0.9369 and 0.9191 for BART, SVM, RF and Logit, respectively. Samtools accuracy was 0.9053 followed by GATK at 0.8738. These results indicate that, on a limited dataset, the trained parameters should generalize well to other platforms and are likely robust to overfitting. Moreover, the trends of higher accuracy of the classifiers compared with GATK and Samtools carried over to the independent test data. Importantly, at specificity levels obtained by GATK (0.8883, Supplementary Table S6), the classifiers obtained sensitivity of 0.9381, 0.9027, 0.9027 and 0.8938 for RF, BART, SVM and Logit, respectively (Supplementary Table S7). At sensitivity levels obtained by GATK (0.8230, Supplementary Table S6), the specificity of the classifiers was 0.9772, 0.9772, 0.9747, and 0.9721 for RF, SVM, BART and Logit, respectively (Supplementary Table S7), whereas GATK specificity was 0.8883. At sensitivity levels obtained by Samtools, the specificity of classifiers reached 1.0, 1.0,1.0 and 0.9797 for RF, BART, SVM and Logit, respectively (Supplementary Table S7), whereas Samtools specificity was 0.9467. Similarly, at specificity levels given by Samtools, the sensitivity of classifiers was 0.8938, 0.8761, 0.8761 and 0.8319 for RF, BART, SVM and Logit, whereas Samtools sensitivity was 0.7611. Thus, on the orthogonal test data, all classifiers outperformed GATK and Samtools in both sensitivity and specificity with BART exhibiting the best overall performance.

Fig. 2.

ROC curves derived from the held-out whole genome shotgun independent test data from four cases show different classifiers' prediction results as well as Samtools and GATK's prediction results. The numbers in the parentheses are the prediction accuracy by using the same threshold as for the exome capture data (except for Samtools and GATK's prediction results).

We next investigated whether the use of classifiers or the expanded set of features contributed to increased performance of our methods. Using the SeqVal1 dataset, we restricted the analysis to only Samtools-derived features (x₁₋₄₀) and compared the results of classifiers with those of the Samtools caller. All classifiers performed statistically better than the Samtools caller (Supplementary Fig. S3a and S3b). For the second experiment, we restricted the analysis to only the GATK features (x₄₁₋₈₀). As for Samtools, the classifiers showed statistically significantly better results than those of the GATK caller (Supplementary Fig. S3c and S3d). These results suggest that the classifiers on the same set of features for both Samtools and GATK better approximated the ‘optimal’ decision boundary without the use of heuristic thresholds employed by the naive methods and demonstrate the clear advantages of the machine learning approaches we used.

Finally, we studied the effect of the additional 26 features we introduced (Table 3, x₈₁₋₁₀₆) to the Samtools and GATK features in order to boost weak mutation signals in the tumour and decrease the influence of germline polymorphisms. We compared the performance of RF and BART on different feature sets: Samtools alone (x₁₋₄₀), GATK alone (x₄₁₋₈₀) our 26 features alone (x₈₁₋₁₀₆) and all features combined (x₁₋₁₀₆). As shown in Supplementary Figure S4, by using all the features, RF and BART showed the best performance in terms of accuracy. However, the improvement attributed to the 26 novel features was incremental and may only apply in rare circumstances. We therefore suggest that while the use of the machine learning classifiers accounts for the majority of improvement over naive methods, further improvement is achievable with the introduction of novel features thus illustrating the power of the flexible framework we used in this study (see also Section 3.3).

3.2 Robustness of classifiers to different feature sets

We used ensemble feature selection to output a set of the most salient, discriminative features for each classifier, leading to four feature sets overall. We then fit each classifier to the exome capture data using only the four selected feature sets output from the ensemble feature selection method. We noted (Table 4) that overall, BART and RF were most robust to the initial set of features and performed similarly for each of the four sets, showing stable performance in the presence of variable initial feature sets. Interestingly, all four methods performed equally well on the features chosen by ensemble feature selection applied to BART (Table 4) with a mean accuracy of 0.9453 compared to 0.9359, 0.9339 and 0.9157 for SVM, Logit and RF chosen features, respectively. The detailed test results of each classifier on different feature sets are given in Supplementary Table S8–S11.

Table 4.

The classification accuracy of classifiers by using different feature sets

Model/Feature	RF_F (18)	BART_F (23)	SVM_F (17)	Logit_F (17)
RF	0.9369	0.9487	0.9448	0.9329
BART	0.9369	0.9428	0.9369	0.9310
SVM	0.9034	0.9408	0.9369	0.9408
Logit	0.8856	0.9487	0.9250	0.9310
Mean	0.9157	0.9453	0.9359	0.9339

Here RF_F means the feature selected by RF classifier. BART_F, SVM_F and Logit_F are similarly defined. The numbers in parentheses are the number of feature selected.

In summary, all classifiers performed better than the naive methods for somatic SNV prediction, with RF and BART showing the best performance. RF classifier is slightly more sensitive (Fig. 2), while BART has slightly higher specificity (Fig. 1d). The performance of SVM and Logit is relatively poor, especially in the presence of outliers as can be seen from Figure 1d. Importantly, both RF and BART are less sensitive to different feature sets compared to SVM and Logit (Table 4). Overall, the data support using RF and BART over SVM and Logit and suggest that RF may achieve better sensitivity while BART will achieve higher specificity, though both methods are extremely comparable.

3.3 Discriminative features are different for tumour and normal data

The description of the set of features selected by BART is given in Supplementary Table S12. The features fell into five broad categories: (i) allelic count distribution likelihoods: provided by both Samtools and GATK; (ii) base qualities such as the sum of reference base qualities, sum of non-reference base qualities, sum of squares of non-reference base quality ratio; (iii) strand bias such as sum of the pooled estimation of strand bias on both strands; (iv) mapping qualities such as the mean square mapping quality; and (v) tail distance such as sum of squares of tail distance for non-reference bases and sum of squares of non-reference tail distance (minimum distance of variant base to the ends of the read) ratio. Notably, the features are often different in the tumour and normal. For example, the reference base qualities (x₆) are selected in the normal, but for tumour both reference (x₂₆) and non-reference base qualities (x₂₈) are selected. Other tumour-specific features included sum of tail distance of the non-reference bases (x₃₇), allele frequency for each non-reference allele (x₆₃) and variant confidence normalized by depth (x₇₁). Therefore, BART assigned unequal weights to the features in the normal and tumour, suggesting that the improved accuracy is due to treating the tumour and normal data differentially to optimize the contribution of the discriminant features. We note in Supplementary Table S12 that BART selected several of the new features we designed (x₈₃, x₉₆, x₉₇, x₉₉, x₁₀₁, x₁₀₂, x₁₀₅). These were not in Samtools or GATK, and some were a combined calculation from the tumour and normal data. This illustrates the advantage of the classifiers' ability to add arbitrary features and the importance of simultaneous (not independent) treatment of the tumour and normal data.

3.4 Sources of errors and subclassification of wild-types

We subgrouped the wild-type positions (false positives from the original predictions) by their feature vectors in order to characterize false positives due to distinct sources of error. Using the wild-type positions from Seqval1, we identified the features which were not unimodal with the dip statistic (Hartigan, 1985) and selected 28 features with P <0.1. We then used PCA to project the features to the first seven principal components, and modelled the wild-types in the 7D space (the first seven principal components account for about 95% of the variance) using a mixture of Gaussian distributions clustering algorithm fit with EM. We used the Bayesian information criteria (BIC) score (Supplementary Material) to select six clusters (Supplementary Fig. S5a and S5e). The number of wild-types in Group 1 to Group 6 was 37, 189, 43, 181, 6 and 31, respectively. We attributed the six events in Group 5 to outliers and excluded this group from further analysis. We then identified discriminant features of the different groups, using an analysis of variance (ANOVA) test followed by a multiple comparison test on each feature (Supplementary Table S13).

Broadly the groups had the following characteristics. Group 1 (black) featured high values for x₁₀₂ and x₁₀₃ indicating disproportionate mapping qualities in the tumour compared with the normal. Thus, the tumour reads harbouring variants mapped with higher qualities than the normal reads harbouring variants at the same genomic location. In addition, Group 1 exhibited strand bias as shown by high values of (x₉₆ and x₉₇). The events in this group had low values for x₅₇ and x₇₇ which indicated low genotype qualities (confidence in the genotype call). Taken together, these data suggest that the combination of poor mapping quality of the normal reads and the strand bias may be affecting the callers' ability to accurately call these variants.

Group 2 (red) is characterized by high values of x₉₆ suggesting strand bias (Supplementary Fig. S6). We examined the surrounding sequence content around these variants and found the majority of the variants in this group had a common tri-nucleotide sequence GGT, changing to GGG (Supplementary Fig. S7), a pattern which has been discovered in whole genome methyl-Seq experiments Meacham et al. (2011a,b). Thus, we expect the false positive events in this group to be induced by systematic artefacts owing to sequencing errors at specific tri-nucleotide sequences as well as PCR artefacts inducing strand bias.

The discriminative features for Group 3 (green) events were characterized by mapping quality-related features (x₁₀, x₁₁, x₅₀, x₇₀, x₄₉, x₆₉). Thus, these wild-types may be the result of misaligned reads, or simply repetitive regions that are difficult to unambiguously sequence. To investigate this, we computed the UCSC mapability (http://genome.ucsc.edu/cgi-bin/hgTrackUi?db=hg18&g=wgEncodeMapability) of each site as shown in Supplementary Figure S8. The mappability of a site depicts the uniqueness of the reference genome in a window size of 35. Overall, Group 3 wild-types have considerably lower mappability scores than the other groups and therefore can be best explained by characteristics of the genome at these positions that make variant calling error prone.

For the wild-types in Group 4 (blue), the pooled estimated strand biases are zero (x₉₆ and x₉₇). This is because these two features were computed after Samtools internal base quality filter threshold of 13, and the variant alleles had small base qualities so they did not pass this filter. The Samtools caller utilizes this base quality filter and therefore did not call these positions as variants (large x₃₉ and x₄₀). Group 4 wild-types were also characterized by the GGT to GGG systematic sequencing artefact (Supplementary Fig. S9) we observed for Group 2 and therefore is fundamentally similar to Group 2, but may be easier to detect owing to poor base qualities at the site of the sequencing error.

Interestingly, Group 6 (magenta) exhibited very similar patterns to the true somatic mutations (yellow) and thus made them challenging to interpret. Upon inspection, many of these positions had weak signals for a variant in the normal data, but perhaps not enough to induce a variant call. The tumour data, conversely [as shown by (x₆₂, x₆₃, x₇₁, x₇₃)] exhibited strong signals for a variant. Thus, the weak signals in the normal data were likely being prematurely thresholded out by the naive methods. Indeed, the Samtools caller called 13 of the 31 Group 6 events as somatic while GATK called 29 of the 31 events as somatic. The characteristics of the positions in Group 6 underscore the strength of simultaneously considering the tumour and normal features that we suspect enhances the ability of the classifier to choose better decision boundaries.

4 DISCUSSION

We studied the use of feature-based classifiers for the purpose of somatic mutation detection in tumour/normal pair NGS data. Using an extensive set of ground truth positions, we trained four different machine learning classifiers using features extracted from existing software tools and novel features we computed ourselves. All four classifiers statistically significantly outperformed popular software packages used in a naive way to detect somatic mutations, treating the tumour and normal data independently. Results were consistent between a cross-validation analysis of the training data and a completely independent test dataset derived from an orthogonal sequencing platform. Our results encapsulate three key results: (i) machine learning classifiers can be trained using principled machine learning techniques to significantly improve somatic mutation detection; (ii) feature selection analysis revealed that our classification method selects different features in the tumour and normal datasets to optimize classification ability, underscoring that simultaneous rather than independent analysis of the paired data is important; and (iii) we identified five distinct groups of false positive results. This last result indicates that feature-based analysis of ‘negative’ or wild-type positions can be helpful to guide future developments in software pipelines that operate upstream of variant calling.

Limitations and future work: the results presented herein rely on third-party software tools for which there is some feature overlap. Future implementations of our framework will make use of the bamtools API (Barnett et al., 2011) to compute features and remove any redundancy and dependence on third-party software packages. In addition, the majority of our conclusions in this study were based on application to exome capture data. Although test data were derived from a limited set of whole genome shotgun data, and results suggested reasonable generalization, it will be of considerable interest to train our classifiers on a sufficiently large training set derived from whole genome shotgun studies as this is likely to be the standard approach for cancer genome interrogation in the coming years. Finally, we focused our work to support somatic SNV mutation detection from tumour/normal paired data; we expect that the framework could easily be adapted to somatic indel detection and to single sample analyses of NGS genomes for studying human or other organism variation, given sufficient training data.

5 CONCLUSION

Our results underscore the advantages of developing cancer-specific tools for NGS data that can capitalize on the unique experimental design of tumour/normal paired data. Our conclusions support the notion that principled feature-based machine learning classification frameworks will be well placed to leverage evolving trends in the cancer NGS field, thereby reducing the burden of downstream validation efforts with more accurate predictions.