Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Jan 17.
Published in final edited form as: J Biomech Eng. 2008 Aug;130(4):041003. doi: 10.1115/1.2913332

Gender Differences in Capitate Kinematics are Eliminated After Accounting for Variation in Carpal Size

Michael J Rainbow 1, Joseph J Crisco 2,✉, Douglas C Moore 3, Scott W Wolfe 4
PMCID: PMC3259565  NIHMSID: NIHMS313029  PMID: 18601445

Abstract

Previous studies have found gender differences in carpal kinematics, and there are discrepancies in the literature on the location of the flexion/extension and radio-ulnar deviation rotation axes of the wrist. It has been postulated that these differences are due to carpal bone size differences rather than gender and that they may be resolved by normalizing the kinematics by carpal size. The purpose of this study was to determine if differences in radio-capitate kinematics are a function of size or gender. We also sought to determine if a best-fit pivot point (PvP) describes the radio-capitate joint as a ball-and-socket articulation. By using an in vivo markerless bone registration technique applied to computed tomography scans of 26 male and 28 female wrists, we applied scaling derived from capitate length to radio-capitate kinematics, characterized by a best-fit PvP. We determined if radio-capitate kinematics behave as a ball-and-socket articulation by examining the error in the best-fit PvP. Scaling PvP location completely removed gender differences (P = 0.3). This verifies that differences in radio-capitate kinematics are due to size and not gender. The radio-capitate joint did not behave as a perfect ball and socket because helical axes representing anatomical motions such as flexion-extension, radio-ulnar deviation, dart throwers, and antidart throwers, were located at distances up to 4.5 mm from the PvP. Although the best-fit PvP did not yield a single center of rotation, it was still consistently found within the proximal pole of the capitate, and rms errors of the best-fit PvP calculation were on the order of 2 mm. Therefore, the ball-and-socket model of the wrist joint center using the best-fit PvP is appropriate when considering gross motion of the hand with respect to the forearm such as in optical motion capture models. However, the ball-and-socket model of the wrist is an insufficient description of the complex motion of the capitate with respect to the radius. These findings may aid in the design of wrist external fixation and orthotics.

Keywords: carpal kinematics, pivot point, in vivo, capitate

Introduction

Due to the capitate’s rigid attachment to the third metacarpal and central position in the carpus, it has been designated the keystone of the wrist and an indicator of overall wrist position [1]. Anatomically, the proximal pole of the capitate is nearly hemispherical, and it articulates in a hemispherically shaped fossa created by the scaphoid and lunate. The proximal convex surfaces of the scaphoid and lunate, in turn, articulate with the scaphoid and lunate fossa of the distal radius. Based on this anatomical arrangement, it seems reasonable to assume that the motion of the capitate with respect to the radius (radio-capitate kinematics) approximately behaves as a ball and socket. If it were an ideal ball-and-socket joint, there would exist a single fixed pivot point (PvP) through which all helical axes of motion (HAMs) intersect.

Previous studies of radio-capitate kinematics have shown that all HAMS nearly intersect one another within a tolerance of a few millimeters [2,3]. Although most studies have shown that the 2D axes of rotation or 3D PvP resides in the proximal pole of the capitate (e.g., Refs. [4–9]), there are discrepancies in the literature regarding the distance of flexion/extension axes from radio-ulnar deviation axes ranging between 2 mm and 7.5 mm [2,10]. Previous studies have also found differences in the location of HAMs between men and women [11]. From these studies, it can be shown that the location of the radio-capitate HAM is closer to the capitate centroid in woman than in men.

It has been proposed, but not proven, that gender differences in HAM location are due to carpal size, not function. This is not unreasonable given that simple isometric scaling eliminates gender differences in carpal size and bone volume differences [11]. If carpal bone size is the largest factor contributing to male-female discrepancies in HAM location, then normalizing kinematics by bone size should eliminate these differences [11].

The differences in the HAM location with the direction of wrist motion is more difficult to reconcile. The variability in the distance of flexion/extension and radio-ulnar deviation HAMs across previous studies may be due to the fact that the previous calculations have been hampered by relatively small sample sizes and imprecise analytical methods. Also, to the best of our knowledge, no previous study has accounted for intersubject variability in HAM or PvP location by normalizing kinematics by carpal bone size.

The purpose of this study was to examine the separation of HAMs as a function of wrist position by using a large database of in vivo wrist kinematics, derived from markerless bone registration (MBR) of sequential computed tomography (CT) scans. In this dataset, we include the traditional anatomical motion paths of flexion/extension and radial/ulnar deviation, as well as motion paths that are considered to be important in activities of daily living, such as the dart thrower’s path [12]. We also examine whether normalizing by capitate size eliminates differences in radio-capitate PvP location (with respect to the capitate centroid) across subjects. Furthermore, we test the effect of kinematic scaling on gender differences.

We hypothesized that gender-related differences in best-fit PvP location would be eliminated when scaled by capitate size. To examine HAM separation as a function of direction of motion, we used the null hypothesis that a single, fixed PvP exists through which all anatomically and functionally defined radio-capitate HAMs pass.

Methods

A digital anatomic database containing CT volume images of both healthy wrists of 13 male (25.6 years old, range 22–34) and 14 female (23.6 years old, range 21–18) subjects in a total of 233 wrist positions, distributed throughout a complete range of wrist motion, was established after IRB approval and informed consent. For each subject, a high resolution neutral scan of both left and right wrists was segmented by using analyze™ (Mayo Clinic Foundation, Rochester, MN) image processing software. The segmentation procedure yielded separate point clouds representing the outer cortical surface of each carpal bone. Closed surfaces for each carpal bone and distal radius were created by tessellating the point clouds using geomagic software (Raindrop Geomagic, Research Triangle Park, NC). To facilitate direct comparison of the kinematic data from the left and right wrists, all left wrists were mathematically converted to right wrists by inverting each individual CT slice at the image processing stage [13].

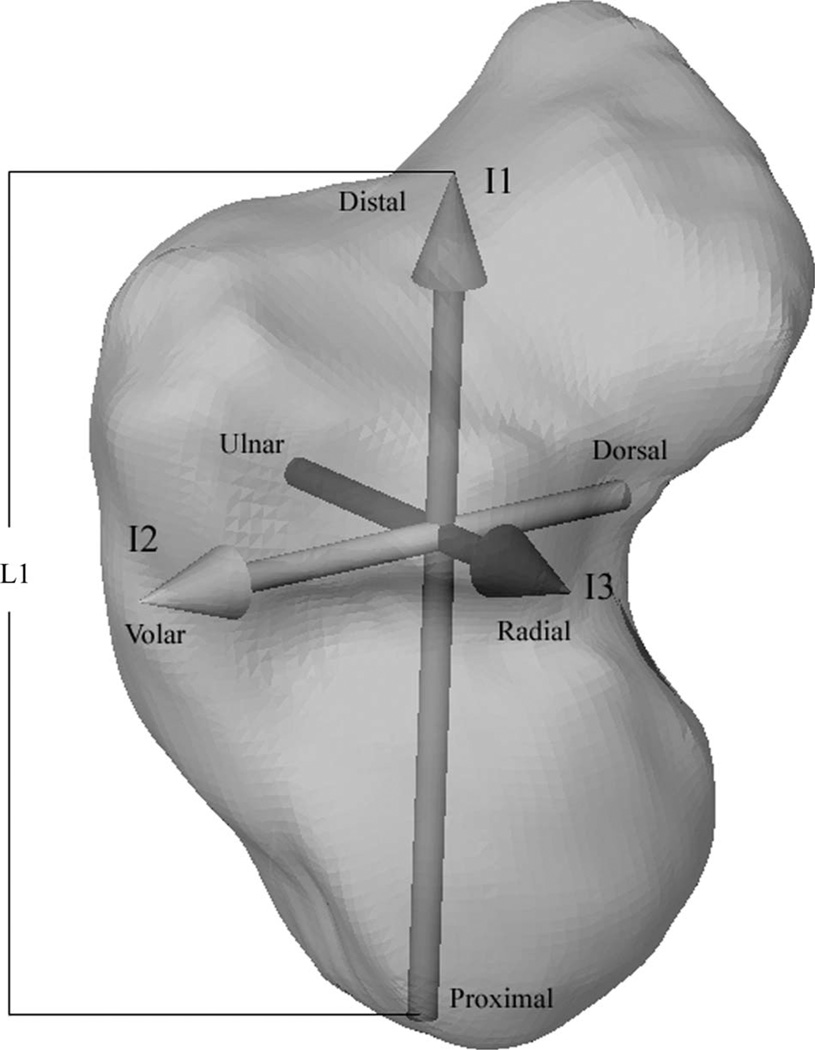
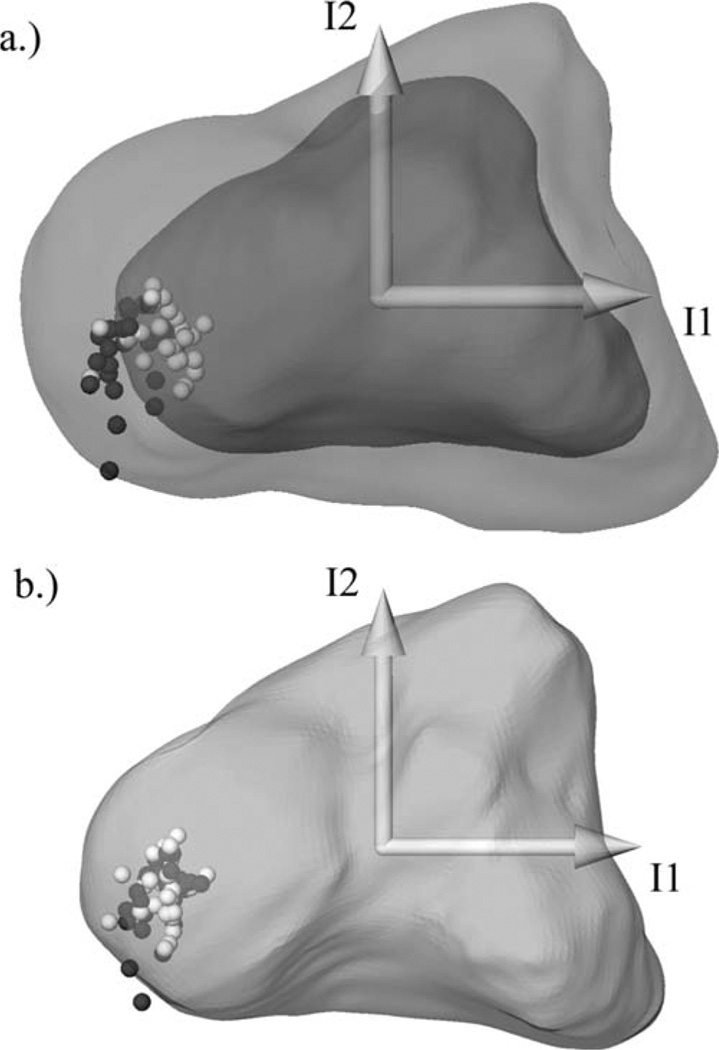
Kinematic transformations from the neutral wrist position to each subsequent position were calculated using a MBR algorithm [14] based on tissue classified distance fields [15]. For each wrist, the MBR algorithm registered the neutral position point clouds to all other CT volumes, creating six-degree-of-freedom global transformations from the neutral scan to each subsequent position. Radio-capitate transformations were generated by registering both the radius and the capitate in each position to the radius of the neutral scan, and then by computing the relative motion of the capitate with respect to the radius. Capitate volumes, centroids, and principal inertial axes were computed using previously established methods [16,17]. A capitate-based coordinate system was established using the capitate’s inertial properties, with the origin at the capitate’s centroid. The orientations of the inertial axes (I1, I2, and I3) that defined the coordinate system were proximal-distal (I1), dorsal-volar (I2), and ulnar-radial (I3) (Fig. 1). The capitate’s shape and orientation are inherent such that its inertial axes are found to be in general alignment with the standard anatomical directions.

Fig. 1.

Fig. 1

Open in a new tab

The capitate coordinate system based on inertia: I1, I2, and I3 = first, second, and third principal inertial axes. L1 is the length of the capitate from the proximal surface to the distal surface along I1. L2 and L3 are similarly defined but corresponding to I2 and I3, respectively.

The best-fit radio-capitate PvP was generated using a least square spherical joint technique. A detailed derivation of the algorithm can be found in the Appendix of Piazza et al. [18]. Briefly, the best-fit PvP was determined for each wrist by using the radio-capitate kinematics to compute the location of two points, one fixed in the capitate coordinate system, the other fixed in the radial coordinate system, whose distance was minimized across the motions of the capitate [18]. If the articulation behaved like a perfect ball and socket and there was no measurement error, these two points would be coincident. Because we employ a radius-fixed coordinate system in our analysis, we report the best-fit PvP of the radius-fixed coordinate system. Each subject’s kinematics (characterized by the PvP) was then reported with respect to the capitate-based coordinate system. The mean separation of the two best-fit PvPs throughout the range of motion was also calculated as a measure of the validity of the functional joint algorithm applied to radio-capitate kinematics. A second set of PvPs was computed for each wrist by isometrically scaling the original PvPs to the average subject by multiplying the I1, I2, and I3 components of the PvP by the scaling factor described below.

To facilitate comparison of the HAM locations and PvPs across subjects, radio-capitate kinematics were scaled to the values of an average wrist. Scaling factors for capitate size were based on length measurements. For each capitate, the distance was calculated along I1, from the proximal to distal surfaces and defined as L1. Likewise, L2, and L3 were found by computing the volar to dorsal and radial to ulnar lengths along I2 and I3.

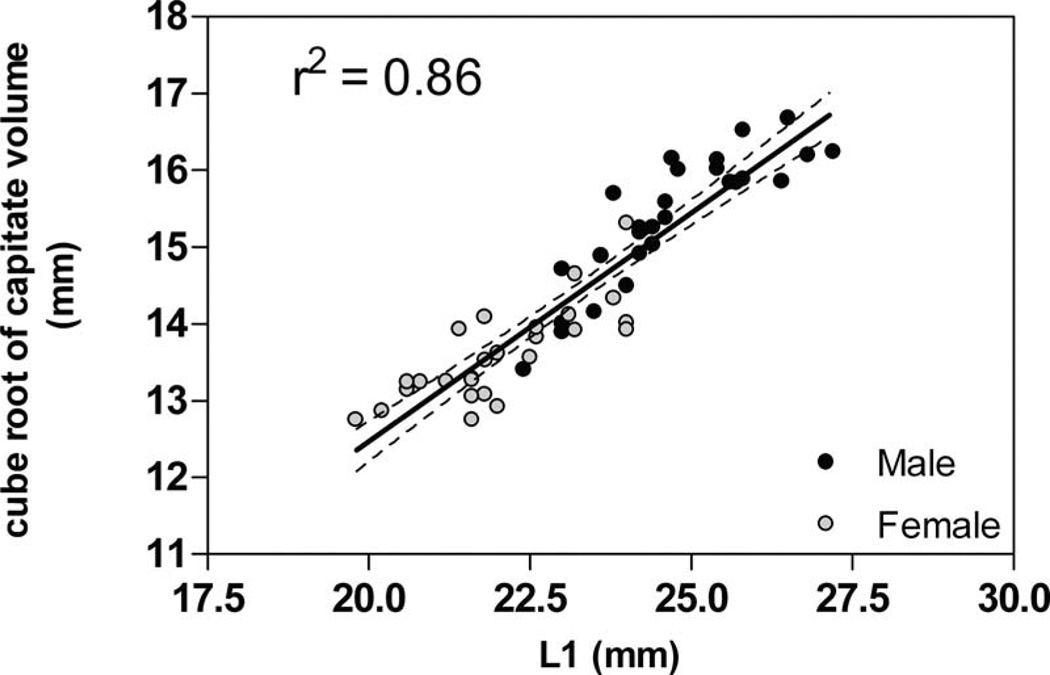
L1 was chosen as the isometric scaling parameter and the measure of overall capitate size because it was found to correspond best to capitate volume (Fig. 2). To determine this, each inertial length was compared to the cube root of capitate volume. Linear regression analysis of this comparison yielded r-squared values for L1, L2, and L3 of 0.86, 0.59, and 0.19, respectively. The average capitate volume and L1 length were calculated across all wrists (n = 54). A subject whose L1 value was closest to the group average (n = 54), in this case less than 2% difference, was chosen as the average subject. The scaling factor for each subject was then determined by computing the ratio of the average subject’s L1 values (L1avg) to that of each subject.

Fig. 2.

Fig. 2

Open in a new tab

There is a positive linear relationship between capitate long axis length and volume. Note that female capitates are smaller than males in both L1 and volume.

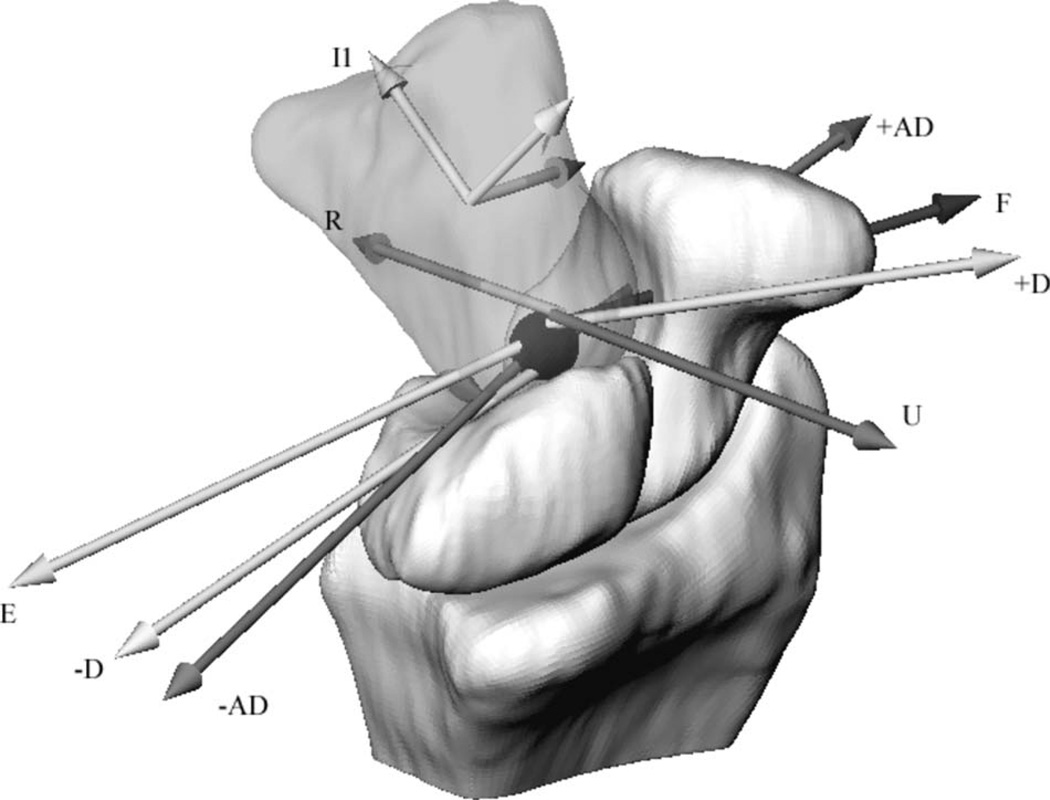
The single, fixed PvP hypothesis was tested by determining if each HAM intersected the PvP within a tolerance of 0.5 mm. The distance (d) was calculated, for each subject, from the PvP to the closest point on each HAM. HAMs from all subjects were grouped into motion bins of flexion (F), extension (E), ulnar deviation (U), radial deviation (R), positive dart throwers (ulnar flexion, +D), negative dart throwers (radial extension −D), positive antidart throwers (radial flexion, +AD), and negative antidart throwers (ulnar extension, −AD) [13]. The HAMs were placed into a specific motion bin if they possessed less than 10 deg of any other motion. To find the representative HAM associated with each motion, HAM locations were scaled, and a quaternion average was performed on all of the HAMs of each bin [19]. The representative HAMs were useful in visualizing the relationship between the capitate and the PvP.

To examine the dependence of PvP location (PvP0) on capitate size (L1), linear regression was performed on the I1, I2, and I3 components of PvP0 (PvPI1,I2, and I3) versus L1. This was done for the scaled and unscaled PvPs. Our hypothesis that gender differences are due to carpal size was tested by comparing male and female PvP0 values for both the unscaled and scaled cases. For each case, a Student’s t-test was performed to determine the significance of the mean differences between male and female PvP0. To test our hypothesis that radio-capitate kinematics behave as a ball and socket, HAMs were postulated to pass through the PvP if d was less than or equal to 0.5 mm. A one-population t-test with a hypothetical mean of 0.5 mm was performed on each motion bin.

Results

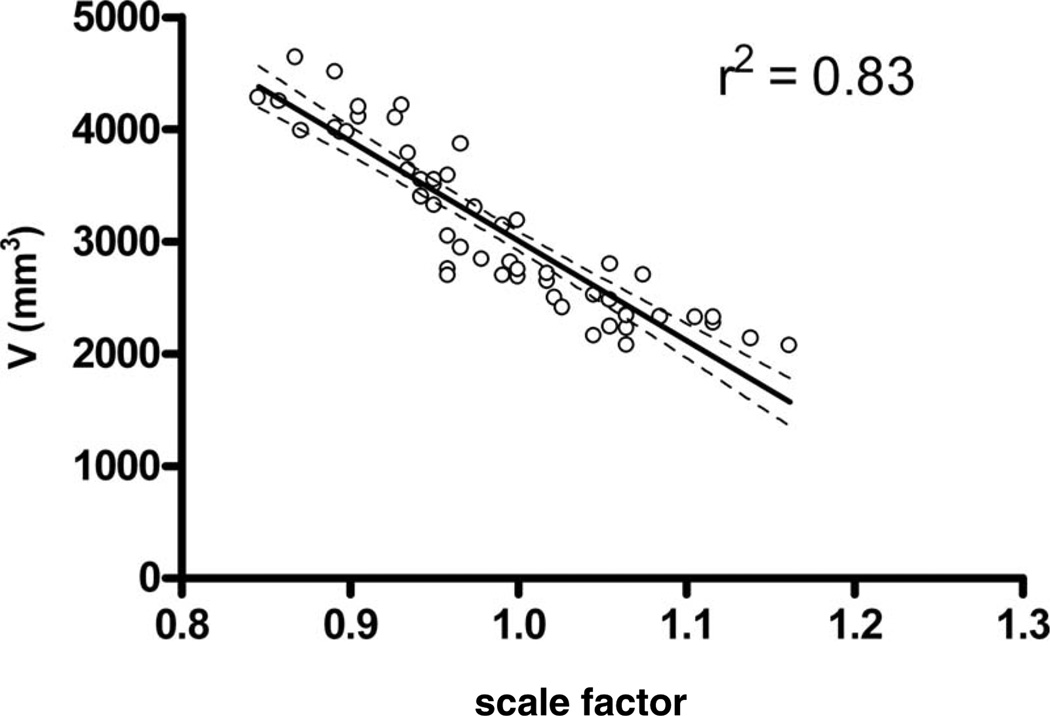
The mean capitate volumes for males were significantly greater than females at 3625 ± 620 mm3 and 2540 ± 350 mm3, respectively. These values were calculated in a previous study; however, the means for men differ from that study due to a slightly smaller sample size in the current study (n = 13, instead of n = 14) [11]. The mean L1 values for males and females were 24.7 ± 1.3 mm and 22.1 ± 1.2 mm, respectively. The smallest capitate’s PvP location, which belonged to a female, was scaled up 16.2%, while the largest, belonging to a male, was scaled down 15.4% (Fig. 3).

Fig. 3.

Fig. 3

Open in a new tab

The smallest capitate’s PvP location was scaled up 16.2%, while the largest was scaled down 15.4%. Small changes in scaling factor correspond to large changes in volume.

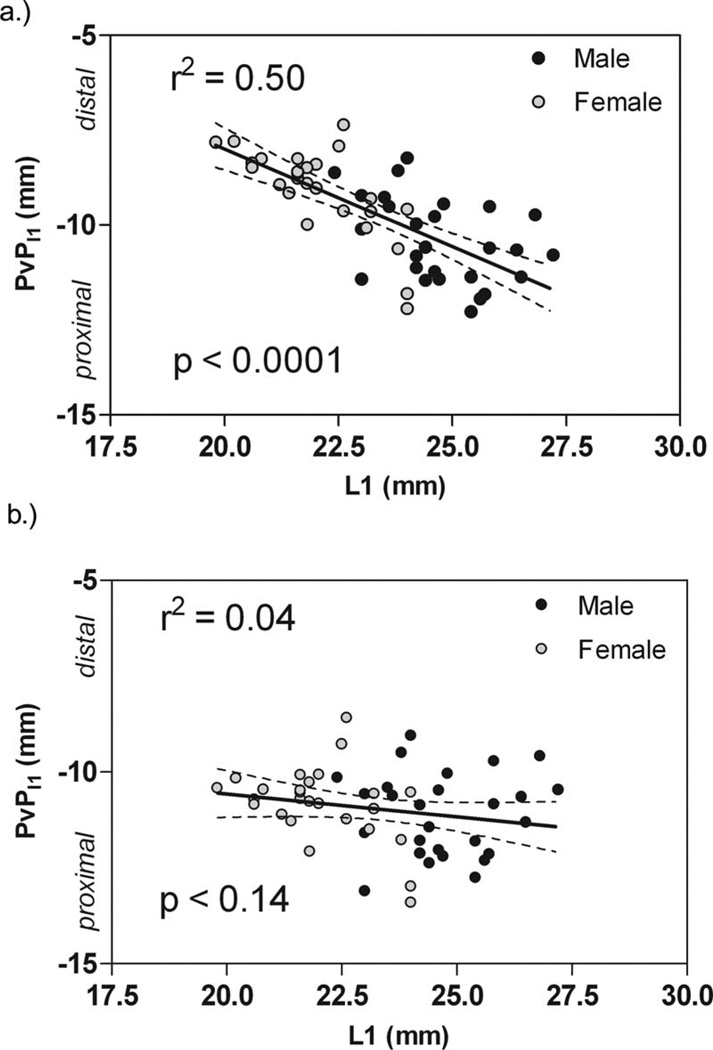
Regression analysis of the unscaled PvPI1 versus L1 revealed that the PvP moved further from the capitate’s centroid as L1 increased (P < 0.0001) (Fig. 4(a)). Also, PvP locations of males and females fell on the same continuum. When isometric scaling was applied to PvP0, the dependence of PvPI1 on the capitate length was completely removed (P = 0.14) (Fig. 4(b)). No dependence was found of PvPI2 or PvPI3 on the capitate length in either the unscaled or the scaled case, with P values for scaled PvPI2 = 0.90 and PvPI3 = 0.40, and unscaled PvPI2 = 0.48 and PvPI3 = 0.48.

Fig. 4.

Fig. 4

Open in a new tab

Location of best-fit PvP from capitate centroid along I1. PvPI1 becomes more negative as it approaches the proximal pole of the capitate. (a) Although the R2 value is low, a trend can be seen that reveals a relationship between capitate size and PvP location; as the capitates get larger, the distance from capitate centroid to the PvP increases. (b) Scaled PvP locations. The relationship between capitate size and PvP location vanishes.

The unscaled PvP0 was located (P = 0.0001) significantly closer to the capitate centroid in females than in males. Scaling removed these gender differences, increasing P to a nonsignificant value of 0.3, supporting our hypothesis that simple isometric scaling would remove gender differences in PvP0. Linear regression analysis revealed that the dependence of PvP location on capitate size was removed with the scaling of the capitate (Fig. 5).

Fig. 5.

Fig. 5

Open in a new tab

Capitate PvP for each subject visualized in a lateral view of the capitate inertial coordinates, male (black), female (white). (a) Unscaled PvPs visualized within the smallest female (inner) and largest male (outer) capitates (registered to the inertial coordinate system). (b) PvPs scaled to L1avg, visualized within the average subject’s capitate. Both male and female PvPs tend toward the center of the proximal pole.

The single, fixed PvP model was not supported because significant differences (P < 0.0001) were found in the distance d for each motion bin (Table 1). Although the PvP did not serve as the intersection point of all HAMs, it was consistently found within the proximal pole of the capitate (Fig. 6). The average distance of a scaled PvP from the average of all PvPs was 1.9 ± 1.1 mm. The average separation of capitate-fixed and radius-fixed PvPs was 1.7 ± 0.6 mm. Qualitatively, the individual HAM axes for each motion bin were in the same general anatomical location with respect to the PvP. For example, flexion axes were located volar and distal to the PvP, extension axes tended to be located more proximal, ulnar deviation was distal, and radial deviation was distal and radial (Table 1 and Fig. 6).

Table 1.

Pos = motion bin. d = the mean distance between HAM location and PvP for each motion bin. std = the standard deviation of d. n = number of positions in each motion bin. Average ROM = average total capitate rotation for each HAM. Direction with respect to PvP = relative position of the average helical axis to the average PvP. F = flexion, E = extension, U = ulnar deviation, R = radial deviation, +D = positive dart thrower path, −D = negative dart thrower path, +AD = positive anti dart thrower path, −AD = negative antidart thrower path.

Distance of HAM axis to PvP
Pos d (mm)a std (mm) n Average ROM (std) Direction with respect to PvP
F 3.6 3.0 25 25 deg (19 deg) Volar distal
E 3.4 3.0 63 36 deg (18 deg) Proximal
U 4.5 2.0 23 26 deg (15 deg) Distal
R 3.0 1.6 10 17 deg (12 deg) Distal radial
+D 4.2 2.2 32 31 deg (14 deg) Distal volar
−D 3.4 1.7 33 36 deg (16 deg) Distal volar
+AD 4.1 2.3 31 36 deg (29 deg) Volar
−AD 1.8 1.1 159 43 deg (19 deg) Dorsal
Open in a new tab
a

All distances of HAM location to the PvP were statistically different from a hypothetical mean of 0.5 mm.

Fig. 6.

Fig. 6

Open in a new tab

The average of all scaled PvPs (black sphere). Representative HAMs for each motion bin. Refer to Table 1 for abbreviations.

Discussion

In vivo sequential CT scans were analyzed to examine gender differences in capitate kinematics and to explore the possibility that radio-capitate kinematics can be modeled as a ball-and-socket articulation. The unscaled PvPs were shown to have a near linear relationship with the proximal-distal length of the capitate. As capitate size increased across subjects, the PvP moved further from the capitate centroid. Once the PvPs were scaled to the average subject, the relationship between PvP location and capitate size was removed.

Gender differences in PvP location were also removed by using capitate length as a scaling factor, confirming that gender differences in capitate kinematics are simply a function of carpal size and not function. Our results are consistent with the findings of Neu et al. who also found that, in general, a female’s radio-capitate HAM is located closer to the capitate centroid than a male’s [2] (Fig. 5(a)).

Although the best-fit radio-capitate PvP was consistently found within the proximal pole of the capitate (Fig. 3(b)), with an average RMS error of 1.7 ± 0.6 mm, the distance of the closest point on the HAM from the PvP (d) varied with the direction of wrist motion (up to 4.5 mm). This verifies that the best-fit radio-capitate PvP should not be interpreted as an ideal ball-and-socket articulation. However, with errors on the order of 2 mm, the best-fit PvP may be used as a reasonable wrist joint center when studying segmental motion of the hand with respect to the forearm. The variation in PvP0 is on the same order of magnitude as the errors seen in biomechanical models of other joints created by using skin-mounted markers [20].

Numerous studies using a wide variety of two-dimensional (2D) and three-dimensional (3D) techniques have sought to quantify the rotational motion of the capitate. 2D studies have commonly used in vivo planar radiographic techniques, whereas previous 3D studies have typically used motion-tracking systems on cadaver wrists. Most studies have shown that the 2D axis of rotation or the 3D PvP resides in the proximal pole of the capitate [4,10,21,22]. However, discrepancies in literature exist in the distance of flexion/extension and radio-ulnar deviation axes from the PvP that range from 2 mm from each other to 7.5 mm [2,10]. Previous studies have methodological limitations, including the inability of a 2D study to measure out of plane motion [4], and the fact that previous 3D studies have been limited by the need for invasive procedures to attach markers to the carpal bones [10].

The current study addresses many of these limitations because of the increased accuracy of the MBR technique and its application to a relatively large number of healthy, normal subjects. While previous studies have revealed a great deal about the complexities of carpal motion, there have been relatively few studies that have examined radio-capitate kinematics using nonorthogonal, or combined, wrist motions, such as the dart thrower’s motion [13,23,24]. Furthermore, to the best of our knowledge, no previous study has examined the effects of normalizing radio-capitate kinematics by capitate size. The current study demonstrates that normalizing HAM or PvP location to the long axis length of the capitate facilitates the combination of male and female datasets of radio-capitate kinematics.

The most prominent limitation of this study is the small number of static positions used as input for the functional joint algorithm used to calculate the best-fit PvP. This algorithm is most often used with passive, high-speed optical motion capture systems. With capture rates of 60 Hz and up, hundreds of positions can be used as input into the least-squares, best-fit PvP algorithm. However, accurate and repeatable marker placement algorithms for high-speed optical motion analysis in the hand and wrist of living subjects have not yet been developed, and the MBR technique is considerably more accurate than skeletal models derived from skin surface markers [25].

Another potential limitation of this study is the relatively large number of negative antidart thrower’s positions compared to other motions such as radial deviation. This may cause the PvP to be biased toward this position. However, the PvP was calculated on a subject by subject basis based on motions derived from targeted wrist positions in our CT protocol. Therefore, the PvP calculation represented the full range of wrist motion for each subject. One possible reason for the greater number of binned antidart thrower’s positions is that both extension and ulnar deviation have the largest ranges of motion. Radial deviation has a limited range of motion, so it follows that there would be limited positions of pure radial deviation in similar ranges of motion. Because the PvP was calculated on a subject by subject basis, and each subject had CT images taken representing their entire range of wrist motion, the uneven number of positions in each bin does not negatively affect this analysis.

One potential application of the best-fit radio-capitate PvP is an estimation of the wrist joint center in an upper extremity model created by using optical motion capture and skin mounted surface markers. These models are becoming increasingly popular in the analysis of upper extremity function [26–28]. Another possible application of these data may be the creation of regression equations by which the best-fit PvP, and thus the proximal pole of the capitate, can be calculated by using its relationship to palpable bony landmarks. When considering carpal kinematics, the capitate does not rotate about a fixed center point for all motions (with respect to the radius). An improved understanding of the capitate center of motion, and its relationship to functional motion planes of the wrist, is important as a design consideration for articulated external fixation devices, wrist orthotic design, and prosthetic replacement of the wrist.

Acknowledgment

This study was supported by NIH AR44005 and NIH HD052127.

Footnotes

Contributed by the Bioengineering Division of ASME for publication in the Journal of Biomechanical Engineering.

Paper presented at the ORS 2007.

Contributor Information

Michael J. Rainbow, Department of Orthopaedics, The Warren Alpert Medical School of Brown University/Rhode Island Hospital, 1 Hoppin Street, CORO West, Suite 404, Providence, RI 02903

Joseph J. Crisco, Email: joseph_crisco@brown.edu, Department of Orthopaedics, The Warren Alpert Medical School of Brown University/Rhode Island Hospital, 1 Hoppin Street, CORO West, Suite 404, Providence, RI 02903.

Douglas C. Moore, Department of Orthopaedics, The Warren Alpert Medical School of Brown University/Rhode Island Hospital, 1 Hoppin Street, CORO West, Suite 404, Providence, RI 02903

Scott W. Wolfe, Hand and Upper Extremity Center, Hospital for Special Surgery, Weill Medical College of Cornell University, 523 East 72nd Street, New York, NY 10021

References

  • 1.Patterson RM, Nicodemus CL, Viegas SF, Elder KW, Rosenblatt J. High-Speed, Three-Dimensional Kinematic Analysis of the Normal Wrist. J. Hand Surg. [Am] 1998;23(3):446–453. doi: 10.1016/S0363-5023(05)80462-9. [DOI] [PubMed] [Google Scholar]
  • 2.Neu CP, Crisco JJ, Wolfe SW. In Vivo Kinematic Behavior of the Radio-Capitate Joint During Wrist Flexion-Extension and Radio-Ulnar Deviation. J. Biomech. 2001;34(11):1429–1438. doi: 10.1016/s0021-9290(01)00117-8. [DOI] [PubMed] [Google Scholar]
  • 3.Wolfe SW, Neu C, Crisco JJ. In Vivo Scaphoid, Lunate, and Capitate Kinematics in Flexion and in Extension. J. Hand Surg. [Am] 2000;25(5):860–869. doi: 10.1053/jhsu.2000.9423. [DOI] [PubMed] [Google Scholar]
  • 4.Youm Y, McMurthy RY, Flatt AE, Gillespie TE. Kinematics of the Wrist. I. An Experimental Study of Radial-Ulnar Deviation and Flexion-Extension. J. Bone Jt. Surg., Am. Vol. 1978;60(4):423–431. [PubMed] [Google Scholar]
  • 5.Kobayashi M, Berger RA, Nagy L, Linscheid RL, Uchiyama S, Ritt M, An KN. Normal Kinematics of Carpal Bones: A Three-Dimensional Analysis of Carpal Bone Motion Relative to the Radius. J. Biomech. 1997;30(8):787–793. doi: 10.1016/s0021-9290(97)00026-2. [DOI] [PubMed] [Google Scholar]
  • 6.Moritomo H, Murase T, Goto A, Oka K, Sugamoto K, Yoshikawa H. Capitate-Based Kinematics of the Midcarpal Joint During Wrist Radioulnar Deviation: An In Vivo Three-Dimensional Motion Analysis. J. Hand Surg. [Am] 2004;29(4):668–675. doi: 10.1016/j.jhsa.2004.04.010. [DOI] [PubMed] [Google Scholar]
  • 7.Kaufmann R, Pfaeffle J, Blankenhorn B, Stabile K, Robertson D, Goitz R. Kinematics of the Midcarpal and Radiocarpal Joints in Radioulnar Deviation: An in Vitro Study. J. Hand Surg. [Am] 2005;30(5):937–942. doi: 10.1016/j.jhsa.2005.05.016. [DOI] [PubMed] [Google Scholar]
  • 8.Kaufmann RA, Pfaeffle HJ, Blankenhorn BD, Stabile K, Robertson D, Goitz R. Kinematics of the Midcarpal and Radiocarpal Joint in Flexion and Extension: An In Vitro Study. J. Hand Surg. [Am] 2006;31(7):1142–1148. doi: 10.1016/j.jhsa.2006.05.002. [DOI] [PubMed] [Google Scholar]
  • 9.McMurtry RY, Youm Y, Flatt AE, Gillespie TE. Kinematics of the Wrist. II. Clinical Applications. J. Bone Jt. Surg., Am. Vol. 1978;60(7):955–961. [PubMed] [Google Scholar]
  • 10.Savelberg HH, Otten JD, Kooloos JG, Huiskes R, Kauer JM. Carpal Bone Kinematics and Ligament Lengthening Studied for the Full Range of Joint Movement. J. Biomech. 1993;26(12):1389–1402. doi: 10.1016/0021-9290(93)90090-2. [DOI] [PubMed] [Google Scholar]
  • 11.Crisco JJ, Coburn JC, Moore DC, Upal MA. Carpal Bone Size and Scaling in Men Versus in Women. J. Hand Surg. [Am] 2005;30(1):35–42. doi: 10.1016/j.jhsa.2004.08.012. [DOI] [PubMed] [Google Scholar]
  • 12.Wolfe SW, Crisco JJ, Orr CM, Marzke MW. The Dart-Throwing Motion of the Wrist: Is It Unique to Humans? J. Hand Surg. [Am] 2006;31(9):1429–1437. doi: 10.1016/j.jhsa.2006.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Crisco JJ, Coburn JC, Moore DC, Akelman E, Weiss AP, Wolfe SW. In Vivo Radiocarpal Kinematics and the Dart Thrower’S Motion. J. Bone Jt. Surg., Am. Vol. 2005;87(12):2729–2740. doi: 10.2106/JBJS.D.03058. [DOI] [PubMed] [Google Scholar]
  • 14.Crisco JJ, McGovern RD, Wolfe SW. Noninvasive Technique for Measuring In Vivo Three-Dimensional Carpal Bone Kinematics. J. Orthop. Res. 1999;17(1):96–100. doi: 10.1002/jor.1100170115. [DOI] [PubMed] [Google Scholar]
  • 15.Marai GE, Laidlaw DH, Crisco JJ. Super-Resolution Registration Using Tissue-Classified Distance Fields. IEEE Trans. Med. Imaging. 2006;25(2):1–11. doi: 10.1109/TMI.2005.862151. [DOI] [PubMed] [Google Scholar]
  • 16.Crisco JJ, McGovern RD. Efficient Calculation of Mass Moments of Inertia for Segmented Homogenous Three-Dimensional Objects. J. Biomech. 1998;31:97–101. doi: 10.1016/s0021-9290(97)00108-5. [DOI] [PubMed] [Google Scholar]
  • 17.Coburn JC, Upal MA, Crisco JJ. Coordinate Systems for the Carpal Bones of the Wrist. J. Biomech. 2007;40(1):203–209. doi: 10.1016/j.jbiomech.2005.11.015. [DOI] [PubMed] [Google Scholar]
  • 18.Piazza SJ, Eroemia A, Okita N, Cavanagh PR. Assessment of the Functional Method of Hip Joint Center Location Subject to Reduced Range of Hip Motion. J. Biomech. 2004;37(3):349–356. doi: 10.1016/s0021-9290(03)00288-4. [DOI] [PubMed] [Google Scholar]
  • 19.Coburn J, Crisco JJ. Interpolating Three-Dimensional Kinematic Data Using Quaternion Splines and Hermite Curves. ASME J. Biomech. Eng. 2005;127(2):311–317. doi: 10.1115/1.1865195. [DOI] [PubMed] [Google Scholar]
  • 20.Hicks JL, Richards JG. Clinical Applicability of Using Spherical Fitting to Find Hip Joint Centers. Gait and Posture. 2005;22(2):138–145. doi: 10.1016/j.gaitpost.2004.08.004. [DOI] [PubMed] [Google Scholar]
  • 21.Brumbaugh RB, Crowninshield RD, Blair WF, Andrews JG. An In-Vivo Study of Normal Wrist Kinematics. ASME J. Biomech. Eng. 1982;104(3):176–181. doi: 10.1115/1.3138345. [DOI] [PubMed] [Google Scholar]
  • 22.Volz RG, Lieb M, Benjamin J. Biomechanics of the Wrist. Clin. Orthop. Relat. Res. 1980;149:112–117. [PubMed] [Google Scholar]
  • 23.Werner FW, Green JK, Short WH, Masaoka S. Scaphoid and Lunate Motion During a Wrist Dart Throw Motion. J. Hand Surg. [Am] 2004;29(3):418–422. doi: 10.1016/j.jhsa.2004.01.018. [DOI] [PubMed] [Google Scholar]
  • 24.Ishikawa J, Cooney WP, III, Niebur G, An KN, Minami A, Kaneda K. The Effects of Wrist Distraction on Carpal Kinematics. J. Hand Surg. [Am] 1999;24(1):113–120. doi: 10.1016/S0266-7681(99)90057-8. [DOI] [PubMed] [Google Scholar]
  • 25.Neu CP, McGovern RD, Crisco JJ. Kinematic Accuracy of Three Surface Registration Methods in a Three-Dimensional Wrist Bone Study. ASME J. Biomech. Eng. 2000;122(5):528–533. doi: 10.1115/1.1289992. [DOI] [PubMed] [Google Scholar]
  • 26.Kuo LC, Su FC, Chiu HY, Yu CY. Feasibility of Using a Video-Based Motion Analysis System for Measuring Thumb Kinematics. J. Biomech. 2002;35(11):1499–1506. doi: 10.1016/s0021-9290(02)00083-0. [DOI] [PubMed] [Google Scholar]
  • 27.Miltner O, Williams S, Schmidt R, Siebert CH, Rau G, Zilkens KW, Disselhorst-Klug C. Arm Motion Analysis: A New Method and Its Clinical Application. Z. Orthop. Ihre Grenzgeb. 2003;141(2):171–176. doi: 10.1055/s-2003-38648. [DOI] [PubMed] [Google Scholar]
  • 28.Riener R, Straube A. Inverse Dynamics as a Tool for Motion Analysis: Arm Tracking Movements in Cerebellar Patients. J. Neurosci. Methods. 1997;72(1):87–96. doi: 10.1016/s0165-0270(96)02168-1. [DOI] [PubMed] [Google Scholar]

RESOURCES