Excitation threshold for subharmonic generation from contrast microbubbles

Abstract

Six models of contrast microbubbles are investigated to determine the excitation threshold for subharmonic generation. The models are applied to a commercial contrast agent; its characteristic parameters according to each model are determined using experimentally measured ultrasound attenuation. In contrast to the classical perturbative result, the minimum threshold for subharmonic generation is not always predicted at excitation with twice the resonance frequency; instead it occurs over a range of frequencies from resonance to twice the resonance frequency. The quantitative variation of the threshold with frequency depends on the model and the bubble radius. All models are transformed into a common interfacial rheological form, where the encapsulation is represented by two radius dependent surface properties—effective surface tension and surface dilatational viscosity. Variation of the effective surface tension with radius, specifically having an upper limit (resulting from strain softening or rupture of the encapsulation during expansion), plays a critical role. Without the upper limit, the predicted threshold is extremely large, especially near the resonance frequency. Having a lower limit on surface tension (e.g., zero surface tension in the buckled state) increases the threshold value at twice the resonance frequency, in some cases shifting the minimum threshold toward resonance.

INTRODUCTION

Encapsulated microbubbles are excellent scatterers of ultrasound and can significantly improve the contrast of diagnostic ultrasound images (de Jong et al., 1991; Ferrara et al., 2007; Goldberg et al., 2001). They also generate super- and subharmonic signals under strong excitations, which can be used for harmonic (imaging at twice the excitation frequency) (Chang et al., 1996) and subharmonic (imaging at half the excitation frequency) imaging (Forsberg et al., 2000; Shankar et al., 1998). Recently, the ambient pressure dependent variation of subharmonic response from contrast microbubbles has been proposed as a noninvasive estimator of the organ-level blood pressure (Adam et al., 2005; Andersen and Jensen, 2010; Forsberg et al., 2005; Frinking et al., 2010; Katiyar et al., 2011; Leodore et al., 2007; Shi et al., 1999). In vitro experiments with a number of contrast agents registered 5–15 dB decrease with 188 mm Hg increase in ambient pressure (Adam et al., 2005; Leodore et al., 2007). Estimation of pressure using subharmonic response has been successfully demonstrated in vivo as well (Forsberg et al., 2005). However, a complete understanding of the nonlinear physics underlying the subharmonic scattering from contrast microbubbles is currently missing. For free bubbles, unlike higher harmonics, subharmonic response is seen only above a threshold excitation; the minimum threshold excitation was shown by a perturbative analysis to occur at twice the linear resonance frequency (f₀) of the bubble (Eller and Flynn, 1968; Neppiras, 1969; Prosperetti, 1977). However, contrast microbubbles are encapsulated by a layer of surface active molecules, such as lipids, proteins, and surfactants, which protects them against premature dissolution (Katiyar and Sarkar, 2010; Katiyar et al., 2009; Sarkar et al., 2009). The encapsulation affects oscillation and thereby the linear and nonlinear scattering. Several models of encapsulation have been created to describe the dynamics of contrast microbubbles (Chatterjee and Sarkar, 2003; Church, 1995; de Jong et al., 1994; Hoff et al., 2000; Marmottant et al., 2005; Paul et al., 2010; Sarkar et al., 2005). In this paper, we numerically investigate the subharmonic response from a commercially available contrast microbubble, specifically the threshold for subharmonic generation from Sonazoid (GE Health Care, Oslo, Norway) comparing the predictions by several of these models.

Recently, we have shown that theoretical models predict both increase and decrease of subharmonic response from a single microbubble with ambient pressure depending on the ratio of the excitation frequency normalized by the natural frequency (Katiyar et al., 2011). The result was explained by investigating the subharmonic resonance curve—the subharmonic response shows a distinct peak in the neighborhood of a particular value of that ratio (~1.6 for a 2μm radius bubble). One would expect that the peak subharmonic response would occur where generating subharmonic is easiest, i.e., where subharmonic threshold is minimum. As noted earlier, performing a small amplitude expansion of the Rayleigh–Plesset (RP) equation showed that this threshold for free bubbles occurs when it is excited at twice the resonance frequency (Eller and Flynn, 1968; Neppiras, 1969; Prosperetti, 1974). Using a similar analysis on an encapsulation model due to de Jong et al. (1994) showed a minimum subharmonic threshold also at twice the resonance frequency (Shankar et al., 1999). Note that the model is based on friction and elasticity parameters used to model the damping and the restoring forces from the encapsulation. The same article also reported maximum subharmonic response from Optison (GE Health Care, Princeton, NJ) at an excitation frequency of 2 MHz, purportedly twice the resonance frequency. The resonance frequency was computed using the same model of encapsulation applied to Optison. For the contrast agent Definity (Lantheus Imaging, N. Billerica, MA), a similar analysis was performed using the linear viscoelastic model due to Church (1995)—a lower threshold for subharmonic was found when excitation frequency was closer to twice the resonance frequency (Kimmel et al., 2007).

In view of the meager literature, there remains a critical need for further investigation of the subharmonic threshold for various contrast microbubbles available today. Above a critical excitation level, contrast microbubbles are destroyed (Ammi et al., 2006; Chatterjee et al., 2005a; Chomas et al., 2001). Determining the threshold for subharmonic generation is crucial for nondestructive subharmonic applications. As mentioned earlier, the classical result of minimum threshold at twice the resonance frequency was obtained using a perturbative analysis of free bubbles and a few early encapsulation models that are largely based on linear elastic behavior of the encapsulation. On the other hand, subharmonic response is generated when a contrast microbubble executes large nonlinear oscillations. There, such linear models might be inappropriate, warranting more sophisticated nonlinear constitutive models for the encapsulation. Recently, considerable effort has been devoted toward developing rigorous models for the encapsulation (Chatterjee and Sarkar, 2003; Chatterjee et al., 2005b; Doinikov and Dayton, 2007; Hoff et al., 2000; Marmottant et al., 2005; Sarkar et al., 2005; Tsiglifis and Pelekasis, 2008). We have developed Newtonian (Chatterjee and Sarkar, 2003) and viscoelastic (Sarkar et al., 2005) (zero-thickness) interfacial rheological models of the encapsulation; the molecular nature of the encapsulation and thereby the directional anisotropy justified such a two-dimensional continuum model in contrast to finite thickness models, e.g., Church (1995); Hoff et al. (2000); Doinikov and Dayton (2007). We applied the model to Sonazoid contrast agent to determine its characteristic parameters using experimentally measured attenuation and scattering data. For large oscillations, responsible for subharmonic response, nonlinear changes of surface elasticity representing rupture and buckling of the encapsulation (Marmottant et al., 2005) or strain-softening (Paul et al., 2010) have also been incorporated.

In this paper, we execute a detailed numerical investigation of a number of encapsulation models to determine the excitation threshold for subharmonic generation as a function of excitation frequency. Specifically, we consider (1) our Newtonian model, (2) the de Jong model, (3) the Church–Hoff model, (4) our constant elasticity model, (5) the Marmottant model, and (6) our strain-softening exponential elasticity model (EEM). Each of these models obtains two terms in the RP equation governing the bubble dynamics—they represent damping and the elastic resistance of the encapsulation. In Sec. 2, we describe all of them as interfacial rheological models with an effective radius dependent surface tension and a dilatational surface viscosity. Note that the surface dilatational elasticity is the derivative of the surface tension with respect to the change in area fraction. In Sec. 3, we show how different radius dependence of effective surface tension leads to different variations of the subharmonic threshold with normalized excitation frequency (f∕f₀). Finally, Sec. 4 discusses and summarizes the results.

MATHEMATICAL FORMULATION AND NUMERICAL SOLUTION

Free bubble dynamics

To simulate the dynamics of a free microbubble, we use the following form of the RP equation:

$$\begin{array}{c}\multicolumn{1}{c}{\mathrm{\rho }(R\stackrel{\mathrm{··}}{R}+\frac{3}{2}{\stackrel{·}{R}}^2)=P_G-\frac{2\mathrm{\gamma }}{R}-4\mathrm{\mu }\frac{\stackrel{·}{R}}{R}-p_0+p_A(t)-\frac{R}{c}\frac{{\mathit{dP}}_G}{\mathit{dt}},}\end{array}$$ (1)

where R is the spherical bubble radius, $\stackrel{·}{R}$ and $\stackrel{\mathrm{··}}{R}$ are the first and the second order time derivatives of the bubble radius R, ρ is the liquid density, µ is the liquid viscosity, γ is the gas–liquid surface tension, p₀ is the ambient pressure, p_A is the excitation pressure with amplitude P_A, and c is the sound velocity in liquid. The last term in Eq. 1 represents compressibility; such a compressible form has been shown to remain numerically stable at high Mach numbers (Brenner et al., 2002). We assume that the gas content of the bubble does not change (i.e., gas diffusion neglected). The gas pressure P_G inside is given by the polytropic law:

$$P_G=P_{G_0}{\left(\frac{R_0}{R}\right)}^{3k},$$ (2)

where R₀ is the initial bubble radius, P_G0 is the initial gas pressure inside the bubble, and k is the polytropic exponent. Incorporating Eq. 2 in Eq. 1, we get

$$\begin{array}{c}\multicolumn{1}{c}{\rho (R\stackrel{\mathrm{··}}{R}+\frac{3}{2}{\stackrel{·}{R}}^2)=P_{G_0}{\left(\frac{R_0}{R}\right)}^{3k}(1-\frac{3k\stackrel{·}{R}}{c})-\frac{2\mathrm{\gamma }}{R}-4\mathrm{\mu }\frac{\stackrel{·}{R}}{R}-p_0+p_A.}\end{array}$$ (3)

The resonance frequency (f₀) for a free bubble is given by

$$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0+\frac{2\mathrm{\gamma }}{R_0}(3k-1))},$$ (4)

where γ=γw, the pure air–water surface tension

Encapsulated bubble dynamics

Most encapsulation models for contrast microbubbles modify the RP equation adding terms representing the contributions due to viscoelastic stresses generated in the encapsulation. Here, we show for several models that the viscoelastic terms can be expressed as two effective interfacial stress terms—one due to an effective dilatational surface viscosity κ^s(R) and the other due to an effective surface tension γ(R). Therefore, the bubble dynamics can be modeled by a modified RP equation:

$$\begin{array}{c}\multicolumn{1}{c}{\mathrm{\rho }(R\stackrel{\mathrm{··}}{R}+\frac{3}{2}{\stackrel{·}{R}}^2)=P_{G_0}{\left(\frac{R_0}{R}\right)}^{3k}(1-\frac{3k\stackrel{·}{R}}{c})-\frac{2}{R}\mathrm{\gamma }\left(R\right)-\frac{4\stackrel{·}{R}}{R^2}{\mathrm{\kappa }}^s-4\mathrm{\mu }\frac{\stackrel{·}{R}}{R}-p_0+p_A.}\end{array}$$ (5)

For the encapsulated bubble dynamics, we are considering the de Jong model (de Jong et al., 1994), the Church–Hoff model (Hoff et al., 2000), the Marmottant model (Marmottant et al., 2005), and three of our interfacial models—Newtonian (Chatterjee and Sarkar, 2003), constant elasticity (Sarkar et al., 2005), and exponential elasticity (Paul et al., 2010) models. For all these models, the effective surface tension γ(R) and the interfacial dilatational surface viscosity κ^s(R) are provided in the following. Note that the Church–Hoff model assumes a finite thickness for the encapsulation with bulk properties; effective interfacial properties are therefore explicit functions of the shell thickness.

• (A)
  Newtonian model (Sarkar et al., 2005):

  $$\mathrm{\gamma }\left(R\right)=\mathrm{\gamma }\mathrm{,}{\mathrm{\kappa }}^s(R)={\mathrm{\kappa }}^s$$ (6)

  are both constant, i.e., independent of initial as well as instantaneous bubble radius during radial oscillations. Note that for several contrast agents such as Optison and Sonazoid, this model predicted large values of surface tension γ (Chatterjee and Sarkar, 2003). The resonance frequency f₀ for the Newtonian model is given by

  $$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0+\frac{2\mathrm{\gamma }}{R_0}(3k-1))}.$$ (7)
• (B)
  de Jong model (de Jong et al., 1994):

  $$\mathrm{\gamma }\left(R\right)={\mathrm{\gamma }}_w+S_p(\frac{R}{R_0}-1),{\mathrm{\kappa }}^s(R)=\frac{S_f}{16\mathrm{\pi }}.$$ (8)

  Here S_p is the shell elasticity parameter and S_f is the encapsulation friction parameter. Note that the effective surface tension varies linearly with instantaneous bubble radius and initially it is equal to _γw. The resonance frequency (de Jong et al., 1994) is given by

  $$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0+\frac{2{\mathrm{\gamma }}_w}{R_0}(3k-1)+\frac{2S_p}{R_0})}.$$ (9)
• (C)
  Church–Hoff model (Hoff et al., 2000):

  $$\mathrm{\gamma }\left(R\right)=6G_s{d}_{{\mathit{sh}}_0}\frac{R_0^2}{R^2}(1-\frac{R_0}{R}),{\mathrm{\kappa }}^s(R)=3{\mathrm{\mu }}_s{d}_{{\mathit{sh}}_0}\frac{R_0^2}{R^2}.$$ (10)

  Here G_s, μ_s, and d_sh0 are the shear modulus, the shear viscosity, and the thickness of the encapsulation. The initial value of the effective surface tension γ(R) is zero. The resonance frequency for the Church–Hoff model (Hoff et al., 2000) is given by

  $$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0+12G_s\frac{d_{{\mathit{sh}}_0}}{R_0})}.$$ (11)
• (D)
  Constant elasticity model (Sarkar et al., 2005):

  $$\text{γ}(R)={\text{γ}}_0+E^s\beta ,\text{\hspace{0.17em}and\hspace{0.17em}}{\kappa }^s={\kappa }^s.$$ (12)

  Here E^s is the constant dilatational surface elasticity, $\mathrm{\beta }=(R^2-R_E^2)∕R_E^2$ is the area fraction increase, and _γ0 is the reference surface tension at the undeformed state with radius R_E,

  $$R_E=R_0{(1-\frac{{\mathrm{\gamma }}_0}{E^s})}^{-1∕2}.$$ (13)

  R_E is obtained from the condition of pressure equilibrium (P_G0=p₀⇒γ(R)=0) at R=R₀. The resonance frequency (Sarkar et al., 2005) is given by

  $$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0-\frac{4{\mathrm{\gamma }}_0}{R_0}+\frac{4E^s}{R_0})}.$$ (14)
• (E)
  Marmottant model (Marmottant et al., 2005):

  $$\begin{array}{cc}\multicolumn{1}{c}{}& \mathrm{\gamma }\left(R\right)=\{\begin{array}{ccc}\multicolumn{1}{c}{0}& \mathrm{for}\hfill & R\le R_{\mathrm{buckling}}\hfill \\ \multicolumn{1}{c}{\mathrm{\chi }(\frac{R^2}{R_{\mathrm{buckling}}^2}-1)}& \mathrm{for}\hfill & R_{\mathrm{buckling}}\le R\le R_{\mathrm{rupture}},\hfill \\ \multicolumn{1}{c}{{\mathrm{\gamma }}_w}& \mathrm{for}\hfill & R\ge R_{\mathrm{rupture}}\hfill \end{array}\hfill \\ \multicolumn{1}{c}{}& {\mathrm{\kappa }}^s(R)={\mathrm{\kappa }}^s.\hfill \end{array}$$ (15)

  Here χ is the elastic compression modulus, R_buckling=R₀[1+γ(R₀)^∕χ]-1∕2, and R_rupture=R_buckling[ 1+γ_ω∕χ ]^−1∕2. In this model, the effective surface tension varies in an extremely small range of radial oscillation (R_rupture-R_buckling≤0.05R₀). Above R_rupture the interface acts as a pure air–water interface, and below R_buckling it is in a buckled state where the effective surface tension is zero. The resonance frequency for the Marmottant model (Marmottant et al., 2005; van der Meer et al., 2007) is given by

  $$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0-\frac{2\mathrm{\gamma }\left(R_0\right)}{R_0}(3k-1)+\frac{4\mathrm{\chi }}{R_0})}.$$ (16)
• (F)
  EEM (Paul et al., 2010):

  $$\text{γ}(R)={\text{γ}}_0+E^s\beta ,E^s=E_0^s\beta \text{exp}(-{\text{α}}^s\beta )\text{\hspace{0.17em}and\hspace{0.17em}}{\kappa }^s={\kappa }^s.$$ (17)

Here $\mathrm{\beta }=(R^2-R_E^2)∕R_E^2$ is the area fraction, and R_E is the equilibrium radius with zero elastic stress:

$$R_E=R_0{[1+\left(\frac{1-\sqrt{1+4{\mathrm{\gamma }}_0{\mathrm{\alpha }}^s∕E_0^s}}{2\mathrm{\alpha }}\right)]}^{-1∕2}.$$ (18)

γ₀ is the constant surface tension in the undeformed state. $E_0^s$ and ^αs are model constants. Note that the interfacial elasticity E^s is assumed to be decreasing exponentially with increasing radius representing a strain softening behavior. The resonance frequency for an encapsulated bubble due to the viscoelastic EEM is given by

$$f_0=\frac{1}{2\mathrm{\pi }{R}_0}\sqrt{\frac{1}{\mathrm{\rho }}(3{\mathit{kp}}_0+\frac{2E_0^s}{R_0}\left(\frac{\sqrt{1+4{\mathrm{\gamma }}_0{\mathrm{\alpha }}^s∕E_0^s}}{{\mathrm{\alpha }}^s}\right)(1+2{\mathrm{\alpha }}^s-\sqrt{1+4{\mathrm{\gamma }}_0{\mathrm{\alpha }}^s∕E_0^s}))}.$$ (19)

Encapsulation parameter estimation

We have developed a procedure to estimate the model parameters using attenuation of ultrasound through a suspension of microbubbles; it was applied to contrast agents Optison and Sonazoid (Chatterjee and Sarkar, 2003; Paul et al., 2010). Here, we only briefly mention the method. Using the linearized RP equation specific to an encapsulation model, one can compute the attenuation due to a single encapsulated bubble. Knowing size distribution, the attenuation due to a suspension of the agent can be computed. An error function between the measured attenuation and the modeled attenuation is formulated; minimizing it the model-specific characteristic parameters of the contrast microbubble are obtained. The unique feature of our characterization approach is that after determining the characteristic parameters using attenuation, the model was investigated for validation against a second experimental observation—scattered subharmonic response. Here, we use the experimentally measured attenuation through Sonazoid bubbles and its size distribution to obtain the parameters for all models under investigation. The model-specific encapsulation parameters used in the numerical simulations are listed in Table TABLE I..

Table 1.

Characteristic properties of Sonazoid microbubbles according to various encapsulation models. For Levovist microbubbles, only theChurch–Hoff model is applied.

Encapsulation model	Contrast agent (gas∕encapsulation)	Parameters	f0|R0=3μm (MHz)
Newtonian model (Chatterjee and Sarkar, 2003)	Sonazoid (C4F10∕lipid)	γ = 0.6 N∕m, κs = 1 × 10−8 N s∕m, k = 1.07	1.845
de Jong model (de Jong et al., 1994)	Sonazoid (C4F10∕lipid)	Sp = 0.89 N∕m, Sf = 6.67 × 10−7 N s∕m, k = 1.07	1.7
Church–Hoff model (Andersen and Jensen, 2009; Hoff et al., 2000)	Sonazoid (C4F10∕lipid)	Gs = 52 MPa, μs = 0.99 Pa s, dsh0 = 4 nm, k = 1.07	1.805
Levovist (air∕galactose-palmitic acid)	Gs = 88 MPa, μs = 1.3 Pa s, dsh0 = 6 nm, k = 1.07	2.514
Constant elasticity viscoelastic model (Sarkar et al., 2005)	Sonazoid (C4F10∕lipid)	γ0 = 0.019 N∕m, Es = 0.51 N∕m, κs = 1.2 × 10−8 N s∕m, k = 1.07	1.661
Marmottant model (Marmottant et al., 2005)	Sonazoid (C4F10∕lipid)	γ(R0) = 0.02 N∕m, χ = 0.53 N∕m, κs = 1.2 × 10−8 N s∕m, k = 1.07	1.728
Viscoelastic EEM (Paul et al., 2010)	Sonazoid (C4F10∕lipid)	γ0 = 0.019 N∕m, $E_0^s$ = 0.55 N∕m, α = 1.5, κs = 1.2 × 10−8 N s∕m, k = 1.07	1.742

Note that Sonazoid has a mean radius of 1.6μm (Hoff, 2001;Sontum et al., 1999). We find that for such a radius, none of the above-presented models predicts subharmonic response for excitation amplitudes, where it has been experimentally observed, i.e., the predicted subharmonic thresholds for this radius are much higher than the experimental observations. Specifically, we measured the subharmonic threshold for Sonazoid to be μm~200–350 kPa at frequencies 2–6 MHz (Paul et al., 2010), whereas the models predict no subharmonic for a bubble of radius 1.6μm at these excitation parameters; the minimum subharmonic threshold for this radius is computed as ~500 kPa. However, note that the scattered response of Sonazoid is generated by bubbles of all sizes in its population. The model prediction accounting for the entire bubble population matched extremely well with the experimentally observed subharmonic response (Paul et al., 2010), indicating major contributions from bubbles bigger than the average. Therefore, the number average radius (= 1.6μm) is not representative of the bubbles that are responsible for subharmonic response. We find such a representative radius by computing a subharmonic response weighted average of the bubble distribution:

$$R_{\mathrm{subharmonic}}=\frac{{\int }_{R_{\text{min}}}^{R_{\text{max}}}R{\mathrm{\sigma }}_{\mathrm{subharmonic}}(R;P_A,f)N(R)\mathit{dR}}{{\int }_{R_{\text{min}}}^{R_{\text{max}}}{\mathrm{\sigma }}_{\mathrm{subharmonic}}(R;P_A,f)N(R)\mathit{dR}}.$$ (20)

In the neighborhood of the experimentally observed subharmonic threshold, 200–400 kPa, and at 2 and 3 MHz excitation frequencies, R_subharmonic≈3μm. Therefore, we have presented our results for a Sonazoid bubble of radius 3μm, unless otherwise stated, and the resonance frequency is computed using this value (Table TABLE I.). We have also briefly considered effects of radius variation.

For the free and the encapsulated bubbles, Eqs. 3, 5 are solved, respectively, using a stiff solver (ODE15s) in MATLAB^® (Mathworks Inc., Natick, MA) with initial conditions R=R₀ and $\stackrel{·}{R}=0$. The scattered pressure P_s(t) by a bubble is (Paul et al., 2010)

$$P_S(r,t)=\mathrm{\rho }\frac{R}{r}(2{\stackrel{·}{R}}^2+R\stackrel{\mathrm{··}}{R}).$$ (21)

We use the Fast Fourier Transform (FFT) routine of MATLAB to obtain the power spectrum. For the FFT, we only use the part of the simulation where transients have subsided. We use the peak values corresponding to the different frequencies (i.e., fundamental or different harmonic) in contrast to an integrated value around the peak used in other references (Andersen and Jensen, 2009; Frinking et al., 2010). The resonance frequency used to normalize excitation frequency for a particular model is model specific and has been determined by appropriate formula. We use ρ = 1 000 kg∕m³, μ = 0.001 kg∕m s, and c = 1485 m∕s. To determine the threshold for subharmonic generation, we obtain the variation of subharmonic component with excitation pressure. At low excitation pressures, there is no subharmonic component distinct from the noise level. With increasing excitation pressure, the subharmonic component appears; it grows quickly followed by gradual saturation and eventual disappearance. The excitation pressure just above which a distinct subharmonic peak appears is selected as the subharmonic threshold.

RESULTS

Free bubble dynamics

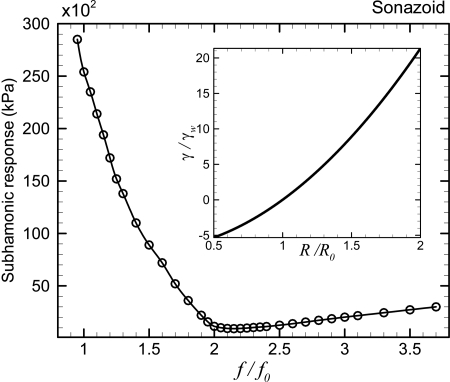
For a free bubble of radius 3μm, the frequency dependent subharmonic threshold at different excitation frequencies normalized by the resonance frequency is plotted in Fig. 1. The minimum threshold is obtained at twice the resonance frequency in conformity with the previous theoretical work on radial oscillations of a free bubble (Eller and Flynn, 1968; Prosperetti, 1977). The absolute value of the minimum threshold obtained is 48 kPa. Note that there is a local minimum of the subharmonic threshold near the resonance frequency. The simulation does not show any subharmonic response for frequencies 1.15≤f∕f₀≤1.35. However at slightly different radius R₀=2μm (also shown in Fig. 1), we find subharmonic response in the entire frequency range considered. Further numerical investigation shows that, for R₀≤2μm, the subharmonic threshold is obtained for the whole range of frequency. However, the threshold increases with decreasing radius. As has been shown in Sec. 2, for an encapsulated microbubble, the interfacial stresses due to the deforming encapsulation changes the effective surface tension. Next, we discuss its effects.

Figure 1.

Variation of the subharmonic threshold of a free bubble with normalized excitation frequency.

Encapsulated bubble dynamics

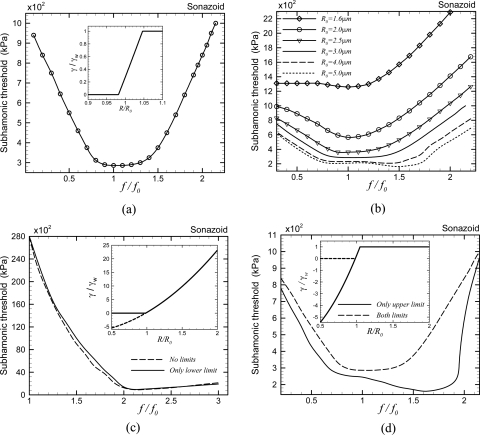
• (A)Newtonian model: The Newtonian model is one of the simplest modifications to the RP equation. It predicted an unusually large value for the surface tension γ, but was able to predict experimentally observed fundamental as well as subharmonic scattering from Sonazoid and Optison microbubbles (Chatterjee and Sarkar, 2003; Sarkar et al., 2005). In Fig. 2 , the global minimum of the subharmonic threshold is obtained at twice the resonance frequency, along with a local minimum at the resonance frequency. In the range of excitation frequency (0.8 ≤ f∕f₀ ≤ 2.3), the predicted values of the subharmonic threshold (385–570 kPa) are in close proximity to those obtained experimentally for a suspension of Sonazoid microbubbles (200–350 kPa) (Sarkar et al., 2005). The numerically predicted subharmonic thresholds of this model are also less than the destruction threshold range (600 kPa–1.6 MPa) of Sonazoid microbubbles (Shi et al., 2000).
• (B)de Jong model: In Fig. 3, we plot the subharmonic threshold for a Sonazoid contrast microbubble using the de Jong model (de Jong et al., 1994). The inset in Fig. 3 (the solid line) shows a linear variation of the effective surface tension with instantaneous radius. Similar to the free bubble case, the de Jong model also predicts a global minimum of the subharmonic threshold near twice the resonance frequency. However, unlike the free bubble model and the Newtonian model, this model does not show any local minimum near the resonance frequency. From the inset of Fig. 3, note that this model predicts much larger values of the effective surface tension (γ(R)>>_γw) for an expanding bubble (R>R₀). This restricts bubble oscillations and thereby results in a much larger subharmonic thresholds (650 kPa–3.3 MPa) than the experimentally observed values (200–350 kPa) in the frequency range 0.8<f∕f₀<3. It has been proposed, e.g., in the Marmottant model that the encapsulation experiences a rupture as the radius increases and the surface tension thereafter is limited by its value at the pure air–water interface (Marmottant et al., 2005). We therefore apply an upper limit on the effective surface tension such that γ≤_γw (shown by the dashed line in the inset of Fig. 3). Note that this modification of the higher values of the effective surface tension does not affect the subharmonic threshold variation at frequencies around twice the resonance frequency, particularly for f∕f₀>2 (shown with dashed line in Fig. 3). However, the large subharmonic thresholds around the resonance frequency are drastically reduced. Thus we conclude that increasing surface tension for an expanding bubble contributes to the larger subharmonic threshold around the resonance frequency. However, overall variation of the threshold curve retains the V shape with a minimum at twice the resonance frequency.
• (C)Church–Hoff model: In Fig. 4 , we plot the subharmonic threshold for Sonazoid according to the model originally proposed by Church (1995) and later modified by Hoff et al. (2000). In the inset, we show the variation of the effective surface tension with bubble radius. In comparison with the model by de Jong, this model limits the increase in the effective surface tension during bubble expansion. For the given model-specific properties of Sonazoid microbubbles (Andersen and Jensen, 2009), the effective surface tension increases to a maximum of 2.57 times the air–water surface tension value. On the other hand, during compression, this model predicts a steep increase in compressive interfacial stress (γ∕_γw=-70 at R∕R₀=0.5). This model, for Sonazoid, predicts a global minimum of the subharmonic threshold at twice the resonance frequency. However, the minimum is quite shallow and there also exists another local minimum of comparable magnitude near the resonance frequency. Although the curve with two minima is similar to what is seen for a free bubble as well as the Newtonian model for an encapsulated bubble, there is a wider frequency band (0.6≤f∕f₀≤2.2) in which the subharmonic thresholds are of comparable magnitude and much smaller than those outside this frequency range. Our main interest lies in the qualitative features of a model which are robust to slight variation of model parameters. Therefore, to further explore this model, we apply it to another contrast agent, Levovist (Schering AG, Berlin, Germany) (parameters are listed in the same Table TABLE I.). We plot the threshold and the effective surface tension in the same figure (Fig. 4). For Levovist, this model predicts larger negative values of surface tension (γ∕_γw=-150 at R∕R₀=0.5) for bubbles in compression. We see here that the minimum at the resonance frequency is slightly deeper than the one at twice the resonance. This further substantiates our conclusion that the minimum has a wider valley between the values from resonance to twice the resonance with two shallow minima at those points. The precise feature of the curve depends on the specific values of the model parameters.
• (D)Constant elasticity model: The zero-thickness Newtonian interfacial rheology model by Chatterjee and Sarkar (2003) was later modified by incorporating a dilatational surface elasticity E^s. The inclusion of a surface elasticity in the modified RP equation allowed them to obtain a realistic value of surface tension (lower than that at the air–water interface) for the Sonazoid microbubbles. However, the constant elasticity model was not able to predict the experimentally observed subharmonic scattering (Sarkar et al., 2005). This can also be seen in Fig. 5 , where we see that the lowest threshold occurring near twice the resonance frequency is 920 kPa, which is much larger than the values (200–350 kPa) observed experimentally. Similar to the de Jong model, this model predicts a single minimum subharmonic threshold near twice the resonance frequency and no minimum around resonance. The curve is also asymmetric in that for f∕f₀≥2, values of the subharmonic threshold are much smaller than those for f∕f₀<2. In the inset of Fig. 5, note that due to the quadratic increase of the effective surface tension with instantaneous radius, this model predicts a steep increase in the tensile stress (γ∕_γw=20 at R∕R₀=2) during expansion. Such large tensile stresses limit the radial expansion resulting in the extremely large subharmonic thresholds.
• (E)Marmottant model: Next we consider the model developed by Marmottant and co-workers (Marmottant et al., 2005) in Fig. 6 . Unlike the free bubble and other encapsulation models, it does not predict any minimum subharmonic threshold at any particular value of excitation frequency; rather it predicts lower subharmonic thresholds over a wider frequency band 0.8<f∕f₀<1.4 [Fig. 6a]. Keeping the encapsulation properties the same, we investigate the effects of the initial bubble radius on the subharmonic threshold [Fig. 6b]. Subharmonic threshold increases with decreasing initial bubble radius. Note that for none of these radii, threshold is minimum around twice the resonance frequency. For larger microbubbles, the valley of lower thresholds is over a wider frequency band. Decreasing the radius shrinks the frequency band of the lower subharmonic thresholds, converging on the resonance frequency. For a polydisperse bubble distribution, minimum threshold would occur at different frequencies for different sizes. Also note that for 1.6μm—the number average radius of Sonazoid—the subharmonic threshold is too high. The Marmottant model [Eq. 15] prescribes three different ranges of variation of the effective surface tension with instantaneous bubble radius. The variation is linear with area fraction, and therefore quadratic with radius between a lower limit—buckling radius, below which surface tension becomes zero (γ=0 for R<R_buckling)and an upper limit—rupture radius where the surface tension becomes identical to that of an air–water interface γ=_γw for  R>R_rupture. We investigate the effects of these two limits on subharmonic thresholds by relaxing them. Note that the initial surface tension is nonzero (0.02 N∕m). In Fig. 6c, we plot the threshold without any limits whereby the form of the Marmottant model becomes identical to the constant elasticity model (12). Consequently, the results are also similar to the one in Fig. 5, with a much larger minimum threshold (930 kPa) near twice the resonance frequency, and no minimum at the resonance. The threshold values are much larger than the ones (200–350 kPa) experimentally observed. Therefore, one or both of these limits on the effective surface tension cause the minimum threshold to shift away from twice the resonance frequency to a valley around the resonance frequency simultaneously lowering the absolute values of threshold there. Next, we only remove the upper limit, in that we allow the surface tension to increase above γ_w for R>R_rupture but impose the lower limit (γ=0 for R≤R_buckling) on the effective surface tension [dashed line in Fig. 6c]. Imposing only the lower limit, i.e., non-negative surface tension, does not significantly alter the result. Therefore the lower limit, without the upper limit, does not play a significant role in subharmonic threshold. In Fig. 6d, only the upper limit on the effective surface tension (γ=_γw for R≥R_rupture) is applied but it is allowed to become negative during compression (shown in the inset with a solid line). The subharmonic threshold shows a minimum over a broad valley of excitation frequency (from the resonance frequency to twice the resonance frequency) similar to the original Marmottant model. Therefore, we note that applying the upper limit on the surface tension drastically reduces the threshold values, particularly at lower frequencies (f∕f₀<2). Further applying the lower limit slightly increases the thresholds and shifts the minimum away from twice the resonance frequency.
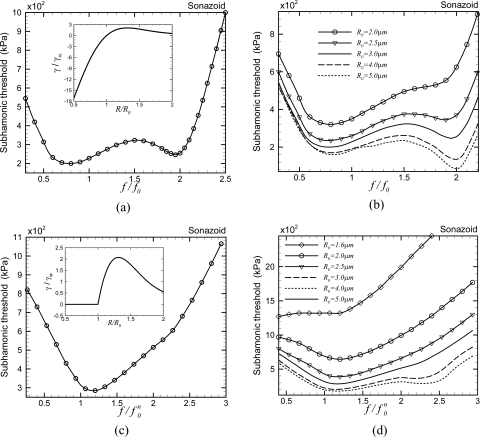
• (F)EEM: Finally, we consider the EEM. To incorporate the effects of strain softening, we modified the constant elasticity model by assuming the interfacial elasticity to decrease exponentially with increasing surface area (Paul et al., 2010). The resulting surface tension versus bubble radius is shown in the inset of Fig. 7a . The model gives rise to a broad valley of lower threshold values from the resonance frequency to twice its value with shallow minima at those two values [Fig. 7a]. Note that the model has an upper limit on surface tension, twice the value at a pure air–water interface, similar to the Marmottant model as well as Church–Hoff model. However, unlike the Marmottant model, it allows surface tension to be negative. In conformity with the above-presented discussion for the Marmottant model, where we show that the upper limit on the surface tension during the expansion phase is critical in determining the subharmonic threshold, we find here that the broad features are similar to the Marmottant and the Church–Hoff models. In Fig. 7b, we see the effects of variation of the initial radius—larger bubble radii sharpen the minimum near twice the resonance frequency, while for smaller radii the minimum is near but at slightly lower value than the resonance frequency, similar to the Marmottant model shown in Fig. 6b.

Figure 2.

Variation of the subharmonic threshold of a Sonazoid microbubble with normalized excitation frequency as predicted by the Newtonian interfacial rheological model.

Figure 3.

Variation of the subharmonic threshold of a Sonazoid microbubble with normalized excitation frequency according to the de Jong model. Inset: Variation of the effective surface tension with instantaneous radius for the same contrast microbubble. Solid line: The original de Jong model. Dashed line: The de Jong model with an upper limit on the effective surface tension [γ=_γw for γ(R)>_γw].

Figure 4.

Variation of the subharmonic threshold of a Sonazoid and a Levovist microbubble with normalized excitation frequency as predicted by the Church–Hoff model. Inset: Variation of the effective surface tension with instantaneous radius for these contrast agents.

Figure 5.

Variation of the subharmonic threshold of a Sonazoid microbubble with excitation frequency as predicted by the constant elasticity viscoelastic model. Inset: Variation of the effective surface tension with instantaneous radius for the same contrast agent.

Figure 6.

Variation of the subharmonic threshold of a Sonazoid microbubble with normalized excitation frequency (a) as predicted by the Marmottant model. Inset: Variation of the effective interfacial tension with instantaneous radius for the same contrast agent. (b) Effect of the radius variation on the same model keeping everything else the same. (c) Marmottant model without any limit on effective surface tension (solid line) and with only a lower limit on the effective surface tension (γ=0 for R≤R_buckling) (dashed line). (d) Marmottant model with only an upper limit on the effective surface tension (γ=_γw for R>R_rupture) (solid line) and the original Marmottant model (dashed line).

Figure 7.

Variation of the subharmonic threshold of a Sonazoid microbubble with normalized excitation frequency (a) as predicted by the viscoelastic EEM. Inset: The variation of the effective surface tension with instantaneous radius for the same contrast agent. (b) Effects of radius variation on viscoelastic EEM. (c) Non-negative [γ=0 if γ(R)<0] viscoelastic EEM. (d) Effects of radius variation on the non-negative [γ=0 if γ(R)<0] viscoelastic EEM. For the non-negative cases (c) and (d), $f_0^n$ is defined in the text.

Finally, we investigate the effects of non-negativity imposed in the buckled state similar to the Marmottant model. The zero surface tension in the buckled state for R<R_buckling facilitates compression which gave rise to “compression-only” behavior observed for certain contrast microbubbles (Marmottant et al., 2005). We have recently shown that the compression-only behavior is a low-excitation phenomenon and can also be predicted by the EEM model, if the non-negativity is enforced on the effective surface tension (Paul et al., 2010). However, imposing non-negativity makes γ(R) not differentiable at R=R₀ [inset of Fig. 7c], making linearization impossible and thereby resonance frequency unobtainable analytically. Note that for the above-considered Marmottant model, initial surface tension γ(R₀)=0.02N∕M; using zero γ(R₀) in the Marmottant model would lead to identical nondifferentiability. Numerically, we find that resonance (maximum fundamental response) occurs at different frequencies in the range 0.7f₀–0.8f₀ (f₀ is the resonance frequency for the original EEM model) for different excitations, even for very small excitations. We choose $f_0^n=0.75f_0$ to normalize the excitation frequency in Fig. 7c. Imposing non-negativity gives a single minimum threshold at the resonance frequency. This is consistent with what we saw before for the Marmottant model that imposing non-negativity shifts minimum threshold toward the resonance frequency. Figure 7d investigates the effects of radius variation with non-negative EEM model to note that for larger bubble radii, there actually exists a second minimum at twice the resonance frequency which disappears for R₀≤4μm. It should be noted that imposing strict non-negativity leads to a bubble never achieving a state of compression. On the other hand, compressive stress leads to buckling of the encapsulation.

DISCUSSION AND SUMMARY

In this paper, we have performed a detailed numerical investigation of the threshold excitation for subharmonic generation according to six different models of contrast microbubbles—(1) Newtonian model, (2) de Jong model, (3) Church–Hoff model, (4) constant elasticity model, (5) Marmottant model, and (6) strain-softening exponentially elasticity model. We have presented each of these models in a common interfacial rheological form where their encapsulation stresses are defined by two terms—an effective radius dependent surface tension γ(R) and an effective dilatational viscosity ^κs(R). Through their appearance in the generalized RP equation they govern the dynamics of a single contrast microbubble. Here, we argue that the qualitative behavior of the subharmonic thresholds according to different models is determined by the effective interfacial rheological parameters in that model.

Simulated subharmonic thresholds for free bubble and one with a Newtonian encapsulation (the same as the free bubble but with a larger value of surface tension and a nonzero dilatational interfacial viscosity) both display a minimum at twice the resonance frequency as predicted by classical perturbative analysis. There also exists a distinct local minimum near the resonance frequency. The absolute value of the subharmonic threshold is higher for Sonazoid according to the Newtonian model compared to a free bubble of the same size because of the larger surface tension value for the former. The values are in close proximity to what has been found experimentally (Paul et al., 2010).

Although de Jong and constant elasticity models assume linear and quadratic variation, respectively, of effective surface tension with radius, both predict very high surface tension in the expansion phase and thereby much higher and unrealistic threshold values with a single minimum around twice the resonance. The overall feature of the threshold curves is also similar for these two models. Note that this also explains the failure of the constant elasticity model to predict the subharmonic response as reported in Sarkar et al. (2005).

The Church–Hoff model was originally developed by Church treating the encapsulation as a viscoelastic layer of finite thickness having a bulk viscosity and a bulk elastic modulus. Hoff later derived a small thickness version of the same. Here we obtain an effective zero-thickness interfacial representation of the stresses. The effective surface tension is found to vary as a polynomial of the inverse of bubble radius; it does not grow beyond a certain value, but can decrease steeply during compression. Note that the Church–Hoff model assumes a linear bulk elastic property for the encapsulation material and the constant elasticity model assumes a linear interfacial elastic property. Doinikov et al. (2009) stated that these two models and the de Jong model are qualitatively identical. In contrast, we note here that the effective surface tension term in each model is qualitatively different, and so are their subharmonic responses. The upper limit on surface tension is also there in the Marmottant and the exponential elasticity models. In the Marmottant model, for radius above a critical value (R>R_rupture) the encapsulation ruptures and the surface tension assumes the value of an air–water interface. The EEM was developed motivated by the failure of the constant elasticity model that insinuated “strain-softening” as the bubble grows. Here the surface elasticity exponentially decreases causing the surface tension to initially increase with radius, but finally saturate. An effective surface tension with an upper bound for these models (in contrast to larger surface tension values in the growth phase for others) makes the bubble less stiff during expansion, giving rise to lower thresholds for subharmonic generation specifically near resonance. The threshold curves for all three models have a broad valley of low threshold values around the resonance and twice the resonance frequencies with shallow minima at both. The threshold minima at resonance and twice the resonance are comparable and depend on radius and the property values.

Note that the classical perturbative results about subharmonic threshold being at twice the resonance frequency were obtained with the assumption of small overall damping of the system. This is also the case for the perturbative analysis of free bubbles. (Eller and Flynn, 1968; Prosperetti, 1977). Eller and Flynn specifically showed that with the introduction of damping the threshold curve changes from a V shape for an undamped system to a rounded U shape with the minimum at twice the resonance frequency increasing with damping. The encapsulation introduces additional damping represented by the interfacial dilatational viscosity ^κs(R) into bubble dynamics. The total nondimensional damping of an encapsulated bubble is

$$\begin{array}{c}\multicolumn{1}{c}{\mathrm{\delta }={\mathrm{\delta }}_{\mathrm{liquid}}+{\mathrm{\delta }}_{\mathrm{rad}}+{\mathrm{\delta }}_{\mathrm{encapsulation}},{\mathrm{\delta }}_{\mathrm{liquid}}=\frac{4\mathrm{\mu }}{{\mathrm{\rho }\mathrm{\omega }}_0{R}_0^2},{\mathrm{\delta }}_{\mathrm{rad}}=\frac{3{\mathit{kP}}_{G0}}{{\mathrm{\rho }\mathrm{\omega }}_0{R}_{0}c},{\mathrm{\delta }}_{\mathrm{encapsulation}}=\frac{4{\mathrm{\kappa }}^s}{{\mathrm{\rho }\mathrm{\omega }}_0{R}_0^3}.}\end{array}$$ (22)

With the material parameters listed in Table TABLE I., which are experimentally determined for Sonazoid, one obtains _δliquid≈0.04, _δrad≈0.006, and _{δencapsulation}≈0.13. The encapsulation increases the damping by an order of magnitude compared to a free bubble. Increased damping typically decreases nonlinear response, and hinders subharmonic generation. Indeed among all three damping terms, _{δencapsulation} increases most rapidly with decreasing radius. Figures 67 show that with decreasing radius, with the same material parameters, the absolute value of the threshold increases, and the distinct minimum at twice the resonance frequency disappears.

The surface tension variation for each of these models is different, except for the upper bound. The Marmottant model is identical to the constant elasticity model between a lower (buckling) and an upper (rupture) limit R_buckling<R<R_rupture—quadratic variation of effective surface tension with γ=0 for R≤R_buckling and γ=_γw for R≥R_rupture. The EEM model does not have any lower limit, and here the constant elasticity model is modified by assuming the dilatational surface elasticity to soften exponentially with area fraction. Despite these differences, the threshold curves look qualitatively similar, although precise details depend on parameter values and bubble radii. For instance, increasing the bubble radius (keeping the property values the same) makes the minimum at twice the resonance more prominent than the one near resonance for both the Marmottant and EEM models.

Removing the upper limit (γ=_γw for R≥R_rupture) in the Marmottant model, i.e., allowing the surface tension to increase in the expansion phase, drastically changes the threshold curve—it becomes similar to those due to the de Jong and the constant elasticity models giving rise to much higher threshold values especially at the resonance frequency. On the other hand, removing only the lower limit (γ=0 for R≤R_buckling) does not change the curve much; it promotes the minimum at twice the resonance frequency. Similarly, imposing such a lower limit on the EEM model degrades the minimum at twice the resonance frequency.

We conclude that the minimum threshold for subharmonic generation from an encapsulated contrast microbubble is not necessarily at twice the resonance frequency. Depending on the model, it occurs in a range from resonance to twice the resonance frequency. The actual minimum for a contrast agent would also depend on the bubble size distribution. Finally, here we study a specific contrast agent Sonazoid using models with a fixed set of material properties. Changing them would affect the subharmonic threshold, an effect to be investigated in the future.