Abstract
Bubbles excited by lithotripter shock waves undergo a prolonged growth followed by an inertial collapse and rebounds. In addition to the relevance for clinical lithotripsy treatments, such bubbles can be used to study the mechanics of inertial collapses. In particular, both phase change and diffusion among vapor and noncondensable gas molecules inside the bubble are known to alter the collapse dynamics of individual bubbles. Accordingly, the role of heat and mass transport during inertial collapses is explored by experimentally observing the collapses and rebounds of lithotripsy bubbles for water temperatures ranging from 20 to 60 °C and dissolved gas concentrations from 10 to 85% of saturation. Bubble responses were characterized through high-speed photography and acoustic measurements that identified the timing of individual bubble collapses. Maximum bubble diameters before and after collapse were estimated and the corresponding ratio of volumes was used to estimate the fraction of energy retained by the bubble through collapse. The rebounds demonstrated statistically significant dependencies on both dissolved gas concentration and temperature. In many observations, liquid jets indicating asymmetric bubble collapses were visible. Bubble rebounds were sensitive to these asymmetries primarily for water conditions corresponding to the most dissipative collapses.
INTRODUCTION
For shock-wave lithotripsy (SWL) treatments, Coleman et al.1 noted the possibility that bubbles may contribute to both stone comminution and renal tissue injury. Moreover, Bailey et al.2 detected cavitation in urine and in tissue as shock waves were applied to a pig kidney. Accordingly, the dynamics of bubbles excited by lithotripter shock waves have received significant attention. Some studies have explored how bubbles near a rigid surface respond to an incident shock wave in order to understand the potential for bubbles to damage the surface (i.e., to enhance stone comminution).3, 4, 5, 6 Other studies have considered the interaction between an incident shock wave and a free-field bubble.7, 8 Yet other work has involved the evolution of a bubble cloud as multiple shock waves are applied.9, 10, 11, 12
In addition, the simplified case of a single, spherical bubble excited by a lithotripter shock wave has been studied to elucidate basic bubble behaviors. In particular, Church13 used such a model to investigate the diffusion of noncondensable gases into lithotripsy bubbles. As predicted by Church and later tested experimentally by Sapozhnikov et al.,14 these bubbles undergo prolonged growth to a radial size on the order of 1 mm, followed by an inertial collapse that occurs hundreds of microseconds after passage of the original shock wave. Because typical lithotripter shock waves last for only about 5–10 μs, the inertial collapse is an unforced Rayleigh collapse that can be readily modeled. As such, observations of the collapses and rebounds of lithotripsy bubbles have been compared to model predictions in order to gain an understanding of the physics relevant to violent bubble collapses.15 Moreover, lithotripsy bubbles are comparable to laser-induced bubbles, which also undergo a prolonged growth and an unforced collapse. Indeed, the collapses and rebounds of millimeter-sized bubbles generated by a focused laser have been used to investigate the physics of collapsing bubbles.16, 17, 18
In previous work, it has been shown that the dynamics of a collapsing vapor bubble can be strongly influenced by the presence of a small amount of noncondensable gas.15, 18, 19, 20 The mechanism behind this sensitivity arises from mass diffusion among vapor and noncondensable gas molecules inside the bubble. During collapse, vapor molecules near the liquid-gas interface (i.e., the bubble wall) condense. If the collapse is rapid enough, a shell of noncondensable gas molecules is left adjacent to the bubble wall so that the rate of condensation is limited by diffusive transport of vapor through the shell of noncondensable gas. Such diffusive transport behavior inside a collapsing bubble may be called vapor trapping. Although the sensitivity to vapor trapping was identified, previous experimental observations of lithotripsy bubbles or laser-induced bubbles did not systematically explore this diffusion problem. Instead, observations were made for air bubbles in water using the same water conditions throughout. When reported, these conditions generally corresponded to degassed water at room temperature. One exception involved a study of laser-induced bubbles at both low (10 °C) and high (35 °C) temperatures,21 which demonstrated measurably larger rebounds at the higher temperature.
Here, we hypothesize that varying the temperature and dissolved gas content of the water will alter the bubble contents and the associated diffusive behavior among vapor and noncondensable gases. In turn, the collapses and rebounds will be affected, thereby providing insight into the underlying diffusive behavior. In addition, testing at elevated temperatures may permit exploration of thermally controlled collapses, for which the rate of collapse is limited by thermal diffusion in the liquid and the corresponding saturation vapor pressure at the bubble wall. In the present work, we characterize the collapses and rebounds of millimeter-sized lithotripsy bubbles under various water conditions. These experiments are primarily intended to provide quantitative measurements that can be compared to model predictions. In a concurrent paper, we propose a reduced-order bubble model that utilizes the experimental data presented here.22 In addition, these observations provide direct insight into the impact that in vivo conditions may have on the collapses of lithotripsy bubbles, which have typically been studied at room temperature in degassed water.
METHODS
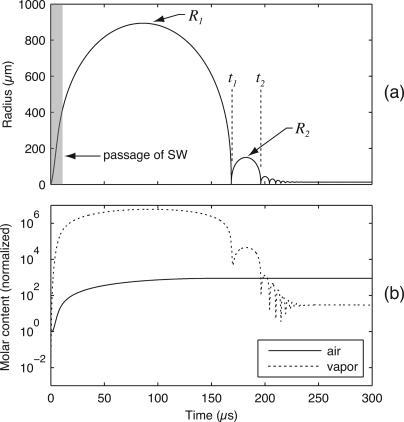
Based on calculations from a model comparable to that presented by Matula et al.,15 Fig. 1 illustrates the basic features of the dynamics of lithotripsy bubbles. The shaded region on the left side of Fig. 1a represents the duration of an incident shock wave; after the shock wave passes, the bubble continues to grow to a maximum size R1 before collapsing inertially at time t1. After collapse, the bubble rebounds to maximum radius R2 and collapses again at time t2. In Fig. 1b, the molar content of the bubble is plotted for an air bubble in water, showing that the amount of vapor can significantly exceed the amount of noncondensable gas.15 The premise behind this work is that ambient water conditions affect the makeup of the bubble as it reaches R1 and begins its collapse. In turn, the contents of the collapsing bubble affect heat and mass transport processes and the energy lost during an inertial collapse. Accordingly, we propose to observe the collapses and rebounds of lithotripsy bubbles under varying water conditions in order to elucidate the attendant transport processes.
Figure 1.
Dynamics of a typical lithotripsy bubble as characterized by (a) the radial dynamics and (b) the gaseous content inside the bubble (note that the plot displays the molar content normalized by the bubble’s initial state). Plotted curves were generated using a model comparable to that from Matula et al. (Ref. 15). The radial dynamics are characterized by prolonged bubble growth after passage of the incident shock wave, followed by an unforced inertial collapse and subsequent rebounds. Consideration of the bubble’s contents demonstrates that the quantity of vapor can easily exceed that of noncondensable gases.
At times corresponding to R1 and R2, the kinetic energy of the water vanishes so that the energy of the flow comprises the pressure-volume potential energy of the bubble. Assuming that the bubble is expanded against a constant pressure, the ratio of bubble volumes (R2∕R13 represents the fraction of energy retained by the bubble through collapse. This normalization strategy was also adopted by Vogel and Lauterborn16, 17 and suggests that bubble behavior through collapse can be quantified simply by measuring R1 and R2. With this approach, we note that details of the incident shock wave are important only to the extent that they determine R1. Moreover, the initial bubble size prior to shock-wave arrival is not important unless the initial quantity of dissolved gas is significant compared to the amount that diffuses into the bubble prior to collapse. For initial sizes on the order of microns and maximum sizes R1 on the order of a millimeter as shown in Fig. 1b, this initial amount of noncondensable gas is negligible.13, 14 As a final note on the bubble’s initial conditions, the characteristic length for diffusion among gas and vapor molecules will be of the same order as the bubble radius when the bubble approaches R1 and the dynamics are slow.15, 20 As such, it is reasonable to assume that the contents of the bubble are spatially homogeneous at the start of collapse, regardless of the particular path by which R1 is reached.
Based on the preceding discussion, the dynamics of unforced collapses of lithotripsy bubbles should be specifically sensitive to the water conditions. To explore these dynamics, the collapses and rebounds of lithotripsy bubbles were observed for water under nine separate test conditions obtained by combination of three nominal temperatures (20, 40, and 60 °C) and three nominal concentrations of dissolved gases (10%, 50%, and 85%). These conditions are labeled cases A–I in Table TABLE I.. The selected temperatures approximately represent room temperature, a physiological body temperature, and an elevated temperature that can be reached in therapeutic ultrasound applications. The selected levels of dissolved gases approximate degassed, intermediate, and saturated conditions. Table TABLE I. shows both nominal and as-tested conditions. To characterize the bubble dynamics in terms of maximum radii R1 and R2, high-speed photography was used in conjunction with passive acoustic detection of the collapse events at t1 and t2 [see Fig. 1a]. Details regarding the experimental arrangement for data acquisition (see Fig. 2) as well as the procedures used for data analysis are described in detail below.
Table 1.
Test conditions in water—nominal and measured.
| Dissolved O2 content | |||
|---|---|---|---|
| Temperature | 10% | 50% | 85% |
| Case A | Case B | Case C | |
| 20 °C | 31 bubble observations | 37 bubble observations | 30 bubble observations |
| (min: 18.5 °C, 7.4%) | (min: 19.5 °C, 47.3%) | (min: 19.7 °C, 79.0%) | |
| (max: 19.6 °C, 9.6%) | (max: 21.5 °C, 50.4%) | (max: 21.4 °C, 84.3%) | |
| Case D | Case E | Case F | |
| 40 °C | 42 bubble observations | 20 bubble observations | 23 bubble observations |
| (min: 39.5 °C, 7.8%) | (min: 39.3 °C, 47.1%) | (min: 38.5 °C, 81.0%) | |
| (max: 40.6 °C, 10.6%) | (max: 40.4 °C, 49.1%) | (max: 40.4 °C, 83.7%) | |
| Case G | Case H | Case I | |
| 60 °C | 46 bubble observations | 43 bubble observations | 22 bubble observations |
| (min: 59.6 °C, 8.5%) | (min: 59.0 °C, 48.8%) | (min: 58.1 °C, 69.1%) | |
| (max: 61.6 °C, 14.4%) | (max: 61.1 °C, 56.2%) | (max: 61.2 °C, 79.3%) | |
Figure 2.
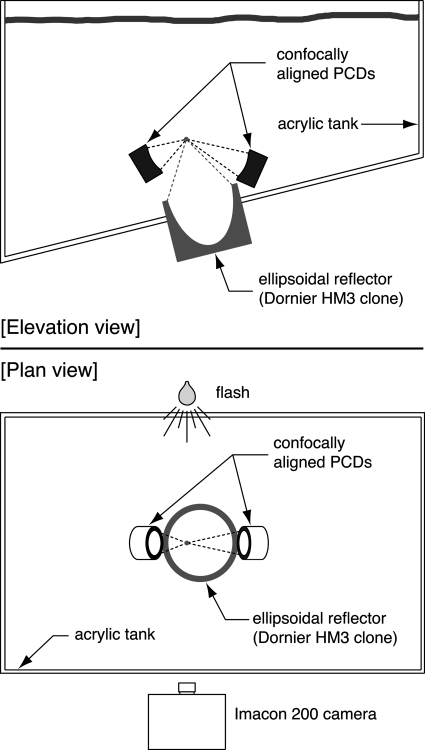
(Color online) Schematic of the experimental arrangement. Passive cavitation detectors (PCDs) inside the test tank are aligned confocally with the lithotripter. A high-speed camera is set up outside the tank to photograph bubbles in the focal region using backlighting from a noncollimated flash source.
Experimental arrangement
Maintenance of water conditions
The water used in the experiments was tap water with table salt added to achieve an approximate conductivity of 600 μS∕cm, which is necessary for proper operation of an electrohydraulic lithotripter. Prior to acquisition of data, the water was recirculated through a flow system to perform the following functions: (1) filtration characterized by a removal of particulates larger than 2 μm (Nexis C series cartridge, Pall Corporation, East Hills, NY); (2) liquid degassing using a Liqui-Cel 4×13 membrane contactor (Membrana, Charlotte, NC) in conjunction with a diaphragm vacuum pump (Vacuubrand MZ 2C pump, BrandTech Scientific, Inc., Essex, CT); and (3) heating with a 4.5 kW stainless steel circulation heater (Gaumer Company, Inc., Houston, TX).
In order to maintain a given set of conditions from Table TABLE I. during testing, the temperature and dissolved oxygen concentration of the water were measured roughly every 30 minutes. An Oxi 330i meter with a CellOx 325 probe (WTW Wissenschaftlich-Technische Werkstätten GmbH, Wellhelm, Germany) was used to measure dissolved oxygen concentrations and was calibrated each day measurements were taken. Because this meter only functions up to 50 °C, measurements pertaining to the 60 °C water conditions utilized an indirect approach. With this approach, the dissolved oxygen content was measured at approximately 50 °C, both before and after observations occurred. These measurements were then interpreted as a percentage of the saturation concentration at 60 °C. Some uncontrolled changes in dissolved gas content inevitably took place while bubble observations were made and while the water underwent heating and cooling. However, consistent concentration measurements were found to be possible, and these measurements imply that the intended test conditions at 60 °C were maintained reasonably well. For temperature measurements, readings from the thermistor built into the CellOx 325 probe were used. At temperatures above 50 °C, these readings were not available; instead, measurements were taken directly with a type K thermocouple connected to a Fluke 179 multimeter (Fluke Corporation, Everett, WA).
The ranges of water conditions recorded during bubble observations are summarized within parentheses in Table TABLE I.. In general, temperature was controlled to the nominal target temperature ±1 °C. Dissolved oxygen concentrations were somewhat more difficult to control, especially at 60 °C. However, because these measurements were acquired within 10 cm of the water’s surface, the actual variations at the lithotripter’s focus were likely smaller (the focus was about 46 cm beneath the surface). With the exception of case I, measurements of dissolved oxygen content were controlled approximately to the target level ±5%.
At this point, it is instructive to consider the extent to which measurements of dissolved oxygen concentration accurately reflect the state of dissolved atmospheric gases in water. Here, degassing is performed by applying some level of vacuum to the water within the gas contactor. If we assume that equilibrium is achieved at the gas contactor and that the applied vacuum equally reduces the partial pressures of all atmospheric gases, then the concentrations of all dissolved gases will be the same fraction of saturation conditions at atmospheric pressure. In this way, reporting the % saturation of dissolved oxygen at any given temperature is representative of the overall state of dissolved gases as long as equilibrium is maintained by applying a vacuum to the gas contactor. Such equilibrium was maintained for test conditions at 20 and 40 °C. However, we note that water was heated and cooled between 50 and 60 °C without re-establishing equilibrium at the gas contactor. Under such conditions, differences in the variation of gas solubilities with temperature could have led to variations in the concentrations of some gases relative to saturation conditions. Consideration of the solubilities of argon, oxygen, and nitrogen suggests that dissolved oxygen concentrations should have remained representative of each of these gases. In contrast, the solubility of carbon dioxide is much more sensitive to temperature than is the solubility of oxygen. Nonetheless, the relative scarcity of carbon dioxide in atmospheric air implies that the concentration of oxygen remained a reasonable metric for the state of dissolved gases in the liquid.
Acoustics configuration
The acoustical setup includes the shock-wave source, passive cavitation detectors (PCDs), and the walls of the test tank, which are all depicted in Fig. 2. Shock waves were generated by the APL-UW lithotripter,23 which is an electrohydraulic source designed to simulate the original Dornier HM3 lithotripter. In order to excite a suitable cavitation field, new electrodes used for fewer than 200 shots were fired at typical voltages near 21 kV.
To detect the collapses of individual bubbles, the approach developed by Cleveland et al.24 was adopted in that two spherically focused PCDs were aligned confocally with the lithotripter. It was determined that PCDs with broadband frequency characteristics were required to resolve temporally the collapses of individual bubbles. Accordingly, broadband detectors fabricated as prototypes25 at the Center for Industrial and Medical Ultrasound (Applied Physics Laboratory, University of Washington, Seattle, WA) were used. The active element of the PCDs was a sheet of polyvinylidene fluoride film that was 25 μm thick. This sheet conformed to a concave spherical shape against an epoxy backing to produce a focused broadband receiver with an aperture of 50 mm. Two PCD geometries were used, possessing focal distances of 10 cm and 15.4 cm. Used as sources driven at 3.6 MHz, the -6 dB focal regions were characterized as ellipsoids with the following length × width characteristics: 17 mm × 1.2 mm (PCD with 10 cm focal length) and 47 mm× 2 mm (PCD with 15.4 cm focal length).
Data from the PCDs were captured on a digital oscilloscope with a sampling frequency of 50 MHz, dc coupling, and a 50 Ω input impedance. One PCD was routed through an analog high-pass filter set at 200 kHz (model 3202, Krohn-Hite Corp., Brockton, MA) before being digitally captured on the oscilloscope. This analog filtering facilitated immediate interpretation of the signal. All saved data from PCDs were downloaded from the oscilloscope over a GPIB connection using a personal computer and a custom Labview program (National Instruments, Austin, TX). Note that the oscilloscope and the high-speed camera were triggered concurrently, so that PCD traces were temporally aligned with the images captured by the Imacon 200 high-speed camera. To further assist in the interpretation of acquired PCD signals, PCD orientations relative to the high-speed images were recorded. As shown in Fig. 2, the PCDs were positioned so that their acoustic axes resided within the focal plane of the camera. By taking photographs of alignment pointers attached to each PCD, both the focal location and the orientation of the acoustic axis of each PCD was identified in subsequent photographs. This information in conjunction with the -6 dB focal regions described above were used to define regions in each image to which the PCDs were sensitive.
Optics configuration
An Imacon 200 high-speed camera (DRS Technologies, Parsippany, NJ) was used to capture images of the collapses and rebounds of bubbles excited by lithotripter shock waves. The camera is capable of capturing sequences of 14 image frames at rates up to 200 million frames per second using seven separate charge-coupled devices (CCDs). Each image frame comprises 980 pixels in height × 1200 pixels in width, where each pixel contains an 8-bit grayscale value. The camera was used with a 105 mm lens and a PK-13 extender ring (Nikon, Inc., Melville, NY). The f∕stop was set at the smallest possible value (f∕2.5) to allow passage of maximum light. The remainder of the optical settings were adjusted through the software used to control the camera. As such, the internal iris was set at f∕2, the exposure duration was set at 1 μs, and the gain for each CCD was set at zero (the lowest available level). This optical configuration yielded a pixel size of about 19 μm, as determined by the calibration of 53.2 pixels per millimeter described below.
The physical setup of the camera and lighting are illustrated in Fig. 2. Bubbles were backlit using light from a noncollimated flash source (Photogenic PowerLight 2500DR, Bartlett, IL). Also, a single sheet of white office paper was taped to the acrylic wall of the test tank to diffuse light from the flash. The standoff distance between the front edge of the 105 mm lens and the optical plane of focus was about 45 cm. For this arrangement, the depth of focus was determined to be about 1.5 cm; moving beyond this range, objects became blurry though still visible. Notably, the −6 dB focal region of the APL-UW lithotripter was reported to be about 1 cm transverse to the acoustic axis.23 Given that the optical focal plane of the present setup contained the acoustic axis of the lithotripter, it is reasonable to expect that the full breadth of the cavitation field transverse to the acoustic axis was visible in the photographs.
Data analysis
Image processing and calibration
To calibrate measurements of bubble radius from high-speed photographs, an image processing algorithm was developed and calibrated. The software algorithm was implemented in matlab (The MathWorks, Natick, MA) and consisted of the following basic steps:
-
(1)
Selection of a target bubble for analysis, thereby defining an analysis window of 150 × 150 pixels.
-
(2)
Utilization of the “graythresh” function in matlab to identify a grayscale threshold level that identifies the edges of photographed bubbles. This step was necessary to account for frame-to-frame lighting variations typical of the multiple-CCD camera used to capture images.
-
(3)
Image segmentation based on the identified threshold.
-
(4)
Application of morphological operations to obtain a representation of the bubble as a singly connected region.
-
(5)
Determination of bubble diameter by measuring the width of the segmented bubble region along 18 separate directions. The median of width measurements was adopted in order to limit the impact of spurious noise in the segmented image. This approach presumes that the bubble is approximately spherical as it grows to reach a maximum size.
Accordingly, the image processing provided a measurement of bubble diameter in pixels. To calibrate this value to physical units, a photograph of a ruler was taken to determine a scaling of 53.2 pixels per millimeter. Last, we note that the results of all automated measurements were reviewed manually to correct occasional segmentation errors.
In addition, optical effects pertinent to bubbles were considered. In particular, we explored the impact of light diffraction for a spherical target as well as light refraction at the air-water interface. To this end, the image processing algorithm was tested on photographs of both glass and nylon spheres that were taken using the optical configuration described above. With this approach, photographs of opaque nylon spheres are assumed to include relevant diffraction effects, while transparent glass spheres also include refraction effects. Both types of spheres had a nominal diameter of 2.38 mm and were characterized by direct micrometer measurements. First, we note that within a given photographic sequence, frame-to-frame diameter measurements were quite consistent with standard deviations less than 1% of the estimated diameter. As such, the image processing algorithm successfully adapted to variable lighting conditions among different image frames. In addition, using the predetermined scaling of 53.2 pixels per millimeter, absolute diameter estimates of both types of spheres were within about 2% of the micrometer measurements. We conclude that diffraction and refraction effects are not especially large and that an accuracy of about 2% can be expected for measurements of bubble radii on the order of 1 mm. This 2% uncertainty corresponds to roughly the width of one pixel. Assuming a similar one-pixel uncertainty for smaller bubbles, the smallest rebounds observed in this work (from case A) would have about an 8% uncertainty for radii estimated from photographs.
PCD signal processing
Recorded traces from PCDs were post-processed in matlab to enhance their utility in identifying bubble collapses. First, signals were bandpass filtered between 0.8 and 3 MHz with a 200th-order finite impulse response filter. These bandpass frequencies were chosen to maintain good temporal resolution for discerning the timing of individual collapses, while still removing much of the high-frequency noise. Then, each trace was synchronized with the corresponding photographic images. Time zero was set to correspond to the arrival of the shock wave at the lithotripter’s focus, while propagation delays associated with each PCD’s focal length were accounted for.
Normalization of bubble rebounds
For millimeter-sized bubbles, surface tension can be neglected so that the energy possessed by a spherical bubble when its radial velocity vanishes is a pressure-volume potential energy. For the expansion of a vapor bubble to maximum radius Rm in a liquid with static pressure p0, this energy can be expressed as
| (1) |
where p is the saturation vapor pressure of the liquid.16 For the lithotripsy bubble dynamics illustrated in Fig. 1, the pressure difference p0-pν remains constant. Although p is a function of temperature in general, the bubble dynamics are slow and isothermal26 when R1 and R2 are measured; p can be evaluated at the ambient water temperature at these times. Accordingly, the energy retained by the bubble through its collapse can be normalized relative to the bubble’s initial energy using the volume ratio (R2∕R13. For convenience, this ratio is termed “rebound energy” in the discussion of results below.
Using photographic images of a bubble’s collapse and rebound, R1 and R2 can be measured directly using the image processing algorithm described above. For R1, the bubble is relatively large and its radius can be estimated reliably from photographs. While this same approach often works for R2, the limited temporal and spatial resolution of the camera can present challenges in estimating R2. As noted by Vogel and Lauterborn,16R2 can also be estimated if the collapse times t1 and t2 are known. Because the bubble rebound is characterized by an inertial growth and collapse, the maximum radius R2 can be calculated by assuming that t2-t1 represents the duration of two Rayleigh collapses
| (2) |
where ρ0 is the liquid density. With this approach, R2 can also be estimated from PCD data. However, Vogel and Lauterborn note a complication associated with Eq. 2. They observed that for bubbles collapsing asymmetrically, Eq. 2 can overpredict the maximum radius R2 by as much as 50%.
Independent estimates of R2 from photographs and PCD data were generally similar. Because PCD data can be expected to overestimate R2 when bubble asymmetries are present, lower estimates from image data are likely more accurate. However, for some of the smaller rebounds, blurry images of bubbles were found to yield measurements of R2 that were larger than those inferred from PCD data. In such cases, the PCD data should provide a better estimate as an upper bound on the maximum radius. Aside from potential overestimates from analyzed images, the relatively small number of image frames implies that underestimates could occur when the true maximum bubble size was not observed. For the smallest bubble rebounds, the temporal sampling of image frames could account for about a 12% underestimate of the maximum radius. Hence, even in a worst-case scenario, this bias would be on the order of the one-pixel measurement uncertainty described above. Considering the possibility for image-based estimates to be biased either high or low and the availability of collapse-time estimates from PCD data as an upper bound, we take R2 to be the smaller of these estimates.
RESULTS
Test observations
Each time a shock wave was fired by the lithotripter, high-speed photographs of the cavitation field and corresponding PCD traces were captured. Shock waves were fired at a rate much slower than one per second, so bubbles did not accumulate between shocks. Many shock waves produced either no significant bubbles or dense clusters of bubbles that did not include an inertial collapse of an isolated bubble. Such data were not saved for further analysis. Data that were saved and ultimately analyzed possessed two main characteristics: (1) a sparse cavitation field containing a bubble whose motion could be correlated with PCD data and (2) an inertial collapse and rebound that were not disturbed by acoustic reflections within the tank.
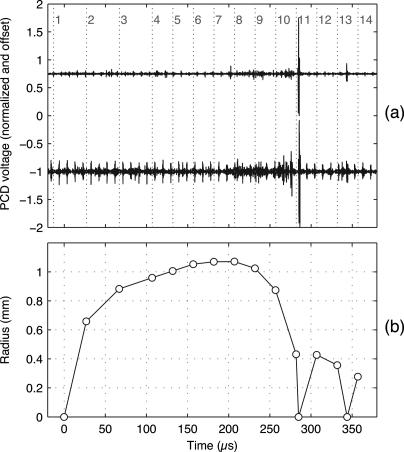
The cavitation field produced by each shock wave was evaluated first when data from each shock wave were captured and then either saved or discarded. Later, the suitability of individual bubbles for analysis was evaluated again, using input from several of the authors to assign “acceptable,” “marginally acceptable,” or “unacceptable” grades to each target bubble. Grading criteria involved the overall density of bubbles in the field of view, the distance between the target bubble and nearby bubbles, and the dominance of the target bubble. Here, dominance refers to not only the bubble size, but also the collapse timing. Bubbles that collapsed later were judged to be more dominant because their rebounds would be less affected by the main collapses of other bubbles. Given the focal depth of the images and the beamwidth of the lithotripter shock wave, images included bubbles throughout the 1.5 cm focal depth of the camera. Because the images do not provide out-of-plane depth information on bubble positions, it was not possible to make meaningful estimates of the distances between bubbles or to apply quantitatively explicit grading criteria (though a visible one-diameter gap was used as a guideline for the minimum spacing between similarly sized bubbles). Despite the qualitative nature of the grading process, trends in the results were not affected by inclusion of the marginal bubbles in the analysis; accordingly, the uncertainty of the grading process likely had minimal impact. Figure 3 shows a sample photographic image sequence with a target bubble that was judged to acceptably represent the inertial collapse and rebound of a single bubble. As exemplified by Fig. 4, data from the captured images were successfully correlated with PCD data to provide a clear estimate of the bubble’s radius-time curve.
Figure 3.
Sample photographic sequence in which the image frames proceed from top to bottom, left to right. Each frame includes a time stamp, two highlighted regions identifying the −6 dB sensitive regions of the PCDs, and a 2.8 mm square box outlining a target bubble for analysis. In the referenced time scale, the shock wave arrived at the center of the field of view at time zero. The image sequence was captured under case A conditions.
Figure 4.
(Color online) Processed data corresponding to the photos from Fig. 3. (a) Measured PCD voltages that have been filtered, normalized to obtain peak absolute values of 1, and offset by ±1 for plotting on the same axes. Vertical dotted lines with numbers indicate the timing of sequential image frames from the camera. Note that a short pressure spike near frame 11 marks the target bubble’s primary inertial collapse, while another spike between frames 13 and 14 marks the subsequent collapse of the bubble’s rebound. Note that the upper trace corresponds to the smaller PCD focal area highlighted in Fig. 3. (b) Radius-time curve based on analysis of photographic image frames. In addition, a radius of zero has been set at time zero and at times corresponding to the PCD spikes.
Regarding the acoustics of the tank, two distinct types of reflection were observed to interfere with bubble collapses and rebounds. The first type was detected by tracking the responses of small, nondominant bubbles in photographic images. The arrival of a reverberated pressure wave was observed to re-excite bubbles that had disappeared after being originally excited by the focused shock wave.27 The arrival time of this wave was found to vary with the height of the water in the tank. Moreover, this timing was consistent with a scattering of the focal shock wave, such that a scattered wave traveled from the focal region to the water surface and back. To address this issue, the water level was raised to delay this reflected wave and prevent its interference with bubble rebounds.
The presence of a second type of reflection was gleaned from the shapes of measured radius-time curves. As shown in Fig. 4b, the bubble appears ready to collapse at about 120 μs; however, the bubble then grew more prior to collapsing. This pattern of secondary bubble growth was observed consistently. The radius-time curves of some bubbles even exhibited a distinct “double hump” shape, suggesting that an imminent collapse was reversed by the arrival of a tensile wave. Such behavior is qualitatively different from the extended bubble growth that has been predicted within a cloud of interacting lithotripsy bubbles.9, 28 Moreover, this behavior does not appear to be directly related to the electrohydraulic generation of the shock wave. Shock-wave generation does involve the creation of a vapor bubble that eventually collapses to produce a secondary pressure wave; however, vapor-bubble collapse happens much later, after milliseconds.29 We propose that secondary pressure waves are caused by reverberations within the brass ellipsoidal reflector. Simulation of these reverberations and the pressures reradiated into the tank suggests that this mechanism may explain our observations.30 To minimize the influence of these secondary pressure waves caused by ringing in the reflector, we only consider bubbles that underwent a Rayleigh collapse that began at least 160 μs after the arrival of the focused shock wave. The specific value of 160 μs was determined empirically from observations of many bubbles.
Careful evaluation of the acoustic conditions within the test tank allowed the collection of a set of observations that represent the bubble dynamics rather than unintended effects of the test environment. However, these observations were still inherently noisy in that the cavitation field was not repeatable. To address this issue, thousands of shock waves were fired and many observations were saved and analyzed for each test condition in order to build statistical confidence. Overall, the collapses and rebounds of 294 bubbles were found to meet the requirements outlined above and therefore were used in the analysis. For these observations, the maximum radius R1 ranged from about 0.7 to 1.2 mm, while rebound energies were not found to be sensitive to R1. Again, the term “rebound energy” represents the fraction of energy retained through collapse as defined by the volumetric ratio (R2∕R13.
Compiled rebound data
In order to interpret the acquired data, two types of statistical analysis were used. For rebounds corresponding to a single test condition, the sample mean and standard deviation were used to characterize central tendency and variance. For data involving more than one test condition, the rebounds from each test condition were compared to one another with analysis of variance (ANOVA) estimates. The ANOVA estimates represent a generalization to multiple groups of the t-test, which is used to assess the statistical significance of the difference in means between two normally distributed groups.
First, group means were compared across all nine test conditions with ANOVA estimates calculated in matlab. Figure 5 displays the results, showing estimated sample means and corresponding 95% confidence intervals. Intervals that do not overlap imply that the corresponding test conditions have different means at the 0.05 level. There are significant differences among various test conditions, while the case A rebounds are most different from all others. The uniqueness of case A is notable; the room-temperature, degassed conditions that are most common for in vitro cavitation studies are significantly different from the in vivo conditions roughly represented by case F. Overall, it is apparent that both dissolved gas content and temperature influenced bubble rebounds. In the prior literature, the sensitivity to dissolved gases was not anticipated for comparable laser-induced bubbles.18
Figure 5.
Comparison of sample means across all test conditions. One-way ANOVA is performed on all analyzed data. The plot shows estimated means in conjunction with 95% confidence intervals. Any cases with confidence intervals that do not overlap have means that are significantly different at the 0.05 level. The different symbols are used to facilitate visual identification of different dissolved gas levels.
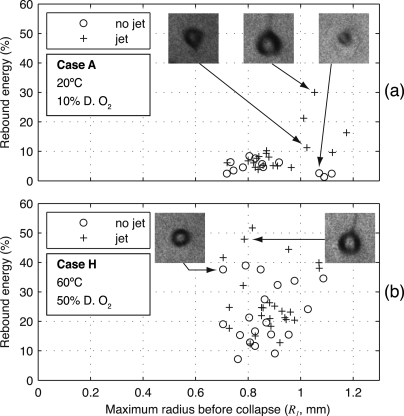
Although it is insightful to broadly compare all analyzed data, heterogeneity within the data for some test conditions merits consideration. In particular, we consider the sensitivity of rebounds to the presence of bubble asymmetries. Although the photographic images lacked the resolution to discern the bubble’s shape during late stages of collapse, a liquid jet was clearly visible during many of the rebounds. Often, the jet remained visible for tens of microseconds. To illustrate the influence of bubble asymmetries, Fig. 6 contains scatter plots of bubble rebounds from cases A and H, distinguishing among bubbles in which a liquid jet was or was not visible (note that similar scatter plots for all cases are provided in Ref. 27). Although the lack of a visible jet does not necessarily imply that the bubble maintained its sphericity through collapse, we refer to such bubbles as “symmetric” below. For case A, all symmetric rebounds were small with fractional energies below 10%; however, several of the asymmetric rebounds were quite large with energies as high as 30%. By comparison, symmetric and asymmetric rebounds for case H were equally mixed at low and high rebound energies.
Figure 6.
Scatter plot of bubble rebound energies for test conditions from (a) case A and (b) case H. The plots sort the observations based on symmetry, distinguishing bubbles for which an involuted liquid jet was visible during the rebound. Inset photographs represent the indicated data points, showing bubbles with and without jets during their rebounds. Each inset photograph corresponds to a height and width of 2.8 mm. For case A, the asymmetric collapses corresponded to larger rebound energies; this trend was not present for case H collapses.
The apparent sensitivity of case A rebounds to asymmetries may seem counterintuitive. Asymmetries leading to liquid jets imply the conversion of energy into nonvolumetric oscillation modes; hence, we might expect smaller rebounds when jets were visible. However, this phenomenon was explained by Vogel and Lauterborn in studying the collapses of laser-induced bubbles near a solid boundary.16 They demonstrated that bubbles collapsing symmetrically radiate larger acoustic transients and have smaller rebounds. Under the conditions tested (although not explicitly reported, we assume degassed water at room temperature), they found up to 90% of the energy lost during collapse to be radiated in an acoustic transient. Because asymmetric bubbles achieve lower internal pressures during collapse, they radiate less acoustic energy.6 Hence, for violent collapses that involve acoustic radiation as the dominant damping mechanism, asymmetric bubbles will tend to have larger rebounds. For less violent collapses, asymmetries can be expected to have less of an impact on rebounds, as was observed for case H.
For each test condition, a t-test comparison of the sample means for symmetric and asymmetric collapses was performed. For cases A–D, the means were significantly different at the 0.05 level. While only one symmetric collapse for case E prevented such a comparison, the means were not significantly different for cases F–I. Considering Fig. 5, rebounds were only sensitive to asymmetries for the conditions with the smallest rebounds. This result is consistent with the interpretation that asymmetries primarily affect damping by acoustic radiation, which in turn is most important for highly damped rebounds. To summarize all of the analyzed rebounds while distinguishing the symmetric collapses, sample means and standard deviations are plotted in Fig. 7. More specifically, for each test condition, the mean ± one standard deviation is plotted both for symmetric collapses and for all collapses. The relevant number of observations is listed above each of the plotted statistics.
Figure 7.
Compiled data for bubble rebound energies for cases A–I. For each data set considered, the mean rebound energy is plotted as a circle or a triangle, while the vertical bar represents the mean ± one standard deviation. Note that these vertical bars thus have a different meaning from those in Fig. 5, which denote confidence intervals. For each “case,” two data sets are plotted: collapses with no visible jet on the left (open circles) and all collapses on the right (filled triangles). The number above each data set is the number of observations. Accordingly, for case A conditions, there were 12 observed collapses with no visible jet out of 31 total collapses.
DISCUSSION AND CONCLUSIONS
The collapses and rebounds of lithotripsy bubbles were explored across a range of water conditions in order to elucidate the dynamics of inertial bubble collapses and the attendant heat and mass transport processes. Bubble responses were characterized by high-speed photography of bubbles and acoustic measurements of bubble collapse times, thereby enabling estimation of the fraction of energy retained by the bubble through collapse and into the ensuing rebound. Although bubble rebounds were observed to be affected by acoustic reflections within the test tank, two main types of reflections were identified and addressed. The data recorded in this effort are inherently “noisy” given the random nature of the cavitation field. Potential sources of variability include interactions of the target bubble with other bubbles, acoustic reflections in the test tank that were not identified, and asymmetries during bubble collapses. In spite of such variability, statistical analysis of the data reveals meaningful trends in that bubble rebounds are influenced by both dissolved gas content and temperature.
Among the conditions tested, case I (60 °C, 85% dissolved oxygen) deserves some particular attention. Case I data have a mean that is surprisingly lower than that from cases F, G, and H. This apparent anomaly could be indicative of the actual bubble physics; however, the test conditions involved unique circumstances. During the case I testing, dissolved oxygen concentrations were measured to remain below saturation; nonetheless, quasistatic bubble growth was observed on surfaces inside the tank. Considering the solubility properties of the various atmospheric gases, it seems likely that carbon dioxide had reached a state of supersaturation. Carbon dioxide is particularly likely to have been involved because its solubility is more sensitive to temperature than the other gases. As such, carbon dioxide approaches saturation conditions fastest as temperature increases. In addition, the high absolute solubility of carbon dioxide implies fast bubble growth under supersaturated conditions.31 Case I tests were apparently conducted under unique conditions in which one or more gases were very close to their saturation threshold. Accordingly, it was very difficult to limit the presence of bubble nuclei, thereby making the study of single-bubble behavior especially difficult.
Using statistical analyses across all test conditions, we can synthesize an interpretation of the data that best represents the idealized situation of a single, spherical bubble that is often addressed in models. As a starting point, we take the symmetric collapses from Fig. 7 to be most representative of cases A–D. For the remaining test conditions, symmetric collapses were not statistically distinguishable from asymmetric ones; moreover, very few symmetric collapses were observed for cases E and F. Accordingly, we consider the data from all collapses to best represent cases E–I. Based on the lone symmetric data point for case E, it is reasonable to speculate that more data may have confirmed a lower rebound energy than implied by the average of all data.
Beyond the selection of data sets represented in Fig. 7, we further examine the data from case A in comparison with observations of comparable laser-induced bubbles. Akhatov et al.18 reported a rebound energy of about 2.4% for spherical collapses in distilled water at 23 °C. In their setup, they were able to evaluate the symmetry of collapses more carefully than was done in the present effort. Hence, considering their water conditions to be comparable to case A, we would expect their results to reflect more symmetric and less energetic rebounds. Indeed, their data at 2.4% are lower than the symmetric average for case A (4.7%). If we further refine our interpretation of case A data to only include the smallest several rebounds (presumed to be the “most” symmetric), we obtain a rebound energy that effectively matches the value from Akhatov et al. Such consistency with prior results provides some validation of the present data, especially noting that completely different experimental techniques were used.
ACKNOWLEDGMENTS
We thank our collaborators at the Center for Industrial and Medical Ultrasound. In particular, we thank Brian MacConaghy and Adam Maxwell for fabrication of the PCDs and Francis Olson for other equipment design and fabrication. This work was supported by the National Institutes of Health (Grant Nos. DK 43881, DK070618, EB007643 and T32 Bioengineering Cardiovascular Training grant) and the National Space Biomedical Research Institute through NASA Grant No. NCC 9-58.
References
- Coleman A., Saunders J., Crum L., and Dyson M., “Acoustic cavitation generated by an extracorporeal shockwave lithotripter,” Ultrasound Med. Biol. 13, 69–76 (1987). 10.1016/0301-5629(87)90076-7 [DOI] [PubMed] [Google Scholar]
- Bailey M., Pishchalnikov Y., Sapozhnikov O., Cleveland R., McAteer J., Miller N., Pishchalnikova I., Connors B., Crum L., and Evan A., “Cavitation detection during shock-wave lithotripsy,” Ultrasound Med. Biol. 31, 1245–1256 (2005). 10.1016/j.ultrasmedbio.2005.02.017 [DOI] [PubMed] [Google Scholar]
- Pishchalnikov Y., Sapozhnikov O., Bailey M., Williams J., Cleveland R., Colonius T., Crum L., Evan A., and McAteer J., “Cavitation bubble cluster activity in the breakage of kidney stones by lithotripter shockwaves,” J. Endourol. 17, 435–446 (2003). 10.1089/089277903769013568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iloreta J. I., Fung N. M., and Szeri A. J., “Dynamics of bubbles near a rigid surface subjected to a lithotripter shock wave. Part 1. Consequences of interference between incident and reflected waves,” J. Fluid Mech. 616, 43–61 (2008). 10.1017/S0022112008003066 [DOI] [Google Scholar]
- Calvisi M. L., Iloreta J. I., and Szeri A. J., “Dynamics of bubbles near a rigid surface subjected to a lithotripter shock wave. Part 2. Reflected shock intensifies non-spherical cavitation collapse,” J. Fluid Mech. 616, 63–97 (2008). 10.1017/S0022112008003054 [DOI] [Google Scholar]
- Johnsen E. and Colonius T., “Numerical simulations of non-spherical bubble collapse,” J. Fluid Mech. 629, 231–262 (2009). 10.1017/S0022112009006351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankin G. N., Simmons W. N., Zhu S. L., and Zhong P., “Shock wave interaction with laser-generated single bubbles,” Phys. Rev. Lett. 95, 034501 (2005). 10.1103/PhysRevLett.95.034501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaseboer E., Fong S. W., Turangan C. K., Khoo B. C., Szeri A. J., Calvisi M. L., Sankin G. N., and Zhong P., “Interaction of lithotripter shockwaves with single inertial cavitation bubbles,” J. Fluid Mech. 593, 33–56 (2007). 10.1017/S002211200700852X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanguay M., “Computation of bubbly cavitating flow in shock wave lithotripsy,” Ph.D. thesis, California Institute of Technology, Pasadena, CA (2004). [Google Scholar]
- Hamilton M. F., Ilinskii Y. A., Meegan G. D., and Zabolotskaya E. A., “Interaction of bubbles in a cluster near a rigid surface,” Acoust. Res. Lett. Online 6, 207–213 (2005). 10.1121/1.1930967 [DOI] [Google Scholar]
- Pishchalnikov Y., Sapozhnikov O., Bailey M., Pishchalnikova I., Williams J., and McAteer J., “Cavitation selectively reduces the negative-pressure phase of lithotripter shock pulses,” Acoust. Res. Lett. Online 6, 280–286 (2005). 10.1121/1.2127115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pishchalnikov Y. A., McAteer J. A., and J. C.Williams, Jr., “Effect of firing rate on the performance of shock wave lithotriptors,” Br. J. Urol. Int. 102, 1681–1686 (2008). 10.1111/j.1464-410X.2008.07896.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church C. C., “A theoretical study of cavitation generated by an extracorporeal shock wave lithotripter,” J. Acoust. Soc. Am. 86, 215–227 (1989). 10.1121/1.398328 [DOI] [PubMed] [Google Scholar]
- Sapozhnikov O. A., Khokhlova V. A., Bailey M. R., J. C.Williams, Jr., McAteer J. A., Cleveland R. O., and Crum L. A., “Effect of overpressure and pulse repetition frequency on cavitation in shock wave lithotripsy,” J. Acoust. Soc. Am. 112, 1183–1195 (2002). 10.1121/1.1500754 [DOI] [PubMed] [Google Scholar]
- Matula T. J., Hilmo P. R., Storey B. D., and Szeri A. J., “Radial response of individual bubbles subjected to shock wave lithotripsy pulses in vitro,” Phys. Fluids 14, 913–921 (2002). 10.1063/1.1433970 [DOI] [Google Scholar]
- Vogel A. and Lauterborn W., “Acoustic transient generation by laser-produced cavitation bubbles near solid boundaries,” J. Acoust. Soc. Am. 84, 719–731 (1988). 10.1121/1.396852 [DOI] [Google Scholar]
- Vogel A., Lauterborn W., and Timm R., “Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary,” J. Fluid Mech. 206, 299–338 (1989). 10.1017/S0022112089002314 [DOI] [Google Scholar]
- Akhatov I., Lindau O., Topolnikov A., Mettin R., Vakhitova N., and Lauterborn W., “Collapse and rebound of a laser-induced cavitation bubble,” Phys. Fluids 13, 2805–2819 (2001). 10.1063/1.1401810 [DOI] [Google Scholar]
- Matsumoto Y. and Takemura F., “Influence of internal phenomena on gas bubble motion (effects of thermal-diffusion, phase-change on the gas-liquid interface and mass diffusion between vapor and noncondensable gas in the collapsing phase),” JSME B Fluids Therm. Eng. 37, 288–296 (1994). [Google Scholar]
- Toegel R., Gompf B., Pecha R., and Lohse D., “Does water vapor prevent upscaling sonoluminescence?,” Phys. Rev. Lett. 85, 3165–3168 (2000). 10.1103/PhysRevLett.85.3165 [DOI] [PubMed] [Google Scholar]
- Lauterborn W., Eick I., and Philipp A., “Approaching bubble dynamics with lasers, holography, and computers,” in Bubble Dynamics and Interface Phenomena, edited by Blake J. R., Proceedings of an IUTAM Symposium (Kluwer Academic, Dordrecht, The Netherlands, 1994), pp 299–310.
- Kreider W., Bailey M. R., Sapozhnikov O. A., and Crum L. A., “A reduced-order, single-bubble model for therapeutic ultrasound,” J. Acoust. Soc. Am. (accepted 2011). [DOI] [PMC free article] [PubMed]
- Cleveland R. O., Bailey M. R., Fineberg N., Hartenbaum B., Lokhandwalla M., McAteer J. A., and Sturtevant B., “Design and characterization of a research electrohydraulic lithotripter patterned after the Dornier HM3,” Rev. Sci. Instrum. 71, 2514–2525 (2000). 10.1063/1.1150643 [DOI] [Google Scholar]
- Cleveland R. O., Sapozhnikov O. A., Bailey M. R., and Crum L. A., “A dual passive cavitation detector for localized detection of lithotripsy-induced cavitation in vitro,” J. Acoust. Soc. Am. 107, 1745–1758 (2000). 10.1121/1.428572 [DOI] [PubMed] [Google Scholar]
- Owen N. R., Bailey M. R., Crum L. A., Sapozhnikov O. A., and Trusov L. A., “The use of resonant scattering to identify stone fracture in shock wave lithotripsy,” J. Acoust. Soc. Am. 121, EL41–EL47 (2007). 10.1121/1.2401266 [DOI] [PubMed] [Google Scholar]
- Storey B. and Szeri A., “A reduced model of cavitation physics for use in sonochemistry,” Proc. R. Soc. London, Ser. A 457, 1685–1700 (2001). 10.1098/rspa.2001.0784 [DOI] [Google Scholar]
- Kreider W., “Gas-vapor bubble dynamics in therapeutic ultrasound,” Ph.D. thesis, University of Washington, Seattle, WA (2008). [Google Scholar]
- Arora M., Ohl C. D., and Lohse D., “Effect of nuclei concentration on cavitation cluster dynamics,” J. Acoust. Soc. Am. 121, 3432–3436 (2007). 10.1121/1.2722045 [DOI] [PubMed] [Google Scholar]
- Coleman A., Whitlock M., Leighton T., and Saunders J., “The spatial distribution of cavitation induced acoustic emission, sonoluminescence and cell lysis in the field of a shock wave lithotripter,” Phys. Med. Biol. 38, 1545–1560 (1993). 10.1088/0031-9155/38/11/001 [DOI] [PubMed] [Google Scholar]
- Sapozhnikov O., Kreider W., Bailey M., Khokhlova V., and Curra F., “Effect of elastic waves in the metal reflector on bubble dynamics at the focus of an electrohydraulic lithotripter,” J. Acoust. Soc. Am. 123, 3367–3368 (2008). 10.1121/1.2933978 [DOI] [Google Scholar]
- Epstein P. S. and Plesset M. S., “On the stability of gas bubbles in liquid-gas solutions,” J. Chem. Phys. 18, 1505–1509 (1950). 10.1063/1.1747520 [DOI] [Google Scholar]