SUMA

Abstract

Surface-based brain imaging analysis offers the advantages of preserving the topology of cortical activation, increasing statistical power of group-level statistics, estimating cortical thickness, and visualizing with ease the pattern of activation across the whole cortex. SUMA is an open source suite of programs for performing surface-based analysis and visualization. It was designed since its inception to allow for a fine control over the mapping between volume and surface domains, and for very fast and simultaneous display of multiple surface models and corresponding multitudes of datasets, all while maintaining a direct two-way link to volumetric data from which surface models and data originated. SUMA provides tools for performing spatial operations such as controlled smoothing, clustering, and interactive ROI drawing on folded surfaces in 3D, in addition to the various level-1 and level-2 FMRI statistics including FDR and FWE correction for multiple comparisons. In our contribution to this commemorative issue of Neuroimage we touch on the importance of surface-based analysis and provide a historic backdrop that motivated the creation of SUMA. We also highlight features that are particular to SUMA, notably the standardization procedure of meshes to greatly facilitate group-level analyses, and the ability to control SUMA’s graphical interface from external programs making it possible to handle large collections of data with relative ease.

Introduction

SUMA (an abbreviation of SUrface MApping) is a freely available, open-source suite of software programs for processing and visualizing neuroimaging data defined over 2-manifold surface models in 3-space.

Triangulated cortical surface models are created from segmentations of MRI volumes and can approximate the cortical sheet at the grey matter-CSF boundary, the grey matter to white matter boundary, or intermediate layers. Such models can be created by a variety of software packages and easily imported into SUMA. Surface models can also be created that represent the brain hull, the surface of the skull, or implanted ECOG electrode arrays. Data mapped onto these surface models can be functional MRI activation maps, anatomical attributes such as labels, cortical thickness, or electrical or magnetic recordings of brain activity. Univariate data processing tools for level-1 and level-2 analyses are the same as those used for voxel data - all AFNI’s (Cox, 1996) voxelwise programs can handle surface-based data, while spatial operations such as smoothing, clustering, and regions-of-interest drawing have their own implementation in SUMA. The visualization part of SUMA allows for very fast and simultaneous display of multiple surface models and corresponding multitudes of datasets, all while maintaining a direct two-way link to volumetric data from which surface models and data originated.

In this retrospective article, we touch briefly on the motivation for the use of surface models and the circumstances prompting the creation of SUMA a little less than 10 years ago, and expand on a few aspects of data analysis and presentation that are particular to SUMA. To keep the tedium of software descriptions to a minimum, we include links to downloadable self-executing interactive demonstrations of some features described herein.

Why Surfaces?

The cortical surface is a highly convoluted sheet comprised of gyri and deeply buried sulci that make it difficult to appreciate its topographic organization. Mapping such data onto cortical surface models is the natural way to view organizations such as retinotopy, somatotopy, and tonotopy. More recently, cortical resting-state FMRI correlation patterns were used to define functional areas (Cohen et al., 2008). Anatomists who sought to understand the cortical layout by studying nonhuman primates first appreciated the value of cortical surface models. In the early days, brain contours of each slice were outlined manually with flexible wires which were then painstaking strengthened, or with pencil and tracing paper (Van Essen and Maunsell, 1980) - tasks reserved for the most patient and meticulously organized among us. Fortunately, computational approaches arrived to make this process simpler. The group of Van Essen, long a pioneer of the use of surface models, produced software known as SureFit/CARET to create cortical surface models from MRI data (Van Essen et al., 2001). About the same time, Anders Dale, Martin Sereno, Bruce Fischl (Dale et al., 1999) and colleagues produced the FreeSurfer software (http://surfer.nmr.mgh.harvard.edu), which also created high-quality surfaces from MRI data. A multitude of surface creation software followed; famous among them are BrainVoyager (http://www.brainvoyager.com), BrainVisa (http://brainvisa.info), and mrVista (http://white.stanford.edu/software).

Although surface-based analysis is restricted to the cortex, it offers advantages with imaging data: 1- The preservation, enhancement, and visualization of topological detail in FMRI volumes. Neighboring voxels in the volume are not necessarily sampling the signal of neighboring regions of the cortex. This often leads to a spatial aliasing of the FMRI signal, that gets more pronounced when one isotropically smoothes the data in the volume. By mapping data from the volume domain onto the surface domain, one can then smooth along the surface, thereby preserving and enhancing topological detail present in the brain. An example of this would be the analysis of retinotopic data, where isotropic smoothing in the volume can destroy the fine topology of the activation pattern. 2- Increase in statistical power. Multiple studies have shown increases in statistical power when group statistics (level-2) are carried out on the cortical surface compared to the volume-domain (Anticevic et al., 2008; Fischl et al., 1999b). This appears to be the case whether or not nonlinear warping is utilized (Argall et al., 2006). The increase in power is likely due to improved smoothing and domain matching across subjects. In other words, the data at each node in the surface comes from gray matter voxels (assuming proper alignment between surfaces and volumes and neglecting partial volume effects), even if nonlinear warping is not used. The same is not true of affine registered volumes. Proper domain matching is important, especially when comparing data from groups with consistent differences in the anatomy, e.g. young vs. old subjects. Without proper alignment and relevant tissue matching, the same voxel in volume template space from a young subject group will likely reflect different brain tissue than in the elderly group, potentially leading to artificial differences in FMRI measures between the two groups. 3- Cortical thickness. Using two surfaces modeling the inner and outer layers of gray matter, cortical thickness estimates can readily be obtained and compared across subjects. 4- Beautiful renditions of cortex and data.

To be sure, all these advantages can be achieved in volume-based approaches, but at a greater computational complexity. For example domain matching in the volume can be improved under highly nonlinear warps, but that is still rarely done despite marked improvements in registration software (Ashburner, 2007; Klein et al., 2009). It remains easier to deform the surface for the purposes of alignment because there is simply less to align than in the volume.

And Then Came SUMA

In the early days of FMRI surface-based analysis, much of the effort went into creating the surfaces out of MRI volumes - a complex task to be sure - but manipulating surfaces or data, or relating the surfaces to the volumetric data from which they originated was cumbersome at best. In the mid to late nineties, by the time one got done analyzing retinotopic data on a flattened version of the cortical surface, multiple steps were needed to find out where a particular node on the flat (or inflated) map came from in the volume. Even surface display was difficult and sluggish: one moved a slider bar to set viewing angles and then clicked a button to refresh the display. Now the user simply clicks on the brain and moves it around until the desired view is achieved, or with a mouse flick sends the brain twirling gently in space - a task particularly mesmerizing for toddlers and grizzled scientists alike. This interactivity requires high-performance graphics hardware that is now readily available on handheld devices. However, in the early days displaying surface models was only available on expensive high-end Silicon Graphics Incorporated machines, and interactivity was very limited. For instance, as a graduate student in the mid nineties, where home-grown tools were the norm for creating and mapping data onto cortical surfaces, I (author ZSS) was asked to compare FMRI signal properties in visual areas that had been delineated by FMRI retinotopy on flattened models of the occipital cortex. To my chagrin, the only way to read the data values off of the flattened occipital maps was by reverse mapping node colors back to data values per the color scale! That was because a colorized rendering of the data was the end point of the mapping process; data values were not preserved in the process. Needless to say, that project did not go far. Such difficulties in relating surfaces to the volume made it harder to detect anomalies in the segmentation, or in the functional data. It was also difficult to view in detail the meshes modeling the cortical surfaces, a problem particularly vexing when trying to understand the source of errors in the geometry or the triangulation of dense surface meshes. Such frustrations, coupled with an interest in the spatial properties of the BOLD response and the irresistible lure of beautiful 3D cortical renderings begat SUMA and shaped its structure and features.

SUMA was first released on the 4th of March 2002, about 1 year after I joined Bob Cox at the Scientific and Statistical Computing Core at NIMH. Unencumbered by the task of creating surface models and their myriad derivates, SUMA’s design focus was on controlling the mapping between volume and surface domains, concurrent display of all geometric variants of the same surface and maintaining an interactive and direct link between the surface and volume domains. Initially SUMA used surface models created by Caret (Van Essen et al., 2001), FreeSurfer, and BrainVoyager. With the advent and adoption of GIFTI http://www.nitrc.org/projects/gifti, surfaces and data from other platforms such as BrainVisa are now readily utilized. The rapid development and the high level of interactivity of SUMA at the first release were due to multiple factors: 1- A first-hand experience with what was missing in surface-based analysis: the ability to see and access the data on the surface and relate surface and data to the volume. 2- A MATLAB-based prototype of the mapping process that I had developed for my own use during a post-doc in Peter Bandettini’s group. 3- An efficient organization of surfaces and data structures and the use of C language and basic OpenGL libraries. 4- Leveraging AFNI’s existing functions for handling and rendering volumetric data.

Standardizing Surface Meshes for Group Comparisons

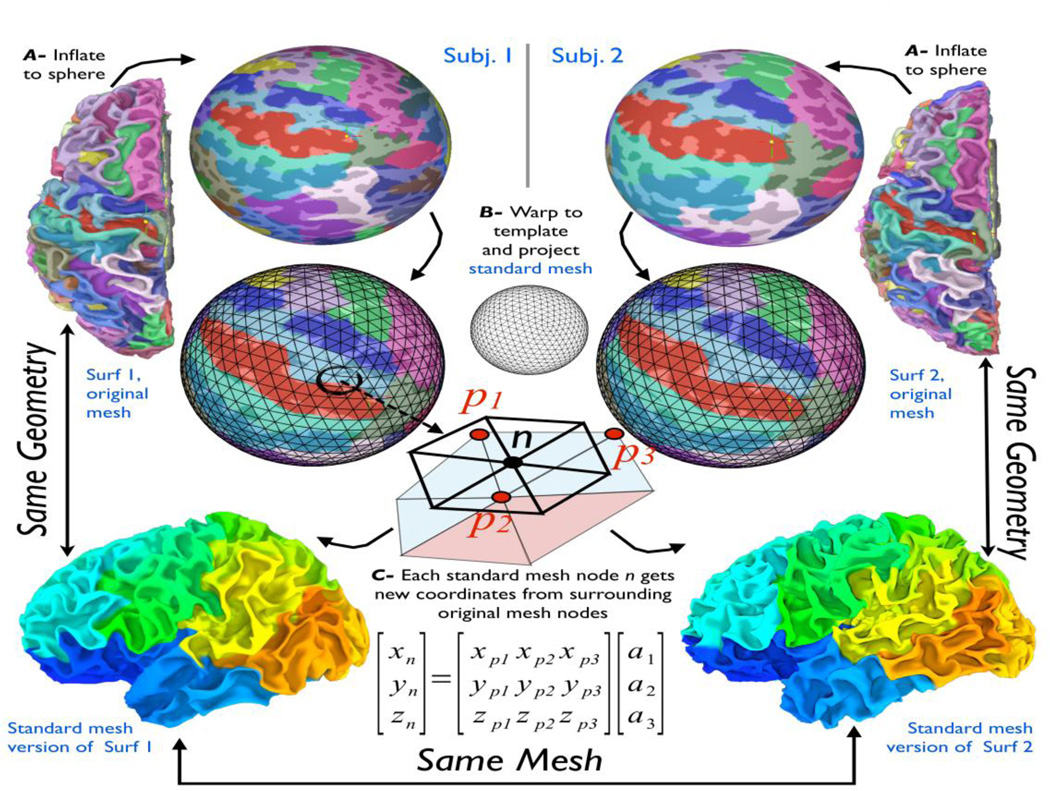
Before discussing the handling of data on surface models, we describe the process by which we take a set of surfaces and re-create them with a new ‘standard’ mesh that is shared by all subjects in a group study. A standard-mesh version of a surface is virtually identical in 3D shape to the original one; however, each node of the new mesh encodes the same cortical location across subjects, within the accuracy of the warping-to-template step. We detail this procedure, which is particular to SUMA, because this simple process greatly facilitates the handling of group statistics when multiple subject surfaces are not created to be topologically isomorphic, as is the case with FreeSurfer and Caret (for example).

Figure 1 shows the common approach for performing group analysis in the surface-domain. The first step (Fig. 1A) involves inflating a subject’s surface to a sphere, then deforming the spherical mesh (Fig. 1B) so that sulcal depth patterns match those of a template (Fischl et al., 1999a). In volume-based analysis, the analogous step is transforming the brain to a standard-template space. Other approaches match selected sulcal patterns or patterns derived from functional data. To what extent warping improves the final results remains the subject of debate. However, it has been repeatedly shown that group analysis on the cortical surface, even without nonlinear registration, results in increased statistical power. Regardless of the warping approach, the procedure for collecting group data then involves mapping each subject’s data from a 3D voxel grid to his individual surface model, and then interpolating into a common domain that is defined by a new standard mesh. This is necessary because data values are attached to the nodes forming the surface (topology) and not to a spatial location (geometry). When the discrete surface topology differs, it is necessary to perform the analysis on a common mesh. This double interpolation step onto the standard model must be repeated for each new dataset, as is done in the volume space; however, it is largely unnecessary on surfaces because the data domain is explicitly defined and not confined to a regular grid. With SUMA, instead of mapping a subject’s data value onto the template mesh, we re-create each subject’s original surface using the mesh of the standard model (shown at a very coarse level in the illustration). In other words, instead of assigning to each node n of the standard mesh a data value interpolated from data on the subject’s original mesh (p.), we now assign to that node a new set of coordinates Xn based on the coordinates of the subject’s original mesh Xp. (Fig. 1-C). When the process is repeated for all the nodes of the standard mesh, its geometry becomes essentially identical to that of the original surface: 99.9% of nodes of the standard-mesh surface are within 0.01mm of the original surface¹ (Saad et al., 2004). The spherical template coordinate system is now embedded in the mesh of the newly created standard surfaces. In the bottom-most row of Fig. 1, each node of the standard-mesh surface of each subject is colorized based on its index. Nodes with similar numbers (colors) now correspond to the same location in template space regardless of their coordinates in subject space. Within the SUMA pipeline, we begin by creating standard-mesh surfaces of each of the subject’s original surfaces, and we utilize the standard-mesh versions for all subsequent analyses. On such standard meshes, functional data mapped directly from the volume to node n on one subject’s surface can be directly compared to data mapped to node n on another subject’s surface. Performing group-level computations on data defined on these isomorphic meshes is then readily carried out with any of the univariate analysis tools applicable in the volume.

Figure 1.

The process of transforming original- to standard- mesh surfaces. See text for details. a₁, a₂, and a₃ are the barycentric coordinates of node n in the triangle formed by nodes p₁,p₂,p₃. Node colors of original-mesh surfaces (top two rows) show FreeSurfer’s cortical parcellations. Colors on standard-mesh surfaces (bottom row) reflect each node’s index.

Typical Pipeline

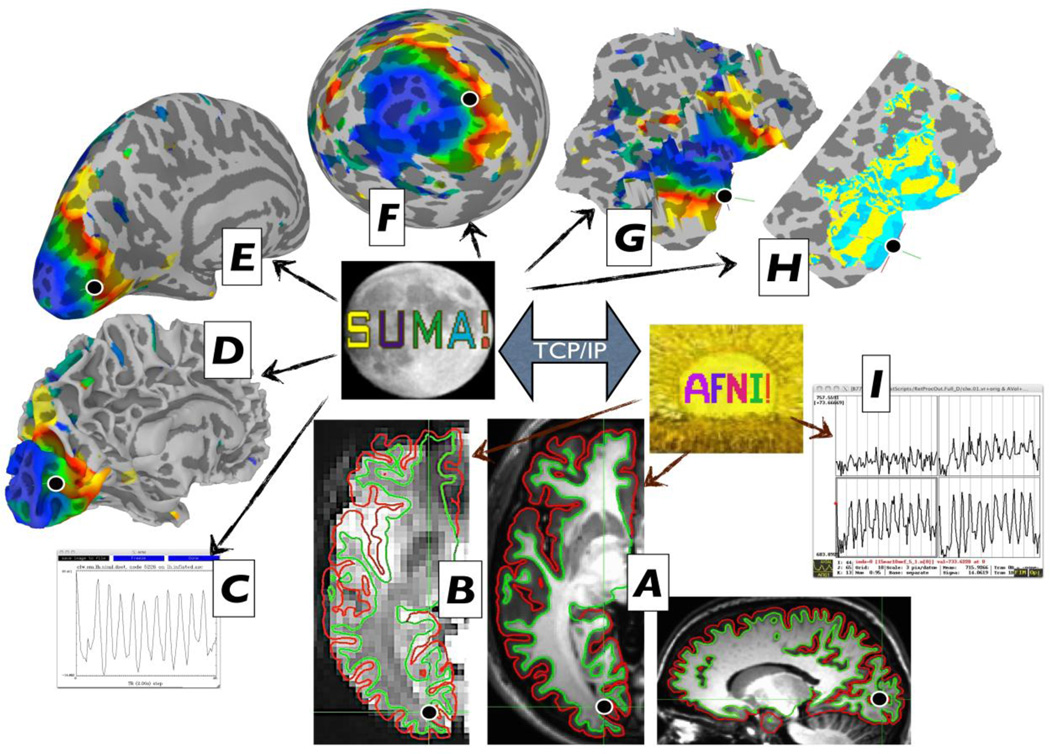
Once standard-mesh surfaces are created, they are brought into alignment with data volumes often acquired at a different scanning session. The overlay of anatomically correct surfaces atop anatomical volume (Fig. 2A) and EPI time series (Fig. 2B) gives direct feedback as to the quality of the surfaces and their alignment with EPI time series as volumes and surfaces are navigated. Shell/Volume Intersection: Motion-corrected EPI time series (or level-1 regression results) are mapped onto standard-mesh surface models before any smoothing (beyond that inherent to motion correction) occurs in the volume. When surfaces modeling the inner and outer boundaries of the gray matter are available, one has greater control over how voxel values in the gray matter are mapped onto the surface. Our recommended approach is to integrate all gray matter voxels that fall along a direction defined by corresponding node pairs from the bounding surfaces (green and red contours in Figure 2A–B). The endpoints for the integration can be modified to change the integration range, including a simple intersection at an intermediate depth in the gray matter. Smoothing is performed on the surface for the same reasons it is applied in the volume. However, controlled smoothing on the surface is more difficult than in the volume. Smoothing by or to a certain FWHM involves approximated iterative methods that can fail in practice to achieve the desired smoothing level (Hagler et al., 2006). SUMA’s SurfSmooth gets around this problem by iteratively smoothing and estimating the current smoothness level of the noise in the data. The noise in the data is either taken from the residual time series after a regression analysis, or by a high-order detrending of the data to reduce stimulus-response-related upward bias of the smoothness estimate. In the default usage, the program can select appropriate iterative kernel smoothing parameters while taking into account the mesh density and the desired additive or target FWHM. Simulations using the method detailed in (Hagler et al., 2006) verify that SurfSmooth achieves in practice the specified smoothness levels. Level-1&2 analyses are carried out using the same AFNI programs used for voxel-based tests. For multiple-comparisons correction, SUMA provides the FDR approach with all statistical datasets, or FWE correction based on Monte Carlo simulations that estimate the likelihood of observing spatial clusters of a particular size given an uncorrected p-value and the smoothness of the data.

Figure 2.

The linkage between data rendering modes. SUMA and AFNI directly control surface-and volume-based renderings, respectively (thin arrows). The two programs are independent but communicate together via TCP/IP. Data shown is from the sample data for the retinotopy analysis pipeline (http://afni.nimh.nih.gov/pub/dist/tgz/AfniRetinoDemo.tgz) courtesy of Peter J. Kohler and Sergey V. Fogelson.

Surface and Volume Domain Linkage

SUMA, at the moment, has little support for displaying volumetric data and relies on AFNI for that purpose. Figure 2 is an illustration of the graphical interface in a typical session. All the images displayed are cropped versions of the live display. The main constraint for how much can be shown is screen space. From SUMA, anatomically correct (e.g. non-inflated) surfaces are sent to AFNI and their intersection with the volume is displayed on all slice renderings (Fig. 2AC). Each surface model is shown in separate but linked interactive surface viewers (Fig. 2D–G). All the renderings are connected, so that a click on any of the surfaces updates the crosshair location on all surfaces and time series windows (Fig. 2C), and jumps to the corresponding location in all the volume views including volume-based time series graphs (Fig. 2I). Vice versa, selecting a voxel close to the surface causes crosshairs in SUMA windows to jump to the closest node. Surface annotations and volume atlas information about crosshair locations are also updated (not shown). The display supports a layering of multiple datasets that can be blended in different forms, including node coordinate bumping as shown on the flattened cortical view in Fig. 2G. While retinotopy is old hat in terms of FMRI techniques, those who attempt it can testify to the difficulty in getting it right despite cookbook recipes for the approach (Warnking et al., 2002), and that being able to readily access the various stages of the data processing is particularly important in assessing the results (Fig. 2H). While SUMA is tightly connected to AFNI, the two programs are independent; they communicate by sending commands and associated data via shared memory or network sockets using TCP/IP. Commands and data are packaged in a simplified version of XML, which, unlike XML itself, also allows for binary data. This communication mode is at the core of SUMA and AFNI’s ability to communicate together and with other programs. For example, the skull stripping program 3dSkullStrip can communicate with both SUMA, and AFNI, sending the envelope of the brain with each iteration to SUMA and the processed volume to AFNI. Doing this helped us refine the skull striping algorithm as we tested it on difficult brain images for humans and other species. Both AFNI and SUMA remain available for user interaction during the process.

Hands-Off GUI Control

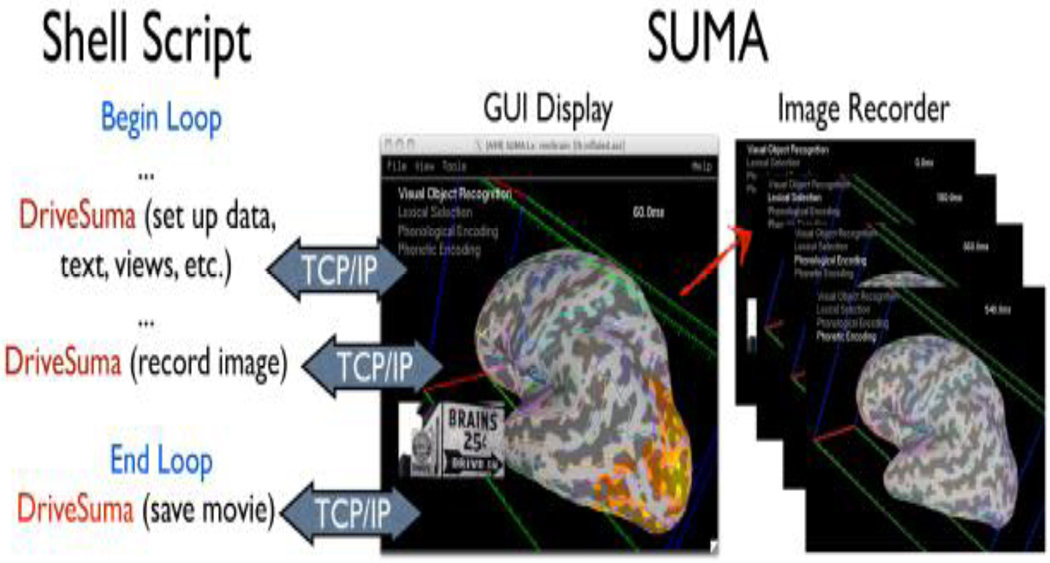
Another useful aspect of the communication support is the ability to script the behavior of the graphical interface. This is easily done by issuing commands via the command-line program DriveSuma. Such scripting can be used to create complex summaries of the data as in Figure 3, which shows one frame from a movie depicting MEG beamformer results (Cheyne et al., 2006) 0 to 600 msec after the stimulus. This particular movie was generated entirely automatically including text annotations and pictures.

Figure 3.

Illustration for driving SUMA’s GUI from the command line with DriveSuma. The example here illustrates the functioning of a script that automatically generates a movie of MEG SAM data from 0 to 600 ms after stimulus delivery. (Data and script to generate this movie are courtesy of Chunmao Wang, and available at http://afni.nimh.nih.gov/pub/dist/tgz/SumaMovieDemo.tgz)

The ability to wade through a large number of datasets and readily access the data remains crucial for MRI and FMRI studies. Twenty years into FMRI, and we still struggle in practice with mundane issues such as image registration when data is less than optimal. This can be particularly challenging when scanning unhealthy populations and in great numbers. Thanks to fully automated pipelines, analyzing thousands of datasets is no more strenuous than analyzing a few, not counting computation time. However, group differences can reflect biases in some of the processing stages that can later be incorrectly attributed to brain anatomical or functional changes. It is important to be able to navigate the data from each subject and at various key processing steps. The recent efforts which have resulted in the wide adoption of NIFTI and GIFTI formats facilitate the exchange and examination of large data sets such as FCON1000 (Biswal et al.) or ADNI(Jack et al., 2008; Mueller et al., 2005), regardless of the package in which they processed. An example that takes advantage of the SUMA standard-meshes approach, the cross-program communication, the scripting of GUI control, and ease of visualization is illustrated by running @Install_InstaCorr_Demo (part of the AFNI/SUMA installation), which sets up an interactive seed-based group resting state connectivity mapping using data from the FCON1000 dataset. A user’s click on the surface sends a seed location to AFNI’s 3dGroupInCorr program, which performs group seed-based correlations on one or two groups, then performs one- or two- sample t-tests with or without subject-level covariates, and sends all the statistical results back for display in SUMA. We detailed this feature, not only because it is really cool, but also to say that being able to interactively query and navigate large collections of datasets leads to insights into the data that are otherwise hard to find when looking only at summary results. It remains quite striking to watch resting state patterns shift as the cursor is dragged along the surface, revealing the high level of detail present in the data; e.g., as reflected in the bilateral homology of correlations (Jo et al., 2011).

Future Features

For software developers, user feedback is mostly of the negative variety. If we were to summarize the appeal of SUMA from the smaller but quite positive sample, it would be the ease with which multiple surfaces and associated data are displayed and related to the volume, and the way group analysis can be carried out. Eye candy images are also a big plus. Currently, SUMA remains under active development. The authors’ SUMA-specific code exceeds 250,000 lines of C for the graphical interface and three dozen command-line programs. Continuing with the theme of ready access to data, we plan to make more information readily available with minimal interface clutter. For example, beyond parcellation results (FreeSurfer), and various volume-based atlas queries currently supported, it would be useful to provide selective anatomical or functional connectivity information, whether atlas-based or data-derived. A researcher examining a set of SPM blobs would benefit from seeing, after pointing to a region of interest, what connectivity or co-activation information exists from that region to the rest of the brain. Queries could be conducted on datasets present on one’s computer or more likely from websites containing extensive databases such as BrainMap http://www.brainmap.org. The new XML-based connectivity format CIFTI http://www.nitrc.org/projects/cifti would help facilitate such information exchanges.

Summary

SUMA is a suite of programs for performing surface-based analysis and visualization. It was written to facilitate viewing sets of multiple dense surfaces while maintaining the linkage between them, and to allow for a fine control of and simplify the once tedious process from mapping volume data to the surface domain, through the group statistics stage. SUMA’s graphical interface allows for fast, simultaneous, and linked rendering of a large number of surfaces, along with composite displays of multiple datasets with contouring options for representing parcellations or atlas regions and translucent overlaying of continuous valued datasets. The surface displays are intimately connected to the volumetric data, allowing for direct verification of surface to volume correspondence. The SUMA GUI is fully scriptable, making it uniquely suited to navigate and summarize results from large numbers of datasets with minimal effort.