Abstract
Multiphysics modeling, which integrates the models studied in different disciplines so far, is an indispensable approach toward a comprehensive understanding of biological systems composed of diverse phenomena. However, the variety of the models is narrower than the actual diverse phenomena because of the difficulty in coupling independent models separately studied in different disciplines for the actual coupled phenomena. In this study, we develop a mathematical model coupling an enzymatic reaction and mineralization formation. As a test case, we selected an in vitro transcription system where a transcription reaction occurs along with the precipitation formation of magnesium pyrophosphate (Mg2PPi). To begin, we experimentally elucidated how the transcription reaction and the precipitation formation are coupled. In the analysis, we applied a Michaelis-Menten-type equation to the transcription reaction and a semiempirical equation describing the correlation between the induction period and the supersaturation ratio to the precipitation formation, respectively. Based on the experimental results, we then integrated these two models. These models were connected by supersaturation that increases as the transcription reaction proceeds and becomes the driving force of the precipitation. We believe that our modeling approach could significantly contribute to the development of newer multiphysics models in systems biology such as bone metabolic networks.
Introduction
Biological systems are composed of diverse phenomena and their interactions. The study of the biological systems composed of diverse phenomena in living organisms is a key factor in advancing our system-level understanding of biological systems. Multiphysics modeling, which integrates the models studied in different disciplines so far, is a powerful technique to analyze and understand such complex biological systems. Unlike most models that are based only on reaction kinetics, multiphysics modeling faces difficulty in coupling different types of models that have been separately studied in different disciplines. Deep understanding of interaction mechanisms by which the separate phenomena are coupled is also required.
The number of phenomena for which models have been proposed is limited when compared with the actual number of diverse phenomena. Hence, it is important to propose and study a variety of models that can be used toward a more comprehensive understanding of biological systems.
In living organisms, there are the phenomena involving the coupling of enzymatic reactions and mineralization (precipitation, calcification, and crystallization). For example, bone metabolic networks are composed of a series of enzymatic reactions and hydroxyapatite crystal formation (1). The models for these two phenomena have been independently studied. As is well known, enzymatic reactions have been analyzed based on reaction kinetics and modeled based on the rate equation or the Michaelis-Menten equation. Other modeling frameworks such as generalized mass action, S-system (2, 3), and lin-log kinetics (4) have been studied to analyze a large system and its dynamic behavior.
On the other hand, mineralization can be separated into two processes—nucleation (which we address in this article) and particle growth. Nucleation is important because it determines whether mineralization occurs through a phase transition from liquid to solid. Nucleation occurs when a solution is supersaturated, and a delay time from the establishment of supersaturation to the experimental detection of nucleation exists (5, 6, 7). The delay time is known as the induction period. According to a semiempirical correlation (6, 8, 9) or classical nucleation theory (7, 10, 11), nucleation is modeled by the relational expression of the supersaturation ratio, which is the degree of the supersaturation, and its induction period. Several models for enzymatic reactions and mineralization have been intensively studied; however, to our knowledge, a model coupling enzymatic reactions and mineralization has not been proposed thus far.
The purpose of our study is to develop a multiphysics model coupling an enzymatic reaction and mineralization by taking nucleation into consideration. We analyzed an in vitro transcription reaction as a test case, because it has been known that the two dominant phenomena of an enzymatic reaction and a precipitation formation occur in the system. In the enzymatic reaction, RNA polymerase (RNAP) produces RNA, the main product, and pyrophosphate (PPi), the byproduct, with Mg2+ as a cofactor. PPi released by the reaction binds with Mg2+ to form Mg2PPi, which is easy to precipitate. The influence of this Mg2PPi precipitation on the transcription reaction has been investigated because the precipitation affects the productivity of RNA in the transcription reaction (12, 13, 14). In one study, Young et al. (14) developed a mathematical model for analyzing the productivity of RNA. In addition, Arnold et al. (15) developed a mathematical model of in vitro transcription involving Mg2PPi precipitation from the standpoint of kinetics study. However, these studies have not considered the supersaturated state of Mg2PPi and the nucleation of the Mg2PPi precipitation formation. In our study, we first conducted experimental analyses of the test reaction and subsequently developed a model to explain the reaction.
In the experimental section of the study, we measured the time course of the production of RNA and PPi as a first step toward understanding the system. Based on these time-course results, we conducted three experiments to investigate the synthesis rate in the transcription reaction, the induction period of the Mg2PPi precipitation formation, and the influence of the precipitation on the transcription reaction. We confirmed the existence of the induction period by measuring the time course of turbidity in the solution and analyzed the relationship between the induction period and the supersaturation ratio by using the empirical correlation. Based on these results, we considered the behavior of precipitation formation during the in vitro transcription reaction. In the modeling phase, we developed a model based on the experimental results and performed numerical simulations to verify the model. The model was developed by incorporating the induction period as the delay time in the model of the transcription reaction. By comparing the results of the numerical simulations with those obtained from the experiments, we validated our developed model. Our modeling approach can potentially enable the development of mathematical models for analyzing bone metabolic networks.
Materials and Methods
In vitro transcription assay
The standard transcription mixture was composed of 7.4 nM linear template DNA, 0.1 μM T7 RNAP, 8 mM Mg(OAc)2, 0.8 mM of each NTP, 5 mM Dithiothreitol, 2 mM Spermidine, and 40 mM Tris-HCl (pH 8.0). The linear template DNA was amplified from the pk7-CAT plasmid (16) by polymerase chain reaction using PrimeSTAR HS DNA polymerase (Takara Bio, Shiga, Japan) and purified using an Illustra GFX PCR Purification Kit (GE Healthcare UK, Little Chalfont, UK). The length of the transcribed RNA was 868 nt, and the numbers of each of the composite bases (A, G, C, and U) were 231, 202, 189, and 246 nt, respectively. T7 RNAP was prepared in-house according to a previously described method (17). The reaction was performed on a 30–130 μL scale at 37°C. Each assay in our study was conducted after incubation for different lengths of time.
Measurement of RNA, PPi, Mg, and turbidity
The RNA concentration was quantified using a RiboGreen RNA Quantitation Kit (Molecular Probes, Eugene, OR). A 100-μL sample was mixed with 100 μL of the 200-fold diluted RiboGreen reagent in a 96-well plate, and the fluorescence (Ex. 485 nm, Em. 535 nm) was measured using an ARVO HTS 1420 multilabel counter (PerkinElmer, Waltham, MA). The PPi concentration was quantified using a Pyrophosphate reagent (Sigma-Aldrich, St. Louis, MO). A 200-μL sample was mixed with 100 μL of Pyrophosphate reagent in a 96-well plate. The Mg concentration was quantified using a QuantiChrom Magnesium Assay Kit (BioAssay Systems, Hayward, CA). The other procedures that are not described in this section were carried out according to the manufacturer's protocols. Turbidity was measured as the absorbance at 405 nm (18) using an ARVO HTS 1420 multilabel counter (PerkinElmer).
Time-course assay
For the time course of RNA and PPi, a 30-μL transcription mixture was prepared for each time point. After incubation, the mixture was centrifuged at 15,000 rpm for 1 min. A 5-μL supernatant was obtained from the mixture and diluted with 195 μL of TE buffer (10 mM Tris-HCl, pH 8.0, 1 mM EDTA). This solution was used for the measurement of PPi concentration. The remaining transcription mixture solution (25 μL) was diluted 400-fold with TE buffer, and this solution was used for the measurement of RNA concentration. When the white precipitation of Mg2PPi was observed, the solution was vortexed until the pellet of the precipitation was no longer evident.
For the time course of RNA, PPi, Mg, and turbidity, a 130-μL transcription mixture was prepared for each time point. After incubation, the transcription mixture was vortexed. A 100-μL suspended mixture was obtained from the transcription mixture for the measurement of turbidity. Subsequently, a 5-μL suspended mixture was taken from the 30-μL remaining transcription mixture solution and diluted 400-fold with TE buffer. This solution was used for the measurement of RNA concentration. Furthermore, the 25-μL remaining transcription mixture solution was centrifuged at 15,000 rpm for 1 min, and two 5-μL supernatants were obtained from this solution. One supernatant was diluted with 195 μL of TE buffer for the measurement of PPi concentration, and the other supernatant was diluted with 45 μL of 10% trichloroacetic acid for the measurement of Mg concentration. The procedures for the measurement of Mg concentration were based on those in the study by Kim et al. (19).
Equilibrium calculation of ionic species
The equilibrium relations and their association constants used in the calculations were as follows: pKHNTP = 6.95, pKMgNTP = 4.42 (15), pKMg2NTP = 1.69, pKMgHNTP = 1.49, pKHPPi = 8.94, pKMgPPi = 5.42, pKMg2PPi = 2.33, pKH2PPi = 6.13, pKMgHPPi = 3.05, and pKTris+ = 8.1 (15). The association constants were based on Kern and Davis (12) unless otherwise stated. The mass balance equations are
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The concentrations of ionic species were calculated by substituting the appropriate equilibrium equations and given total concentrations into the mass balance equations. A method proposed by Storer and Cornish-Bowden (20) was used for the iterative calculation of the ionic concentration. The total concentrations of Mg, NTP, and PPi were varied depending on the initially added concentration and the progress of the transcription reaction. The total Tris concentration was kept constant at 40 mM. The total H concentration was kept constant at 25 mM. When the transcription reaction was conducted, the total H concentration was varied from 25 mM as the reaction proceeded.
Measurement and analysis of induction period
The standard transcription mixture was modified by eliminating the template DNA. Various concentrations of tetrasodium pyrophosphate solution were added to this mixture to vary the PPi concentration in the mixture. A 120-μL mixture was prepared for each time point. After incubation, the mixture was vortexed, and a 100-μL suspended mixture was obtained for the measurement of turbidity.
To extract the induction period from the time course of turbidity in the analysis of precipitation, we conducted a fitting procedure using a sigmoidal curve described by (21)
| (6) |
and the induction time is given by t1/2 − 2τ. The supersaturation ratio (Ω) was calculated by using the equation
| (7) |
where α denotes the activity of ions, γ denotes the activity coefficient of ions, and Ksp denotes the solubility product of Mg2PPi. In our study, we assumed that the activity coefficients were 1.0. The solubility coefficient Ksp is 2.5 × 10−4 mM3 (H. Nanbu, K. Nakata, N. Sakaguchi, and Y. Yamazaki. 2000. Mineral composition, U.S. Patent 6,074,675). In Eq. 7, when Ω = 1, Mg2PPi is in equilibrium. When Ω < 1, Mg2PPi is undersaturated and when Ω > 1, Mg2PPi is supersaturated; precipitation can start at this state. All of the fitting procedures were carried out using MATLAB (The MathWorks, Natick, MA).
Results
Time-course analysis of RNA and PPi under several conditions
We first measured the time course of RNA and PPi quantities at various concentrations of the dominant factors in the transcription reaction—T7 RNAP, NTP, and Mg(OAc)2—to understand how each factor influences the transcription reaction. The condition of the mixture at 0.1 μM T7 RNAP, 0.8 mM NTP, and 8 mM Mg(OAc)2 concentrations was set as the standard condition.
First, we focused on the synthesis rate of RNA. When the T7 RNAP and Mg(OAc)2 concentrations were increased, the synthesis rate in the initial part of the reaction increased and subsequently gradually saturated over the latter part of the reaction. On the other hand, when the NTP concentration was increased, the synthesis rate increased up to a concentration value of 1.6 mM; subsequently, it sharply decreased with increasing NTP concentration.
Second, we focused on the duration time of the transcription reaction. When analyzed in terms of T7 RNAP (Fig. 1 A), the duration time generally decreased as the concentration of T7 RNAP increased. On the other hand, when analyzed in terms of NTP (Fig. 1 B), the duration time increased as the NTP concentration was increased up to a value of 1.6 mM. At higher NTP concentrations (3.2 and 4.0 mM), the reaction persisted for >120 min. When the reaction was analyzed in terms of Mg(OAc)2 (Fig. 1 C), the duration time increased as the Mg(OAc)2 concentration increased from 8 to 14 mM. At lower Mg(OAc)2 concentrations (2 and 4 mM), the reaction persisted for >120 min. Moreover, at the Mg(OAc)2 concentration of 20 mM, the reaction persisted although the synthesis rate significantly decreased at ∼45 min.
Figure 1.
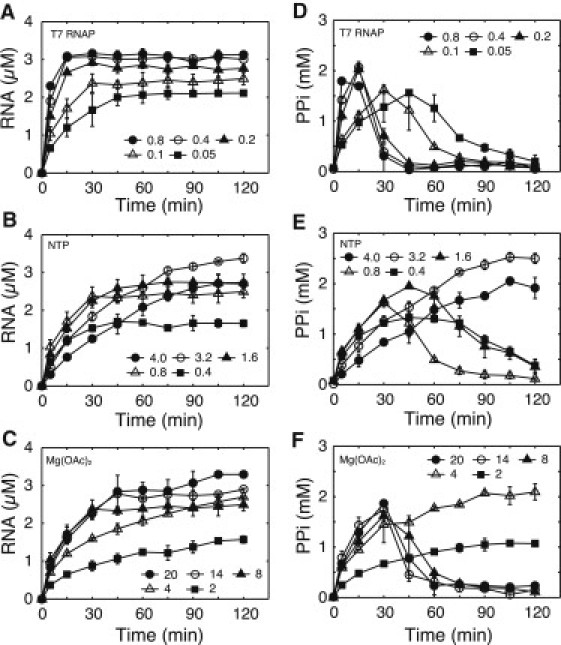
Experimentally measured time course of RNA and PPi simultaneously measured from the same sample at (A and D) T7 RNAP concentrations varying from 0.05 to 0.8 μM, (B and E) each of the NTP concentrations varying from 0.4 to 4.0 mM, and (C and F) Mg(OAc)2 concentrations varying from 2 to 20 mM. The time points were 0, 5, 15, 30, 45, 60, 75, 90, 105, and 120 min. (Error bars) Standard deviation of duplicate experiments. The details of this experiment are described in Materials and Methods.
Thirdly, we focused on the time course of the PPi concentration in the reaction mixture. The time at which the PPi concentration started to decrease was coincident with the time at which the transcription reaction stopped under the conditions that the T7 RNAP and NTP concentrations were varied (Fig. 1, A, B, D, and E). On the other hand, under the condition that the Mg(OAc)2 concentration was varied, the times were not coincident at the Mg(OAc)2 concentration of 14 and 20 mM (Fig. 1, C and F).
Experimental analysis of synthesis rate of RNA
To more quantitatively evaluate the influence of the relationship between NTP and Mg(OAc)2 on the synthesis rate, we measured the initial rate at various concentrations of NTP and Mg(OAc)2 (Fig. 2 A). The initial rate gradually saturated with increasing NTP concentration at higher Mg concentrations (14 and 20 mM). However, at lower Mg(OAc)2 concentrations (2, 4, and 8 mM), the initial rate showed a one-time increase and subsequently decreased. As the Mg(OAc)2 concentrations were decreased, the NTP concentrations at which the initial rate started to decrease shifted to lower values. From previous studies, it is known that NTP4− ion binds with Mg2+ ion to form several kinds of complexes such as MgNTP2−, Mg2NTP, and MgHNTP− (12), and the transcription reaction by T7 RNAP requires both MgNTP2− and Mg2+ ions for the reaction to progress (14, 22). Consequently, we evaluated the synthesis rate using a Michaelis-Menten type equation based on Young el al. (14), given as
| (8) |
where [MgNTP2−] denotes the lowest value among [MgATP2−], [MgGTP2−], [MgCTP2−], and [MgUTP2−] concentrations. We calculated [MgNTP2−] and [Mg2+]free values using the equilibrium calculations (see Materials and Methods) and fitted the predicted initial rates to the values measured in Fig. 2 A; this is shown in Fig. 2 B. In the case where the measured initial rate was negative, we substituted zero for the actual negative value. As a result, the predicted values were fully consistent with the measured values (R2 = 0.96), and the obtained parameters were kapp = 2.04 min−1, K1 = 0.23 mM, and K2 = 0.094 mM.
Figure 2.
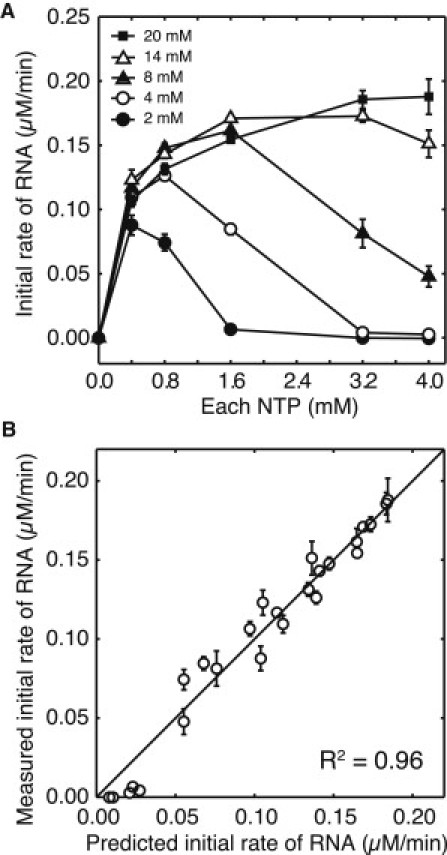
Analysis of the initial rate of the transcription reaction. (A) Experimentally measured initial rate of RNA at the various concentrations of each NTP (0.0, 0.4, 0.8, 1.6, 3.2, and 4.0 mM) and Mg(OAc)2 (2 mM; solid circles, 4 mM; open circles, 8 mM; solid triangles, 14 mM; open triangles, and 20 mM; solid squares) concentrations. The RNA concentration was measured after 5-min incubation, and the initial rate was obtained by dividing the concentration by 5. (Error bars) Standard deviation of triplicate experiments. (B) Fitting result of predicted initial rates of RNA to measured ones obtained in panel A. Predicted initial rate was calculated using Eq. 8, and a nonlinear least-square method was used (R2 = 0.96).
Experimental analysis of nucleation process of Mg2PPi precipitation
To investigate the induction period of the Mg2PPi precipitation formation, we obtained the time course of Mg2PPi concentration by measuring the turbidity of the mixture without the transcription reaction (Fig. 3 A). The PPi concentrations were varied from 0.75 to 2.50 mM, and the Mg(OAc)2 concentration was maintained constant at 4 mM. As a result, at PPi = 0.75 mM, the turbidity of the mixture was nearly constant for ∼100 min and then gradually increased. As the initially added PPi concentration was increased, this period of constant turbidity sharply decreased. This result confirmed that the induction period existed and varied depending on the PPi concentration. In general, it is known that the induction period of sparingly soluble compounds is decreased in inverse proportion to the supersaturation ratio. Therefore, we calculated the supersaturation ratio using Eq. 7 and extracted the induction period in the time-course data by fitting Eq. 6 (see Materials and Methods). Fig. 3 B shows the plot of the induction period against the supersaturation ratio (obtained from Fig. 3 A), thereby showing that the induction period is inversely proportional to the supersaturation ratio similar to other sparingly soluble compounds. In addition, the induction period can be expressed as the semiempirical correlation (6, 8, 9)
| (9) |
where K and r are empirical constants obtained via fitting to experimental data. We fitted this equation to the data obtained from Fig. 3 B. As a result, we obtained the actual parameters in our experimental system (K = 1.01 × 107, r = 3.33, R2 = 0.99). Moreover, the induction period can be expressed using an equation derived from classical nucleation theory when the nucleation process during the induction period is homogeneous (7, 10, 11). Whether or not the nucleation is homogeneous can be investigated using a logarithm plot (logTind versus 1/log2 Ω). Our results by the logarithm plot indicated the possibility that the nucleation process in our experiments was not homogeneous (see Fig. S1 in the Supporting Material). Therefore, we used Eq. 9 for the description of the induction period.
Figure 3.
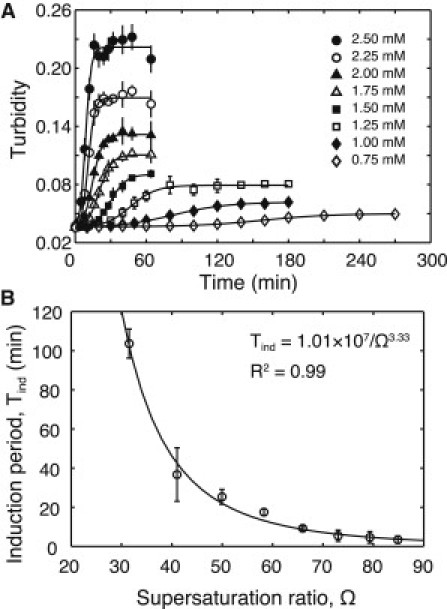
Analysis of induction period of the Mg2PPi precipitation formation without the transcription reaction. (A) Experimentally measured time course of turbidity at various PPi concentrations from 2.50 to 0.75 mM (plots). The time points were 0, 2, 5, 8, 12, 16, 20, 24, 28, 32, 40, 48, and 64 min (2.50, 2.25, 2.00, 1.75, and 1.50 mM), 0, 10, 20, 30, 40, 50, 60, 80, 100, 120, 140, 160, and 180 min (1.25 and 1.00 mM), and 0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 210, 240, and 270 min (0.75 mM). (Error bars) Standard deviation of triplicate experiments. (Lines) Fitting Eq. 6 to the mean value of the above experimental data. (B) Plot of induction period as a function of supersaturation ratio (plots) and fitting result obtained using Eq. 9 (shown as a line). The induction period was extracted from the time course data in panel A (see Materials and Methods). The supersaturation ratio was calculated by the equilibrium calculation (see Materials and Methods) and Eq. 7, where [Mg2+]total = 4 mM, each [NTP4−] total = 0 mM, [Tris] total = 40 mM, [H+] total = 25 mM, and [PPi4+] total were the added concentrations. The induction period and the supersaturation ratio are shown in Table S1 in the Supporting Material.
Influence of Mg2PPi precipitation on transcription reaction
To validate whether or not Mg2PPi precipitation directly causes the stoppage of the RNA synthesis, we conducted two additional experiments. In the first experiment, we added pyrophosphatase (PPase), which hydrolyzes PPi into Pi, to the time course assay. In the second experiment, we simultaneously measured the time course of RNA, PPi, Mg, and turbidity. Fig. 4 A shows the time course of RNA and PPi with/without PPase under standard conditions. RNA synthesis stopped after ∼30 min without the addition of PPase, whereas it continued for at least 1 h with PPase addition. The PPi concentration was kept at nearly zero in the presence of PPase, thereby indicating that PPase was active in the transcription reaction. Fig. 4 B shows the simultaneously measured time course of RNA, PPi, Mg, and turbidity under standard conditions. The increase in turbidity was coincident with the decrease in PPi and Mg concentrations and the stoppage of the RNA synthesis. These results indicated that the occurrence of the Mg2PPi precipitation strongly inhibited the RNA synthesis by causing the decrease in Mg2+ concentration in solution.
Figure 4.
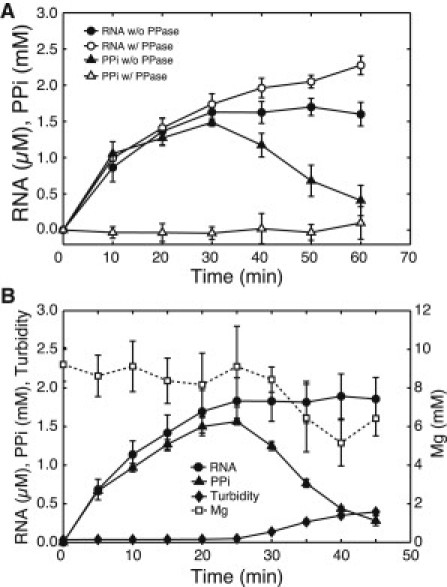
(A) Time course of RNA and PPi simultaneously measured under standard conditions with/without PPase. The time points were 0, 10, 20, 30, 40, 50, and 60 min. (Error bars) Standard deviation of triplicate experiments. (B) Time course of RNA, PPi, Mg, and turbidity simultaneously measured under standard conditions. The Mg concentration is plotted on the secondary y axis. The time points were 0, 5, 10, 15, 20, 25, 30, 35, 40, and 45 min. (Error bars) Standard deviation of quadruplicate experiments.
Model development
A schematic diagram of the model is shown in Fig. 5, and we describe the model as the following three parts: transcription reaction; precipitation formation and its connection with transcription reaction; and influence on transcription reaction after precipitation.
Figure 5.
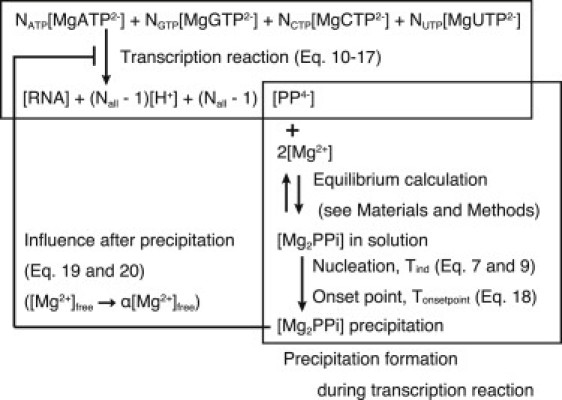
Schematic diagram showing the relationship between the transcription reaction and Mg2PPi precipitation formation during the transcription reaction in our in vitro transcription system.
Transcription reaction
The synthesis rate of transcription reaction expressed by Eq. 8 can be rewritten as
| (10) |
The rate of release of PPi4−, the consumption rates of each NTP, and the rate of release of hydrogen ions are expressed as (14)
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where Nall denotes the length of the RNA. NATP, NGTP, NCTP, and NUTP denote the numbers of ATP, GTP, CTP, and UTP consumed per molecule of RNA, respectively. In addition, we assumed the inactivation of T7 RNAP during the transcription reaction; this assumption was based on the results of the study by Arnold et al. (15). The inactivation rate is expressed as
| (17) |
where kd is 0.014 min−1.
Precipitation formation and its connection with transcription reaction
The precipitation formation was calculated based on Eq. 9, and the induction period was the important index of the precipitation formation. As the transcription reaction proceeded, PPi4− and H+ were released and each NTP was consumed. Then, 1), by substituting these total ionic concentrations into the equilibrium calculation, the free ionic concentrations of Mg2+ and PPi4− were calculated; 2), by substituting these free ionic concentrations into Eq. 7, the supersaturation ratio was calculated; and 3), by substituting the supersaturation ratio into Eq. 9, the induction period was calculated.
Moreover, it was considered that the onset point of the precipitation formation moved in a direction opposite to the progress of the reaction as shown in Fig. 6. This dynamics was implemented using the following procedure. At step n, the predicted onset point of the precipitation (Tonsetpoint) was first calculated by adding the reaction time t (n) to the induction period Tind (n):
| (18) |
Tonsetpoint (n) was then compared with Tonsetpoint (n−1) because Tonsetpoint (n) may be larger than Tonsetpoint (n−1), depending on the decease rate of Tind. The smaller Tonsetpoint was selected as the predicted onset point because the onset point does not move in the direction of the reaction progress after the nucleation starts. At step n+1, if t (n+1) is larger than the predicted onset time that was selected at step n, then the precipitation begins. The step size in the numerical simulation is 0.01 (min). This value is sufficiently small compared with the change of the induction period.
Figure 6.
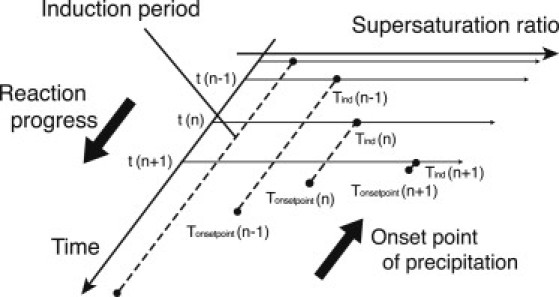
Schematic diagram of the Mg2PPi precipitation formation during transcription reaction. The values t (n), Tind (n), and Tonsetpoint (n) denote the reaction time, the induction period, and the onset point of the precipitation at step n, respectively.
Influence on transcription reaction after precipitation
After the Mg2PPi precipitation began, the Mg2PPi concentration in the solution decreases. The decrease of the Mg2PPi concentration was expressed as each decrease of the Mg2+ and PPi4- concentrations in the solution ((19), (20)). Based on Quintana et al. (23), the rate of decrease of Mg2+ is expressed as
| (19) |
where Nratio denotes the ratio of Mg2+ contained in the Mg2PPi precipitation and the value was 2.0 in the calculation.
The rate of change of PPi4− was calculated by adding the rate of decrease of PPi4− to Eq. 11,
| (20) |
where kprecip is 1.0 min−1, and [Mg2PPi]eq is 0.014 mM. The [Mg2PPi]eq concentration value was calculated using
| (21) |
Moreover, the term α[Mg2+]free (α = 0.007) was used instead of [Mg2+]free in Eq. 10.
Numerical simulation
Fig. 7 shows the time course of RNA calculated by numerical simulation using the developed model when the initial concentrations of T7 RNAP, NTP, and Mg were varied. As observed in Fig. 7 A, the time at which the transcription reaction stopped reduced as the T7 RNAP concentration increased. This result was consistent with the experimental result shown in Fig. 1 A. As observed in Fig. 7 B, the time at which the reaction stopped gradually increased as the NTP concentration was increased from 0.4 to 1.6 mM, whereas the reaction persisted at NTP concentrations of 3.2 and 4.0 mM. These results were in good accordance with the experimental results shown in Fig. 1 B except for that at 1.6 mM. In Fig. 7 C, when the Mg concentration was 8 mM, the reaction stopped after ∼30 min. At lower Mg concentrations (2 and 4 mM), the reaction did not stop unlike the case at 8 mM and was gradually saturated. At higher Mg concentrations (14 and 20 mM), whereas the synthesis rate significantly decreased after ∼20 min, the reaction persisted for 120 min. Although the synthesis rate in the calculated results did not fully coincide with the experimental ones, the overall profile of the calculated results agreed with the experimental results.
Figure 7.
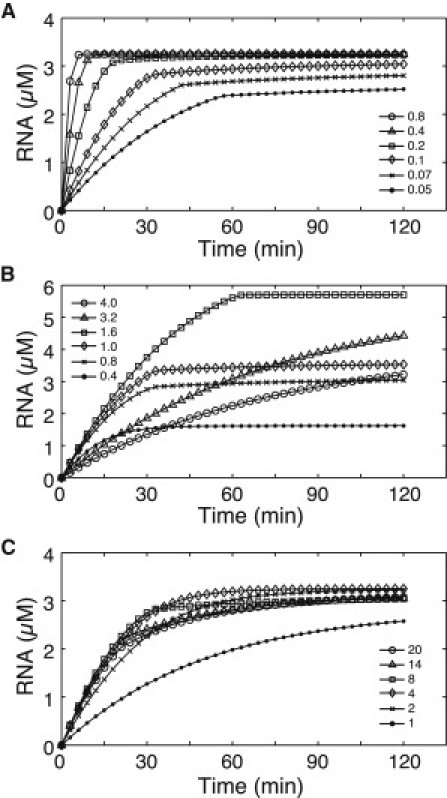
Time course of RNA calculated by our developed model for (A) T7 RNAP concentrations varying from 0.05 to 0.8 μM, (B) NTP concentrations varying from 0.4 to 4.0 mM, and (C) Mg(OAc)2 concentrations varying from 1 to 20 mM. Unless otherwise stated, the initial values of other concentrations were [RNA] = 0, [PPi4−] = 0, [ATP4−] = 0.8 mM, [GTP4−] = 0.8 mM, [CTP4−] = 0.8 mM, [UTP4−] = 0.8 mM, [H+] = 25 mM, [T7 RNAP] = 0.1 μM, and [Mg2+] = 8 mM.
Discussion
To begin, we discuss the development of our multiphysics model coupling the transcription reaction and the precipitation formation. In previous studies, a couple of models of in vitro transcription have been developed taking into account the Mg2PPi precipitation formation (12, 13, 14). However, these models did not consider the nucleation process involved in the precipitation formation. In the previous studies, the Mg2PPi precipitation formation was analyzed based on the assumptions.
In the first case, the assumption was that the precipitation starts immediately after the concentration of Mg2PPi exceeds the solubility limit (13, 14). If this was the case, the PPi4− released by the transcription reaction should start to decrease at the same PPi4− concentration under the same Mg2+ concentration.
In the second case, the assumption was that the precipitation starts immediately after PPi4− is released by the transcription reaction (12). If this was the case, the PPi4− released by the transcription reaction should start to decrease at the same time as the release of PPi4−. However, as shown in Fig. 1 D, PPi4− started to decrease at different PPi4− concentrations (additional data are shown in Fig. S2).
In this experiment, the Mg2+ concentration in the solution should remain constant because T7 RNAP has little influence on the concentrations of ionic species. Our results indicated that the Mg2PPi precipitation started some time after Mg2PPi became supersaturated. Therefore, we considered the existence of an induction period for the Mg2PPi precipitation formation and validated it by the experiment measuring the turbidity of the solution. The increase in turbidity could be considered as the onset of the Mg2PPi precipitation because the increase in the turbidity was coincident with the decrease in PPi and Mg (Fig. 4 B). As expected, the existence of induction period was observed in Fig. 3 A. Moreover, the induction period was inversely proportional to the supersaturation ratio (Fig. 3 B). In this study, the nucleation process was incorporated into the model of the transcription reaction as the delay time of the induction period, expressed as Eq. 9 (Fig. 5). Moreover, we incorporated Eq. 18 into the model to describe the movement of the onset point of the precipitation induced by the coupling of transcription reaction and the induction period (Fig. 6).
Next, we discuss the relationship between the transcription reaction and the Mg2PPi precipitation after the onset of the precipitation. Our results indicated that the onset of the Mg2PPi precipitation strongly inhibited the transcription reaction (Figure 1, Figure 4). Kern and Davis (12) reported a similar result and concluded that this was due to a lack of free Mg2+ in solution. We reached the same conclusion because the rate of the transcription reaction was dependent on free Mg2+ concentration (Fig. 2 B) and the transcription reaction did not stop under conditions of higher Mg(OAc)2 concentration (Fig. 1, C and F). In this situation, a question about the decrease in free Mg2+ concentration caused by the precipitation arises. In Fig. 4 B, the Mg2+ concentration was assumed to have rapidly decreased at the same time as the onset of the precipitation because the transcription reaction stopped at the same time as the precipitation (at ∼25 min). However, in fact, the Mg2+ concentration did not decrease as expected.
These results indicated the free Mg2+ concentration available for the transcription reaction is lower than the concentration that we predicted by means of ion equilibrium. Therefore, to incorporate the gap of the free Mg2+ concentration into the model under a minimal assumption, we introduced a parameter, the decrease rate α, after the onset point of the precipitation. The parameter α was introduced as the term α[Mg2+]free in the synthesis rate of RNA (Eq. 10) instead of the normal free Mg2+ concentration ([Mg2+]free). The value of the parameter was chosen by trial and error. By introducing the parameter, the phenomenon that the transcription stops immediately after the onset point of the precipitation was shown in the result of the numerical simulation. Because the mechanism of the transition from liquid to solid is quite complex (24) and we cannot analyze the moment of the transition, it is difficult to directly reveal the gap by experiments.
We discuss here two phenomenological possibilities causing the gap of the free Mg2+ concentration. The first one is the existence of an electrical double layer, which is the layer of positive and negative ions around the precipitation (25). This electrical double layer may affect the free Mg2+ concentration and then decrease the concentration by more than that assumed only by ion equilibrium. The second one is the physical interaction between the RNA polymerase and the Mg2PPi precipitation at the moment of the transition. In the transcription reaction, PPi4− ion is released from the incorporated MgNTP2− through the dephosphorylation by RNA polymerase. Therefore, if the Mg2PPi precipitation occurs immediately after the PPi4- ion is released, the precipitation that occurs close to the RNA polymerase may inhibit the transcription reaction by the physical interaction. In this case, the transcription reaction may stop even if the free Mg2+ concentration is sufficient. A single-molecule assay (22) may enable us to analyze the possibility.
Then, we discuss the differences between the experimental results (Fig. 1, A–C) and the numerical results calculated by the developed model (Fig. 7). On the whole, the time at which the transcription reaction stopped or at which the synthesis rate decreased in the calculated results agreed with the time in the experimental results except for that under the conditions at 1.6 mM NTP, 14 mM Mg(OAc)2, and 20 mM Mg(OAc)2. A possible reason for this difference is the difference between the actual concentrations of the ion species and the concentrations calculated by our equilibrium calculation. The validation of our equilibrium calculation was difficult because it was hard to directly measure the concentrations of free ions and ionic complexes. Therefore, to obtain the clues for improving the equilibrium calculation, we measured the decrease in the total Mg concentration in the solution induced by the Mg2PPi precipitation, and compared the measured total Mg concentration with the calculated one. Fig. S3 shows the total Mg concentrations obtained by the experiment and the calculation.
We focused on the added PPi concentration from 0 to 3 mM because this range of the concentration was used to calculate the ionic concentrations in the time course assay. In this range, the tendency of the total Mg concentration was consistent between the experiment and the calculation. However, the rate of increase in the Mg concentration induced by the addition of NTP was not consistent between them. Although the increase rate due to the addition of NTP changed nonlinearly in the experimental result, the increase rate changed linearly in the calculated one. From this result, we concluded that the differences in the experimental and calculated results of the time course of RNA and PPi might be attributed to the accuracy of our equilibrium calculation of the interaction between Mg and NTP. If we could obtain the actual concentrations of free ions and ionic complexes, our equilibrium calculation could be improved by more detailed analyses.
Finally, we discuss the advantages of our multiphysics model developed by integrating the model of the enzymatic reaction and that of the mineralization. One application of our developed model is the system-level analysis of bone formation in living organisms. The mineralization in the bone formation is the crystallization of hydroxyapatite, which is a calcium phosphate compound. Similar to our model, the source of the inorganic Pi in the hydroxyapatite is produced by the enzymatic reaction (by phosphatase enzyme) (26, 27, 28). This enzymatic reaction is then coupled with other enzymatic reactions to constitute the reaction network (29). In other words, the crystallization is one of the components in the reaction network, and a reaction network that such contains diverse phenomena by nonenzymatic reaction has been difficult to study by using conventional systems biology.
Although the crystallization in living organisms is more complex than our experimental system because of the compartmentalization by matrix vesicles and the interaction of collagen fibril, our multiphysics model will contribute to the development of a comprehensive mathematical model for the bone metabolic network as a first step. Moreover, by integrating a mathematical model such as compartment models (30, 31) that can treat the compartmentalization by cell membranes and the membrane transport into our model, it may be possible to address the above problem. On the other hand, our study revealed the time-delayed negative feedback regulation through the supersaturated state and enabled us to treat this regulation with the mathematical model. In biological systems, temporal dynamics such as periodic phenomena is important to highly regulate the system. It is known that the feedback regulation with delay time generates biochemical oscillation (32). Similar to the finding in our experimental system, a time-dependent mechanism may be found by introducing the influence of the delay time through the supersaturated state into the above crystallization process.
Conclusion
In this study, we developed a multiphysics model coupling an enzymatic reaction and mineralization formation. As a test case, we selected an in vitro transcription system involving the transcription reaction and precipitation formation: 1), We experimentally revealed how the transcription reaction and the precipitation formation are coupled. 2), We developed the multiphysics model by applying a Michaelis-Menten-type equation to the transcription reaction and the model derived from the semiempirical correlation for the precipitation, respectively, and coupling those models. We believe that our findings and modeling approach will contribute to the development of models for dynamical systems.
Acknowledgments
The authors thank Prof. Akihiko Konagaya, Prof. Isao Ono, Dr. Takayoshi Matsuda, and Dr. Naoya Tochio for their valuable suggestions.
S.A. is supported by the Junior Research Associate Program of RIKEN.
Editor: Doug Barrick.
Footnotes
Three figures and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(11)05415-4.
Supporting Material
References
- 1.Hessle L., Johnson K.A., et al. Millan J.L. Tissue-nonspecific alkaline phosphatase and plasma cell membrane glycoprotein-1 are central antagonistic regulators of bone mineralization. Proc. Natl. Acad. Sci. USA. 2002;99:9445–9449. doi: 10.1073/pnas.142063399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Savageau M.A. Biochemical systems analysis. II. The steady-state solutions for an n-pool system using a power-law approximation. J. Theor. Biol. 1969;25:370–379. doi: 10.1016/s0022-5193(69)80027-5. [DOI] [PubMed] [Google Scholar]
- 3.Voit E.O. Cambridge University Press; Cambridge, UK: 2000. Computational Analysis of Biochemical Systems: A Practical Guide for Biochemists and Molecular Biologists. [Google Scholar]
- 4.Visser D., Heijnen J.J. Dynamic simulation and metabolic re-design of a branched pathway using lin-log kinetics. Metab. Eng. 2003;5:164–176. doi: 10.1016/s1096-7176(03)00025-9. [DOI] [PubMed] [Google Scholar]
- 5.Tantayakom V., Fogler H.S., et al. Chavadej S. Kinetic study of scale inhibitor precipitation in squeeze treatment. Cryst. Growth Des. 2005;5:329–335. [Google Scholar]
- 6.Lancia A., Musmarra D., Prisciandaro M. Measuring induction period for calcium sulfate dihydrate precipitation. AIChE J. 1999;45:390–397. [Google Scholar]
- 7.Guan B., Yang L., Wu Z. Effect of Mg2+ ions on the nucleation kinetics of calcium sulfate in concentrated calcium chloride solutions. Ind. Eng. Chem. Res. 2010;49:5569–5574. [Google Scholar]
- 8.Prisciandaro M., Lancia A., Musmarra D. Calcium sulfate dihydrate nucleation in the presence of calcium and sodium chloride salts. Ind. Eng. Chem. Res. 2001;40:2335–2339. [Google Scholar]
- 9.Packter A. The precipitation of sparingly soluble alkaline-earth metal and lead salts: nucleation and growth orders during the induction period. J. Chem. Soc. A. 1968;0:859–862. [Google Scholar]
- 10.Ohlinger K.N., Young T.M., Schroeder E.D. Kinetics effects on preferential struvite accumulation in wastewater. J. Environ. Eng. 1999;125:730–737. [Google Scholar]
- 11.Kofina A.N., Koutsoukos P.G. Spontaneous precipitation of struvite from synthetic wastewater solutions. Cryst. Growth Des. 2005;5:489–496. [Google Scholar]
- 12.Kern J.A., Davis R.H. Application of solution equilibrium analysis to in vitro RNA transcription. Biotechnol. Prog. 1997;13:747–756. doi: 10.1021/bp970094p. [DOI] [PubMed] [Google Scholar]
- 13.Kern J.A., Davis R.H. Application of a fed-batch system to produce RNA by in vitro transcription. Biotechnol. Prog. 1999;15:174–184. doi: 10.1021/bp990008g. [DOI] [PubMed] [Google Scholar]
- 14.Young J.S., Ramirez W.F., Davis R.H. Modeling and optimization of a batch process for in vitro RNA production. Biotechnol. Bioeng. 1997;56:210–220. doi: 10.1002/(SICI)1097-0290(19971020)56:2<210::AID-BIT10>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 15.Arnold S., Siemann M., et al. Reuss M. Kinetic modeling and simulation of in vitro transcription by phage T7 RNA polymerase. Biotechnol. Bioeng. 2001;72:548–561. [PubMed] [Google Scholar]
- 16.Kim D.M., Kigawa T., et al. Yokoyama S. A highly efficient cell-free protein synthesis system from Escherichia coli. Eur. J. Biochem. 1996;239:881–886. doi: 10.1111/j.1432-1033.1996.0881u.x. [DOI] [PubMed] [Google Scholar]
- 17.Zawadzki V., Gross H.J. Rapid and simple purification of T7 RNA polymerase. Nucleic Acids Res. 1991;19:1948–1955. doi: 10.1093/nar/19.8.1948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mori Y., Nagamine K., et al. Notomi T. Detection of loop-mediated isothermal amplification reaction by turbidity derived from magnesium pyrophosphate formation. Biochem. Biophys. Res. Commun. 2001;289:150–154. doi: 10.1006/bbrc.2001.5921. [DOI] [PubMed] [Google Scholar]
- 19.Kim T.W., Kim D.M., Choi C.Y. Rapid production of milligram quantities of proteins in a batch cell-free protein synthesis system. J. Biotechnol. 2006;124:373–380. doi: 10.1016/j.jbiotec.2005.12.030. [DOI] [PubMed] [Google Scholar]
- 20.Storer A.C., Cornish-Bowden A. Concentration of MgATP2- and other ions in solution. Calculation of the true concentrations of species present in mixtures of associating ions. Biochem. J. 1976;159:1–5. doi: 10.1042/bj1590001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nielsen L., Khurana R., et al. Fink A.L. Effect of environmental factors on the kinetics of insulin fibril formation: elucidation of the molecular mechanism. Biochemistry. 2001;40:6036–6046. doi: 10.1021/bi002555c. [DOI] [PubMed] [Google Scholar]
- 22.Thomen P., Lopez P.J., et al. Heslot F. T7 RNA polymerase studied by force measurements varying cofactor concentration. Biophys. J. 2008;95:2423–2433. doi: 10.1529/biophysj.107.125096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Quintana M., Sánchez E., et al. Borja R. Kinetics of phosphorus removal and struvite formation by the utilization of by-product of magnesium oxide production. Chem. Eng. J. 2005;111:45–52. [Google Scholar]
- 24.Anderson V.J., Lekkerkerker H.N.W. Insights into phase transition kinetics from colloid science. Nature. 2002;416:811–815. doi: 10.1038/416811a. [DOI] [PubMed] [Google Scholar]
- 25.Kostoglou M., Karabelas A.J. Comprehensive modeling of precipitation and fouling in turbulent pipe flow. Ind. Eng. Chem. Res. 1998;37:1536–1550. [Google Scholar]
- 26.Ciancaglini P., Yadav M.C., et al. Millán J.L. Kinetic analysis of substrate utilization by native and TNAP-, NPP1-, or PHOSPHO1-deficient matrix vesicles. J. Bone Miner. Res. 2010;25:716–723. doi: 10.1359/jbmr.091023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moochhala S.H., Sayer J.A., et al. Simmons N.L. Renal calcium stones: insights from the control of bone mineralization. Exp. Physiol. 2008;93:43–49. doi: 10.1113/expphysiol.2007.040790. [DOI] [PubMed] [Google Scholar]
- 28.Sayer J.A., Carr G., Simmons N.L. Nephrocalcinosis: molecular insights into calcium precipitation within the kidney. Clin. Sci. 2004;106:549–561. doi: 10.1042/CS20040048. [DOI] [PubMed] [Google Scholar]
- 29.Roberts S.J., Stewart A.J., et al. Farquharson C. Human PHOSPHO1 exhibits high specific phosphoethanolamine and phosphocholine phosphatase activities. Biochem. J. 2004;382:59–65. doi: 10.1042/BJ20040511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stefanini M.O., Wu F.T., et al. Popel A.S. A compartment model of VEGF distribution in blood, healthy and diseased tissues. BMC Syst. Biol. 2008 doi: 10.1186/1752-0509-2-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fletcher P.A., Li Y.-X. An integrated model of electrical spiking, bursting, and calcium oscillations in GnRH neurons. Biophys. J. 2009;96:4514–4524. doi: 10.1016/j.bpj.2009.03.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Novák B., Tyson J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008;9:981–991. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


