Kinetics and Mechanics of Two-Dimensional Interactions between T Cell Receptors and Different Activating Ligands

Abstract

Adaptive immune responses are driven by interactions between T cell antigen receptors (TCRs) and complexes of peptide antigens (p) bound to Major Histocompatibility Complex proteins (MHC) on the surface of antigen-presenting cells. Many experiments support the hypothesis that T cell response is quantitatively and qualitatively dependent on the so-called strength of TCR/pMHC association. Most available data are correlations between binding parameters measured in solution (three-dimensional) and pMHC activation potency, suggesting that full lymphocyte activation required a minimal lifetime for TCR/pMHC interaction. However, recent reports suggest important discrepancies between the binding properties of ligand-receptor couples measured in solution (three-dimensional) and those measured using surface-bound molecules (two-dimensional). Other reports suggest that bond mechanical strength may be important in addition to kinetic parameters. Here, we used a laminar flow chamber to monitor at the single molecule level the two-dimensional interaction between a recombinant human TCR and eight pMHCs with variable potency. We found that 1), two-dimensional dissociation rates were comparable to three-dimensional parameters previously obtained with the same molecules; 2), no significant correlation was found between association rates and activating potency of pMHCs; 3), bond mechanical strength was partly independent of bond lifetime; and 4), a suitable combination of bond lifetime and bond strength displayed optimal correlation with activation efficiency. These results suggest possible refinements of contemporary models of signal generation by T cell receptors. In conclusion, we reported, for the first time to our knowledge, the two-dimensional binding properties of eight TCR/pMHC couples in a cell-free system with single bond resolution.

Introduction

An essential component of adaptive immune responses is the capacity of T lymphocytes to detect foreign peptides bound to major histocompatibility complex molecules (pMHC) on the surface of virus-infected cells or specialized cells that have ingested and processed microbial pathogens. This recognition event is a remarkable feat because a T lymphocyte bearing typically 50,000 identical receptors (TCRs) is able to scan within a few minutes the surface of a cell exposing >100,000 different pMHC complexes and detect a few or even a single (1, 2) cognate peptide differing from self-peptides by a few or even a single amino acid. In addition to remarkable specificity and sensitivity, the recognition event may trigger a variety of responses ranging from lymphocyte unresponsiveness or anergy to full activation (3). It is therefore not surprising that intense efforts have been made to determine the criteria used by a T lymphocyte to select a particular outcome after briefly encountering a given pMHC.

A number of separate reports have supported the view that the TCR response is determined by some physical-chemical property of TCR/pMHC interaction such as affinity (4, 5, 6, 7), dissociation rate of the complex (8, 9, 10, 11), or the association rate (11). However, although most authors found a positive correlation between the lifetime of TCR/pMHC complexes and T lymphocyte activation, some discrepancies remain (12). In addition, two points remain incompletely understood.

First, because interaction lifetime is a random event that may display important fluctuations, it is difficult to understand how T lymphocytes can discriminate between quite similar ligands with exquisite accuracy. It was suggested that the involvement of a complex series of time-requiring reactions in TCR signaling might be necessary to overcome this paradox (13, 14). This was the basis of the so-called kinetic proofreading hypothesis.

Second, the aforementioned studies of the interaction between TCR and pMHC were performed using soluble molecules (i.e., three-dimensional or 3D conditions) using techniques such as surface plasmon resonance. It has long been emphasized that measured three-dimensional parameters could not fully account for the behavior of surface-attached (2D conditions) molecules (15, 16, 17, 18) because of major differences in diffusion conditions and the forces that the interacting molecules are subjected to.

During the last two decades, a number of methods, including laminar flow chambers, atomic force microscopy, biomembrane force probes, or optical traps have yielded very useful information on interactions between surface-attached molecules at the single bond level (19). However, it is only recently that TCR/pMHC interactions could be monitored at the single bond level. A kinetic study performed with single-molecule fluorescence resonance energy transfer (FRET) microscopy showed that the dissociation rate of bonds formed between cell-bound TCR and pMHC was 4–12-fold higher than on soluble molecules, and this was ascribed to an active participation of lymphocyte cytoskeleton (20).

In other experiments, mechanical studies showed that the dissociation rate of bonds involving cell-attached TCR and pMHC could be 8300-fold higher than reported for soluble molecules. Further, quite surprisingly, the pMHC with maximal activating potency displayed higher dissociation rate, in contrast with conclusions from three-dimensional studies (21). One possible complicating factor in these studies is the fact that cellular responses that affect the measured binding parameters, such as cytoskeletal processes, are influenced by TCR signaling. Thus the higher off-rate measured with more potent ligands may be a consequence of stimulating cytoskeletal processes.

Here, we used a laminar flow chamber to probe the interaction between a recombinant TCR and eight pMHC complexes previously shown to have varying activation potency in functional assays. As recently reviewed in Pierres et al. (22), the laminar flow chamber operating at a low shear rate is an efficient way of probing the kinetics of association and force-induced dissociation of weak molecular bonds at the single molecule level. The use of model surfaces instead of cells allowed us to probe intrinsic two-dimensional molecular properties in the absence of potentially confounding cellular effects. These 2D binding properties were compared with 3D binding properties and pMHC activation potency. We found: 1), there is an essential agreement between 3D dissociation rate and 2D dissociation rate measured with the lowest disrupting force. 2), the force resistance is not entirely accounted for by spontaneous bond duration. 3), the activation potency is positively correlated with bond duration and, surprisingly, correlated negatively with bond mechanical strength. Our results may provide new insights into potential mechanisms of signal generation by TCR/pMHC interactions.

Materials and Methods

Molecules

1G4 TCR is specific for the peptide 157–165 derived from the tumor-associated protein NY-ESO-1 protein presented on HLA-A2 (23). Soluble forms of the 1G4 TCR and pMHC variants were produced as previously described in Aleksic et al. (11). Briefly, wild-type or mutant forms of HLA-A2 heavy chain (residues 1–278) with C-terminal BirA tag and β₂-microglobulin were expressed as inclusion bodies in Escherichia coli, refolded in vitro in the presence of synthesized peptides, and purified using size-exclusion chromatography. Purified pMHC was biotinylated in vitro by BirA enzyme (Avidity, Hounslow, England). The 1G4 TCR α and β subunits were expressed in Escherichia coli as inclusion bodies, refolded in vitro, and purified using size exclusion chromatography. As suggested by their names, all pMHCs differed by a single amino acid of the peptide (3A, 3Y, 6T, 9L, or 9V) or the MHC (H70, H74, or R65) (11).

Preparation of surfaces and microspheres

24 × 24 mm² glass slides (Assistent, Sondheim, Germany) were rinsed twice in ethanol, then rinsed thoroughly with water. Glass slides were then cleaned in a mix of 70% sulphuric acid (Fisher Bioblock, Illkirch, France) and 30% H₂O₂ (50% in water; Sigma-Aldrich, St-Quentin Fallavier, France) for 10 min, then rinsed thoroughly with deionized water and stocked in deionized water. Glass slides were coated with a poly-L-lysine solution (150,000–300,000 Da, 100 μg/mL; Sigma-Aldrich) in 0.02 M phosphate buffer, pH 7.4 for 30 min, rinsed in phosphate-buffered saline (PBS), then incubated in a glutaraldehyde solution (2.5% in 0.1 M borate buffer, pH 9.5; Sigma-Aldrich) for 10 min, and rinsed in PBS. Glass slides were then incubated in a solution of bovine serum albumin (BSA; 90 μg/mL; Sigma-Aldrich) and biotinylated BSA (10 μg/mL; Sigma-Aldrich) in PBS for 30 min, then rinsed with PBS. Glass slides were incubated for 30 min in a blocking solution of glycine (0.2 M in PBS), rinsed in PBS, then incubated in a streptavidin solution (10 μg/mL in PBS; Sigma-Aldrich) for 30 min, then rinsed with PBS. Glass slides were incubated with biotinylated pMHC in PBS, at different concentrations, for 1 h, then mounted in the flow chamber.

Dynabeads M500 tosylactivated microspheres (Invitrogen, Cergy Pontoise, France) were coated first with a mouse anti-histidine tag antibody (MCA1396; Serotec, Colmar, France), according to the manufacturer's protocol. Briefly, microspheres were rinsed in 0.1 M pH 9 borate buffer, incubated 24 h at 37°C in antibody solution in 0.1 M pH 9 borate buffer, then rinsed in PBS, and incubated in a blocking solution of tris(hydroxymethyl)aminomethane 0.1 M and BSA 0.1% for 4 h at 37°C. Microspheres were stored in this solution at 4°C with 0.1% sodium azide added, and incubated in histidine-tagged TCR molecules for 1 h before experiment. It was checked that these incubation times were sufficient to ensure irreversible binding of the reagents on the timescale of experiments (not shown).

Flow chamber setup and data analysis

We used a custom-made flow chamber with a machined Plexiglas top forming a 0.2 × 2 × 6 mm³ chamber (height × width × length), the functionalized glass slide forming the bottom, maintained by a machined aluminum plate bolted to the top. Vacuum grease was used as a gasket. Flow was established using a 5 mL glass syringe mounted on a syringe pump (A-99; Razel, St. Albans, VT). Microspheres were suspended in PBS with 0.1% BSA in the flow chamber.

An inverted microscope (Olympus France, Rungis, France) in bright-field illumination equipped with a 20× lens and a standard video camera was used to follow the two-dimensional trajectory of the beads and to measure their adhesion to the underlying substrate. Video signal was digitized at video rate (25 Hz) by a digitization card (Hauppauge France, Paris, France) and compressed on-the-fly by the freeware VirtualDubMod using the DivX 5.1.1 codec. Microsphere positions were determined using a custom-made software written in C++. Arrest detection and duration measurement was done using a custom-made software written in the Igor environment (WaveMetrics, Lake Oswego, OR). Statistics of molecular-bond formation and rupture were determined by counting the frequency and duration of microspheres arrest events in the laminar flow as previously described in Robert et al. (24). Briefly, a microsphere was considered as arrested if its position did not change by >dx = 0.5 μm in dt = 0.2 s, and if its velocity before the arrest corresponded to that of a moving sedimented bead.

The adhesion frequency was defined as the number of arrests divided by the total time spent by the microspheres after sedimentation in the velocity range of moving sedimented beads. The frequency of specific binding under a given condition (i.e., wall shear rate and ligand surface density) was estimated by subtracting the binding frequency measured with nonpeptide-specific TCR bearing microspheres from the binding frequency measured with peptide-specific TCR bearing microspheres. An arrest was considered to continue as long as the arrest criterion was satisfied, which yields an apparent duration d_app. The true arrest duration d_true was derived from the apparent duration d_app with the correction d_true = d_app+(t−2dx/v), where v is the most probable velocity of the beads (25).

Statistical analysis

Presented conclusions are based on the determination of ∼11,000,000 microsphere coordinates and recording of ∼7106 binding events. However, the intrinsic randomness of single molecule events made it useful to estimate the statistical significance of presented data. The error in the fraction of surviving bonds was derived from the number of counted arrests on the basis of binomial law (26). The significance of correlations was obtained after calculating a Pearson correlation coefficient r by using the normal transform: z = (n−3)²/2 ln[(1+r)/1−r)], where n is the number of pairs (26). Bootstrapping (27) was performed with a custom-made software.

Results

We readily observed the formation of single specific TCR/pMHC bonds that displayed multiphasic rupture kinetics

In a first series of experiments, microspheres coated with the 1G4 TCR (23) were driven along a series of surfaces coated with eight specific pMHC ligands previously shown to interact with 1G4 with affinity constants ranging between 1.1 × 10⁴ and 29 × 10⁴ M⁻¹, and activation potencies spanning a sevenfold range (11). The shear rate was kept at a low value of 20 s⁻¹, thus generating a pulling force of 34 picoNewtons on surface-attached spheres (28). The motion was monitored with a computer-assisted method allowing 20-ms time resolution and 40-nm spatial accuracy (29). Previous experiments have shown that these conditions allow single ligand-receptor bonds to generate detectable arrests of moving spheres (22, 30). Fully sedimented spheres flowed along the surface with a velocity of ∼25 μm/s, and they displayed binding events with a frequency between ∼0.1 s⁻¹ and 1 s⁻¹.

These binding events could be ascribed to a specific TCR/pMHC interaction because their frequency exhibited a 5–10-fold decrease when 1G4 was replaced with another TCR (G10) that does not bind to these pMHCs in solution (not shown).

Arrest durations were recorded and a typical plot of bond survival versus time is shown in Fig. 1 A. The curve displayed upward concavity, similar to results previously obtained for avidin-streptavidin (31), integrin-fibronectin (32), or cadherin-cadherin (25) interactions. We checked that this feature was due to a time-dependent strengthening of individual bonds rather than to the formation of additional bonds by changing the surface density of pMHCs: whereas the binding frequency displayed an up-to-fourfold decrease after pMHC dilution, the distribution of arrest durations was not changed (Fig. 2). The stopping events could thus be considered to be mediated by single molecular bonds (33).

Figure 1.

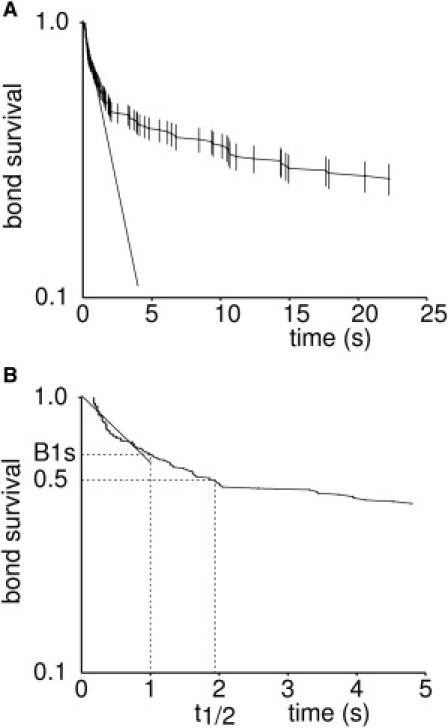
Bond rupture follows a complex kinetic behavior that can be robustly represented by the fraction of bonds surviving 1 s after formation. The figure shows a typical survival plot of bonds formed between microspheres coated with 1G4 TCR and surfaces coated with ESO-9V pMHC complex. Wall shear rate was 20 s⁻¹. (A) Vertical bar length is twice the standard error calculated on the basis of binomial law (162 binding events at time zero). (Straight line) Least-square linear fit calculated on [0 s,1 s] time interval. (B) Enlarged initial part of the curve. The slope of the linear fit (straight line), fraction of surviving bonds at 1 s (B1s), and median bond lifetime (t_1/2) are shown.

Figure 2.

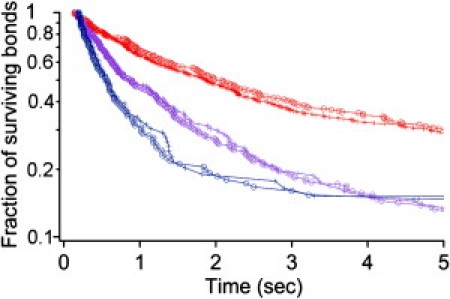
Independence of rupture kinetics on pMHC density supports the assumption that single bonds are observed. For each pMHC, binding frequency and detachment curves were determined for at least two pMHC coating densities. The assumption that binding events were mediated by single bonds was based on the finding that twofold decrease of coating density resulted in approximately twofold decrease of adhesion frequency whereas survival curves were unaltered. A typical example is shown: ESO-3A peptide studied at 20 (red), 40 (purple), and 80 (blue) s⁻¹ shear rate with coating densities of 0.5 μg/mL (crosses) or 1 μg/mL (circles). The mean number of binding events used to build each curve is 262 (range: 79–548).

The bond-strengthening phenomenon that we describe has been reported by several different laboratories and termed the “history dependence of bond dissociation” (34, 35). This is indicative of the existence of a number of different bound states potentially formed by a given ligand-receptor couple (30, 31, 36). As a consequence, it is not straightforward to account for the dissociation behavior of a well-defined ligand-receptor couple with a single parameter (Fig. 1, A and B).

The fraction of bonds surviving at least 1 s gives a robust account of bond lifetime during the first 10–20 s after ligand-receptor association

The statistics of bond duration were determined for the eight pMHC variants and three different values of the shear rate (20, 40, and 80 s⁻¹). Typical detachment curves are shown on Fig. 3.

Figure 3.

Survival statistics of the rupture of bonds formed with eight pMHCs display minimal crossing between curves, supporting the feasibility of accounting for these curves with a single parameter such as B1s. The rupture kinetics of bonds formed with eight pMHCs and TCR 1G4 was studied at 20 s⁻¹ wall shear rate. The survival during the first 5 s is shown. (Color codes are indicated in the inset.) These plots are based on 1827 arrest durations (between 110 and 356 events per curve).

A natural way of translating experimental data into quantitative lifetime parameters is to fit survival curves to mathematical models. The simplest model involves a single fitted parameter and would be applicable if bond rupture followed monophasic kinetics with a time-independent rupture frequency k_off, yielding

$$B\left(t\right)=\text{exp}\left(-k_{\text{off}}t\right),$$ (1)

where B(t) is the fraction of bonds surviving at time t after formation. However, experimental curves were not consistent with this assumption because they did not appear as straight lines on semilog plots. Another possibility would be to assume a single first-order Markovian unbinding process,

$$B\left(t\right)=A_0+A_1\text{exp}\left(-k_{\text{off}}^{\prime }t\right),$$ (2)

where A₀, A₁, and k_off are three fitted parameters, where k′_off would be equal to the off-rate if bond rupture followed monophasic kinetics. This model allowed accurate fitting of all survival curves (not shown). However, a single parameter (among A₀, A₁, and k′_off) could not give an adequate account of bond lifetime. Thus, although k′_off appeared an attractive candidate, the fitted k′_off values for pMHC variants R65 and 6T were, respectively, 1.44 and 1.45 at 20 s⁻¹ shear rate, whereas the survival curves were markedly different (Fig. 3).

A simple way of accounting for a full detachment curve with a single parameter was suggested by the observation that crossings between survival curves were rare (e.g., ESO-6T and ESO-3Y at 20 s⁻¹ shear rate) and the rank of bond survival yielded by tested pMHCs was nearly unchanged during the first 10 s after attachment. Thus, bond survival at a given time t_ref after association can provide a satisfactory index of bond lifetime. Hopefully, B(t_ref) might account for the information drawn by a T lymphocyte from a cycle of TCR/ligand association/dissociation, whatever the underlying mechanism.

To choose the reference time t_ref for bond survival determination, we used the binomial law to estimate the statistical accuracy of survival information (26): As shown in Fig. 1 A, the relative accuracy of survival determination decreased with time, due to a concomitant decrease of the number of remaining bonds. The fraction of bonds surviving 1 s after association (B1s) was therefore tentatively used as a single robust parameter to account for bond lifetime.

We used bootstrapping (27) to assess the robustness of the B1s parameter: starting from the 162 arrest durations exemplified on Fig. 1, we generated 25 survival curves by random sampling with repetition of 80 arrest durations from the 162 experimental values. The slope of the regression line on the (0.1 s) time interval, parameter B1s and the median duration of arrests were calculated, yielding mean values of −0.588 (standard deviation or SD = 0.127, coefficient of variation CV = SD/mean = 0.22), 0.62 (SD = 0.051, CV = 0.083), and 2.59 s (SD = 1.35, CV = 0.52). Thus, B1s might be considered to provide a reproducible account of bond rupture during the first few seconds after attachment. Interestingly, the estimate of B1s CV matched the estimate obtained with binomial distribution (26), which yielded 0.052.

Note that parameter B1s was strongly correlated with the fraction of bonds surviving 5 s (B5s) and 20 s (B20s), because Pearson correlation coefficients between B1s and B5s, and between B1s and B20s were 0.9826 and 0.9525, respectively. This suggested that our conclusions should not be strongly dependent on the choice of 1 s as a reference time.

Two-dimensional bond lifetimes obtained with the flow chamber are consistent with previously reported three-dimensional values

We next examined whether 3D lifetime measurements could yield a satisfactory account of the lifetime of 2D interactions. Under 3D conditions, the expected fraction of bonds surviving at time t after attachment is

$$B_{3\text{D}}\left(t\right)=\text{exp}\left(-k_{\text{off}}t\right),$$ (3)

where B_3D(t) is the fraction of bonds surviving at time t after formation under 3D conditions and k_off is the conventional dissociation rate. Thus, we compared the experimental survival fractions obtained with the flow chamber and the values of B_3D(t) obtained with the dissociation rates k_off determined using the Biacore analysis system (Biacore Life Sciences, GE Healthcare, Waukesha, WI).

We then compared bond survival at time 1 s and zero force (Biacore) or when bonds were subjected to hydrodynamic forces (flow chamber). Using an estimate of 32 nm for the total length of the bond maintaining a microsphere at rest (pMHC + TCR + anti-Histag, represented ∼8 immunoglobulin domains of 4 nm each), the force on the bond was calculated to be 34, 68, and 136 pN at wall shear rates of 20, 40, and 80 s⁻¹, respectively (30). Note that this estimate is only weakly dependent on bond length because it is inversely proportional to the square root of the bond length (30). Experimental data are shown in Fig. 4 A, suggesting a qualitative agreement between two- and three-dimensional parameters, with two groups of more transient and more durable bonds appearing with both methods. An interesting outlier was peptide ESO-6T that exhibited highest resistance to stronger forces and rather low bond lifetime in presence of low forces.

Figure 4.

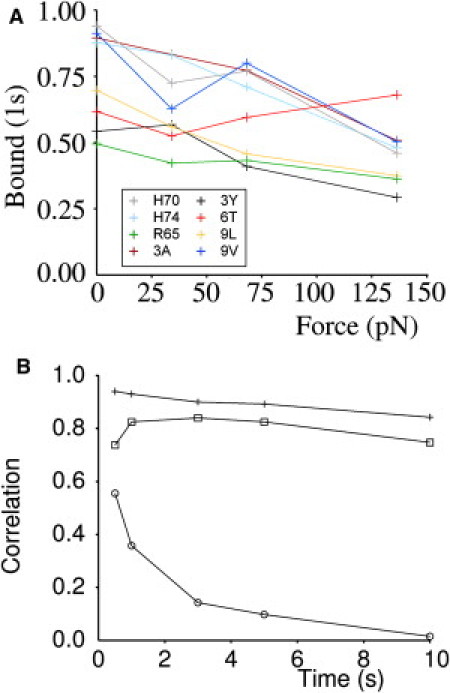
Correlation between three-dimensional dissociation rates and bond survival at time t_ref in the flow chamber depends on the flow rate, not on t_ref. (A) Bond survival at time 1 s is shown for eight pMHC/TCR pairs under three-dimensional conditions, corresponding to F = 0 pN, and under two-dimensional conditions with 20, 40, and 80 s⁻¹ flow rate, corresponding to estimated forces of 34, 68, and 136 pN on bonds. (B) The Pearson correlation coefficient was calculated between the experimental survival fraction measured in the flow chamber at different times under a wall shear rate of 20 (squares), 40 (crosses), or 80 s⁻¹ (circles) and the value expected on the basis of three-dimensional measurements, i.e., exp(−k_offt). The curves shows that three-dimensional (force-free) dissociation is strongly correlated to two-dimensional survival in presence of low forces, but not higher forces, for a wide range of time values, supporting the robustness of this conclusion.

We tried to make the comparison of two- and three-dimensional data more quantitative and less dependent on the threshold time by calculating correlation coefficients with survival fractions measured at times 0.5, 1, 3, 5, and 10 s under wall shear rates of 20, 40, and 80 s⁻¹. Results are shown in Fig. 4 B, yielding the following conclusions: 1), With the lowest two flow rates, the correlation between two- and three-dimensional survival at time t was fairly constant when t was <10 s. The correlation coefficients r measured at 1 s were, respectively, 0.8271 (P = 0.0084) and 0.9332 (P = 000168) at 20 and 40 s⁻¹ shear rate. These values were not significantly different because the normal transforms of r differed by only 1.13 standard deviations (P = 0.26). 2), with the highest flow rate, the correlation between two- and three-dimensional was low (ranging between 0.572 and 0.144) and not significant (P ranging between 0.15 and 0.75). Thus, three-dimensional measurements were found to give a satisfactory account of the lifetime of surface-attached bonds subjected to low forces.

The flow chamber yielded new information on the mechanics of bond rupture as compared to three-dimensional studies

The simplest interpretation of our results would be that the forces exerted by flow might decrease the survival of stressed bonds in proportion to a parameter unrelated to k_off. Indeed, the mean fraction of bonds surviving at least 1 s in the flow chamber was, respectively, 0.63 ± 0.15 SD, 0.62 ± 0.16 SD, and 0.45 ± 0.12 SD for the eight peptides tested at shear rates of 20, 40, and 80 s⁻¹. A straightforward way of following this interpretation consisted of using as a guideline the framework elaborated by Bell (15) that was found to hold in previous studies on, for example, selectin/ligand interactions using flow chambers (37). The basic assumption is that the rupture frequency of a bond subjected to a disrupting force F is

$$k_{\text{off}}\left(F\right)=k_{\text{off}}\left(0\right)\text{exp}\left(F/F°\right),$$ (4)

where F° is a force parameter that is a characteristic property of a given ligand-receptor couple and may vary independently of the dissociation rate measured at zero force. Taking the logarithm of both sides of Eq. 4, we obtain

$$\text{ln}\left[k_{\text{off}}\left(F\right)\right]=\text{ln}\left[k_{\text{off}}\left(0\right)\right]+F/F°.$$ (5)

Replacing k_off(F) with ln(B1s), tentative parameters k_off(0) and F° could be derived from the regression lines of ln[k_off(F)] on F determined for all tested pMHCs complexes. Seven pMHCs yielded positive F° values ranging between 68 and 562 pN, and a single peptide (ESO-6T) displayed a catch-bond behavior with a negative F° of −213 pN. Interestingly, the estimated values of k_off[0] and F° were not correlated (r = 0.41, P = 0.58) whereas k_off[0] was well correlated to the three-dimensional k_off obtained with Biacore measurements (r = 0.8915, P = 0.0014). Results are summarized on Table 1.

Table 1.

Summary of two-dimensional (2D) and three-dimensional (3D) properties of TCR/pMHC pairs

Peptide	EC50 μg/mL	koff (3D) s−1	kon × 1000 M−1 s−1 (3D)	F° (pN) (2D)	Bond survival 1 s (flow 25 μm/s)	koff(0) s−1 (2D)	1000 × Adhesion efficiency (2D)
3A	70 ± 15	0.11	32.1	67.6 ± 45.3	0.834 ± 0.057	0.076 ± 0.068	0.38 ± 0.05
H74	107 ± 12	0.13	5.4	77.2 ± 15.1	0.831 ± 0.056	0.133 ± 0.030	2.35 ± 0.30
H70	151 ± 19	0.06	0.7	57.1 ± 27.4	0.727 ± 0.083	0.130 ± 0.098	0.76 ± 0.10
9V	180 ± 19	0.09	21.1	181.7 ± 319.2	0.630 ± 0.074	0.271 ± 0.236	25.70 ± 3.33
6T	228 ± 62	0.48	7.8	−212.8 ± 25.3	0.527 ± 0.065	0.751 ± 0.038	0.46 ± 0.06
3Y	240 ± 50	0.61	24.7	136.6 ± 40.3	0.569 ± 0.053	0.477 ± 0.093	1.86 ± 0.23
9L	426 ± 113	0.37	9	198.0 ± 48.1	0.562 ± 0.052	0.512 ± 0.0056	1.64 ± 0.21
R65	479 ± 12	0.7	8	563.1 ± 283.9	0.424 ± 0.056	0.788 ± 0.064	0.95 ± 0.12

EC50 is the pMHC concentration for 50% maximal stimulation of interferon production (11). Three-dimensional k_off and k_on were obtained with Biacore (11). Two-dimensional F° and k_off(0) were obtained by extrapolation of flow chamber results with Bell's formula (15). Calculations and error estimates were performed according to Snedecor and Cochran (26) as implemented in the software Excel (Microsoft, Redmond, WA). Adhesion efficiency is shown as a number of arrests per 20-ms interval when surfaces are coated with 1 μg/mL pMHC solution. The coefficient of variation was estimated at 12.8% from nine series of measurements and used to calculate the expected error. Wall shear rate is 20 s⁻¹.

Adhesion efficiencies yielded with the flow chamber are not correlated to three-dimensional association rates

Although there is no straightforward way of deriving 3D association rates from measurements performed with a flow chamber (15, 38), it was interesting to determine whether 2D adhesion efficiencies and 3D association rates were correlated. Taking advantage of the linear relationship between adhesion efficiencies measured with the flow chamber and concentrations of pMHC solutions used for surface coating, we compared 3D association rates and adhesion efficiencies defined as ratios between adhesion frequencies (in arrest per second) and pMHC concentration: no significant correlation was found between 3D association rate and 2D adhesion efficiency measured at 20 s⁻¹ shear rate (r = 0.2635, P = 0.546).

The overall conclusion was that three-dimensional measurements gave only a partial account of the molecular interactions occurring on cell surfaces. An obvious question was thus to ask whether our experimental data provided new insight into the relationship between the two-dimensional interaction parameters of TCR with pMHC and T cell response.

In accordance with previous reports, bond lifetime is positively correlated to the activation potency of pMHCs

As shown in Fig. 5 A, our results were fully consistent with previous reports disclosing a positive correlation between bond lifetime measured under three-dimensional conditions and pMHC activation potency (11): The correlation coefficient between the pMHC concentration required for half-maximal induction of interferon production (EC₅₀) and the three-dimensional dissociation rate (k_off) or the two-dimensional dissociation rate extrapolated at zero force (k_off(0)) were, respectively, 0.7492 (P = 0.03) and 0.8012 (P = 0.014). These values are not significantly different from each other (P = 0.99) and are both significantly different from zero. To ensure that our conclusions were not dependent on any quantitative model, we also calculated the Spearman (rank) correlation coefficient ρ between EC₅₀ and k_off or k_off(0): we obtained, respectively, 0.7380 (P = 0.04) and 0.9048 (P = 0.001), thus confirming the finding of a strong positive correlation between activating potency and bond lifetime of different TCR/pMHC couples.

Figure 5.

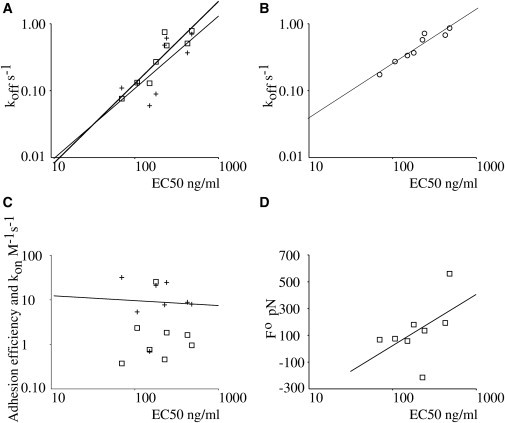
pMHC activation potency as represented by EC50 is better correlated to dissociation rate k_off than to association rate or bond strength. Further results suggest that correlation is optimal with two-dimensional k_off measured in presence of a disrupting force of ∼56 pN. (A) Correlation between EC₅₀ for interferon production and k_off(0) estimated with Biacore (crosses, three-dimensional conditions, thin line is regression line) or the flow chamber (squares, two-dimensional conditions, thick line is regression line). (B) Correlation between EC₅₀ and k_off(F) estimated with the flow chamber with a disruptive force of 56 pN. (C) Lack of correlation between EC₅₀ and adhesion efficiency measured under three-dimensional (crosses) and two-dimensional (squares) conditions. (D) Positive correlation between EC₅₀ and force coefficient estimated with the flow chamber, indicative of an negative correlation between activation potency and bond strength.

In contrast, as clearly illustrated in Fig. 5 C, neither two-dimensional adhesion frequency nor three-dimensional association rates were significantly correlated with EC₅₀ because correlation coefficients were, respectively, r = −0.1453 (P = 0.74) and r = −0.3100 (P = 0.47).

Unexpectedly, our results strongly suggest that bond strength is negatively correlated to activation potency

Because the unstressed lifetime and mechanical strength of TCR/pMHCs interactions varied independently, we tested whether mechanical strength was correlated with activation potency. Somewhat unexpectedly, a positive correlation (r = 0.6380, P = 0.091) was found between EC₅₀ and the force parameter F°. Similar conclusions were obtained with rank correlations (ρ = 0.6428, P = 0.0097). These results strongly suggested that bond strength was negatively correlated with activation potency.

We looked for a more intuitive interpretation of these findings by looking for the force F_m that might optimize the correlation between EC₅₀ and k_off(F) as tentatively calculated with Eq. 4. We found that using 56 pN for F_m yielded a Pearson correlation coefficient of 0.909 between EC₅₀ and k_off(F_m), as shown in Fig. 5 B. Note that the estimates of k_off in presence of a force of 56 pN were derived from regression lines obtained with aforementioned Eq. 5.

Because the determination of k_off(0) and F° involved a fairly complex formula, resulting in a fairly high uncertainty (Table 1), it was important to test whether the estimate of F_m was sensitive to calculation artifacts. Thus, we used a simpler interpolation procedure by assuming that the proportion B1s of bonds surviving at 1 s in the flow chamber was linearly dependent on the particle velocity: the correlation between B1s and EC₅₀ was maximum for a particle velocity of ∼34 μm/s, corresponding to an estimated force exerted on bonds of 46 pN, which is quite comparable to the estimate of 56 pN obtained with more involved calculations. This supported the robustness of our estimate.

Our conclusions are not dependent on the simplified analysis used to process experimental data

Although the reduction of complex dissociation curves to a single number is robust, this simplification entailed a substantial loss of information, which may therefore have prevented us from identifying new connections between TCR binding properties and T cell activation. This risk was an incentive to perform a number of more complicated analyses. In addition to the monoexponential model described by Eq. 1, we also considered a two-state binding model involving a first binding state (f) and a complete binding state (c), yielding five fitting parameters. However, these calculations did not alter our conclusions (not shown).

Discussion

Point 1

To begin, we used a model system to compare the interaction properties of eight TCR/pMHC couples under two-dimensional and three-dimensional conditions. Then, we looked for correlations between two-dimensional parameters and biological activities. This approach is of interest for four reasons: 1), TCR engagement is the primary event in the adaptive immune response. 2), The unique mechanistic interest of the TCR/pMHC interaction is supported by a number of reports suggesting that T cell activation is both qualitatively and quantitatively dependent on the physical properties of interaction with pMHC. 3), The use of eight different ligands differing by a single amino acid is a powerful way of correlating binding properties with function. 4), Using a single molecule pair born by model surfaces allowed us to eliminate interpretative problems generated by additional molecular interactions or active cellular phenomena. A key finding is the ability of a single parameter, i.e., the fraction B(t_ref) of bonds surviving at time t_ref, to account for dissociation kinetics that were obviously multiphasic (Fig. 3), and indeed might involve several separate processes, as suggested by many authors (39, 40, 41). Clearly, this parameter is insufficient to account for the molecular basis of bond rupture. However, we think our results are consistent with the hypothesis that this parameter is of high biological significance. It is plausible that a T lymphocyte might test a TCR/ligand interaction by determining whether it survived for a given interval, whatever the precise molecular pathway followed for rupture.

Point 2

Dissociation rates estimated with the Biacore analysis were tightly correlated with those obtained with the flow chamber. This was not a trivial point; interactions between surface-bound molecules differ from interactions between soluble molecules in two ways: First, after dissociation, molecules may be maintained at a suitable binding distance by surfaces for a significant amount of time. Second, a disrupting force is applied after forced contact. It is therefore conceivable that the agreement between two-dimensional and three-dimensional data be optimal under a given nonzero shear rate. This possibility is consistent with, although not statistically proven by, our results.

Point 3

The force parameter F° that we derived was poorly correlated with k_off(0) (r = 0.2410; P = 0.58). This result is in line with data reported in a recent review (42): the correlation coefficient between k_off(0) and F° in eight ligand/receptor couples was not significantly different from zero (r = 0.4145; P = 0.32). Although this conclusion may seem counterintuitive, it may be easily understood based on the simple Bell model: the force parameter is essentially dependent on the distance between the minimum and the maximum on the energy landscape, whereas k_off(0) is strongly dependent on the height of this barrier (15). Also, it is well known that Bell model is only an approximation, as illustrated with the recent discovery of catch bonds (43, 44), which display nonmonotonous survival/force curves as exemplified in some curves shown in Fig. 4 A.

Point 4

The absence of correlation between association rates (k_on) measured with Biacore and adhesion efficiencies estimated with the flow chamber (r = 0.2635 ; P = 0.55) is consistent with the complexity of two-dimensional association rates, which has been emphasized by many authors (18, 38, 45). Indeed, 2D association rates are highly dependent on the size and flexibility of linker molecules, which may generate big differences between two- and three-dimensional measurements. In addition, the recently disclosed complexity of energy landscapes characterizing biomolecule complexes may hamper the very significance of association rates as used in conventional frameworks (28). Estimated values of association rates are highly dependent on the concentration of functional pMHCs, which may display significant variations due to a possible release of peptide during the course of experiments or surface preparation. Further investigations are thus required to explain the differences between 2D and 3D association rates we report here.

Point 5

This final point concerns the biological significance of our results. The strong correlation between bond lifetime and pMHC activation potency is consistent with a number of previous reports suggesting the same conclusion. The interest of our results is that we used surface-attached molecules, thus mimicking biological conditions more adequately than soluble molecules. The finding of a negative correlation between bond strength and peptide potency is new, to our knowledge, and was quite unexpected. However, this reminds us of the well-known concept of serial triggering (46, 47). According to this model, individual pMHC molecules engage and trigger multiple TCRs in sequence. Serial triggering predicts that there is an optimal TCR/pMHC half-life: short half-lives are insufficient for triggering individual TCRs whereas very longer half-lives reduce the total number of productive TCR engagements by limiting repeated TCR engagements.

It has long been remarked that the requirement to detect a small number of cognate pMHCs among high levels of self-pMHC molecules within a few minutes is a formidable challenge for T lymphocyte recognition. Both sensitivity and specificity might be improved if relative movements of lymphocyte/APC membranes, by introducing mechanical pulling and pushing forces, decreased bond lifetime and enhanced association, respectively (48). In this way, a potent MHC might form a bond with long half-life but low mechanical strength, so that TCR/APC contacts might be readily reversed by active cellular processes and reformed within a short period of time, thus enhancing serial triggering. This hypothesis would be consistent with the previously emphasized importance of the motile lymphocyte machinery in contact areas (46, 49), and is consistent with the finding that T lymphocyte membranes spontaneously display nanometer-scale transverse undulations (50). This is also in line with a recent report on the existence of mechanical pulsations of 20–100 pN amplitude disclosed on fibroblasts studied with atomic force microscopy (51). Obviously, it would be attractive to speculate that the pMHC potency could be increased if they could be ruptured by the forces locally exerted by the lymphocyte membrane. Thus, it would certainly be instructive to subject lymphocytes to the measurements that were successfully performed on fibroblasts (51).

Note, however, that the molecular mechanisms of signal generation as a consequence of TCR engagement remain poorly understood and much work remains to be done in order to fully elucidate the TCR biorecognition mechanisms. Indeed, as clearly shown in a recent review (52) the importance of multivalent interactions, e.g., as a consequence of local clustering, remains poorly understood. Also, although we used the stimulation of interferon γ-production as a gold standard for defining pMHC potency, it will be important to relate the TCR/pMHC interaction to much earlier readouts of TCR signaling, which is a formidable challenge (52, 53). Therefore, fundamental biophysical studies such as this are required for full elucidation of the TCR biorecognition problem.

Editor: Michael Edidin.