3-Picolyl Azide Adenine Dinucleotide as a Probe of Femtosecond to Picosecond Enzyme Dynamics

Abstract

Functionally relevant femtosecond to picosecond dynamics in enzyme active sites can be difficult to measure because of a lack of spectroscopic probes that can be located in the active site without altering the behavior of the enzyme. We have developed a new NAD⁺ analog 3-Picolyl Azide Adenine Dinucleotide (PAAD⁺), which has the potential to be a general spectroscopic probe for NAD-dependent enzymes. This analog is stable and binds in the active site of a typical NAD-dependent enzyme formate dehydrogenase (FDH) with similar characteristics to natural NAD⁺. It has an isolated infrared transition with high molar absorptivity that makes it suitable for observing enzyme dynamics using 2D IR spectroscopy. 2D IR experiments show that in aqueous solution, the analog undergoes complete spectral diffusion within hundreds of femtoseconds consistent with the water hydrogen bonding dynamics that would be expected. When bound to FDH in a binary complex, it shows picosecond fluctuations and a large static offset, consistent with previous studies of the binary complexes of this enzyme. These results show that PAAD⁺ is an excellent probe of local dynamics and that it should be a general tool for probing the dynamics of a wide range of NAD-dependent enzymes.

Introduction

Enzyme motions can span from femtosecond to millisecond timescales both on the exterior of the protein as well as in the active site.^1–4 Characterizing these protein motions is essential to understanding the structure-dynamics-function relationship in enzymes. There is a growing interest in understanding enzyme motions at femtosecond to picosecond time scales as it has been suggested that protein dynamics modulate the activation barrier and influence the complex energy landscape of the catalyzed reaction.^5–9 The importance of fast dynamics at enzyme active sites is also invoked to explain anomalous kinetic isotope effects and their temperature dependence.^10–13 These results were interpreted in the context of Marcus-like models that link environmental reorganization of the active site to the catalyzed H-transfer reactions and specifically suggest a role for femtosecond to picosecond dynamics that modulate the donoracceptor distance and, thus, the reaction rate. The potential for such motions to influence the catalyzed reaction is a subject of much debate in the community. Such dynamics were, until recently, experimentally inaccessible, but, with the advent of nonlinear vibrational techniques like 2D IR spectroscopy, it is now possible to access these motions directly.^14–17

Several proteins have previously been studied by nonlinear vibrational spectroscopies including myoglobin,^{18, 19} hemoglobin,²⁰ neuroglobin,²¹ native and unfolded cytochrome c,²² cytochrome P450,²³ horseradish peroxidase,²⁴ HIV-1 reverse transcriptase,²⁵ carbonic anhydrase²⁶ and formate dehydrogenase.^{27, 28} In all of these studies a small molecule or ion is bound to the protein and serves as a vibrational reporter of the protein dynamics. Unfortunately, the probes in these studies cannot readily be extended to a broad range of enzymes as the chromophores used in those studies are system specific and, therefore, lack generality. Another approach that is commonly used to make proteins accessible to vibrational spectroscopy is site-specific labeling either with isotopes or non-natural amino acids in which a spectroscopic label has been incorporated.^29–35 Such modifications are sometimes challenging for large proteins, can result in limited quantities of material, and, in some cases, can compromise the integrity of the native protein structure. More importantly, the protocol for incorporating the spectroscopic label must be developed anew for every new protein to be studied. Although these challenges do not prohibit the widespread application of these approaches, they do make them sufficiently difficult that these labeling schemes have not been widely adopted for 2D IR applications yet. Thus there is a need for general spectroscopic reporters that can bind to the active sites of many enzymes with minimal perturbation to the native structure of the protein and that are suitable for use with 2D IR spectroscopy.

One approach to address this problem is to label a cofactor or coenzyme that can be used in a wide range of systems. Mid–IR active analogs of NAD⁺ represent an excellent target for developing such a probe of protein dynamics because NAD⁺ is a ubiquitous cofactor for many enzymes. As a cofactor, it binds in the active site and should be a good reporter of protein dynamics in the binding pocket of enzymes. Chromophores substituted at the 3-position of the nicotinamide ring of NAD⁺ are likely to preserve their biological function and bind to the active site in a way that is similar to native NAD⁺.^36–39 Probes that have strong transition moments and transition frequencies that are well separated from other absorption bands are ideal for spectroscopic studies. We have recently shown that an azido-derivatized analog of NAD⁺, azido-NAD⁺, has the potential to be a general probe to investigate the active site dynamics of NAD-dependent enzymes.⁴⁰ This analog exhibits binding and kinetic properties that are similar to native NAD⁺ for a number of enzymes, suggesting that the analog binds to the enzyme with minimal perturbations to the active site structure. For azido-NAD⁺ we have also studied its spectroscopic characteristics.⁴¹ The azido group of the analog is sensitive to hydrogen bond fluctuations in water as would be expected, but this probe has a weak transition moment compared to that for the azide anion, which limits its utility. In general, enzymes have poor solubility and are difficult to study with 2D IR even with strong chromophores. Because the 2D IR signal scales as ε^ı, having a probe with higher molar absorptivity would make it much easier to study enzyme motions. An NAD⁺ analog retaining all the other characteristics of azido-NAD⁺ but with a high molar extinction coefficient would access the active site dynamics of a wide range of proteins. Such a probe would be ideal for 2D IR spectroscopy of enzyme dynamics.

Here, we report the synthesis and characterization of picolyl azide adenine dinuceotide (PAAD⁺), a derivative of NAD⁺ with a high molar absorptivity for the azido antisymmetric stretching vibration. We report the spectral dynamics of this analog in water, which are governed by hydrogen bond fluctuations and are similar to those for azido-NAD⁺ and other small chromophores in water. We also show that the binary complex of PAAD⁺ with the enzyme formate dehydrogenase (FDH) exhibits dynamics that are consistent with what we would expect for this complex based on our previous work with this enzyme. These results reveal the potential of this analog to report enzyme dynamics in FDH and a wide range of other NAD- and NADP-dependent enzymes.

Experimental Methods

Chemicals

3-picolyl chloride hydrochloride, sodium azide, sodium biocarbonate, NADase, NAD⁺, and all solvents were obtained from Sigma Aldrich and used as received. Formate dehydrogenase (FDH, Candida boidinii) is obtained from Roche Diagnostics, Germany.

Synthesis of 3-picolyl azide

In a round bottom flask, 3.4 g (26 mmols) of 3-picolyl chloride hydrochloride dissolves in 50 mL of water and reacts with 2.6 g (40 mmols) of sodium azide. The reaction continues for 16 hours at 50 °C and then sodium biocarbonate quenches it. An oily product is obtained after extraction with methylene chloride. The ¹H-NMR shows peaks at 4.16 (2H,s), 7.3–7.38 (1H, m), 7.72–7.76 (1H, m), 8.6 (2H, s). ¹³C-NMR shows peaks at 123.4, 135.5, 130.9, 141.1, 141.9, 51.9. This compound is soluble in a mixture of 25% DMF in water and has an infrared absorption peak at 2107 cm⁻¹ that has a full width at half maximum (FWHM) of 26 cm⁻¹.

Synthesis of 3-picolyl azide adenine dinuceotide (PAAD⁺)

The synthetic protocol is similar to that for azido-NAD⁺.⁴⁰ In short, NADase from pig brain effects the base exchange of picolyl azide for NAD⁺ at 37 °C under dark conditions. The product, PAAD⁺ is obtained in high purity (> 95 %) as white powder with similar solubility and stability as native NAD⁺ in water. An LC-MS analysis reveals one prominent peak with m/z 675.9, which is assigned to PAAD⁺. The compound shows an infrared absorption at 2119 cm⁻¹ with a FWHM of 22 cm⁻¹ in water.

Enzymatic studies

PAAD⁺ is an inhibitor for the enzyme FDH. The measurements of the dissociation constant, K_d, for PAAD⁺ with FDH are carried out on a MicroCal VP-ITC isothermal calorimeter. For these measurements, FDH is titrated with PAAD⁺. The concentration of FDH is 0.1 mM and the concentration of PAAD⁺ is approximately 1 mM. All solutions are degassed for 15 minutes prior to the experiments to prevent bubble formation. Aliquots of 14 µL of the ligand solution are added to the enzyme solution. Heats of dilution are subtracted from the raw data, and the data are analyzed using a single-site binding model⁴² to determine the dissociation constant.

Infrared Pump-Probe Spectroscopy

An amplified Ti:Sapphire laser system (Spectra Physic, Spitfire) generates 800 nm pulses of 80 fs duration with approximately 4 mJ of energy per pulse at a 1 kHz repetition rate. A portion of this output, about 800 µJ per pulse, pumps an optical parametric amplifier (OPA) based on a β-barium borate (BBO) crystal (θ = 27°, type II). The OPA generates two tunable near-infrared pulses, signal and idler, with a combined pulse energy of 270 µJ. The signal and idler are tuned such that the difference in the energies of the photons from each beam is equivalent to the energy of the mid-infrared light needed to excite the azido-NAD⁺ sample, 2140 cm⁻¹. These are then mixed in a AgGaS₂ difference frequency generation (DFG) crystal (θ = 50°, type II) that produces nearly transform limited pulses with a pulse duration of approximately 100 fs and a pulse energy of 6 µJ.

A wedged CaF₂ substrate separates a small portion of the infrared light for use as a probe beam. The remaining infrared light is used as a pump beam. An infrared pulse shaper based on a germanium acousto-optic modulator built according to the design of Shim et al^{43, 44} chops the pump beam on alternating laser shots. A half-wave plate and polarizer in the pump beam set the polarization of the pump at the magic angle relative to the probe beam to remove the reorientation contribution to the signal. A computer-controlled translation stage varies the time delay between pump and probe pulses. The pump and probe beams are aligned parallel to one another separated by about 2 cm. A 90° off-axis parabolic mirror with an effective focal length of 100 mm focuses the beams into the sample where they have a spot size of approximately 80 µm. After a second parabolic mirror recollimates the beams, an iris isolates the probe beam. A zero-dispersion stretcher with a slit at the Fourier plane frequency narrows a portion of the 800 nm light from our femtosecond amplifier to a transform-limited bandwidth of approximately 1 cm⁻¹. The narrowed 800 nm beam upconverts the infrared probe beam in a MgO-doped LiNbO₃ crystal (θ = 46.5°, type I) into the visible. An imaging spectrometer (300 mm focal length, 1200 grooves/mm grating) disperses the upconverted probe beam and a CMOS camera with 1024 pixels measures the spectrum of each individual laser shot. Using adjacent probe spectra, we calculate the change in optical density caused by the pump beam.

2D IR spectroscopy

In heterodyned 2D IR spectroscopy, we measure the vibrational echo response as a function of one frequency variable ω₃ and two time variables τ, the evolution time, and T, the waiting time. Three femtosecond infrared pulses focus into the sample and generate the vibrational echo response. The time delay between the first and second pulses is τ and that between the second and third pulses is T. For heterodyned detection, the signal overlaps with a fourth, local oscillator, pulse and passes through a monochromator to select the frequency ω₃. A liquid-nitrogen-cooled mercury cadmium telluride (MCT) detector measures the interference between the signal and local oscillator. We scan the monochromator to generate the ω₃ spectrum for each value of τ. As τ is stepped for a fixed value of T, the interference between signal and local oscillator produces an interferogram at each monochromator frequency. A numerical Fourier transform of each interferogram gives the ω₁ spectrum at each value of ω₃. A liquid sample holder made of CaF₂ windows separated by a 25 µm spacer holds the sample which contains a solution with an approximately 30 mM concentration of the PAAD⁺ chromophore either in buffer alone or with the enzyme FDH in slight excess relative to PAAD⁺.

At each waiting time, we generate a 2D spectrum that functions as a correlation map showing how well correlated are the frequencies of the oscillators in our sample at time T with their initial values. If the frequencies of the oscillators have not changed much during the waiting time, then the line shape will be elongated along the diagonal. As the protein samples different conformations as a result of the enzyme dynamics, however, the line shape will rotate toward the horizontal axis. The evolution of this line shape reports the spectral diffusion dynamics of the chromophore that arise due to the structural fluctuations of the system that cause the molecules to lose the memory of their initial frequencies. The frequency-frequency correlation function (FFCF), which is given by <δω(t)δω(0)>, connects the experimental results to the underlying dynamics. This function shows the correlation between the frequencies of the ensemble of oscillators at time zero and a time T later. We employ the center line slope (CLS) method to determine the FFCF from the 2D IR data as described by Kwak et al.^{45, 46} In this analysis, frequency slices are taken from the 2D IR spectrum for fixed values of ω₁. We then locate the frequency ω₃ at which the signal goes through its maximum for each slice in ω₁. This collection of points in ω₃ and ω₁ is called the center line, and the slope of this line, the CLS, as a function of the waiting time, T, is proportional to the FFCF. Plotting the CLS as a function of T, we fit this curve to a sum of exponentials with an offset retaining the fewest terms necessary for accurately fitting the decay. The time constants of this decay are the time scale for the decay of the FFCF as well and reflect the time scale of the structural fluctuations. To determine the absolute amplitude of the FFCF, we take the time constants of the exponentials and their relative amplitudes from the fit of the CLS decay and use those to fit the infrared absorption line shape with the absolute amplitude of the FFCF and a motionally narrowed contribution to the line shape, if necessary, as adjustable parameters.

Results

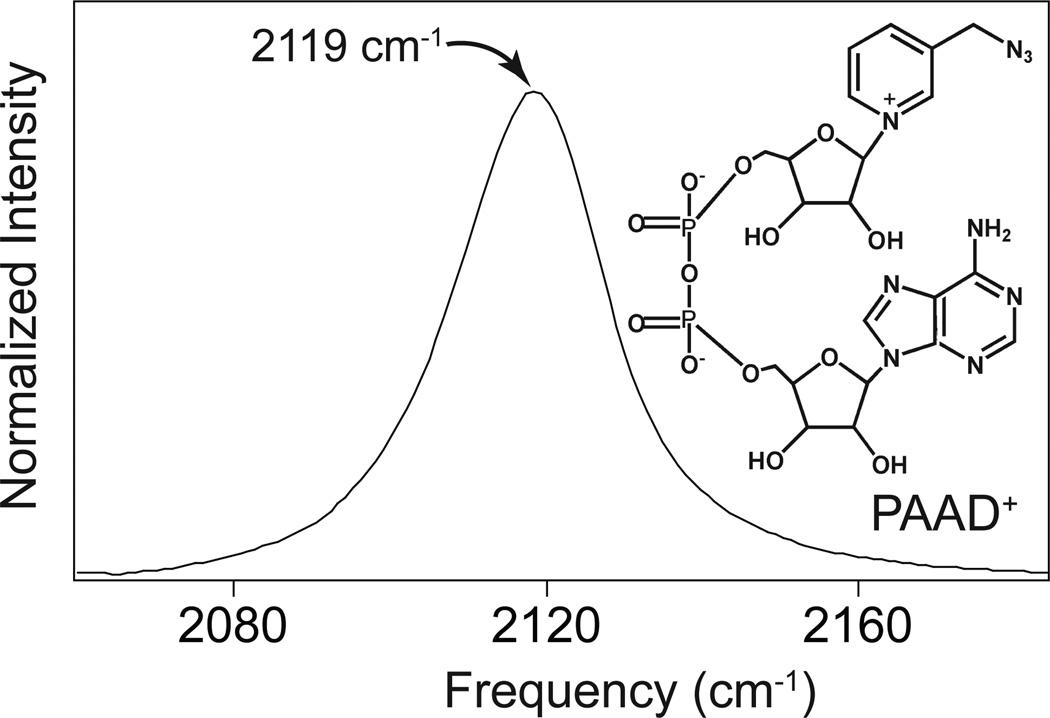
The preparation of the analog PAAD⁺ is analogous to the synthesis of azido-NAD⁺. PAAD⁺ is stable, soluble in water, and can be obtained in high purity. This molecule is structurally analogous to native NAD⁺ except that an azido group with a methylene linker replaces the amide in the nicotinamide ring. As with native NAD⁺, PAAD⁺ has a characteristic UV absorption at 260 nm with an extinction coefficient similar to that for the native cofactor. This transition results from the electronic absorption of the adenine moiety present in both molecules. Unlike native NAD⁺, however, this analog has a strong absorbance in the infrared near 5 µm. Figure 1 shows the linear infrared absorption spectrum and structure of PAAD⁺. The molar absorptivity of PAAD⁺ is ~2000 M⁻¹cm⁻¹ at 2119 cm⁻¹, which is similar to that for the azide anion. This large molar absorptivity circumvents the major limitation of the azido-NAD⁺ analog we have reported previously.

Figure 1.

Infrared spectrum and structure of PAAD⁺.

PAAD⁺ is an inhibitor for FDH. Although this result is not surprising given that the redox potential of the picolyl azide ring is likely to be rather different from the nicotinamide ring, it does mean that the binding geometry of PAAD⁺ in the enzyme is ambiguous. Fortunately, our 2D IR results show clear indications that the picolyl azide is bound inside the protein and is not solvent exposed as described below. The binding studies of the binary complex of PAAD⁺ with FDH by ITC result in a K_d of 7 µM, which is comparable to the K_M for NAD⁺ of 37 µM,^{47, 48} so it is likely that this analog binds in the active site in a way that is similar to that for the natural coenzyme, NAD⁺.

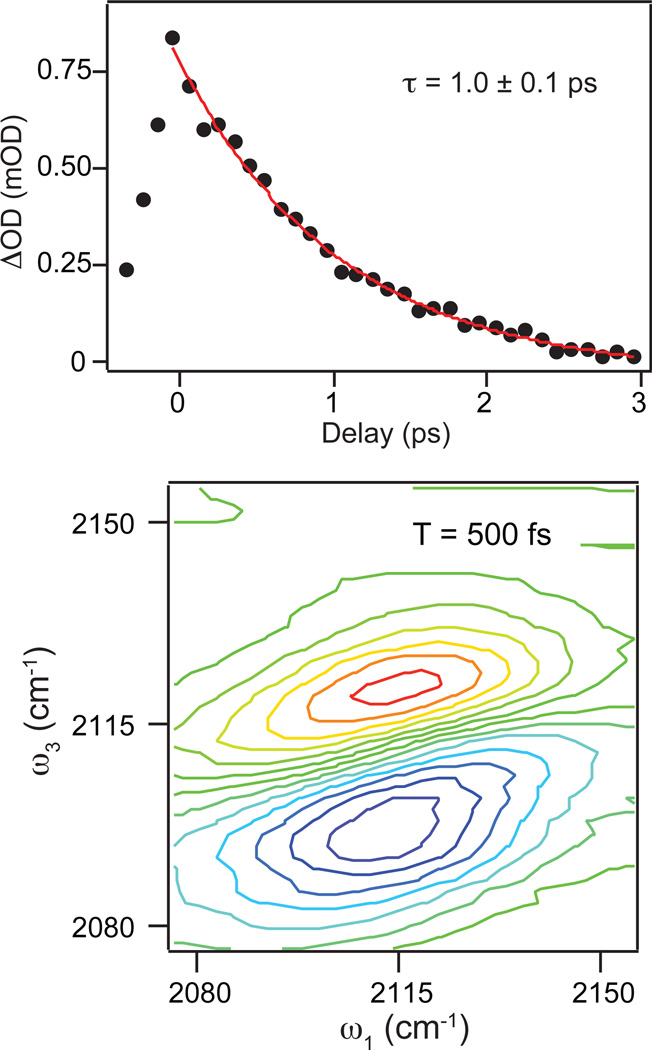
The top panel of Figure 2 shows the decay of the excited-state-absorption contribution to the dispersed pump-probe spectrum measured in the magic-angle polarization geometry. The black dots represent the measured data and the red line is a fit to the decay with a time constant of 1.0 ± 0.1 ps. The ground-state-bleach signal (data not shown) decays with a similar time constant, but exhibits an additional weak contribution to the decay likely resulting from the weakly anharmonically coupled states that are populated in the relaxation of the excited state population.

Figure 2.

(Top) Decay of the excited state absorption contribution to the frequency-dispersed pump-probe measurements for PAAD⁺ in water measured with relative pump and probe polarizations at the magic angle. The excited state decays to zero with a single exponential time constant of 1.0 ±0.1 ps. (Bottom) 2D IR spectrum of PAAD⁺ in water at T = 500 fs illustrating the full 2D IR lineshape of the raw spectrum.

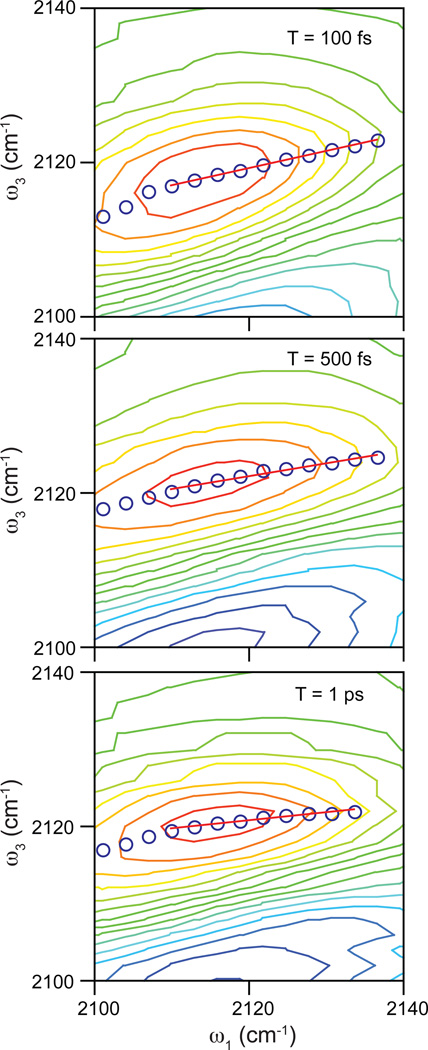
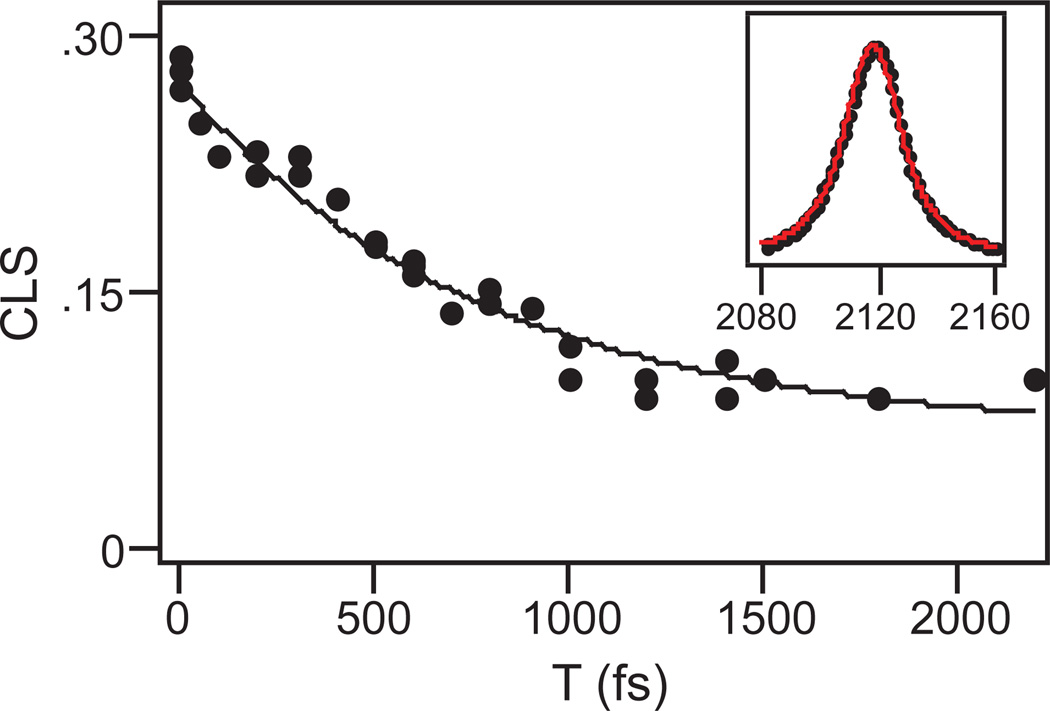
The bottom panel of Figure 2 shows a typical 2D IR spectrum of PAAD⁺ in water at T = 500 fs. The red contours indicate positive signals corresponding to ground state bleaching and stimulated emission signal pathways. These features are elongated along the diagonal at early waiting times and rotate toward the horizontal axis at longer waiting times. This change is a signature of spectral diffusion, in which the environmental conformations are sampled and, therefore, the frequencies of the probe vibrations change. As noted in the experimental section, we use the CLS method to determine the FFCF from the 2D IR data. Figure 3 shows this analysis for 2D IR spectra of PAAD⁺ in water at T = 100 fs (top), 500 fs (middle), and 1 ps (bottom). The open blue circles indicate the frequencies of the peaks in ω₃ for each value of ω₁ corresponding to the center line. Shown in red is the linear fit to the center line. The FFCF decay is proportional to the decay of the slope of the center line as a function of T. Figure 4 shows the decay of the CLS as a function of T for PAAD⁺ in water. A single exponential function with an offset fits the CLS decay well. The time constant for the exponential is 800 ± 100 fs. This model is a generalized Kubo line shape model for the FFCF, i.e. C(t) = Δ₁²e^−t/τ + Δ₂², where Δ₁ and Δ₂ reflect the magnitude of the frequency fluctuations and τ is the time constant for the decay of the FFCF. We get τ and the relative amplitudes of the two components from the CLS decay and the absolute amplitudes for the Δ’s are determined by fitting to the linear absorption spectrum. The parameters that result from the fitting are Δ₁ = 0.91 ps⁻¹, τ = 800 fs, and Δ₂ = 0.52 ps⁻¹. As seen in the inset of Figure 4, the experimental (black) and simulated (red) absorption spectra agree well.

Figure 3.

Representative 2D IR spectra of PAAD⁺ in water for waiting times of 100 fs (top), 500 fs (middle), and 1 ps (bottom) focusing on the positive feature that we analyze to extract the frequency correlations. Blue circles correspond to the center line points determined from the spectrum. The red line is the linear fit to the center line.

Figure 4.

Decay of the CLS as a function of the waiting time T for PAAD⁺ in water. Points are the CLS values for each value of T. The solid line is the fit to the data. The inset shows the infrared absorption spectrum of PAAD⁺ (black points) and the fit to the spectrum (red line).

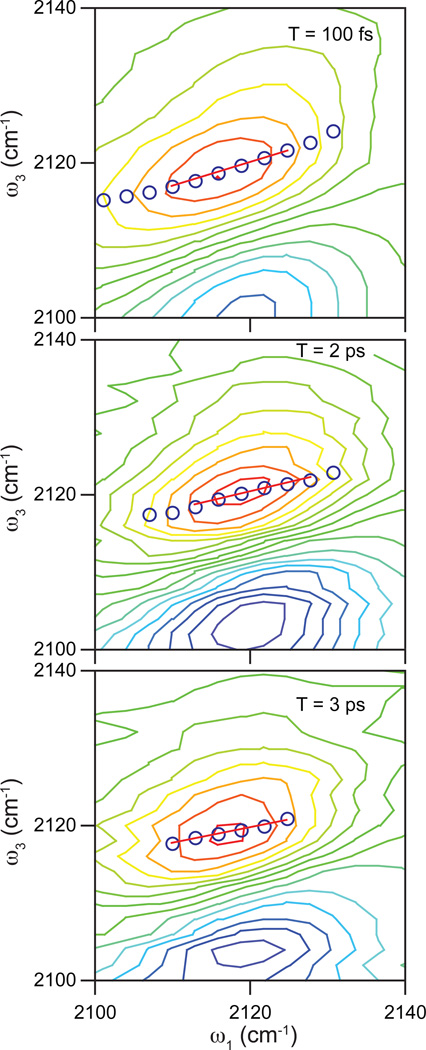
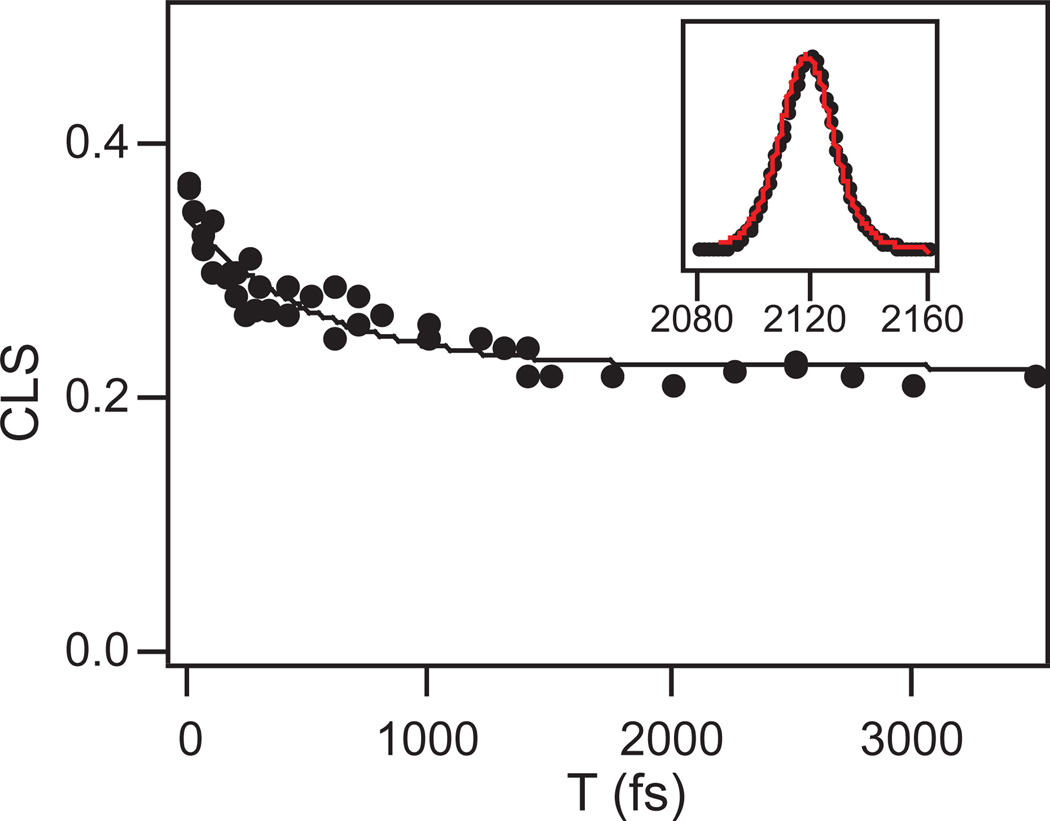
Figure 5 shows 2D IR spectra of the binary complex of FDH with PAAD⁺ at T = 100 fs (top), 2 ps (middle), and 3 ps (bottom). Figure 6 shows the CLS decay as a function of the waiting time, T, for the binary complex. The CLS data are presented as dots and the fit is the solid line. A single exponential with a static offset and a time constant of 500 ± 100 fs fits the decay of the CLS well. To model the FFCF in this complex, we again use a generalized Kubo line shape function of the form, C(t) = Δ₁²e^−t/τ + Δ₂². The inset in Figure 6 shows the fit to the infrared absorption spectrum using the parameters from the fit to the CLS decay and adjusting the total amplitude of the FFCF to fit the absorption line shape. The resulting FFCF parameters from the fitting are Δ₁ = 0.97 ps⁻¹, τ = 500 fs, and Δ₂ = 1.34 ps⁻¹. The simulated spectrum with these parameters is in good agreement with the linear absorption spectrum.

Figure 5.

Representative 2D IR spectra of the PAAD⁺-FDH binary complex for waiting times of 100 fs (top), 2 ps (middle), and 3 ps (bottom) focusing on the positive feature that we analyze to extract the frequency correlations. Blue circles correspond to the center line points determined from the spectrum. The red line is the linear fit to the center line.

Figure 6.

Decay of the CLS as a function of the waiting time T for the PAAD⁺-FDH binary complex. Points are the CLS values for each value of T. The solid line is the fit to the data. The inset shows the infrared absorption spectrum of PAAD⁺ (black points) and the fit to the spectrum (red line).

Discussion

Careful comparison of the infrared spectra of free PAAD⁺ in solution with that for PAAD⁺ bound to FDH shows no significant differences. That there is no apparent difference in these spectra does not mean, however, that they do not exhibit distinct underlying dynamics. The infrared absorption line shape is often not a good measure of the underlying dynamics that give rise to the line shape because it is determined by the integral of the correlation function, and many different FFCFs can be integrated to give the same line shape even though the associated dynamics differ. In contrast, 2D IR can probe these differences. A key feature of 2D IR is its ability to uniquely determine the FFCF. Our experimental analysis clearly shows that PAAD⁺ exhibits distinct spectral dynamics depending on whether it is bound to FDH or free in solution, suggesting that it binds in the active site and that it will be a suitable probe of enzyme dynamics.

Based on our measurements of PAAD⁺ in water it is logical to conclude that the frequency fluctuations of the azido stretching vibration are determined by the water hydrogen bond dynamics. The FFCF of PAAD⁺ in water is similar to that for other small chromophores.^{41, 49–53} The time scale of spectral diffusion, 800 fs, is consistent with these earlier measurements and with the conclusions of those studies that this time scale reflects the hydrogen bond fluctuations around the chromophore, in this case the azido moiety of PAAD⁺. In solution, NAD⁺ is a mixture of folded and unfolded forms with the aromatic rings stacked parallel to one another in a π-stacking interaction. One might expect this equilibrium to contribute to the frequency fluctuations of the azido vibration. The equilibrium exchange between the folded and the unfolded structure should be slow compared to the time window for our measurement suggesting that such a contribution would appear at long times. In addition, unlike azido-NAD⁺, PAAD⁺ has a methylene linker between the azide and the pyridine ring that should increase the orientational flexibility of the azido group and could also contribute to the decay of the FFCF at long waiting times. In our experiments on PAAD⁺ in water we do observe a small static contribution indicative of dynamics that occur beyond our experimental time scale that could reflect the slow equilibrium exchange between folded and unfolded conformers or rotations about the dihedral angles associated with the methylene group. Nevertheless, this contribution is about a fourth of the amplitude of the 800 fs component. Thus we conclude that local hydrogen bond fluctuations of water molecules in the first solvation shell around the azido group have the greatest influence on the decay dynamics of the FFCF for PAAD⁺ in water. In addition to the 2D IR measurements, the pump-probe experiments for PAAD⁺ in water show that the excited vibration relaxes in 1 ps, which is typical for azido stretching vibrations.^{41, 53–55} Although this time scale is short, it is adequate for sampling the dynamics on the hundreds of femtoseconds to few picoseconds time scale. Based on our 2D IR measurements, it appears that the lifetime for PAAD⁺ bound to FDH may be somewhat longer thus enabling the measurement of 2D IR spectra at somewhat longer waiting times than are accessible in water. We have not measured the pump-probe decay for PAAD⁺ bound to FDH primarily because the sample concentration would be much lower than that used for the experiments in water making that measurement substantially more difficult. Nevertheless, we can conclude that, although the population lifetime for the azido stretching vibration of PAAD⁺ is short, it is adequate for sampling the femtosecond to picosecond dynamics of enzymes.

PAAD⁺ bound to FDH shows distinct spectral diffusion dynamics from those seen in water, and the resulting FFCF agrees well with that seen in previous studies of enzyme dynamics. PAAD⁺ in the binary complex with FDH decays to a large static offset. The decay of the FFCF in the binary complex exhibits a 500 fs time constant, and the static contribution to the FFCF represents 65% of the overall decay. This result is consistent with the FFCFs of other small molecules bound to proteins and is expected since proteins typically exhibit dynamics at a wide range of time scales from femtoseconds to milliseconds. The motions of the protein that occur on time scales longer than the measurement time appear as a static contribution to the FFCF and frequently contribute 20–50% of the overall decay. For the FDH-PAAD⁺ binary complex, we collect 2D IR spectra for waiting times up to 3.5 ps indicating that the population lifetime of the bound chromophore is somewhat longer than in the free state as noted above. These results suggest that PAAD⁺ should be a good general probe of enzyme active-site dynamics of NAD-dependent enzymes. Based on the similarity of the dissociation constants for PAAD⁺ as compared to the native coenzyme, NAD⁺, we anticipate that PAAD⁺ binds to FDH in a way that is similar to NAD⁺ with the picolyl azide ring located in the active site where the nicotinamide ring would normally be.⁵⁶ Of course PAAD⁺ is missing the key amide group that is present in NAD⁺. Although the methylene-linked azido group of PAAD⁺ retains the H-bond accepting ability of this amide, the H-bond donating capability is lost in this substitution. This difference between NAD⁺ and PAAD⁺ has the potential to alter the binding of PAAD⁺ and its interactions with the enzyme active site, which could limit the applicability of this cofactor as a probe of enzyme dynamics in some enzymes.

The FFCF of the PAAD⁺-FDH complex is similar to that for the FDH-azide binary complex that we have studied previously.²⁷ Both of these complexes have a significant static component that comprises more than 50% of the initial value of the FFCF. As with the FDH-azide binary complex, the binary complex of PAAD⁺ with FDH likely represents a structure that is well removed from the transition-state-analog conformation represented by the ternary complex, FDH-NAD⁺-azide. In the ternary complex, we observed the surprising result that the FFCF decays to zero on the picosecond time scale. We explained this unusual result on the grounds that the ternary complex is a mimic of the transition state and therefore resides in a deep potential minimum in which one would anticipate a narrow conformational distribution and fast fluctuations about the average configuration. The presence of the static component in the FFCF decay of the FDH-azide binary complex was presented as evidence in support of this hypothesis since the binary complex does not resemble the transition state structure. The current result for the binary complex of FDH with PAAD⁺ lends further support to this conclusion. Here too the complex is removed from the transition state structure, and, again, we observe a significant static contribution to the decay. A key test of the potential of PAAD⁺ as a probe of enzyme dynamics is whether the ternary complex with PAAD⁺ and azide exhibits complete decay of the FFCF on the picosecond time scale. Such a result would demonstrate that PAAD⁺ does not significantly perturb the active site structure and dynamics of the transition-state-analog complex. These experiments are presently underway.

Conclusion

We report the synthesis, characterization and kinetics of an azido analog of NAD⁺, PAAD⁺. It binds to FDH with an affinity comparable to native NAD⁺. PAAD⁺ exhibits a strong infrared absorption at 2119 cm⁻¹ associated with the azido antisymmetric stretching vibration, a region suitable for enzymatic studies. It has a high molar extinction coefficient comparable to that of the azide ion, which makes it an ideal spectroscopic probe of enzyme dynamics. Our results show that the azido antisymmetric stretch of PAAD⁺ is sensitive to the dynamics in its local environment. In aqueous solution, the spectral diffusion is nearly complete within hundreds of femtoseconds whereas when bound to FDH, PAAD⁺ shows a substantial static contribution to the FFCF. This observation is consistent with other enzymes where slow motions influence the FFCF.

The ability of PAAD⁺ to bind, form kinetically relevant complexes with the enzyme and to report the active-site dynamics show that PAAD⁺ can be a general spectroscopic tool to probe the femtosecond to picosecond dynamics of numerous NAD⁺ dependent and other systems, where NAD⁺ plays a role. Studies of this probe bound to different enzymes both wild type and mutants are currently underway.