Abstract
Motor learning changes the activity of cortical motor and subcortical areas of the brain, but does learning affect sensory systems as well? We examined in humans the effects of motor learning using fMRI measures of functional connectivity under resting conditions and found persistent changes in networks involving both motor and somatosensory areas of the brain. We developed a technique that allows us to distinguish changes in functional connectivity that can be attributed to motor learning from those that are related to perceptual changes that occur in conjunction with learning. Using this technique, we identified a new network in motor learning involving second somatosensory cortex, ventral premotor cortex, and supplementary motor cortex whose activation is specifically related to perceptual changes that occur in conjunction with motor learning. We also found changes in a network comprising cerebellar cortex, primary motor cortex, and dorsal premotor cortex that were linked to the motor aspects of learning. In each network, we observed highly reliable linear relationships between neuroplastic changes and behavioral measures of either motor learning or perceptual function. Motor learning thus results in functionally specific changes to distinct resting-state networks in the brain.
Introduction
Neural plasticity at a systems level is reflected in the ability of the brain to alter its functional organization as a result of experience. In work on motor learning, studies of plasticity have primarily focused on motor function and motor areas of the brain. The extent to which motor learning affects sensory systems has received less attention. Recent behavioral work has shown that motor learning results in systematic perceptual changes to both the sensed position of the limb (Haith et al., 2008; Cressman and Henriques, 2009; Ostry et al., 2010) and perceptual acuity (Wong et al., 2011). These changes appear to play a functional role in the learning process in that, after learning, movements follow trajectories that are aligned with shifted perceptual boundaries. The effects of learning on perceptual function are not limited to limb movement. In previous work, it has been shown that changes in the perception of speech sounds accompany speech motor learning (Nasir and Ostry, 2009; Shiller et al., 2009).
Previous studies have reported changes in activation in sensory areas in conjunction with motor learning (Lotze et al., 2003; Pleger et al., 2003; Hlustík et al., 2004; Floyer-Lea and Matthews, 2005). These studies as a group share a problem in interpretation. There is a confound such that differences in activation that are observed after learning may simply reflect changes in motor performance between pre-learning and post-learning measures. Here we eliminate this problem by using resting-state functional magnetic resonance imaging (fMRI) to assess changes in the functional connectivity (FC) of brain areas after motor learning. Scanning during resting-state conditions enables us to rule out the possibility that differences in activation that are observed after learning are attributable to differences in how the task is performed in pre-learning versus post-learning scans.
One previous study has reported changes in resting-state FC in association with motor learning (Albert et al., 2009). Effects are observed in a frontoparietal network and a cerebellar network. The extent to which these changes are related to behavioral indices of learning is unknown, as is whether the changes reflect adaptation in sensory or motor systems or the two in combination. Here we introduce a technique for incorporating behavioral measures into resting-state connectivity analyses. The method allows us to identify networks whose connectivity changes with learning and specifically to dissociate changes in connectivity that are related to motor learning from those related to perceptual changes that occur in conjunction with learning. The power of this technique lies in its ability to distinguish changes in neural function that are directly related to behavioral measures in both motor and sensory domains.
We find that changes in brain networks that occur in combination with motor learning can be partitioned into those that are primarily motor in nature and those that reflect the perceptual changes that arise during motor learning. The sensory networks that are strengthened in conjunction with learning are the same as those involved in somatosensory perceptual learning and decision-making (Romo et al., 2002; de Lafuente and Romo, 2006). Thus, the process of motor learning appears to engage the perceptual learning network.
Materials and Methods
We studied learning by having subjects reach straight ahead to a single visual target while a robot applied forces to the arm in a lateral direction in proportion to movement velocity. Vision of the arm was blocked throughout the training procedure. Measures of BOLD activation under resting-state conditions were obtained ∼1 h after training trials in the absence of load and again on the following day ∼1 h after force-field learning. On each day, subject's perception of limb position was assessed using an adaptive staircase technique (Taylor and Creelman, 1967).
Subjects.
Thirteen right-handed volunteers of either sex between the ages of 21 and 44 years participated in this study. The McGill University Research Ethics Board approved all experimental procedures.
Experimental setup.
A 2 degree of freedom (DOF) planar robotic arm (InMotion2; Interactive Motion Technologies) was used for psychophysical parts of study. Subjects were seated in front of the robot and held the handle with their right hand. They performed reaching movements in a horizontal plane. The start position, target, and a cursor that represented the position of the subject's hand were all projected on a semi-silvered mirror that was placed horizontally just above the subject's arm. The visual feedback appeared in the same plane as the arm. Two white circles, 20 mm in diameter, represented the start and target positions; a 12 mm yellow circle indicated the subject's hand position. Subjects were not able to see their hand or arm, and all experiments were done under conditions of low ambient light. The seat height was adjusted for each subject individually, to give an 80° abduction angle at the shoulder. The position of the robot handle was recorded by means of optical encoders at the robot joints (Gurley Precision Instruments).
Experimental task.
Subjects participated in three sessions on three separate days. The first day (day 0) familiarized subjects with the psychophysical procedure. In this session, subjects completed three blocks of trials. In the first block, they were trained to make straight reaching movements to the same target location that was used on subsequent days for the experimental manipulation. In the second and third blocks, subjects practiced the perceptual testing procedure, in which the subject's perception of the boundary between left and right was estimated.
The experimental manipulation was performed in the second and third sessions (experimental days 1 and 2), which took place at the same time on consecutive days. On each day, the session began with a series of reaching movements to the visual target. Subjects then moved to the Montreal Neurological Institute (MNI) imaging facility. The scanning phase took approximately one hour. During the resting state scans subjects were instructed to rest quietly with their eyes closed and to stay awake. Subjects then returned to the laboratory and completed a perceptual test. On the last day of study, the perceptual test was followed by a final block of reaching movements (Fig. 1A).
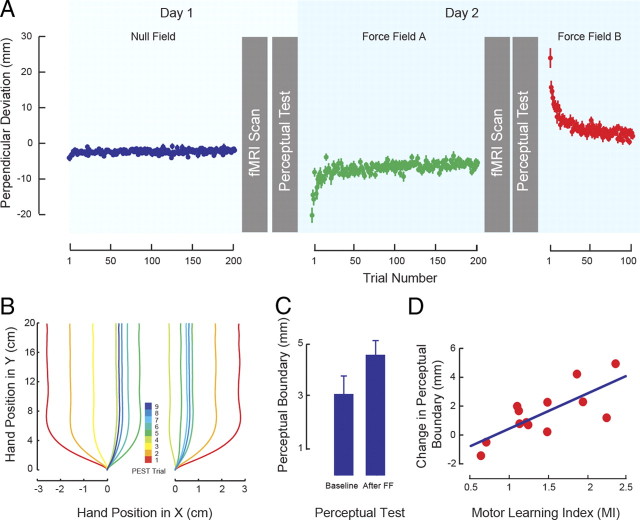
Figure 1.
A, Sequence of experimental procedures showing evolution of PD during training averaged across subjects. B, Representative hand paths during perceptual testing starting from the left (left panel) and right (right panel). The color code gives the trial number in the PEST sequence. C, Motor learning results in changes to the sensed position of the limb. The figure shows the mean ± SEM perceptual boundary under baseline conditions and after force-field learning (After FF). D, Subjects who show greater motor learning (MI) have greater shifts in the perceptual boundary. The solid line gives the best linear fit.
Reaching movements.
Subjects made straight-ahead reaching movements to a single visual target that was 20 cm from the start point in the midsagittal plane. The desired maximum velocity was 0.5 ± 0.04 m/s. Visual feedback of movement speed was provided as soon as the subject's hand entered the target zone. After the feedback, the robot returned the subject's hand to the start position.
The familiarization session (day 0) started with 50 movements under null field conditions. On day 1 of the actual experiment, subjects completed 200 reaching movements under null field conditions. On day 2, subjects made 200 reaching movements in a counterclockwise force field (force field A) before they went for the resting-state scan. When subjects returned from the day 2 scan (and after perceptual testing), they completed a final block of 100 reaching movements in a clockwise force field (force field B). The clockwise force field was applied according to Equation 1:
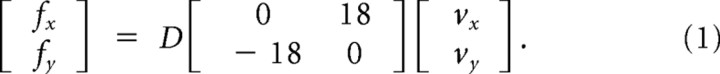 |
In this equation, x and y are lateral and sagittal directions, fx and fy are the commanded force to the robot, and vx and vy are hand velocity in Cartesian coordinates. D defines the direction of force field. For a clockwise field, D was set to 1; in the counterclockwise condition, D was −1.
Perceptual judgments.
Subject's perception of the boundary between left and right was estimated using the PEST procedure (parameter estimation by sequential testing), as described previously by Ostry et al. (2010). In the current study, subjects were asked to hold their hand at the start position as indicated by a yellow cursor (the subjects' arm was blocked from view). After a semi-random wait time of 500 ± 500 ms, the robot was programmed to move the subjects' hand outward toward the target following a fork-shaped pattern (Fig. 1B) under position servo control. Subjects were instructed not to resist the action of the robot. The programmed sequence was as follows. As soon as the hand had been moved 5 mm, both the target and the yellow circle that indicated hand position disappeared. At 15 mm from the start, the robot gradually shifted the hand laterally either to the left or the right over a period of 300 ms by an amount that was updated on a trial-by-trial basis. The limb was maintained at this lateral position for the remainder of the outward movement. Thus, at the end of each movement, the subjects' hand was either to the left or the right of the actual target position. When robot reached its final position, subjects were asked to indicate whether or not the hand had been moved to the right. On each trial, the magnitude of the lateral deviation of the hand was modified in an adaptive manner (Taylor and Creelman, 1967), until an estimate of the perceived boundary between left and right was obtained. On each PEST run, which typically involved 8–16 movements, a single estimate of the perceptual boundary was obtained. On successive PEST runs, the initial displacement direction alternated between left and right. The lateral displacement on the first movement of each run was randomly selected from a uniform distribution with values ranging from 20 to 30 mm (in both directions). All of our subjects were easily able to correctly discriminate the direction of the first arm deflection. On the next trial, the deflection was reduced by 10 mm, and this was repeated on successive trials until the subject reported a change in the direction of lateral displacement. At this point, we reduced the step size by half, and the next displacement was in the opposite direction. The algorithm terminated whenever the step size for the upcoming movement fell below 1 mm.
Data analysis.
Hand position and the force applied by the subject to the robot handle were both sampled at 400 Hz. The recorded signals were low-pass filtered at 40 Hz using a zero-phase-lag Butterworth filter. Position signals were numerically differentiated to produce velocities. The start and end of each trial were defined at the time at which hand tangential velocity went above or fell below 5% of peak velocity. The resulting time series was resampled to have the same number of data points in each trial. For analysis purposes, we calculated the maximum perpendicular deviation of the hand (PD) from a straight line connecting movement start and end positions (Malfait et al., 2002). In this way, we obtained quantitative estimates of movement straightness.
Each block of perceptual tests had six PEST runs, three starting from the right and three from the left. We obtained an estimate of the perceptual boundary between right and left for each subject and each experimental condition separately by fitting a logistic function to that subject's entire set of lateral deviations and associated binary (yes/no) responses. The 50% point of the psychometric function was taken as the perceptual boundary. A perceptual index (PI) was defined as the change in the perceptual boundary normalized by the mean absolute value of the perceptual boundaries on day 1 and day 2.
We quantified motor learning ∼90 min after learning force field A by measuring the extent to which this previous experience interfered with learning of force field B, which produced force in the opposite direction; greater interference indicated greater retention of force field A. For each subject, we calculated PD averaged over the first three trials in force field A and over the first three trials in force field B, with both measures taken relative to each subject's average PD over the last 50 null field trials (ΔPDA and ΔPDB, respectively). We normalized for differences between subjects by dividing ΔPDB by ΔPDA on a per-subject basis. The resulting ratio, or motor learning index (MI), is given in Equation 2. MI scores >1.0 indicate interference caused by force field A learning on initial performance in force field B. The greater the value of MI, the greater the learning and also retention of force field A:
 |
fMRI acquisition.
All data were acquired using a 1.5 tesla Siemens Sonata MR scanner at the MNI. The whole-brain functional data were acquired using a T2*-weighted EPI sequence (eight head-coil channels; resolution, 4 mm isotropic; 32 slices; 64 × 64 matrix; TE, 50 ms; TR, 3000 ms; flip angle, 90°; generalized autocalibrating partially parallel acquisitions with an acceleration factor of 2). The functional images were superimposed on a T1-weighted anatomical image (1 mm slice thickness; 256 × 256 matrix; TE, 9.2 ms; TR, 27 ms; flip angle, 30°). A T2-weighted structural image, aligned with the EPI images (4 mm slice thickness; 256 × 256 matrix; 32 slices; TE, 83 ms; TR, 5000 ms; flip angle, 180°), was also acquired to enhance the registration transformation from the EPI to T1-weighted scan. Each session began with two 12-min resting-state fMRI scans, separated by an 18-min T2-weighted structural scan and a T1-weighted high-resolution anatomical scan. A final 7-min scan involved arm movement in a block design.
Image preprocessing.
Data processing was performed using FSL (FMRIB Software Library) software packages [www.fmrib.ox.ac.uk, FMRIB (Functional MRI of the Brain), Oxford, UK; FSL version 4.1 (Smith et al., 2004; Woolrich et al., 2009)]. Image preprocessing consisted of the following: (1) the removal of the first two volumes in each scan series (volumes acquired before equilibrium magnetization was reached), (2) slice time correction (using Fourier-space time-series phase shifting), (3) non-brain removal using Brain Extraction Tool (Smith et al., 2004), (4) motion correction (using a six-parameter affine transformation implemented in FLIRT (FMRIB Linear Image Registration Tool) (Smith et al., 2004), (5) global intensity normalization (because there may be global intensity differences between BOLD runs, multiplicative differences can be factored out by scaling each run to a global mean), (6) spatial smoothing (Gaussian kernel of FWHM, 6 mm), and (7) temporal high-pass filtering (Gaussian-weighted least-squares straight-line fitting with σ = 100.0 s).
To achieve the transformation between the low-resolution functional data and standard space (MNI 152: average T1 brain image constructed from 152 normal subjects), we performed two transformations. The first was from the T2*-weighted image to the T1-weighted structural image (using a 6 DOF transformation), and the second was from T1-weighted structural image to the average standard space (using a 12 DOF linear affine transformation; voxel size, 2 × 2 × 2 mm).
It has been shown that removing physiological noise (cardiac- and respiratory-related signals) substantially improves the results of the FC analysis at rest (Krüger and Glover, 2001). For physiological noise removal, we used the method reported previously (Shehzad et al., 2009). This method uses average signals taken over sections of white matter (WM) and CSF, plus the global signal as nuisance regressors. To extract the WM and CSF time series, we segmented each individual's high-resolution structural T1 image, using an automatic segmentation program implemented in FSL (Smith et al., 2004). The resulting segmented WM and CSF images were then thresholded to ensure 80% tissue type probability. Each thresholded mask was then applied to that individual's time series, and the mean time series was calculated by averaging the time series from all voxels within the mask. The global signal accounts for several potential sources of physiological noise assuming that fMRI experiments are concerned with local changes in neuronal activity and that global signals represent uninteresting sources of noise (Desjardins et al., 2001). The global signal was calculated by averaging the time series over all voxels in the brain. In total, nine nuisance regressors were used: WM, CSF, global signal, and six motion parameters (x, y, and z translations and rotations obtained from the motion-correction step in preprocessing). For each individual, a separate multiple regression analysis was performed on the time series of nuisance signals using the FEAT (FMRIB Expert Analysis Tool) toolbox (Beckmann et al., 2003). In this way, the nuisance signals are modeled and the residual image represents the corrected signal. We further applied temporal bandpass filtering (Butterworth filter with zero-phase lag) to the resulting residual image to retain frequencies in the 0.009–0.08 Hz band because, in resting-state fMRI, we expect a neuronal activity-related signal within this range (Fox et al., 2005; Fox and Raichle, 2007).
Movement imaging analysis.
After preprocessing (except for physiological noise removal, which is specific to the resting-state functional data), the regressor for arm movement versus baseline was modeled with a boxcar function, and another regressor was added to represent the temporal derivative of the stimulation timing. The regressors were then convolved with a double-gamma hemodynamic response function (HRF). For each participant, a first-level GLM analysis was performed using FEAT, which is part of FSL. Then the Z statistic images were input to a group-level GLM. The group-level analysis used the FEAT mixed-effects model with a stringent cluster thresholding (Z ≥ 3.5, corrected, using Gaussian random field theory, cluster significance threshold of p = 0.01). Threshold activation maps were then overlaid on the MNI standard image to define anatomical locations of activations by using the Harvard–Oxford cortical and subcortical and Juelich histological atlases.
Region of interest selection.
We selected seven regions of interest (ROIs) in areas reported previously to have significant changes in activation attributable to motor learning. These regions include contralateral primary motor cortex (M1) (Grafton et al., 1992; Steele and Penhune, 2010), dorsal premotor cortex (PMd) (Shadmehr and Holcomb, 1997), supplementary motor area (SMA) (Padoa-Schioppa et al., 2004), ventral premotor cortex (PMv) (Mitz et al., 1991), posterior parietal cortex BA7 (PPC) (Shadmehr and Holcomb, 1997), basal ganglia, caudate nucleus (BG) (Doyon et al., 2009), and ipsilateral cerebellar cortex (adjacent to posterior–superior fissure) (Imamizu et al., 2000; Pasalar et al., 2006). Because we also wanted to assess sensory plasticity in association with motor learning (Eickhoff et al., 2005), we added two additional ROIs that are known to play a significant role in perceptual learning: primary somatosensory cortex (SI; BA1/2) (Pleger et al., 2003) and second somatosensory cortex (SII) within the parietal operculum (Romo et al., 2002; Pleger et al., 2003). Each of these areas was defined based on the Juelich histological (cyto-architectonic and myelo-architectonic) atlas (Eickhoff et al., 2005). The caudate nucleus and cerebellar lobules were defined using the Harvard–Oxford subcortical structural atlas (Desikan et al., 2006) and probabilistic cerebellar atlas (Diedrichsen et al., 2009), respectively.
An arm movement task was used as a localizer to identify seed coordinates for connectivity analyses. Specific coordinates in each of the ROIs were selected on the basis of activation peaks obtained from a block-design analysis of arm movements, which were recorded at the end of the scanning session. The design involved alternate blocks of movement and rest (six 36-s blocks of each), cued with a color-coded blinking visual stimulus at the frequency of ⅓ Hz. The movement blocks involved slow cyclic movements of the right arm that were ∼15 cm in amplitude in an outward direction away from the body in the sagittal plane. The subjects practiced this task outside the scanner to ensure consistency of movement across subjects. The direction of movement was similar to that using the robotic device, although at a lower speed was used to minimize movement artifact in the scanner.
The preprocessing of the block-design data followed the same steps as the resting-state data, except that physiological noise was not removed. In this way, we made sure that the selected seed voxel in each ROI corresponded somatotopically to areas activated by subjects' arm movements. The MNI coordinates of seed voxels, the Z value of the peak activity in the movement block, and their anatomical labels are listed in Table 1. We used this same set of seed coordinates for all individuals. We verified that Z values for individual subjects were high (Z > 2.0) at the seed locations shown in Table 1. One exception was caudate nucleus, in which for three individuals the Z value at the group-level peak was lower, between Z = 1 and Z = 1.5. We obtained the average BOLD time series of each ROI and each subject by defining a spherical mask (radius of 6 mm) around the seed in standard space. We resampled this mask first to the T1-weighted structural image of each subject and from there to the low-resolution functional space of that subject. For each subject, the average time course of the BOLD signal within the transformed mask in the functional space was calculated.
Table 1.
Seed coordinates of selected ROIs in MNI space (given in mm), their anatomical labels, and the corresponding Z value of the activation peak during movement
| ROI | Anatomical label | MNI coordinates |
Z value | ||
|---|---|---|---|---|---|
| x | y | z | |||
| MI | L primary motor cortex BA4 | −32 | −30 | 68 | 6.1 |
| PMd | L dorsal premotor cortex BA6 | −26 | −22 | 66 | 5.7 |
| SMA | L supplementary motor area proper | −2 | −8 | 58 | 4.6 |
| PMv | L ventral premotor cortex BA6 | −34 | −16 | 52 | 5 |
| SI | L primary somatosensory cortex BA2 | −36 | −38 | 58 | 5.5 |
| SII | L secondary somatosensory cortex, OP1 | −62 | −20 | 20 | 4.7 |
| PPC | L posterior parietal cortex, BA7 | −22 | −56 | 64 | 5.3 |
| CB | R cerebellum, lobule VI | 32 | −52 | −28 | 5 |
| BG | L basal ganglia, caudate | −16 | −8 | 22 | 3.7 |
Each ROI is a sphere of radius 6 mm with its center located at the activation peak. L, Left; R, right.
FC analysis using behavioral factors.
The mean BOLD time course of each ROI identified above was used as a predictor in a per-subject GLM to assess the FC of that ROI with every other voxel in the brain. We included the time derivative of the signal of each ROI as a regressor in the GLM to account for possible time differences in the HRF of different cortical areas, as well as the latency for signal propagation from one cortical area to another (see below, Response latency correction). This analysis produced maps of all voxels that were positively and negatively predicted with the mean time course of an ROI. This was followed by between-subjects analyses that were performed using a mixed-effects model (FLAME) implemented in FSL (Beckmann et al., 2003). In this analysis, we used either the MI or PI as regressors, as well as regressors modeling each subject's overall mean across sessions and runs. Specifically, one set of regressors modeled the common effect between days for each subject. This comprised the overall mean of each subject across all four runs (two runs from day 1 and two from day 2). The second regressor, which is the regressor of interest, modeled the difference between days based on the subject-specific MI or PI weights. The applied regressor of interest, after orthogonalization with respect to other regressors, comprises −MI/2 for the scans on day 1 and +MI/2 for the scans on day 2 (and the same for PI). Thus, instead of using the binary contrast day 2 − day 1 as the contrast of interest in the GLM, we used a graded variable that was based on each subject's behavioral performance.
We ran two separate analyses involving MI and PI to identify those changes to FC that were more strongly related to the retention of motor learning than to the change in perception. Corrections for multiple comparisons at the cluster level were performed using Gaussian random field theory (minimum Z > 2.7; cluster significance, p < 0.05, corrected). To correct for multiple ROIs, we identified as statistically significant those clusters that had a probability level of better than p = 0.05/9 (in which 9 is the number of ROIs). This between-subjects analysis produced thresholded Z score maps of activity associated with each ROI.
Response latency correction.
To correct for response latency between two different brain regions into our analysis, we used a method similar to that of Henson et al. (2002). If the time course of an arbitrary voxel, y(t), is a scaled (by α) version of the BOLD time series of a selected ROI, r(t), but shifted by a small amount, dt, then using a first-order Taylor expansion, we can write the following:
where r′(t) is the first derivative of r(t) with respect to t. We use r(t) and r′(t) as two basis functions in the subject-level GLM to estimate the parameters β1 and β2, in which β1 = α and β2 = α.dt. This enables us to cancel out the combined effect of the various latencies of HRF between two brain regions and the signal propagation delay between them. Because the β2 values include the effects of both factors, a separate assessment of response latency was not possible. Accordingly, the β2 values were discarded and the analysis focused on the β1 weights that reflect instantaneous FC.
Correspondence of ΔFC and index type.
Because psychophysical measures of motor learning and perceptual change, MI and PI, are themselves correlated, the strength of some functional connections will change in conjunction with both of these factors. To separate the dependence of each connection on MI, PI, or both factors, we removed the portion of the total variance attributable to MI and PI together and calculated the residual “mi” and “pi,” which are uncorrelated with PI and MI, respectively (see below, Variance decomposition). We then constructed a vector for each connection between an ROI and target cluster whose elements were each subjects' change in FC from day 1 to day 2 (ΔFC). This vector was correlated with a vector of associated mi or pi measures. Finally, we performed paired-sample t tests (p < 0.001, uncorrected) to assess the correspondence between neural (ΔFC) and behavioral measures (mi or pi) for each link separately.
Variance decomposition.
The variance attributable to MI can be decomposed into a part that is correlated with PI and a residual uncorrelated component (mi). Similarly, the variance attributable to PI can be decomposed into a mutual component (M) and a residual component that is uncorrelated with MI:
 |
The solution to the above equations is:
 |
Results
Comparison of motor and perceptual adaptation
We examined the relationship between FC and each of motor learning and perceptual change. Figure 1A shows the experimental sequence in which movement training and perceptual tests are interleaved with scanning sessions in which resting-state FC is assessed. Figure 1A also gives the maximum PD attributable to the force field over the course of learning. It can be seen that movements are straight under null field conditions. Application of the load (force field A) results in increases in movement curvature that approach baseline over the course of training. When the direction of load application is reversed (force field B) after the second scanning session, there is a large initial deviation in the opposite direction that likewise approaches baseline values with training. Figure 1B provides a representative example of the perceptual testing sequence. An adaptive algorithm is used to move the limb passively over a series of paths that quickly converge to provide an estimate of the perceptual boundary. Figure 1C shows a reliable change in the sensed position of the limb from the pre-learning to the post-learning perceptual tests (t(12) = 3.11, p < 0.01). Moreover, as seen in Figure 1D, the shift in the perceptual boundary is highly correlated with motor learning as evaluated by MI (r = 0.75, p < 0.005). The evident linear trend underscores the effect of motor learning on perceptual recalibration on a per-subject basis.
Correspondence between neural plasticity and behavioral performance
We conducted analyses to investigate changes in the sensorimotor network in conjunction with motor learning. These analyses enabled us to assess the possibility of changes over the entire brain with respect to our selected ROIs. They also enabled us to test for differences in FC from day 1 to day 2 that were related to motor learning, to perceptual change, or to the two in combination. We found that, in several cases, ΔFC was dependent to varying degrees on both the extent of motor learning and the amount of perceptual change. We consider these possibilities in turn below.
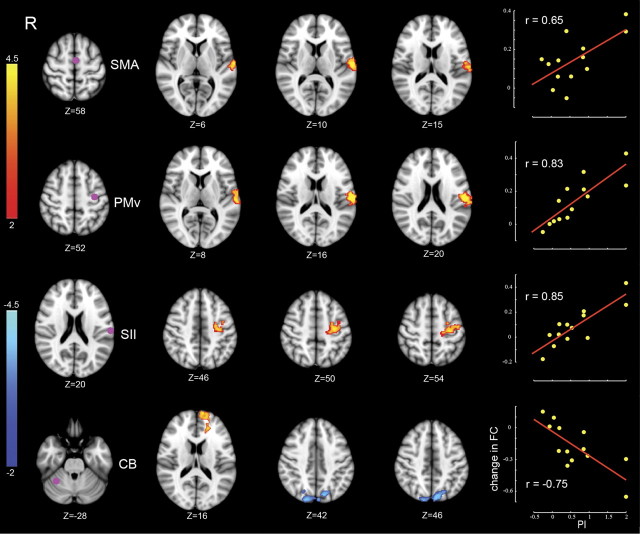
Figure 2 shows the results of the whole-brain analyses, focusing on changes in connectivity that were most strongly related to perceptual function. Each row in the figure shows an ROI at the left (purple dot) and, in the middle, the location of clusters whose ΔFC from day 1 to day 2 was correlated with the amount of perceptual change. The right shows that ΔFC was greater for subjects who showed larger perceptual shifts. The primary changes in connectivity associated with changes to perceptual function are seen in the connection between SII and frontal motor areas (PMv and SMA) and between right anterior cerebellar cortex (lobule VI) and clusters in superior parietal lobule (SPL; BA7) and prefrontal cortex (BA10). Table 2 lists the locations of significant clusters corresponding to each ROI, the associated MNI coordinates of peaks of activity, and their anatomical labels.
Figure 2.
Changes in connectivity in relation to perceptual change. Each row corresponds to a specific ROI whose FC is changed in relation to perceptual learning. Left column, Location of ROIs. Two middle columns, Clusters showing significant change in connectivity with the corresponding ROI. Color-coded statistical Z score maps (corrected p < 0.05 for spatial extent) showing increases in positive correlation (coded in red to yellow) and negative correlation (coded in dark to light blue) from day 1 to day 2 with respect to PI (z-coordinates of cross-sections are reported in MNI space). Right column, The linear trend between individual changes in FC and associated PI values on a per-subject basis. ΔFC gives the change in FC averaged over the significant clusters (the change in FC in the bottom row is shown with respect to the blue-coded clusters alone). The value of r represents the Pearson's product-moment correlation coefficient.
Table 2.
Summary of results using the PI as a regressor to predict FC
| ROI | pcorr | Z value | MNI coordinate |
Z value day 1 | Z value day 2 | Cluster's anatomical label | ||
|---|---|---|---|---|---|---|---|---|
| x | y | z | ||||||
| SII | 0.01 | 4.2 | −30 | −18 | 48 | −0.06 | 4.47 | L BA4, primary motor cortex |
| 3.95 | −26 | −12 | 46 | 1.8 | 4.11 | L BA6, ventral premotor cortex | ||
| 3.8 | −42 | −12 | 56 | 1.54 | 3.62 | L BA6, premotor cortex | ||
| SMA | 0.002 | 4.39 | −62 | −16 | 12 | 4.6 | 7.4 | L SII, OP1 |
| 3.4 | −58 | −20 | 20 | 3.3 | 5.2 | L SII, OP1 | ||
| PMv | 0.0000 | 6.1 | −62 | −18 | 16 | 0.04 | 4.65 | L SII, OP1 |
| 4.2 | −56 | −18 | 28 | 4.2 | 6.35 | L inferior parietal lobule | ||
| CB | 0.0007 | 4.08 | −8 | −84 | 50 | −0.1 | −3.7 | L superior parietal lobule |
| 4.02 | 36 | −80 | 24 | −1.2 | −2.9 | R inferior parietal lobule | ||
| 0.0001 | 4.39 | −10 | 66 | 16 | 0.45 | 3.8 | L SFG, BA 10 | |
The table shows clusters whose correlation with the corresponding ROI changed reliably with motor learning. pcorr is the corrected cluster-level p value related to the regressor of interest (PI). The associated Z score for the peak is shown in the Z value column. Z value day1 and Z value day 2 give Z scores at the location of maximum activation based on values averaged over subjects on days 1 and 2, respectively. A negative Z score indicates an anti-correlation between the ROI time series and the time series of activation peak. L, Left; R, right; SFG, superior frontal gyrus.
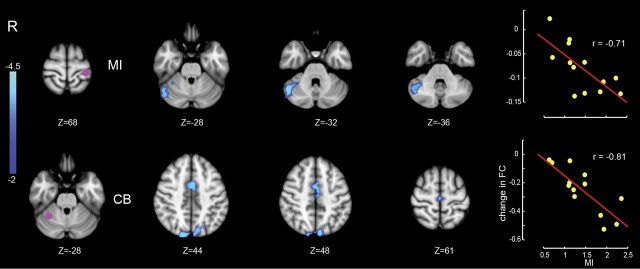
Figure 3 shows the corresponding analysis for those changes in connectivity that were only related to motor learning. As in Figure 2, each row gives the location of the ROI (left panel, purple dot). The middle panels show the locations of clusters whose connectivity from day 1 to day 2 changed in conjunction with motor learning. The right panel shows that greater changes in connectivity were observed for subjects who displayed greater motor learning. The major change in connectivity related to motor learning was in the link between right cerebellar cortex adjacent to posterior–superior fissure (lobule VI, Crus I) and left M1 and SMA. There was also a reliable change in FC between right cerebellar cortex and the SPL. The negative correlation is consistent with the inhibitory relationship between cerebellar cortex and cortical motor areas.
Figure 3.
Changes in connectivity in relation to motor learning (MI). Display conventions are as in Figure 2.
Tables 2 and 3 provide a summary of changes in FC from day 1 to day 2. The Z-scores on day 1 and day 2 correspond to the group-level correlations on day 1 and day 2, respectively. For the perceptual network comprising left SII, PMv, and SMA, the general pattern of change is an elevation of a positive correlation from pre-learning to post-learning. For the motor learning network, comprising right cerebellum (CB), left M1, and SMA, the general pattern of change is from no (or an insignificant negative) correlation to a significant negative correlation. In all cases, the magnitude (absolute value) of correlation increased from pre-learning to post-learning.
Table 3.
Summary of results using MI as a regresssor to predict FC
| ROI | pcorr | Z value | MNI coordinate |
Z value day 1 | Z value day 2 | Cluster's anatomical label | ||
|---|---|---|---|---|---|---|---|---|
| x | y | z | ||||||
| MI | 0.02 | 4.94 | 50 | −58 | −32 | −2.50 | −6.54 | R cerebellum, Crus I |
| 3.32 | 34 | −48 | −28 | −1.60 | −3.87 | R cerebellum, lobule VI | ||
| CB | 0.001 | 4 | −6 | −12 | 46 | −1.3 | −4.8 | L SMA proper |
| 3.85 | −2 | 0 | 44 | 2.47 | −2.19 | Anterior cingulate gyrus | ||
| 0.007 | 4.3 | −8 | −80 | 52 | 1.11 | −3.21 | L superior parietal lobule | |
| 3.86 | 8 | −84 | 42 | −1.5 | −4.5 | R superior parietal lobule | ||
| PMv | 0.0001 | 5.26 | −60 | −12 | 16 | 1.18 | 4.7 | L SII, OP4 |
| SMA | 0.0007 | 4.3 | −64 | −10 | 8 | 3.24 | 6.43 | L SII, OP4 |
| SII | 0.04 | 4.14 | −42 | −12 | 56 | 1.54 | 3.62 | L BA6, premotor cortex |
| 3.83 | −34 | −16 | 48 | 1.94 | 5.23 | L BA4, primary motor cortex | ||
Details as in Table 2. Anatomical labeling is determined based on the Juelich histological atlas (Eickhoff et al., 2005). OP4 is also known as the parietal ventral area. L, Left; R, right.
A number of links showed changes in FC that were statistically reliable with respect to both motor and sensory measures but showed stronger correlations to sensory performance. In particular, the links between SII and PMv and between SII and SMA showed a higher correlation across subjects (on the order of ∼0.3) between ΔFC and perceptual change attributable to learning (PI) than between ΔFC and MI. Another difference is that peaks in activity differed somewhat for changes in connectivity correlated with sensory versus motor indices of learning. Specifically, with an ROI in SMA or PMv, the peak of activity related to motor learning (MI measure) lies in the parietal ventral area (the more rostral part of SII, also called OP4). In contrast, for the same ROI, the peak in activity related to perceptual change is located at S2 (the more caudal part of SII, also known as OP1). This difference is in line with the results of anatomical and functional brain imaging, in which it has been shown that the parietal ventral area has more connections with frontal motor regions than the rostral part of SII (Eickhoff et al., 2010).
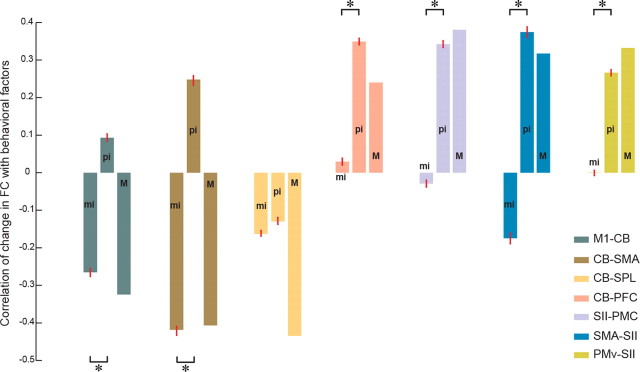
As noted above, many identified links were dependent on both motor learning and perceptual recalibration measures. To further investigate the correspondence of each link with MI, PI, or both factors, we separated the variance in the psychometric variables to obtain measures of mutual variance, M, between MI and PI, and residual variance attributable to either motor learning (mi) or perceptual change (pi) alone, that is, uncorrelated with the other measure. Figure 4 shows the mean ± SEM correlation between ΔFC from day 1 to day 2 and each variance component. ΔFC is calculated for each ROI separately over all significant voxels in a cluster. Examination of the figure reveals two distinct patterns. For links between frontal motor areas and CB (shown at the left), the mi factor correctly explains the direction of change in FC with learning. That is, changes in FC are negatively correlated with motor learning. For the four links shown at the right of the figure (see CB-PFC, SII-PMC, SMA-SII, and PMv-SII), the pi factor dominates the pattern of change in connectivity with motor learning. For the CB-SPL link, both motor and sensory factors are significantly different from zero and correctly explain ΔFC.
Figure 4.
Dependence of changes in FC on uncorrelated sensory (pi) and motor (mi) indices of learning. Mean correlation between individual changes in FC and exclusively motor (mi), sensory (pi), or mutual (M) components. SEs are specified using red bars. The mean and SE for a specific link is calculated over significant voxels (Z > 2.7) defined on the union of clusters associated with MI and PI. Each color-coded link comprises a pair of regions in which the first region represents the location of the ROI and the second region represents the area in which the activated cluster is located. *p < 0.001, significant differences in the correlation between ΔFC with mi and pi (Wilcoxon's rank-sum test). PMC, Premotor cortex.
To test the specificity of our results, we examined a number of other resting-state networks (Fox et al., 2005). We assessed changes with motor learning in the default mode network, a network that routinely shows decreases in activity during task performance, and the task-positive network, a network that exhibits increases in activity during cognitively demanding tasks. We examined FC associated with three previously defined seeds in the default mode network [medial prefrontal cortex, (MNI; 1, 47, 4), posterior cingulate cortex (5, 49, 40), and lateral parietal cortex (45, 67, 36)] and three seeds in the task positive network [intraparietal sulcus (25, 57, 46), the frontal eye field region of the precentral sulcus (25, 13, 50), and the middle temporal region (45, 69, 2)] (Fox et al., 2005). We conducted the same FC analyses as described in Materials and Methods. Neither the task-positive nor the default mode network showed a significant change in FC in relation to either motor or perceptual measures of learning.
We also verified that contralateral, but not ipsilateral, cerebral cortex is central to the pattern of changes that is measured during the resting-state period after motor learning. We examined seven seed locations in the ipsilateral cerebral cortex (right M1, PMd, PMv, SI, SII, PPC, and BG) and one seed location in contralateral CB, at the same locations in the opposite hemisphere as those given in Table 1. The only significant change in connectivity in this analysis in conjunction with either MI or PI was between a seed in left CB and a cluster in right SPL (the peak of the cluster in MNI; 8, −80, 38). Thus, the only regions that showed bilateral changes in FC in association with learning were cerebellar cortex and SPL. The remainder of the significant changes in connectivity were contralateral to the limb that made the movements.
We considered the possibility that the negative correlations shown in Figure 3 may be caused, as suggested by Murphy et al. (2009), by the removal of the global signal, a common preprocessing step in the resting-state fMRI analyses. To test for this possible confound, we reanalyzed our data without removing the global signal as part of nuisance signal correction. This analysis resulted in maps of change in connectivity that were very similar to those shown in Figures 2 and 3. Our finding is consistent with the conclusion that removal of the global signal does not introduce any major confound in group-level results (Fox et al., 2009).
Discussion
This study showed that functionally specific changes to both sensory and motor areas of the brain can be obtained under resting-state conditions 1 h after force-field learning. These effects were observed at a time at which plastic changes were ongoing (Brashers-Krug et al., 1996). The measures of neural plasticity were highly correlated with both sensory and motor indices of learning, such that subjects who learned more also showed greater changes in FC. We were able to attribute differences in the observed patterns of connectivity to either motor learning or perceptual change. We found that changes in connectivity between right cerebellar cortex (lobule VI and Crus I; adjacent to the posterior–superior fissure) and left frontal motor areas (M1 and SMA) depended only on motor learning. In contrast, the connections between left SII and both left PMv and SMA were more strongly dependent on perceptual change (Figs. 2, 3). We found that the connection between CB and SPL was equally dependent on both sensory and motor indices. This latter finding is consistent with the results of recent anatomical studies that show a link between CB and PPC and hypothesize its role in perceptual processing (Strick et al., 2009). This distributed pattern of cerebellar–frontal–parietal changes is consistent with the idea that a distributed pattern of sensory and motor plasticity accompanies motor learning.
At a behavioral level, we found that, across subjects, the magnitude of perceptual change varied with the degree of motor adaptation (Fig. 1D). We were able to detect this correlation by using a new measure of motor learning that involved the use of a force field that was opposite in direction to that experienced over the course of the initial training. In so doing, the final block of force-field trials acted, in effect, as an assistive load that amplified the after-effect of limb displacement attributable to the initial learning. This increased our sensitivity to detect the amount of retention from the initial force field by measuring the amount of negative transfer (Brashers-Krug et al., 1996).
We observed changes in perceptual function after motor learning that involve SII, SMA, and ventral premotor cortex. Romo and colleagues (Romo et al., 2002; Romo and Salinas, 2003; de Lafuente and Romo, 2006) have shown that perceptual decision-making and the transformation of sensory information into action take place in a distributed manner in these same areas. SII has also been implicated in somatosensory perceptual learning in humans (Pleger et al., 2003; Hodzic et al., 2004). Motor learning may thus result in changes to the perceptual learning and decision-making circuitry. The observation that perceptual-related plasticity involves changes in higher-order somatosensory areas, such as SII and PPC, but not low-level centers, such as the subdivisions of SI, is consistent with this conclusion.
Brain areas involved in force-field learning have been studied previously by Shadmehr and Holcomb (1997) using positron emission tomography and under resting-state conditions by Albert et al. (2009). As in the study by Shadmehr and Holcomb, we observe changes associated with learning involving cerebellar cortex, contralateral PMd, and PPC. Our findings allow us to extend these results by showing the ways in which neural connectivity is tied to behavioral measures of learning. We find that subjects who learned more had a greater increase in strength of the related neuronal networks (Figs. 2, 3, right columns). Moreover, our techniques allow us to partition both the behavioral measures and the underlying brain circuitry into changes that are primarily sensory versus those that are motor in nature.
In the present study, all of the observed negative correlations involve cerebellar cortex. There is a multisynaptic inhibitory circuit from cerebellar cortex to frontal motor areas. Purkinje cells in cerebellar cortex form inhibitory synapses with deep cerebellar nuclei, which in turn send excitatory output to cerebral cortex through thalamus. When activity in cerebellar cortex increases, activity in target regions in cerebral cortex decreases and vice versa. There are several neuroimaging studies that have reported negative correlation between cerebellar cortex and frontal motor areas. Shehzad et al. (2009) reported reliable negative connectivity under resting-state conditions between cerebellar cortex and SMA. Similarly, Yan et al. (2009) have observed negative correlations between cerebellar cortex and anterior cingulate cortex. In one of the few studies that have evaluated changes in connectivity during motor learning, Ma et al. (2010) found that effective connectivity from CB to M1 became increasingly negative during task execution over several sessions of learning.
Christensen et al. (2007) reported the results of a recent study implicating a related sensorimotor network in movement production. They found that activation in PMv was correlated with activity in somatosensory cortex during voluntary movement without proprioceptive feedback. Moreover, the strength of FC between SII and SI increased during movement without sensory feedback compared with normal movement (Christensen et al., 2007). The basic similarity of these results to those of the present study may indicate that learning-related activity in PMv modulates activity in somatosensory areas that interpret and compare sensory inflow with the memory of past experiences. However, causality and the directionality of the modulation cannot be inferred from our FC analysis. Other types of analysis, such as effective connectivity analysis (Bullmore et al., 2000), or functional tests using transcranial magnetic stimulation to modulate the activity of certain brain areas before and after learning could be useful in deducing causality within the network responsible for sensorimotor plasticity.
Footnotes
This research was supported by National Institute on Child Health and Human Development Grant HD048924, the Natural Sciences and Engineering Research Council (Ottawa, ON, Canada), and Le Fonds Quebecois de la Recherche sur la Nature et les Technologies (Quebec, QB, Canada). We thank Guillaume Houle for help.
References
- Albert NB, Robertson EM, Miall RC. The resting human brain and motor learning. Curr Biol. 2009;19:1023–1027. doi: 10.1016/j.cub.2009.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Jenkinson M, Smith SM. General multilevel linear modeling for group analysis in FMRI. Neuroimage. 2003;20:1052–1063. doi: 10.1016/S1053-8119(03)00435-X. [DOI] [PubMed] [Google Scholar]
- Brashers-Krug T, Shadmehr R, Bizzi E. Consolidation in human motor memory. Nature. 1996;382:252–255. doi: 10.1038/382252a0. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Horwitz B, Honey G, Brammer M, Williams S, Sharma T. How good is good enough in path analysis of fMRI data? Neuroimage. 2000;11:289–301. doi: 10.1006/nimg.2000.0544. [DOI] [PubMed] [Google Scholar]
- Christensen MS, Lundbye-Jensen J, Geertsen SS, Petersen TH, Paulson OB, Nielsen JB. Premotor cortex modulates somatosensory cortex during voluntary movements without proprioceptive feedback. Nat Neurosci. 2007;10:417–419. doi: 10.1038/nn1873. [DOI] [PubMed] [Google Scholar]
- Cressman EK, Henriques DY. Sensory recalibration of hand position following visuomotor adaptation. J Neurophysiol. 2009;102:3505–3518. doi: 10.1152/jn.00514.2009. [DOI] [PubMed] [Google Scholar]
- de Lafuente V, Romo R. Neural correlate of subjective sensory experience gradually builds up across cortical areas. Proc Natl Acad Sci U S A. 2006;103:14266–14271. doi: 10.1073/pnas.0605826103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Desjardins AE, Kiehl KA, Liddle PF. Removal of confounding effects of global signal in functional MRI analyses. Neuroimage. 2001;13:751–758. doi: 10.1006/nimg.2000.0719. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Balsters JH, Flavell J, Cussans E, Ramnani N. A probabilistic MR atlas of the human cerebellum. Neuroimage. 2009;46:39–46. doi: 10.1016/j.neuroimage.2009.01.045. [DOI] [PubMed] [Google Scholar]
- Doyon J, Bellec P, Amsel R, Penhune V, Monchi O, Carrier J, Lehéricy S, Benali H. Contributions of the basal ganglia and functionally related brain structures to motor learning. Behav Brain Res. 2009;199:61–75. doi: 10.1016/j.bbr.2008.11.012. [DOI] [PubMed] [Google Scholar]
- Eickhoff SB, Stephan KE, Mohlberg H, Grefkes C, Fink GR, Amunts K, Zilles K. A new SPM toolbox for combining probabilistic cytoarchitectonic maps and functional imaging data. Neuroimage. 2005;25:1325–1335. doi: 10.1016/j.neuroimage.2004.12.034. [DOI] [PubMed] [Google Scholar]
- Eickhoff SB, Jbabdi S, Caspers S, Laird AR, Fox PT, Zilles K, Behrens TE. Anatomical and functional connectivity of cytoarchitectonic areas within the human parietal operculum. J Neurosci. 2010;30:6409–6421. doi: 10.1523/JNEUROSCI.5664-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Floyer-Lea A, Matthews PM. Distinguishable brain activation networks for short- and long-term motor skill learning. J Neurophysiol. 2005;94:512–518. doi: 10.1152/jn.00717.2004. [DOI] [PubMed] [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafton ST, Mazziotta JC, Presty S, Friston KJ, Frackowiak RS, Phelps ME. Functional anatomy of human procedural learning determined with regional cerebral blood flow and PET. J Neurosci. 1992;12:2542–2548. doi: 10.1523/JNEUROSCI.12-07-02542.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haith A, Jackson C, Miall R, Vijayakumar S. Unifying the sensory and motor components of sensorimotor adaptation. Presented at 22nd Annual Conference on Neural Information Processing Systems; December; Vancouver, Canada. 2008. [Google Scholar]
- Henson RN, Price CJ, Rugg MD, Turner R, Friston KJ. Detecting latency differences in event-related BOLD responses: application to words versus nonwords and initial versus repeated face presentations. Neuroimage. 2002;15:83–97. doi: 10.1006/nimg.2001.0940. [DOI] [PubMed] [Google Scholar]
- Hlustík P, Solodkin A, Noll DC, Small SL. Cortical plasticity during three-week motor skill learning. J Clin Neurophysiol. 2004;21:180–191. doi: 10.1097/00004691-200405000-00006. [DOI] [PubMed] [Google Scholar]
- Hodzic A, Veit R, Karim AA, Erb M, Godde B. Improvement and decline in tactile discrimination behavior after cortical plasticity induced by passive tactile coactivation. J Neurosci. 2004;24:442–446. doi: 10.1523/JNEUROSCI.3731-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imamizu H, Miyauchi S, Tamada T, Sasaki Y, Takino R, Pütz B, Yoshioka T, Kawato M. Human cerebellar activity reflecting an acquired internal model of a new tool. Nature. 2000;403:192–195. doi: 10.1038/35003194. [DOI] [PubMed] [Google Scholar]
- Krüger G, Glover GH. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn Reson Med. 2001;46:631–637. doi: 10.1002/mrm.1240. [DOI] [PubMed] [Google Scholar]
- Lotze M, Braun C, Birbaumer N, Anders S, Cohen LG. Motor learning elicited by voluntary drive. Brain. 2003;126:866–872. doi: 10.1093/brain/awg079. [DOI] [PubMed] [Google Scholar]
- Ma L, Wang B, Narayana S, Hazeltine E, Chen X, Robin DA, Fox PT, Xiong J. Changes in regional activity are accompanied with changes in inter-regional connectivity during 4 weeks motor learning. Brain Res. 2010;1318:64–76. doi: 10.1016/j.brainres.2009.12.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malfait N, Shiller DM, Ostry DJ. Transfer of motor learning across arm configurations. J Neurosci. 2002;22:9656–9660. doi: 10.1523/JNEUROSCI.22-22-09656.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitz AR, Godschalk M, Wise SP. Learning-dependent neuronal activity in the premotor cortex: activity during the acquisition of conditional motor associations. J Neurosci. 1991;11:1855–1872. doi: 10.1523/JNEUROSCI.11-06-01855.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasir SM, Ostry DJ. Auditory plasticity and speech motor learning. Proc Natl Acad Sci U S A. 2009;106:20470–20475. doi: 10.1073/pnas.0907032106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostry DJ, Darainy M, Mattar AA, Wong J, Gribble PL. Somatosensory plasticity and motor learning. J Neurosci. 2010;30:5384–5393. doi: 10.1523/JNEUROSCI.4571-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padoa-Schioppa C, Li CS, Bizzi E. Neuronal activity in the supplementary motor area of monkeys adapting to a new dynamic environment. J Neurophysiol. 2004;91:449–473. doi: 10.1152/jn.00876.2002. [DOI] [PubMed] [Google Scholar]
- Pasalar S, Roitman AV, Durfee WK, Ebner TJ. Force field effects on cerebellar Purkinje cell discharge with implications for internal models. Nat Neurosci. 2006;9:1404–1411. doi: 10.1038/nn1783. [DOI] [PubMed] [Google Scholar]
- Pleger B, Foerster AF, Ragert P, Dinse HR, Schwenkreis P, Malin JP, Nicolas V, Tegenthoff M. Functional imaging of perceptual learning in human primary and secondary somatosensory cortex. Neuron. 2003;40:643–653. doi: 10.1016/s0896-6273(03)00677-9. [DOI] [PubMed] [Google Scholar]
- Romo R, Salinas E. Flutter discrimination: neural codes, perception, memory and decision making. Nat Rev Neurosci. 2003;4:203–218. doi: 10.1038/nrn1058. [DOI] [PubMed] [Google Scholar]
- Romo R, Hernández A, Zainos A, Lemus L, Brody CD. Neuronal correlates of decision-making in secondary somatosensory cortex. Nat Neurosci. 2002;5:1217–1225. doi: 10.1038/nn950. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Holcomb HH. Neural correlates of motor memory consolidation. Science. 1997;277:821–825. doi: 10.1126/science.277.5327.821. [DOI] [PubMed] [Google Scholar]
- Shehzad Z, Kelly AM, Reiss PT, Gee DG, Gotimer K, Uddin LQ, Lee SH, Margulies DS, Roy AK, Biswal BB, Petkova E, Castellanos FX, Milham MP. The resting brain: unconstrained yet reliable. Cereb Cortex. 2009;19:2209–2229. doi: 10.1093/cercor/bhn256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiller DM, Sato M, Gracco VL, Baum SR. Perceptual recalibration of speech sounds following speech motor learning. J Acoust Soc Am. 2009;125:1103–1113. doi: 10.1121/1.3058638. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Steele CJ, Penhune VB. Specific increases within global decreases: a functional magnetic resonance imaging investigation of five days of motor sequence learning. J Neurosci. 2010;30:8332–8341. doi: 10.1523/JNEUROSCI.5569-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strick PL, Dum RP, Fiez JA. Cerebellum and nonmotor function. Annu Rev Neurosci. 2009;32:413–434. doi: 10.1146/annurev.neuro.31.060407.125606. [DOI] [PubMed] [Google Scholar]
- Taylor MM, Creelman CD. PEST: efficient estimates on probability functions. J Acoust Soc Am. 1967;41:782–787. [Google Scholar]
- Wong JD, Wilson ET, Gribble PL. Spatially selective enhancement of proprioceptive acuity following motor learning. J Neurophysiol. 2011;105:2512–2521. doi: 10.1152/jn.00949.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith SM. Bayesian analysis of neuroimaging data in FSL. Neuroimage. 2009;45:S173–S186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
- Yan H, Zuo XN, Wang D, Wang J, Zhu C, Milham MP, Zhang D, Zang Y. Hemispheric asymmetry in cognitive division of anterior cingulate cortex: a resting-state functional connectivity study. Neuroimage. 2009;47:1579–1589. doi: 10.1016/j.neuroimage.2009.05.080. [DOI] [PubMed] [Google Scholar]