Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2011 Sep 21;20(2):217–223. doi: 10.1038/ejhg.2011.173

On the statistical properties of family-based association tests in datasets containing both pedigrees and unrelated case–control samples

Tero Hiekkalinna 1,2,*, Harald HH Göring 3, Brian Lambert 4, Kenneth M Weiss 4, Petri Norrgrann 1,2, Alejandro A Schäffer 5, Joseph D Terwilliger 1,2,6,7,8,9
PMCID: PMC3260916  PMID: 21934707

Abstract

A common approach to genetic mapping of loci for complex diseases is to perform a genome-wide association study (GWAS) by analyzing a vast number of SNP markers in cohorts of unrelated cases and controls. A direct motivation for the case–control design is that unrelated, affected individuals can be easier to collect than large families with multiple affected persons in the Western world. Despite its higher potential power, investigators have not actively pursued family ascertainment in part because of a dearth of methods for analyzing such correlated data on a large scale. We examine the statistical properties of several commonly used family-based association tests, as to their performance using real-life mixtures of families and singletons taken from our own migraine and schizophrenia studies, as well as population-based data for a complex trait simulated with the evolutionary phenogenetic simulator, ForSim. In virtually every situation, the full likelihood-based methods in the PSEUDOMARKER program outperformed those implemented in FBAT, GENEHUNTER TDT, PLINK (family-based options), HRR/HHRR, QTDT, TRANSMIT, UNPHASED, MENDEL, and LAMP. We further show that GWAS is much more powerful when family samples are used rather than unrelateds, on a genotype-by-genotype basis.

Keywords: power, type-I error, genetic linkage analysis, linkage disequilibrium, family-based association, genome-wide association studies

Introduction

Linkage analysis can be powerful for the localization of genes of large effect to chromosomal regions, though with imprecise resolution. Regions identified through linkage analysis often contain many genes, making identification of the disease-predisposing alleles difficult. After a finding of significant linkage, association analysis can aid in fine mapping,1, 2, 3, 4, 5, 6, 7, 8, 9, 10 as it measures the effects of recombination over many meioses that historically connect affected individuals to one another. Association mapping can be done using either families or ‘unrelated' singleton individuals, while linkage analysis requires families, as it measures correlations in genotype among relatives.

In this study, statistical properties of commonly used family-based association tests were evaluated. We compared the performance of the following software packages: FBAT,11, 12 GENEHUNTER TDT,13 PLINK (family-based options, ie, TDT),14 HRR/HHRR,15 QTDT,16, 17 TRANSMIT,18 UNPHASED,19 MENDEL,20 LAMP,21, 22 and PSEUDOMARKER.23 Different software applying the same or similar tests may have different properties due to differences in implementation. We compared performance using simulated data based on datasets ascertained for studies of migraine24, 25 and schizophrenia26 in Finland, on which joint association and linkage studies are ongoing. In addition, we used our phenogenetic evolutionary simulator, ForSim,27 to simulate data under an oligogenic model with environmental and genetic factors contributing to disease in a population.

Materials and methods

Methods to be compared

Haplotype relative risks (HHRR)

The HHRR program randomly extracts one triad (one affected child and two genotyped parents) from each pedigree. The alleles of the child are added to the ‘case' sample, and the non-transmitted alleles of the parents are added to the ‘control' sample. If no triad is available, one affected individual is added to the ‘case' sample with no matching control. Alleles found in all singleton cases and controls are added to their respective samples, and a likelihood-based test of equality of the allele frequencies in these two samples is performed.15 P-values are obtained by randomization.

Transmission/disequilibrium test (TDT)

The TDT28, 29 approach extracts all triads from pedigrees and analyzes them as if they were independent triads drawn from the population. This test contrasts the alleles transmitted and not transmitted from parents heterozygous at the marker locus, and is a test of the null hypothesis of association but no linkage against the alternative of both association and linkage. It is often mistakenly referred to as a family-based association test, implying that a significant test statistic indicates the presence of linkage disequilibrium (LD), which is untrue whenever multiple related affecteds are included in the analysis.30, 31 We compared the implementations of the TDT with GENEHUNTER, QTDT, and PLINK.

Other score tests and modifications of TDT to handle more complex family structures

The TDT has been generalized in the form of a general score test32 of linkage in the presence of LD, and several software packages implement variations of the TDT to test null hypotheses about linkage and association. TRANSMIT uses a score vector averaged over all possible configurations of parental haplotypes and transmissions consistent with the observed data, while FBAT derives the expected distribution of transmissions based on sufficient statistics for the nuisance parameters under the null hypothesis of linkage and no association. UNPHASED is similar to TRANSMIT, in how it deals with missing data (see the appendix of the UNPHASED publication).19 When applied to larger pedigrees, these methods break the pedigrees into component nuclear pedigrees and model the covariances between them to control for the effects of linkage. QTDT works with scores of the transmission of alleles through general pedigrees, by conditioning on deeper common ancestry to test for association conditional on linkage. We omitted PDT33 from our detailed comparisons. Although our simulation study showed that PDT gave valid type-I error rates, the power was far lower than every other test considered, so we dropped it from further study – this is largely because PDT cannot analyze families with missing parental genotypes unless unaffected siblings are genotyped, and in these real datasets, more than half of parents were unavailable for genotyping and unaffected siblings were not ascertained.

Likelihood-based approaches - PSEUDOMARKER

We have developed statistical algorithms for the joint analysis of linkage and LD across combinations of various pedigree structures and singleton individuals,30 and implemented them in PSEUDOMARKER.23 This software can compute the likelihood of any pedigree as a function of the recombination fraction between trait and marker loci, marker locus allele frequencies, and LD between trait and marker loci (parameterized as marker allele frequencies conditional on which trait locus allele is on the same haplotype). This likelihood can be maximized assuming linkage, LD, neither, or both, providing a framework for testing hypotheses about linkage and LD.

PSEUDOMARKER uses a modified version of the ILINK program of the FASTLINK 4.1P34, 35, 36, 37, 38 version of the LINKAGE package35 to model LD with conditional allele frequencies, and uses a ‘direct-search' algorithm to maximize the likelihood over this complex set of confounded parameters.39, 40 Here, we focus on the statistic comparing the likelihood maximized over both linkage and LD with that maximized over linkage, assuming absence of LD:

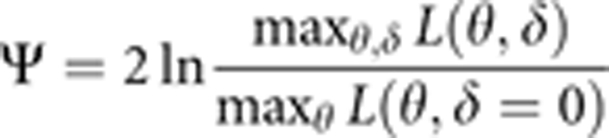graphic file with name ejhg2011173e1.jpg

(where θ denotes the recombination fraction and δ the LD parameters). For this analysis, we used a deterministic parametric model assuming an infinitesimal disease allele frequency, and probability 0 of being affected without a risk genotype (ie, no so-called ‘phenocopies'). Formally, MRec={(P(D)=0.00001; P(Aff∣DD)=0.00001; P(Aff∣D+ or ++)=0)}. Under MRec, the penetrance ratio between homozygous disease-allele carriers (DD) and all other genotypes is infinite, forcing all affecteds to have genotype DD, and the rarity of the disease allele makes all obligate carriers D+ and all other unaffected founders ++. Although this model does not represent the actual etiology, it has been shown elsewhere to lead to a statistical framework that is stochastically equivalent to various model-free methods, including the affected sib-pair mean test, TDT, HHRR, and case–control test.30, 41

Other likelihood-based algorithms

Performing likelihood-based analysis of linkage and LD jointly is not new; we have done this 20 years ago.6 The capability to model LD with haplotype frequencies has long been included in the LINKAGE package,35 and LD was used for fine mapping many disease genes cloned in the 1980s and 1990s.1, 3, 4, 5, 6, 7, 8, 10, 42, 43, 44 In the past decade, two other software packages have implemented joint analysis of linkage and LD: LAMP and MENDEL. However, MENDEL does not perform adequately under MRec because it conditions disease allele frequencies on the marker alleles found on each haplotype, constraining the overall disease allele frequency.45 With the disease allele frequency set to a small number, the constrained numerical maximization generally misses the global optimum. LAMP uses the Lander–Green algorithm46 to compute the likelihood, which places limits on the family size one can analyze; some portions of our real datasets could not be processed by LAMP. Furthermore, LAMP restricts the recombination fraction between marker and trait loci to 0, which is unreasonable for imprecisely specified models.47

Simulations

To evaluate the statistical properties of programs for testing for LD in the presence of linkage, a simulation study was performed. Because our main interest is testing for LD conditional on linkage, the null hypothesis is linkage but no association. We also evaluated programs under the alternative null hypothesis of no linkage and no association (to examine properties of joint tests of linkage and LD). In all, 42 combinations of analysis options from 10 programs were evaluated. Supplementary Table 1 lists program options and their abbreviations that appear in our summarized power and type-I error rate results.

The ascertained pedigree structures being used in ongoing studies of migraine24, 25 and schizophrenia26 in Finland were used for simulation analyses. The migraine sample included multigenerational pedigrees, whereas the schizophrenia sample consisted of mostly nuclear pedigrees. We simulated genotype data only for individuals who were genotyped in the real dataset. Detailed statistics about the datasets are shown in Table 1. An additional 199 unrelated controls were added to the schizophrenia pedigree collection, and 884 controls and 270 cases to the migraine sample,48 consistent with the real studies.

Table 1. Migraine and schizophrenia pedigree statistics.
  Migraine Schizophrenia
Pedigrees 84 438
Individuals 1099 2535
Founders 366 914
Average pedigree size 13.08 (4–47) 5.79 (3–14)
     
Generations (%)    
 2 11.9 99.5
 3 56.0 0.5
 4 32.1 —
     
Phenotyped    
 All 398 (36.2%) 918 (36.2%)
 Founders 26 (7.1%) 60 (6.6%)
     
Genotyped    
 All 810 (73.3%) 1906 (75.2%)
 Founders 147 (40.2%) 442 (48.4%)
     
Additional singletons    
 Cases 270 —
 Controls 884 199
Open in a new tab

ForSim

Additionally, we generated data for a complex multifactorial trait in an entire population with the phenogenetic evolutionary simulator, ForSim,27 to verify that our conclusions are not dependent on simple monogenic models. This phenogenetic simulation yielded hundreds of functional variants in each of five unlinked genes. All variants were presumed to influence the trait in an additive fashion, with effect sizes simulated when they arose by mutation, subject to natural selection on the resulting phenotypes. We simulated a population over 10 000 generations in which such variants were allowed to accumulate, with the disease prevalence of 9% in the last generation. ForSim generated a population comprised of 10 000 multigenerational pedigrees (more than 120 000 individuals) and 1000 random controls. From this pool of pedigrees, we randomly sampled 25, 50, 100, 200, and 300 pedigrees with at least two affected individuals. We selected one common functional SNP for analysis, which showed the strongest evidence of linkage and association with disease in the population, (allele frequency 0.124, estimated odds ratio 1.673). This odds ratio measures not just the functional effect of this SNP, but also the effects of LD with other functional variants. To mimic realistic patterns of missing data, 75% of founders were assumed to be unavailable for genotyping. One random control was included in the analysis for every missing (ungenotyped) founder individual.

Type-I error rate simulations

We simulated datasets assuming complete linkage and no LD, and estimated empirically the frequency with which certain critical values were exceeded. These simulations were done assuming the etiological model MRec in the schizophrenia nuclear families, and using MDom={(P(D)=0.00001; P(Aff∣DD or D+)=0.00001; P(Aff∣++)=0)} in the migraine families (which had intergenerational transmission of disease). The null hypothesis was complete linkage (θ=0) and no LD (δ=0). These extreme models were used to maximize the effects of linkage on the statistical properties of the resulting conditional test statistics. Empirical null distributions were estimated from 1000 replicates of the migraine and schizophrenia pedigree sets, simulated with the (Fast)SLINK program,49, 50 (modified by TH to use a more sophisticated random number generator).

Power simulations

The power was estimated for each program/analysis option combination using further simulated datasets in which complete linkage between marker and trait locus was assumed, and for which LD and etiological parameters were varied. The disease prevalence was assumed to be 10% for migraine and 1% for schizophrenia. We assumed a diallelic trait locus with alleles (D, +) and a diallelic marker locus with marker alleles (1, 2) having frequencies of (0.1 and 0.9), with P(D)=0.1. In one set of simulations, the effect size of the risk allele was varied with LD held constant, and in another, the effect size was held constant with the strength of LD varied. More details can be found in Supplementary Methods.

Results

Type-I error rates

The empirical type-I error rates were estimated for 0.01 and 0.05 significance levels for both migraine and schizophrenia data sets, as shown in Supplementary Tables 2–5, together with 95% confidence intervals. The relative patterns in type-I error appear to remain the same deeper into the tail of the distribution, but estimates had much larger confidence intervals (data not shown) because of the small number of replicates we were able to perform in several months.

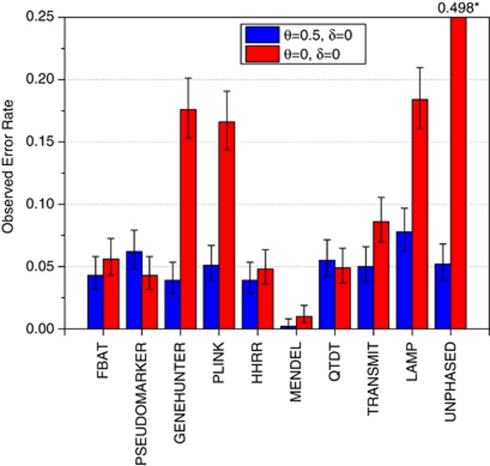
Under the null hypothesis of no linkage and no association, all programs provided valid tests, except LAMP, which always showed excess type-I error rates, especially when the unconstrained genetic model (free) was used. In Figure 1, we graph the type-I error rates for the analysis options recommended in each program's documentation for analysis of pedigree data in the presence of missing data. The blue columns in Figure 1 represent the type-I error rates for the null–null model (no linkage and no association), with error bars showing the 95% CI for those estimates. See Supplementary Tables 2, 3 for comparisons of all programs and analysis options.

Figure 1.

Figure 1

Open in a new tab

Type-I error rates are presented for the author-recommended analysis options for testing for LD in the presence of linkage. Full details for all program options are in Supplementary Tables 2–5. The following analysis options were used from each program in this figure: FBAT's robust variance estimator and recessive model, PSEUDOMARKER MRec LD-given linkage, GENEHUNTER TDT, PLINK's sib-TDT, HHRR (allele-based randomized), MENDEL association given linkage using MRec*,fixed1, QTDT with no additional options, TRANSMIT's robust estimator and multiple nuclear families, LAMP's recessive model, and UNPHASED's ‘missing' and ‘parentrisk' options (with controls, cc). Blue columns represent empirical error rates estimated from the Finnish schizophrenia dataset – simulation of no linkage and no association. Other statistics from each program behaved similarly, with most being valid tests in this situation, with the notable exception of LAMP, and for LAMP the invalidity extended over the range of analysis models available in the program. The red columns are empirical error rates estimated from the Finnish schizophrenia dataset – simulation of complete linkage and no association. GENEHUNTER, PLINK, UNPHASED, and LAMP had elevated type-I error rates. Similar results were obtained for migraine families as well, and the pattern was the same for α=0.01. Results are based on 1000 replicates.

For the null hypothesis of linkage but no association (Figure 1, red columns, and Supplementary Tables 4, 5), the programs FBAT, HHRR, MENDEL (association given linkage) and QTDT were valid across all null simulations. HHRR performed robustly as expected, but MENDEL (association given linkage) was overly conservative. Other programs were anticonservative, namely: GENEHUNTER TDT, PLINK, MENDEL (gamete competition), and TRANSMIT. TRANSMIT was much worse on migraine pedigrees than on schizophrenia pedigrees, because it ignores relationships among nuclear families within multigenerational pedigrees. TRANSMIT's type-I error rates were somewhat lower (though still anticonservative) when their robust estimator or bootstrapping were used to correct for multiple affected individuals within a nuclear pedigree. MENDEL's gamete competition option is anticonservative in the presence of linkage, because it is a generalized version of TDT; thus, its null hypothesis with full pedigrees is no linkage, as is the case for GENEHUNTER TDT. UNPHASED had an enormous type-I error rate on the schizophrenia dataset and its performance was even worse when the software options ‘missing' (ie, allowing for missing genotypes) and ‘parentrisk' (ie, multiple affected sibs in the presence of linkage) were used, as recommended in the user manual for situations where parental genotype data are missing. Adding controls (option cc) to the analysis completely destroyed the performance of UNPHASED – the type-I error rate rose to almost 50% at the 0.05 significance level. MENDEL (gamete competition), TRANSMIT, and UNPHASED had type-I error rates of 100% when parental genotypes were unknown in affected sib-ships in the presence of linkage (Supplementary Table 6).

LAMP was anticonservative in all tests, perhaps as a side effect of the method maximizing the likelihood over the disease allele frequency and penetrances conditional on prevalence and model constraints (eg, dominant, recessive, etc). It is well-known that likelihood ratio tests can behave irregularly when one is estimating numerous constrained non-orthogonal nuisance parameters jointly with the parameter of interest.51

The PSEUDOMARKER type-I error rate was at the expected level in schizophrenia pedigrees (MRec) and in migraine pedigrees (MDom).

Power

We included only those programs/options in our power analyses that provided valid type-I error rates. For this reason, LAMP was dropped (despite the excessive type-I error rate, it still showed less nominal power than PSEUDOMARKER). For the same reason, GENEHUNTER TDT, and PLINK were omitted from power comparisons. Some analysis options of TRANSMIT and UNPHASED had valid type-I error estimates under the hypothesis of complete linkage and no association, and those options were used in power simulations.

Power was estimated at the 0.0001 significance level. The choice of 0.0001 is based on the rationale that, asymptotically, a lod score of 3.0 has a point-wise significance level of 0.0001, which is generally considered as minimally significant in genome-wide linkage analysis. The same general patterns are seen at other significance levels examined (data not shown).

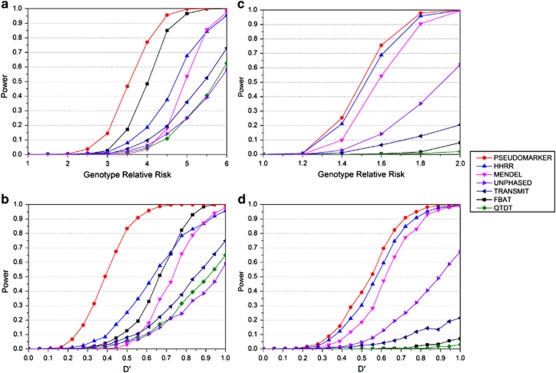
Under all genotype relative risk models considered in the schizophrenia pedigrees, PSEUDOMARKER was more powerful than FBAT, MENDEL, HHRR, TRANSMIT, QTDT, and UNPHASED (Figure 2a). The reasons for this likely include: (a) relationships in the pedigrees are used correctly, (b) recombination fraction and allele frequencies are estimated from the data, and (c) all available data are used. The tests based on TDT and HHRR utilized only a subset of the data (ie, triads), which is the primary reason for reduced power. When comparing power across different levels of LD (Figure 2b), the same trend in relative power resulted and tests based on the TDT, such as TRANSMIT, QTDT, and UNPHASED, had low power, even under complete linkage and LD (D′=1 and θ=0).

Figure 2.

Figure 2

Open in a new tab

(a) Schizophrenia data with recessive model, the genotype relative risk scan and (b) the D′ scan and genotype relative risk fixed to six. As in Figure 1, the analysis models recommended by the authors are used here, if that test was valid according to the simulations in Figure 1. When the type-I error rates were not correct from Figure 1, we substituted other statistics from those programs that were giving accurate type-I error rates as follows: the analysis model and option for each the programs were: PSEUDOMARKER (MRec LD-given linkage), FBAT (recessive), MENDEL (MRec*,fixed1, association given linkage), HHRR (allele-based randomized), TRANSMIT (one), QTDT, UNPHASED (plain, cc). (c) Migraine data with dominant model, the genotype relative risk scan, and (d) the D′ scan and genotype relative risk fixed to two. The analysis model and option for each of the programs were: PSEUDOMARKER (MDom LD-given linkage), FBAT (dominant), MENDEL (MDom*,fixed1, association given linkage), HHRR (allele-based randomized), TRANSMIT (nonuc, ro), QTDT, UNPHASED (plain, cc). Results are based on 1000 replicates.

The differences in power between TDT-based tests on one side and HHRR, MENDEL and PSEUDOMARKER on the other were even greater on the migraine pedigrees (Figure 2c). Under the dominant model, FBAT and QTDT had less than 10% power at all examined levels of genotype relative risk. When investigating power as a function of the strength of LD (Figure 2d), PSEUDOMARKER and MENDEL were the most powerful as well, because they were able to analyze the extended pedigrees in full. HHRR was surprisingly powerful as well, because it includes the available singletons in the analysis (Table 1).

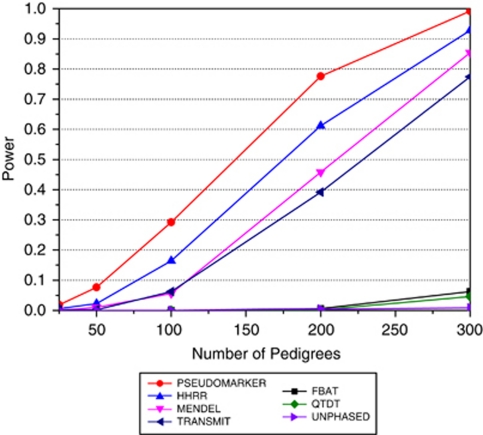
Using ForSim-generated data (Figure 3), the trend was similar to that from the migraine pedigrees. PSEUDOMARKER, HHRR, and MENDEL were far more powerful than TRANSMIT, FBAT, QTDT, and UNPHASED, verifying that these conclusions hold not just for simple monogenic models.

Figure 3.

Figure 3

Open in a new tab

The ForSim-simulated data; there was one population, five chromosomes, three genes per chromosome (one gene per chromosome contributing to the disease phenotype additively). ForSim-generated data which contained 10 000 multigenerational pedigrees and 1000 controls. SNP selected for analysis was linked and associated with the trait, with allele frequency 0.124, and estimated odds ratio of 1.673. Various numbers of pedigrees (25, 50, 100, 200, and 300) were randomly sampled w/o replacement and power was computed at α=0.0001 level, based on 500 replicates. The analysis model and option for each the programs were: PSEUDOMARKER (MRec LD-given linkage), FBAT (recessive), MENDEL (MRec*,fixed1, association given linkage), HHRR (allele-based randomized), TRANSMIT (one), QTDT, UNPHASED (plain, cc). Between the five specific numbers of pedigrees tested (x-axis), power estimates are made by linear interpolation.

Comparative merits of ascertainment of different family structures

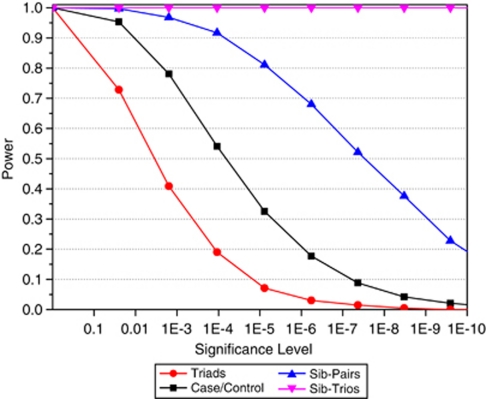
We have shown the benefits of PSEUDOMARKER for analysis of a mixture of families and singletons, but have not proven the wisdom of analyzing mixtures of relationship structures. The advantages of sampling multiplex pedigrees have been described in many papers proposing GWAS, back to the seminal study of Risch and Merikangas.52 We compared four commonly used sampling schemes, namely singletons, triads, sib-pairs, and sib-trios, and assumed everyone sampled would be genotyped, and that unrelated controls were available as well (to estimate the frequency of the risk allele in unaffected persons). We assumed 4000 individuals were available for genotyping – either 2000 cases and 2000 controls, 1000 triads and 1000 controls, 800 sib-pairs (including parents) and 800 controls, or 667 sib-trios and 665 controls. A recessive risk allele with frequency of 0.1 and a relative risk of four was simulated, and it was assumed that this allele was genotyped in our study for simplicity. Figure 4 shows the relative power of the PSEUDOMARKER test for LD with linkage as a nuisance parameter. As expected, power is lowest for samples of triads (three genotypes needed to get the equivalent of one case and one control), and the power per genotype consistently increases as the number of affected individuals in a family increases, despite fewer independent chromosomes being sampled from the population.

Figure 4.

Figure 4

Open in a new tab

Power increase from sampling family data rather than unrelated individuals: total sample size (number of genotyped individuals) is identical for each data structure. Singletons=2000 cases and 2000 controls. Triads=1000 triads and 1000 controls. Sibpairs=800 sibpairs and 800 controls. Sib trios=667 sib trios and 665 controls. In all, 4000 total individuals per sample. This is for a model with complete LD, complete linkage, and a recessive model with relative risk of four, disease allele frequency of 10%, and disease prevalence of 10%. The test statistic used was recessive PSEUDOMARKER LD-given linkage.

Which null hypothesis to test?

If one is testing for LD conditional on linkage, one must be careful to make sure the likelihood under the null hypothesis of linkage and no LD is, in fact, a function of linkage. If one has a dataset consisting solely of triads and singletons, under the null hypothesis of linkage and no LD, the likelihood is not a function of the recombination fraction, while under the alternative hypothesis of linkage and LD, the likelihood is a function of both. This degenerate case leads to a well-known pathology where the difference in free parameters under null and alternative hypotheses is greater than implied by the test statistic's formulation. In such a dataset, a test comparing the likelihood of both linkage and LD in the alternative with the null of no association is stochastically equivalent to the joint test of linkage and LD against the null hypothesis of no linkage and no LD. In Supplementary Table 6, PSEUDOMARKER seems anticonservative if one assumes the test is conditional on linkage, giving an empirical type-I error rate of 0.1. However, if one assumes (correctly) that this was a joint test, rather than a conditional test, owing to the composition of the dataset, the P-values are accurate.

A fair question to ask is ‘how much family material is needed to perform a truly conditional test?' One needs the likelihood to be a function of the recombination fraction in the absence of LD, with sufficiently many informative meioses that the traditional lod score approximately follows its asymptotic distribution, to ensure the null hypothesis likelihood in the conditional test is non-degenerate. As shown in Supplementary Figure 1, the exact P-value for a lod score of 3 converges to roughly 10−4 when there are as few as 20 informative meioses. To this end, we added sibpairs to a dataset consisting of triads and singletons to see how many informative meioses would be needed for a conditional test of association given linkage to be valid. As shown in Table 2, adding as few as 10 sibpairs reduced the empirical type-I error rates to expected levels, independent of the number of triads and controls, as predicted.

Table 2. The effect of adding fully genotyped sib-pairs (eg, linkage information) to analysis of type-I error rate (α=0.05 significance level) of PSEUDOMARKER recessive LD-given linkage test, when the dataset consisted solely of triads and controls.

# of sib-pairs 200 triads and 200 controls 500 triads and 500 controls 600 triads and 600 controls
0 0.09 0.10 0.10
1 0.09 0.09 0.10
5 0.06 0.06 0.09
10 0.05 0.05 0.05
15 0.06 0.04 0.05
20 0.06 0.06 0.05
25 0.05 0.06 0.05
30 0.04 0.05 0.05
50 0.05 0.06 0.06
100 0.04 0.05 0.04
Open in a new tab

The true (ie, generating) model of inheritance was MRec, with complete linkage between disease and SNP marker (minor allele frequency 0.1). Results are based on 1000 replicates.

Discussion

Methods that analyze an entire dataset jointly, appropriately partitioning linkage and LD information, outperform methods that subdivide pedigrees into arbitrary homogeneous structures, provided the null hypothesis is appropriate. If a dataset has no information about linkage in the absence of LD, or vise versa, conditional testing is not meaningful, however. If one wishes to test for LD-given linkage, applying a TDT approach to multiple related individuals is not appropriate, as its null hypothesis is LD and no linkage.

We have demonstrated (Figure 1) that even when statistical approaches claim to test for LD conditional on linkage, this is not always true in practice for TRANSMIT, UNPHASED, PLINK, and LAMP. TDT-based methods in GENEHUNTER, MENDEL (gamete competition), and other packages provide valid tests, however, of the null hypothesis of no linkage and no LD. Joint tests must be applied carefully if there is prior evidence of linkage, as one cannot discriminate whether one has detected linkage or LD from such an analysis, and inference of the latter is inappropriate in general.

The algorithms implemented in PSEUDOMARKER outperformed the other packages; however, the simple HHRR approach of selecting one trio per family for analysis, discarding the remainder of the data, performed surprisingly well (because disease alleles enter the pedigree only once in most cases). Therefore, we advocate application of the simpler HHRR for genome-wide analysis, with targeted follow-up analysis of the complete dataset using PSEUDOMARKER for markers of particular interest, either because of prior evidence of involvement in disease or because of ‘interesting' statistical results from the simpler HHRR analysis, accepting of course, that there is a chance that we may miss the global optimum. We have automated this procedure in a script as follows: (1) apply the HHRR and traditional lod score analysis for all markers in a genome scan (2) select all markers exceeding user-specified thresholds for significance on either or both of these tests for subsequent automated analysis with PSEUDOMARKER.

The PSEUDOMARKER program and automated analysis script and documentation are freely available for academic use via http://www.helsinki.fi/~tsjuntun/ pseudomarker/index.html.

Acknowledgments

This research work was funded by the FiDiPro program of the Academy of Finland, Grants MH84995, MH59490 and RR017515 from the National Institutes of Health, the Helsingin Sanomat Centennial Foundation, Biomedicum Helsinki Foundation, Emil Aaltonen Foundation, Otto A. Malm Foundation, Jenny and Antti Wihuri Foundation, Finnish Cultural Society, and the SBC Foundation are gratefully acknowledged. This research was supported in part by the Intramural Research Program of the NIH, NLM (AAS). Maija Wessman, Verneri Anttila, Mari Kaunisto, and Tiina Paunio are acknowledged for providing Finnish migraine and schizophrenia pedigree structures for simulation studies. Markus Perola and Leena Peltonen-Palotie are greatly acknowledged for their guidance and support over the years. The great majority of simulations were executed on the Linux-based supercomputers of the Finnish IT Center for Science (CSC). CSC is greatly acknowledged. Thanks to three reviewers for numerous helpful suggestions to improve the manuscript.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary Tables
Click here for additional data file. (288.5KB, doc)
Supplementary Methods
Click here for additional data file. (25.5KB, doc)

References

  1. Pekkarinen P, Hovatta I, Hakola P, et al. Assignment of the locus for PLO-SL, a frontal-lobe dementia with bone cysts, to 19q13. Am J Hum Genet. 1998;62:362–372. doi: 10.1086/301722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Enattah NS, Sahi T, Savilahti E, Terwilliger JD, Peltonen L, Järvelä I. Identification of a variant associated with adult-type hypolactasia. Nat Genet. 2002;30:233–237. doi: 10.1038/ng826. [DOI] [PubMed] [Google Scholar]
  3. Kerem B, Rommens JM, Buchanan JA, et al. Identification of the cystic fibrosis gene: genetic analysis. Science. 1989;245:1073–1080. doi: 10.1126/science.2570460. [DOI] [PubMed] [Google Scholar]
  4. Nikali K, Suomalainen A, Terwilliger J, Koskinen T, Weissenbach J, Peltonen L. Random search for shared chromosomal regions in four affected individuals: the assignment of a new hereditary ataxia locus. Am J Hum Genet. 1995;56:1088–1095. [PMC free article] [PubMed] [Google Scholar]
  5. Hellsten E, Vesa J, Speer MC, et al. Refined assignment of the infantile neuronal ceroid lipofuscinosis (INCL, CLN1) locus at 1p32: incorporation of linkage disequilibrium in multipoint analysis. Genomics. 1993;16:720–725. doi: 10.1006/geno.1993.1253. [DOI] [PubMed] [Google Scholar]
  6. Tienari PJ, Terwilliger JD, Ott J, Palo J, Peltonen L. Two-locus linkage analysis in multiple sclerosis (MS) Genomics. 1994;19:320–325. doi: 10.1006/geno.1994.1064. [DOI] [PubMed] [Google Scholar]
  7. Haberhausen G, Schmitt I, Köhler A, et al. Assignment of the dystonia-parkinsonism syndrome locus, DYT3, to a small region within a 1.8-Mb YAC contig of Xq13.1. Am J Hum Genet. 1995;57:644–650. [PMC free article] [PubMed] [Google Scholar]
  8. Raha-Chowdhury R, Bowen DJ, Stone C, et al. New polymorphic microsatellite markers place the haemochromatosis gene telomeric to D6S105. Hum Mol Genet. 1995;4:1869–1874. doi: 10.1093/hmg/4.10.1869. [DOI] [PubMed] [Google Scholar]
  9. Satsangi J, Parkes M, Louis E, et al. Two stage genome-wide search in inflammatory bowel disease provides evidence for susceptibility loci on chromosomes 3, 7 and 12. Nat Genet. 1996;14:199–202. doi: 10.1038/ng1096-199. [DOI] [PubMed] [Google Scholar]
  10. Hästbacka J, de la Chapelle A, Kaitila I, Sistonen P, Weaver A, Lander E. Linkage disequilibrium mapping in isolated founder populations: diastrophic dysplasia in Finland. Nat Genet. 1992;2:204–211. doi: 10.1038/ng1192-204. [DOI] [PubMed] [Google Scholar]
  11. Laird NM, Horvath S, Xu X. Implementing a unified approach to family-based tests of association. Genet Epidemiol. 2000;19 (Suppl 1:S36–S42. doi: 10.1002/1098-2272(2000)19:1+<::AID-GEPI6>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
  12. Rabinowitz D, Laird N. A unified approach to adjusting association tests for population admixture with arbitrary pedigree structure and arbitrary missing marker information. Hum Hered. 2000;50:211–223. doi: 10.1159/000022918. [DOI] [PubMed] [Google Scholar]
  13. Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES. Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet. 1996;58:1347–1363. [PMC free article] [PubMed] [Google Scholar]
  14. Purcell S, Neale B, Todd-Brown K, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Terwilliger JD. A powerful likelihood method for the analysis of linkage disequilibrium between trait loci and one or more polymorphic marker loci. Am J Hum Genet. 1995;56:777–787. [PMC free article] [PubMed] [Google Scholar]
  16. Abecasis GR, Cardon LR, Cookson WO. A general test of association for quantitative traits in nuclear families. Am J Hum Genet. 2000;66:279–292. doi: 10.1086/302698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Abecasis GR, Cookson WO, Cardon LR. Pedigree tests of transmission disequilibrium. Eur J Hum Genet. 2000;8:545–551. doi: 10.1038/sj.ejhg.5200494. [DOI] [PubMed] [Google Scholar]
  18. Clayton D. A generalization of the transmission/disequilibrium test for uncertain-haplotype transmission. Am J Hum Genet. 1999;65:1170–1177. doi: 10.1086/302577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dudbridge F. Likelihood-based association analysis for nuclear families and unrelated subjects with missing genotype data. Hum Hered. 2008;66:87–98. doi: 10.1159/000119108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lange K, Cantor R, Horvath S, et al. Mendel version 4.0: a complete package for the exact genetic analysis of discrete traits in pedigree and population data sets Am J Hum Genet 200169(Suppl50411462172 [Google Scholar]
  21. Li M, Boehnke M, Abecasis GR. Joint modeling of linkage and association: identifying SNPs responsible for a linkage signal. Am J Hum Genet. 2005;76:934–949. doi: 10.1086/430277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Li M, Boehnke M, Abecasis GR. Efficient study designs for test of genetic association using sibship data and unrelated cases and controls. Am J Hum Genet. 2006;78:778–792. doi: 10.1086/503711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hiekkalinna T, Schäffer AA, Lambert BW, Norrgrann P, Göring HHH, Terwilliger JD. PSEUDOMARKER: a powerful program for joint linkage and/or linkage disequilibrium analysis on mixtures of singletons and related individuals. Hum Hered. 2011;71:256–266. doi: 10.1159/000329467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Wessman M, Kallela M, Kaunisto MA, et al. A susceptibility locus for migraine with aura, on chromosome 4q24. Am J Hum Genet. 2002;70:652–662. doi: 10.1086/339078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kaunisto MA, Tikka PJ, Kallela M, et al. Chromosome 19p13 loci in Finnish migraine with aura families. Am J Med Genet B Neuropsychiatr Genet. 2005;132:85–89. doi: 10.1002/ajmg.b.30082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ekelund J, Hovatta I, Parker A, et al. Chromosome 1 loci in Finnish schizophrenia families. Hum Mol Genet. 2001;10:1611–1617. doi: 10.1093/hmg/10.15.1611. [DOI] [PubMed] [Google Scholar]
  27. Lambert BW, Terwilliger JD, Weiss KM. ForSim: a tool for exploring the genetic architecture of complex traits with controlled truth. Bioinformatics. 2008;24:1821–1822. doi: 10.1093/bioinformatics/btn317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Spielman RS, McGinnis RE, Ewens WJ. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM) Am J Hum Genet. 1993;52:506–516. [PMC free article] [PubMed] [Google Scholar]
  29. Terwilliger JD, Ott J. A haplotype-based ‘haplotype relative risk' approach to detecting allelic associations. Hum Hered. 1992;42:337–346. doi: 10.1159/000154096. [DOI] [PubMed] [Google Scholar]
  30. Göring HH, Terwilliger JD. Linkage analysis in the presence of errors IV: joint pseudomarker analysis of linkage and/or linkage disequilibrium on a mixture of pedigrees and singletons when the mode of inheritance cannot be accurately specified. Am J Hum Genet. 2000;66:1310–1327. doi: 10.1086/302845. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Spielman RS, Ewens WJ. The TDT and other family-based tests for linkage disequilibrium and association. Am J Hum Genet. 1996;59:983–989. [PMC free article] [PubMed] [Google Scholar]
  32. Schaid DJ. General score tests for associations of genetic markers with disease using cases and their parents. Genet Epidemiol. 1996;13:423–449. doi: 10.1002/(SICI)1098-2272(1996)13:5<423::AID-GEPI1>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
  33. Martin ER, Monks SA, Warren LL, Kaplan NL. A test for linkage and association in general pedigrees: the pedigree disequilibrium test. Am J Hum Genet. 2000;67:146–154. doi: 10.1086/302957. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Cottingham RW, Jr, Idury RM, Schäffer AA. Faster sequential genetic linkage computations. Am J Hum Genet. 1993;53:252–263. [PMC free article] [PubMed] [Google Scholar]
  35. Lathrop GM, Lalouel JM. Easy calculations of lod scores and genetic risks on small computers. Am J Hum Genet. 1984;36:460–465. [PMC free article] [PubMed] [Google Scholar]
  36. Lathrop GM, Lalouel JM, Julier C, Ott J. Strategies for multilocus linkage analysis in humans. Proc Natl Acad Sci USA. 1984;81:3443–3446. doi: 10.1073/pnas.81.11.3443. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lathrop GM, Lalouel JM, White RL. Construction of human linkage maps: likelihood calculations for multilocus linkage analysis. Genet Epidemiol. 1986;3:39–52. doi: 10.1002/gepi.1370030105. [DOI] [PubMed] [Google Scholar]
  38. Schäffer AA, Gupta SK, Shriram K, Cottingham RW., Jr Avoiding recomputation in linkage analysis. Hum Hered. 1994;44:225–237. doi: 10.1159/000154222. [DOI] [PubMed] [Google Scholar]
  39. Dennis JE, Jr, Torczon V. Direct search methods on parallel machines. SIAM J Optim. 1991;1:448–474. [Google Scholar]
  40. Torczon V. On the convergence of the multidirectional search algorithm. SIAM J Optim. 1991;1:123–145. [Google Scholar]
  41. Terwilliger JD, Göring HH. Gene mapping in the 20th and 21st centuries: statistical methods, data analysis, and experimental design. Hum Biol. 2000;72:63–132. [PubMed] [Google Scholar]
  42. Trembath RC, Clough RL, Rosbotham JL, et al. Identification of a major susceptibility locus on chromosome 6p and evidence for further disease loci revealed by a two stage genome-wide search in psoriasis. Hum Mol Genet. 1997;6:813–820. doi: 10.1093/hmg/6.5.813. [DOI] [PubMed] [Google Scholar]
  43. Simard LR, Prescott G, Rochette C, et al. Linkage disequilibrium analysis of childhood-onset spinal muscular atrophy (SMA) in the French-Canadian population. Hum Mol Genet. 1994;3:459–463. doi: 10.1093/hmg/3.3.459. [DOI] [PubMed] [Google Scholar]
  44. Terwilliger JD, Weiss KM. Linkage disequilibrium mapping of complex disease: fantasy or reality. Curr Opin Biotechnol. 1998;9:578–594. doi: 10.1016/s0958-1669(98)80135-3. [DOI] [PubMed] [Google Scholar]
  45. Cantor RM, Chen GK, Pajukanta P, Lange K. Association testing in a linked region using large pedigrees. Am J Hum Genet. 2005;76:538–542. doi: 10.1086/428628. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Lander ES, Green P. Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA. 1987;84:2363–2367. doi: 10.1073/pnas.84.8.2363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Clerget-Darpoux F, Bonaïti-Pellié C, Hochez J. Effects of misspecifying genetic parameters in lod score analysis. Biometrics. 1986;42:393–399. [PubMed] [Google Scholar]
  48. Kaunisto MA, Kallela M, Hämäläinen E, et al. Testing of variants of the MTHFR and ESR1 genes in 1798 Finnish individuals fails to confirm the association with migraine with aura. Cephalalgia. 2006;26:1462–1472. doi: 10.1111/j.1468-2982.2006.01228.x. [DOI] [PubMed] [Google Scholar]
  49. Ott J. Computer-simulation methods in human linkage analysis. Proc Natl Acad Sci USA. 1989;86:4175–4178. doi: 10.1073/pnas.86.11.4175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Weeks DE, Ott J, Lathrop GM. SLINK: a general simulation program for linkage analysis. Am J Hum Genet. 1990. p. A204.
  51. Barndorff-Nielsen OE, Cox DR. Inference and Asymptotics. London: Chapman & Hall/CRC Monographs on Statistics & Applied Probability; 1994. [Google Scholar]
  52. Risch N, Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Tables
Click here for additional data file. (288.5KB, doc)
Supplementary Methods
Click here for additional data file. (25.5KB, doc)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES