An MR image-guided, voxel-based partial volume correction method for PET images

Abstract

Purpose: Partial volume effect in positron emission tomography (PET) can cause incorrect quantification of radiopharmaceutical uptake in functional imaging. A PET partial volume correction method is presented to attenuate partial volume blurring and to yield voxel-based corrected PET images.

Methods: By modeling partial volume effect as a convolution of point spread function of the PET scanner, the reconstructed PET images are corrected by iterative deconvolution with an edge-preserving smoothness constraint. The constraint is constructed to restore discontinuities extracted from coregistered MR images but maintains the smoothness in radioactivity distribution. The correction is implemented in a Bayesian deconvolution framework and is solved by a conjugate gradient method. The performance of the method was compared with the geometric transfer matrix (GTM) method on a simulated dataset. The method was evaluated on synthesized brain FDG–PET data and phantom MRI–PET experiments.

Results: The true PET activity of objects with a size of greater than the full-width at half maximum of the point spread function has been effectively restored in the simulated data. The partial volume correction method is quantitatively comparable to the GTM method. For synthesized FDG–PET with true activity 0 μci/cc for cerebrospinal fluid (CSF), 228 μci/cc for white matter (WM), and 621 μci/cc for gray matter (GM), the method has improved the radioactivity quantification from 186 ± 16 μci/cc to 30 ± 7 μci/cc in CSF, 317 ± 15 μci/cc to 236 ± 10 μci/cc for WM, 438 ± 4 μci/cc to 592 ± 5 μci/cc for GM. Both visual and quantitative assessments show improvement of partial volume correction in the synthesized and phantom experiments.

Conclusions: The partial volume correction method improves the quantification of PET images. The method is comparable to the GTM method but does not need MR image segmentation or prior tracer distribution information. The voxel-based method can be particularly useful for combined PET/MRI studies.

INTRODUCTION

Positron emission tomography (PET) is an important tool for the diagnosis and longitudinal study of neurological diseases and also has been widely used to differentiate between benign and malignant tumors, determine tumor stages, and assess therapies.¹ Recently, PET has been used as a molecular imaging technique to image molecular or protein interaction during biological processes.² However, despite the continual improvement of the physical characteristics of PET machine, PET is still impaired by its low spatial resolution compared with other imaging modalities such as magnetic resonance imaging (MRI) or computed tomography (CT). The limited spatial resolution induces partial volume effect (PVE) in the images, which significantly biases the quantitative measurement of regional radioactivity concentration.^{3, 4} Such bias could result in incorrect estimation of local tracer concentration and eliminate the subtle change in metabolism or physiology as a function of an event or time.⁵ Correction of this effect has been demonstrated to effectively improve the sensitivity and accuracy of PET quantification of physiological activities.^{6, 7, 8, 9, 10, 11}

There are two distinct phenomena resulting in the partial volume effect in PET.^{4, 12} First is the relatively low spatial resolution of PET so that one image voxel might consist of different tissues. The second phenomenon is image blurring from the scanner’s point spread function (PSF). The response of a scanner to a radioactivity point source shows a bell shape instead of a perfect impulse function. This point spreading effect causes radioactivity spillover between voxels. A number of methods have been proposed for PET partial volume effect correction (PVC). Broadly, the correction can be categorized into two classes: correction during PET reconstruction from sinograms of radioactivity events and correction on postreconstruction PET images. Each category can be subdivided into voxel-based and region-of-interest (ROI)-based approaches.

ROI-based postreconstruction PVC attempts to recover true radioactivity in the region level with the assumption of homogeneous radioactivity distribution within each region of interest. Usually, these ROIs are obtained by segmenting or classifying the coregistered anatomical images into a number of nonoverlapping compartments.¹³ A typical ROI-based method is the geometric transfer matrix (GTM) method, where a regional spread function is computed for each ROI by forward projection¹⁴ or PSF convolution¹⁵ of the region assuming unit radioactivity, and then linear equations are formed to solve the regional correction. The method is initially proposed for the brain and is extended to arbitrary numbers of ROIs,¹⁶ which discusses a general theory considering explicit noise models and error estimation in a least square fitting framework. These methods not only require registration and segmentation of anatomical images but also need the knowledge about regional structural and functional correspondence to satisfy the assumption of regionally homogeneous radioactivity.

With the knowledge of object shape and assumption of a homogeneous radioactivity, model fitting-based methods simultaneously recover the size and the activity of the object.^{17, 18, 19} The methods use mathematic models of the shape of the interesting object with a limited number of parameters, such as describing spheroid or ellipsoid-shape tumors with the location and axis lengths,^{17, 19, 20} or cylinder blood vessels with the position and widths.¹⁸ These methods can be understood as a type of deconvolution with greatly simplified object geometry and radioactivity distribution. These simplifications make it difficult to apply to whole-body PET images consisting of objects with various shapes and activities. Although the methods do not require anatomic information, initial knowledge about the object location is necessary for convergence of the optimization to the correct solution.

Other than providing corrected radioactivity for ROIs, voxel-based PVC restores activity in each voxel and yields improved images which enables better visual assessment and allows further quantitative evaluation. By segmenting brain into cerebrospinal fluid (CSF), white matter (WM), and gray matter (GM) from MRI or CT images, the method in Ref. 21 attempted to correct the brain region of WM and GM under the assumption of zero radioactivities in CSF. The methods have been extended to a three-compartment method to accommodate more heterogeneous distribution of the tracer.²² Another tissue compartment was added to include brain atrophy.²³ These compartment-based methods require tissue segmentation and assume uniform distribution in each compartment except the one for correction, thereby generated partially corrected PET images.

A novel multiresolution method was proposed to utilize anatomical MRI images but eliminates image segmentation and the assumption of uniform radioactivity within a region.²⁴ The method decomposed high-resolution MR images into different scales using a discrete wavelet transformation. True radioactivity was restored by synthesizing the detail information from MR images into PET images. Stemming from the methodology, a structural–functional synergistic resolution recovery method was proposed to use anatomical probabilistic atlases instead of CT or MRI for wavelet decomposition.²⁵ The method does not need MR image segmentation or PET point spread function. Instead, they rely on the positive relationship of high-frequency information between PET and MRI. The method was modified by replacing MR images with the deconvoluted PET so eliminated the need for anatomical images.²⁶

Deconvolution-based partial volume correction could generate voxel-based improved images without the need of anatomical images. Several authors attempted the methods with different forms of smoothing regularization to limit noise amplification. Several deconvolution methods have been evaluated for PET data.^{27, 28} These papers showed improved quantification than uncorrected images, and almost similar performance with the GTM method. But these methods were only evaluated on Monte Carlo simulated PET database instead of clinical data. Another iterative deconvolution method has been proposed using the one-step regularization procedure,²⁹ which achieved recovery of radioactivity similar to that achieved by methods incorporating anatomical images.

In this paper, we present an MRI-guided partial volume correction method that eliminates the segmentation requirement for MR images. The method utilizes edge information on MR images rather than tissue class information, and thus, it could yield partial volume corrected images for whole-body PET scans. The methodology, experiments, and validation are described in detail in the following sections.

MATERIALS AND METHODS

Bayesian-based partial volume correction of PET images

Assume i(r) is the postreconstruction PET image after scanning a true spatial distribution of radioactivity o(r) by a PET scanner with a 3D point spread function of h(r). r is the 3D coordinate of an image voxel. The image formation is considered as a linear and space invariant distortion of the levels and distribution of radioactivity. Spatial independent Gaussian noise is considered for the present work. Under these conditions, PET imaging is a convolution process and is modeled as

$$i(r)=o(r)\otimes h(r)+n(r),$$ (1)

where r is a three-element vector ([x, y, z]^T) representing a point in a three-dimensional space or a two-element vector ([x, y]^T) in two dimensions. n(r) is a Gaussian distributed noise, and the operator ⊗ denotes a convolution. Equation 1 can be expressed in the frequency domain as

$$I(j)=O(j)H(j)+N(j),$$ (2)

where capitalization denotes the Fourier transform of a variable, and j is the conjugate spatial frequency. Convolution becomes a multiplication operation in the frequency domain, so the computation is greatly speeded up when a fast Fourier transform algorithm is available.

The goal of partial volume correction is to restore the true radioactivity o(r) by deconvolution of the observed PET i(r). It becomes a least square minimization denoted as

$$J^{\mathit{deconvolution}}=\sum _r{(i(r)-o(r)\otimes h(r))}^2.$$ (3)

Solving o(r) by minimization of J usually leads to noise amplification and severe ring artifacts. In order to find a unique and stable solution for J, prior knowledge about o(r) is required to regularize the minimization.

Viewing PET as a probabilistic mapping of the objects’ radioactivity to an intensity count sampled at each voxel of the image, partial volume correction can be considered as maximization of a posteriori probability to obtain the true radioactivity o providing the observed image i, PSF, and prior information about o. According to Bayesian’ theorem, a posteriori probability can be expressed as

$$p(o|i)=\frac{p(i|o)p(o)}{p(i)}.$$ (4)

p(o|i) is aposteriori probability of o accompanied with an observation i. p(i) is the probability of observing PET i and is a constant here. p(o) is the prior information about true PET activity. p(i|o) is the posterior probability density of observing image i given true radioactivity o. Based on the assumption of signal-independent Gaussian noise model, p(i|o) is denoted as

$$p\left(i\right|o)=\exp (-\frac{1}{2{\sigma }_n^2}\sum _r{(i\left(r\right)-o\left(r\right)\otimes h\left(r\right))}^2),$$ (5)

where ${\sigma }_n^2$ is a Gaussian noise variance which could be estimated from background or tissue regions with uniform radioactivity distribution and assumed to be spatial independent.

Prior information from anatomical MRI

In a Bayesian framework, prior information regarding the true distribution of radioactivity is important for partial volume correction. We modeled the true radioactivity as a Markov Random Field (MRF) and described the prior information as intensity interaction between voxels in order to account for the regularization of local smoothness. The prior information is described by Gibbs formulation as

$$p(o)=\frac{1}{G}\exp (-\lambda \sum _{c\in C}{U}_c(o)),$$ (6)

where U_c(o) is Gibbs potential defined on each possible set c of voxels, G is a normalizing factor, and the cliques C determine the range of voxel interactions. In the proposed method, only the interaction between neighboring voxels is considered and the prior information is expressed as

$$p(o)=\frac{1}{G}\exp (-\lambda \sum _r\sum _{k\in N(r)}\frac{w_{\mathit{rk}}}{d_{\mathit{rk}}}{(o(r)-o(k))}^2),$$ (7)

where N(r) is neighborhood around voxel r, that is, 26 voxels in 3D or 8 pixels in 2D, d_rk is the Euclidian distance between voxel r and k, and w_rk is a weighting coefficient. The prior information constrains, the local smoothness between neighboring voxels by the square of intensity difference, and w_rk determines the weight to enforce this regularization. For example, w_rk = 1 will lead to equal intensity between two neighboring voxel and w_rk = 0 will release any intensity constraint.

We manipulate w_rk to generate an appropriate prior regularization for PET partial volume correction. In PET, we can consider the true radioactivity is smooth at two voxels once intensity difference is less than a small threshold μ but discontinuous when two voxels having intensity difference of more than a greater threshold v. This prior is similar to an edge preserving deconvolution.³⁰ However, PET is contaminated by significant partial volume effect that blurs image edges and makes it difficult to identify tissue boundaries just through thresholds of intensity. Fortunately, aligned MRI provides the edge information for PET with much higher contrast and resolution. True radioactivity edges will appear at the edges of MRI because a region belonging to one tissue class in MRI should have same tracer activity. Therefore, the smoothness regularization needs to be removed when an MRI edge presents. However, the regularization ought to be kept when PET signal shows smoothness via the small radioactivity threshold μ, even although MRI shows an intensity discontinuity. Based on these observations, w_rk is defined as

$$\begin{array}{c}{w}_{rk}=\exp (-{(\frac{\Delta o_{\mathit{rk}}}{\mu })}^2)+[1-\exp (-{(\frac{\Delta o_{\mathit{rk}}}{\mu })}^2)]\exp (-{(\frac{\Delta o_{\mathit{rk}}}{\nu })}^2)\exp (-{(\frac{\Delta l_{\mathit{rk}}}{\kappa })}^2)\\ \approx \{\begin{array}{cc}1& \left|\Delta o_{rk}\right|\ll \mu \\ 0& \left|\Delta o_{rk}\right|\gg \nu \\ 1& \mu <\left|\Delta o_{rk}\right|<\nu and\left|\Delta l_{rk}\right|\ll \kappa \\ 0& \mu <\left|\Delta o_{rk}\right|<vand\left|\Delta l_{rk}\right|\gg \kappa \end{array}\end{array}$$ (8)

where Δo_rk = o_r − o_k and Δl_rk = MRI_r − MRI_k. μ and ν are radioactivity thresholds with μ < ν. κ is a threshold to determine an edge present in MRI, by which an edge is considered to appear if the intensity difference between the neighboring voxels is greater than κ. If |Δo_rk| is smaller than μ which indicates substantial smoothness between voxel r and k at PET, w_rk ≈ 1 to switch on the constraint for PET activity continuity. If |Δo_rk| is greater than ν denoting there is an edge between r and k, w_rk ≈ 0 to switch off the intensity constraint. For neighboring voxels, who have radioactivity difference between μ and ν, MRI edge information is employed to ensure that there is an edge in the corrected image by w_rk ≈ 0 if MRI presents an edge with |Δl_rk| > κ.

MRI-guided partial volume correction

The true radioactivity is restored by maximizing a posteriori probability as

$$o=\arg \underset{o}{\max }p(o|i)=\arg \underset{o}{\max }[p(i|o)p(o)].$$ (9)

With the definition of p(i|o) in Eq. 5 and p(o) in Eq. 8, the maximization becomes a minimization of the following cost function:

$$\begin{array}{c}o=\arg \underset{o}{\min }J(o)\\ =\arg \underset{o}{\min }[{\displaystyle \sum _r{(i(r)-o(r)\otimes h(r))}^2}\\ +\lambda {\displaystyle \sum _r{\displaystyle \sum _{k\in N(r)}\frac{w_{rk}}{d_{rk}}{(o(r)-o(k))}^2],}}\end{array}$$ (10)

where λ is a parameter to balance the convolution and the MRF smoothness constraint, which is chosen heuristically in this paper but will be simultaneously estimated based on image noise distribution.

The correction (o) is sought by minimization of the cost function J using a conjugate gradient (CG) method. CG minimization requires analytical derivatives of the cost function with respect to the true radioactivity in each voxel, which is given as

$$\begin{array}{c}\multicolumn{1}{c}{\frac{\partial J}{\partial o(r)}=2(o(r)\otimes h(r)-i(r))•h(r)+4\lambda \sum _{k\in N(r)}\frac{w_{\mathit{rk}}}{d_{\mathit{rk}}}(o(r)-o(k)),}\end{array}$$ (11)

where • denotes a correlation computation. Because PSF h is a symmetric Gaussian function, the correlation is equivalent to a convolution operation. The convolution is computed in Fourier domain described in Eq. 2 thereby to achieve a better computation speed.

A conjugate gradient method with guaranteed descent is applied for minimization.³¹ This conjugate gradient scheme guarantees descent by using a new descent condition that avoids the jamming that can happen in the Powell’s method. The minimization is performed by iterate update of the conjugate direction and the solution that is denoted as o^m+1 = o^m + αd^m. m is the iteration number, d^m is the conjugate direction, and α is a positive step size which is determined by a line search. We derive it according to $\frac{\mathit{dJ}(o^m+\alpha d^m)}{d\alpha }=0$ and have the following updated equation in iteration m:

$$a=\frac{(I-o^m\otimes H)(\nabla o^m\otimes H)-\frac{\lambda }{N}{\displaystyle \sum _r}{\displaystyle \sum _{k\in N(r)}}\frac{w_{\mathit{rk}}}{d_{\mathit{rk}}}[(o_r^m-o_k^m)(\nabla o_r^m-\nabla o_k^m)]}{{(\nabla o^m\otimes H)}^2+\frac{\lambda }{N}{\displaystyle \sum _r}{\displaystyle \sum _{k\in N(r)}}\frac{w_{\mathit{rk}}}{d_{\mathit{rk}}}{(\nabla o_r^m-\nabla o_k^m)}^2}.$$ (12)

The conjugate gradient method achieves a better performance than common conjugate gradient methods. We restart the algorithm, resetting the descent direction to the steepest descent direction, if the CG scheme cannot significantly improve the minimization of the cost function in Eq. 10 initialized or the iteration number is reached 50. Postreconstruction PET image is used as the initial value for the CG minimization, which ends if there is no further improvement between two consecutive restarts.

In summary, the partial volume correction starts with MRI and PET images with the knowledge of PET scanner’s point spread function. The next step is to register MRI to PET images using a rigid-body image registration algorithm³² if only rigid motion presents. For better edge extraction, MR images can be processed using a diffusion filtering or other edge enhancement methods. We interpolated PET to the MRI resolution using a sync interpolation in our experiments and then defined the thresholds for both images and the weight (λ). The correction is implemented by the conjugate gradient minimization of the cost function at Eq. 10 initialized with the reconstructed PET. The minimization is ended when there is no further improvement between consecutive iterations or the maximal iteration number was reached (n = 500). Usually, a median filter is applied to the result in order to remove possible isolated voxels with very high magnitudes.³³

PET point spread function and images preprocessing

It is widely accepted that PET PSF can be approximated as an anisotropic three-dimensional Gaussian function that is written as

$$h(r)=\frac{1}{{(2\pi )}^{3/2}{\sigma }_x{\sigma }_y{\sigma }_z}\exp (-\frac{1}{2}[\frac{x^2}{{\sigma }_x^2}+\frac{y^2}{{\sigma }_y^2}+\frac{z^2}{{\sigma }_z^2}]),$$ (13)

where σ = [σ_x, σ_y, σ_z] is the standard deviation in each direction. The point spread function can be measured by fitting the Gaussian function to PET images of a point radioactivity source. Full-width at half maximum (FWHM) of different PET machines have been reported and the standard deviation can be related to FWHM as $\sigma =\mathit{FWHM}/2\sqrt{2\ln 2}$.

In comparison with PET resolution, we consider PSF of MR imaging to be an impulse response. But MRI could be degraded by noise and tissue fraction-based partial volume effect³⁴ that affects edge extraction for PET partial volume correction. Therefore, MR image preprocessing is important for accurate PET partial volume correction. The segmented or classified MR image presents the best boundary information for PET partial volume correction, and an MRI intensity-based classification might be enough for the purpose.³⁵ A variety of image processing methods can be used to improve MRI quality. We use an edge-preserving diffusion filtering to attenuate image noise in MR images but maintain the edges.³⁶ The diffusion filtering smoothes regions with a gradient lower than a threshold but preserves edges with gradients higher than the threshold. κ in Eq. 8 is used as the gradient threshold for MRI diffusion filtering.

Experiments with synthesized images

The algorithm was first validated using a synthetic dataset. The synthetic dataset started with a given true radiotracer distribution on a 256 × 256 image which consisted of four rows of disks with different sizes and contrast ratios in a background intensity of 50. Each row had five horizontal disks of decreasing diameter of 30, 20, 16, 10, and 8 pixels, and each column had same size disks with a decreasing intensity of 65, 60, 45, and 30 which were intensity contrasts of 30%, 20%, 10%, and 40% with respect to the background. An MR image was synthesized with the same size and disks distribution with the synthesized true tracer image, but the MR intensity given to a disk was different from each other in order to characterize different tissue types. The background of the MR image was given an intensity of five. The true radioactivity image was added with Gaussian white noise of different levels (1%, 5%, 8%, 10%, and 12%) relative to the background activity. Then, the noisy PET was convoluted with a Gaussian function having FWHMs of 10 pixels in x- and y-axes. The convolution induced signal contamination between neighboring regions and accordingly simulated the point spread function blurring of the true radioactivity signal. In order to account for tissue fraction effect, the convoluted PET image was down sampled by extracting a point at every two pixels along each axis. The synthesized data were applied to evaluate the correction method on PET images with variable statistical quality and resolutions. The PSF and image size were given with a unit of pixel which can be easily mapped to typical MRI and PET resolutions.

The restored signal intensity was compared with the true PET in lines traversing the centers of each disk in a row. The mean intensity in the disks was calculated before and after the correction in each of the disks and then quantitatively compared with the true tracer intensity. The comparison was performed by recovery ratio, which was defined as percentage of O/I_true for correction and I/I_true for original PET. Therefore, the ratio was greater than 100%, if the object was in a hot background (object radioactivity is less than the background), and it is less than one if the object was in a cold background. Recovery error was calculated as absolute value of the difference between the recovery ratios to one, which characterized the error percentage to represent the true signal. Our experiments demonstrated the quality of partial volume recovery of objects with different sizes (3.0, 2.0, 1.6, and 1.0, 0.8 times of FWHM) and different contrasts (10%, 20%, 30%, and 40%). We also performed PVC using the GTM method on the synthesized data with the ROI defined from MRI. GTM method is considered as the reference numerical approach for partial volume correction in PET.

We also used the synthesized image to assess the proposed method in the cases where image content of MRI and PET was no longer correlated. For example, two distinct structures in MRI have same radioactivity intensity, or one region in MRI has an inhomogeneous radiotracer distribution in PET. We removed the disks in the middle row with an intensity of 45 in the true radioactivity image and generated a PET image for correction. MR image was unchanged, so different structures in MRI at the middle row had the same true radioactivity. In the other case, without altering the PET image, the first row of disks in MRI was removed and set as the background intensity. Another configuration was present in which a subregion in the first row of MRI had structure information. The data were used to demonstrate whether the method can recover local regions in PET without affecting other areas without clear structural information available. This could happen for tumor metabolic quantification from a whole-body scanning where global anatomical information might not be salient in the aligned MRI but with identifiable tumors for correction. For these cases, the threshold for PET was carefully selected in order to recognize the boundaries from PET.

Alignment of MRI and PET is essential for correction of the partial volume in PET using MRI anatomical information. The robustness of the proposed algorithm to small spatial misalignment was studied by introducing artificial displacement of the synthesized PET with regards to MRI. A set of PET image was generated by 1, 2, and 3 pixels shift to left and 1°, 2°, and 3° of rotations clockwise. Five percent Gaussian noise was considered for all the PET images. The recovery error was calculated for each disk using the ROIs in MRI and was tabled with the object’s size.

Phantom imaging experiments

A phantom was designed to evaluate the performance of the partial volume correction method. The phantom consisted of a hollow 10 × 10 × 40 mm square and a hollow 30-mm diameter sphere in a plastic box container. The square and sphere were filled with FDG solution with activities of 25 μci/cc and 16 μci/cc, respectively. The phantom was first imaged by a microPET scanner system (R4, Siemens Preclinical Solutions, Knoxville, TN) and then reconstructed by the OSEM method with 16 subsets and four iteration. The PET was reconstructed with a dimension of 128 × 128 × 63 mm³ and a resolution of 0.845 × 0.845× 1.215 mm³. After PET imaging, the FDG solution was removed and 0.1% Gd-DTPA solution was given to the square and sphere, respectively. A T1-weighted MR image of the phantom was acquired using a 9.4T small animal scanner (Bruker BioSpin GmbH, Rheinstetten, Germany). The MRI had a dimension of 198 × 218 × 45 mm and a voxel size of 0.2 × 0.2 × 0.5 mm. Rigid-body registration of MRI and PET images was performed using Analyze 6.0 (AnalyzeDirect, Inc., Overland Park, KS). The microPET R4 machine has an FWHM of 1.85 mm at the axial direction and 1.66 mm at the radial direction within the field of view of a size of 6.3 × 6.3 cm.³⁷ The PSF of the scanner was created by a 3D Gaussian function with the given FWHMs. Since the center transverse section of the sphere was much greater than the FWHMs, the average radioactivity within the center region of 1-cm diameter was considered as the true radioactivity for evaluation. We selected different transverse sections from the sphere to get ROIs with varied sizes, and evaluated the method based on the recovery of true radioactivity at these ROIs with regard to the object’s size.

Brain PET experiments

We evaluated the proposed method on a publicly available dataset of 16 Monte Carlo simulated dynamic brain FDG–PET volumes³⁸ that has been used for PVC validation.²⁸ The dataset was simulated by the PET–SORTEO Monte Carlo simulated software²⁷ that models PET imaging with the Exact-ECAT HR+ scanner operating in a 3D mode. The simulation accounts for the specific scanner and most of the phenomena appeared in radioactivity signal acquisition and allow faithful reproduction of PET tomography image formation. The realistic anatomical models were derived from human brain MR images, which were partitioned into white matter, gray matter, and CSF according to the properties of FDG uptake. Constant activity of 8.45 and 22.99 kBq/cc was assigned to WM and GM, respectively, activity of zero was given to CSF and background. Images of the FDG distribution were simulated, and the data were reconstructed by the filtered back projection with 0.3 mm⁻¹ frequency cutoff hanning filter. The filter produces images with a low noise level but a poor resolution compared with other filter. The resulting PET volumes had a size of 128 × 128 × 63 mm³ with a resolution of 2.11 × 2.11 × 2.43 mm³ and were well aligned with the original MR volumes. The dimension of MR volume was 256 × 256 × 63 mm³, and its voxel size was 1.0 × 1.0 × 1.0 mm³. The PSF of the simulated scanner was approximated by a 3D Gaussian function. The FWHM of the PSF was derived by imaging a point source located at 5 cm from the center of the field of view of the scanner. For the simulated FDG–PET data, the FWHM was 9.2 mm in axial and radial directions. The original anatomical MRI, the true FDG activity model, and the simulated PET volumes provide a reliable dataset for quantitative evaluation of the PET–PVC algorithm. One of 16 PET volumes was used to tune the parameters in the method, and the other 15 volumes were corrected using the proposed method. The results were evaluated in four regions of interest, which were defined based on anatomical models from the MRI segmentation.

The proposed method has been applied to correct partial volume effect in a clinical PET study using the [¹¹C]-PIB agent. PET data were acquired using a Siemens HRRT dedicated brain PET scanner. The PET images were reconstructed by the 3D iterative ordered-subset expectation maximization (OSEM3D) method with 16 subsets and 6 iterations, and then the images were smoothed by a 4-mm 3D Gaussian function. The voxel size is 1.22 × 1.22 × 1.22 mm³. The FWHM of the HRRT scanner was determined as 5.5 mm according to our experiments and the published study.³⁹ For the subject, T1-weighted MR images were acquired using a 3T Siemens MR scanner with the resolution of 1 × 1 × 1 mm³ and an acquisition matrix of 240 × 256 × 176 mm³. The MR images were processed by a diffusion filtering to reduce image noise and to enhance MRI edges. A piece of edge was delineated on the MR images, and parameter κ was determined as the average neighboring voxel intensity differences across the edge divided by the square root of 3. By this mean, we ensure w = exp(−3) at the MRI edges. An ROI with visually homogeneous tracer activity was delineated on the PET, and the intensity standard deviation in the ROI was computed as the parameter of μ. Similar to the way of determining κ on MR images, we determined the parameter ν from the manually delineated edges on the PET. In this experiment, we determined the parameter λ in a trial-and-error fashion. The corrections of partial volume effect by the proposed method were performed on one PET image with a number of λs. Then, we removed those λs from which the corrected PET activity in the delineated homogeneous ROI had greater than 5% change of the mean activity as compared to the original PET. Finally, the λ that generated visually optimal correction of the PET was determined. Several values that are close to the determined λ were also tested in order to examine whether the λ could be further refined. These determined parameters were used for the correction of the whole PET volume.

RESULTS

Results from synthesized images

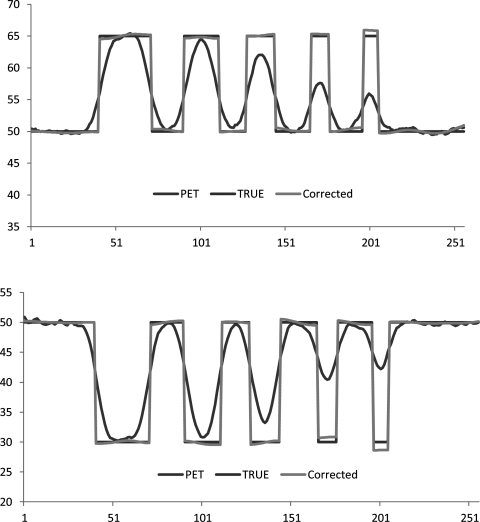
The method is first evaluated on a simulated data as shown in Fig. 1 that shows a synthesized 2D image of a true tracer distribution, a simulated PET, a synthesized MR image, and the resultant partial volume corrected PET image. The partial volume correction method was guided by the structural information from MR image. As compared to the original noncorrected PET image, the contrast of the corrected image was improved and is closer to the true value. The quantitative comparison of PET restoration is shown in Fig. 2 that displays the signal profiles from uncorrected PET, true intensity, and corrected intensity cross the centers of circular objects. The matching of corrected signals with the true signals illustrates that the partial volume correction algorithm restores the true activity from the uncorrected PET.

Figure 1.

Partial volume correction of a simulated 256 × 256 2D image. (a) A synthesized 2D image of true tracer distribution. Circular objects with different sizes and tracer intensities are in a background with an intensity of 50. From left to right, the rows are objects having diameters of 3, 2, 1.6, 1, and 0.8 times of PSF FWHM. From top to bottom, the columns are objects having contrasts of 30%, 20%, 10%, and 40% relative to the background. (b) A simulated PET by convolving PSF with image from (a) with 5% Gaussian noise. (c) A synthesized MR images where different intensities are assigned to the circular objects so that edge information is present. (d) The resultant partial volume corrected PET image which is corrected from (b).

Figure 2.

Signal profiles of uncorrected PET, true intensity, and corrected intensity cross the centers of simulated circular objects that are shown in Fig. 1a. Top: profiles from the first row of simulated circular objects. Bottom: profiles from the last row of simulated circular objects.

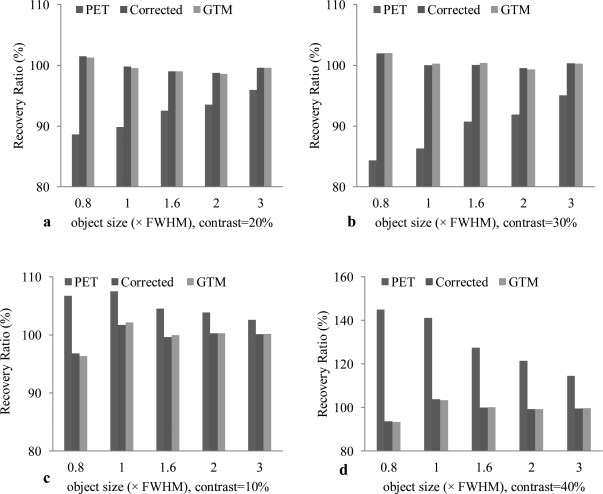
Figure 3 compares the average intensity in each object without correction (PET), with correction using the proposed algorithm (corrected), and using geometrical transformation method (GTM). Different intensity contrasts and different object sizes were used to test the partial volume correction method. When the objects are in a cool background, i.e., the background intensity is lower than those of the objects [Figs. 3a, 3b], the correction method increases the intensity in order to match the true intensity. Because the objects intensities are lower than the background and because the background spills some intensity into the objects, the partial volume correction leads to the decrease of the object intensity in order to restore the true intensity. The GTM method was used as a gold standard for comparison. The synthesized MR image delineates the ROI for each circular object, which is used for quantification of the correction method in each region. The proposed method achieves similar results compared to the GTM method but the proposed method does not require MR classification or segmentation as needed by the GTM method.

Figure 3.

Comparison of the average intensity in each object without correction (PET), with correction using the proposed algorithm (corrected), and with correction using the GTM. Each figure shows the comparison of the average intensity at different object sizes (0.8, 1.0, 1.6, 2.0, 3.0 × FWHM) and at different contrast (a: 20%, b: 30%, c: 10%, and d: 40%). (a) is for the four circular objects in the first row of the simulated image (Fig. 1), (b) is for the circular objects in the second row. The objects are in a cool background (background intensity is lower than the objects). After correction, the intensity increased. (c) and (d) are the objects in the third and last rows, respectively. The objects intensity is lower than the background, thus the correction leads to the decrease of the intensity and thus it is close to the true intensity.

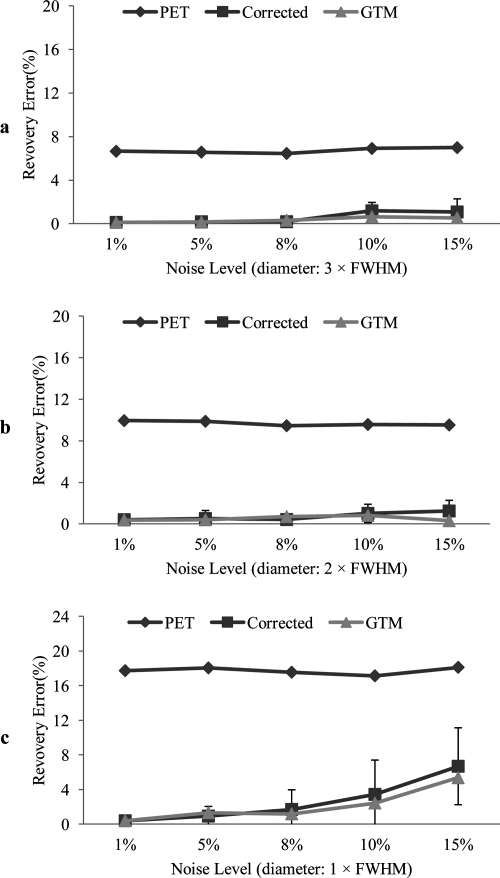
We quantify the signal restoration by recovery errors, i.e., the percentage of signal difference from the measured intensity over the true intensity. Figure 4 shows the intensity recovery errors of the circular objects for the uncorrected PET, corrected images using our method and using the GTM method. Noise at the levels of 1%, 5%, 8%, 10%, and 15% are added to the images. Recovery errors of the objects with the object sizes of 3, 2, and 1 times of FWHM are evaluated. The noise level of less than 15% leads to a less than 5% recovery error for the objects with different sizes using the proposed correction method.

Figure 4.

Intensity recovery errors of the circular objects from uncorrected PET (PET), corrected images using the proposed method (corrected), and the result from the GTM method (GTM) at different image noise levels. The recovery error is the percentage of signal difference compared to the true intensity. Noise levels of 1%, 5%, 8%, 10%, and 15% are added to the images for evaluating the robustness of the proposed method. Recovery errors of the objects with the sizes of 3, 2, and 1 times of FWHM are shown in a, b, and c, respectively. The error bars are calculated from the four objects with different contrasts but with the same object size. Only the result of the proposed method has shown the error bars.

The misregistration between MRI and PET can significantly affect the MRI-based PET partial volume correction. Table TABLE I. shows the recovery errors that illustrate the effect of the misregistration on the PVC results using the proposed method. The PET image is shifted by 0, 1, and 2 pixels or is rotated by 1°, 2°, and 3° and is then corrected using the proposed method. The average intensity within each circular object that was delineated from MRI is calculated and compared with the true intensity. The results are separated and compared according to the object size. Significant intensity restoration has been achieved using the method even with 2-pixel translation or 3-degree rotation for those objects with a size of no less than the FWHM of the machine’s PSF.

Table 1.

Recovery errors of the proposed method (I) and uncorrected PET (II) with respect to the misregistration between PET and MRI. The PET image is shifted by 0, 1, and 2 pixels or is rotated by 1°, 2°, and 3° and is then corrected using the proposed method. The average intensity within each circular object is calculated and compared with the true intensity for the calculation of the recovery error. The results are separated and compared according to the object sizes. The standard deviation is from the four objects with different contrasts but with the same size.

		Object size (× FWHM)
I. Corrected recovery error (%)		0.8	1	1.6	2	3
X shift (pixel)	0	3.2 ± 2.2	1.4 ± 1.7	0.4 ± 0.4	0.7 ± 0.4	0.3 ± 0.1
	1	5.0 ± 3.8	2.3 ± 0.6	1.2 ± 1.5	0.6 ± 0.7	0.3 ± 0.1
	2	7.3 ± 5.7	2.9 ± 2.9	1.8 ± 2.8	1.8 ± 2.6	0.9 ± 1.3
	3	5.8 ± 5.0	2.9 ± 2.8	4.5 ± 6.6	3.7 ± 5.3	2.3 ± 3.0
Rotate (degree)	1	2.2 ± 2.1	1.3 ± 0.9	1.1 ± 1.4	0.9 ± 0.7	1.6 ± 2.4
	2	6.9 ± 6.3	3.0 ± 2.4	3.8 ± 5.2	2.7 ± 4.0	2.9 ± 3.8
	3	11.8 ± 10.5	6.7 ± 8.1	7.5 ± 9.2	5.5 ± 6.9	5.4 ± 6.7

		Object size (× FWHM)
II. Uncorrected recovery error (%)		0.8	1	1.6	2	3
X shift (pixel)	0	19.7 ± 17.2	18.1 ± 15.6	12.2 ± 10.4	10.0 ± 7.9	6.5 ± 5.4
	1	21.1 ± 18.2	18.4 ± 15.1	12.8 ± 11.0	10.0 ± 8.6	6.7 ± 5.5
	2	21.4 ± 18.8	18.0 ± 15.8	12.7 ± 11.2	10.4 ± 8.9	6.9 ± 6.1
	3	22.4 ± 19.2	18.9 ± 16.8	13.5 ± 11.8	10.7 ± 9.1	7.5 ± 6.3
Rotate (degree)	1	21.5 ± 18.8	17.8 ± 15.5	12.6 ± 10.7	10.3 ± 8.8	7.2 ± 6.2
	2	22.4 ± 19.5	18.6 ± 15.8	13.2 ± 11.5	10.5 ± 9.2	7.8 ± 7.0
	3	24.4 ± 20.9	20.1 ± 18.5	14.2 ± 12.4	11.5 ± 10.7	8.9 ± 8.2

Figure 5 shows the partial volume correction results when there is no corresponding information between PET and MR images. This is of particular interesting because a tumor may be seen on PET but not visible on MR images, or vice versa. In the first case [Fig. 5a], there is no object in the PET image, which could correspond to the ones in the second row on MR images. The corrected image [Fig. 5c] was affected by the object information on MRI. In the second case [Fig. 5d], the MR image does not show the objects that could correspond to the circular objects in the first row on the PET image [Fig. 5e]. Hence, there is no structural information for correcting these objects. However, the proposed correction method is able to restore the objects in PET without MRI information, as shown in Fig. 5f. In the third case, MRI [Fig. 5g] recognizes a small object in the first row to give local anatomical information for PET [Fig. 5h]. The result illustrates that the PVC method is able to accurately recover the object when local structural information becomes available.

Figure 5.

Partial volume correction results when there is no corresponding information between PET and MR images. (a) A synthesized MRI. (b) An uncorrected PET. Note that there are four objects in the second row on the MR image but there are no corresponding objects in PET in the same second row. It is important to note that the corrected image (c) was not affected by the objects in the second row in the MR image. A synthesized MRI (d) shows no objects in the first row; however, there are four objects on the PET image (e) in the first row. Thus, no structural information is provided for correcting these objects. By selecting a correct threshold, the proposed correction method is able to restore the objects in PET without MRI information, as shown in image (f). In (g), the MR image recognizes a small object in the first row to give a local anatomical information for PET in (h). The correction result in (i) illustrates that the proposed method is able to recover the object when a local structural information is available.

Phantom experiment results

The phantom consists of a square and a sphere with FDG tracer filled for PET imaging and with Ga-DTPA contrast agent filled for MRI. Figure 6 shows the correction results of the phantom experiment. The MR image volume was first registered with the PET image volume using our registration methods.^{40, 41, 42, 43, 44} Two image slices are selected to show correction results. The image quality was improved from the proposed partial volume correction method.

Figure 6.

Partial volume correction results of a PET phantom study. The phantom consists of a square and a sphere filled with FDG tracer for PET and with Ga-DTPA contrast agent for MRI. Two image slices of the phantom MRI and PET are shown in the two rows. (a) MR image slice, (b) corresponding PET image slice, (c) corrected result using the proposed method, (d) another MR image slice, (e), and (f) PET images before and after the partial volume correction.

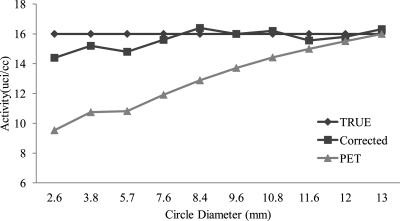
Furthermore, the radioactivity restoration of the sphere is also improved (Fig. 7). In order to show the partial volume effect with respect to different object sizes, MR image slices were selected from the sphere at different level positions where the center of the sphere has a larger diameter, while the top and bottom of the sphere have an area of smaller diameter. Hence, the MR image slices show circular objects with different diameters to demonstrate the partial volume correction with respect to object sizes. Mean activity of the selected region before and after the correction is shown and also compared with the true intensity. The FDG quantification from the corrected PET images is closer to the true activity as compared to the uncorrected images, especially when the object size is small and thus the partial volume effect is severe. The significant improvement of FDG quantification demonstrates the effectiveness of the proposed partial volume correction method.

Figure 7.

Radioactivity restoration for the objects with different sizes in the phantom experiment. The true activity was measured from the mean PET intensity within the center sphere with a radius of 5 mm, which is a homogeneous region with minimal partial volume effect. The objects were selected from different slices of the sphere object in the phantom MR image and they were in circular shapes with different diameters when the image slice was selected at different positions. This is to demonstrate the partial volume correction with respect to object sizes. Mean activity of the selected region before and after correction was shown and is also compared with the true intensity.

Brain PET study

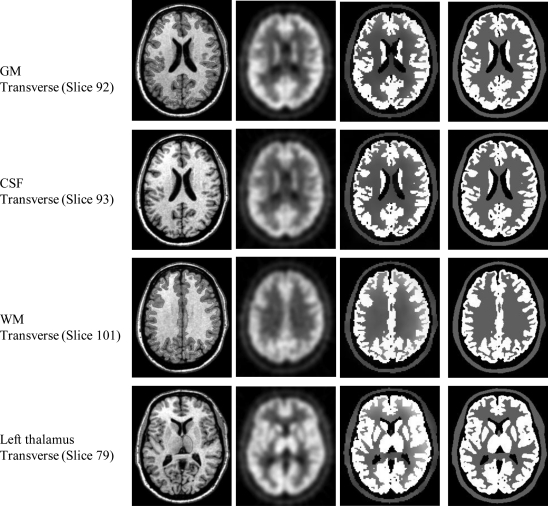
The partial volume correction method has been evaluated by simulated human brain FDG–PET database. Figure 8 shows both the real MR images and the PET images without and with correction. The true activity distribution is available from this database for validation. The MR images provide the structural information for the partial volume correction of PET images. The resultant images show the FDG distribution within the brain. As the MR images provide high-resolution anatomic information for the tissue types, the partial volume correction method is able to restore the FDG distribution with the prior knowledge of tissue types (GW, WM, and CSF). The restored FDG distribution has much clear edge as compared to the blurred, uncorrected PET images.

Figure 8.

Partial volume correction of simulated human brain FDG–PET images in the database. Each row shows the result for one slice in the 3D volume dataset. The first column is the real MR images. The second column is the aligned PET images interpolated to MRI resolution. The third column is the partial volume correction results showing the activity distribution of FDG in the brain. The true FDG distribution from the database is displayed in the fourth column. Four slices were selected, and each slice has a defined ROI which is delineated by the red line. From top to bottom, the objects are GM, CSF, WM, and left thalamus. These objects have been used for the following region-based quantitative evaluation of radioactivity recovery after partial volume correction.

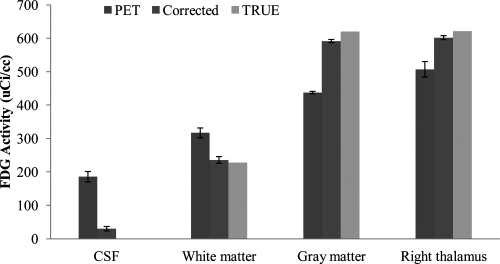
On MR images, four ROIs (GM, WM, CSF, and left thalamus) are defined to quantitatively evaluate the partial volume correction methods. Sixteen FDG–PET brain volumes were corrected. Figure 9 shows the average FDG radioactivity within the four ROIs from the true, uncorrected PET and corrected results. The true activity is 0 μci/cc for CSF, 228 μci/cc for WM, 621 μci/cc for GM, and 621 μci/cc for left thalamus. The plot shows the region radioactivity has been improved from 186 ± 16 μci/cc to 30 ± 7 μci/cc for CSF, from 317 ± 15 μci/cc to 236 ± 10 μci/cc for WM, and from 438 ± 4 μci/cc to 592 ± 5 μci/cc for GM after the partial volume correction.

Figure 9.

Average FDG radioactivity within four ROIs (GM, WM, CSF, and left thalamus) from the true, the uncorrected PET, the corrected results (corrected), and the true activity from the database (TRUE). The results are obtained from correction experiments of 16 simulated FDG–PET and real MRI volumes. The true activity is 0 μci/cc for CSF, 228 μci/cc for WM, 621 μci/cc for GM, and 621 μci/cc for left thalamus. The region radioactivity has been improved from 186 ± 16 μci/cc to 30 ± 7 μci/cc for CSF, from 317 ± 15 μci/cc to 236 ± 10 μci/cc for WM, and from 438 ± 4 μci/cc to 592 ± 5 μci/cc for GM after the partial volume correction.

In our experiment, the smoothness weight λ balances deconvolution and image smoothness constraint. One MRI and PET dataset are selected to determine appropriate λ for optimal signal recovery. The average activity within the four ROIs (white matter, gray matter, CSF, and left thalamus) is calculated from the true, the uncorrected PET, and corrected results with different smoothness weight in Table TABLE II.. By considering the radioactivity restoration for all the objects, λ = 5 was selected and was used for all the experiments.

Table 2.

Correction of simulated brain PET images versus the smoothness weight λ. One MRI and PET dataset are selected. The average activity within four ROIs (white matter, gray matter, CSF, and left thalamus) is calculated from the true, the uncorrected PET, and corrected results with different smoothness weight. By considering the radioactivity restoration for all the five objects, λ = 5 is selected for our experiments.

			Correction with λ
ROI	TRUE	PET	0.1	1	3	5	10
WM	228	266	238	228	234	230	242
GM	616	442	549	580	582	595	558
CSF	0	190	45	39	29	25	21
Right thalamus	621	537	604	602	597	605	593

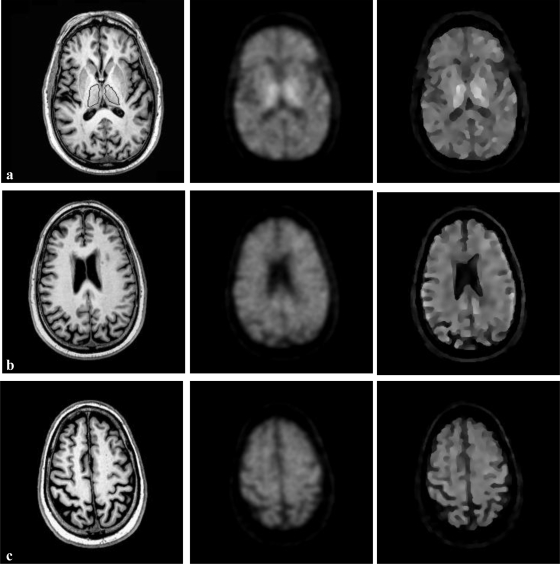
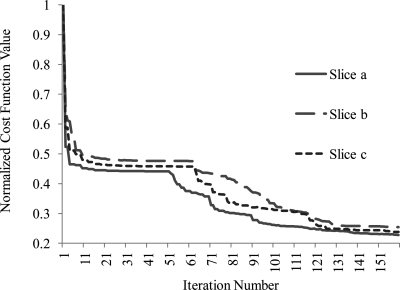
The correction results of the real clinical PET data are shown in Fig. 10. The three PET slices in the middle column are substantially smooth and edge-blurring because of PET partial volume effect. By utilizing MRI anatomical information, the proposed method significantly improves the resolution of the corrected PET images as shown in the third column. We calculated the percentage change of the mean activity in the segmented caudate between the corrected and original PET images. The result shows the activity in the segmented caudate has approximately 17% improvement resulting from the proposed correction method. Figure 11 shows the convergence behaviors of the correction method for three slices. These optimizations approximately converge after 150 iterations, and the plot indicates the stability of the algorithm.

Figure 10.

Partial volume correction of three slices (a, b, c) in the clinical patient dataset. Each row shows the result for one slice in the 3D volume dataset. The first column is the real patient MR images. The second column is the aligned real PET images from the same patient and the image was interpolated to the MRI resolution. The third column is the partial volume correction results. The MR image on the top shows the delineation of the caudate ROI.

Figure 11.

Convergence behaviors of the PET correction method for three image slices. The normalized cost function value for a slice is the cost function value at an iteration divided by the cost of its first iteration.

DISCUSSION

We developed an MRI-based method to efficiently correct partial volume effect in reconstructed PET images. As various multimodalities image registration algorithms become available, fusion and registration of MRI and PET images have been widely used in clinical applications. Because combined scanners such as PET/CT, SPECT/CT, and PET/MRI (Refs. ^{1, 45}, and ⁴⁶) are demonstrating their utilities in patient care and disease management, anatomical and functional images can be acquired at the same imaging session and then be superposed to aid in clinical decision making. Based on the development of image registration methods and utilization of combined imaging modalities, anatomical image-guided methods can be a more natural choice for PET partial volume correction.

However, most current methods focus on brain PET imaging and typically employ tissue type information via MR image segmentation or classification. These methods suffer from the accuracy of anatomical image segmentation and they may be difficult for other applications such as metabolism quantification in tumors or whole-body function studies where image segmentation is a challenging task. Our proposed method incorporates edge information in MRI to guide PET partial volume correction without MRI segmentation. The method provides a partial volume corrected PET image by deconvolution of an initially reconstructed PET image with an edge-preserving smoothness constraint. Because MRI and PET are aligned, the edge information from MRI can be used to guide the PET partial volume correction. This concept has been demonstrated by most region-based correction methods.^{14, 47} However, those methods need prior information of PET tracer distribution in order to correctly combine or separate anatomical structures into regions with distinct tracer concentrations. Our proposed method avoids the problem by a design of the edge-preserving constraint. The constraint can optionally remove edges that are visible in MRI but not PET and can also render edges that are shown in PET (e.g., tumor) but not in MRI. Our experiments of simulated images demonstrate the ability of the method to recover true trace distribution directly from MR images. The simulation study shows that the proposed method has similar performance with the conventional GTM method. The phantom experiments and evaluation with FDG brain PET database demonstrate the improvement of radioactive tracer quantification after our partial volume correction. The method improves the resolution of the corrected PET for the clinical dataset. Figure 10 also shows minor activity artifacts in the corrected PET, mainly because the PSF that we used from the literature may be different from the one of our PET scanner. When applying this correction method to a particular PET scanner, experiments measuring its PSF will help to improve the image quality.

The partial volume correction can compensate both the system point spread function and the tissue fraction effect. MRI usually provides much higher resolution images than PET, so it can be reasonably assumed that each voxel is a single tissue type which is not the case in PET. Typically, MRI is interpolated to PET resolution for image correction thus leads to blurred edges due to tissue fraction effect. But interpolation of PET images to MRI resolution incurs inaccurate estimation of radioactivity. According to our experiments of different combination of interpolation approaches, no significant quantification difference happens. A deconvolution-based method needs the full knowledge of the point spread function, that is, the probability to detect an event occurrence in the image space when a point source presents. PSF usually depends on the position of the point source. With space variant PSF, Fourier-based methods are no longer applicable, but fortunately the variations across the field of view are somewhat decreased likely, owing to the Compton scatter effect. Extensive experiments showed a very small change in PSF within a region centered at the field of view.⁴⁸ In our current experiments, objects are located at the center region of PET FOV. We consider a constant PSF within their dimensions. Our experiments of the simulated dataset show that we could perform partial volume correction within a small region and do not affect other areas. Therefore, we may be able to divide the whole space into small segments, and each segment has a constant PSF even though the PSF is space-variant in the whole image. Through correction in each segment with varied PSF, we can account for the effect of space-variant PSF. The other benefit of local correction is to correct a given region or regions with tumors so as to improve tumor metabolic quantification.

Several parameters need be determined before performing the correction. Parameters μ, ν, and κ are smoothness and edge thresholds determined by the PET and MR images, which can be obtained from manually delineated ROIs as what we did for the clinical PET dataset. The threshold κ is used to separate edge points from homogeneous MR regions. Good delineation of MRI edges will lead to better edge enhancement and smoothness within regions. Various image enhancement methods can be used to improve MR images and edge delineation. We use a diffusion filtering to preprocess MR images because diffusion filtering smoothes image noise but preserves the edges. Image segmentation techniques can also be employed to intensify the edges in MRI. Binary parametric images of MR edges may be able to generate boundary restoration of radiotracer activity. However, because of possible MRI/PET misregistration and MRI tissue fraction effect, a Gaussian smoothness of the binary edge may augment the robustness of the partial volume correction. Another two thresholds for PET image gradients are needed. A small one is used to identify homogeneous neighboring pixels, and a greater one is to determine obvious discontinuous pixels. Noise level positively affects the selection of the small threshold. Thereby PET images may need to be filtered before correction. The other important parameter is the weight of λ that balances the ratio of smoothness constraint and signal deconvolution. The constraint regularizes region homogeneity, which is disturbed by the noise during deconvolution. So, a bigger parameter may be selected for a higher noise level. The threshold could be analytically derived with some assumptions about image distribution in the future.³⁰

The restoration method is derived in a Bayesian framework with an MRF model for prior information regularization. The cost function could equivalently result from penalized maximum likelihood or deterministic least square approaches. We select two-element neighboring pixels for Gibbs formulation although more complicate pixels interactions might improve the result. The model ensures the convexity of the criterion and a unique minimum solution. The minimization is performed by a conjugate gradient method, whose convergence to a stationary point is guaranteed because of the quadratic criterion function. The analytic solution for the line search step size [Eq. 12] also greatly speeds up the minimization. Typically, 3∼4 CG restarts with 50 iterations in each restart are enough for correction of a PET image with the size of 256 × 256 pixel, which approximately takes 6 s for the method programmed by the Interactive Data Language on an Intel CPU 6600 computer. The solution is bounded between zero and a maximal uptake. The non-negative constraint is implemented in iterations by a projective strategy.⁴⁹ But a few isolated pixels of very high intensity might emerge because pixel differences with very large magnitude incur the same cost as smaller intensity differences.³³ Therefore, a median filer was applied to remove these isolated points.

In conclusion, we developed an MRI-guided partial volume correction method that can improve both PET quantification and image contrast. The method does not require MR image segmentation or prior information about the radiotracer distribution. It can offer a partial volume correction approach for a broad range of applications of PET or combined MR/PET imaging.