Controlled vocabularies and semantics in systems biology

Abstract

The use of computational modeling to describe and analyze biological systems is at the heart of systems biology. Model structures, simulation descriptions and numerical results can be encoded in structured formats, but there is an increasing need to provide an additional semantic layer. Semantic information adds meaning to components of structured descriptions to help identify and interpret them unambiguously. Ontologies are one of the tools frequently used for this purpose. We describe here three ontologies created specifically to address the needs of the systems biology community. The Systems Biology Ontology (SBO) provides semantic information about the model components. The Kinetic Simulation Algorithm Ontology (KiSAO) supplies information about existing algorithms available for the simulation of systems biology models, their characterization and interrelationships. The Terminology for the Description of Dynamics (TEDDY) categorizes dynamical features of the simulation results and general systems behavior. The provision of semantic information extends a model's longevity and facilitates its reuse. It provides useful insight into the biology of modeled processes, and may be used to make informed decisions on subsequent simulation experiments.

Introduction: semantics in computational systems biology

Models as abstract representations of observed or hypothesized phenomena are not new to the life sciences. They have long been used as tools for organizing and communicating information. However, the form those models take in systems biology has changed dramatically. Traditional representations of biomolecular networks have used natural language narratives augmented with block-and-arrow diagrams. While useful for describing hypotheses about a system's components and their interactions, those representations are increasingly recognized as inadequate vehicles for understanding complex systems (Bialek and Botstein, 2004). Instead, formal, quantitative models replace these static diagrams as integrators of knowledge, and serve as the centerpiece of the scientific modeling and simulation cycle. By systematically describing how biological entities and processes interrelate and unfold, and by the adoption of standards for how these are defined, represented, manipulated and interpreted, quantitative models can enable ‘meaningful comparison between the consequences of basic assumptions and the empirical facts’ (May, 2004).

The ease with which modern computational and theoretical tools can be applied to modeling is leading not only to a large increase in the number of computational models in biology, but also to a dramatic increase in their size and complexity. As an example, the number of models deposited in BioModels Database (Le Novère et al, 2006; Li et al, 2010a) is doubling roughly every 22 months while the average number of relationships between variables per model is doubling every 13 months. The models published with the first release of BioModels Database contained on average 30 relationships per model, and this number rose to around 100 in the 17th release. Standardization of the encoding formats is required to search, compare or integrate such a large amount of models. We have argued that the standards used in descriptions of knowledge in life sciences can be divided into three broad categories: content standards, syntax standards and semantic standards (see for instance the matrix in Le Novère, 2008). Content standards provide checklists or guidelines as to what information should be stored for a particular data type or subject area. Examples of such Minimum Information checklists are hosted on the MIBBI portal (Taylor et al, 2008). Syntax standards provide structures for formatting the information requested in a content standard. Frequent examples are representation formats, for instance using an XML language. Semantic standards provide a unified, common definition for all words, phrases or vocabulary used to describe a particular data type or subject area. By using standards from these three categories in concert, model descriptions can achieve both human and computational usability, reusability and interoperability, and it has even been claimed that ‘the markup is the model’ (Kell and Mendes, 2008).

Computational models, expressed in representation formats such as the Systems Biology Markup Language (SBML; Hucka et al, 2003), CellML (Lloyd et al, 2004) and NeuroML (Gleeson et al, 2010), still require much human interpretation. While syntax standards define the format for expressing the mathematical structure of models (i.e. the variables and their mathematical relationships), they define neither what the variables and the mathematical expressions represent, nor how they were generated. Where this critical information is communicated through free-text descriptions or non-standard annotations, it can only—if at all—be computationally interpreted with complex text-mining procedures (and hardly even with those; Ananiadou et al, 2006). Existing modeling tools that work only with unannotated models are therefore restricted to a fraction of the overall model information available, omitting the crucial semantic portion encoded in non-standard annotations. Furthermore, textual descriptions of semantics can be ambiguous and error-prone. Subsequent activities such as model searching, validation, integration, analysis and sharing all suffer as a result; software tools are of limited use without standardized, machine-readable data. The extent of semantic information associated with models is potentially unlimited and susceptible to rapid evolution. Thus, to provide for maximum flexibility, semantic information should be defined independently of the standard formats used for model encoding. This allows for easy updates and extensions of the vocabulary as science evolves, without invalidating previously encoded models. Making use of ontologies, as one approach of encoding semantics, has gained momentum in life sciences over the last decade (Smith, 2003). Ontologies are formal representations of knowledge with definitions of concepts, their attributes and relations between them expressed in terms of axioms in a well-defined logic (Rubin et al, 2008). Ontologies include information about their terms, especially definitional knowledge, and provide a single identifier for each distinct entity, allowing unambiguous reference and identification. In addition, ontologies can be augmented with terminological knowledge such as synonyms, abbreviations and acronyms. Widely used and established examples include the Gene Ontology (Ashburner et al, 2000), the Foundational Model of Anatomy (Rosse and Mejino, 2003) and BioPAX (Demir et al, 2010). Ontologies used in conjunction with standard formats provide a rich, flexible, fast-evolving semantic layer on top of the stable and robust standard formats.

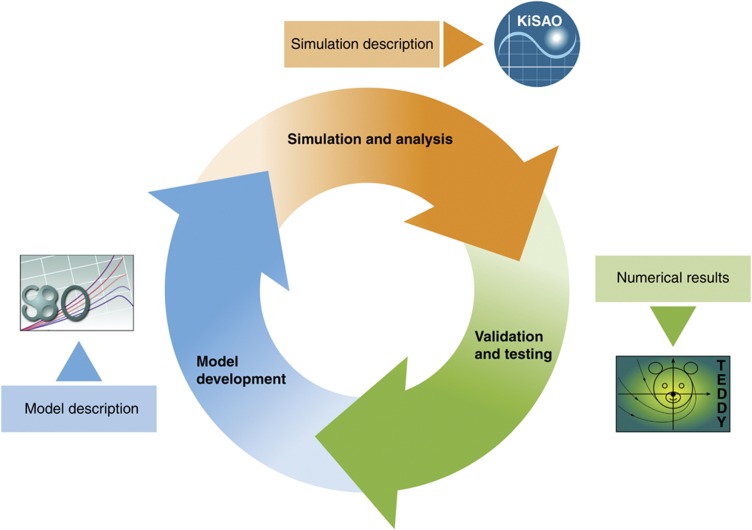
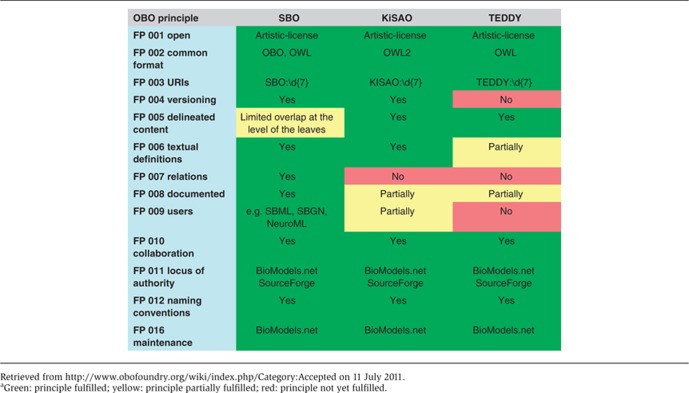
While existing ontologies adequately cover the biology encoded in models, we extend the idea to model-related information. We describe three ontology efforts to standardize the encoding of semantics for models and simulations in systems biology. These publicly available, free consensus ontologies are the Systems Biology Ontology (SBO), the Kinetic Simulation Algorithm Ontology (KiSAO) and the Terminology for the Description of Dynamics (TEDDY). Together, they provide stable and perennial identifiers, referencing machine-readable, software-interpretable, regulated terms. These ontologies define semantics for the aspects of models, which correspond to the three steps of the modeling and simulation process as shown in Figure 1. The efforts we introduce here are at different stages of development and have different levels of community support; SBO is a well-established software tool, KiSAO gathers increasing community support and TEDDY is as yet in its infancy, being primarily a research project. The purpose of our work is to provide practical tools for computational systems biology and as such, the development of the ontologies presented here is largely driven by the needs of the projects using them. However, their focus and coverage is not voluntarily restricted and any community requirements will, in general, be accommodated. All three ontologies aim to fill specific niches in the concept space covered by the Open Biomedical Ontology (OBO) foundry (Smith et al, 2007). The level of compliance with the OBO foundry principles is described for each of the three ontologies in Table I.

Figure 1.

Flowchart depicting the role of SBO, KiSAO and TEDDY in the process of developing and analyzing models.

Table 1. Compliance of the ontologies with the accepted OBO principles^a.

Model structure: SBO

SBO describes the entities used in computational modeling. It provides a set of interrelated concepts that can be used to specify, for instance, the type of component being represented in a model, or the role of those components in systems biology descriptions. Annotating entities with SBO terms allows for unambiguous and explicit understanding of the meaning of these entities. In addition, using SBO terms in different representation formats facilitates mapping between elements of models encoded in those formats. SBO is currently composed of seven vocabulary branches: systems description parameter, participant role, modeling framework, mathematical expression (whose constituent terms refer to the previous three branches), occurring entity representation, physical entity representation and metadata representation (Box 1). The concepts are related through ontological subsumption relationships (subclassing), as well as via mathematical constructs expressed in the Mathematical Markup Language (MathML) Version 2 (Ausbrooks et al, 2003). If an SBO term carries a mathematical expression then each symbol used within that expression has to be defined by another SBO term. This procedure increases the richness of the information obtained when using such terms, and lends itself to further computational processing.

Structure and content of SBO.

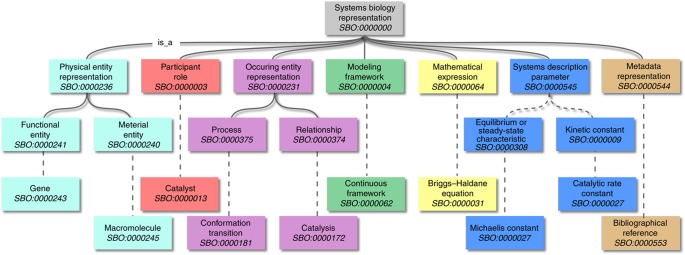SBO terms are presently distributed in seven orthogonal branches described below. See also the graph, where dashed lines indicate that intermediate terms have been omitted.Physical entity representation: Identifies the material or functional entity, which is represented by the model's constituent (ontologists call such entities ‘continuant,’ because they endure over time). Functional entities are those entities that are defined by the function they perform, and include channel, metabolite and transporter entities. The vocabulary for material entities identifies the physical type of an entity, and includes terms such as macromolecule and simple chemical.Participant role: Identifies the role played by an entity in a modeled process or event, and how it will be affected by it. Examples include roles such as catalyst, substrate, competitive inhibitor. Note that this is different from the meaning of the symbol representing the entity in a mathematical expression, which is described in the systems description parameter vocabulary introduced below.Modeling framework: Identifies the formal framework into which a given mathematical expression or model component is assumed to be translated. Some examples include deterministic framework, stochastic framework and logical framework. Such contextual information is crucial for interpreting a model description as intended by the author. This branch of SBO is only meant to state the context in which to interpret a mathematical expression, not to express any constraint on the methods to use when instantiating simulations.Occurring entity representation: Identifies the type of process, event or processual relationships involving physical entities (ontologists call such entities ‘occurrent’ because they unfold over time). The process branch lists types of biochemical reaction, such as cleavage and isomerization. The relationship branch depicts types of control that are exerted on biochemical reactions, such as inhibition and stimulation. When a formula representing such biological events appears in a model, it is frequently difficult to deduce from the formula alone the process that the expression represents; this vocabulary allows the constructs to be annotated in order to make this meaning clear.Systems description parameter: Defines a parameter used in quantitative descriptions of biological processes. This set of terms includes forward unimolecular rate constant, Hill coefficient, Michaelis constant and others, which can be used to identify the role played by a particular constant or variable in a model. In addition to the subclassing links provided as a relationship between SBO terms, a parameter can be defined as a function of other SBO terms through a mathematical construct.Mathematical expression: Classifies a mathematical construct used when modeling a biological interaction. In particular, this SBO vocabulary contains a taxonomy of rate equations. Example terms include mass action kinetics, Henri–Michaelis–Menten kinetics and Hill equation. Each term definition contains a mathematical formula, where symbols are defined using three of the vocabularies above (i.e. modeling framework, participant role and systems description parameter). An illustrated example for term Briggs–Haldane rate law SBO:0000031 is shown below.Metadata representation: Describes the sort of information added to a model description that does not alter the meaning or the behavior of the model. An example for such metadata is a controlled annotation.The branches of SBO are linked to the root by standard is_a relationships (Smith et al, 2005). Terms within each branch are also linked in this way, which means any instance of a child term is also an instance of its parent term. In the cases where a term includes a mathematical expression, each child term represents a more refined version of the mathematical expressions defined by the parent.In addition to its stable identifier and term name, an SBO term also contains a definition, synonyms, a list of relationships to child and parent terms, and optionally can also contain a mathematical formula. Free-text comments may be included by the creator of the term for clarification or reference purposes. A log of the history of the term, including creation and modification details, is also available.[Term]id: SBO:0000031name: Briggs–Haldane rate lawdef: The Briggs–Haldane rate law is a general rate equation that does not require the restriction of equilibrium of Henri–Michaelis–Menten or irreversible reactions of Van Slyke, but instead makes the hypothesis that the complex enzyme–substrate is in quasi-steady-state. Although of the same form as the Henri–Michaelis–Menten equation, it is semantically different since Km now represents a pseudo-equilibrium constant, and is equal to the ratio between the rate of consumption of the complex (sum of dissociation of substrate and generation of product) and the association rate of the enzyme and the substrate.comment: Rate law presented by GE Briggs and JBS Haldane (1925): ‘A note on the kinetics of enzyme action, Biochem J, 19: 338–339.’is_a: SBO:0000028 ! kinetics of unireactant enzymesmathml:

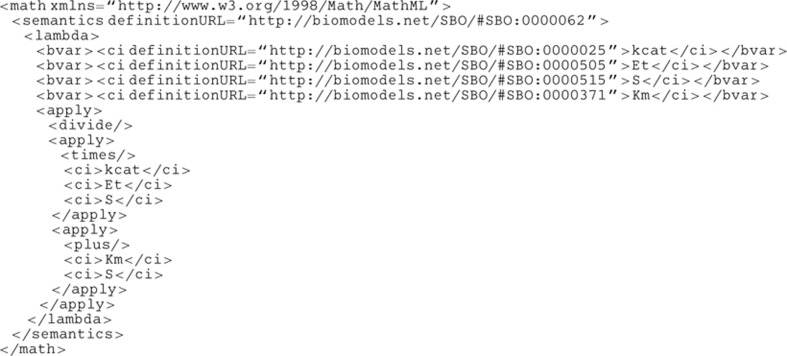SBO is an open ontology, developed by the community of its users. It is accessible in different formats (OBO format; Day-Richter, 2006; Web Ontology Language; W3C OWL working group, 2009; SBO-XML) under the terms of the artistic license (http://www.opensource.org/licenses/artistic-license-2.0). A number of software tools facilitate the development and exchange of the ontology. The resource is accessible programmatically through Web Services, with a Java library available to aid consumption (Li et al, 2010b). SBO, related documentation and associated resources are freely available at http://biomodels.net/sbo/. SBO is also available through the NCBO BioPortal (Noy et al, 2009; ontology 1046, http://purl.bioontology.org/ontology/SBO) and the OBO Foundry.

SBO is developed as a standard ontology, abiding by a set of common development principles, as described by the OBO Foundry (Open Biomedical Ontologies Foundry, http://www.obofoundry.org/wiki/index.php/Category:Accepted). The OBO initiative is an open, community-level collaborative effort to create and apply standardized methodologies in ontology development. Authors of ontologies belonging to this effort are committed to maintain and continually improve their resource, based on community feedback and advancements in their scientific field. SBO itself is an OBO Foundry candidate ontology. The analysis of the compliance level of a candidate ontology with the OBO principles is carried out as part of a formal review, usually by an OBO Foundry coordinator. SBO underwent such a review at the Third Annual OBO Foundry Workshop. The details of the review are publicly available (http://www.ebi.ac.uk/sbo/main/static?page=OBO_status).

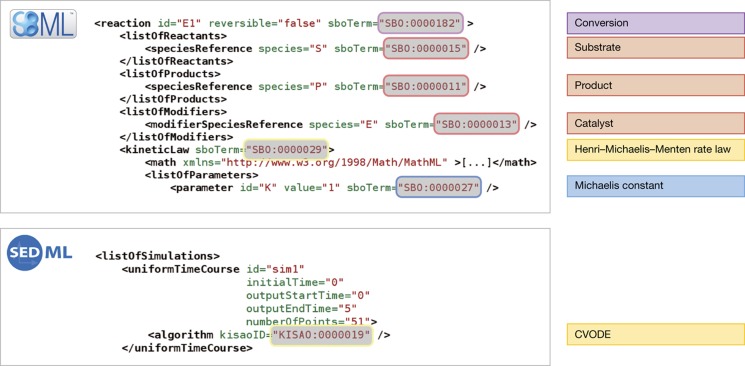
Several representation formats in systems biology have already developed formal ties to SBO. Since Level 2 Version 2, SBML elements carry an optional sboTerm attribute, that precisely defines the meaning of encoded model entities (species, compartments, parameters and other elements) and their relationships (variable assignments, reactions, events, etc.), see for instance Figure 2. Information provided by the value of an sboTerm may facilitate distinguishing between, for example, a simple chemical or a macromolecule. Roles played by those entities in processes, such as being an enzyme or an allosteric activator, can also be specified. Furthermore, a model's mathematical formulae may embody implicit assumptions made by the modeler at the time of the model's creation, such as the use of a steady-state approximation rather than a fast equilibrium assumption for enzymatic reactions. Interpretation of SBO terms by software tools enables, for example, checking the consistency of a rate law, and converting reactions from one reference modeling framework to another (e.g. using continuous or discrete variables). Use of SBO terms in SBML is supported by the software libraries libSBML (Bornstein et al, 2008) and JSBML (Dräger et al, 2011), which provide methods to check for instance whether a term is a subelement of another term, whether a term fits to a certain model component, or to query model elements (for instance, check if myTerm is an ‘enzymatic catalyst’). Tools such as semanticSBML (Krause et al, 2010) rely, among others, on SBO annotations to search for models or to integrate individual models into a larger one. A growing number of applications have been created to facilitate the addition of SBO terms to model descriptions. Web applications such as Saint (Lister et al, 2009) and libraries such as libAnnotationSBML (Swainston and Mendes, 2009) can be used to suggest and add appropriate biological annotations, including SBO terms, to models. Other applications such as SBMLsqueezer (Dräger et al, 2008) help identify SBO terms based on existing model components, to further generate appropriate mathematical relationships on top of biochemical maps. SBO terms can be added to experimental data before inclusion in databases, to facilitate their reuse in systems biology projects (Swainston et al, 2010). SBO terms also enable the generation of a visual representation from other encoding formats, for instance SBML. The Systems Biology Graphical Notation (SBGN; Le Novère et al, 2009) is a set of visual languages to represent models and pathways in systems biology. Each symbol from the list of SBGN glyphs corresponds to an SBO term, which provides its precise definition. Reaching out from the realm of systems biology, support of SBO terms via sboTerm attributes is planned in the forthcoming release of NeuroML v2. The CellML initiative also plans to incorporate support for SBO by providing annotation of components with ‘MIRIAM’ URIs (Le Novère et al, 2005).

Figure 2.

Use of SBO and KiSAO from within SBML and SED-ML. The SBML code on the upper left makes reference to the SBO terms on the upper right. The SED-ML code on the lower left makes reference to the KiSAO term on the lower right.

The use of SBO is not restricted to the development of quantitative models. Using SBO, resources providing quantitative experimental information, such as SABIO Reaction Kinetics (SABIO-RK; Wittig et al, 2006), are able to explicitly state the meaning of measured parameters as well as provide information on how they were calculated. In addition, because SBO terms are organized within a relationship network tree, it is possible to infer the relationships between different parameters, and choose the desired level of granularity (depth in the tree). Another example for the application of SBO terms is the combination of structural constraints imposed by SBML (which element contains or refers to which SBO term, as described in the XML schema and the specification document), with the semantic addition of the ontology as described by Lister et al (2007). This provides a computationally accessible means of model validation, and ultimately a means of semantic data integration for models (Lister et al, 2010). SBO fills a niche not covered by any other ontology. While some existing ontologies have a limited overlapping concept space with SBO, such as the Ontology for Physics in Biology (OPB; Cook et al, 2008), none provides features such as the mathematical formulae corresponding to common biochemical rate laws, expressed in ready-to-reuse MathML. OPB is a high-level ontology with a broader scope than SBO. Subbranches of the latter can be cross-referenced at the level of the leaves of the former.

The current coverage of SBO has largely been dictated by the needs of the systems biology community in the last half decade, specifically biochemical modeling. As the field expands so will SBO. Because of the global collaborations that are currently unfolding, in the forthcoming years, the ontology will have to cover the needs of the computational neurosciences, pharmacometrics and physiology. As other computational modeling fields mature, it is anticipated that the scope of SBO will broaden further to cover all modeling in the life sciences.

As the number of terms in SBO increases, there is a growing need to be able to handle scenarios where the content or concept space of SBO impinges upon that of another ontology. In order to maintain orthogonality (one of the primary goals of the OBO Foundry effort), this problem can be handled in SBO through the use of:

• (a) MIREOT (Courtot et al, 2011), which allows the direct import of terms from an external ontology into a target ontology. This methodology can be used to import single terms, or indeed entire branches, of an external ontology. It allows deferral of the development of some parts of SBO to more appropriately positioned ontology engineers, and is also applicable where the concepts dealt with by the external ontology are thought to be incidental to SBO's main concept space.

• (b) Cross-products, where the intersections refer to terms that are essentially a product of terms originating in different ontologies. This method has been used to extend, for example, the Gene Ontology (Mungall et al, 2010), and may have some utility for SBO.

• (c) Modularization algorithms such as described in Grau et al (2007), which would allow to extract part of an ontology while retaining all inferences from the original resource.

Simulation procedures: KiSAO

SBO adds a semantic layer to the formal representation of models in systems biology, resulting in a more complete definition of both the structure and the meaning of computational models. However, formal representations of models do not always provide information about the procedures to follow to analyze and work with the model. A plethora of different results can be generated using a given model (or set of models), depending on the simulation procedure used, the specific simulation algorithms employed and the transformations applied to the variables. Many simulation procedures, and variations thereof, already exist, and more are being regularly introduced. Not all simulation algorithms lead to valid simulation outcomes when run on a specific model. In addition, many algorithms are available only in a limited number of simulation tools, and not all algorithms are publicly available. To enable the execution of a simulation task, even if the original algorithm is not available, it is important to identify both the algorithm intended to be used, as well as analogous algorithms with similar characteristics, that are able to provide comparable results. KiSAO is an ontology developed to address the problem of describing and structuring existing simulation algorithms in an appropriate way. It enables unambiguous references to existing algorithms from simulation experiment descriptions and retrieving information about similar simulation methods. KiSAO furthermore allows the precise identification of the simulation approaches used in each step of the simulation.

KiSAO presents a hierarchy of algorithms, which are linked to their characteristics and parameters (cf Box 2). The hierarchy is based on derivation and specialization: more general algorithms are ancestors of more specific ones, for instance tau-leaping method is a descendant of accelerated stochastic simulation algorithm and ancestor of trapezoidal tau-leaping method and Poisson tau-leaping method. Since algorithms are linked to the characteristics they possess, and KiSAO is encoded in OWL, one can reason over the ontology. It is also possible to build algorithm classifications based on any of the characteristics or a combination of several ones. Characteristics currently incorporated into KiSAO include the type of variables used for the simulation (discrete or continuous), the spatial description (spatial or not spatial), the system's behavior (deterministic or stochastic), the type of time steps used by the algorithm (fixed or adaptive), the type of solution (approximate or exact) and the type of method (explicit or implicit). The characteristic-based algorithm classification can be used to provide, for example, possible alternatives to the algorithm covered by a single software package. KiSAO is therefore an ontology to define, with the desired level of abstraction, the algorithms suitable for use within a given simulation setup.

Structure and content of KiSAO.

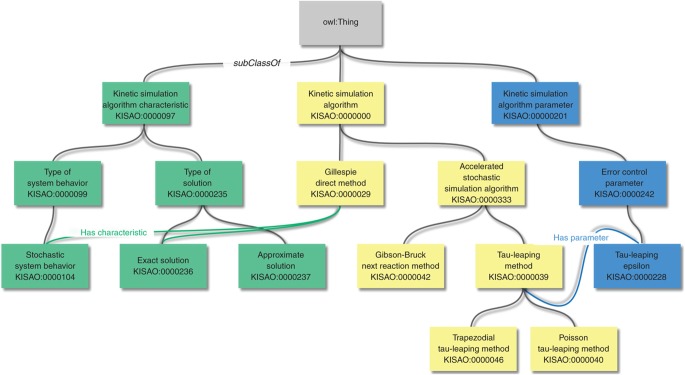KiSAO consists of three main branches, representing simulation algorithms, their characteristics and parameters. The elements of each algorithm branch are linked to characteristic and parameter branches using has characteristic and has parameter relationships accordingly.The algorithm branch itself is hierarchically structured using subClassOf relationships, which denote that the descendant algorithms were derived from, or specify, more general ancestors (i.e. equivalent to the OBO is_a). Every algorithm is annotated with a definition, synonymous names and references to the publication describing it. Some of the algorithms are also annotated with the names of the tools that implement them. In addition to self-contained algorithms, the algorithm branch contains hybrid methods, combining or switching between several algorithms. For example, LSODA automatically selects between non-stiff Adams and stiff BDF algorithms. To represent such interalgorithm dependencies, the complex methods are linked to the algorithms they use by is hybrid of and uses relationships.The characteristic branch of KiSAO classifies both model and numerical kinetic characteristics. Model characteristics include the type of variables used for a simulation—an indication of how the model can be simulated (discrete or continuous), and information on the spatial resolution. Numerical kinetic characteristics include the system's behavior (deterministic or stochastic) as well as the kind of timesteps (fixed or adaptive).The parameter branch describes error, granularity and method switching control parameters, annotated with names, synonyms and descriptions. Information about parameter types is represented using has type relationship, for instance relative tolerance__has type__xsd:double.owl:Class: kisao:KISAO_0000039 owl:Annotations:   rdfs:label ‘tau-leaping method,’   rdfs:comment ‘Approximate acceleration procedure of the Stochastic Simulation Algorithm [urn:miriam:biomodels.kisao:KISAO_0000029] that   divides the time into subintervals and ‘leaps’ from one to another, firing all the reaction events in each subinterval.’,   owl:Annotations:     rdfs:comment ‘Gillespie DT. Approximate accelerated stochastic simulation of chemically reacting systems. The Journal of Chemical Physics,     Vol. 115 (4):1716–1733 (2001). Section V.’   rdfs:seeAlso ‘urn:miriam:doi:10.1063/1.1378322,’   owl:Annotations:     oboInOwl:SynonymType ‘EXACT’   oboInOwl:Synonym ‘tauL,’   isImplementedIn ‘ByoDyn,’   isImplementedIn ‘Cain,’   isImplementedIn ‘SmartCell,’ owl:SubClassOf:  KISAO_0000333 # ‘accelerated stochastic simulation algorithm’ KISAO_0000245 some KISAO_0000237, # ‘has characteristic’ some ‘approximate solution’ KISAO_0000259 exactly 1 KISAO_0000228, # ‘has parameter’ exactly 1 ‘tau-leaping epsilon’

KiSAO is an open ontology, accessible in OWL2 format via the project homepage (http://biomodels.net/kisao/) or through the NCBO BioPortal (ontology 1410, http://purl.bioontology.org/ontology/KiSAO). To facilitate the use of the ontology from within simulation tools and simulation description manipulating software, a free Java library is available (http://biomodels.net/kisao/libkisao.html). The library provides methods to query KiSAO for algorithms, their parameters, characteristics and interrelationships.

The information about algorithm parameters and their types allows simulation tools to check which parameters need to be specified for the chosen simulation procedure (for instance, absolute and relative tolerances) or even to perform an update of the user interface containing parameter input fields on-the-fly.

An important use of KiSAO terms is to improve the description of simulation procedures. To date, users must rely on free-text explanations accompanying a model to understand how best to perform a simulation. These explanations often need to be extracted from publications or database entries. Sometimes a script written for a specific simulation environment is provided with a model. The descriptions are specific for a given simulation software package, orrely upon proprietary algorithms, and are therefore rarely reusable in other software systems. The need for a tool-independent, machine-readable description of a simulation experiment has lead to the recent creation of the Simulation Experiment Description Markup Language (SED-ML; Köhn and Le Novère, 2008). SED-ML permits complete description of a simulation experiment by (a) specifying the models to use, (b) specifying the simulation tasks to perform and (c) defining how to report the results. Each algorithm mentioned in an SED-ML file must be identified by a KiSAO term (Figure 2).

The content of KiSAO is not covered by any other ontology at the moment. The Software Ontology (SWO; http://www.ebi.ac.uk/efo/swo) is a subproject of the Experimental Factor Ontology project to describe software used in bioinformatics. It contains an algorithm branch, but that does not currently cover modeling and simulation. The Biomedical Resource Ontology (Tenenbaum et al, 2011) contains an algorithm branch with a few related terms such as numerical method and PDE solver. However, those terms do not describe the algorithm themselves but the software resources providing access to those algorithms. Other upper ontologies could be used to ‘plug in’ KiSAO. For example, the SemanticScience Integrated Ontology (Chepelev and Dumontier, 2011) incorporates a term algorithm, which is a natural ancestor of kisao:kinetic simulation algorithm. EMBRACE Data and Methods ontology (Lamprecht et al, 2011) is another upper ontology candidate for KiSAO, which contains a branch modeling and simulation. The current emphasis is on structural biology. Plugging KiSAO into a well-crafted upper ontology will facilitate its integration with other OBO ontologies.

KiSAO's current content has been gathered from simulation tools documentation, scientific literature, and key modeling and simulation textbooks. As SED-ML expressiveness increases and it is used within more domains, different types of simulations and analysis will have to be covered. Together with that expanding scope will come representation problems for instance relationships between different types of numerical analyses, possibly very different from kinetic simulation. The description of hybrid algorithms, involving the synchronization of different approaches is also a problem that will become increasingly more important as the tools become more sophisticated.

Numerical results: TEDDY

Given a computational model (semantically enriched with SBO terms) and a ‘recipe’ for producing a simulation experiment (described in part using KiSAO terms), there remains the problem of describing the observed behavior in a systematic and machine-readable manner (Knüpfer et al, 2006). The usual approach nowadays involves free-text explanations accompanying a model, e.g.:

‘Depending on the values of these parameters, at least two types of solutions are possible: the system may converge toward a stable steady state, or the steady state may become unstable, leading to sustained limit-cycle oscillations (Figure 1b and c).’ (Elowitz and Leibler, 2000).

While this form of description is concise and pleasant to read, it is not in a form that can be readily interpreted by software tools. Over the last three decades, the success of bioinformatics applications in molecular biology can be attributed mostly to one type of task: comparing sequences. The equivalent task in computational systems biology is comparing dynamical behaviors, tackling questions such as ‘How do I find a model describing the protein X and displaying a periodic oscillation?’ ‘What behavioral features do all the models have in common?’ ‘Which model displays a behavior matching my experimental data?’ Answering these questions requires a means of formally characterizing the qualitative dynamical behaviors of both models and experimental results. Indeed, numerical results of simulation experiments are structurally similar to numerical results of biological experiments. Aligning both is at the core of model parameterization, validation and testing.

TEDDY is an ontology designed to fulfill this need. It comprises four branches: the classification of the concrete temporal behaviors observed in a simulation (the trajectories), the diversifications and relationships between behaviors, the characteristics of specific behaviors and the functional motifs generating particular types of behaviors (Box 3). TEDDY terms should be sufficient to qualify, with variable levels of detail, the critical features of numerical results obtained from simulations as well as those from experimental measurements. Such a qualification could ultimately be extracted from a formal encoding of the results, such as the SAX representation of time series (Lin et al, 2007).

Structure and content of TEDDY.

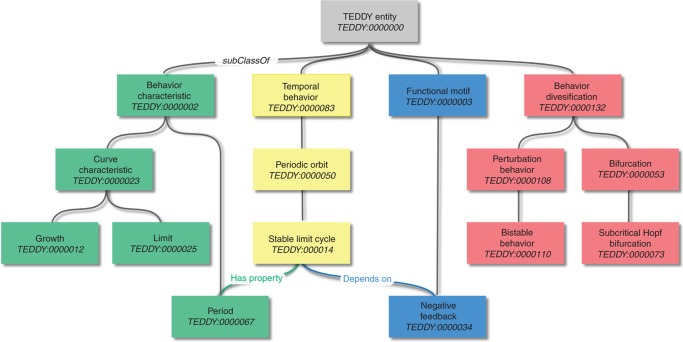TEDDY contains four branches, which are linked through a variety of relationships. Within a branch, most of the terms are linked by subClassOf relationships.Temporal behavior describes the way a dynamical system changes with respect to some aspect of the environment (note that a system here can be a variable, a subset of the model's variables or the complete model). Simple examples are limit cycle and fixed point. More complex examples are heteroclinic orbit and half-stable behavior. Temporal behaviors can be related by two relationships, adjacentTo and convergeTo.Behavior characteristic is a quantitative property that characterizes temporal behaviors. Temporal behaviors can be related to behavior characteristics using hasProperty. For instance, a periodic oscillation is characterized by a property period, a steady-state by a property limit. Behavior diversification describes the way one or several temporal behaviors are modified or related upon interaction with information external to the system considered. For instance, in a Hopf bifurcation, the possible behaviors change by varying a parameter. Behavior diversification can be related to temporal behaviors using the relationships hasPart, hasSubPart, hasOnPart and hasSuperPart. Functional motif describes the structures of a submodel that may generate specific temporal behaviors, such as negative feedback or switch. Functional motifs are related to temporal behaviors using the relationships dependsOn and realizes.owl:Class: TEDDY_0000053 owl:Annotations:   Reference ‘http://www.egwald.com/nonlineardynamics/bifurcations.php,’   Definition ‘A ‘characteristic’ describing a qualitative (topological) change in the orbit structure of a system.’   DisplayName ‘bifurcation’owl:SubClassOf:   TEDDY_0000132, # behavior diversification  TR_0008 min 1 owl:Thing, # hasSuperPart   TR_0006 min 1 owl:Thing # hasSubPart

Because of the complexity of the relationships between dynamical behaviors, their diversifications and characteristics and their functional motifs, TEDDY is encoded in OWL. TEDDY is available from the project home page (http://biomodels.net/teddy/), with a browsable version provided through NCBO BioPortal (ontology 1407, http://purl.bioontology.org/ontology/TEDDY).

TEDDY only provides the vocabulary for naming the critical dynamical features of models, and relating them within one set of numerical results. In order to comprehensively describe the overall dynamics of a model, including different behaviors with regard to different conditions and the relations between them, an additional language framework is needed. This could in turn be used in conjunction with efforts like the Systems Biology Result Markup Language (Dada et al, 2010).

TEDDY is currently a research project, and although much thought was put in its design, its structure is still susceptible to change rapidly. The priority is now to cover the most common dynamical behaviors encountered in biology, and develop procedures to use the ontology in a way to allow reasoning and validation.

Use of ontologies across the modeling and simulation pipeline

Activities in systems biology are often depicted as a modeling–hypothesis–experiment cycle (Kitano, 2002). Prior biological knowledge forms the basis for designing the model, and in turn the modeling activity generates hypotheses that feed the experimental investigation. Within the main cycle, the modeling and simulation process itself is in fact a cycle (Figure 1). The ontologies described in this article support the multiple steps of this pipeline.

Systematically annotating model components with SBO terms helps not only to document the hypothesis behind the choice of a mathematical representation, but also specify how to interpret it. An example is the ‘Michaelis–Menten’ equation, which can be an abstracted view of several alternative chemical reaction schemes (Le Novère et al, 2007). SBO terms can even be used to propose appropriate mathematical constructs, as shown in the software SBMLsqueezer, and fetch the necessary information from databases such as SABIO-RK. Automatic documentation procedures such as SBML2LATEX (Dräger et al, 2009) can directly link controlled vocabulary term identifiers to their unambiguous definitions, which can also be included into a human-readable report on the model structure. Other related ontologies can also be used to enhance the semantics of mathematical description, such as OPB.

The growing complexity of computational models in systems biology makes it more difficult to create models from scratch. In parallel, the increasing number of models available increases the likelihood that a given component has already been published. As such, modelers may decide to reuse portions of existing models as building blocks. Annotation of model components with SBO terms can be used in model search strategies (Schultz et al, 2011). Annotation of existing models with TEDDY terms is also potentially an effective way of discovering components of interest by allowing queries such as ‘Find a model of MAPK cascade that oscillates’ or ‘Find a model of MAPK cascade that can exhibit bistability.’ We anticipate that the same procedure will also make TEDDY extremely useful for synthetic biology, where modularity is seen as a core feature in the construction of novel systems from composable parts. Once appropriate building blocks have been identified, merging them into larger models may be helped by ontologies (Krause et al, 2010). SBO can be used to identify model structures that are equivalent although expressed in different formats, and to identify identical model components to act as interfaces between submodels.

In order to run the simulations, modelers need to know the algorithms applicable to simulate the original building blocks, which is the information provided by KiSAO terms. The ontology also supports the retrieval of similar algorithms available in other simulation toolkits. Note that identifying an algorithm for reuse does not ensure that software claiming to implement the algorithm did so faithfully, without errors or ad hoc hypotheses potentially leading to different results in subsequent simulations when compared with the original.

Finally, numerical results, from both experimental measurements and simulations, can be annotated with TEDDY. This information allows verification based, for instance, on temporal logic. Such procedures can be performed during the parameterization of the model, to analyze the results of simulations or to retrieve models based on the potential results of simulation procedures.

Conclusion

Ontologies are quickly becoming an invaluable tool in computational biology. This is largely due to their expressiveness and their capacity for extension and enrichment without disruption to the end user. Ontologies are the perfect media to encode domain knowledge. Because different tools or approaches can share the same ontologies, they become the de facto glue between heterogeneous kinds of information, providing for a true integrative biology. We showed how using three different ontologies augments models and increases their usability by software tools. Semantically improved models will provide more meaningful and reliable information, ultimately resulting in a richer pool of integrated data. However, even the best ontology is only a worthy effort until used. Encouraging a widespread use of SBO, KiSAO and TEDDY, as well as any future similar efforts is and will remain a challenge. With increased adoption, we expect to reach the tipping point. When, due to the amount of annotated models available, the benefits will outweight the effort required for curation. The existence of coordinated efforts such as COMBINE (http://co.mbine.org/) may also help.