A Pattern Mining Approach for Classifying Multivariate Temporal Data

Abstract

We study the problem of learning classification models from complex multivariate temporal data encountered in electronic health record systems. The challenge is to define a good set of features that are able to represent well the temporal aspect of the data. Our method relies on temporal abstractions and temporal pattern mining to extract the classification features. Temporal pattern mining usually returns a large number of temporal patterns, most of which may be irrelevant to the classification task. To address this problem, we present the minimal predictive temporal patterns framework to generate a small set of predictive and non-spurious patterns. We apply our approach to the real-world clinical task of predicting patients who are at risk of developing heparin induced thrombocytopenia. The results demonstrate the benefit of our approach in learning accurate classifiers, which is a key step for developing intelligent clinical monitoring systems.

I. Introduction

Advances in data collection and data storage technologies have led to the emergence of complex multivariate temporal datasets, where data instances are traces of complex behaviors characterized by multiple time series. Such data appear in a wide variety of domains, such as health care, sensor measurements, intrusion detection, motion capture, environmental monitoring and many more. Designing algorithms capable of learning from such complex data is one of the most challenging topics of data mining research.

This work primarily focuses on developing methods for analyzing electronic health records (EHRs). Each record consists of multiple time series of clinical variables collected for a specific patient, such as laboratory tests, medication orders and physiological parameters. The record may also provide information about the patient’s diseases, surgical interventions and their outcomes. Learning classification models from this data is extremely useful for patient monitoring, outcome prediction and decision support.

The task of temporal modeling in EHR data is very challenging mostly because the time series for clinical variables are acquired asynchronously, that is, they are measured at different time moments and they are irregularly sampled in time. Hence, most time series feature extraction techniques [1], [2], [3] cannot be applied on this data.

The key step for analyzing EHR data is to define a language that can adequately represent the temporal dimension of the data. Our approach uses temporal abstractions [4] and temporal logic [5] in order to define patterns able to describe temporal interactions among multiple time series. For example, this allows us to define complex temporal patterns like “the administration of heparin precedes a decreasing trend in platelet counts”.

The next step is to automatically mine temporal patterns that are important to describe and predict the studied medical condition. Our approach adopts the frequent pattern mining paradigm. However, we are not interested in finding all frequent temporal patterns, but only those that are important for the classification task. To address this, we present the minimal predictive temporal patterns (MPTP) framework, which relies on a statistical test to effectively filter out non-predictive and spurious temporal patterns.

We demonstrate the usefulness of our framework on a real-world clinical task of predicting patients who are at risk of developing heparin induced thrombocytopenia (HIT), a life threatening condition that may develop in patients treated with heparin. We show that incorporating the temporal dimension is crucial for this task. In addition, we show that the MPTP framework provides useful features for classification and can be beneficial for knowledge discovery because it returns in a small set of discriminative temporal patterns that are easy to analyze by a domain expert.

Our main contributions are summarized as follows:

• We propose a novel temporal pattern mining approach for classifying complex EHR data.

• We extend our minimal predictive patterns framework [6] to the temporal domain.

• We present an efficient mining algorithm that integrates pattern selection and frequent pattern mining.

II. Related Research

Our work relies on temporal abstractions [4] as a preprocessing step to represent the numeric time series data in an interval-based format. The problem of mining temporal patterns from time interval data is a relatively young research field. Most existing approaches [7], [8], [9], [10], [11], [12], [13] extend sequential pattern mining methods [14], [15] to handle time interval data¹. All of these related methods have been mainly applied in an unsupervised fashion to mine temporal association rules. Our work is different because we are mostly interested in mining predictive temporal patterns and using them as features in a classification model.

III. Methodology

Let D = {< x_i, y_i >} be a dataset such that x_i ∈ X is the electronic health record for patient i up to time t_i, and y_i ∈ Y is a class label associated with a medical condition at time t_i. Our objective is to learn a function f: X → Y that can predict accurately the class labels for future patients. Learning f directly from X is very difficult because the instances consist of multiple irregularly sampled time series of different length. Therefore, we want to learn a space transformation ψ: X → X′ that maps each instance x_i to a fixed-size feature vector ${\mathit{x}}_{\mathit{i}}^{\prime }$ that preserves the predictive temporal characteristics of x_i as much as possible.

We propose using the following steps to obtain ψ:

1. Convert the time series variables into a higher level description using temporal abstractions.

2. Mine the minimal predictive temporal patterns Ω.

3. Transform each EHR instance x_i to a binary vector ${\mathit{x}}_{\mathit{i}}^{\prime }$ of size equal to |Ω|, where every feature in ${\mathit{x}}_{\mathit{i}}^{\prime }$ corresponds to a specific temporal pattern P ∈ Ω and its value is 1 if x_i contains P; and 0 otherwise.

After applying this transformation, we can use a standard machine learning method (e.g., SVM, decision tree, naïve Bayes, or logistic regression) on { $<{\mathit{x}}_{\mathit{i}}^{\prime },y_i>$} to learn function f.

A. Temporal Abstraction

The goal of temporal abstraction [4] is to transform the time series for all clinical variables to a high-level qualitative form. More specifically, each clinical variable (e.g., series of white blood cell counts) is transformed into an interval-based representation 〈v₁[b₁, e₁], …, v_n[b_n, e_n]〉, where v_i ∈ Σ is an abstraction that holds from time b_i to time e_i and Σ is the abstraction alphabet that represents a finite set of all permitted abstractions.

The most common clinical variables in EHR data are: medication administrations and laboratory results.

Medication variables are usually represented in an interval-based format and they specify the time interval during which a patient was taking a specific medication. For these variables, we simply use abstractions that indicate whether the patient is on the medication: Σ = {ON, OFF}.

Lab variables are usually numerical time series that specify the patient’s laboratory results over time. For these variables, we use two types of temporal abstractions:

• Trend abstraction uses the following abstractions: Decreasing (D), Steady (S) and Increasing (I), i.e., Σ = {D, S, I}. In our work, we segment the lab series using the sliding window method [16], which keeps expanding each segment until its interpolation error exceeds some error bound. The abstractions are determined from the slopes of the fitted segments. For more information about trend segmentation, see [16].

• Value abstraction uses the following abstractions: Very Low (VL), low (L), Normal (N), High (H) and Very High (VH), i.e., Σ = {VL, L, N, H, VH}. We use the 5th, 25th, 75th and 95th percentiles on the lab values to define these 5 states: a value below the 5th percentile is very low (VL), a value between the 5th and 25th percentiles is low (L), and so on.

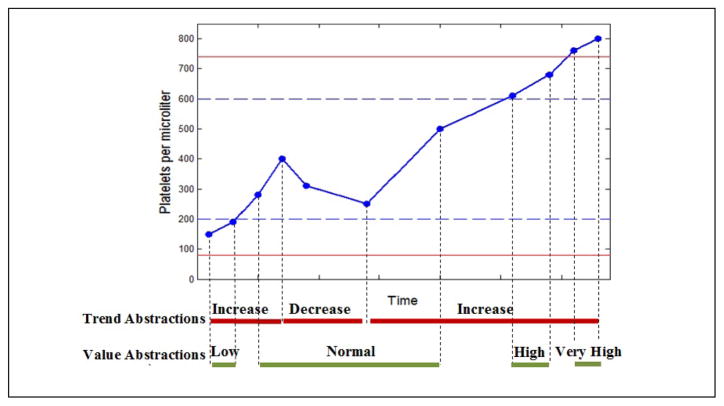
Figure 1 shows the trend and value abstractions on a time series of platelet counts of a patient.

Figure 1.

An example illustrating the trend and value abstractions. The dashed lines represent the 25th and 75th percentiles and the solid lines represent the 5th and 95th percentiles.

State Sequence Representation

We define a state to be an abstraction for a specific variable. For example, state E: V_i = D represents a decreasing trend in the values of temporal variable V_i. We also use the shorthand notation D_i to denote this state, where the subscript indicates that D is abstracted from the i^th variable. We define a state interval to be a state that holds during an interval, that is, state interval (E, b_i, e_i) is a realization of state E in a data instance and has specific start time (b_i) and end time (e_i).

Definition 1

A state sequence is a series of state intervals, where the state intervals are ordered according to their start times:

$$\langle (E_1,b_1,e_1),(E_2,b_2,e_2),\dots ,(E_l,b_l,e_l)\rangle :b_i\le e_i\wedge b_i\le b_{i+1}$$

Note that we do not require e_i to be less than b_i+1 because the states are obtained from multiple temporal variables and their intervals may overlap.

After abstracting all temporal variables, we represent every instance (i.e., patient) in the database D as a state sequence. As a result, D can be viewed as a set of state sequences. We will use the terms instance and state sequence interchangeably hereafter.

B. Temporal Relations

Allen’s temporal logic [5] describes the relations for any pair of state intervals using 13 possible relations. However, it suffices to use the following 7 relations: before, meets, overlaps, is-finished-by, contains, starts and equals because the other relations are simply their inverses. Allen’s relations have been used by the majority of research on mining time interval data ([7], [8], [11], [12]).

Most of Allen’s relations require equality of one or two of the intervals end points. That is, there is only a slight difference between overlaps, is-finished-by, contains, starts and equals relations. These relations are too specific for pattern discovery when the time information in the data is noisy (not precise) [9], which is the case in EHR data.

Therefore we opt to use only two temporal relations, before (b) and co-occurs (c), which we define as follows: Given two state intervals E_i and E_j:

• (E_i, b_i, e_i) before (E_j, b_j, e_j) if e_i < b_j

• (E_i, b_i, e_i) co-occurs with (E_j, b_j, e_j), if b_i ≤ b_j ≤ e_i, i.e. E_i starts before E_j and there is a nonempty time period where both E_i and E_j occur.

C. Temporal Patterns

In order to obtain temporal descriptions of the data, basic states are combined using temporal relations to form temporal patterns.

Definition 2

A temporal pattern is defined as P = (〈S₁, …, S_k〉, R) where S_i is the i^th state of the pattern and R is an upper triangular matrix that defines the temporal relations between each state and all of its following states:

$$R_{i,j}=S_{i}r{S}_j:i\in \{1,\dots ,k-1\}\wedge j\in \{i+1,\dots ,k\}\wedge r\in \{b,c\}$$

The size of pattern P is the number of states it contains. If size(P)=k, we say that P is a k-pattern. Hence, a single state is a 1-pattern (a singleton). We also denote the space of all temporal patterns of arbitrary size by TP.

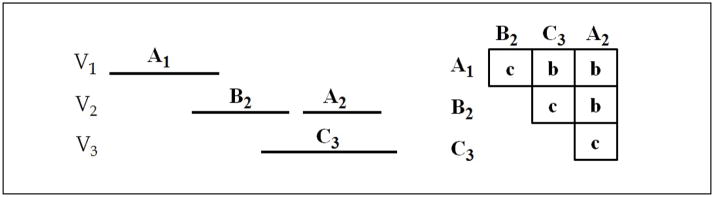
Figure 2 graphically illustrates a 4-pattern with states 〈A₁, B₂, C₃, A₂〉, where the states are abstractions of temporal variables V₁, V₂ and V₃ using abstraction alphabet Σ = {A, B, C}. The half matrix on the right represents the temporal relations between every state and the states that follow it.

Figure 2.

A temporal pattern with states 〈A₁, B₂, C₃, A₂〉 and temporal relations R_1,2 = c, R_1,3 = b, R_1,4 = b, R_2,3 = c, R_2,4 = b and R_3,4 = c.

Interesting patterns are usually limited in their temporal extensions, i.e., it would not be interesting to use the before relation to relate states that are temporally very far away from each other. Therefore, the definition of temporal patterns usually comes with a specification of a window size that defines the maximum pattern duration.

In our task, we are interested in detecting events (medical conditions) that may happen at a specific time t_i during patient x_i hospitalization period. Hence, recent measurements of the clinical variables of x_i (close to t_i) are usually more predictive than distant measurements [17]. The approach taken in this paper is to define windows of fixed widths that are aligned with t_i for every x_i and only mine temporal patterns that can be observed inside these windows.

Definition 3

Let T = 〈(E₁, b₁, e₁), …, (E_l, b_l, e_l)〉 be a state sequence that is visible within a specific window. We say that pattern P = (〈S₁, …, S_k〉, R) occurs in T (or that P covers T), denoted as P ∈ T, if there is an injective mapping π from the states of P to the state intervals of T such that:

$$(S_i=E_{\pi (i)})\wedge ((E_{\pi (i)},b_{\pi (i)},e_{\pi (i)})R_{i,j}(E_{\pi (j)},b_{\pi (j)},e_{\pi (j)}))\forall i\in \{1,\dots ,K\}\wedge j\in \{i+1,\dots ,k\}$$

Notice that checking the existence of a temporal pattern in a state sequence requires: (1) matching all k states of the patterns and (2) checking that all k(k − 1)/2 temporal relations are satisfied.

Definition 4

P = (〈S₁, …, S_k1〉, R) is a subpattern of $P^{\prime }=(\langle S_1^{\prime },\dots ,S_{k_2}^{\prime }\rangle ,R^{\prime })$, denoted as P ⊆ P′, if there is an injective mapping π from the states of P to the states of P′ such that:

$$S_i=S_{\pi (i)}^{\prime }\wedge R_{i,j}=R_{\pi (i),\pi (j)}^{\prime }\forall i\in \{1,\dots ,k_1\}\wedge j\in \{i+1,\dots ,k_1\}$$

Definition 5

The support of temporal pattern P in database D is the number of instances that contain P:

$$\mathit{sup}(P,D)=\mid \{T_i:T_i\in D\wedge P\in T_i\}\mid$$

Note that the support definition satisfies the Apriori property [18]:

$$\forall P,P^{\prime }\in TP\text{if}P\subseteq P^{\prime }\Rightarrow \mathit{sup}(P,D)\ge \mathit{sup}(P^{\prime },D)$$

We define a rule to be an implication of the form P ⇒ y, where P is a temporal pattern and y ∈ Y is a specific value of the target class variable. We say that rule P ⇒ y is a subrule of rule P′ ⇒ y′ if P ⊆ P′ and y = y′.

Definition 6

The confidence of rule P ⇒ y is the proportion of instances from class y in all instances covered by P:

$$\text{conf}(P\Rightarrow y)=\frac{\mathit{sup}(P,D_y)}{\mathit{sup}(P,D)}$$

where D_y denotes all instances in D that belong to class y.

The confidence of rule R: P ⇒ y is the maximum likelihood estimation of the probability that an instance covered by P belongs to class y. If R is a predictive rule, then its confidence should be larger than the prior probability of y in the data.

D. Mining Frequent Temporal Patterns

In this section, we present the algorithm for mining frequent temporal patterns. We chose to utilize the class information and mine frequent patterns from each class separately. The algorithm takes D_y: the state sequences from class y and min-sup_y: a user specified minimum support threshold. It outputs all frequent temporal patterns in D_y:

$$\{P\in TP:\mathit{sup}(P,D_y)\ge \mathit{min}-{\mathit{sup}}_y\}$$

The mining algorithm performs an Apriori-like level-wise search [18]. It first scans the database to find all frequent 1-patterns. Then, it performs the following two phases to obtain the frequent k-patterns:

1. The candidate generation phase: To generate candidate k-patterns using the frequent (k−1)-patterns.

2. The counting phase: To count the generated candidates and remove the infrequent ones.

In the following, we discuss how to improve the efficiency of each phase.

1) Candidate Generation

We generate a candidate (k+1)-pattern by adding a new state (1-pattern) to the end of a frequent k-pattern. Let us assume that we are extending pattern P = (〈S₁, …, S_k〉, R) with state S_k+1 in order to generate candidate P′ = (〈S₁, …, S_k, S_k+1〉, R′). First, we set $R_{i,j}^{\prime }=R_{i,j}$ for i ∈ {1, …, k − 1} ∧ j ∈ {i + 1, …, k} so that P ⊂ P′. In order to fully define P′, we still need to specify the temporal relations between states S₁, …, S_k and the new state S_k+1, i.e., we should define $R_{i,k+1}^{\prime }$ for i ∈ {1, …, k}. Since we have two possible temporal relations (before and co-occurs), there are 2^k possible ways to specify the missing relations. That is, 2^k possible candidates can be generated when adding state S_k+1 to pattern P. However, many of these candidates are not necessary to generate because they are incoherent, as we see in the following.

Definition 7

A temporal pattern P is incoherent if there does not exist any valid state sequence that contains P.

We introduce the following two propositions to avoid generating incoherent candidates when extending frequent pattern P = (〈S₁, …, S_k〉, R) with state S_k+1.

Proposition 1

P′ = (〈S₁, …, S_k, S_k+1〉, R′) is incoherent if $R_{i,k+1}^{\prime }=c$ and S_i and S_k+1 are extracted from the same variable.

Proposition 2

P′ = (〈S₁, …, S_k, S_k+1〉, R′) is incoherent if $R_{i,k+1}^{\prime }=c\wedge \exists j>i:R_{i,j}^{\prime }=b$.

We omit the proofs of these simple propositions due to space limitation.

Example 1

Assume we want to extend pattern P = (〈A₁, B₂, C₃, A₂〉, R) in Figure 2 with state B₃ to generate candidates of the form (〈A₁, B₂, C₃, A₂, B₃〉, R′). The relation between A₂ and the new state B₃ can be either before or co-occurs: $R_{4,5}^{\prime }=b$ or $R_{4,5}^{\prime }=c$. However, according to proposition 1, C₃ and B₃ cannot co-occur because they both belong to temporal variable $V_3(R_{3,5}^{\prime }\ne c)$. Also, according to proposition 2, B₂ cannot co-occur with $B_3(R_{2,5}^{\prime }\ne c)$ because B₂ is before $A_2(R_{2,4}^{\prime }=b)$ and A₂ should start before B₃. Similarly, A₁ cannot co-occur with $B_3(R_{1,5}^{\prime }\ne c)$ because A₁ is before $A_2(R_{1,4}^{\prime }=b)$. Therefore, instead of naively generating all 2⁴ = 16 candidates, we generate only 2 candidates.

2) Speeding up the Counting Phase

Even by eliminating incoherent patterns, the mining algorithm is still computationally expensive because for every generated candidate, we need to scan the entire database in the counting phase to check whether or not it is a frequent pattern. So can we omit portions of the data that are guaranteed not to contain the candidate we are counting? The proposed solution is inspired by [19] that developed the vertical data format for itemset mining and later expended it to sequential pattern mining [15].

The idea is to associate every frequent pattern P with a list of identifiers for all state sequences that contain P:

$$P.id-\mathit{list}=\langle i_1,i_2,\dots ,i_n\rangle :T_{i_j}\in D_y\wedge P\in T_{i_j}$$

Clearly, sup(P; D_y) = |P.id-list|.

Definition 8

The potential id-list (pid-list) of pattern P is the intersection of the id-lists of its subpatterns:

$$P.\mathit{pid}-\mathit{list}={\cap }_{S\subset P}S.id-\mathit{list}$$

Proposition 3

∀P ∈ TP: P.id-list ⊆ P.pid-list

Proof

Assume T_i is a state sequence in the database such that P ∈ T_i. By definition, i ∈ P.id-list. We also know that T_i must contain all subpatterns of P according to the Apriori property: ∀S ⊂ P: S ∈ T_i. Therefore, ∀S ⊂ P: i ∈ S.id-list ⇒ i ∈ ∩_S⊂P S.id-list = P.pid-list.

Putting it all together, we compute the id-lists in the counting phase (based on the true matches) and the pid-lists in the candidate generation phase. The key idea is that when we count a candidate, we only need to check the state sequences in its pid-list because:

$$i\notin P.\mathit{pid}-\mathit{list}\Rightarrow i\notin P.id-\mathit{list}\Rightarrow P\notin T_i$$

This offers a lot of computational savings since the pid-lists get smaller as the size of the patterns increases, making the counting phase much faster.

Figure 3 shows the candidate generation algorithm. After generating coherent candidates (line 3), we apply the standard Apriori pruning [18], which states that for a (k+1)-candidate to be frequent, all of its k-subpatterns must be frequent as well (lines 5 and 6). In our implementation, we hash all patterns in F_k, so that searching the subpatterns in F_k requires only k operations. Now that we found all k-subpatterns, we simply intersect their id-lists to compute the pid-list of the candidate (line 7). Note that the cost of the intersection is linear because the id-lists are always sorted according to the order of the instances in the database. Line 8 is used to mine the minimal predictive temporal patterns and will be explained later in Section III-F. Finally, line 9 applies an additional pruning to remove candidates that are guaranteed not to be frequent according to the following implication of proposition 3:

$$\mid P.\mathit{pid}-\mathit{list}\mid <\mathit{min}-{\mathit{sup}}_y\Rightarrow \mathit{sup}(P,D_y)<\mathit{min}-{\mathit{sup}}_y$$

Figure 3.

A high-level description of candidate generation. The algorithm takes as input the frequent k-patterns (F_k) and returns the candidate (k+1)-patterns (Cand) together with their pid-lists.

E. Minimal Predictive Temporal Patterns

Applying frequent pattern mining on data usually results in a very large number of temporal patterns, most of which may be unimportant for the classification task. Using all of these patterns as features can hurt the classification performance due to the curse of dimensionality. Therefore, it is crucial to develop effective methods to select a subset of patterns that are likely to improve the classification performance.

The task of pattern selection is more challenging than the standard task of feature selection due to the nested structure of patterns: if P is frequent, all instances covered by P are also covered by all of its subpatterns, which are also in the result of the frequent mining method (the Apriori property). This nested structure causes the problem of spurious patterns, which we will define and then explain using an example.

Definition 9

A temporal pattern P is a spurious pattern if P is predictive when evaluated by itself, but it is redundant given one of its subpatterns.

Example 2

Assume that having very low platelet counts (PLT) is an important risk factor for heparin induced thrombocytopenia (HIT). If we denote pattern PLT=VL by P, we expect conf (P ⇒ HIT) to be much higher than the HIT prior. Now assume that there is no causal relation between the patient’s potassium (K) level and his risk of HIT, so a pattern like K=N (normal potassium) does not change our belief about the presence of HIT. If we combine these two patterns, for example P′:K=N before PLT=VL, we expect that conf (P′ ⇒ HIT) ≈ conf (P ⇒HIT). The intuition behind this is that the instances covered by P′ can be seen as a random sub-sample of the instances covered by P. So if the proportion of HIT cases in P is relatively high, we expect the proportion of HIT cases in P′ to be high as well.

The problem is that if we examine P′ by itself, we may falsely conclude that it is a good predictor of HIT, where in fact this happens only because P′ contains the real predictive pattern P. Having spurious patterns in the mining results is undesirable for classification because it leads to many redundant and highly correlated features. It is also undesirable for knowledge discovery because spurious patterns can easily overwhelm the domain expert and prevent him/her from understanding the real causalities in the data.

Having discussed these problems, we propose the minimal predictive temporal patterns framework for selecting predictive and non-spurious temporal patterns for classification.

Definition 10

A frequent temporal pattern P is a minimal predictive temporal pattern (MPTP) with respect to class y if rule P ⇒ y is significantly more predictive than all of its subrules.

In order to complete the definition, we define the MPTP statistical significance test and explain how to address the issue of multiple hypothesis testing.

The MPTP Significance Test

Assume we want to check whether temporal pattern P is an MPTP with respect to class y. Suppose that P covers N instances in the entire database D and covers N_y instances in D_y (the instances from class y). Let best_conf be the highest confidence achieved by any subrule of P ⇒ y:

$$\mathit{best}\_\mathit{conf}=\underset{s\subset P}{max}(\mathit{conf}(S\Rightarrow y))$$

The null hypothesis presumes that N_y is generated from N according to the binomial distribution with probability best_conf. We perform a one sided statistical test and calculate its p-value:

$$p-\mathit{value}={Pr}_{\mathit{binom}}(x\ge N_y;N,\mathit{best}\_\mathit{conf})$$

This p-value is the probability of observing N_y or more instances of class y out of the N instances covered by P if the true underlying probability is best_conf. If the p-value is smaller than a significance level α (e.g., p-value < 0.01), then this hypothesis is very unlikely and we conclude that P ⇒ y is significantly more predictive than all its subrules, hence P is an MPTP.

This test can filter out many spurious patterns. Going back to example 2, we do not expect spurious pattern K=N before PLT=VL to be an MPTP because it does not predict HIT significantly better that the real pattern: PLT=VL.

Correcting for Multiple Hypothesis Testing

When testing the significance of multiple patterns in parallel, it is possible that some patterns will pass the significance test just by chance (false positives). This is a concern for all techniques that rely on statistical tests. In order to tackle this problem, the significance level should be adjusted by the number of tests performed during the mining. In this work, we adopt the FDR (False Discovery Rate) technique [20], which directly controls the expected proportion of false discoveries in the result (the type I error). FDR is a simple method for estimating the rejection region so that the false discovery rate is on average less than α. It takes as input sorted p-values: p₍₁₎ ≤ p₍₂₎ ≤ … ≤ p_(m) and estimates k̂ that tells us that hypothesis associated with p₍₁₎, p₍₂₎, …, p_(k̂) are significant. We apply FDR to post-process all potential MPTP (patterns satisfying the MPTP significance test) and select the ones that satisfy the FDR criteria.

F. Mining Minimal Predictive Temporal Patterns

The algorithm in Section III-D describes how to mine all frequent temporal patterns from D_y. In this section, we explain how to mine the MPTP set from D_y. To do this, the algorithm requires another input: D_¬y, which is the instances in the database that do not belong to class y: D_¬y = D − D_y.

The process of testing whether temporal pattern P is an MPTP is not trivial because the definition demands checking the pattern against all its subpatterns. That is, for a k-pattern, we need to compare it with all of its 2^k − 1 subpatterns!

In order to avoid this inefficiency, we associate every frequent pattern P with two values:

1. P.mcs (Maximum Confidence of Subpatterns) is the maximum confidence of all proper subpatterns of P:

   $$P.\mathit{mcs}=\underset{S\subset P}{max}(\mathit{conf}(S\Rightarrow y))$$ (1)
2. P.mc (Maximum Confidence) is the maximum confidence of P and all of its proper subpatterns:

   $$P.mc=max(\mathit{conf}(P\Rightarrow y),P.\mathit{mcs})$$ (2)

Note that P.mcs is all we needed to perform the MPTP significance test for pattern P. However, we need a way to compute P.mcs without having to access all subpatterns. The idea is that we can reexpressed P.mcs for any k-pattern using the maximum confidence values of its (k−1)-subpatterns:

$$P.\mathit{mcs}=\underset{S\subset P}{max}(S.mc):\mathit{size}(S)=k-1$$ (3)

This leads to a simple dynamic programming type of algorithm for computing these two values. Initially, for every frequent 1-patterns P, we set P.mcs to be the prior probability of class y in the data and compute P.mc using expression (2). In the candidate generation phase, we compute mcs of a new candidate k-pattern using the mc values of its (k−1)-subpatterns according to expression (3) (Figure 3: line 8). Then, we compute the mc values for the frequent k-patterns, and repeat the process for the next levels.

1) Lossless Pruning

The MPTP significance test can help us to reduce the search space. The idea is to prune pattern P if we guarantee that none of P’s superpatterns will be an MPTP. However, since the algorithm is applied in a level-wise fashion, we do not know the superpatterns of P. To overcome this difficulty, we define the optimal superpattern of P, denoted as P^*, to be a hypothetical pattern that covers all and only the instances of class y in P, i.e., sup(P^*, D_y) = sup(P, D_y) and sup(P^*, D_¬y) = 0. Clearly, P cannot generate any superpattern that predicts y better than P^*. Now, we prune P if P^* is not an MPTP with respect to P.mc (the highest confidence achieved by P and its subpatterns). Note that this pruning is anti-monotonic and is guaranteed not to miss any MPTP.

Example 3

Assume that the support of pattern P in D_y is 10 and that P.mc = 0.75. We can safely prune P because Pr_binom(x ≥ 10; 10, 0.75) = 0.056, which is not significant at significance level α = 0.01.

2) Lossy Pruning

This section describes a lossy pruning technique that speeds up the mining at the risk of missing some MPTPs. We refer to the patterns mined with the lossy pruning as A-MPTP (Approximated MPTP). The idea is to prune P if it does not show any sign of being more predictive than its subpatterns. To do this, we simply perform the MPTP significance test, but at a higher significance level α₂ than the significance level used in the original MPTP significance test: α₂ ∈ [α, 1]. If P does not satisfy the MPTP test with respect to α₂, we prune P. Note that α₂ is a parameter that controls the tradeoff between efficiency and completeness. So if we set α₂ = 1, we do not perform any lossy pruning. On the other end of the spectrum, if we set α₂ = α, we prune every non-MPTP pattern, which leads to very aggressive pruning!

IV. Experimental Evaluation

In this section, we test and present results of our temporal pattern mining approach on the problem of predicting patients who are at risk of developing heparin induced thrombocytopenia (HIT) [21]. HIT is a prothrombotic disorder induced by heparin exposure with subsequent thrombocytopenia (low platelets in the blood) and associated thrombosis (blood clot). It is a life-threatening condition if it is not detected and managed properly. Hence, it is extremely important to detect the onset of the condition.

A. Dataset

We use data acquired from a database that contains 4,281 electronic health records of post cardiac surgical patients [22]. From this database, we selected 220 instances of patients who were considered by physicians to be at risk of HIT and 220 instances of patients without the risk of HIT. The patients at risk of HIT were selected using information about the heparin platelet factor 4 antibody (HPF4) test orders. The HPF4 test is ordered for a patient when a physician suspects the patient is developing HIT and hence it is a good surrogate of the HIT-risk label. The HIT-risk instances included clinical information up to the time HFP4 was ordered. The negative (no HIT-risk) instances were selected randomly from the remaining patients. These instances included clinical information up to some randomly selected time.

For every instance, we consider the following 5 clinical variables: platelet counts (PLT), activated partial thromboplastin time (APTT), white blood cell counts (WBC), hemoglobin (Hgb) and heparin orders. PLT, APTT, WBC and Hgb are numerical time series and we segment them using trend and value abstractions (Section III-A). Heparin orders are already in an interval-based format that specifies the time period the patient was taking heparin. We set the window size of temporal patterns to be the last 5 days of every patient record.

B. Classification Performance

In this section, we test the ability of our methods to represent and capture temporal patterns important for predicting HIT. We compare our methods, MPTP and its approximate version A-MPTP, to the following baselines:

1. Last_values: The features are the most recent value of each clinical variable.

2. Last_abs: The features are the most recent abstractions of the clinical variables.

3. TP_all: The features are all frequent temporal patterns.

4. TP_IG: The features are the top 100 frequent temporal patterns according to information gain (IG).

5. TP_chi: The features are the frequent temporal patterns that are statistically significant according to the χ² test with significance level α = 0.01. This method applies FDR to correct for multiple hypothesis testing.

The first two methods (1–2) are atemporal and do not rely on any temporal ordering when constructing their features. On the other hand, methods 3–5 use temporal patterns that are built using temporal abstractions and temporal logic. However, unlike MPTP and A-MPTP, they select the patterns using standard feature selection methods without considering the nested structure of the patterns.

We set the significance level α = 0.01 for MPTP and A-MPTP, and we set the pruning parameter α₂ = 0.25 for A-MPTP (see Section III-F2). We set the minimum support (min-sup) to be 10% of the number of instances in the class for all compared methods.

We judged the quality of the different feature representations in terms of their induced classification performance. More specifically, we use the features extracted by each method to build an SVM classifier and evaluate its performance using the classification accuracy and the area under the ROC curve (AUC).

Table I shows the classification accuracy and the AUC for each of the methods. All classification results are reported using averages obtained via 10-folds cross validation.

Table I.

The classification accuracy (%) and the area under the ROC curve (%) for different feature extraction methods.

Method	Accuracy	AUC
Last_values	78.41	89.57
Last_abs	80.23	88.43
TP_all	80.68	91.47
TP_IG	82.50	92.11
TP_chi	81.36	90.99
MPTP	85.68	94.42
A-MPTP	85.45	95.03

The results show that temporal features generated using temporal abstractions and temporal logic are beneficial for predicting HIT, since they outperformed methods based on atemporal features. The results also show that the MPTP and A-MPTP are the best performing methods. Note that although the temporal patterns generated by TP_all, TP_IG, and TP_chi subsume or overlap MPTP and A-MPTP patterns, they also include many irrelevant and spurious patterns that negatively effect their classification performance.

C. Knowledge Discovery

In order for a pattern mining method to be useful for knowledge discovery, the method should provide the user with a small set of understandable patterns that are able to capture the important information in the data.

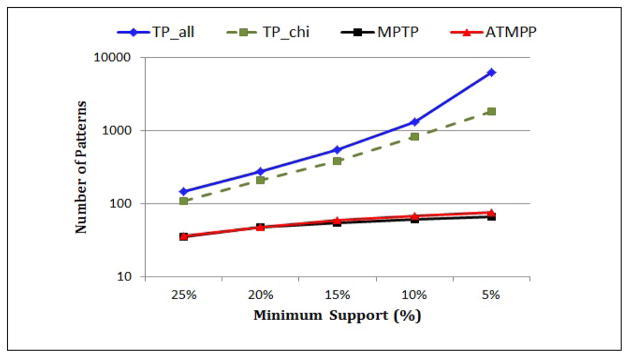
Figure 4 compares the number of temporal patterns (on a logarithmic scale) that are extracted by TP_all, TP_chi, MPTP and A-MPTP under different minimum support thresholds. Notice that the number of frequent temporal patterns (TP_all) exponentially blows up when we decrease the minimum support. Also notice that TP_chi does not help much in reducing the number of patterns even though it applies the FDR correction. For example, for min-sup=5%, TP_chi outputs 1,842 temporal patterns that are statistically significant! This clearly illustrates the spurious patterns problem that we discussed in Section III-E.

Figure 4.

The number of patterns return by TP_all, TP_chi, MPTP and A-MPTP for different minimum supports.

On the other hand, the number of MPTPs is much lower than the other methods and it is less sensitive to the minimum support. For example, when min-sup=5%, the number of MPTPs is about two orders of magnitude less than the total number of frequent patterns.

Finally notice that the number of A-MPTPs may in some cases be higher than the number of MPTPs. The reason for this is that A-MPTP performs less hypothesis testing during the mining (due to its aggressive pruning), hence FDR is less aggressive with A-MPTPs than with MPTPs.

Table II shows the top 5 MPTPs according to the p-value of the binomial statistical test, measuring the improvement in the predictive power of the pattern with respect to the HIT prior in the dataset. Rules R₁, R₂ and R₃ describe the main patterns used to detect HIT and are in agreement with the current HIT detection guidelines [21]. Rule R₄ relates the risk of HIT with high values of APTT (activated partial thromboplastin time). This relation is not obvious from the HIT detection guidelines. However it has been recently discussed in the literature [23]. Finally R₅ suggests that the risk of HIT correlates with having high WBC values. We currently do not know if it is a spurious or an important pattern. Hence this rule requires further investigation.

Table II.

The top 5 MPTPS according to their p-values. Sup denotes the proportion of data that the patterns cover and conf denotes the confidence of the rules.

Rule	Sup	Conf
R1: PLT=VL ⇒ HIT-risk	0.41	0.85
R2: Hep=ON co-occurs with PLT=D ⇒ HIT-risk	0.28	0.88
R3: Hep=ON before PLT=VL ⇒ HIT-risk	0.22	0.95
R4: Hep=ON co-occurs with APTT=H ⇒ HIT-risk	0.2	0.94
R5: PLT=D co-occurs with WBC=H ⇒ HIT-risk	0.25	0.87

D. Efficiency

In this section, we study the effect of the different techniques we proposed for improving the efficiency of temporal pattern mining. We compare the running time of the following methods:

1. TP_Apriori: Mine the frequent temporal patterns using the standard Apriori algorithm.

2. TP_id-lists: Mine the frequent temporal patterns using the vertical id-list format described in Section III-D2.

3. MPTP: Mine the MPTP set using the vertical format and the lossless pruning described in Section III-F1

4. A-MPTP: Mine the approximated MPTP set using the vertical format, the lossless pruning and the lossy pruning described in Section III-F2.

The experiments were conducted on a Dell Precision T7500 machine with an Intel Xeon 3GHz CPU and 16GB of RAM. All algorithms are implemented in MATLAB.

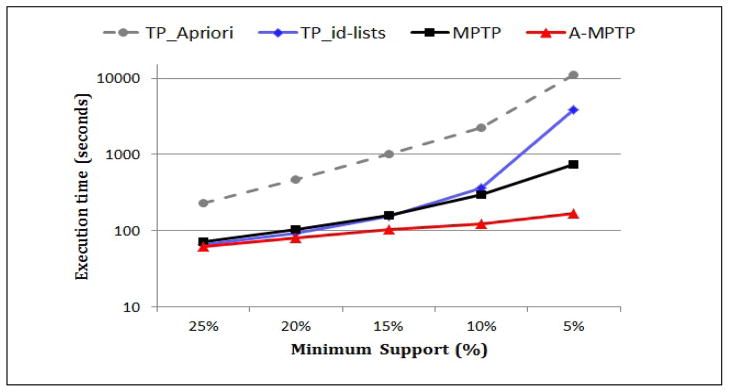
Figure 5 shows the execution times (on a logarithmic scale) of the above methods using different minimum support thresholds. We can see that using the vertical data format greatly improves the efficiency of frequent temporal pattern mining as compared to the standard Apriori algorithm. For example, for min-sup=10%, TP_id-lists is more than 6 times faster than TP_Apriori.

Figure 5.

The running time of TP_Apriori, TP_id-lists, MPTP and A-MPTP for different minimum supports.

Notice that the execution time of frequent temporal pattern mining (both TP_Apriori and TP_id-lists) blows up when the minimum support is low. On the other hand, MPTP controls the mining complexity and the execution time increases much slower than frequent pattern mining when the minimum support decreases. Finally, notice that A-MPTP is the most efficient method. For example, for min-sup=5%, A-MPTP is around 4 times faster than MPTP, 20 times faster than TP_id-lists and 60 times faster than TP_Apriori.

V. Conclusion

The integration of classification and pattern mining has recently attracted a lot of interest in data mining research and has been successfully applied on static data [24], [6], graph data [25] and sequence data [26]. This work proposes a pattern-based classification framework for multivariate time series data. Our approach relies on temporal abstractions and temporal logic to construct the classification features. We also propose the minimal predictive temporal patterns framework and present an efficient algorithm to directly mine these patterns. An important benefit of our approach is that it can handle complex irregularly spaced temporal data, such as electronic health records. This makes it a promising candidate for many applications in the medical field, such as patient monitoring and decision support.