Effects of pH on proteins: Predictions for ensemble and single molecule pulling experiments

Abstract

Protein conformations change among distinct thermodynamic states as solution conditions (temperature, denaturants, pH) are altered or when they are subject to mechanical forces. A quantitative description of the changes in the relative stabilities of the various thermodynamic states is needed to interpret and predict experimental outcomes. We provide a framework based on the Molecular Transfer Model (MTM) to account for pH effects on the properties of globular proteins. The MTM utilizes the partition function of a protein calculated from molecular simulations at one set of solution conditions to predict protein properties at another set of solution conditions. To take pH effects into account we utilized experimentally measured pK_a values in the native and unfolded states to calculate the free energy of transferring a protein from a reference pH to the pH of interest. We validate our approach by demonstrating that the native state stability as a function of pH are accurately predicted for CI2 and protein G. We use the MTM to predict the response of CI2 and protein G subject to a constant force (f) and varying pH. The phase diagrams of CI2 and protein G as a function of f and pH are dramatically different, and reflect the underlying pH-dependent stability changes in the absence of force. The calculated equilibrium free energy profiles as function of the end-to-end distance of the two proteins show that, at various pH values, CI2 unfolds via an intermediate when subject to f. The locations of the two transition states move towards the more unstable state as f is changed, which is in accord with the Hammond-Leffler postulate. In sharp contrast, force-induced unfolding of protein G occurs in a single step. Remarkably, the location of the transition state with respect to the folded state is independent of f, which suggests that protein G is mechanically brittle. The MTM provides a natural framework for predicting the outcomes of ensemble and single molecule experiments for a wide range of solution conditions.

Introduction

Recent experimental advances, especially in single molecule techniques^1,2, have made it possible to obtain detailed mechanistic insights into the folding of proteins over a wide range of external conditions. For example, singe molecule FRET (smFRET) experiments have been used to probe the characteristics of the ensemble of unfolded states under folding conditions, providing a glimpse of the nature of the collapse transition in proteins³. Developments in single molecule force spectroscopy, which probe the response of proteins subject to mechanical force (f), have been used to map the entire folding landscape of proteins described by the end-to-end distance of the molecule^4–6. These experiments have been remarkably successful in measuring the roughness of the energy landscape⁷, estimating barriers to folding⁸, and characterizing minimum energy compact structures^9,10 that are sampled during the folding process. In the majority of the smFRET experiments, folding or unfolding is initiated using chemical denaturants^11,12, whereas in pulling experiments external force is applied to select points on the protein to control folding. More recently, the global response of proteins to f in the presence of osmolytes and denaturants, and pH changes have also been reported^10,13. The wealth of data emerging from these studies demand computational models for which exhaustive simulations at conditions that mimic those used in experiments can be performed¹⁴.

Besides denaturants^15–17, protein folding or unfolding can also be initiated by altering pH¹⁸. Although a number of experimental studies have reported the pH-dependence of protein stability^19–22 there are very few theoretical approaches which have addressed the thermodynamic aspects of pH-dependent folding. In principle, all atom molecular dynamics simulations can be used to model pH-dependent effects on protein folding. Such an approach has found success in predicting and interpreting pK_a values of titratable groups within the native and unfolded ensembles^23–25. However, calculating other pH-dependent protein properties using all-atom models is difficult because of inaccuracies in force-fields²⁶ and the inability to adequately sample both the folded and denatured conformational space.

One of the most widely used thermodynamic models for pH effects on proteins was created by Tanford and coworkers, who showed that from knowledge of the pK_a values of titratable groups it is possible to predict the change in protein native state stability as a function of pH¹⁷. This thermodynamic model cannot be used to calculate the distribution of pH-dependent properties of proteins because it neglects the ensemble nature of folding. It is limited to making estimates of changes in the stability and the difference in the number of bound protons between the native and unfolded states.

The limitations of the thermodynamic model can be overcome using the Molecular Transfer Model (MTM), which we originally introduced to account for osmolyte effects on proteins²⁷. Although the MTM can be used in conjunction with all-atom models for proteins, we used a coarse-grained representation of proteins^27,28 so that the partition function of the system could be precisely computed at a given solution condition. Knowledge of the partition function can be used to compute any thermodynamic property at another solution condition by appropriate reweighting. The MTM utilizes the Tanford Model^17,29 to estimate the free energy cost of transferring each microstate (i.e., protein conformation) from one solution condition to another. Thus, the MTM is a post-simulation processing technique, which allows for a rapid prediction of the thermodynamic properties of proteins under a wide range of external conditions by performing simulations at one solution condition^27,30,31.

Here, we further develop the MTM to model pH effects on protein properties. We validate our approach by demonstrating that the methodology accurately predicts experimentally measured changes in the native state stability as function of pH. We further establish the efficacy of the MTM by calculating the pH-dependent response of proteins subject to an external mechanical force, f. Simulations at constant force and varying pH for chymotrypsin inhibitor 2 (CI2)^32,33 and protein G^34,35 show dramatically different behavior. Both the diagram of states as a function of f and pH and the free energy profiles depend on the protein. Our results are consistent with experimental data from a constant pulling speed force experiment³⁶ and offer a number of testable predictions.

Methods

Molecular Transfer Model for pH effects on proteins under tension

The MTM²⁷ utilizes protein conformations from C_α side chain model (C_α – SCM) coarse grained simulations (see below), experimentally measured or theoretically computed amino acid transfer free energies and the Weighted Histogram Equations³⁷ (WHAM) to predict how changes in external conditions alter the thermodynamic properties of a protein. The MTM equation for predicting the average of a quantity A at a given pH, temperature, and f value is

$$\langle A({pH}_2,T,f)\rangle =Z{({pH}_2,T,f)}^{-1}\sum _{k=1}^R\sum _{t=1}^{n_k}\frac{A_{k,t}{e}^{-\beta E_P(k,t,{pH}_2,f)}}{{\sum }_{m=1}^R{n}_m{e}^{F_m-{\beta }_m{E}_m(k,t)-f_{m}x(k,t)}},$$ (1)

where Z(pH₂, T, f) is the partition function. In Eq. 1, R is the number of independent simulated trajectories, n_k is the number of protein conformations in the k^th simulation, A_k,t is the value of property A for the t^th conformation, β = 1/k_BT, where k_B is Boltzmann constant and T is the temperature. The potential energy E_P of the t^th conformation in the k^th simulation at a pH value denoted pH₂, and under external force f is E_P (k, t, pH₂, f) = E_P (k, t, pH₁) + G_tr(k, t, pH₂) − fx(k, t), where E_P (k, t, pH₁) is the potential energy of the system at pH = pH₁, ie. the pH conditions at which the simulations are carried out in this study (see below). The free energy, ΔG_tr(k, t, pH₂), of transferring the t^th conformation in the k^th simulation from a solution at pH₁ to a solution at pH₂. f is the external pulling force and x is the end-to-end distance vector of the protein projected onto the direction of the applied force. In the denominator of Eq. 1, n_m and F_m are, respectively, the number of conformations and the free energy of the m^th simulation. The values of F_m are obtained self consistently at the simulated solution conditions as described in reference³⁷.

To estimate ΔG_tr(k, t, pH₂) we use a model developed by Tanford and coworkers¹⁷ in which the free energy of transferring a titratable group p in conformation l of the protein from pH₁ to pH₂ is

$$\delta g_{p,l}=-k_B\mathit{Tln}\left[\frac{{10}^{{pH}_2}+{\mathrm{\Theta }}_N(l){10}^{{pK}_{N,p}}+{\mathrm{\Theta }}_D(l){10}^{{pK}_{D,p}}}{{10}^{{pH}_1}+{\mathrm{\Theta }}_N(l){10}^{{pK}_{N,p}}+{\mathrm{\Theta }}_D(l){10}^{{pK}_{D,p}}}\right],$$ (2)

where Θ_N (l) and Θ_D(l) are Heaviside step functions that identify a conformation l as being either native or denatured. Θ_N (l) (Θ_D(l)) equals 1 if conformation l is native (denatured) and 0 otherwise. pK_N,p and pK_D,p are the pK_a values for group p in the native and denatured states respectively. We use pK_N,p values that have been determined experimentally^34,38 (see Table S1). Details on classifying conformations as native and denatured are given below. Finally $\mathrm{\Delta }{G}_{tr}(k,t,{pH}_2)={\sum }_{p=1}^{N_p}\delta g_{p,l}$, which is the sum of the δg_p,l values that are calculated using Eq. 2.

Coarse-Grained models for proteins

We model the 65 residue long protein CI2, and 56 residue protein G using the C_α-SCM^27,28 in which each amino acid is represented as two interaction sites, one of which is located at the α carbon position of the backbone. For all amino acids except glycine, the other interaction site is located at the center-of-mass of the SC. We use a Go model version³⁹ of the C_α-SCM. Thus, side chains that are in contact or backbone groups that form hydrogen bonds in the crystal structure have attractive non-bonded Lennard-Jones interactions while all other non-bonded interactions are repulsive. Sequence dependent effects are modeled using non-bonded interaction parameters based on the Miyazawa-Jernigan statistical potential⁴⁰. The excluded volume of an amino acid side chain is proportional to its experimentally measured partial molar volume in solution.

The potential energy E_P of a C_α-SCM conformation is $E_P=E_A+E_{HB}+E_{NB}^N+E_{NB}^{NN}$, which is the sum of potential energy terms corresponding to angles (E_A), hydrogen bonds (E_HB), and native ( $E_{NB}^N$) and non-native ( $E_{NB}^{NN}$) non-bonded interactions. We use the Shake algorithm⁴¹ to hold the bond lengths fixed in the simulations, hence there is no energy term corresponding to this constraint. The functional forms of the terms in the C_α-SCM force field are

$$E_A=\sum _{i=1}^N{K}_A{({\theta }_i-{\theta }_{i,0})}^2+\sum _{i=1}^{N_D}\sum _{j=1}^3{K}_{D_j}(1+\mathit{cos}(n_j{\phi }_i-{\delta }_{ij}))+\sum _{i=1}^{N_{Ch}}{K}_{Ch}{({\mathrm{\Psi }}_i-{\mathrm{\Psi }}_{i,0})}^2,$$ (3)

$$E_{HB}+E_{NB}^N=\sum _{i=1}^{N_{HB}}{\epsilon }_{HB}\left[{\left(\frac{r_{HB,i}^0}{r_i}\right)}^{12}-2{\left(\frac{r_{HB,i}^0}{r_i}\right)}^6\right]+\sum _{i=1}^{N_N}{\epsilon }_i^N\left[{\left(\frac{r_{\mathit{min},i}}{r_i}\right)}^{12}-2{\left(\frac{r_{\mathit{min},i}}{r_i}\right)}^{12}\right],$$ (4)

$$E_{NB}^{NN}=\sum _{i=1}^{N_{NN}}{\epsilon }_i^{NN}\left[{\left(\frac{r_{\mathit{min},i}}{r_i}\right)}^{12}\right].$$ (5)

On the right hand side (RHS) of Eq. 3, and from left to right, the summation corresponds, respectively, to bond angle, dihedral angle and improper dihedral angle energy terms. The improper dihedral term is used to model chirality about the C_α interaction site. On the RHS of Eq. 4 we model hydrogen bonds found in the crystal structure as a Lennard-Jones potential (first term) with a well-depth set to ε_HB and the positions of the minima $r_{HB,i}^0$ are set by the interaction site distance in the crystal structure. The second summation term in Eq. 4 accounts for native interactions between sites and is treated using the Lennard-Jones potential whose well-depth is set using the Miyazawa-Jernigan statistical potential and minima location r_min,i corresponds to the distance in the crystal structure. Non-native interactions (Eq. 5) between sites are treated as short-ranged and repulsive, with the r_min,i being proportional to the experimentally measured partial molar volume of the amino-acid type. The force-field parameters used for CI2 and protein G are in Table S2, and additional details on the model can be found in our previous study²⁷. We use the crystal structures with PDB codes 2CI2⁴² and 1GB1⁴³ for CI2 and protein G, respectively.

Simulation details

We use Hamiltonian Replica Exchange (HREX)^44,45 in the canonical (NVT) ensemble to obtain equilibrium simulations of CI2 and protein G at constant force (f) applied in the positive x-direction to the C-terminal C_α interaction site of the protein. In the simulations, the N-terminal C_α interaction site is fixed at the origin. In the HREX simulation independent trajectories (replicas) are simulated at different temperatures and at different f values using Langevin dynamics⁴⁶ with a damping coefficient of 0.8 ps⁻¹ and an integration time-step of 6 fs. The non-bonded interactions were truncated at 20 Å with a switch function applied starting at 18 Å. We use CHARMM (version c33b2) to simulate the time evolution of the replicas⁴⁷. Every 5,000 to 7,000 integration time-steps the coordinates of the proteins were saved for each replica and then exchanged, either between neighboring temperatures or between neighboring external tensions (i.e., Hamiltonians) according to exchange criteria that preserve detailed balance⁴⁴. It total, 90,000 exchanges, alternating between temperature and force values, were attempted. The first 10,000 exchanges were discarded to allow for equilibration.

For CI2, five temperature windows (300, 317, 330, 345, 380) K and eight f values (f = 0.00, 0.35, 3.47, 8.68, 9.03, 9.38, 9.73, 10.42, 13.89) pN were used for a total of forty replicas. For protein G four temperature windows (310, 320, 330, 370 K) and ten f values (f = 0.00, 0.35, 1.60, 2.85, 4.10, 5.35, 6.60, 7.85, 9.10, 10.42, 13.89 pN) were used for a total of forty replicas. Swap acceptance ratios of between 10 and 40% were achieved in the HREX runs. The equilibrium properties of the proteins at temperatures and constant pulling forces other than those values explicitly simulated were calculated using Eqs. 1 and 6.

Analysis

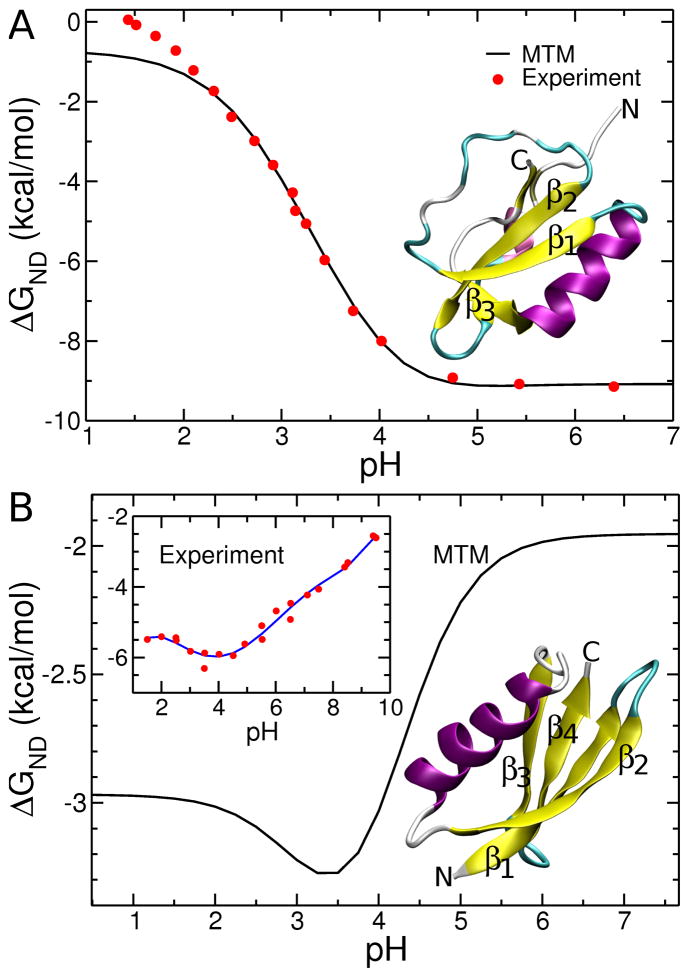
A conformation is native if the root-mean-squared-distance (RMSD) of the C_α interaction sites are within 5 Å, for protein G, or 11 Å, for CI2, of the corresponding C_α atoms in the crystal structure, otherwise it is classified as denatured. These RMSD thresholds were determined as the upper limit on the integral of the RMSD probability densities at the melting temperature (i.e., the maximum in the heat capacity trace) that yielded a value of 0.5. This method is illustrated in Fig. S1. This means we assumed that at the melting temperature CI2 is a two state system. Structurally, CI2’s larger threshold arises from the disordered random coil regions in the native state ensemble (see Fig. 1A).

Figure 1.

Stability of the native state, relative to the denatured state ensemble (ΔG_ND = −k_BTln(P_N/P_D), where P_N and P_D are the probabilities of being in the native and denatured ensembles, respectively) as a function of pH. Panel A is for CI2 and B is for protein G. Native state structures are shown of CI2 and protein G in a secondary structure representation based on crystal structures with PDB accession codes of 2CI2 and 1GB1 respectively. Experimental data (red circles) in A are from³⁸. Because experimental data for wild-type protein G is unavailable we show in the inset in B experimental data (red circles) for a triple mutant protein G (T2Q, N8D, N37D)³⁵. The blue line is a 5^th order polynomial fit to the data and is used to guide the eye. For the CI2 the temperature in the simulations was 302 K and in the experiment was 298 K. For the protein G the simulation temperature was 317 K and in the experiment it was 298 K.

A key step in applying the MTM is in the choice of the reference pH (‘pH₁’ in the equations above) in the post-simulation analysis. To choose the reference pH we first calculated the native stability of these two proteins at 300 K. For CI2 we identified a pH value for which the calculated and experimentally measured stabilities are similar³⁸. Using this criterion we obtained a value of 3.5 for the reference pH. We then determined the temperature at which the calculated stability exactly equaled the experimental value of 6.0 kcal/mol at pH 3.5. This occurs at a simulation temperature of 302 K. In this way we set the overall free energy of this system to match the experiment at a single pH value. This procedure provided a reference solution condition (T=302 K, pH 3.5) from which predictions at all other pH values are made by reweighting of the partition function using the MTM procedure in Eqs. 1 and 6. Thus, despite the fact that there are no hydrogens in the coarse-grained simulation model, the thermodynamic effects of differential proton binding to N and D can still be accounted for within the MTM theory, as demonstrated by the successful comparisons between simulations and experiments. Experimental data of pK_a values and stability versus pH for wild-type protein G does not exist. Therefore, we chose a simulation temperature (318 K) that resulted in a native stability typical for such small proteins (−3.0 kcal/mol) and set pH₁ to 2.3. The trends and conclusions presented below are insensitive to the choice of reference pH, especially when such stability matching is carried out.

Two-dimensional native state stability phase diagrams (e.g., ΔG_ND(f, pH), etc.) are computed by rewriting Eq. 1 in terms of the probability of being folded as a function of f and pH using⁴⁸

$$P_N(f,pH)=Z{({pH}_2,T,f)}^{-1}\sum _{k=1}^R\sum _{t=1}^{n_k}\frac{{\mathrm{\Theta }}_N(k,t)e^{-\beta E_P(k,t,{pH}_2,f)}}{{\sum }_{m=1}^R{n}_m{e}^{F_m-{\beta }_m{E}_m(k,t)-f_{m}x(k,t)}},$$ (6)

where ΔG_ND(f, pH) = −k_BTln(P_N (f, pH)/(1 − P_N (f, pH))). All terms in Eq. 6 are the same as in Eq. 1 except we use the Heaviside step function Θ_N (k, t), which is one if conformation (k, t) is native and zero otherwise. We calculate f_m using P_N (f_m, pH) = 0.5.

Results

The Molecular Transfer Model for pH effects on proteins

The theory of the MTM hinges on the observation that if the partition function Z(A)(= Σ_j e^−βE(j,A)) is known at some solution condition A, and if the free energy cost ΔG_tr(A → B) of transferring each protein conformation from A to an arbitrary solution condition B is known, then the partition function in B is Z(B) = Σ_je^{−βE(j,A)−βΔG_tr(j,A→B)}. In other words, the potential energy of the j^th conformation in B is the sum of potential energy in A (E(j, A)) and the reversible work of transferring conformation j from A to B. In the current study, A and B differ in pH. In practice, the precision of the MTM, which is a mean field-like approximation to the exact partition function, is limited only by the accuracy of the protein model Hamiltonian (i.e., the force field), the errors in the ΔG_tr model, and the extent of sampling in A.

We use the Aune-Tanford pH model⁴⁹, which is among one of the most widely used theories to account for pH effects on protein stability¹⁷, to compute the free energy, ΔG_tr(pH₁ → pH₂), of transferring a protein conformation from pH₁ to pH₂. The change in the experimentally measured native (N) state stability with respect to the denatured (D) state (ΔG_ND), due to a change in pH is fit using,

$$\mathrm{\Delta }{G}_{tr}(l,{pH}_1\to {pH}_2)=-k_{B}T\sum _{k=1}^{N_t}ln\left[\frac{{10}^{{pH}_2}+{10}^{{pK}_{k,l}}}{{10}^{{pH}_1}+{10}^{{pK}_{k,l}}}\right],$$ (7)

where the summation is over the N_t titratable groups and pK_k,l is the pK_a value of the k^th titratable group in the l^th protein conformation. It can be shown that Eq. 7 is a mean field result obtained by integrating over all possible protonation states of a protein with N_t independent titratable groups in the native and denatured states⁵⁰. The success of Eq. 7 in modeling experimental ΔG_ND versus pH not only offers insight into the mechanism of pH denaturation, but also provides a means to estimate the free energy cost of transferring individual protein conformations from one solution pH to another.

To implement the MTM for pH effects, we use Hamiltonian Replica Exchange simulations⁴⁴ of the C_α side-chain coarse grained model²⁸ of protein G and CI2 to calculate the partition function Z(A). We use experimental pK_a values (Table S1), to estimate the free energy cost of transferring the conformations (Eq. 7) sampled in the simulations that we classify as belonging to either the native or denatured ensembles based on suitable order parameters. To optimize the accuracy of the calculated partition function from the simulations we use the Weighted Histogram Equations (see Methods for details)³⁷.

The Molecular Transfer Model accurately models pH denaturation

We first calculated the thermodynamic properties of CI2 and protein G as a function of pH at f = 0. The MTM prediction of the dependence of ΔG_ND(pH) on pH for CI2 is in excellent agreement with experiment (Fig 1A)³⁸. Just as in the experiment, we find that the stability of CI2 decreases monotonically in a sigmoidal fashion as pH decreases. Although there are small differences between the experimental and simulation ΔG_ND(pH) data at pH less than 2, the overall agreement with experiment shows that the MTM accurately models pH effects on the thermodynamics of folding and unfolding.

We also calculated ΔG_ND as a function of pH (Fig 1B) for wild-type protein G for which experimental data are not available. However, pH-dependent ΔG_ND(pH) for a triple mutant (T2Q, N8D, N37D) of protein G³⁵ has been measured. Although mutations can alter the native state stability, it is likely that the response of ΔG_ND to pH for the wild-type and the mutant will be qualitatively similar. With this caveat, we note that the overall shape of the calculated ΔG_ND as a function of pH for wild-type protein G is similar to the experimental data from the triple mutant (Fig. 1B). They both exhibit non-monotonic trends with minima located in the pH range of 3 to 4. In addition, the difference in stability at two different pH values, ΔG_ND(pH = 7) − ΔG_ND(pH = 3.4) is similar for the wild type and the triple mutant, with values of 1.3 and 1.7 kcal/mol, respectively. This suggests that the three mutations to titratable groups in the wild type protein do not drastically alter the characteristics of the thermodynamic response of protein G to pH changes. The non-monotonic dependence of ΔG_ND on pH observed for protein G contrasts with the monotonic-dependence observed for CI2 (Fig. 1A).

Force-pH and force-temperature phase diagrams

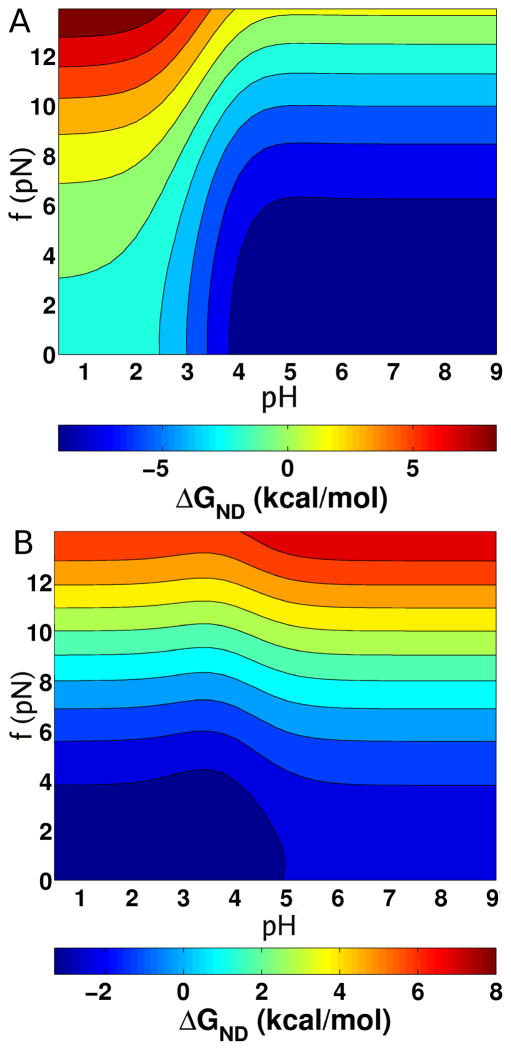
The versatility of the MTM is illustrated by probing the response of protein G and CI2 when, as is done in constant force single molecule pulling experiments, a tensile force f is applied to their N and C termini at various pH values. Such constant force pulling simulations are at equilibrium. We calculated the phase diagram for both CI2 and protein G as a function of pH and f (Fig. 2). Based on the destabilization of the native state of CI2 at acidic pH at f = 0 (Fig. 1A) we expect that the midpoint force required to unfold CI2 should decrease as pH decreases. This expectation is borne out in the pH range from 2 to 9 (Fig. 2A). For CI2, decreasing pH facilitates force unfolding by stabilizing the denatured state. As a result, the force required to unfold CI2 decreases as pH decreases (Fig. 2A).

Figure 2.

Force-pH phase diagram. (A) The [f, pH] diagram displays ΔG_ND(f, pH) for CI2 at a simulation temperature of 302 K. The solid lines correspond to lines of iso-stability. The scale for ΔG_ND(f, pH) is given below. (B) Same as (A) except it is for protein G at a simulation temperature of 317 K.

The [f,pH] phase diagram for protein G (Fig. 2B) differs qualitatively from the one for CI2. In contrast to CI2, for protein G increasing the pH above 3.4 destabilizes the native state ensemble, which implies that smaller forces are needed to unfold protein G (Fig. 2B). These results show that the mechanical response of proteins are strongly pH-dependent and can have opposite trends, which reflects the underlying stability of the proteins.

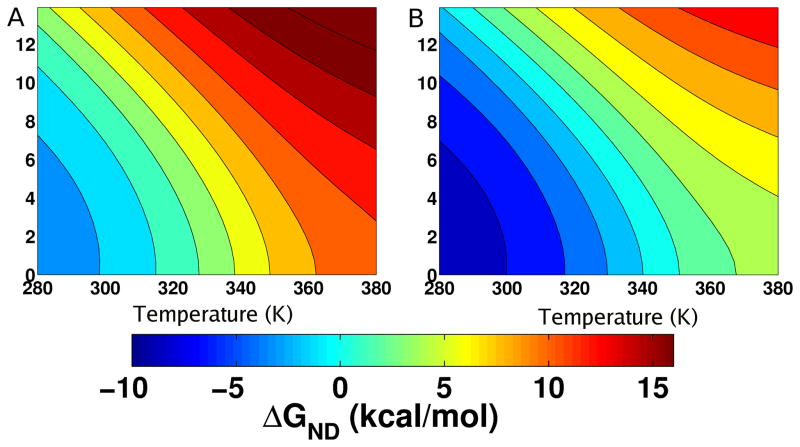
We also calculated for CI2 the [f,T] phase diagram at two pH values (Fig. 3). The locus of points separating the folded, partially folded (see below), and unfolded structures is reminiscent of previously calculated [f,T] phase diagrams for simpler lattice and off-lattice models^51,52. Not surprisingly, the region of stability increases as temperature decreases (compare the extent of blue regions in Figs. 3A and 3B). The force required to destabilize CI2’s native state increases as the temperature is lowered. Furthermore, at T = 280 K and pH 3.5 only at f > 12 pN (Fig. 3B) is the native state unstable, whereas at pH = 1.0 this occurs for f > 8 pN.

Figure 3.

Force-temperature phase diagram for CI2. (A) Contours of this phase diagram at pH=1.0 are lines of iso-stability in ΔG_ND(f,T). Blue regions correspond to a thermodynamically stable native state while red corresponds to the unfolded state. (B) The [f,T] diagram is for pH=3.5. Enhanced stability at higher pH is reflected in large [f,T] regions in which the native state is stable.

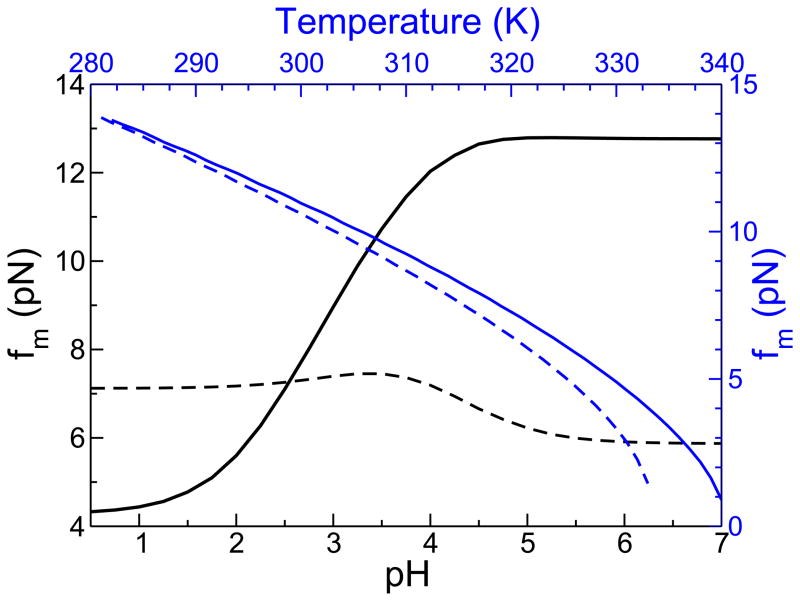
Force midpoints

From the phase diagrams the pH-dependent midpoint unfolding force, f_m, can be determined using ΔG_ND(f_m,pH) = 0. Similarly, T-dependent f_m can be computed using ΔG_ND(f_m, T) = 0. At high (pH > 5) and low pH (pH < 2) values we find f_m is largely unchanged for both proteins (Fig. 4). For CI2, the interplay between native state stabilization with increasing pH and the counteracting f-induced destabilization results in a population of partially structured conformations at f < f_m and pH > 4 (see blue regions in Fig. 2A). At intermediate pH values (2 < pH < 5) f_m for CI2 is an increasing function of pH (Fig. 4), which is a reflection of the enhanced stability of the native state at f = 0 (Fig. 1A). In contrast, at intermediate values of pH f_m for protein G exhibits non-monotonic behavior with a maximum at pH = 3.4, which coincides with the pH at which the native state stability is largest when f = 0 (Fig. 1B).

Figure 4.

The force midpoint at various temperatures and pH. The temperature scale is on top in blue and the corresponding scale for f_m is on the right. Solid lines are for CI2 and the dotted lines are for protein G, with blue corresponding to temperature and black to pH changes. Unless otherwise stated, the solution conditions for CI2 are 302 K and pH 3.5, and for protein G the conditions are 317 K and pH 2.3.

Although the dependence of f_m on pH differs greatly for the two proteins the T-dependent f_m results exhibit qualitatively similar behavior (blue curves in Fig. 4). Increasing temperature affects all interactions whereas changing pH only affects titratable groups. Temperature effects are global and pH effects are more localized. As a consequence, ΔG(f,pH) and ΔG(f, T) are different, which leads to the predictions in Fig. 4.

pH-dependent free energy profiles

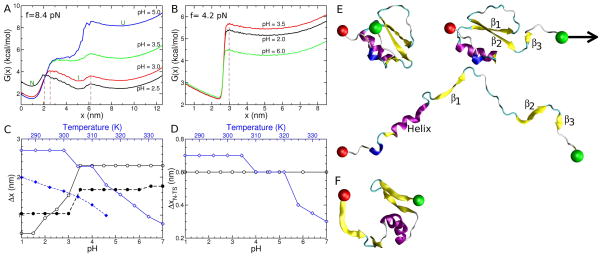
Single molecule force experiments are routinely used to obtain the f-dependent free energy profiles G(x) where x is the end-to-end distance of the protein projected onto the pulling direction^53,54. The free energy profiles in principle can yield both the barrier height to unfolding and the location of the transition state assuming that x is an appropriate reaction coordinate. It is also possible to extract the intrinsic ruggedness of the folding landscape at f = 0 using the f-dependent kinetics of unfolding at different temperatures^55,56. This would require doing explicit kinetic simulations or experimentally measuring the unfolding rates. We first calculated G(x) at several pH values for CI2 at f=8.4 pN and protein G at f=4.2 pN (Figs. 5A and 5B).

Figure 5.

pH and temperature effects on the mechanical response of CI2 and protein G at a constant tension force of 8.4 pN and 4.2 pN, respectively. The free energy profile G(x) = −k_BTln(P(x)), where P(x) is the probability of finding a given x value, as a function of the end-to-end distance of the protein, projected onto the pulling vector, for (A) CI2 and (B) protein G at different pH values as labeled. The temperature is 302 K and 317 K in (A) and (B), respectively. Brown dashed lines indicate transition state locations at pH=2.5 and 3.0 in (A), and pH=3.5 in (B). The location of the native, intermediate, and fully unfolded basins of attraction in G(x) are marked by the labels N, I, and U, respectively. (C) For CI2, the distance, Δx, between the native and first transition state (Δx_N–TS), and intermediate and second transition state (Δx_I–TS) are shown as a function of pH (lower axis) and temperature (upper axis). The black symbols correspond to pH and blue symbols are for temperature. In both cases solid lines show Δx_N–TS and dashed lines correspond to Δx_I–TS. (D) Same as (C) but for protein G. No intermediate basin of attraction exists for protein G, so only the distance between the native and transition state (Δx_N–TS) is reported. (E) Sample conformations (top to bottom) from the native, intermediate and unfolded states of CI2 during simulations at 300 K and f = 8.68 pN. β-strands 1 through 3 are labeled and the direction in which the constant tension is applied to the C-terminus (green sphere) is indicated by the black arrow. The N-terminal residue, fixed in space during the simulation is shown as a red sphere. (F) Simulation structure of protein G with x=3.09 nm from the replica at T=320 K and f = 4.1 pN in the replica exchange simulations.

For CI2, we observe three basins of attraction in G(x) over a range of pH values (Fig. 5A), which suggests that CI2 undergoes a two-stage force induced unfolding transition in which a partially folded state is populated between the fully folded and fully unfolded basins. To obtain structural insights into the nature of the intermediate we calculated the fraction of native contacts for various structural elements within the native topology of CI2 (see structure in Fig. 1A) as a function of x. The analysis indicates (Fig. S2) that the transition from the native to the intermediate basin (located between 2 and 6 nm in G(x)) corresponds to the unfolding of β-strand 3 (residues 75 and 76 in PDB 2CI2) resulting in the loss of tertiary interactions with β-strand 2 (residues 65 to 71) and the α-helix (residues 32 to 42). The transition to the unfolded basin (located at x > 7 nm) corresponds to the unfolding of the rest of the structural elements in the protein (i.e., β-strands 1–2, and interaction of these strands with the α-helix). Sample structures of the native, intermediate and unfolded conformations from the simulations of CI2 under these conditions are consistent with this analysis (Fig. 5E).

The pH-dependent free energy profiles for protein G under tension have only two basins of attraction (Fig. 5B), which implies that force induced unfolding occurs in a single step. The free energy barrier to unfolding increases from 2.1 kcal/mol at pH 6.0, to 3.4 kcal/mol at pH 3.5. Because the curvature near the native basin and barrier top are roughly independent of pH (Fig. 5B) it follows from Kramers’s theory that transition rates between the folded and unfolded states are determined entirely by the barrier height. Thus, the calculated G(x) profiles in conjunction with Kramers’s theory predict that the unfolding rate k_U (f) increases by a factor of 10 as pH increases from 6.0 to 3.5. The predictions for free energy profiles and the inferred changes in unfolding rates are amenable to experimental tests.

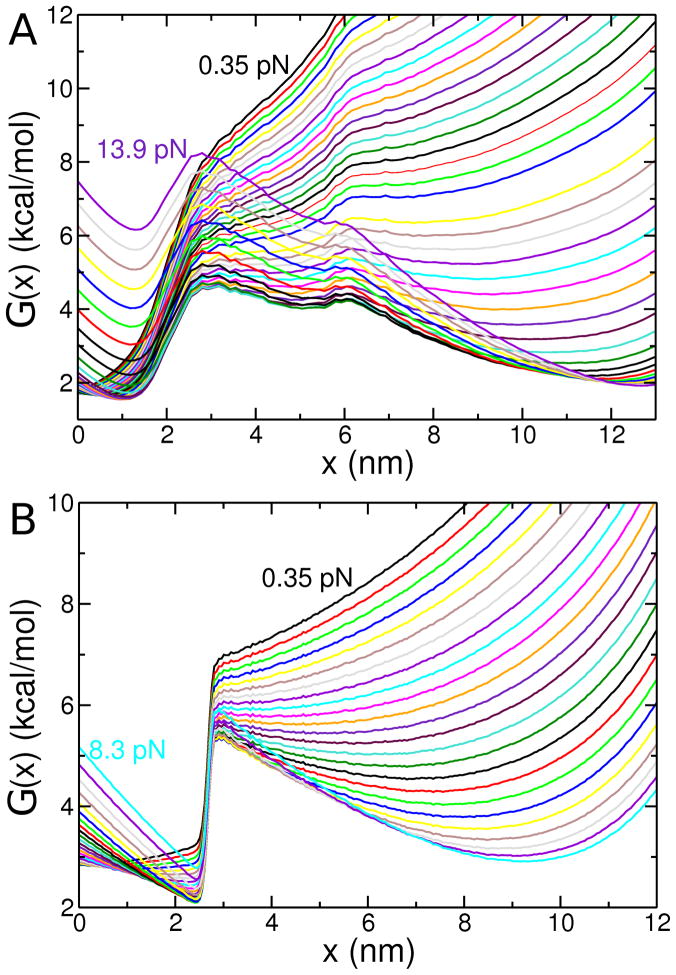
In order to ascertain the generality of our conclusions we show in Fig. 6 the free energy profiles over a wide range of forces. Just as in Fig. 5 we find that for CI2 there is force-induced folding intermediate, suggesting that the two transition states persist at all relevant f values. Remarkably, the invariance of the location of the TS is preserved at all forces. Both these figures show in a rather dramatic manner that the mechanical responses of CI2 and protein G are very different, which reflects the underlying variations in the native topology⁵² (see below for additional discussions).

Figure 6.

Equilibrium free energy profiles G(x) at various constant tension forces at pH 3.5 for (A) CI2 at 302 K and (B) protein G at 317 K. As indicated in the panels, the force values range from 0.35 pN up to 13 pN for CI2 and from 0.35 pN 8.3 pN for protein G. Successive profiles differ by approximately 0.35 pN of applied tension. Comparisons between (A) and (B) reveal vividly the dramatic differences in the compliance between these two proteins, thus underscoring the importance of native structure.

pH and temperature dependent movements in transition state location suggest Hammond-Leffler behavior

According to the Hammond-Leffler postulate⁵⁷ the transition state (TS) should resemble the least stable species in the reaction. Although originally proposed for reactions of small organic molecules, Hyeon and Thirumalai⁵⁸ showed that the Hammond postulate is also applicable to force unfolding of biomolecules regardless of the nature of the reaction coordinate. For proteins under tension this implies that the location, x_TS, of the TS, should either be independent of f or move towards the native state when f increases.

The G(x) profiles for CI2 at f=8.4 pN (Fig. 5A) show that there are two transition states, one between the native and intermediate, whose distance is Δx_N–TS with respect to the location of the native state, and the other between the intermediate and fully unfolded ensemble, whose distance is Δx_I–TS. Fig. 5C shows that Δx_N–TS and Δx_I–TS are independent of pH when pH exceeds 3.5. As pH increases, resulting in enhanced stability of both N with respect to I and I with respect to U (Fig. 5A), Δx_N–TS and Δx_I–TS increase with a dramatic jump at a pH=3.0. These results imply that the locations of the two transition states move closer to the less stable species, which is in accord with the Hammond-Leffler postulate. As a corollary, we expect and find (Fig. 5C) that upon an increase in temperature Δx_N–TS and Δx_I–TS should decrease as both the folded and intermediate states are destabilized relative to the unfolded state. Although these observations do not establish the adequacy of the one-dimensional reaction coordinate to describe f-induced unfolding of CI2 they support the generality of the Hammond-Leffler postulate for interpreting force spectroscopy results⁵⁵.

The abrupt change in Δx_N–TS and Δx_I–TS at pH 3 range from about 1.7 to 2.0 nm (Fig. 5C). Similarly, the change in Δx_N–TS is 2.3 nm as the temperature is increased from 300 to 340 K. Such large changes in TS locations are not typically observed in constant loading rate AFM experiments. For example, the maximum value of x_N–TS observed in filamin ≈ 0.7 nm⁵⁹. The observed changes for CI2 are similar to the values obtained in the transition from intermediate to the unfolded states in RNase H using laser optical tweezer experiments⁴. The large variations in Δx_N–TS and Δx_I–TS for CI2 shows that besides experimental conditions the native state topology must also play a critical role in response to f.

In sharp contrast to CI2, the TS changes in the unfolding of protein G are dramatically different. The TS location Δx_N–TS is independent of pH (Figs. 5B and 5D), which implies that protein G behaves as a brittle material when subjected to f at all pH values. As the temperature increases Δx_N–TS decreases (Fig. 5D) in two steps, one at 305 K and the other at 320 K. In comparison, to CI2 the values of Δx_N–TS are roughly in the range observed for several proteins using AFM experiments. The value of Δx_N–TS changes by 0.4 nm as the temperature increases from 280 K to 340 K. The decrease in Δx_N–TS, reflecting the movement of the TS closer to the native state, as temperature increases is consistent with the Hammond-Leffler postulate.

Discussion

We have introduced a way to account for pH effects on proteins within the framework of the Molecular Transfer Model. Our formulation overcomes the key limitations of the Tanford Thermodynamic model⁴⁹, which is restricted to predicting only changes in protein stability due to changes in pH. Besides accomplishing this goal, the MTM also offers a molecular interpretation of folding and unfolding over a broad range of external conditions, including the response to f and pH. In principle, the MTM can be combined with all-atom simulations to calculate pH effects on proteins. As a matter of practice, however, currently such simulations under sample the partition function of proteins and therefore do not yield statistically significant results for the self-assembly of proteins.

Applications of the f-dependent response to pH of proteins using the MTM have revealed a number of surprising predictions. In particular, we found that f_m had a non-linear dependence on pH; f_m increases at acidic pH for protein G where as it decreases for CI2. These results correlate with the pH-dependence of ΔG_ND at f = 0, a conclusion also reached from single molecule force experiments³⁶. We have also shown that the movement of the transition state location follows Hammond-Leffler behavior at all forces and solution conditions examined here. Large or discontinuous changes in transition state location inferred from the free energy profiles provide structural evidence for plasticity or brittleness of forced-unfolding of CI2 and protein G. We note that the sequence of events during an unfolding event cannot be directly calculated from the Hamiltonian replica exchange simulations, which are restricted to obtaining the measurable equilibrium free energy profiles. Brownian dynamics or all all-atom molecular dynamics simulations have to be performed to obtain the force-induced unfolding kinetics. Nevertheless, using our previous study⁵², which established a link between the structure of the native state and potential unfolding pathways, we can suggest the plausible structural origin of the brittleness of protein G. Our earlier work⁵² showed that upon application of force unfolding occurs by a shearing-type motion of β-sheets that are arranged in an anti-parallel manner. Using this result we surmise that protein G unfolds by shearing (or sliding) of the strands in the β-sheets (most likely the C-terminal strands) with respect to each other. Hence, the transition is abrupt involving a f-independent transition state (Figs. 5 and 6). In contrast unfolding is gradual in the plastic protein CI2 in which the TS move in response to f (Figs. 5 and 6). Explicit kinetic simulations are needed to enumerate the force-induced unfolding pathways, and to further confirm the drastically different responses to f predicted for these proteins.

Our results can be compared at a qualitative level to single molecule constant pulling speed experiments on ubiquitin³⁶ in which pH effects were studied. Those experiments found³⁶ that the unfolding force of ubiquitin is a constant over a range of pH values (6 to 10) and decreased at acidic pH. These findings are qualitatively consistent with our results for CI2 (Figure 4A). A major prediction from our results is that such pH-dependent trends depend critically on the specific protein under study. For example, f_m for protein G shows the opposite trend observed in CI2; f_m increases slightly at more acidic pH values (Figure 4B).

In single molecule pulling experiments, with x as the only experimentally accessible coordinate, identification of the TS location with the ensemble of TS structures in the multidimensional landscape is a challenging problem. It is possible that at f > f_m the pulling coordinate is a good reaction coordinate because at large forces the molecule is likely to be aligned along the f direction, thus forcing it to unfold along the coordinate conjugate to f. Recently, we showed that the suitability of x as a reaction coordinate is determined by the interplay between compaction (determined by protein stability) and tension (dependent on x_TS and the barrier to unfolding)⁶⁰. A test of the adequacy of x as a reaction coordinate is captured by the experimentally measurable molecular tensegrity parameter, $s=\frac{f_c}{f_m}$, where the unfolding critical force, f_c, equals $\frac{\mathrm{\Delta }{G}^{‡}}{x_{TS}}$, and ΔG^‡ is the height of the free energy barrier. For CI2, with its two transition states, the values of s₁ (N → TS) and s₂ (I → TS₂) are 0.019 and 0.005 at pH = 3.0. The theory of Morrison et. al.⁶⁰ predicts that at this pH x is a good reaction coordinate for both the transitions because it is likely that the ensemble of conformations starting from Δx_N–TS (Δx_I–TS) would reach I and N (I and U) with equal probability (p_fold ≈ 0.5). For protein G at pH = 6.0, s = 0.058, which also lies in the range for which x is likely to be a good reaction coordinate as assessed by the theory outlined in⁶⁰.

A number of assumptions underlie our application of the MTM, including the temperature independence of pH transfer free energies (Δ G_tr(k, t, pH₂)), and the use of the independent site model of titration. In addition, there are other assumptions^17,50 that are inherent to the Aune-Tanford model that should be kept in mind in specific applications of our theory. However, the excellent agreement between experiments and simulations demonstrated here (Fig. 1) and in previous applications of MTM^27,31 suggests that this assumption is reasonable for the proteins and solution conditions studied here.

To predict pH effects on proteins we utilized experimentally measured pK_a values of titratable side-chains of protein G and CI2^34,38. In the absence of such experimental data pK_a values calculated using quantum chemical methods can be utilized. Alternatively, the MTM could potentially be utilized to solve the inverse problem of predicting pK_a values from either simulation structures alone, or from known changes of protein properties as a function of pH⁶¹. The MTM could also be used to test different functional forms that go beyond the two-state mean-field assumption of Eq. 7⁵⁰.

The Molecular Transfer Model is a significant advance in our ability to model in a natural way the effects of osmolytes and pH on the folding of proteins. By combining thermodynamic models and physio-chemical data the MTM incorporates the effects of osmolytes and pH into simulations in a physically transparent and theoretically rigorous manner. Consequently, reliable simulations can be performed to predict measurable quantities, which enables a direct comparison to experiments^27,30,31,62.