Timing Facilitated Site Transfer of an Enzyme on DNA

Abstract

Many enzymes that react with specific sites in DNA exhibit the property of facilitated diffusion, where the DNA chain is used as a conduit to accelerate site location. Despite the importance of such mechanisms in gene regulation and DNA repair, there have been few viable approaches to elucidate the microscopic process of facilitated diffusion. Here we describe a new method where a small molecule trap (uracil) is used to clock a DNA repair enzyme as it hops and slides between damaged sites in DNA. The “molecular clock” provides unprecedented information: the mean length for DNA sliding, the 1D sliding constant, the maximum hopping radius and time frame for DNA hopping events. In addition, the data establish that the DNA phosphate backbone is a sufficient requirement for DNA sliding.

With the original observation that the lac-repressor was able to locate its DNA target site faster than the Smoluchowski diffusion limit¹, it has since been proposed that DNA binding proteins and enzymes enhance the efficiency of locating their individual DNA target sites by reducing the dimensionality of the search through a process known as facilitated diffusion on the DNA chain². In recent years, numerous bulk solution and single molecule measurements have thoroughly established that facilitated diffusion is a general property of protein-DNA interactions, both in vitro^3–8 and in vivo^9,10. Although facilitated diffusion mechanisms are now generally accepted to involve both 1D sliding and 3D hopping events on the DNA chain^3,4,11–15, these individual pathways have never been simultaneously detected and mechanistically defined for any protein-DNA interaction. There is good reason for this deficiency. While single molecule studies have measured the speed of various proteins sliding on DNA, and also their mean sliding lengths^12–20, limits in resolution of the method can lead to uncertainty in the mechanistic interpretation of these measurements. In particular, what may be construed as sliding may in fact involve microscopic 3D excursions of the protein from DNA, where the residence time and distances are too short to be resolved by current single molecule approaches^3,15,21. Different limitations apply to ensemble kinetic approaches, where the kinetic pathways of interest are very rapid, and often occur after the slower steps of catalysis or product release, obscuring the time scales for hopping and sliding events that may be occurring.

In this report, we describe an entirely new “molecular clock” approach to dissect sliding and hopping events of the human DNA repair enzyme uracil DNA glycosylase (hUNG) on DNA, and to determine microscopic details of its target search process that have been previously inaccessible (Fig. 1). The highly optimized target search by hUNG allows it to locate and excise damaged uracil bases in either single stranded or duplex DNA, making this enzyme a master catalyst in uracil damage repair, as well as adaptive immunity²².

Figure 1.

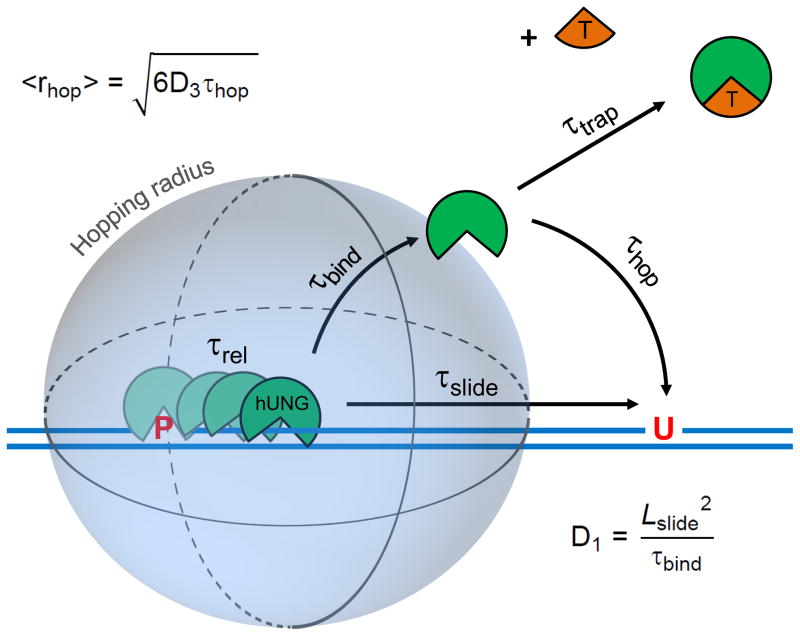
The molecular clock approach for timing pathways for facilitated diffusion on DNA. The molecular clock begins when hUNG is released from the abasic site product (P) produced from its excision of uracil from one site in DNA and then begins its journey to the second site (U) by either hopping or sliding. The rate-limiting product release step occurs with a characteristic release time (τ_rel), after which hUNG is bound non-specifically to DNA with a lifetime τ_bind = 1/k_off. The hopping pathway involves one or more dissociation events from non-specific DNA to generate a free enzyme molecule that is still very close to the original DNA chain from which it dissociated. The free lifetime (τ_hop) of a dissociated enzyme molecule following the hopping pathway will depend on its 3D diffusion constant (D₃) and its distance from the DNA chain (r). In contrast, the sliding pathway involves direct transfer of an enzyme molecule to the second site without dissociation. The sliding length (L_slide) will depend on how long the enzyme remains bound to non-specific DNA (τ_bind) and its 1D diffusion constant (D₁). The timing mechanism of the clock is provided by the concentration and diffusion constant of a small molecule trap (T) that can capture hopping, but not sliding enzyme molecules. The molecular clock can be used to calculate D₁ and the hopping radius (<r_hop>), which is the distance at which half of the hopping enzyme molecules are trapped and half find the second target site successfully by hopping (see text).

Results

Timing DNA hopping and sliding pathways

Molecular clocks are molecules that react with a known time constant, and therefore, allow the clocking of other molecular events that occur on a similar time scale. A classic example are the radical clocks²³, but other molecular clocks have been used successfully to measure lifetimes of reactive intermediates that occur during a variety of chemical transformations^24,25. In the present case we wish to clock the DNA hopping and sliding pathways used by the human DNA repair enzyme, uracil DNA glycosylase (hUNG), as it departs one target site in DNA and transfers to a second nearby site in the same DNA molecule (Fig. 1). To separately clock the hopping and sliding pathways for transfer, we envisioned that a small molecule active site-directed inhibitor of the enzyme would selectively trap enzyme molecules that had dissociated from the DNA during a hopping event, while leaving sliding enzyme molecules unperturbed because their active sites would be shielded from the trap by DNA. The ideal trap (T) should have the following properties: (i) The trap should not bind too tightly to the enzyme, otherwise all of the enzymes molecules will be in the inhibited ET form and the rate of reaction will be prohibitively slow. Thus, a weak binding trap is essential (K_i ~ 1 mM). (ii) The trap must be sufficiently soluble such that high millimolar concentrations can be achieved. This is an essential requirement because the trap must densely populate the solution volume surrounding the dissociated enzyme such that the trap has an opportunity to diffuse to the enzyme active site during the lifetime of the hopping event. In other words, 1/k_trap[T] = τ_trap must be comparable to the lifetime of the dissociated hopping enzyme (τ_hop) (Fig. 1). (iii) Finally, the trap must not bind to DNA and interfere with the sliding pathway. In the case of hUNG, these trap criteria were met by the previously characterized active site inhibitor uracil (U)²⁶, which has a K_i = 0.3 mM²⁷, solubility in water of at least 20 mM at 37 °C, and it does not interfere with binding of hUNG to nonspecific DNA (Supplementary Results, Supplementary Fig. 1).

Intramolecular Site Transfer by hUNG

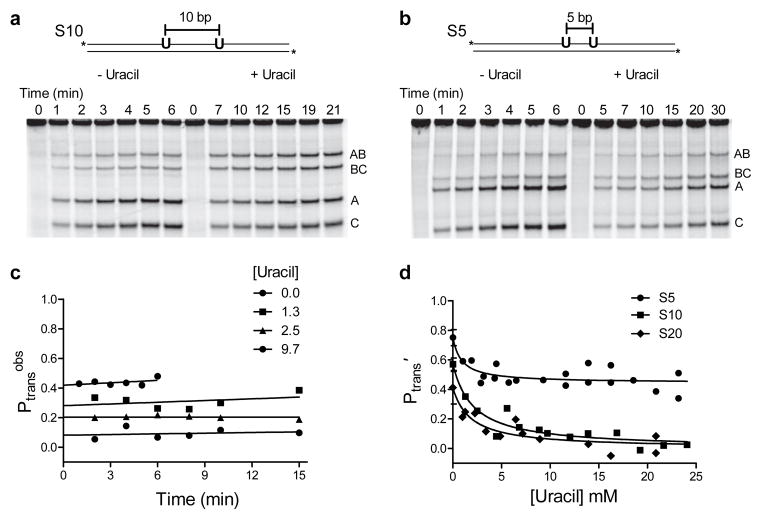
To measure facilitated transfer of hUNG between two uracil sites spaced 5 to 55 bp apart on the same strand in duplex DNA (designated as S5, S6, S10, S20 and S55) in the presence and absence of the uracil trap, we employed an assay that had been previously developed to study facilitated diffusion of Escherichia coli UNG (eUNG)⁷. This initial rate, steady-state assay quantifies the fraction of enzyme molecules that react at one uracil site and then transfer and excise uracil at the second site without dissociating to bulk solution (Fig. 2a, b)⁸. After appropriate sample processing (see Methods), the uracil excision events produce discrete fragments of the product DNA. Distributive single site excision events lead to the larger fragments AB and BC, while processive double excision events lead to an excess of the smaller fragments A and C (Fig. 2a, b). Thus, intramolecular transfer is qualitatively indicated by an excess of the double excision products A and C relative to the single excision products AB and BC. The overall probability for intramolecular site excision (P_trans) is precisely calculated by linearly extrapolating to zero time the transfer efficiency at each time point in the progress of the reaction (P_trans^obs) using eq 1 (Fig. 2c).

Figure 2.

Facilitated site transfer by human uracil DNA glycosylase (hUNG). In all facilitated transfer assays the hUNG concentration is 5–20 pM and the DNA substrate concentration is 40 nM. (a) Facilitated site transfer of hUNG between two uracil sites on the same DNA strand separated by 10 bps (S10). Reactions in the absence and presence of 10 mM uracil are shown. Facilitated transfer is qualitatively indicated by an excess of double excision fragments (A and C) relative single site excision products (AB and BC). (b) Facilitated site transfer by hUNG between sites separated by 5 bp (S5) in the absence and presence of 10 mM uracil. (c) Observed probability of site transfer (P_trans^obs) as a function of time and uracil concentration for the substrate with a 10 bp site separation. Linear extrapolation to the y axis provides the true transfer probability at zero time (P_trans). (d) P_trans′ as a function of increasing uracil for substrates with 5, 10 and 20 bp site spacings. Each data point represents an individual experiment as in panels a and b and the prime notation indicates correction for the efficiency of excision (see text). The non-linear least squares fits in (d) use a kinetic partitioning model that relates the dependence of the total transfer probability (P_trans′ = P_slide′ + P_hop′) to the uracil trap concentration (Supplementary Methods). Uncut gel images are shown in Supplementary Fig. 6. Error bars represent the mean ± 1 s.d. of at least three independent trials.

$${{\text{P}}_{\text{trans}}}^{\text{obs}}=\frac{[\text{A}]+[\text{C}]-[\text{BC}]-[\text{AB}]}{[\text{A}]+[\text{C}]+[\text{BC}]+[\text{AB}]}$$ [1]

P_trans consists of two distinct and measurable components (P_trans = E × P_trans′): the site transfer probability (P_trans′) and the efficiency (E) of excising the second uracil as opposed to falling off the DNA once the second site is reached⁷. Accordingly, we divide P_trans by the measured E value for the cleavage reaction to isolate the site transfer probability P_trans′ (Supplementary Methods and Supplementary Fig. 2).

In the absence of the uracil trap, P_trans′ for hUNG decreased with increasing site separation from 0.75 ± 0.05 at 5 bp separation to 0.27 ± 0.08 at 55 bp separation (Supplementary Fig. 3). For site spacings between 20 and 55 base pairs, human hUNG showed indistinguishable transfer probabilities as compared to previous measurements of eUNG (Supplementary Fig. 3)⁷. Notably, for spacings greater than 20 bp, P_trans′ for both enzymes followed a 1/r dependence (where r is the site spacing in nm), as expected for a transfer mechanism involving hopping²⁸. Thus, it was remarkable that there was no change in the site search mechanism of these enzymes, even though the human and bacterial genomes differ in size by over 1000-fold, and the former is condensed into chromatin structures that differ significantly from bacterial DNA architectures. Apparently, the search mechanism was optimized early during evolution, and further increases in genome complexity have not provided a selection pressure for further variation.

For hUNG, we made measurements of P_trans′ at very short site spacings from 5 to 10 bp (Fig. 2a, 2b), and deviations from the 1/r dependence expected from hopping were observed (Supplementary Fig. 3). This result suggested that a change to a sliding transfer pathway might be occurring at short site spacings. To explore this possibility further, we measured P_trans′ for S5, S10 and S20 in the presence of increasing concentrations of the uracil trap, with the goal of dissecting P_trans′ into separate sliding and hopping transfer probabilities (P_slide′ and P_hop′, respectively). For substrates S10 and S20, transfer was completely ablated at uracil concentrations greater than 10 mM (Fig. 2a, c, d), indicating that at least one hopping event from the DNA had occurred, even with a short 10 bp spacing. In contrast, for S5 the transfer probability plateaued at P_trans′ = 0.47 ± 0.08, even at the highest uracil concentrations achievable (Fig. 2b, d), indicating that a large fraction of the enzyme molecules that depart the first site make it to the second site 5 bp away without hopping. The curves in Fig. 2d are fitted to eq 2(derived in Supplementary Methods),

$${{\text{P}}_{\text{trans}}}^{\prime }={{\text{P}}_{\text{slide}}}^{\prime }+{\text{P}}_{\text{off}}\left(\frac{k_{\text{hop}}^{\prime }}{k_{\text{hop}}^{\prime }+k_{\text{trap}}[\text{trap}]}\right)$$ [2]

which describes the probability of transfer via two parallel pathways (sliding or hopping) as a function of trap concentration (Fig. 1). It is significant that the experimental findings match the two major expectations from this mechanism: the contribution of the hopping pathway decreases in a hyperbolic manner according to the trap concentration, and a second pathway that is refractory to trap persists at short, but not longer, site spacings.

We excluded other explanations for these results. The decreased intramolecular transfer observed in the presence of uracil does not involve uracil binding to the DNA and subsequent disruption of DNA sliding by the enzyme, because binding of hUNG to nonspecific DNA is unaffected by the presence of uracil (Supplementary Fig. 1). In addition, if uracil binding to DNA were important, this binding should disrupt sliding in all the DNA constructs, yet a non-zero plateau value for P_trans′ persists for S5 between 5 and 20 mM [uracil] (Fig. 2d). In addition, we show below that transfer between two uracils placed five base pairs apart on opposite strands of the DNA is largely negated by the uracil trap, indicating that the plateau value observed with S5 is due to a distinct transfer pathway (likely strand specific sliding, see below). In addition, we excluded the possibility that Group I or II salts in the uracil stock might have disrupted transfer by ICP-MS analysis [all ions < 1:1000 (mol/mol) compared to uracil], and ¹H NMR confirmed the purity of the uracil stock with respect to organic contaminants.

The mean sliding length is four base pairs

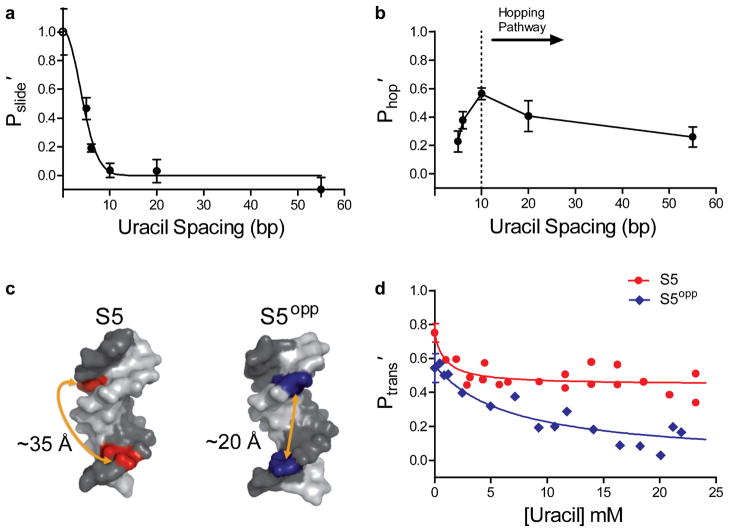
If hUNG uses 1D sliding over distances less than 10 bp, a plot of P_slide′ against uracil spacing (in bp) will follow an S^N dependence, where N = bp² is the number of steps taken in the 1D walk²⁸. To test these expectations, we plotted the sliding contribution (P_slide′) to the overall transfer probability against bp spacing for S5 through S55 (Fig. 3a). The data corresponded well to the 1D random walk model, as the probability of transfer to the second site decreased sharply with increased spacing, with a mean sliding length of 4.2 ± 0.8 bp. A similar plot of the hopping probability (P_hop′) against bp spacing for S5 through S55 showed a broad site spacing dependence as expected for a pathway involving hopping events (Fig. 3b). Notably, this plot shows a downward deviation at spacings less than 10 bp (dotted line, Fig. 3b), indicating that a significant fraction of the transfer events occur by the sliding pathway for spacings less than 10 bp.

Figure 3.

Probability of sliding (P_slide′) and hopping (P_hop′) as a function of site spacing and strand positioning of uracils. The individual contributions of the sliding and hopping pathways at each site spacing were determined by measuring the limiting P_trans′ at high concentrations of uracil (sliding only), and the difference between the P_trans at zero and high concentrations of uracil (hopping only). (a) Site spacing dependence of P_slide′. The non-linear least squares fit to the function P_slide′ = S^N is shown, where S is a constant and N is the site spacing in bp squared²⁸. The maximal efficiency of a sliding enzyme at zero spacing is 1.0 and is equivalent to the efficiency of excision (open circle). The mean sliding length (L_slide) was calculated from the spacing at P_slide′ = 0.5 and was determined to be 4.2 ± 0.8 bp where the error represents the 95% confidence interval of the least squares fit. (b) Site spacing dependence of P_hop′. The dotted line indicates the approximate base pair separation where a change from a predominantly hopping to sliding pathway for facilitated transfer occurs. (c) Structural models of B-DNA helices illustrating the position and approximate distances of two uracils positioned on the same (S5) or opposite DNA strand (S5^opp). Images were made in Pymol^™ using PDB I.D. 2L8Q. (d) Transfer efficiencies for S5 and S5^opp as a function of uracil concentration. Error bars represent the mean ± 1 s.d. of at least three independent trials.

Strand preference and salt dependence of sliding

We reasoned that if the untrappable component to P_trans′ was truly a result of hUNG sliding on a DNA strand or groove, this component (P_slide′) would disappear if the two uracil sites were placed on opposite strands of the DNA³. To test this prediction, transfer efficiencies were measured at increasing concentrations of uracil using a substrate with uracil sites spaced 5 bp apart, but located on opposite strands of the duplex (S5^opp, Fig. 3c). Without the addition of uracil, P_trans′ for S5^opp (0.54 ± 0.08) was found to be lower than S5 (0.75 ± 0.05). Moreover, S5^opp differed markedly in its response to uracil, with P_trans′ falling to nearly zero as the uracil concentration was increased (Fig. 3d). The distinct responses of these substrates to the uracil trap establishes that hUNG reaches a uracil target on the same strand using both hopping and sliding pathways, but that the enzyme must always complete at least one dissociation/reorientation event in order to transfer to a uracil site on the opposite strand even when they are only 5 bp apart³.

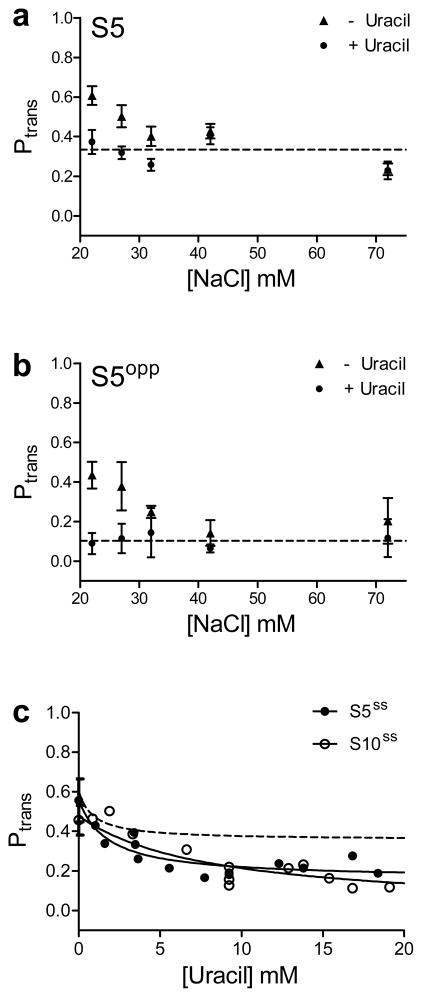
Another expectation is that a sliding enzyme would be insensitive to the ionic strength of the bulk solution², while a hopping enzyme would allow ions to recondense around the DNA chain after dissociation, thereby reducing the transfer efficiency of hopping. We tested the salt concentration dependence of P_trans for both S5 and S5^opp in the presence and absence of 10 mM uracil (Fig. 4a, b). For S5 in the absence of uracil, P_trans diminished by about 50% over the NaCl concentration range ~20–35 mM, and then plateaus at P_trans ~ 0.3 over the range 35 – 75 mM NaCl. (We do not correct P_trans for the uracil excision efficiency (E) in these experiments because E has not been measured at each salt concentration.) For S5 in the presence of uracil, P_trans ~ 0.3 over the entire range of salt concentrations investigated, which is equivalent to the plateau value that is reached in the absence of uracil. For S5^opp, P_trans approaches zero (0.13 ± 0.09, dotted line Fig. 4b) as the salt concentration increases, which is the expected transfer efficiency at high concentrations of uracil (see Fig. 3d). The distinct behaviors of S5 and S5^opp towards added salt and uracil, support the proposal that a sliding (salt resistant) pathway operates with S5, but in the case of S5^opp a hopping event must occur to reach the opposite strand.

Figure 4.

Site transfer dependence with increasing salt and in the context of single stranded DNA. No correction for the cleavage efficiency (E) was made in these transfer measurements. (a & b) Transfer probabilities for substrate S5 and S5^opp with and without the addition of 10 mM uracil as a function of increasing [NaCl]. For both substrates with increasing NaCl, the transfer probabilities plateau at the level observed in the presence of uracil. The average salt-independent values for P_trans in the presence of uracil are indicated by the dotted lines in panels (a) & (b). For both (a) & (b) in the presence of uracil, the P_trans value at 22 mM NaCl is the plateau average with increasing uracil (Fig. 2d and Fig. 4b). (c) hUNG slides on single stranded DNA. Transfer probabilities were measured for a 90mer substrate with uracils positioned 5 and 10 bp apart (S5^ss, S10^ss). The plateau in P_trans for S5^ss andS10^ss equals 0.22 ± 0.04 and 0.16 ± 0.05 respectively. For comparison, the dashed line is the theoretical fit to the data for the duplex form S5 (also with no correction for the cleavage efficiency). Error bars represent the mean ± 1 s.d. of at least three independent trials.

hUNG slides using the DNA phosphate backbone

To gain insight into whether DNA grooves or the phosphate backbone were essential for hUNG sliding, transfer efficiencies were measured on a single stranded DNA substrate. We designed 90 mer sequences containing uracil sites positioned 5 and 10 bp apart (S5^ss andS10^ss) that had no potential for secondary structure formation that might give rise to differential catalytic efficiency at the uracil sites (see Methods).

For S5^ss and S10^ss in the absence of uracil, the measured values for P_trans (0.56 ± 0.11 and 0.46 ± 0.08) were near that of the respective duplex DNA forms (Fig. 4c). In contrast to the behavior of duplex DNA, S5^ss and S10^ss both showed a plateau in P_trans (0.22 ± 0.04 and 0.16 ± 0.05) in response to increasing uracil, indicating that the mean sliding length is longer for single stranded DNA. It is possible that the additional flexibility of single stranded DNA allows enhanced tracking of the phosphate backbone compared to the more rigid duplex DNA, although other mechanisms are certainly possible. The observation of sliding on this single stranded substrate establishes that the major or minor groove of duplex DNA are not essential for sliding and supports a mechanism involving primarily phosphate backbone tracking. Such a mechanism is entirely consistent with the observation that hUNG preferentially locates uracils by sliding on the same DNA strand in duplex DNA (Fig. 3d).

Discussion

The molecular clock allows measurement of several key microscopic aspects of DNA sliding and hopping that have been previously inaccessible. First, the 1D diffusion constant (D₁) may be calculated using eq 3^2,29,30, using the mean sliding length of 4 bp (Fig. 3a), and the binding lifetime of hUNG to non-target DNA (τ_bind = 1/K_D k_on = 3 ms) (Supplementary Methods, Supplementary Fig. 1 and Supplementary Fig. 5).

$${\text{D}}_1=\frac{{L_{\text{slide}}}^2}{{\tau }_{\text{bind}}}$$ [3]

This approach yields D₁ = 6.0 × 10³ bp²/s = 6.9 × 10⁻⁴ μm²/s which is several orders of magnitude less than the theoretical maximum for sliding (~1 × 10⁷ bp²/s or ~1 μm²/s, Supplementary Methods)^2,31,32. As compared to previous single molecule measurements of the human 8-oxoG glycosylase enzyme (hOGG1)¹⁷, an enzyme that recognizes 8-oxoguanine in DNA³³, the 1D diffusion process of hUNG has a higher activation barrier (~7 k_BT as compared to ~k_BT for hOgg1, Supplementary Methods), and a much shorter mean sliding length (4 bp versus versus ~400 bp for hOGG1). Nevertheless, the short lifetime of hUNG on DNA allows it to dissociate often and then rapidly diffuse short distances by 3D diffusion, which efficiently leads to reassociation with the nearby DNA chain. This iterative use of slower short range sliding and rapid 3D hopping is highly desirable because it allows rapid and comprehensive searching of both DNA strands, and this mechanism can operate even in the presence of bound proteins. Accordingly, these results nicely account for the observation that human alkyladenine DNA glycosylase (AAG) can efficiently bypass bound protein obstacles during transfer between two target sites separated by only 50 base pairs¹¹.

A perplexing aspect of barrierless Brownian sliding (such as observed with hOGG1)^16,17 is that it is difficult to envision how such an extraordinarily rapid sliding process is arrested at a damaged site such that enough time is spent at the site to initiate the first steps of site specific recognition. For both hOGG1 and hUNG, these recognition events involve DNA bending, damaged base extrusion and conformational changes in these enzymes that occur on the ms time scale (1–20 ms for hOGG1^34,35), time frames that are much greater than the calculated base pair residence times of ~10⁻⁷ s per bp for barrierless sliding^16,17. In contrast, short range sliding over 4 bp within a bound lifetime of 3 ms gives a mean base pair residence time of about 0.8 ms for hUNG at 37°C, which is compatible with the time scale of uracil base pair opening motions that have been measured, as well as the dynamic motions of the enzyme that have been observed using NMR relaxation methods^36–39.

These results are the first to directly observe a strand specificity for sliding, and a requirement for phosphate backbone tracking. Although single molecule studies have suggested that proteins use rotation coupled movement around the DNA helix consistent with the Schurr model for DNA sliding¹⁶, current single-molecule methods lack the temporal and spatial resolution to exclude other explanations for these observations, such as microscopic hops in combination with strand sliding^3,15,21. Indeed, even with the high resolution of the studies presented here (~5 bp or 1.7 nm), we cannot exclude the possibility that the efficient location of a uracil site on the opposite strand by hUNG might involve a more complicated trajectory such as tumbling or rolling on the DNA helix⁴⁰.

Although hopping is frequently invoked in discussions of target site location mechanisms of enzymes, there have been no direct measurements that define the distances or time scales involved in hopping events. The data present two independent methods to estimate these parameters. The first qualitative approach we call the “DNA ruler”. If the mean hopping distance is defined as the characteristic site spacing where there is an equal probability that a dissociated enzyme molecule will be lost to bulk solution, or alternatively, hop back onto the DNA and locate the second site, this condition is approximately met at a 10 bp site spacing for hUNG (Fig. 3b)³⁰. It is important to point out that all of the transfer events that occur over a 10 bp spacing involve at least one hopping event and no direct sliding transfers (i.e 10 bp is the shortest spacing where all transfer events are trappable by uracil). Thus, 10 bp (3.4 nm) provides a reasonable boundary to the hopping distance. Using this value, and the calculated diffusion constant for hUNG (Supplementary Methods), the upper limit hopping time τ_hop ~ 20 ns can be estimated from eq 4).

$${\tau }_{\text{hop}}=\frac{<{\text{r}}_{\text{hop}}{>}^2}{6{\text{D}}_3}$$ [4]

Such short range hopping events are entirely expected because hUNG shows a preference in locating a site 10 bp away over a site located 20 bp away. If the hopping distance away from the DNA were very large compared to these site spacings, then no preference for transfer between these sites would be observed (i. e. for very long hops each site would be roughly equidistant from the dissociated enzyme). Therefore, the data are only consistent with short, fast microscopic hops which would serve to accelerate movement of the enzyme to new regions of the DNA chain. This qualitative view of short, fast microscopic hopping is quantitatively supported by the molecular clock approach that follows.

What is the characteristic distance that a hopping hUNG molecule diffuses before being trapped by uracil? This parameter, which we call the hopping radius (Fig. 1), may be estimated using the concentration of uracil trap at which 50% of the hopping transfers are eliminated ([uracil]_0.5 = 2.1 mM, Fig. 2d). Under this condition, the time constant for trapping (τ_{trap, 0.5} = 1/[uracil]_0.5 k_trap) is equal to the characteristic lifetime of the free enzyme before it hops back onto DNA (τ_hop), thereby providing a molecular clock for timing hopping events (Fig. 1). The value τ_{trap, 0.5} = 60 ns may be directly calculated from the Smoluchowski diffusion equation (Supplementary equation S3), using the measured diffusion constant of uracil⁴¹. Given that τ_{trap, 0.5} =τ_hop under the condition where 50% of the hopping events are trapped, the Einstein equation may then be used to calculate the distance (<r_hop> = 7 nm) traveled by hUNG in a hopping event of duration τ_hop using a calculated D₃ = 1.4 × 10⁸ nm²/s (Supplementary Methods) for hUNG (eq 5).

$$<{\text{r}}_{\text{hop}}>=\sqrt{6{\text{D}}_3{\tau }_{\text{hop}}}$$ [5]

Importantly, while the value for <r_hop> is based on an estimate of the bimolecular diffusion rate of uracil and hUNG, uncertainty in these values does not significantly affect the calculated value for <r_hop> because of its square root dependence on τ_hop. This estimated time frame and distance for hopping agrees well with the aforementioned approach using the DNA ruler.

The above analysis uses the simplest hopping model with only a single enzyme dissociation event, which is a reasonable assumption given the short spacing between sites (Fig. 1). With this model, the total distance traveled by hUNG during τ_hop is the maximum distance possible for a single hop. If a more complex model employing multiple microscopic hopping steps is used, with each hopping step leading to a possible uracil trapping event, the hopping distance would be reduced from that of the single hop model. However, since hopping is sensitive to increasing ionic strength (Fig. 4a, b), hUNG must escape the ion atmosphere of the DNA (~1 nm)⁴² during hops. Therefore, the data brackets the boundary for hopping in the range of 1 to 7 nm.

The general picture that emerges from these measurements is that frequent hopping events (≥1 hop/3 ms) result in dissociated hUNG molecules that escape the ion atmosphere around the DNA, but these enzyme molecules remain in close proximity to the DNA chain (within 7 nm) allowing very rapid reassociation by hopping (k_hop ~ 20 × 10⁶ s⁻¹). Thus, DNA hopping through solution is rapid compared with scanning, and the two pathways work synergistically along with the dynamic time scale of enzyme and DNA motions to result in efficient recognition of damaged uracil bases.

Methods

Described in the Supplementary Methods are the theory and derivation of equations for the molecular clock approach, hUNG non-specific DNA binding measurements, steady state kinetics of uracil excision, and the determination of the excision efficiency.

Oligonucleotide and protein reagents

Wild type human Uracil DNA Glycosylase (hUNG) was purified as the catalytic N-terminal truncated form (amino acids 82–304). Specifically the DNA encoding the hUNG amino acid sequence was cloned into a pET-21a vector and expressed in Bl21-DE3 E.Coli cells. Briefly, cells containing the hUNG encoding vector were grown in 1 Liter of Luria Broth at 37 °C to an OD₆₀₀ of 0.4 and then to an OD₆₀₀ = 0.6 at 16 °C. hUNG expression was then induced by the addition of IPTG and the cells were grown at 16 °C overnight. The cells were then harvested by centrifugation and then resuspended in Buffer A (50 mM Tris-Acetate pH 7.0, 10 mM NaCl, 1mM DTT) followed by cell lysis using a microfluidizer. The supernatant was then clarified by centrifugation at 40,000 ×g for 45 minutes at 4 °C and directly loaded onto an anion exchange column (UNO-Q12 purchased from BioRad^™). The flow through fractions containing hUNG were then loaded onto a Mono-S cation exchange column (GE) that had been preequilibrated with buffer A. hUNG was then purified by gradient elution with Buffer A containing 800 mM NaCl. The final step was gel filtration using BioRad^™ P-40 resin. The purified protein was then dialyzed and concentrated into 10 mM sodium phosphate pH 8.0, 150 mM NaCl, 1 mM DTT, 50% glycerol and then stored at −20 °C. The concentrations of hUNG stock solutions were determined using the absorbance at 280 nm and an extinction coefficient of 33.68 mM⁻¹ cm⁻¹.

Oligonucleotides were purchased from Integrated DNA technologies (www.idtdna.com) and purified in house by denaturing gel. Concentrations of stock solutions were determined by the absorbance at 260 nm using extinction coefficients calculated from nearest neighbor parameters. All oligonucleotide sequences used in this study are listed in full in the Supplementary Methods.

Intramolecular transfer assay

Each duplex strand was labeled on the 5′ end with P³³ by incubation with [γ³³P] ATP (Perkin-Elmer) and T4 polynucleotide kinase (New England Biolabs). The 5′-labeled strands were then hybridized by heating to 95 °C in a heat block and after 10 minutes the block was allowed to cool to room temperature. Unincorporated [γ³³P] ATP was then removed by gel filtration.

For the intramolecular transfer assay each reaction contained 40 nM ³³P-labeled duplex DNA substrate in 20 mM HEPES pH 7.5, 0.002% Brij 35, 3 mM EDTA (added from stock at pH 8.0), and 1 mM DTT in a total volume of 28 μl total. The pH of all buffer stocks were adjusted with sodium hydroxide giving a final [Na⁺] of 22 mM. The reaction was then initiated by the addition of 2 μl of human UNG (hUNG) to a final concentration of 5–20 pM and incubated at 37 °C. At each time point 4 μl of the reaction mix was taken out and quenched with Uracil DNA Glycosylase Inhibitor (UGI) at a final concentration of 0.1 Units (New England Biolabs) or 50 nM final concentration of a highly potent duplex DNA inhibitor (2′-fluoro-2′-deoxyuridine paired with 4-methylindole in duplex DNA)^7,43, both of which rapidly and efficiently quenched hUNG activity. Following reaction quenching, each aliquot was treated with human abasic endonuclease (APE1) and the nicking enzyme Nt.BbvCI to generate discrete double stranded fragments as previously described⁷. The fragments were then separated on a 10% non-denaturing polyacrylamide gel (19:1 bis-acrylamide ratio, 0.5 mm thickness, run at 20 watts with 1X TBE running buffer in a model S2 sequencing gel apparatus). The gel was dried and exposed to a storage phosphor screen and imaged with a Typhoon 8600 phosphorimager (GE Healthcare).

For experiments in which uracil was present, an appropriate volume according to the final reaction concentration of a 10 mM uracil stock solution in water was dried and then reconstituted in reaction buffer. The intramolecular transfer assay was then performed exactly as above. Control reactions confirmed that the nicking and abasic site cleavage activities of Nt.BbvCI and APE1 proceeded to completion in the presence of high uracil concentrations. Importantly, the uracil solutions were prepared from uracil of the highest available purity (>99%, Sigma-Aldrich catalog# U0750). This purity was confirmed by ¹H NMR. In addition, the uracil stock was shown to be free of group I and II metals by Inductively Coupled Plasma Mass Spectrometry (ICP-MS) at the University of Georgia Center for Applied Isotope Studies (http://www.uga.edu/cais).

For S5^ss and S10^ss, the sequence was designed to eliminate potential secondary structure formation based on Watson-Crick and uracil wobble pairings. Using the hybridization prediction program mFold⁴⁴, it was determined that only a maximum of two neighboring bases could potentially pair making any secondary structure formation unlikely. For the assay, both the 5′ and 3′ ends of the DNA were labeled with [γ³²P] ATP and 3′-deoxyadenosine 5′-triphosphate (Cordycepin 5′-triphosphate),-[α-³²P] respectively by incubation with T4 polynucleotide kinase and terminal transferase (New England Biolabs). The reactions were performed as described above for duplex DNA except that the abasic sites were cleaved by the addition of a final concentration of 1M piperidine followed by heating to 90° C for 20 min. The reaction mix was then dried to completion in a vacuum centrifuge and resuspended in 50 % formamide containing trace amounts of bromophenol blue and xylene cyanol dyes. The samples were then separated on a 0.5 or 0.4 mm thick 10% denaturing (7M urea) polyacrylamide gel run in 1X TBE at 75 watts in a model S2 sequencing gel apparatus. The gels were then exposed to a storage phosphor screen. All gel images were quantified using QuantityOne^™ (Bio-Rad) by the box method. The percentage of intramolecular transfer at each time point (P_trans^obs) was then calculated using eq 1⁸. The percent transfer at zero time (P_trans) was then calculated by linear extrapolation and then divided by the site excision efficiency (E = 0.81, Supplementary Methods) to give P_trans′ (Fig. 2c, d).