Model-driven therapeutic treatment of neurological disorders: reshaping brain rhythms with neuromodulation

Abstract

Electric stimulation has been investigated for several decades to treat, with various degrees of success, a broad spectrum of neurological disorders. Historically, the development of these methods has been largely empirical but has led to a remarkably efficient, yet invasive treatment: deep brain stimulation (DBS). However, the efficiency of DBS is limited by our lack of understanding of the underlying physiological mechanisms and by the complex relationship existing between brain processing and behaviour. Biophysical modelling of brain activity, describing multi-scale spatio-temporal patterns of neuronal activity using a mathematical model and taking into account the physical properties of brain tissue, represents one way to fill this gap. In this review, we illustrate how biophysical modelling is beginning to emerge as a driving force orienting the development of innovative brain stimulation methods that may move DBS forward. We present examples of modelling works that have provided fruitful insights in regards to DBS underlying mechanisms, and others that also suggest potential improvements for this neurosurgical procedure. The reviewed literature emphasizes that biophysical modelling is a valuable tool to assist a rational development of electrical and/or magnetic brain stimulation methods tailored to both the disease and the patient's characteristics.

1. Introduction

Brain rhythms, also known as neuronal oscillations or brain waves, occur at very different scales of space and time. Indeed, single-cell oscillations range from 0.01 Hz to more than 600 Hz [1], corresponding to firing periods between 1.6 ms and 100 s, a ratio of about 6 × 10⁴. Furthermore, some brain oscillations are localized (millimetre scale), whereas others can spread up to several centimetres [2], a ratio of approximately 10³. Brain oscillations as measured by local field potentials, electroencephalographic (EEG) or magnetoencephalographic (MEG) recordings are usually classified as δ (1–4 Hz), Θ (4–7 Hz), α (8–12 Hz), β (13–30 Hz) and γ (30–100 Hz) rhythms. These oscillations are produced by large ensembles of synchronized neuronal activity and the resulting electrophysiological signals in the different frequency bands are associated with different functional states (e.g. sleep, wake and perception).

It is difficult to bridge the gap between behavioural and single-cell data. Similarly it is not obvious to determine which brain rhythms contribute to generating behaviour (e.g. how motor cortex activity generates movement execution), and which rhythms are the consequences of behaviour (e.g. how cerebral activity is induced by proprioceptive afferences). It has been debated whether brain oscillations have a functional role, or if they are an epiphenomenon of other information processing mechanisms [3,4]. One additional difficulty is that brain rhythms coexist and interact continuously with each other. In 1980, Gray et al. [5] used recordings of spike trains in the visual cortex following a visual stimulus (moving bar), and recorded oscillatory, synchronized activity between different regions of the visual cortex. The authors hypothesized that the role of the synchronized oscillations might represent characteristics of the stimulus. Moreover, this might express a general principle in cortical processing as well as in unifying different components of a pattern processed in spatially distributed circuits into a unique representation. Later on, and based on these previous experimental results, Varela [6] proposed that cognitive processes are the result of transient synchronization between neuronal assemblies in common frequency bands, therefore proposing a central role to brain oscillations in behaviour. This putative role of neuronal synchrony in cognitive processes has also been highlighted by Fries [7], who emphasized more specifically that neural synchronization at γ frequencies may play a crucial role in the coordination of cognitive processes [8]. The potential functional role of brain oscillations has been examined thoroughly by Buzsaki in his book Rhythms of the brain [9], where he examines the nature and the functional significance of brain rhythms. He focuses on the principles linking structure and function and argues that network complexity is based on the geometry of recurrent clusters having a small number of pivotal elements as the common thread [10]. He also explores the importance of inhibition and the significance of temporal coherence and patterning as the ‘machine language for the brain’ [10]. These topics, according to Buzsaki's words, ‘represent the middle grounds of brain activities between the microscopic mindless neurons and the wise, performing brain’. Therefore, establishing a relationship between brain spatio-temporal patterns and behaviour appears relevant to understanding information processing by the brain both in physiological and pathological conditions. Overall, understanding how brain rhythms are generated in physiological conditions, but also during the transition towards pathological conditions where brain rhythms change [11], is critical for the conception of innovative brain stimulation methods. This issue of brain rhythms in physiological and pathological conditions has been extensively reviewed in a recent book [12].

Distorting brain rhythms can shift brain function from a physiological to a pathological regime [13] and produce a variety of neurological disorders (motor or psychiatric). Several hypotheses have been proposed on the functional role of neuronal oscillations. As early as 1938, Gibbs et al. [14] proposed that ‘cortical dysrhythmia’, a disruption in brain rhythms, was the cause of neurological and neuropsychiatric disorders. Furthermore, the concept of ‘thalamocortical dysrhythmia’ introduced by Llinas et al. [15] suggests that positive and negative symptoms can be explained by intricate dynamics in thalamic and cortical neurons. At the base of thalamocortical dysrhythmia lies diminished excitatory or increased inhibitory input at the thalamic level, leading to a switch of thalamocortical neurons from tonic to burst firing subsequently entraining thalamic and cortical areas to pathological oscillations around 5 Hz. Current clinical data tend to support this view. Indeed, neurodegenerative disorders such as Parkinson's disease (PD) or Alzheimer's disease appear to be associated with disturbed modulation in brain rhythms with increased synchronized activity around 5 Hz and harmonics in PD [16–19], and increased δ activity (1 to 4 Hz) in Alzheimer's disease [20].

Thus, the notion that abnormal brain rhythms underlie a broad spectrum of neurological and psychiatric disorders is receiving growing experimental and clinical support. Consequently, stimuli producing appropriate neuromodulation normalizing brain rhythms supposed to cause symptoms are likely to result in positive clinical outcomes. In this paper, we focus on a well-known form of therapeutic brain stimulation, namely deep brain stimulation (DBS) in PD, which is today an accepted, well documented and established neuromodulation method. Moreover, this treatment has revealed its therapeutic benefits over the last 20 years by demonstrating a normalization of brain rhythms. In this review, we present how biophysical modelling efforts are exploiting the functional role of brain rhythms to explore underlying physiological mechanisms of DBS in PD, and also models proposing improvements of DBS as it is performed today. Challenges for experimental testing of these models are discussed.

2. Neuromodulation induced by deep brain stimulation in parkinson's disease

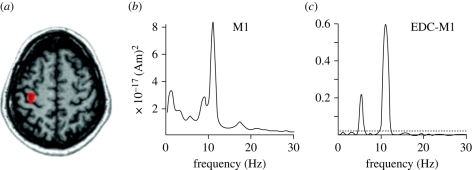
Parkinson's disease is a neurological disorder resulting in motor (tremor, rigidity, slowness of movements and postural instability) and cognitive (speech difficulties and depression) symptoms. The underlying neurological substrate of these symptoms is the gradual destruction of dopaminergic neurons in the substantia nigra pars compacta. However, non-motor symptoms involve not only the central dopaminergic system, but also the noradrenergic, serotoninergic and cholinergic transmitter systems. Decreased dopamine, normally present in numerous brain regions under physiological condition, leads to disrupted activity in both cortical (e.g. primary motor cortex, supplementary motor area and pre-motor cortex) and subcortical structures (e.g. subthalamic nucleus, internal segment of the globus pallidus and ventrointermediate nucleus of the thalamus). This pathological activity is characterized by increased synchrony (i.e. neurons tend to fire simultaneously) in narrow frequency bands. For example, subthalamic neuron firing activity occurs mainly at 5 Hz, which is also a common frequency of Parkinsonian tremor (4–6 Hz [21,22]), whereas primary motor cortex activity is prominent at twice the tremor frequency according to magnetoencephalography recordings (maximal activity at 10 Hz [19]). Figure 1 presents an example of coherence between central nervous system activity (as measured by magnetoencephalography) and muscular activity (as measured by electromyography) at tremor frequency (around 5 Hz), illustrating the potential functional role of abnormal brain rhythms.

Figure 1.

Localization, Fourier transform and coherence values between primary motor cortex activity (as measured by magnetoencephalography) and peripheral rest tremor (as measured by electromyography) in a PD patient. (a) Indication of where the magnetoencephalographic (MEG) signal is recorded (red area). (b) The power spectrum of MEG signal in the primary motor cortex, which features a noticeable peak centred at 10 Hz. (c) The cerebro-muscular coherence between the MEG signal in the primary motor cortex and the electromyographic signal measured at the extensor digitorum communis (EDC) level, with a maximum value around 10 Hz. (Figure modified from Timmermann et al. [19], with permission.)

It is still unclear if pathological brain activity drives PD peripheral tremor or if it is the reverse, but experimental evidence suggests that Parkinsonian tremor originates from low-frequency, synchronized activity of a network of brain structures [19]. This issue has been challenged in works examining motor cortex activity and essential tremor, which suggested that the motor cortex is the generator of essential tremor [19,23,24]. In 1987, Dr Alim-Louis Benabid discovered incidentally that sending electrical pulses at high frequency (greater than 100 Hz) in the thalamic ventrointermediate nucleus of PD patients dramatically relieved tremor [25]. Since then, between 40 000 and 50 000 PD patients benefited from this technique [26] called DBS. DBS is today an established neurosurgical technique, which relieves efficiently motor and non-motor symptoms of PD. Usual targets of DBS include the subthalamic nucleus, the internal segment of the globus pallidus and the thalamus. The paradox is that, even if DBS is an effective therapy for many PD sufferers, the underlying mechanism of action is still unknown. Therefore, clinicians must rely on a trial and error approach to provide appropriate device settings for each patient. Consequently, advances in biophysical modelling might provide innovative solutions based on rational principles, thereby improving this empirical aspect of DBS as it is performed today. One possible direction is by tailoring therapy to the needs of patients and updating stimulation patterns more frequently and adequately.

3. Mathematical models of brain oscillations

It is possible to use different mathematical models to understand how oscillations can emerge in neural networks. A simple illustration is to consider a two-population network (one excitatory and one inhibitory) [27], where each population is described by its firing rate and corresponding evolution equation. By computing the equilibrium point of the system (derivative of the firing rate set to zero for both populations), and linearizing firing rate equations around this point, it is possible to compute the Jacobian matrix and its eigen values that determine the stability of the equilibrium (see [28] for illustrated examples): if they are all negative, then the equilibrium point (corresponding to a steady firing rate for both populations) is stable; otherwise if at least one eigen value is positive, then the equilibrium point is unstable and oscillations appear. Therefore, oscillations are the result of a dynamical instability occurring when control parameters of the system vary (such as connectivity parameters or membrane time constants in this example).

Oscillations and stability of neural networks have been extensively studied from a mathematical modelling perspective. In their pioneer work on neural field theory, Wilson & Cowan showed that, in a neural field model (spatio-temporal dynamics of continuous cortical tissue), the oscillation frequency was directly proportional to the stimulus intensity, in line with increased neural firing rate caused by higher electric stimulation amplitude [29]. Furthermore, under certain conditions, these oscillations could propagate through the network, giving rise to waves of electrical activity propagating in cortical tissue [30]. Along the same lines, Ermentrout & Cowan [31] provided a mathematical study on a network of excitatory and inhibitory populations investigating the conditions (connectivity parameters within and between populations) allowing the emergence of oscillations in networks of excitatory and inhibitory cortical neurons. Their results indicated that strong recurrent inhibition and strong excitatory projections towards excitatory neurons promote high-frequency oscillations, while weak recurrent excitatory and inhibitory projections give rise to low-frequency oscillations, providing a link between network architecture (structure) and activity (function). The influence of time delays induced by finite conduction times of action potentials has also been explored [32,33], and provides evidence that time delays may affect the stability of neural networks. Hutt et al. [34] showed in a neural field model that, with first- and second-order synaptic kinetics, non-stationary patterns (oscillations) could only occur in the presence of time delays above a given value. This suggests that the presence of time delays has a functional role, since it increases the diversity of possible spatio-temporal patterns that can emerge in a neural network. Further, the distribution of delays in neural networks (since all axonal fibres do not exactly have the same length, giving a different spike conduction time) may modulate oscillation frequency [35]. Other works have also intended to link neuronal oscillations in these models in the context of brain function. An interesting concept proposed by Roopun et al. [36] is that two networks oscillating each at its own frequency could cooperate by sharing a common, new oscillation frequency that would add to their own activity; which is possible to link with function emerging from the interaction between these two networks. For example, γ oscillations have been suggested to play a role in stimulus competition [37], while a modelling study simulating neural circuits' hippocampus showed that θ oscillations may serve to encode memory in terms of spatial and temporal information [38]. Therefore, biophysical modelling has already provided numerous insights on the conditions in which neuronal oscillations occur, and at which frequency, and may assist in unravelling the functional role of brain oscillations since it allows variations of any parameter and its consequences on neural networks activity.

4. Biophysical models of deep brain stimulation mechanisms

During the last decade, a growing number of models have attempted to address the problem of DBS in PD (table 1). A pioneering mathematical modelling study with the objective of improving the understanding of DBS effects in PD has been initiated by Tass [41] who used the concept of phase oscillator model to simulate the abnormally synchronized activity measured experimentally in deep brain regions of patients with PD [18]. Indeed, Kuramoto showed in 1975 [42] that it was possible to reproduce synchronization phenomena using a model of the form

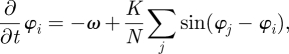4.1

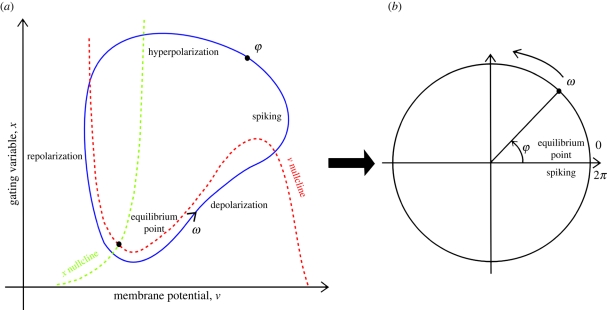
where φ is the oscillation phase and varies between 0 and 2π, i.e. the position of the neuron in its oscillation cycle, K the global coupling factor and N the number of oscillators. Phase oscillators represent a convenient way of modelling neuronal oscillatory activity. If a neuron is regularly spiking at an eigen frequency such that ω = 2πf, there exists a limit cycle in the phase space, i.e. a closed trajectory in the space of the neuron state variables. By mapping this trajectory (figure 2a) on a circle (figure 2b), then the neuron spiking activity can be described using a single variable: its phase φ. By doing so, we assume that a neuron can be seen as an oscillator of fixed frequency.

Table 1.

Summary of the main modelling approaches that have been used to study the question of DBS effects in PD. The main underlying assumptions and possibilities of these models are mentioned.

	single-compartment spiking neuron models	phase oscillator models	multi-compartmental spiking neuron models	neural field models
assumptions	neuron soma membrane is considered a point capacitor. The timing of spikes is relevant to understanding and describing neuronal activity	neuronal regular spiking can be summarized by a single variable: the oscillation phase. Oscillators are then coupled typically using a mean coupling coefficient	neuronal geometry can be decomposed into smaller elements, each being described by Hodgkin–Huxley equations. Such neurons are then ‘synaptically’ connected by coupling together the system of equations describing individual neurons, including synaptic currents	cortical tissue is a continuous medium composed of interconnected neural masses (i.e. a cortical column). The firing rate is relevant to understand and describe neuronal activity
possibilities	describes the time course of the membrane potential in response to synaptic currents, can describe the effect of an arbitrary number of ionic channels with specific properties	describes concisely large neuronal networks, and efficiently reproduces synchronization phenomena caused by coupling between phase oscillators	describes accurately how the membrane potential is affected in space and time by external stimulation and how various parts of the neuron are affected. The effect of external electric stimulation on axonal fibres can be studied	predicts spatio-temporal patterns of neuronal activity (travelling waves, spiral waves and visual hallucinations patterns)
limitations	unable to take into account axonal activation, become rapidly computationally extensive	unable to reproduce specific (brain region-dependent) or complex spiking patterns (bursting, post-inhibitory spiking)	computationally extensive, limiting the number of neurons possibly simulated	no access to single neuron activity. The effect of ionic channel type and kinetics cannot be investigated
examples	[39,40]	[41–44]	[45]	[30,31,34,46]

Figure 2.

Illustration of the relationship between the oscillation phase and the polarization state of the neuron membrane (see [47]). A neuron regularly spiking ((a) for a representation of neuron trajectory in the phase space) can be represented as a point oscillating around a circle with an angular frequency ω = 2πf, the instantaneous position on the circle being the phase φ (b). From (a), one can see that different parts of the limit cycle correspond to different neuronal excitability states.

Therefore, the complexity of neuronal dynamics is captured using a single variable, at the price of losing all relevant information about ionic channel dynamics and possible complex spiking patterns. However, these models have proved useful in understanding the emergence of synchronization in coupled systems [42]. As a first attempt to understand the effects of DBS on neural synchronization and to propose a closed-loop stimulation method using biophysical modelling as a tool, Tass developed several stimulation techniques using networks of phase oscillators [41,43,44] investigating the desynchronization of phase oscillators using stimuli interacting minimally with neural tissue. To do so, Tass used the same model structure as Kuramoto [42], including a stimulation term that modulates not only the phase of the target phase oscillators, but also temporal fluctuations of the phase capturing the noise present in the time course of neurons' membrane potential. In such a phase oscillator network, the synchronization was quantified by the index

4.2

where R(t) is the real part of the time-dependent synchronization, Z(t) its amplitude and φ(t) its phase. A convenient way to illustrate in a simple manner the synchronization Z(t) of coupled phase oscillators is to represent each oscillator on a circle, with its position being its phase. If all phase oscillators are perfectly synchronized, then all oscillators are located on the same single point of the circle; conversely, if all phase oscillators are completely incoherent, then all oscillators are regularly located on the circle. This is illustrated in figure 3.

Figure 3.

Three states of a phase oscillator network, the phase of each neuron being its position on the unit circle. Each black dot indicates the phase of a given neuron (N = 12 here). (a) Neurons have their phases regularly distributed on the circle, so that the amplitude R(t) of the synchronization (coherent neuronal activity) index Z(t) vanishes, resulting in a null vector Z(t). (b) Some neurons have a similar phase, thus there is partial synchronization in the network resulting in non-zero real amplitude R(t) less than 1. (c) All neurons have the same phase yielding complete network synchronization characterized by R(t) = 1 [47].

The situation depicted in figure 3c can roughly represent a network of abnormally synchronized neurons, such as subthalamic nucleus neurons in PD [18], whereas the physiological situation would be close to the one depicted in figure 3a [43]. Therefore, in order to reduce abnormal synchronization in a network of phase oscillators in a closed-loop manner, the parameter R(t) is suitable to monitor since a threshold can be fixed, indicating when the level of synchronization is too high and stimulation should be triggered. Tass [44] showed that the effect of a high-frequency pulse train was to reset the phase of neuronal firing (i.e. preventing the neuron from moving on the circle and to cross the phase spiking value of 2π), thereby preventing neurons from spiking. This explanation is consistent with the clinical observation that DBS and lesion of the subthalamic nucleus provide similar alleviation of motor symptoms [48]. Consequently, this approach provided the first evidence that mathematical models could be complementary to experimental approaches in order to uncover the mechanisms of action of DBS.

Even if the model presented by Tass provided promising insights in the physiological mechanisms of DBS, it should be mentioned that this approach suffers from a lack of biological realism. Indeed, all the complexities of neuronal structure and dynamics are summarized into a single variable without considering complex spiking patterns in DBS targets (such as the subthalamic nucleus; see [49]). In order to overcome these caveats, a more physiologically detailed model was proposed by Terman et al. [39] More specifically, this model used a single-compartment Hodgkin–Huxley model to describe neurons from the subthalamic nucleus and the external segment of the globus pallidus. The motivation of studying these two structures is based on their supposed role in the pathophysiology of PD [50]. Moreover, in vitro culture experiments including synaptically connected subthalamic nucleus and external globus pallidus neurons have exhibited spontaneous low-frequency bursts, similar to the low-frequency oscillations observed in the subthalamic nucleus of patients with PD [51]. Therefore, this network of two subcortical structures has been proposed as a ‘pacemaker’ forcing the motor network (cortex, basal ganglia—that include the subthalamic nucleus and the external globus pallidus—and thalamus) in low-frequency oscillations responsible for the motor impairments of PD [51]. In the work of Terman et al. [39], both nuclei were modelled by eight model neurons of the Hodgkin–Huxley type:

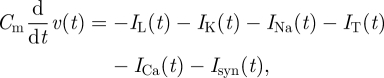4.3

where C_m is the membrane capacitance, I_L the leak current, I_K the potassium current, I_Na the sodium current, I_T the low-threshold calcium current, I_Ca the high-threshold calcium current and I_syn the sum of synaptic currents. Also, excitatory and inhibitory projections were established between and within these two structures according to neuroanatomical knowledge [39]. The level of inhibition from the striatum on the external globus pallidus was the main control parameter to simulate the transition from ‘physiological’ to ‘pathological’ (Parkinsonian) dynamics. Ionic current parameters were selected to fit to the firing patterns observed in vivo for neurons from these two structures. Importantly, the post-inhibitory bursting (burst occurring after hyperpolarizing input) of subthalamic neurons was included, which is important since it cannot be captured using phase models. This specificity pattern turns out to be of particular relevance according to Terman et al. [39], since it can lead to sustained low-frequency bursting activity. Consequently, this modelling approach has contributed to clarifying Plenz & Kitai's [51] experimental results on a potential pathophysiological mechanism for abnormal brain oscillations in PD. This work has also emphasized the relevance of using mathematical modelling to capture non-intuitive dynamical properties of neurons, such as post-inhibitory bursting.

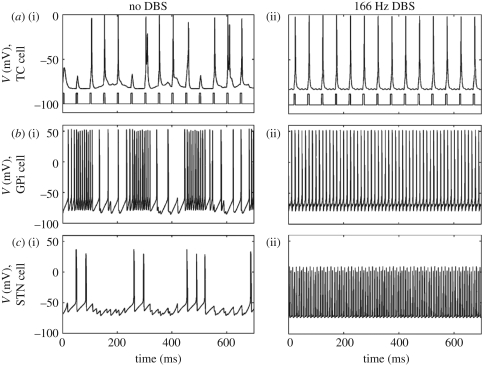
Later on, Rubin & Terman decided to expand this model to a larger network not only including the subthalamo-pallidal network, but also the internal globus pallidus and the thalamus, with the objective to investigate the effect of DBS of the subthalamic nucleus in PD [40]. As a basis to simulate pathological activity of the basal ganglia, the authors used their previously developed network of the subthalamo-pallidal network. The output of these two nuclei was sent to internal globus pallidus neurons that regulate thalamic inhibition. More precisely, two thalamic relay cells were modelled, conveying sensorimotor signal inputs to the cortex. The authors illustrate that, under a physiological situation, the subthalamo-pallidal network has irregular, unsynchronized activity and that thalamic relay cells are able to faithfully relay sensorimotor inputs to the cortex; whereas when the subthalamo-pallidal network has synchronized oscillatory activity, the ability of thalamic relay cells to relay sensorimotor signals is compromised. The capacity of thalamic relay cells to effectively relay incoming signals was quantified using an error index, i.e. the ratio of successfully conveyed signal over the total number of incoming signals. Interestingly, when a high-frequency pulse train simulating DBS is applied to subthalamic nucleus neurons, the authors show two major results: first, subthalamic neurons' activity increases and is phase-locked to DBS pulses; and second, the thalamic relay cells recover their capacity to transmit incoming sensorimotor signals to the cortex. These results are illustrated in figure 4.

Figure 4.

Activity of thalamic relay neurons (a(i,ii), TC cells), internal globus pallidus neurons (b(i,ii), GPi cells) and subthalamic neurons (c(i,ii), STN cells) without DBS—left column—and during DBS applied to subthalamic neurons—right column. (Figure modified from Rubin & Terman [40], with permission.) (a) The incoming sensorimotor inputs are shown on the bottom trace on the activity plot of the thalamic relay cells. Whereas all of these cells exhibit low-frequency bursting in the absence of stimulation—left column—thereby simulating neuronal dynamics in PD, DBS suppresses them and drives neurons to fire in a 1∶1 manner (one spike per stimulation pulse)—right column. Therefore, the pathological rhythm is replaced by another high frequency one that appears compatible with a reliable transmission of sensorimotor signals.

Consequently, the main conclusion of the authors based on this physiologically detailed model was that DBS is able to allow proper relay of motor signals by the thalamus to the cortex. This represented a major step in modelling DBS effects. It has been used to develop on-demand stimulation methods (see below) and has provided an original and plausible hypothesis on the mechanisms of DBS. However, this model suffers from several limitations [52]. First, this model assumes that the thalamus is a simple relay, while it has been shown to have a much more complex role [53]. Second, the model indicates that phase-locked spiking is induced by DBS, whereas DBS has been shown to decrease spiking activity in the subthalamic nucleus [54]. Finally, the authors use monophasic pulses, whereas biphasic, charge-balanced pulses are used clinically for safety and prevent any damage to neural tissue [55].

Recently, a new model of subthalamo-pallidal network activity during DBS has been proposed by Hahn & McIntyre [56]. In order to ground the model in experimental data, the synaptic weights were set using a least-square error optimization algorithm so that the neural structures simulated (external and internal segments of the globus pallidus, subthalamic nucleus) exhibited firing rates close to those recorded in MPTP monkeys (MPTP, or 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine, is a substance that, once absorbed, induces changes in neural activity similar to those observed in PD). Cortical afferences in the β range (13–30 Hz) were modelled as excitatory synaptic inputs to the subthalamic nucleus. Finally, 500 cells were simulated, extending by far the model of Rubin & Terman [40] that included overall less than 30 cells. When DBS was applied to subthalamic neurons at a frequency of 136 Hz, the axons were activated at high frequency as observed experimentally by Hashimoto et al. [57]. The authors observed that bursting in the internal globus pallidus was reduced to values comparable to those observed in experimental recordings in MPTP monkeys. Furthermore, they suggest the existence of a threshold in bursting reduction in internal globus pallidus neurons in order to achieve therapeutic effects. Interestingly, one result from Rubin & Terman's model was also showing that decreased bursting in the internal globus pallidus improved thalamic relay of sensorimotor inputs. Therefore, the modulation of bursting in the internal globus pallidus might be one of the physiological mechanisms of DBS in PD.

Overall, despite the excellent clinical results of DBS, there is still room for improvement in terms of stimulation pattern, stimulation target, side effects or parameter adjustments to name a few. In the following, we present several biophysical modelling works that suggest new ways to electrically stimulate the brain in a more intelligent, real-time, closed-loop manner, as opposed to the DBS pattern used today that remains fixed over time and is not adaptive.

Consequently, from the models reviewed in this section, the combination of experimental studies and the contribution of DBS mathematical models have led to an improved understanding of DBS mechanisms and clinical settings (see [58–61] for reviews). One consistent key concept both from the experimental and biophysical modelling perspectives is that DBS apparently normalizes the activity of a brain structure's network by suppressing tremor-related synchronized activity. Interestingly, the effects of DBS in both experimental settings and most of these biophysical models appear to prevent low-frequency spiking, leading to the following paradox: why does electric stimulation inhibit neural firing, whereas it should intuitively increase it? From the phase oscillators point of view, DBS induces a phase resetting of neurons, preventing them from spiking [41]. Similarly, one proposed explanation based on resonant properties of subthalamic neuron membranes [61] is that subthalamic neurons have a considerably lower eigen frequency than therapeutic DBS frequency. As a consequence, subthalamic neuron membranes cannot respond efficiently to each DBS pulse, resulting only in subthreshold responses. Therefore, it appears that preventing neural oscillations at pathological frequencies is a major mechanism of DBS. This may serve as a starting point for the development of new methods targeting narrow frequency bands of neural activity, only where and when these frequencies are present, thereby optimizing current DBS procedures. With this objective in mind, several groups have proposed methods that could achieve the normalization of pathological brain oscillations using adaptive stimulation, which are reviewed in §5.

5. Biophysical models of possible improvements of deep brain stimulation

Despite its obvious success in relieving the incapacitating symptoms of PD, DBS also suffers from a few drawbacks (e.g. battery replacement, or potential side effects such as trouble of speech, depression or weight gain [62]). Therefore, several groups have been working in the last few years to elaborate more sophisticated methods that could provide at least similar clinical benefits as with classical DBS while being less invasive, less energy-demanding and able to adapt in real time to the fluctuations of symptoms. First of all, let us mention that the alternatives to DBS proposed by these models face several difficulties. Indeed, such methods need to be experimentally tested, which is challenging since existing experimental microrecording equipment has to be modified and approved to be used in humans, or also because recording artefacts caused by stimulation pulses must be efficiently corrected online.

One of the simplest forms of adaptive or closed-loop stimulation can be to stimulate the neuronal target with a linear function of the recorded variable, typically the mean membrane potential. This was proposed in several papers [63–65] in which the modulation of neural synchronization was studied in the presence of a linear feedback stimulus that was applied after a given delay. The principle of this method is illustrated in figure 5.

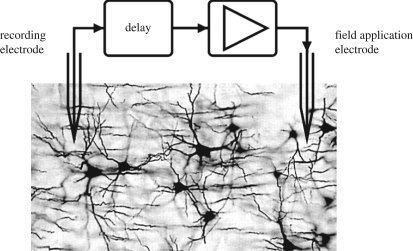
Figure 5.

Principle of the linear delayed feedback method proposed by Rosenblum & Pikovsky [63,64]. The target neural population is monitored using a recording electrode, and after a given delay, a rescaled value of the recorded signal (i.e. a given multiplicative factor is applied) is computed and used as a stimulation signal applied to the target neural population. (Figure adapted from Rosenblum et al. [65] with permission.)

This method includes only two parameters: the delay τ after which the linear feedback is sent back to the network, and the amplification factor ε_f. Therefore, the stimulation term I_f(n) depending on the recorded mean field X(n) at time n is expressed as [65]

5.1

and is added directly as an input current through the neuron membrane. Despite the apparent simplicity of this method, efficient neural desynchronization was obtained in networks based on different neuron models (e.g. [66]). Strong assets of this method include a good robustness with respect to the presence of noise, or imperfections either in the measurement of the mean field or in the effect of the stimulus on target neurons [65]. However, one limitation highlighted by Popovych et al. [67] is that, with inappropriate parameters, linear delayed feedback can enhance neural synchronization and produce a completely opposite effect.

Based on his previously developed phase oscillator network model, Tass developed several stimulation methods effectively desynchronizing networks of phase oscillators. These methods include the use of a high-frequency pulse train followed by a silent time period and finally a single stimulation pulse [43]. This pattern is repeated when needed. It was highlighted that the goal of these methods is not to shut down neural activity, but only to modulate the level of synchrony between neurons [44] following a two-stage action: first, the population of neurons is shifted to a desynchronized state, and then a second stimulus is sent when the population re-synchronizes to block re-synchronization. Interestingly, the power consumption of these new techniques can be notably lower as compared with classical high-frequency train of pulses such as DBS. Furthermore, this method has been extended to the more realistic case of a spatially distributed target in which the stimulation was applied at different sites [68] providing again robust neural desynchronization. Using the same approach of phase oscillator network, Popovych et al. [67] proposed a novel method of closed-loop stimulation of neural networks, still with the objective of desynchronizing abnormally synchronized phase oscillators. The phase oscillator model for one single oscillator j was of the form

5.2

where a is the radius of the oscillator's limit cycle (closed trajectory in its phase space), ω its frequency, C is the coupling coefficient, Z_j(t) is the complex phase, 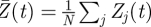is the mean field (mean phase of the network) and S_j(t) is the external stimulus applied to the oscillator j. The authors proposed one method in which the same stimulation signal was applied to each neuron (which is obviously a simplification of reality, where neurons are differently affected depending on the orientation with respect to the field, and their distance with respect to the electrode; see [59]), and which was a function of the delayed mean field (nonlinear, as opposed to the method proposed by Rosenblum & Pikovsky):

5.3

where K is a parameter and τ is the delay. Each of the individual oscillators had a different intrinsic oscillation (i.e. spiking in this approach) natural frequency ω_j Gaussian-distributed, but when sufficiently strong coupling was introduced, network synchronization around a common frequency occurred. Interestingly, when the nonlinear delayed feedback was applied, the network's synchronization decreased drastically and oscillators returned to their natural oscillation frequency [67]. In terms of application, these results could theoretically be used to desynchronize abnormally synchronized subcortical brain regions such as the subthalamic nucleus in PD. It is still debated whether abnormal synchrony may be a cause or only a consequence of a symptom; nonetheless the possibility to provide ‘on-demand’ desynchronization of target structures to improve symptoms is an appealing strategy. However, this possibility remains to be experimentally tested.

Another recent work has investigated the possibility to stimulate the primary motor cortex in PD using a closed-loop stimulation method [46,69]. The aim of this work was to control neural activity both in time and space, while only impacting a targeted frequency band (such as 10 Hz; figure 1) of neural activity. In order to model an electric stimulation applied at several spatial positions, the authors used a continuous neural field model [30,70]. In this class of models, cortical tissue is seen as a continuous two-dimensional sheet of interacting basic units called neural masses, which include of the order of 1000 excitatory and inhibitory neurons. By writing the effective potential ψ(r,t) (i.e. the deviation from the rest potential) under the form of a wave packet, the optimal stimulus to suppress neuronal activity in the frequency band [ω′, ω″] is

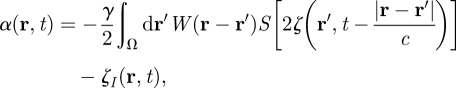5.4

where

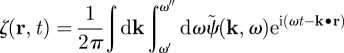and

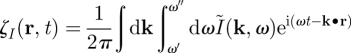with ψ(r,t) the neural field value, W(r − r′) the distance-dependent connectivity function (expressing the type—excitatory or inhibitory—and the strength of connections between neural masses), γ the synaptic coupling strength, c the propagation speed of spikes along axons, I(r,t) the input, ζ(r,t) the noise, α(r,t) the space- and time-dependent stimulus term, and where S is a sigmoid function linking the effective potential and the firing rate, taking into account the variability of firing threshold among neurons. Using this closed-loop stimulation scheme, neuronal oscillations (induced by external bursting input) of a spiking neuron network at the target frequency of 10 Hz (and also harmonics) were considerably dampened while other physiological rhythms were minimally affected [46,69]. Consequently, considering that therapeutic brain stimulation in PD should attenuate a narrow frequency band (say, 9–11 Hz in the cortex, resulting in a decrease of peripheral 4–6 Hz tremor), it is possible to derive theoretically effective stimulation signals able to adapt in real time to recorded neuronal activity. One drawback is that the causal relationship between primary motor cortex activity and Parkinsonian tremor still remains to be demonstrated. The next step is to validate such an approach experimentally by stimulating the cortex of patients with PD.

Models presented above propose new stimulation methods able to normalize neuronal synchronization around pre-determined frequencies by affecting the membrane potential (or the phase in phase oscillator model) in a closed-loop manner. However, one work by Tass & Majtanik [71] aimed at a completely different objective, namely modulating the weight (or efficiency) of synapses. Indeed, since synaptic weights determine the interaction strength between neurons' activity and the emergence of neuronal oscillations, impacting synaptic weights might be an efficient way to modulate neuronal activity. In their model [71], the authors included a synaptic plasticity rule called spike-timing-dependent plasticity in order to simulate the dynamic regulation of synaptic weight depending on the timing of pre- and post-synaptic times [72]. By contrast, the models mentioned above did not include such rules, and had fixed coupling (synaptic) coefficients. The model used by Tass & Majtanik was similar to the Kuramoto model, with the difference that individual couplings are considered instead of a single mean coupling. The model was expressed as

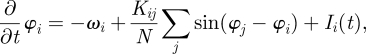5.5

where I_i(t) is the total input received by oscillator i, and with a spike-timing-dependent plasticity rule expressed as [71]

5.6

where ΔK is the variation of synaptic weight, α_p/α_d are the amplitude of potentiation and depression (i.e. increase and decrease in synaptic weight, respectively), τ_p/τ_d are the time scales of potentiation and depression and Δt is the time interval between pre- and post-synaptic spikes. When the input was chosen under the form of a high-frequency train of biphasic pulses (i.e. the pattern used in DBS), neuronal firing was drastically reduced, consistent with in vivo recordings during DBS [54]. The authors tested the effect of the previously developed multi-site stimulation [68], which resulted in a durable modulation of synaptic weights with the effect of decreasing firing activity. Though promising, this method also lacks of any experimental validation that would open the way to clinical applications.

In addition to the aforementioned models, other models are based on an alternative philosophy consisting of monitoring the target brain structure and developing a method affecting the observed variable and resulting in optimized control. Among these studies, Santaniello et al. [73] used an original approach based on control theory, and more specifically on an ARX model (autoregressive model with external inputs). In this approach, a system is considered as a black box, and it is assumed that only the inputs and the outputs are known. Then, in order to control the system towards a targeted state, an algorithm optimizes control so that the state of the system minimally differs from the desired state. Such an approach is valuable to model brain regions, since it avoids taking into account their complexity in terms of geometry and physiology. The ARX model designed to control activity in the target population of neurons (the ventrointermediate nucleus of the thalamus in their study, which is another effective DBS target to alleviate tremor; see [25]) was written as

5.7

with y(k) being the filtered output of the recorded neural population and u(k) its input, k being related to the time at which the recording takes places (t = kT, where T is the time between two recordings). The stimulation (control) term modulates the system's transfer function so that the system will finally reach the targeted state, i.e. network activity exempt from low-frequency oscillations. This method was tested on a neural population simulated by 100 multi-compartmental thalamocortical model neurons. Applying this stimulation method to the target neuron population drastically reduced tremor-related bursting activity, providing appealing evidence that sophisticated models of brain activity might not be necessary to achieve proper control of target neural population. However, physiologically detailed models of neural circuits will probably remain the gold standard to capture nonlinear responses of neural networks and provide an accurate ‘input–output’ function of neural structures.

The model proposed by Feng et al. [74] constitutes another interesting example of closed-loop stimulation paradigm that does not involve a detailed knowledge of the underlying physiological processes taking place in the target brain structure. Indeed, this work is based on the idea that the main condition for an efficient alleviation of Parkinsonian tremor is to decrease the level of synchrony between neurons of the target brain region, in the vein of Tass [41]. This objective is consistent with experimental evidences showing that several brain regions exhibit a high level of synchrony in PD and not in a physiological situation [18]. To achieve this objective, the authors propose to quantify the level of synchrony among the recorded neurons, and to use this quantity to provide appropriate control: if the level of synchrony is high, then stimulation should be applied, and if the level of synchrony is back to physiological levels, stimulation should not be applied. In order to optimize stimulation parameters towards the objective of normalizing neural synchrony, the authors used a genetic algorithm. In brief, this algorithm retains efficient and inefficient stimulation parameter values, and combines together efficient sets of parameters in order to evaluate the efficiency of new stimulation parameter values. To investigate the capabilities of such a stimulation algorithm, the authors used the model of Rubin & Terman [40] (presented above) as a model of the brain structures involved in the generation of Parkinsonian tremor. By doing so, the authors put forward interesting conclusions such as the possibility that stochastic (as opposed to regular) stimulation waveforms are able to induce neuronal firing desynchronization, and thus presumably alleviate symptoms. Such stochastic stimulation patterns would constitute an innovative alternative to the regular DBS pattern clinically used today. However, this outcome conflicts with experimental results found in humans while the regularity of DBS pulses was varied [75], where it was shown that clinical efficiency decreased with increased variability in the inter-pulse period.

Schiff & Sauer [76] proposed another model assuming that detailed knowledge of the neuronal target's physiology might not be needed to achieve efficient control leading to symptoms improvement. The authors use the concept of a Kalman filter, consisting of estimating the state variables of a nonlinear system to predict its state at a later time, based on past measures. The authors used a neural field model [29,30] to describe cortical activity in space and time. The model parameters were selected so that the simulated cortical tissue was exhibiting spiral waves, a phenomenon experimentally observed [77]. To achieve appropriate feedback to the network, the monitored variable was the mean potential of local neural assemblies (termed as neural mass in the formalism of Wilson & Cowan), which was then used by the Kalman filter to predict future mean potential values. Based on this approach and using proportional feedback, the authors show the efficiency of this method to suppress spiral wave activity while consuming little energy. Consequently, this work confirms that methods from control theory might provide appropriate solutions to identify effective and adaptive brain stimulation methods in PD, without the need to develop a sophisticated model of the underlying structures. However, an optimal closed-loop stimulation method based on control theory is yet to be discovered, and again should be experimentally tested to evaluate its relevance and predictive value.

6. Discussion

During more than 20 years, several mechanisms of action have been proposed to explain the efficiency of DBS, such as inhibition of the stimulated structure or normalization of network activity in the cortico-basal ganglia–thalamo-cortical network. Although a quite complete picture of the advantages and drawbacks of DBS is available in the literature, these mechanisms are still debated. Previous biophysical modelling work [43,61] suggests that subthalamic neuron membranes have resonant properties with a resonance frequency notably lower than DBS, and that neuron membranes could not respond to each DBS pulse, but rather respond by a weak transient depolarization. This is compatible with experimental recordings showing that somatic activity is inhibited by DBS [54]. Therefore, both experimental and modelling evidence suggests that DBS in PD has a rapid effect on subthalamic neuron membrane dynamics. Now that DBS mechanisms are partially understood, the time has come to move forward towards intelligent neuromodulation techniques that are able to adapt the stimulation signal in both space and time according to ongoing neuronal activity and to provide optimal symptom improvement. It is becoming obvious that empirical methods of neuromodulation have reached a limit, and that biophysical modelling may overcome these limitations. Several closed-loop therapeutic stimulation models have been published so far [46,71,73,76,78], but none of them have been verified clinically to date. This may be in part caused by scepticism of most clinicians towards biophysical modelling approaches.

Future therapeutic brain stimulation methods should minimally interfere with physiological brain rhythms to prevent potential side effects, but also stimulate with lower levels of current and only when needed, in order to minimize interaction with neuronal tissue and decrease the number of interventions needed for battery replacement. Modelling-driven designs of stimulation waveforms (not necessarily stationary signals, but complex, non-stationary signals with time-varying frequency components and ‘pulse’ period) should also investigate the capability to modulate synaptic plasticity on the long run (of the order of hours) in order to achieve pre-determined objectives of synchronization or desynchronization of neural assemblies in narrow frequency ranges. Also, it might be useful to envision not only alternative stimulation patterns to the high-frequency pulse train used in DBS, but also to use less invasive stimulation methods to deliver therapeutic stimuli. Among these methods, let us cite transcranial magnetic stimulation (TMS), consisting of approaching a coil from the skull, inducing non-invasively a strong magnetic field in brain tissue, currently using either a single pulse or a train of pulses at variable frequencies, typically between 1 and 100 Hz. Promising results have been obtained for the symptomatic treatment of neurological disorders such as PD [79,80] or drug-resistant depression [81,82]. One limiting factor for the clinical use of TMS is that biological mechanisms underlying the response of brain tissue have not been fully elucidated. Another method used recently by the group of Buzsaki [83] is non-invasive transcranial electric stimulation, which entrains cortical neurons in rats, based on the well-known fact that extracellular fields generated around neurons affect their excitability. The authors show that relatively weak electric fields applied through the skull activate neurons either antidromically (through their axons) or anterogradely (via mono- or multi-synaptic connections) in widespread cortical areas. Since cortical neurons are ‘embedded in perpetually active networks transcranial electric stimulation inevitably interacts with network-induced effects’ [83], this technique might be used to produce amplification or interference of brain tissue activity. Therefore, these results imply that therapeutic effects using chronic transcranial electric stimulation can be expected and should be explored.

One critical test for all the modelling approaches presented in this review will be their experimental testing. If it is experimentally shown that some models successfully predict the outcome of new brain stimulation methods, it will give biophysical modelling a strong asset in the development of new therapeutic stimulation techniques. Moreover, it will also provide evidence supporting that mechanisms assumed by these models are likely to occur in the brain. This will also be a unique opportunity to evaluate which models are most appropriate to describe the effect of therapeutic brain stimulation, and which ones fail to predict correct brain response to electrical stimulation. Therefore, subsequent modelling works could focus on the most relevant models, those accurately describing and predicting the response of brain tissue to therapeutic stimulation. For these reasons, the experimental testing of closed-loop stimulation techniques derived from modelling should be an important focus of research in neuroscience.

7. Concluding remarks

Our review of various models of DBS effects, but also models of potential alternatives to DBS, shows that modulation of brain rhythms by specific and innovative stimuli becomes gradually better understood using computational modelling. However, in order to optimally normalize in the long term brain rhythms associated with the symptoms of neurological disorders, a global theory linking neural dynamics, synaptic plasticity and rhythms would be required, which appears to be a tremendous task. Consequently, the use of simplified models of spatio-temporal cortical dynamics and corresponding numerical simulations may be insightful towards the understanding the complex interplay between firing patterns, firing activity, synaptic weights and neural oscillations. Such models should also be helpful to discriminate, among the very large number of possible combinations of stimulation parameters, which ones should be clinically useful.

Also, we have shown that model-driven approaches represent an alternative and a new perspective for treatment development based on rational biophysics principles that may assist usual empirical experimental method based on scientific ‘best-guess’. It is likely that progress in biophysical modelling will undoubtedly lead to significant advances in medicine with the development of efficient neuromodulation stimuli especially designed to produce the desired outcome, i.e. normalized brain activity in pre-determined frequency bands. However, challenges complicate this task, and explain why model-based closed-loop stimulation methods have not been tested experimentally so far. Biophysical models are, like animal models, imperfect in that they represent a simplification of ‘reality’, i.e. the disease and how it affects the patient. An additional difficulty is that PD may take different forms (e.g. tremor-dominant). Therefore, there is a risk that model predictions are inconsistent with experimental or clinical results. This is why biophysical modelling should be based on solid foundations to be a reliable tool providing clinically meaningful predictions. Also, in order to achieve an experimental validation of model-based closed-loop stimulation, it will probably be necessary to make technical compromises. Such project execution will require multi-disciplinary expertise and funding, but also smooth interaction between different disciplines and a good relationship with reliable industrial partners. Another non-scientific issue is that biophysical modelling is sometimes welcomed with scepticism by scientists specialized in experimental studies. The fact that biophysical models regularly prove their usefulness in reproducing, understanding and predicting data should gradually ease the dialogue between experimentalists and theoreticians, but also inspire confidence in investors.