Exocytosis from pancreatic β-cells: mathematical modelling of the exit of low-molecular-weight granule content

Abstract

Pancreatic β-cells use Ca²⁺-dependent exocytosis of large dense core vesicles to release insulin. Exocytosis in β-cells has been studied biochemically, biophysically and optically. We have previously developed a biophysical method to monitor release of endogenous intragranular constituents that are co-released with insulin. This technique involves the expression of ionotropic membrane receptors in the β-cell plasma membrane and enables measurements of exocytosis of individual vesicles with sub-millisecond resolution. Like carbon fibre amperometry, this method allows fine details of the release process, like the expansion of the fusion pore (the narrow connection between the granule lumen and the extracellular space), to be monitored. Here, we discuss experimental data obtained with this method within the framework of a simple mathematical model that describes the release of low-molecular constituents during exocytosis of the insulin granules. Our findings suggest that the fusion pore functions as a molecular sieve, allowing differential release of low- and high-molecular-weight granule constituents.

1. Introduction

Pancreatic β-cells are electrically excitable, and changes in blood glucose couple to stimulation or inhibition of insulin secretion via electrical activity [1,2]. An increase in the submembrane [Ca²⁺]_i caused by β-cell electrical activity triggers exocytotic release of the insulin-containing secretory granules [3]. These belong to the class of large dense core vesicles (LDCVs), so named because they contain an electron-dense central core (seen in electron microscopy) that is often (but not always) surrounded by a halo. It has been estimated that every β-cell contains approximately 10 000 secretory granules [4,5]. In β-cells, the LDCVs are spherical and have a diameter of approximately 0.33 µm [5]. This means that every granule has a volume of about 18 attolitre (al). A β-cell has a volume of approximately 1 picolitre (pl) and thus the granules together occupy close to 20 per cent of the total β-cell volume.

Insulin secretion has previously principally been studied using biochemical techniques (such as radioimmunoassays), but more recently, high-resolution biophysical and optical techniques have been applied. The latter include single-vesicle imaging, capacitance measurements and amperometry [6]. The application of these techniques to pancreatic β-cells has permitted the exploration of processes preceding exocytosis, the exocytotic event itself and the fate of the granule membrane after exocytosis [7].

Exocytosis in β-cells does not only result in the release of insulin. The β-cell LDCVs contain a number of substances in addition to insulin. These include Zn²⁺, adenine nucleotides, Ca²⁺, glutamate, chromogranin, islet amyloid polypeptide, serotonin and dopamine [6,8]. All of them are co-released with insulin during β-cell exocytosis. Although many of these substances are biologically active and are thus likely to exert functional effects following their release, the regulation of these endogenous granule constituents has not been much investigated. To date, the majority of studies of exocytosis in β-cells have focused on the release of insulin [9]. This is probably a reflection of the well-established biological function of the hormone. However, the lack of appropriate techniques to study the release of the other compounds may have contributed.

1.1. Ionotropic membrane receptors can be used to study exocytosis

We have developed a technique that allows high-resolution measurements of ATP and GABA release. This method involves the ‘engineering’ of the β-cells to express P2X₂ (P2X₂R) or GABA_A (GABA_AR) membrane receptors. Normally, these receptors are not expressed at high levels in the rat β-cells (but see [10,11] for the expression of these receptors in human β-cells). P2X₂R and GABA_AR belong to the class of ionotropic receptors and represent ligand-gated ion channels that are activated by extracellular ATP (P2X₂R) or GABA (GABA_AR), respectively. During exocytosis, ATP and GABA are released into the extracellular space, diffuse over the cell surface and are bound to their membrane receptors. For the purpose of this method, the β-cells are forced to express these membrane receptors at very high levels (ideally greater than 10² receptors per µm²). A receptor surface density as high as this corresponds to an average distance between two neighbouring receptor complexes of less than 100 nm [12]. Therefore, as illustrated schematically in figure 1a, the exocytotic release of ATP or GABA results in the activation of a large number of receptors situated close to the release sites, and this in turn leads to the development of membrane currents that can be monitored by patch-clamp recordings from the same cells [13,14]. Unfortunately, there are no insulin-activated ion channels, and the technique can therefore only be applied to measure the release of low-molecular-weight granule constituents. However, it might be worth investigating a possibility to modify insulin by FMRF (neuropeptide Phe-Met-Arg-Phe-NH₂) tagging and to express ionotropic FMRF receptors in the β-cell [15].

Figure 1.

Schematic of electrophysiological detection of ATP or GABA release. (a) ATP and GABA are co-released with insulin and activate GABA_A or P2X₂ receptors in β-cells engineered to express them. The release of GABA or ATP leads to the activation of their respective receptors. The resultant membrane currents can be recorded electrophysiologically by whole-cell patch-clamping as illustrated. (b) Quantal ATP and GABA release recorded electrophysiologically. Measurements were made using the standard whole-cell technique at a holding potential of −70 mV for ATP and at 0 mV for GABA detection. Recording electrodes contained CsCl. The traces shown represent the most common type of events consisting of rapid current spikes.

The electrophysiological properties of the release events observed with the help of ionotropic membrane receptors resemble those that can be measured by carbon fibre amperometry. Thus, the release of ATP and GABA results in short-lived current spikes (figure 1b). However, there are a few important differences between the measurements made by carbon fibre amperometry or by use of ionotropic membrane receptors. An inherent problem with amperometry is that only events that are released close to the carbon fibre are detected; this could be as little as 30 per cent of the total number of release events [13]. In addition, the time course (shape) of current transients reflecting exocytosis is distorted by the diffusion of the released substance from the fusion site to the detecting electrode [16].

These problems are largely circumvented when exocytosis is instead measured using ionotropic receptors. With this method, practically all exocytotic events can be detected because every cell contains several thousand ‘detectors’ that are evenly distributed across the cell surface. The time course of these current transients is governed by the speed of the ligand–receptor interactions. These are known to be very rapid for most (if not all) ligand-gated ion channels and certainly for the P2X₂Rs and GABA_ARs used here. Indeed, comparison of the signals obtained by amperometry and the ionotropic receptors suggests that the membrane receptors respond with sufficient speed to faithfully report exocytosis, and the current transients recorded by the two techniques superimpose [12]. However, as is the case in amperometry, the kinetics of the current responses is influenced by the geometry of the release site (size of cell, granule and fusion pore) as well as the intragranular matrix and not least the intragranular concentration of the compound released. An advantage of the use of an ionotropic receptor-based technique (that pertains specifically to the study of exocytosis in β-cells) is that the cells do not have to be preloaded with the substance being released. In amperometry, the endogenous intragranular serotonin concentration is too low to allow amperometric detection and the cells must therefore be preloaded with serotonin itself or its precursor 5-HTP [12,17], which selectively accumulates in insulin-containing granules [18,19]. This is not necessary with ATP and GABA, which are both normal constituents of the β-cell granules. Admittedly, GABA and ATP release can only be detected after the cells have been engineered to express their respective ionotropic membrane receptors. However, the β-cells appear to tolerate this well as evidenced by a maintained glucose responsiveness [10].

1.2. Pancreatic β-cells contain two types of secretory vesicles: LDCVs and synaptic-like microvesicles

Pancreatic β-cells contain two types of secretory vesicles. In addition to the insulin-containing LDCVs, they also contain synaptic-like microvesicles (SLMVs). Cell membrane capacitance measurements suggest that the SLMVs undergo exocytosis and capacitance steps of 200 aF (attofarad) have been seen in addition to large approximately 3 fF (femtofarad) steps [20]. These capacitance steps correspond (assuming spherical geometry) to vesicle diameters of approximately 80 nm and approximately 300 nm, respectively. It seems likely that the two classes of membrane capacitance changes reflect exocytosis of SLMVs—small capacitance steps—and LDCVs—large capacitance steps. Based on experiments that use the photo-liberation of caged Ca²⁺ in the rat β-cell, it was proposed that an early component of the cell membrane capacitance increase is not associated with any detectable release of serotonin [21]. As serotonin is used as a surrogate marker of the insulin-containing LDCVs, these experiments suggested that the early component of capacitance increase reflects instead the exocytosis of SLMVs (assumed not to contain any serotonin). However, no such discrepancy is observed during membrane depolarization when exocytosis monitored by the two methods shows close temporal agreement [22]. Exocytosis of SLMVs has been proposed to mediate the release of GABA from the β-cells [23]. Using measurements of ATP release in the β-cells expressing P2X₂ receptors, we have examined the hypothesis that exocytosis of SLMVs contributes significantly to the membrane capacitance increase in these cells that occurs without concomitant serotonin release. Our observations suggest that although SLMVs undergo exocytosis (as suggested by the on-cell capacitance measurements), they contribute only marginally (if at all) to the depolarization- and Ca²⁺-induced increase in membrane capacitance. This conclusion is based on the following findings. First, ATP and serotonin (a marker of LDCVs) are nearly always co-released [13]. Second, the amplitude distribution of the currents recorded in β-cells expressing P2X₂Rs is well described by a single Gaussian [12], and there is no sign of additional components that may correspond to the release of ATP mediated by exocytosis of SLMVs (although the technique as such has sufficient resolution to detect them). Third, ATP release is associated with an average capacitance increase of 3.6 fF per event [13], close to that expected for LDCVs. Collectively, these observations suggest that LDCVs represent the principal exocytotic pathway in the β-cell and that it accounts for more than 90 per cent of the capacitance increase. We have also found that exocytosis of LDCVs accounts for the release of GABA in both human and rat β-cells. Thus, a subset of the LDCVs contains GABA, and there is little evidence that the release of this neurotransmitter involves exocytosis of SLMVs. Although both biophysical [20] and optical [24] measurements agree that SLMVs undergo exocytosis in β-cells, the functional significance of this process therefore remains unclear. It may be speculated that it provides a means for membrane repair or insertion of trans-membrane proteins into the plasma membrane.

1.3. Release of transmitters through LDCV fusion pores

During exocytotic fusion of LDCVs with the plasma membrane, the vesicle lumen is initially connected to the extracellular space via a narrow pore (fusion pore). High-resolution on-cell capacitance measurements have shown that this pore is sometimes stable for several tens of milliseconds before its expansion, allowing the estimation of its diameter. The combination of on-cell capacitance measurement with amperometry has revealed that low-molecular-weight substances are able to permeate the fusion pore [25]. Release occurs at a slower rate than after full fusion and gives rise to a ‘pedestal’ or ‘foot’ signal that precedes the larger spike reflecting full fusion (and expansion of the fusion pore). In some cases, the fusion pore does not expand at all but closes again after a variable time, a process called ‘kiss-and-run’ exocytosis. In amperometry, transmitter release during kiss-and-run is visible as a ‘stand-alone foot’ signal [20]. Unfortunately, such stand-alone foot signals are difficult to identify reliably by amperometry as similar events would also result from full fusions occurring at a greater distance from the carbon fibre. This problem is eliminated if ionotropic receptors are used as sensors of exocytosis. Assuming even distribution of the receptors in the plasma membrane (which does indeed appear to be the case; [14]), all exocytotic events will occur at a similar distance from the sensor, and the time course of the measured event will faithfully reflect the release kinetics of the transmitter.

Using this method, we have shown that both ATP and GABA are released during kiss-and-run exocytosis of insulin granules in β-cells [20]. These kiss-and-run events are quantitatively significant as they account for up to 25 per cent of all exocytotic events in these cells. Interestingly, the proportion of kiss-and-run events seems to be regulated. For example, the fraction of kiss-and-run events increases when intracellular cAMP levels are elevated [20]. Peptides, such as insulin, are too large to permeate the fusion pore [26]. Kiss-and-run therefore allows β-cells to selectively release small transmitters. The possible physiological significance of this will be discussed below. Finally, simultaneous monitoring of exocytosis using amperometry and ionotropic receptors has provided evidence that small transmitters are released at different rates through fusion pores that inversely correlate with the size of these transmitters [13]. This suggests that fusion pores may act as filters not only for peptides, but also for small vesicle constituents and that the ease by which these molecules exit via the fusion pore depends on the molecular size.

2. Mathematical model of a current transient

The use of ionotropic membrane receptors to study exocytosis has, as briefly reviewed above, yielded valuable insights into the properties of exocytosis in pancreatic β-cells. It seems possible that additional information can be extracted from the experimental electrophysiological data. To this end, we have developed a simple mathematical model that describes the properties of the current transients that can be recorded during stimulation of exocytosis in β-cells expressing the ionotropic P2X₂ or GABA_A receptors.

2.1. Basic model equation

A two-dimensional section of the geometry and the three-dimensional overview of the release site used are depicted in figures 2 and 3. A spherical granule with a diameter d_gr is attached to the inner side of the plasma membrane and linked to the extracellular space by a cylindrical pore having the diameter d_p and length l_p. The β-cell is a spherical body with the diameter d_c. The whole-cell current I across the cell membrane at any given time t (measured by whole-cell patch-clamp measurements) depends on the instantaneous concentration of ATP or GABA (in the following collectively referred to as the ‘ligand’) at the cell surface and can be found by considering the diffusion of the ligand from the granule lumen into the extracellular space, its spread across the surface of the β-cell and its reversible binding to the ionotropic P2X₂ or GABA_A receptors (in the following referred to as ‘receptors’) expressed on the cell membrane.

Figure 2.

The geometry of the release site set for mathematical modelling of the release of low-molecular-weight substances out of the lumen of the fused pore into the extracellular space. The definition of the geometric parameters is seen. It has to be noted that the geometry of the site is axially symmetric. This allows the solution of the relevant equations in two-dimensional cylindrical coordinates.

Figure 3.

A three-dimensional view of a insulin granule attached to the inner surface of the cell membrane. The relative size of the granule and the cell is seen, with the characteristic size of the latter being approximately 1000 times larger. Triangular objects present demonstrate the grid imposed on the volume for solving the problem of ATP and GABA diffusion by the method of finite elements.

Since the concentration of the ligand c in the bulk extracellular space varies both in time and over the cell surface, we first consider ionic current through a small part ΔS of the cell surface. Assuming that the conductance of a single receptor channel is g_s, the surface density of activated channels is r (that have associated with the ligand) and the reversal potential is V_r, the current ΔI through an elementary surface is

2.1

where V is the holding potential applied to the cell membrane. The whole-cell current I at any given time t is then obtained by integrating equation (2.1) over the whole surface of the cell membrane S_c and is

2.2

Following exocytosis, intragranular ligands are released into the extracellular space and cause a time-dependent and transient activation of the receptors. This is because of the diffusion of the ligand away from the cell surface into the extracellular space. Thus, r is a peak function of time. Then it follows from equation (2.2) that I will vary over time in a way similar to the whole-cell currents experimentally recorded on depolarized β-cells expressing corresponding ionotropic receptors. Consequently, the model of ligand release defined by equation (2.2) can be fitted to the experimental data in order to find estimates of model parameters.

2.2. Equations for the surface concentration of activated channels r

The time course of the whole-cell current (equation (2.2)) is defined by the concentration r of the ligand bound to the surface receptors. This is found by solving a transient surface diffusion and surface reaction problem coupled to the diffusion of the ligand out of the granule into the extracellular space via the fusion pore.

Events that define the whole-cell current (I) take place on the cell surface. The receptors are allowed to move only laterally within the lipid bilayer and do not diffuse into the extracellular space during times necessary to record ionic currents caused by the depolarization of the cells. These receptors are activated by ligand molecules that reach the cell surface by diffusion from the lumen of the fused granule. In this situation, the material balance for receptor species (occupied or not by the ligand) on the cell surface, taking into account both the surface diffusion and the binding of the ligand to the receptor, can be written as

2.3

In the above equation, r₀ is the total number of receptor molecules present on the unit of the cell surface, D_s is the coefficient of the surface diffusion of the receptors and k₊ and k₋ are rate constants for the receptor binding and unbinding of the ligand.

The exit of the ligand from the pore and its concentration c in the extracellular space is described by the diffusion equation:

2.4

In this equation, D is the diffusion coefficient for the ligand in the extracellular space. Equations (2.3) and (2.4) have to be solved together in order to obtain the transport of the ligand in the bulk extracellular space and its binding on the cell surface. The coupling of the two processes is achieved by setting a boundary condition for the bulk's mass balance (equation (2.4)).

2.3. Boundary and initial conditions

The boundary condition for equation (2.4) that couples the rate of the binding reaction with the diffusional flux of the ligand towards the cell surface is given by the relationship

2.5

Here n is a unit vector normal to the cell surface. In essence, this boundary condition states that the component of the diffusional flux of the ligand normal to the cell surface (the term on the left side of the equation) is equal to the rate of the ligand binding in the same point of the cell surface (the term on the right side of the equation).

Insulating boundary conditions have to be set on the inner surfaces of the granule and the pore (figure 2) since there is no flux of the ligand across the granule membrane and the wall of the fusion pore. For the sake of numerical simulations, the zero concentration boundary condition at infinity, that would otherwise be appropriate for this type of a problem, was substituted with a zero-concentration condition on a 60 µm sphere concentric with the sphere representing the cell surface.

The boundary conditions for equation (2.3) are insulating, and they state that there is no loss of bound ligand by diffusion from the cell surface. Thus,

2.6

This is a mathematical expression of the fact that membrane proteins cannot leave the cell membrane in the time frame relevant to this problem and the diffusional flux in the direction perpendicular to the cell surface is equal to zero. Initial conditions for equations (2.3) and (2.4) set concentrations of species at t = 0 as follows: (i) r = 0, (ii) c = 0 in the extracellular space and inside the fusion pore, and (iii) c = c₀ inside the granule.

2.4. Model parameters

Our model contains 11 parameters. These are the diameter of the granule d_gr, the diameter of the cell d_c, the diameter of the pore d_p, the length of the pore l_p, the diffusion coefficient of the hormone in the extracellular space D, the surface diffusion coefficient of the bound hormone in the cell membrane D_s, the surface concentration of the receptor in the cell membrane r₀, the rate constants for the binding of the hormone k₊ and k₋ and the concentration of the hormone in the lumen of the granule. One more parameter has to be introduced into the model because the mobility of the ligand within the granule may be different from its mobility in the bulk extracellular space. Indeed, a considerable part of the granule volume is occupied by the insulin crystals, and there is experimental evidence that secretory granules are filled with a polyelectrolytic matrix that facilitates the packaging of charged and polar molecules within the limited space available inside the granule [27]. To account for these specific conditions, one has to allow the diffusion coefficient in the lumen of the granule d_gr to vary independently of D during the fitting procedure.

In principle, any single or a group of these parameters can be estimated by fitting the model to experimental recordings of current transients caused by the fusion event of a single granule. However, the majority of them are well known from earlier experimental work. This applies to most of the geometric parameters (such as the size of the β-cell, the size of the granule and the length of the fusion pore). The physico-chemical properties of the ligand and its binding to the receptors have also been studied extensively. However, knowledge about the intragranular ligand concentration and the mobility of these molecules within the polyelectrolytic matrix is limited. Also, the diameter of the fusion pore is one other parameter that is hard to measure, and it is likely to expand as granule fusion/exocytosis proceeds. On the basis of numerous investigations by various methods, it has been established that the size of the pore changes rapidly during the initial stages of pore formation before stabilizing at diameters that range between 2 and 12 nm [20,28]. Therefore, the model-based fitting to current transients caused by the release of ligands from the secretion granule can be expected to be useful, first of all, in estimations of the intragranular ligand concentration and the ligand's mobility within the lumen of the granule in different experimental conditions. It can also be used to predict the dynamics of the fusion pore, separately or simultaneously with the intragranular hormone concentration. The latter problem is computationally more complicated since it involves changing boundary conditions and was not attempted here.

2.5. Modification of the model: the use of experimental dose–response curves

For compounds like GABA and ATP, both released by exocytosis of LDCVs in β-cells [13], the dose–response curves for their interaction with the respective membrane receptors are available [29–31]. The above model of current transients can be modified and essentially simplified by the use of these curves. If p(c) represents the fraction of channels activated at the ligand concentration c, then the current through the elementary surface ΔS is equal to

2.7

and I, obtained by integration over the cell surface S_c, is correspondingly

2.8

Thus, the use of dose–response curves removes the necessity to solve the surface diffusion equation (equation (2.3)). As earlier, the concentration of the ligand in the extracellular space and on the cell surface is defined by equation (2.4). In this modification of the model, the insulating boundary conditions have to be expanded to include the cell surface. Otherwise, the boundary conditions and initial conditions are same as previously.

It has to be noted that by defining the whole-cell current by equation (2.7), we introduce dose–response curves into the description of a non-equilibrium situation. This is justifiable for two reasons. First, the dose–response properties of the ligand–receptor interactions were obtained by rapid application of the ligand to the entire cell, an experimental paradigm that approximates what occurs at the fusion site when the ligand is released locally by the exocytosis of an individual LDCV. Second, the diffusion of the ligand out of the LDCV and over the cell surface is slow compared with its binding/unbinding to their respective receptors (approx. from 10 to 30 ms versus several milliseconds [31,32]. Therefore, for LDCVs, the time course of the current responses is primarily defined by the time-dependent diffusion of the ligand over the cell surface with resultant activation of an increasing number of receptors. Consequently, it means that the model, based on these approximations, is only applicable to the release of the ligand out of vesicles of large size. We believe that for this type of vesicles the model represents an acceptable and reasonable first approximation of the process. We acknowledge, however, that taking into account the real binding/unbinding rates and the gating of the ion channel would refine the method (but also make it computationally more complex).

3. Model fitting to experimental current transients

Equations (2.3), (2.7) and (2.8) were fitted to experimental currents recorded from Ins-1 and β-cells expressing P2X₂ or β-cells expressing GABA_A receptor channels. For these simulations, the dose–response function p(c) was as reported previously by Ding & Sachs [31] and Birnir et al. [29] for the P2X₂ and GABA_A receptors, respectively. The diffusion coefficient in the extracellular space for ligands was determined according to the size of the ATP and GABA molecules and set to 406 and 600 µm² s⁻¹, respectively. The diameter of the fusion pore was set to 12 nm since it has been shown by two-photon imaging that there is a subgroup of very fast exocytotic events that lead to the formation of a pore with this diameter [28]. Other parameters used for fitting of the model to experimental current spikes are as summarized in table 1.

Table 1.

Model parameters used for fitting current transients caused by release of ATP and GABA during exocytotic events in β- and Ins-1 cells.

parameter	Ins-1 cells	β-cells
set parameters
cell diameter, dc, µm	12	18
granule diameter, dgr, nm	185	327
pore diameter, dp, nm	12	12
pore length, lp, nm	15	15
ATP diffusion coefficient, DATP, µm2 s−1	406	406
GABA diffusion coefficient, DGABA, µm2 s−1	not determined	600
ATP receptor density, r0ATP, µm−2	83	98
GABA receptor density, r0GABA, µm−2	not determined	8
fitting parameters
granular concentration of ATP or GABA	cgr	cgr
granular diffusion coefficient of ATP or GABA	dgr	dgr

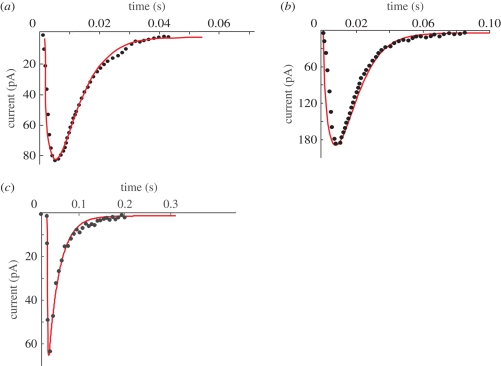
Figure 4 shows examples of representative fits of the model to current spikes from an Ins-1 cell (figure 4a) and a rat β-cell (figure 4b), both expressing the P2X₂ receptor, and a fit for a current transient from a β-cell-expressing GABA receptor (figure 4c). The selected events were, based on their rapid activation and decay [20], assumed to represent examples of full fusion when the fusion pore almost instantaneously expands to its final size (12 nm; [28]). The rapid expansion of the fusion pore makes it impossible to resolve the initial pedestal. Kiss-and-run events (associated with the partial opening of the fusion pore) are characterized by slower activation/deactivation kinetics (figure 6).

Figure 4.

Examples of model fits to whole-cell current transients caused by ATP or GABA release in Ins-1 and rat β-cells engineered to express P2X₂ or GABA_A receptors. (a) A representative current spike recorded from an Ins-1 cell. The fit shown was achieved at 11.3 ± 1.7 mM concentration of ATP in the granular lumen; the effective ATP diffusion coefficient in the granular matrix was 13 ± 3.5 µm² s⁻¹. (b) A similar current spike recorded from a rat cell. The fit shown was achieved at 3.7 ± 0.7 mM concentration of ATP in the granular lumen; the effective ATP diffusion coefficient 121 ± 17 µm² s⁻¹. (c) The fit of the model to a current spike recorded on a rat cell expressing the GABA_A receptor. The fit yielded GABA concentration of 15.9 ± 2.5 mM and the effective diffusion coefficient in the lumen of the granule of 192 ± 31 µm² s⁻¹. In all three panels, the experimental data are shown by full black dots. Fitting curves are in red. Calculations were done using the software package Femlab (Comsol, Stockholm, Sweden). This software is based on the finite-element method and automatically selects the mesh size for each geometry. These simulations were done with the fine-mesh size since it was found that it gave stable and reproducible results.

Figure 6.

The pedestals of current spikes caused by the release of ATP or GABA. (a) Experimental examples of pedestals (red arrows) that precede the large spikes that reflect full fusion and rapid emptying of the LDCV lumen. Schematic of the LDCV before exocytosis (i), just after opening of the fusion pore (allowing exit of ATP and/or GABA) (ii) and after expansion of the fusion pore (full fusion, allowing rapid release of ATP/GABA as well as insulin) (iii). The approximate times at events depicted schematically in (i)–(iii) occur are indicated on the top trace. (b) A 25 ms simulation of ATP and GABA release through a stable 1.4 nm pore that does not undergo the final expansion (hence the absence of large current spikes).

We used the mathematical model to estimate the intragranular ATP and GABA concentration and their mobility within the secretory granules. The intragranular ATP concentration was thus found to be 11.3 ± 1.7 and 3.7 ± 0.7 mM for Ins-1 and rat β-cells, respectively. The corresponding effective diffusion coefficients of ATP within these granules were 13 ± 3.5 and 121 ± 17 µm² s⁻¹. The intragranular ATP concentrations estimated above correspond to the ATP content of 0.055 amol per granule in rat β-cells and to 0.037 amol per granule in Ins-1 cells. The best fit of the model to the current transients caused through the GABA receptor channel was achieved at intragranular hormone concentration of 15.9 ± 2.5 mM and its diffusion coefficient within granule lumen of 192 ± 31 µm² s⁻¹. The intragranular GABA concentration estimated by this method corresponds to a GABA content of 0.32 amol per granule. For comparison, the insulin content of a β-cell LDCV has been estimated to be 1.6 amol. Thus, the stoichiometry between ATP, GABA and insulin in β-cell LDCVs is approximately 1 : 8 : 43.

Figure 5 shows the part of the plasma membrane involved in the creation of a current transient for ATP release from an insulin granule that has just fused with the plasma membrane. The ATP concentrations have been colour-coded. It can be seen that the ATP concentration falls from 1.5 mM (dark red) at the outer mouth of the fusion pore to less than 10 µM (green) within five granule diameters (approx. 1.5 µm) from the release site.

Figure 5.

The extent of cell surface involved in the creation of current spikes. The ATP concentration in the extracellular space is colour-coded. It can be seen on the contour plots that only the part of the cell surface close to the fusion site is involved in the event. ATP concentration falls from 1.5 mM (dark red) at the outer mouth of the fusion pore to less than 10 µM (green) within five granule diameters (approx. 1.5 µm) from the release site.

4. Discussion

The results presented above suggest that the exocytotic release of ATP and GABA detected by ionotropic membrane receptors can be modelled mathematically. The model we have developed enables us to estimate the intragranular concentrations of these low-molecular-weight granule constituents. It has long been recognized that the insulin granules contain large amounts of ATP and other nucleotides [33]. In rat β-cells, the total cellular ATP content has been estimated to be 2 fmol per β-cell [34]. Using a cell permeabilization protocol, approximately 30 per cent of ATP (i.e. 0.6 fmol per cell) in mouse β-cells was found to reside in a non-diffusible pool believed to be contained in the secretory granules [35]. Given that every β-cell contains 10 000 secretory granules, this corresponds to a granule ATP content of 0.06 amol per granule. The latter value corresponds to an intragranular concentration of 3.3 mM when taking into account that a secretory granule has a volume of 18 al. This is similar to that measured in isolated secretory granules [8] and close to the 3.7 mM we now estimate based on the mathematical modelling of the current transients recorded from isolated rat β-cells infected with ATP-sensitive P2X₂ receptors. The granular ATP content (0.055 amol per granule) obtained by this method is clearly also in very good agreement with that which can be estimated from the experimental data.

Similarly, mathematical simulation suggests that the intragranular GABA concentration is 16 mM. This concentration suggests that every GABA-containing granule delivers 0.32 amol of GABA into the islet interstitium during exocytosis. Rat β-cells maintained in tissue culture have been reported to contain approximately 10 fmol GABA per cell [36]. The latter value means that if all 10 000 granules contained the same amount of GABA, then approximately 30 per cent of the cellular pool of GABA would be granular. However, this is likely to be an overestimate since both electrophysiological measurements and electron microscopy indicate that only approximately 20 per cent of the granules contain GABA [13].

It is of interest that the intragranular diffusion coefficient estimated for ATP in secretory granules from primary rat β-cells is approximately 10-fold higher than that obtained from Ins-1 cells. This may reflect the presence of a dense crystal in primary β-cells but not in Ins-1 cells. On the other hand, the fact that similar values were obtained for the diffusion coefficients for ATP and GABA argues that these two molecules behave similarly within the secretory granules of the rat β-cell.

Most of the current spikes we observe develop and decline rapidly. However, occasionally events with more complex time courses are observed (figure 6a). As discussed above, the occurrence of pedestals before the current spikes is likely to reflect the exit of ATP and GABA via a narrow semi-stable fusion pore that sometimes survives long enough to give rise to an experimentally resolved current. Exit of ATP or GABA via the narrow fusion pore that occasionally forms for a short period prior to full fusion accounts for the pedestal that precedes the large spike reflecting full fusion (shown schematically by cartoon below current traces in figure 6a). On-cell capacitance measurements indicate that the fusion pore has a diameter of 1.4 nm [20]. ATP and GABA are fairly small molecules; the two shortest diameters are 1.1 × 0.5 nm and 0.3 × 0.2 nm for ATP and GABA, respectively [13]. Thus, both molecules can be accommodated within the fusion pore.

Figure 6b illustrates the simulated GABA- and ATP-activated membrane currents resulting from the opening of a 1.4 nm fusion pore for 25 ms. In this case, the fusion pore is assumed to remain stable and not to undergo the final expansion. The decay of the currents that occur eventually results from the depletion of the LDCVs of their ATP and GABA contents. Consistent with the experimental data, the relative amplitude of the plateau compared with the peak current is larger in the case of GABA than for ATP. This is likely to be a consequence of ATP being a slightly larger molecule.

We have previously argued that a significant fraction of granular ATP and GABA can be released via the fusion pore [20]. Parallel measurements of ATP and cargo release (fluorescently labelled) have revealed the occurrence of such exocytosis. Thus, the fusion pore may function as a molecular sieve that allows selective release of one molecular species over another. Whether this process can be regulated remains to be examined. Nevertheless, it is possible that selective release of GABA and ATP via the fusion pore may allow these compounds to exert a local paracrine effect on neighbouring islet cells [11,37,38].

5. Conclusions

We have developed a technique to measure exocytosis in β-cells that measures the release of naturally occurring granule constituents and that uses a type of sensor that nature herself has perfected: the ionotropic membrane receptors. This technique can be applied to all compounds with the capacity to activate ionotropic membrane receptors. In addition to ATP and GABA, the list of ionotropic receptors includes compounds like glutamate, glycine, serotonin, acetylcholine and histamine. Peptide hormones may be modified by FMRFamide tagging, thus allowing the release of these to be monitored following expression of ionotropic FMRF receptors. The data obtained with this technique resemble those obtained by carbon fibre amperometry. However, provided the membrane receptors are expressed at high density, the technique we describe here has the advantage that (almost) all exocytotic events are detected, thus allowing correlation with other biophysical (e.g. capacitance measurements) and optical techniques to study secretion. The data are also amenable to mathematical modelling, and this combination allows physiologically significant quantitative data to be extracted. As shown here, this method has been successfully applied to pancreatic β-cells but there is of course no reason why it cannot also be successfully used to study exocytosis in other cell types.