Acoustic radiation force-based elasticity imaging methods

Abstract

Conventional diagnostic ultrasound images portray differences in the acoustic properties of soft tissues, whereas ultrasound-based elasticity images portray differences in the elastic properties of soft tissues (i.e. stiffness, viscosity). The benefit of elasticity imaging lies in the fact that many soft tissues can share similar ultrasonic echogenicities, but may have different mechanical properties that can be used to clearly visualize normal anatomy and delineate pathological lesions. Acoustic radiation force-based elasticity imaging methods use acoustic radiation force to transiently deform soft tissues, and the dynamic displacement response of those tissues is measured ultrasonically and is used to estimate the tissue's mechanical properties. Both qualitative images and quantitative elasticity metrics can be reconstructed from these measured data, providing complimentary information to both diagnose and longitudinally monitor disease progression. Recently, acoustic radiation force-based elasticity imaging techniques have moved from the laboratory to the clinical setting, where clinicians are beginning to characterize tissue stiffness as a diagnostic metric, and commercial implementations of radiation force-based ultrasonic elasticity imaging are beginning to appear on the commercial market. This article provides an overview of acoustic radiation force-based elasticity imaging, including a review of the relevant soft tissue material properties, a review of radiation force-based methods that have been proposed for elasticity imaging, and a discussion of current research and commercial realizations of radiation force based-elasticity imaging technologies.

1. Background

1.1. Soft tissue material properties

Manual palpation of tissue has been a diagnostic tool used by doctors for centuries. Pathological processes, such as the growth of malignant tumours or tissue scarring, often involve replacing healthy tissues with fibrotic tissue and/or increasing the cellular density of tissues. Such pathological changes are often stiffer than their surrounding healthy tissues. The stiffness of tissues can be described by their elastic moduli, which are a measure of a material's resistance to deformation, in compression/tension (Young's modulus, E) and in shear (shear modulus, μ) [1]. Tissues with higher elastic moduli, such as muscle and fibrous tissue, are more resistant to deformation than more compliant tissues, such as fat [2–4]. Tissue deformation occurs in response to a stress (σ) being applied to tissue; in the case of manual palpation, this stress is related to the force exerted by the clinician's fingers over the surface area of an organ or mass. The deformation that occurs in response to this applied stress is known as the strain (ε), and strain is related to the tissue displacement (u) as shown in equation (1.1) [1]:

1.1

where superscript T represents the transpose operation and ∇u represents the spatial displacement gradient. The dynamic displacement response of soft tissues is typically monitored using cross-correlation and Doppler-based autocorrelation (e.g. Kasai's method [5]) methods. The resolution of ultrasonic displacement tracking methods is anisotropic and is typically an order of magnitude better in the axial direction (i.e. fractions of a micrometre [6]) than the lateral direction (tens of micrometres using two-dimensional cross-correlation methods). Conveniently, the micrometre scale displacements generated by radiation force-based methods occur along the direction of wave propagation (in the axial direction); thus, axial displacements are typically the only component of displacement that is monitored using these methods.

While soft tissues are very complex heterogeneous materials, many assumptions are made in the field of elasticity imaging to simplify the analysis and interpretation of elasticity images. Common material assumptions include that the tissue is: linear (i.e. the amount of strain resulting from an applied stress is not a function of the absolute stress applied), elastic (i.e. the tissue returns back to its non-deformed state when an applied stress is removed, and the deformation state is not dependent on the rate of the applied stress) and isotropic (i.e. the tissue's material properties are not orientation dependent). Under these assumptions, stress and strain can be related to each other as [1]:

1.2

The elastic properties of a material can also be determined by monitoring the propagation of shear waves. In contrast to ultrasonic or compressive waves that propagate in the same direction as the tissue displacement, shear waves propagate in a direction orthogonal to the direction of the induced tissue displacement. Under the simplifying material assumptions discussed above, shear wave propagation is governed by the Helmholtz equation:

1.3

where ρ is the material density, ∇² is the Laplacian operator and t is time. The speed of propagating shear (or transverse) waves (c_T) can be related to the shear modulus (μ) by:

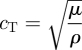1.4

and, the shear modulus is related to Young's modulus by Lai et al. [1]:

1.5

Soft tissues are commonly considered to be incompressible, with a Poisson's ratio (ν) of 0.5 in materials with the assumptions stated above, leading to the relation μ = E/3.

Two common deviations from the simplifying assumptions used to derive the relations above include modelling the tissue as being viscoelastic and/or nonlinear. The introduction of viscosity to the tissue description introduces a dependence of the tissue stiffness on the excitation frequency, where higher frequency excitations yield a stiffer tissue response compared with lower frequency excitations (i.e. the elastic moduli are a function of frequency (E(f) and μ(f)) [7]. As portrayed in equation (1.4), a frequency-dependent shear modulus would result in a frequency-dependent shear wave speed, which is a phenomenon called dispersion. These viscous mechanisms also result in the absorption of energy by the tissue. Tissue nonlinearities (i.e. hyperelastic material models) imply that the strain in response to an applied stress is dependent on the absolute stress that is applied to the tissue (i.e. elastic moduli are a function of strain, E(ε) and μ(ε)).

2. Elasticity imaging methods

All elasticity imaging methods apply a mechanical excitation or stress to tissues, either using an external excitation source, an internal physiological motion source or acoustic radiation force, and measure the resulting tissue deformation (i.e. displacement) in response to that stress, using either ultrasound, magnetic resonance (MR) or optical imaging methods. Based on stress–strain relationships, such as that in equation (1.2), or models of shear wave propagation, such as that in equation (1.3), the measured tissue deformation in response to the applied mechanical excitation can be related to the tissue stiffness.

When elastographic imaging methods were first proposed, the mechanical excitation was derived from physiological tissue motion, such as pulsing blood vessels, and ultrasound was used to monitor the tissue response [8,9]. This was followed by methods using dynamic external vibration to create shear waves within tissue monitored by ultrasound (i.e. sonoelasticity) [10] and methods using external static compression for mechanical excitation monitored by ultrasound (i.e. strain imaging) [11], which were introduced in 1988 and 1991, respectively. The use of acoustic radiation force as a mechanical excitation source was first proposed by Sugimoto in 1990 [12]. This method of excitation can be advantageous when compared with external methods because it is coupled directly within the organ of interest, rather than being coupled through the intervening tissues.

Elasticity imaging techniques provide images related to tissue stiffness that can be either qualitative, portraying relative stiffness differences, or quantitative, providing an estimate of the underlying tissue elastic modulus using reconstruction methods. Excellent reviews of elasticity imaging methods have recently been provided by Greenleaf et al. [13] and Parker et al. [14]. In this article, elasticity imaging methods that use focused acoustic radiation force to provide the mechanical excitation for elasticity imaging are discussed.

2.1. Acoustic radiation force

Acoustic radiation force results from a transfer of momentum from the propagating ultrasonic wave to the tissue through which it is propagating owing to absorption and scattering mechanisms. Following the derivation by Nyborg, modelling tissue as a viscous fluid in response to ultrasonic wave propagation, under plane wave assumptions, acoustic radiation force (F) can be related to the acoustic absorption (α) and speed of sound (c) of the tissue, and the temporal average intensity of the acoustic beam (I) by Nyborg [15,16]:

2.1

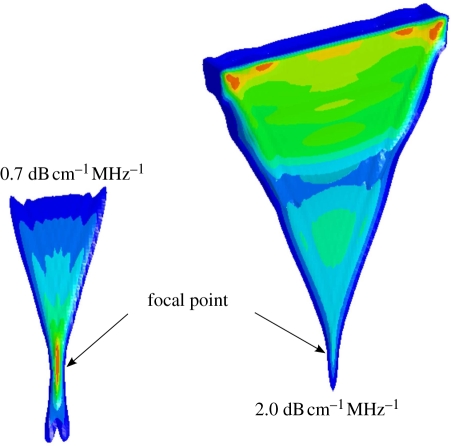
This force is in the form of a body force in the direction of the wave propagation. It is notable that this derivation neglects the contributions of scattering in the computation of the momentum transfer, which seems reasonable in soft tissues where the majority of the attenuation of ultrasound arises from absorption. For a perfect reflector, the radiation force would be twice that for absorption [16]. The spatial distribution of this acoustic radiation field is distributed throughout the geometric shadow of the transducer aperture. Typically, there is a peak in the force field near the focal point, as shown in figure 1; however, for higher frequencies and/or highly attenuating materials, the force field is more uniformly distributed throughout the geometric shadow of the aperture, which is also portrayed in figure 1. Thus, the optimal frequency used for acoustic radiation force tissue excitation varies with depth and is dictated by the tradeoff between attenuation losses in the near field and the focal gain. Through the use of longer and/or higher power acoustic pulses than are typically used in diagnostic ultrasound, transient soft tissue deformation of the order of micrometres (10⁻⁶ m) and fluid streaming of the order of centimetre per second can be generated in vivo.

Figure 1.

Isocontours of acoustic radiation force distribution from a focused linear array in media with two different acoustic attenuation coefficients (0.7 and 2.0 dB cm⁻¹ MHz⁻¹). Red indicates peak radiation force magnitudes with an overall lower peak magnitude in the more attenuating medium. Notice that the peak of the radiation force magnitude occurs at the focus for the lower attenuating material (0.7 dB cm⁻¹ MHz⁻¹), while in the more attenuating medium (2.0 dB cm⁻¹ MHz⁻¹) the radiation force is distributed more evenly throughout the near field, without a strong focal point gain.

As with external mechanical excitation sources, acoustic radiation force can be applied for different temporal durations. Methods have been proposed that apply acoustic radiation force (quasi) statically, where the excitation pulses are applied long enough for the tissue to reach a steady-state response (typically greater than 1 s); transiently, where the excitation pulse is applied as a temporal impulse (i.e. significantly faster than the natural resonant frequencies associated with the dynamic tissue response [7]); or harmonically, where the excitation is applied in a pulsed manner, achieving a sinusoidal tissue excitation of one or more frequencies.

In addition, data processing and display methods for radiation force-based elastographic imaging have been approached in two general categories: (i) those that provide qualitative images of relative differences in tissue stiffness, similar to external compression strain imaging [11], cardiac strain imaging [17] and intravascular ultrasound (IVUS) palpography [18] and (ii) those that provide quantitative estimates of the underlying elastic modulus of tissue, as is done with MR elastography [19]. Each will be treated separately below.

2.2. Steady-state radiation force excitations in fluids

Some methods have employed steady-state radiation force excitations for tissue characterization. Typically, these methods use longer duration (tens of cycles) excitations, or pushing pulses, at a fairly high pulse repetition frequency (PRF; higher than the natural frequency response of the tissue being interrogated), and monitor the tissue response by alternating the excitation beams with conventional imaging beams. In viscous fluids, the application of radiation force generates acoustic streaming, or fluid flow, and the velocity is proportional to the fluid viscosity and boundary conditions [15,20]. Early investigations of the generation of acoustic streaming with diagnostic ultrasound scanners were reported by Starritt et al. [21]. Nightingale et al. [22] first employed this phenomenon clinically to differentiate fluid-filled from solid lesions in the breast, interspersing pushing pulses with pulsed Doppler pulses and monitor the resulting fluid flow using Doppler techniques.

2.3. Steady-state radiation force excitations in soft tissues

Soft tissues are viscoelastic, meaning that their response to mechanical excitation depends on the frequency of excitation. For ultrasonic frequency excitations, soft tissues respond as fluids, where only compressive (i.e. pressure) waves propagate as soft tissues do not support shear stresses at these high frequencies. However, because the acoustic radiation force phenomenon arises from the absorption of acoustic energy and is dependent on the time-average intensity of a compressive ultrasonic wave (equation (2.1)), the excitation frequency of the resulting radiation force excitation is much lower than that of the incident ultrasonic wave (less than 1000 Hz). At these lower frequencies, tissues have been reasonably modelled either as elastic solids, where the stiffness of the tissue is not considered a function of the excitation frequency, or using simple viscoelastic models, such as the Voigt model and the three-parameter solid model [23].

In soft tissues, high PRF acoustic radiation force excitation pulses can be used to effectively create a step excitation of the material (typically for several hundred milliseconds), and both the rise time and steady-state displacement are related to the underlying material stiffness. Either the excitation pulses can be used to monitor the tissue response, or shorter duration imaging pulses can be interspersed with pushing pulses for tissue monitoring. Walker [24] explored this approach, using both elastic material models, and a viscoelastic Voigt model to derive relative material properties from the tissue response [25]. Viola et al. [26] have employed this approach to characterize blood coagulation in vitro in the operating room setting for timely feedback to anaesthesiologists and surgeons using sonorheometry. Mauldin et al. [27] have also employed this approach with a Voigt model, using a scaling constant to account for acoustic attenuation, intensity and other factors that affect the radiation force magnitude.

3. Transient (impulsive) radiation force excitations

3.1. Qualitative methods

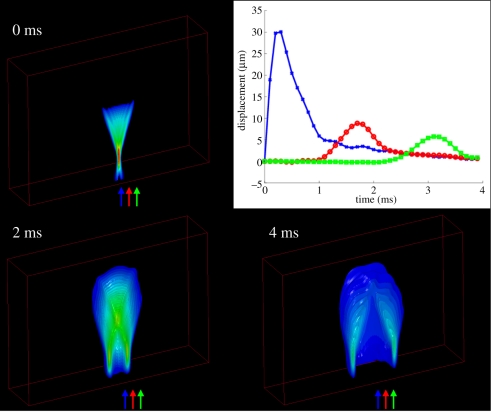
Transient focused acoustic radiation force excitations are typically single pulses that are several hundred cycles in duration (0.05–1 ms). In response to focused, transient excitations, the tissue within the region of excitation (ROE) is deformed, and shear waves are created that propagate away from the ROE, as shown in figure 2. Acoustic radiation force impulse (ARFI) imaging [28] employs temporal impulse-like excitations (pushing pulse durations of less than 1 ms) and monitors the transient tissue displacement response within the ROE using a single diagnostic ultrasonic imaging array. ARFI imaging sequences sequentially interrogate adjacent spatial positions to build up a two-dimensional ARFI dataset that synthesizes the responses from all interrogations. Throughout each ROE, each pixel contains displacement-through-time data (as shown by the blue curve, centred within the ROE at the focal point in the plot in figure 2), allowing for a variety of parameters to be evaluated, including displacement at a given time after excitation, maximum displacement, time-to-peak displacement and time of recovery from peak displacement [28,29]. Equation (1.1) indicates that for a given stress, strain (and displacement) is inversely related to tissue stiffness. ARFI displacement images thus portray relative differences in tissue stiffness, similar to the images generated in elastographic external compression strain imaging [30,31]. These images do not provide quantitative information about tissue stiffness because the magnitude of the applied radiation force varies with tissue attenuation from patient to patient and is difficult to quantify. These qualitative images do, however, provide improved contrast that can be used concurrently with the B-mode images to improve the visualization of anatomical structures and lesions.

Figure 2.

Examples of shear wave propagation represented as isocontours of displacement at different times after impulsive (i.e. <1ms) ARFI excitation in a three-dimensional finite-element simulation of a purely elastic medium with a Young's modulus of 4 kPa and an acoustic attenuation coefficient of 0.7 dB cm⁻¹ MHz⁻¹. The 0 ms isocontour image portrays the radiation force region of excitation (ROE), and the central axis of this displacement profile is the location used to generate qualitative ARFI images as shown in figure 3. The plot in the upper right shows the displacement-through-time profiles at the axial focal depth of the radiation force excitation at three different lateral positions (indicated by the arrows in the isocontour images). Blue, 0 mm; red, 1.5 mm; green, 3 mm.

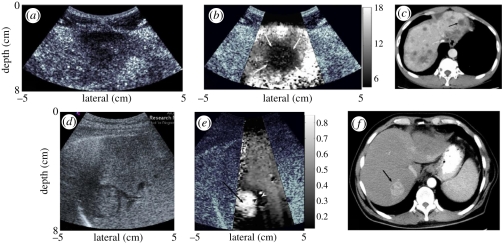
Figure 3 shows ARFI images of liver masses in a study by Fahey et al. [32], where the masses have different displacement contrast relative to the background liver tissue depending on the health of that liver tissue.

Figure 3.

The top row of images shows a metastatic melanoma mass in an otherwise healthy liver background. The mass appears as a hypoechoic region in the B-mode image (a); in the corresponding ARFI image (b), the malignant mass does not displace as much as the background liver tissue and can be interpreted to be stiffer than the liver tissue. This mass is also identified as a region of reduced opacity on the corresponding computed tomographic (CT) image, indicated with an arrow (c). The images in the bottom row show B-mode (d) and ARFI displacement (e) images of a hepatocellular carcinoma in a fibrotic liver. In the ARFI image, the mass appears more compliant (i.e. displaces more) than the stiffer, diseased liver tissue. The corresponding CT image for this hepatocellular carcinoma is shown in (f), with the lesion indicated with an arrow. The greyscale bars in the ARFI images represent displacement in micrometres. (Reproduced with permission from Physics in Medicine and Biology [32]).

Other clinical applications of ARFI imaging that have been studied include monitoring thermal ablation procedures [33], characterizing cardiac [34,35] and vascular tissues [36–40], prostate imaging [41], breast mass imaging [42], gastrointestinal tract imaging [43] and regional anaesthesia guidance [44].

A similar method for monitoring high-intensity focused ultrasound (HIFU) thermal ablation procedures using the HIFU transducer to generate transient radiation force and a separate imaging transducer to monitor the displacement response has been developed by Lizzi et al. [45]. This application is promising as it has the potential to provide low-cost, real-time monitoring of HIFU procedures, which are currently monitored by MR temperature imaging.

3.2. Quantitative methods

The shear waves that are generated by transient radiation force excitations, as shown in figure 2, provide an opportunity for quantification of tissue shear modulus. The propagation speed of the shear waves is several orders of magnitude slower than the speed of sound in soft tissue (i.e. 1–5 m s⁻¹ compared with 1540 m s⁻¹), so ultrasonic correlation and Doppler-based methods can be used to monitor their propagation. Based on wave propagation equations (equation (1.3)), the propagation speed can be related to the underlying tissue shear modulus.

3.3. Shear wave elasticity imaging

Sarvazyan et al. [46] first proposed the quantification of tissue shear modulus using transient, impulse-like focused acoustic radiation forces to generate shear waves within tissues. In this work, they used HIFU pistons to generate radiation force, and MR imaging methods to monitor the resulting shear wave propagation. Nightingale et al. [47] employed the same diagnostic ultrasound array to generate radiation force and monitor the propagation of shear waves, initially using inversion of the Helmholtz equation to quantify shear wave speed in humans in vivo. Bercoff et al. concurrently developed the use of multiple radiation force excitations focused at increasing axial focal depths to create a near plane-wave shear wavefront (i.e. a cylindrical ROE), and monitored the propagation with plane-wave transmit, extensively parallel beam-forming methods, naming this method supersonic shear imaging (SSI) [48]. Plane-wave shear wave fronts can improve the validity of several assumptions associated with the time-of-flight (TOF) shear wave reconstruction methods (discussed below) that are currently implemented in many shear wave elasticity imaging (SWEI)-based methods. Spatially modulated ultrasound radiation force (SMURF), developed by McAleavey et al. [49,50] uses more complex radiation force excitation patterns and a single displacement tracking location that is spatially offset from the excitation to estimate shear wave speed. The complex excitation beam geometry generates shear waves with a known spatial frequency that is modulated temporally by the underlying shear stiffness of the tissue and can be measured at the tracking location.

3.4. Shear wave speed reconstruction methods

Ideally, shear wave speeds can be reconstructed from three-dimensional displacement data using an inversion of the Helmholtz (wave) equation (equation (1.3)), as is commonly used in MR elastography [51,52]. Ultrasonic elasticity imaging, however, is restricted to a single tomographic imaging plane that does not allow for full three-dimensional data reconstruction. Additionally, the presence of jitter in the displacement estimates can yield data with 10–20 dB signal-to-noise ratio (SNR) that is not amenable to second-order differentiation in space and time without excessive amplification of the jitter, leading to variable shear wave speed estimates when employing Helmholtz inversion, as was initially pursued with transient radiation force excitation methods [47,48]. For these reasons, TOF methods are now typically used that take advantage of a priori information about the shear wave propagation direction to estimate wave arrival times and propagation speed.

TOF-based methods employ a priori assumptions, including local homogeneity, and a known direction of propagation, such that the arrival time at adjacent positions can be used to determine the shear wave speed. In TOF methods, it is necessary to determine the arrival time of the shear wave at each spatial location, which can be accomplished using a variety of arrival time metrics (e.g. time of peak displacement and arrival time of the leading edge of the shear wave [53,54]). Once the arrival time has been determined as a function of position, several approaches have been employed to determine the shear wave speed, including linear regression of the position versus arrival time data [53] including outlier removal with, for example, RANdom SAmple Consensus (RANSAC) [55], and arrival time surface fits that are amenable to inverse Eikonal equation solution and level set methods [54,56].

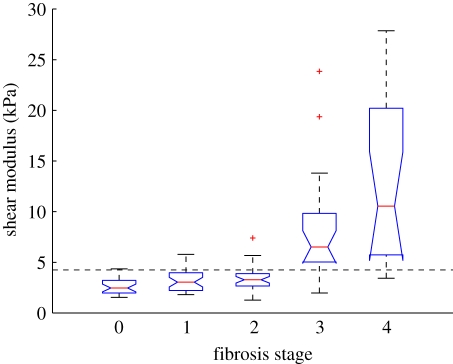
One clinical application of quantitative elasticity imaging methods that has been extensively researched is the potential for non-invasively staging liver fibrosis, which is a diffuse disease process, thus satisfying the TOF-based homogeneity assumptions throughout a large propagation domain. An example of the relationship between radiation force-derived shear modulus estimates and biopsy proven hepatic fibrosis stage is shown in figure 4 [57].

Figure 4.

Liver stiffness, as characterized using transient radiation force excitations and shear wave speed quantification with the RANSAC method, as a function of biopsy-proven fibrosis stage in patients being evaluated for non-alcoholic fatty liver disease. Choosing a shear stiffness threshold of 4.24 kPa allowed F3–F4 fibrosis stages (advanced fibrosis and cirrhosis) to be distinguished from mild to no fibrosis (F0–F2) with 90% sensitivity and specificity (AUC = 0.90) [57].

In shear wave speed reconstruction methods, there is a tradeoff between precision and spatial resolution. The use of larger regression kernels presumes a larger homogeneous region and is typically associated with higher precision and accuracy; however, this comes at the expense of spatial resolution. Smaller regression kernels yield better spatial resolution of the reconstructed shear wave speed data; however, decreasing the size of the kernel is also associated with an increase in the variance of the estimate. The spatial resolution of TOF-based reconstructions is ultimately limited by the need for the wave to propagate over a finite spatial extent in order to quantify its propagation speed.

Fink et al. have extensively developed and reported TOF-based shear wave quantification methods using their SSI excitation techniques and have reported spatial resolution of 1–2 mm [54,58]. SSI imaging approaches have been implemented in several clinical applications, including: monitoring thermal ablation procedures [59], breast imaging (figure 5 [60]), musculoskeletal imaging [61], hepatic imaging [62] and small animal transcranial brain imaging [63], among others. These efforts have led to a recently available commercial SSI product as discussed below.

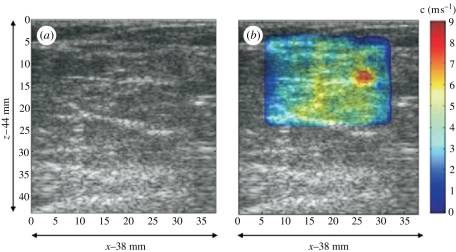
Figure 5.

Characterization of a 5 mm grade III infiltrating ductal carcinoma using SuperSonic Imaging and an L74 linear imaging array (centre frequency 5 MHz). The B-mode image (a) shows a slightly hypoechoic region that is clearly delineated as stiff (red) in the corresponding shear wave velocimetry map (b). (Reproduced with permission from Ultrasound in Medicine and Biology [60]).

Transient excitations have also been used to characterize dispersion (i.e. the frequency dependence of shear wave speed) in soft tissues. An elegant method was presented by Deffieux et al. [58] using a Fourier transform approach to evaluate the phase shifts throughout the propagation domain of an SSI excitation as a function of frequency. Using this method, they quantified dispersion of shear waves in both liver and muscle for shear wave frequencies ranging from 75 to 500 Hz.

With the extensively parallel beam-forming capabilities that are now available on many ultrasound scanners, it is possible to concurrently monitor displacement throughout an imaging plane. Therefore, ARFI (qualitative) and SWEI (quantitative) images can now be generated from a single dataset (figure 6). The SWEI image portrays quantitative information with higher contrast, whereas the ARFI image provides higher spatial resolution.

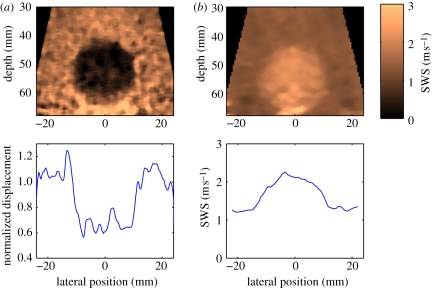
Figure 6.

Matched (a) ARFI and (b) SWEI images of a calibrated elasticity phantom with a 20 mm diameter stiff spherical inclusion. The images were generated from the same dataset, which was obtained with a 4 MHz abdominal imaging array, using parallel receiving beam-forming techniques to monitor the tissue response to each excitation throughout the entire field of view. A total of 88 excitation pulses were located at two focal depths (50 and 60 mm), with a beam spacing of 1 mm. The ARFI image portrays normalized displacement at 0.7 ms after each excitation, whereas the SWEI image portrays reconstructed shear wave speed. The lesion contrast is 0.37 and 0.71 for the ARFI and SWEI images, respectively, and the edge resolution (20–80%) is 1.2 mm (ARFI) and 5.0 mm (SWEI) in the plots from a depth of 50 mm, shown in the bottom row.

3.5. Harmonic tissue excitations with acoustic radiation force

Fatemi & Greenleaf [64,65] proposed the use of interfering ultrasonic beams with slightly offset frequencies (differences ranging from approx. 100 Hz to 10 kHz) to generate oscillating radiation force excitations at the beat frequency in the region of overlap between the two beams. A hydrophone is used to monitor the tissue response, and the excitation beams are swept across the field of view to generate C-scan type images of both vibration amplitude and phase. This technique has been termed vibroacoustography and has been applied in multiple in vitro and in vivo scenarios, including vascular imaging [66], breast imaging [67] and prostate imaging [68], among others.

A variation of this approach has been developed by Konofagou et al. [69,70] termed harmonic motion imaging (HMI), where harmonic oscillations are generated either by the beat frequency of confocal beams as in vibroacoustography or by amplitude modulation of a single excitation beam at the desired frequency. The displacement response is monitored using conventional ultrasonic correlation-based techniques. The peak-to-peak amplitude of the vibrating tissue is used to determine relative differences in tissue stiffness. HMI has shown promise in imaging HIFU-generated thermal ablation lesions [71].

Quantification of shear wave dispersion has been implemented by Greenleaf et al. using a method called shear wave dispersion ultrasound vibrometry (SDUV) [72]. In this method, repeated radiation force excitation pulses are employed in a single location to generate a propagating sinusoidal shear wave with a frequency determined by the excitation pulse-repetition frequency. Differences in the phase of the shear wave at lateral positions are used to determine the wave speed. Dispersion is assessed by analysing shear wave speed differences for different shear wave frequencies. This method has the advantage of narrowband excitation and thus filtering methods can be employed to isolate the tissue response to the SDUV excitation, facilitating the use of lower acoustic output. This method has been applied to several tissues, demonstrating dispersion in liver [73] and blood vessels [74].

Building upon sonoelasticity-based methods, Parker et al. have developed a novel crawling wave method using acoustic radiation force. In this method, amplitude-modulated radiation force excitations of slightly different frequencies are generated in spatially offset positions. The crawling wave interference pattern generated by these excitations propagates at a speed related to the underlying tissue stiffness and can be detected with conventional Doppler techniques [75].

3.6. Methods using spherical point scatterers

Several creative radiation force-based quantitative elasticity approaches have been proposed that involve the use of embedded spheres or gas bubbles to derive mechanical information about the surrounding medium. These approaches are appealing because the motion of the sphere can be modelled using analytical expressions that can be solved to determine the viscoelastic properties of the background material [76–78]. Such methods have been proposed for implementation in the eye using laser-induced gas bubbles [79]. In addition, the radiation force applied to an embedded sphere is generally much greater than that arising in purely absorbing media; thus, lower acoustic output can be used in moderately attenuating media, such as in hydrogels and engineered biological tissues, where a sphere could be incorporated prior to cell growth [80].

3.7. Safety of acoustic radiation force imaging methods

The safety of diagnostic ultrasonic imaging methods is monitored through several metrics, including the thermal index (TI), which provides an estimate of the expected tissue heating, and the mechanical index (MI), which provides a measure of the potential for inducing acoustic cavitation [81]. The methods discussed above use different duration excitation pulses, with steady state and harmonic excitations typically requiring higher cumulative acoustic output than transient excitations. In addition, for transient excitations, owing to geometric spreading and attenuation of the shear wave, the larger the propagation domain over which shear waves are monitored, the higher the required initial acoustic output.

Transient acoustic radiation force-based imaging methods typically employ excitation pulses with similar pulse amplitudes and longer pulse durations (several hundred cycles) than those commonly used for diagnostic imaging (10–20 cycles for Doppler methods). These longer durations could result in increased tissue heating; thus, the thermal response must be monitored to ensure compliance with the diagnostic guidelines. It is fortuitous that it takes less energy to displace tissue several micrometres than to raise its temperature by a fraction of a degree Celsius, owing to differences in the thermal and mechanical material properties. For a single impulsive radiation force excitation, heat loss owing to both perfusion and thermal conduction can reasonably be neglected, and the temperature rise in the tissue can be estimated using [82]:

3.1

where q_v is the rate of heat production per unit volume generated by the absorption of acoustic energy, c_v is the heat capacity per unit volume of the tissue and t is the duration of the excitation. For repeated interrogations, conduction must be addressed, in addition to considering the spatial overlap of the excitations [83]. Both heating owing to acoustic absorption and transducer face heating must be considered when designing sequences for clinical use to maintain temperature rises within diagnostic limits.

The likelihood of the generation of acoustic cavitation in diagnostic ultrasonic imaging is reduced by maintaining an MI < 1.9. Radiation force excitations are typically employed within this limit; thus, non-thermal bioeffects are not expected and no evidence of non-thermal bioeffects associated with such pulses employed in vivo has been reported to date. While unlikely, it is currently not known if the longer duration pulses near this limit are associated with non-thermal bioeffects [81]. In addition, given that the MI of radiation force excitation pulses is generally near this upper limit, it would be expected that ultrasonic contrast agents would cavitate if exposed to these pulses. In addition, no related studies have been performed in the setting of obstetric imaging, where the thermal and mechanical limits for acoustic exposure are considerably lower than those for general imaging.

3.8. Commercial implementations of radiation force-based imaging

Recently, two manufacturers have released commercial implementations of radiation force-based imaging methods, both of which employ transient radiation force excitations. These have been designed such that the pulse sequences are within diagnostic limits for non-obstetric imaging. Siemens Medical Solutions has implemented a version of ARFI imaging on their ACUSON S2000 ultrasound scanner as the Virtual Touch Tissue Imaging tool that provides qualitative images of relative differences in tissue displacement in response to transient acoustic radiation force excitation as described above for ARFI imaging. Clinical studies in Europe and Asia are actively being conducted to evaluate the clinical utility of this imaging modality (e.g. [84–88]). Siemens Medical Solutions has also introduced a tool for radiation force-based shear wave speed estimation as the Virtual Touch Tissue Quantification tool, which is actively being studied in the context of abdominal and thyroid tissue stiffness quantification (e.g. [89–93]).

SuperSonic Imagine released the Aixplorer ultrasound scanner that generates quantitative elasticity images based on shear wave propagation measurements. This system is based on the SSI technology developed by Bercoff et al. [48], employing shear wave speed reconstruction algorithms similar to those reported by McLaughlin & Renzi. [54,56]. Initial clinical applications of the Aixplorer have been in characterizing breast lesions [60], and the system is actively being translated to applications in the liver, thyroid and prostate.

In addition to the new acoustic radiation force imaging systems mentioned above, HemoSonics, LLC, in collaboration with StarFish Medical, has begun the development and clinical testing of a portable point-of-care analyser based upon sonorheometry [26] to characterize blood haemostasis potential in a variety of clinical settings.

4. Discussion

The use of acoustic radiation force as a mechanical excitation source for elasticity imaging has been investigated in research settings since the mid-1990s, and has recently been introduced into the commercial market. These approaches provide a unique tool to directly couple focused stresses within internal organs, overcoming this challenge associated with sources of external vibration. In addition, these methods do not rely on the operator to introduce stress, thus facilitating operator-independent data acquisition. As with external excitation elasticity imaging methods, radiation force imaging methods have been developed that provide both qualitative and quantitative elasticity information. The qualitative methods provide high-resolution structural information, and the wave propagation-based methods provide quantitative elasticity metrics.

To make quantitative elasticity imaging a viable and useful clinical tool, large-scale studies need to be performed to establish elasticity metrics for healthy and diseased tissues. The current literature contains stiffness values for soft tissues that span a wide range, many with measurements made in an ex vivo setting, rather than an in vivo setting, which could impact on the tissue stiffness [2,4,94–96]. Thus, stiffness metrics need to be established as a function of disease state and patient demographics in vivo. While there are many hypotheses for why tissues stiffen or soften in the face of disease (e.g. scarring of the liver leads to increased fibrotic tissue that is stiffer), these disease processes may exhibit differences in their mechanical manifestation based on the aetiology of the disease, pre-existing conditions and other variables associated with the patient's overall health such as blood pressure, perfusion, etc. In addition, given that many assumptions are being made in current implementations of shear wave imaging methods (e.g. linearity, viscoelasticity, etc.), it is important for stiffness metrics to be accompanied with information about the processing algorithms and modes of excitation (e.g. static versus dynamic, frequency of excitation, etc.) to facilitate comparison between methods.

There are additional technical innovations that can be made to improve the likelihood that radiation force-based elasticity imaging methods will have clinical success and utility. As obesity becomes more prevalent in western societies, the ability to image at depth becomes more of a concern. Many target organs for elasticity imaging, such as the liver and kidney, become increasingly difficult to image as the amount of subcutaneous and visceral fat between the ultrasound transducer and the target organs increases. Adipose tissue can be highly attenuating, reducing the ultrasound SNR at depth, which degrades conventional B-mode image quality, compromising the ability to accurately estimate displacement, and reducing acoustic radiation force amplitudes. Improvements in transducer technology to achieve greater acoustic output without transducer lens heating will allow stronger and longer ultrasound pulses to be delivered to the tissue without risking transducer damage [97]. Additionally, improvements in displacement estimation in the presence of noisy signals will allow for improved elasticity imaging without necessarily increasing the acoustic exposure to patients. More advanced algorithms are actively being studied by many research groups [98–100].

Finally, the study of more complex material models to represent soft tissues has the potential to open new doors of clinical opportunity as additional metrics to differentiate disease states are explored. Even more clinical opportunities will probably be generated as additional and future-generation commercial implementations of these technologies are made available to clinicians to facilitate large-scale studies for a variety of disease processes.