Identifying mental states from neural states under mental constraints

Abstract

This article emphasizes how the recently proposed interlevel relation of contextual emergence for scientific descriptions combines ‘bottom-up’ and ‘top-down’ kinds of influence. As emergent behaviour arises from features pertaining to lower level descriptions, there is a clear bottom-up component. But, in general, this is not sufficient to formulate interlevel relations stringently. Higher level contextual constraints are needed to equip the lower level description with those details appropriate for the desired higher level description to emerge. These contextual constraints yield some kind of ‘downward confinement’, a term that avoids the sometimes misleading notion of ‘downward causation’. This will be illustrated for the example of relations between (lower level) neural states and (higher level) mental states.

1. Introduction

The sciences know various types of relationships among domains of descriptions of particular phenomena—most common are versions of reduction and of emergence.¹ Although these domains are not ordered strictly hierarchically, one often speaks of lower and higher levels of description, where lower levels are typically considered as more fundamental. As a rule, phenomena at higher levels of description are more complex than phenomena at lower levels. This increasing complexity depends on contingent conditions, the so-called contexts, that must be taken into account for an appropriate description. The way this can be done constrains the lower level description and entails a kind of downward confinement by higher level contexts, often referred to as ‘downward causation’ [4].

Moving up or down between levels of descriptions also decreases or increases the amount of symmetries relevant at the respective level. A (hypothetical) description at a most fundamental level would have no broken symmetry, meaning that such a description is invariant under all conceivable transformations. This would amount to a description completely free of contexts: everything is described by one (set of) fundamental law(s). The consequence of complete symmetry is that there are no distinguishable phenomena. Broken symmetries provide room for contexts and, thus, ‘create’ phenomena.

The interlevel relation of contextual emergence uses lower level features as necessary (but not sufficient) conditions for the description of higher level features. As will become clear below, it can be viably combined with the idea of multiple realization, a key issue in the debate about supervenience [5,6], which poses sufficient (but not necessary) conditions at the lower level. Both contextual emergence and supervenience are more specific than a patchwork scenario as in radical emergence and more flexible than a radical reduction where everything is already contained at a lower (or lowest) level. Combining them suitably leads to a balanced relationship between bottom-up and top-down influences in the formulation of interlevel relations.

Stephan [7] distinguishes synchronic and diachronic kinds of emergence. The key point in synchronic emergence is the irreducibility of higher level features to lower level features; in diachronic emergence, it is the unpredictability of future behaviour from previous behaviour. Synchronic emergence refers to interlevel relations with no time dependence involved, whereas diachronic emergence refers to temporal intralevel relations allowing us to speak of effects and causes preceding them (‘efficient causation’).

Contextual emergence is a structural relation between different levels of description. As such, it is a synchronic kind of emergence. It does not address questions of diachronic emergence, referring to how new qualities arise dynamically, as a function of time. Moreover, contextual emergence is conceived as a relation between levels of description, not ‘levels of nature’: it addresses epistemic questions rather than issues of ontology. A possible option for how ontological relations may be addressed as well, inspired by Quine's [8] ontological relativity, has been elaborated and applied to scientific examples by Atmanspacher & Kronz [9].

In mature basic sciences such as physics or chemistry, contextual emergence typically substantiates in detail already existing schemes and ideas. As an example, §3 will describe how this works for the relation between mechanics and thermodynamics. The full added value of contextual emergence is to be expected in applications without established theoretical frameworks. A pertinent example is cognitive neuroscience, where levels of description are not yet finally specified or even formalized, and it can be shown how (higher level) mental properties are actively constructed. In §4, it will be demonstrated how this works in detail. But, to begin with, let us have a brief look at the general framework of contextual emergence in abstract terms.

2. The conceptual scheme

The basic idea of contextual emergence is that, starting at a particular ‘lower’ level L of description, a two-step procedure can be carried out that leads in a systematic and formal way (1) from an individual description L_i to a statistical description L_s and (2) from L_s to an individual description M_i at a ‘higher’ level M. This scheme can, in principle, be iterated across any connected set of descriptions, so that it is applicable to any case that can be formulated precisely enough to be a sensible subject of a scientific investigation.

The essential goal of step (1) is the identification of equivalence classes of individual states that are indistinguishable with respect to a particular ensemble property. Insofar as this step implements the multiple realizability of statistical states in L_s by individual states in L_i, it is a key feature of a supervenience relation with respect to states. The equivalence classes at L can be regarded as cells of a partition. Each cell can be regarded as the support of a (probability) distribution representing a statistical state.

The issue of composition or constitution, which is emphasized in alternative types of emergence, is to be treated in the framework of this step (1). In contextual emergence, however, the point is not the composition of large objects from small ones. Rather than size, the point here is that statistical states are formulated as probability distributions over individual states. This way they can at the same time be considered as compositions and as representations of (limited) knowledge about individual states.

The essential goal of step (2) is the assignment of individual states at level M to statistical states at level L. This cannot be done without additional information about the desired level-M description. In other words, it requires the choice of a context setting the framework for the set of observables (properties) at level M that is to be constructed from level L. The chosen context provides constraints to be implemented as a stability criterion at level L. It is crucial that this stability condition cannot be specified without knowledge about the context at level M. In this sense, the context yields a top-down influence or downward confinement.

The notion of a context can be understood in a very broad sense. For instance, given a statistical mechanics description of a many-particle system, the proper contextual framework for a discussion in terms of thermal observables is thermodynamics, yielding observables such as temperature. If one is interested in the behaviour of fluids in particular, the proper contextual framework would be hydrodynamics, yielding observables such as viscosity. Similar kinds of contexts for cognitive neuroscience have been discussed by Bechtel & Richardson [10] or more recently by Dale [11].

The notion of stability induced by context is of paramount significance for contextual emergence. Roughly speaking, stability refers to the fact that some system is robust under (small) perturbations. For example, a (small) perturbation of a homeostatic or equilibrium state does not lead to a completely different state, because the perturbation is damped out by the dynamics, and the initial state will be asymptotically retained (see §3). The more complicated notion of a stable partition of a state space (see §4) is based on the idea of coarse-grained states, i.e. cells of a partition whose boundaries are (approximately) maintained under the dynamics.

Such stability criteria guarantee that the statistical states of L_s are based on a robust partition so that the emergent observables in M_i are well-defined. (For instance, if a partition is not stable under the dynamics of the system at L_i, the assignment of states in M_i will change over time and is ill-defined in this sense.) The implementation of a contingent context at level M as a stability criterion in L_i yields a proper partitioning for L_s. In this way, the lower level state space is endowed with a new, contextual topology (see Atmanspacher [12] and Atmanspacher & Bishop [13] for more details).

From a slightly different perspective, the context selected at level M decides which details in L_i are relevant and which are irrelevant for individual states in M_i. Differences among all those individual states at L_i that fall into the same equivalence class at L_s are irrelevant for the chosen context. In this sense, the stability condition determining the contextual partition at L_s is a relevance condition at the same time.

This interplay of context and stability across levels of description is the core of contextual emergence. Its proper implementation requires an appropriate definition of individual and statistical states at these levels. This means, in particular, that it would not be possible to construct emergent observables in M_i from L_i directly, without the intermediate step to L_s. And it would be equally impossible to construct these emergent observables without the downward confinement arising from higher level contextual constraints.

This way, bottom-up and top-down strategies are interlocked with one another in such a way that the construction of contextually emergent observables is self-consistent. Higher level contexts are required to implement lower level stability conditions leading to proper lower level partitions, which in turn are needed to define those lower level statistical states that are co-extensional with higher level individual states and associated observables.

The following section outlines how this is manifest even in one of the most discussed (and misinterpreted) interlevel relations: that between mechanics and thermodynamics. Then, recent work applying contextual emergence for the relation between brain states and mental states, i.e. bridging neurobiology and psychology, is reviewed. This work, it will be argued, has interesting consequences for the much discussed philosophical topic of mental causation.

3. From mechanics to thermodynamics

As a concrete example, consider the transition from classical point mechanics over statistical mechanics to thermodynamics [14]. Step (1) in the discussion above is here the step from point mechanics to statistical mechanics, essentially based on the formation of an ensemble distribution. Particular properties of a many-particle system are defined in terms of a statistical ensemble description (e.g. as moments of a many-particle distribution function), which refers to the statistical state of an ensemble (L_s) rather than the individual states of single particles (L_i).

An example for an observable associated with the statistical state of a many-particle system is its mean kinetic energy, which can be derived from the distribution of the momenta of all N particles. The expectation value of kinetic energy is defined as the limit N → ∞ of its mean value.

Step (2) is the step from statistical mechanics to thermodynamics. Concerning observables, this is the step from the expectation value of a momentum distribution of a particle ensemble (L_s) to the temperature of the system as a whole (M_i). In many standard philosophical discussions, this step is mischaracterized by the false claim that the thermodynamic temperature of a gas is identical to the mean kinetic energy of the molecules which constitute the gas. In fact, a proper discussion of the details was unavailable for a long time and was not achieved until the work of Haag et al. [15] and Takesaki [16].

The main conceptual point in step (2) is that thermodynamic observables such as temperature presume thermodynamic equilibrium as a crucial assumption, which we call a contextual condition. It is formulated in the zeroth law of thermodynamics and is not available at the level of statistical mechanics. The very concept of temperature is thus foreign to statistical mechanics and pertains to the level of thermodynamics alone. (Needless to say, there are many more thermodynamic observables in addition to temperature. Note also that a feature so fundamental in thermodynamics as irreversibility depends crucially on the context of thermal equilibrium.)

The context of thermal equilibrium (M_i) can be recast in terms of a class of distinguished statistical states (L_s), the so-called Kubo–Martin–Schwinger (KMS) states. These states are defined by the KMS condition that characterizes the (structural) stability of a KMS state against local perturbations. Hence, the KMS condition implements the zeroth law of thermodynamics as a stability criterion at the level of statistical mechanics. (The second law of thermodynamics expresses this stability in terms of a maximization of entropy for thermal equilibrium states. Equivalently, the free energy of the system is minimal in thermal equilibrium.)

Statistical KMS states induce a contextual topology in the state space of statistical mechanics (L_s), which is basically a coarse-grained version of the topology of L_i. This means nothing else than a partitioning of the state space into cells leading to statistical states (L_s) that represent equivalence classes of individual states (L_i). They form ensembles of states that are indistinguishable with respect to their mean energy and can be assigned the same temperature (M_i). Differences between individual states at L_i falling into the same equivalence class at L_s are irrelevant with respect to a particular temperature at M_i.

While step (1) formulates statistical states from individual states at the mechanical level of description, step (2) provides individual thermal states from statistical mechanical states. Along with this step goes a definition of novel, thermal observables. All this is guided by and impossible without the explicit use of the context of thermal equilibrium, unavailable within a mechanical description.

The example of the relation between mechanics and thermodynamics is particularly valuable for the discussion of contextual emergence because it illustrates the two essential construction steps in great detail. In addition to the work quoted, a more recent account of what has been achieved and what is still missing is due to Linden et al. [17].

There are other examples in physics and chemistry which can be discussed in terms of contextual emergence: emergence of geometric optics from electrodynamics [18], emergence of electrical engineering concepts from electrodynamics [18], emergence of chirality as a classical observable from quantum mechanics [14,19], emergence of hydrodynamic properties from many-particle theory [20].

4. Mental states from neurodynamics

In the example discussed in the preceding section, descriptions at L and M are well established so that a formally precise interlevel relation can be straightforwardly set up. The situation becomes more difficult in situations where no such established descriptions are available. This is the case in the areas of cognitive neuroscience or consciousness studies, focusing at relations between neural and mental states (e.g. the identification of neural correlates of conscious states). That brain activity provides necessary but not sufficient conditions for mental states, which is a key feature of contextual emergence, becomes increasingly clear even among practising neuroscientists (see, for instance, the recent opinion article by Frith [21]).

For the application of contextual emergence, the first desideratum is the specification of proper levels L and M. With respect to L, one needs to specify whether states of neurons, of neural assemblies or of the brain as a whole are to be considered; and with respect to M a class of mental states reflecting the situation under study needs to be defined. In a purely theoretical approach, this can be extremely tedious, but, in empirical investigations, the experimental set-up can often be used for this purpose. For instance, experimental protocols include a task for subjects that defines possible mental states, and they include procedures to record brain states.

The following discussion will first address a general theoretical scenario (developed by Atmanspacher & beim Graben [22]) and then a concrete experimental example (worked out by Allefeld et al. [23]). Both are based on the so-called state space approach to mental and neural systems (see Fell [24] for a brief introduction).

It should be mentioned that there are other notable proposals to study mappings between mental states and brain states in a formally developed and empirically applicable way; for instance, the approaches suggested by Balduzzi & Tononi [25,26] or by Hotton & Yoshimi [27,28]. Their detailed relation to contextual emergence remains to be explored in future work.

4.1. Theoretical approach

The first step is to find a proper assignment of L_i and L_s at the neural level. A good candidate for L_i are the properties of individual neurons. Then the first task is to construct L_s in such a way that statistical states are based on equivalence classes of those individual states whose differences are irrelevant with respect to a given mental state at level M. This reflects that a neural correlate of a conscious mental state can be multiply realized by ‘minimally sufficient neural subsystems correlated with states of consciousness’ [29].

In order to identify such a subsystem, we need to select a context at the level of mental states. As one among many possibilities, we may use the concept of ‘phenomenal families’ [29] for this purpose. A phenomenal family is a set of mutually exclusive phenomenal (mental) states that jointly partition the space of mental states. Starting with something like creature consciousness, that is, being conscious versus being not conscious, one can define increasingly refined levels of phenomenal states of background consciousness (awake, dreaming, sleep, …), sensual consciousness (visual, auditory, tactile, …), visual consciousness (colour, form, location, …) and so on.²

Selecting one of these levels (as an example) provides a context that can then be implemented as a stability criterion at L_s. In cases like the neural system, where complicated dynamics far from thermal equilibrium are involved, a powerful method to do so uses the neurodynamics itself to find proper statistical states. The essential point is to identify a partition of the neural state space whose cells are robust under the dynamics. This guarantees that individual mental states M_i, defined on the basis of statistical neural states L_s, remain well-defined as the system develops in time. The reason is that differences between individual neural states L_i belonging to the same statistical state L_s remain irrelevant as the system develops in time.

The construction of statistical neural states is strikingly analogous to what leads Butterfield [30] to the notion of ‘meshing dynamics’. In his terminology, L-dynamics and M-dynamics mesh if coarse graining and time evolution commute. From the perspective of contextual emergence, meshing is guaranteed by the stability criterion induced by the higher level context. In this picture, meshing translates into the topological equivalence of the two dynamics. For details see appendix A.

For multiple fixed points, their basins of attraction represent proper coarse grainings, while chaotic attractors need to be coarse-grained by so-called generating partitions (see appendix A). From experimental data, both can be numerically determined by partitions leading to Markov chains. These partitions yield a rigorous theoretical constraint for the proper definition of stable mental states. The formal tools for the mathematical procedure derive from the fields of ergodic theory [31] and symbolic dynamics [32], and are discussed in some detail in Atmanspacher & beim Graben [22] and Allefeld et al. [23]. Some key issues are compactly surveyed in appendix A.

4.2. Empirical construction

Although there are mathematical existence theorems for generating partitions in hyperbolic systems [33–35], they are generally hard to construct—their cells are inhomogeneous, i.e. they vary in form and size. They are actually known for only a few synthetic examples such as the torus map, the standard map or the Henon map [36–38]. Therefore, algorithms have been suggested to estimate them from experimental time series [39–42].

In the following, I will sketch a workable construction applying contextual emergence to experimental data concerning the relation between mental states and brain dynamics recorded by electroencephalograms (EEGs). In their recent study, Allefeld et al. [23] used data from the EEGs of subjects with sporadic epileptic seizures. This means that the neural level is characterized by brain states recorded via EEG, while the context of normal and epileptic mental states essentially requires a bipartition of that neural state space.

The analytical procedure rests on ideas by Gaveau & Schulman [43], Froyland [44] and Deuflhard & Weber [45]. It starts with a (for instance) 20-channel EEG recording, giving rise to a state space of dimension 20, which can be reduced to a lower number by restricting the analysis to principal components. On the resulting state space, a homogeneous grid of cells is imposed in order to set up a (Markov) transition matrix reflecting the EEG dynamics on a fine-grained auxiliary partition.

The eigenvalues of this matrix yield time scales for the dynamics which can be ordered by size. Gaps between successive time scales indicate groups of eigenvectors defining partitions of increasing refinement—in simple cases, the first group is already sufficient for the analysis. The corresponding eigenvectors together with the data points belonging to them define the neural state space partition relevant for the identification of mental states [46].³

Finally, the result of the partitioning can be inspected in the originally recorded time series to check whether mental states are reliably assigned to the correct episodes in the EEG dynamics. The study by Allefeld et al. [23] shows perfect agreement between the distinction of normal and epileptic states and the bipartition resulting from the spectral analysis of the neural transition matrix.

5. Macrostates in neural systems

Contextual emergence addresses both the construction of a partition at a lower level description and the application of a higher level context to do this in a way adapted to a specific higher level description. Two alternative strategies have been proposed to contruct L_s-states (‘macrostates’) from L_i-states (‘microstates’) previously: one by Amari and co-workers and another one by Crutchfield and co-workers.

Amari and colleagues [47,48] proposed identifing statistical states L_s based on their decorrelation in the neural state space. The macrostate criterion that they require for the stability of these states, however, does not exploit the dynamics of the system in the direct way which a Markov partition or generating partition allows. A detailed comparison of macrostate criteria in contextual emergence and in Amari's approach has been given by beim Graben et al. [49].

Another alternative is the construction of macrostates within an approach called computational mechanics [50]. A key notion in computational mechanics is the notion of a ‘causal state’. Its definition is based on the equivalence class of histories of a process that are equivalent for predicting the future of the process. Since any prediction method induces a partition of the state space of the system, the choice of an appropriate partition is crucial. If the partition is too fine, too many (irrelevant) details of the process are taken into account; if the partition is too coarse, not enough (relevant) details are considered.

As described in detail by Shalizi & Moore [51], it is possible to iteratively determine partitions leading to causal states. This is achieved by minimizing their statistical complexity, the amount of information which the partition encodes about the past. Thus, the approach uses an information theoretical criterion rather than a stability criterion to construct a proper partition for macrostates.

Causal states depend on the ‘subjectively’ chosen initial partition, but are then ‘objectively’ fixed by the underlying dynamics. This has been expressed succinctly by Shalizi & Moore [51]: Nature has no preferred questions, but to any selected question it has a definite answer. Quite similarly, the notion of robust statistical states in contextual emergence combines the ‘subjective’ notion of coarse graining with an ‘objective’ way to determine proper partitions as they are generated by the underlying dynamics of the system.

6. Mental causation

It is a long-standing philosophical puzzle how the mind can be causally relevant in a physical world: the ‘problem of mental causation’.⁴ The question of how mental phenomena can be causes is of high significance for an adequate comprehension of scientific disciplines such as psychology and cognitive neuroscience. Moreover, mental causation is crucial for our everyday understanding of what it means to be an agent in a natural and social environment. Without the causal efficacy of mental states, the notion of free agency would be nonsensical.

One of the reasons why the causal efficacy of the mental has appeared questionable is that a horizontal (intralevel and diachronic) determination of a mental state m by prior mental states seems to be inconsistent with a vertical (interlevel and synchronic) determination of m by neural states. In a series of influential papers and books, Kim [54] has presented his much discussed ‘supervenience argument’ (also known as ‘exclusion argument’), which ultimately amounts to the dilemma that either mental states are causally inefficacious or they hold the threat of overdetermining neural states. In other words: either mental events play no horizontally determining causal role at all, or they are causes of the neural bases of their relevant horizontal mental effects [54].

The interlevel relation of contextual emergence yields a quite different perspective on mental causation. It dissolves the alleged conflict between horizontal and vertical determination of mental events as ill-conceived [55]. The key point is a construction of properly defined mental states from the dynamics of an underlying neural system. This can be done via statistical neural states based on a proper partition, such that these statistical neural states are co-extensive (but not necessarily identical) with individual mental states.

This construction implies that the mental dynamics and the neural dynamics, related to each other by a so-called intertwiner, are topologically equivalent ([22], see also appendix A). Given properly defined mental states, the neural dynamics gives rise to a mental dynamics that is independent of those neurodynamical details that are irrelevant for a proper construction of mental states.

As a consequence, (i) mental states can indeed be causally and horizontally related to other mental states and (ii) they are causally related neither to their vertical neural determiners nor to the neural determiners of their horizontal effects. This makes a strong case against a conflict between a horizontal and a vertical determination of mental events and resolves the problem of mental causation in a deflationary manner. Vertical and horizontal determination do not compete, but complement one another in a cooperative fashion. Both together deflate Kim's dilemma and reflate the causal efficacy of mental states.

In this picture, mental causation is a horizontal relation between previous and subsequent mental states, although its efficacy is actually derived from a vertical relation: the downward confinement of (lower level) neural states originating from (higher level) mental constraints. This vertical relation is characterized by an intertwiner, a mathematical mapping, which must be distinguished from a causal before–after relation. For this reason, the terms ‘downward causation’ or ‘top-down causation’ [4] are infelicitous choices for addressing a ‘downward confinement’ by contextual constraints.

7. Some concluding remarks

• — Viewed superficially, the combination of contextual emergence with supervenience might appear conspicuously close to plain reduction because it ultimately merges necessary and sufficient conditions at the lower level description for higher level terms. However, there is a subtle difference between the ways in which supervenience and emergence are in fact implemented.⁵ While we allude to supervenience in terms of the multiple realization of statistical neural states by individual neural states, only the argument by emergence relates those statistical neural states to mental observables. The important selection of a higher level contextual constraint leads to a stability criterion for neural states, but it is also crucial for the definition of the set of observables with which lower level statistical states are to be associated.

• — Statistical neural states are multiply realized by individual neural states, and they are co-extensive with individual mental states; see also Bechtel & Mundale [57], who proposed precisely the same idea. There are a number of reasons to distinguish this co-extensivity from an identity relation which are beyond the scope of this article; for details, see Harbecke & Atmanspacher [55].

• — Besides the application of contextual emergence under well-controlled experimental conditions, it may be useful also for investigating spontaneous behaviour. If such behaviour together with its neural correlates is continuously monitored and recorded, it is possible to construct proper partitions of the neural state space along the lines of §4.2. Mapping the time intervals of these partitions to epochs of corresponding behaviour may facilitate the characterization of typical paradigmatic behavioural patterns.

• — It is an interesting consequence of contextual emergence that higher level descriptions constructed on the basis of proper lower level partitions are compatible with one another. Conversely, improper partitions yield, in general, incompatible descriptions [58]. As ad hoc partitions usually will not be proper partitions, corresponding higher level descriptions will generally be incompatible. This argument was proposed by Atmanspacher & beim Graben [22] for an informed discussion of how to pursue ‘unity in a fragmented psychology’, as Yanchar & Slife [59] put it.

• — Another application of contextual emergence refers to the symbol grounding problem posed by Harnad [60]. The key issue of symbol grounding is the problem of assigning meaning to symbols on purely syntactic grounds, as proposed by cognitivists such as Fodor & Pylyshyn [61]. This entails the question of how conscious mental states can be characterized by their neural correlates (see Atmanspacher & beim Graben [22]). Viewed from a more general perspective, symbol grounding has to do with the relation between analogue and digital systems, the way in which syntactic digital symbols are related to the analogue behaviour of a system they describe symbolically. This might open up a novel way to address the problem of how semantic content arises as a reference relation between symbols and what they symbolize. This problem is not restricted to cognition; it may also be a key to understand the transition from inanimate matter to biological life in information theoretical terms [62].

• — For additional directions of research in cognitive science, psychology and psycholinguistics that are related to contextual emergence, see [63–66]. They are similar in spirit, but differ in their scope and details.

Appendix A.

Generating partitions and topological equivalence

Consider a partition 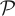= (A₁, A₂, … , A_m) over a state space X in which the states of a system are represented. Then a simple version of the entropy of the system is the well-known Shannon entropy

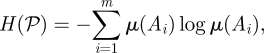A 1

where μ(A_i) is the probability that the system state resides in partition cell A_i.

The dynamical entropy of a system in a state space representation requires considering its dynamics Φ:X → X with respect to a partition ,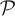

A 2

In words, this is the limit of the entropy of the union of partitions of increasing dynamical refinement. The refinement is dynamical because it is generated by the dynamics Φ itself, expressed by Φ 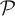, Φ² 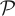, and so forth.

A special case of a dynamical entropy of the system with dynamics Φ is the Kolmogorov–Sinai entropy [67,68]

A 3

This supremum over all partitions 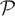is assumed if 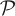is a generating partition, otherwise H(Φ, 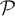) < H_KS. (Every Markov partition is generating, but not vice versa.) A generating partition 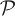_g minimizes correlations among partition cells A_i, so that they are stable under Φ and only correlations owing to Φ itself contribute to H(Φ, 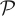_g). Boundaries of A_i are (approximately) mapped onto one another. Spurious correlations owing to blurring cells are excluded, so that the dynamical entropy indeed takes on its supremum.

The Kolmogorov–Sinai entropy is a dynamical invariant of dynamical systems. It vanishes for regular (e.g. periodic), completely predictable systems and diverges for completely unpredictable random systems. For chaotic systems, neither purely regular nor purely random, its value characterizes the degree to which their future behaviour is predictable.

Since the cells of a generating partition are dynamically stable, they can be used to define dynamically stable symbolic states, whose sequence provides a symbolic dynamics Γ [69]. This dynamics is a faithful representation of the underlying dynamics only for generating partitions. The technical term ‘faithful’ expresses that the underlying dynamics Φ and the properly constructed symbolic dynamics Γ are topologically equivalent.

Another way to say that Φ and Γ are topologically equivalent derives from the mapping π of states in X to symbolic states. If Φ is the dynamics of neural states p, and Γ is the dynamics of mental states m, then Φ and Γ are related by

A 4

where π is now a mapping from the neural state space to the mental state space.

If π is continuous and invertible, and its inverse π⁻¹ is also continuous, π is called an intertwiner and we can write

A 5

The intertwiner π is topology-preserving if the partition yielding the equivalence classes of individual neural states in X is generating. (The topology of one state space is preserved in another one, if and only if any state change in one state space implies a state change in the other.) For generating partitions of X, there is therefore a one-to-one correspondence between statistical neural states in X and individual mental states.

The synchronic (vertical) and diachronic (horizontal) relations π, Φ, Γ can be represented diagrammatically as:

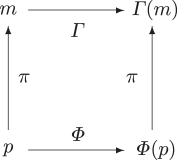
and equations (A 4) and (A 5) express that this diagram is commutative: the concatenated mappings p → m → Γ(m) and p → Φ(p) → Γ(m) lead to the same result. Compare the commutativity of coarse graining and time evolution in Butterfield [30].