The indentation of pressurized elastic shells: from polymeric capsules to yeast cells

Abstract

Pressurized elastic capsules arise at scales ranging from the 10 m diameter pressure vessels used to store propane at oil refineries to the microscopic polymeric capsules that may be used in drug delivery. Nature also makes extensive use of pressurized elastic capsules: plant cells, bacteria and fungi have stiff walls, which are subject to an internal turgor pressure. Here, we present theoretical, numerical and experimental investigations of the indentation of a linearly elastic shell subject to a constant internal pressure. We show that, unlike unpressurized shells, the relationship between force and displacement demonstrates two linear regimes. We determine analytical expressions for the effective stiffness in each of these regimes in terms of the material properties of the shell and the pressure difference. As a consequence, a single indentation experiment over a range of displacements may be used as a simple assay to determine both the internal pressure and elastic properties of capsules. Our results are relevant for determining the internal pressure in bacterial, fungal or plant cells. As an illustration of this, we apply our results to recent measurements of the stiffness of baker's yeast and infer from these experiments that the internal osmotic pressure of yeast cells may be regulated in response to changes in the osmotic pressure of the external medium.

1. Introduction

Just as one might ‘poke’ an object to have a qualitative sense of its material properties, materials scientists often use an indentation test to make quantitative measurements of an object's elasticity [1–3]. Indentation is a useful technique because it is repeatable and non-destructive. For small scale applications in biology, it is common to use an atomic force microscope (AFM) in an indentation test to obtain high levels of accuracy that would not otherwise be possible [4]. While several studies have focused on determining the mechanical properties of both animal and plant cells using variants of the indentation test [5,6], a question of particular interest for plant, fungal and bacterial cells is the turgor pressure within the cell. Indeed, differences in turgor pressure could be important for the regulation of growth [7]. It has been suggested previously [8–11] that indentation using an AFM would allow the turgor pressure of bacteria to be measured. However, this previous work relied on an ad hoc approach to the equations of elasticity rather than using classical shell theory.

From a fundamental point of view, the indentation of unpressurized elastic shells has received a great deal of theoretical attention [12–15]. Much of the early work focused on axisymmetric geometries but more recently the simple problem of indentation has been used as a starting point in understanding some of the more complicated geometries that arise when an object with an intrinsic curvature is subject to different external loads [16,17]. By contrast, very little work has concerned the indentation of a pressurized elastic shell, despite its technological importance in applications such as pressure vessels [18] or capsules designed for drug delivery [19,20]. However, numerical simulations have been carried out for the case of a thick, fluid-filled shell with a constant volume [21] and for a thin shell (or membrane) subject to a constant internal pressure [20].

Here, we carry out a comprehensive investigation of the indentation of spherical pressurized shells, combining an analytical study of the equations of shells with finite-element simulations and macroscopic experiments. After the formulation of the problem of interest, we successively focus on the regimes of small and large indentations. We show that in each of these regimes the shell has a characteristic stiffness and determine analytical expressions for these stiffnesses in terms of the material properties of the system. Finally, we apply these results to previous microscopic experiments on the indentation of polymeric capsules [20] and of baker's yeast [22]. In particular, our approach allows us to investigate the regulation of the osmotic pressure of yeast cells.

2. First observations and formulation

Our model system is shown schematically in figure 1a. We consider an elastic shell of natural radius R, thickness h, Young's modulus E, Poisson ratio v that is subject to an internal pressure (or pressure difference) p. The shell is then deformed by the action of a point-like force, F. Numerical simulations were performed using the commercial finite-element package Abaqus (SIMULIA, Providence, RI, USA), a commercial finite-element package, with material properties R = 1 m, E = 70 GPa and v = 0.3. (Three-node thin quadratic axisymmetric shell elements were used in all calculations and a mesh sensitivity study was carried out to ensure that the results are minimally sensitive to the element size.) To simulate the response of a pressurized shell, a uniform internal pressure was first applied to the shell. A point load was then applied, while the internal pressure was kept constant, and the relationship between applied force F and maximum displacement w₀ was determined for a range of internal pressures and shell thicknesses. An image of the deformed shell from simulations is shown in figure 1b.

Figure 1.

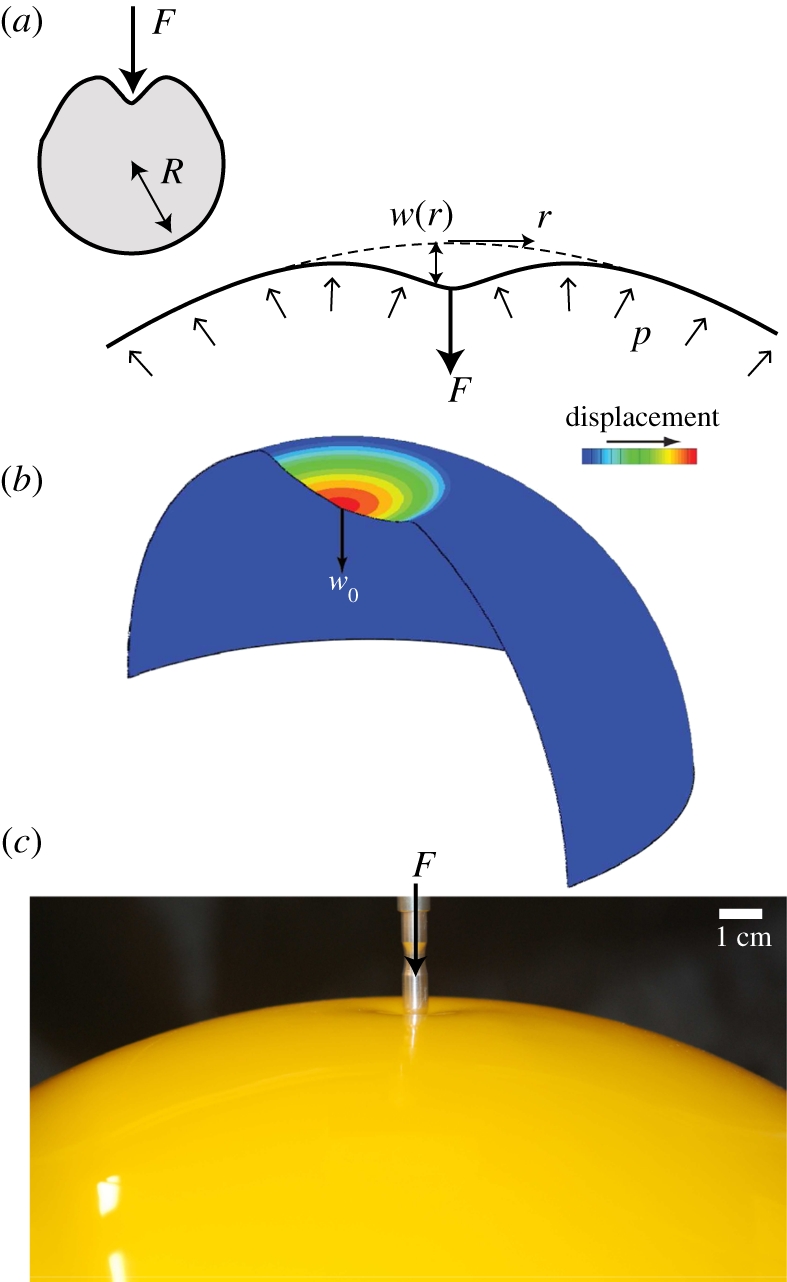
The indentation of an inflated spherical shell considered here. (a) Idealized set-up and notation for the problem: a spherical shell of thickness h and undeformed radius R is subject to an internal pressure, p, while also being loaded by a vertical point force F at a pole. This causes a vertical deflection w(r) and, in particular, a displacement w(0) = −w₀ at the point of application of the force. (b) Three-dimensional cross section of a deformed shell with w₀ = 13 cm from numerical simulations with E = 70 GPa, v = 0.3, R = 1 m, h = 2 mm and p = 10⁴ Pa. (c) Image showing the experimental set-up in which a Pezzi ball (Ledragomma) is inflated and loaded by an indentor.

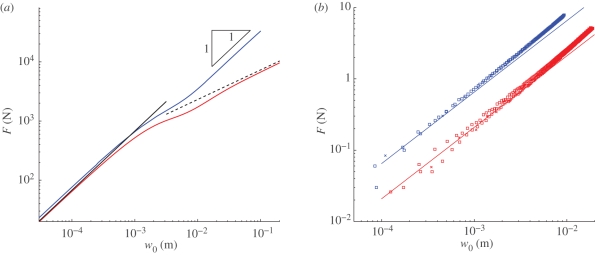
Two typical force–displacement curves are shown in figure 2a. The first curve shows the force–displacement curve in the absence of an internal pressure. In this case, we recover the two classical results for an unpressurized shell: for 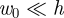, F ∼ w₀, as shown by Reissner [13], while for 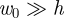, 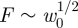as shown by Pogorelov [14]. However, with an internal pressure the results in figure 2a show that there are two separate linear regimes. Further analysis reveals that the prefactor of this linear relationship in the first regime, k₁, differs from that in the unpressurized case. In this article, we focus on understanding the presence of these linear regimes and determining the two linear stiffnesses, k₁ and k₂, in terms of the material properties of the system.

Figure 2.

Force-displacement curves in indentation tests. (a) In the absence of a pressure difference, p = 0 (red curve) the numerical results recover the asymptotic results of Reissner [13] (solid line) and Pogorelov [14] (dashed line). However, with p = 10⁵ Pa (blue curve), a new linear regime is observed at large displacements. Here, E = 70 GPa, v = 0.3, R = 1 m, h =2 mm. (b) Experimental results obtained with a Pezzi ball with internal pressure p = 1.2 kPa (red) and p = 5.4 kPa (blue). Results are shown for loading at a speed of 200 µm s^-1 (squares) and unloading at 1000 µm s⁻¹ (crosses). In each case, two runs are shown with every 20th point plotted. The lack of a significant discrepancy between repeated experiments demonstrates the reproducibility of our results as well as the unimportance of frictional and rate effects. The two solid lines represent the linear force laws F = k₁ w₀ with the appropriate value of k₁ predicted by theory (see §3).

In order to test the experimental applicability of our approach, we also performed a series of indentation tests using an inflated rubber ball (Pezzi ball, Ledragomma) of radius R =18.5 cm, shell thickness h = 1 mm. Young's modulus was measured to be E = 2.3 MPa (by determining the linear relationship between internal pressure and shell circumference) and we assume that the Poisson ratio v = 0.5, as is typical of rubbers. The ball was inflated to a known pressure and then loaded using a hemispherical cap indentor (figure 1c) at a constant speed. (The radius of curvature of the indentor ≈ 3 mm, which is significantly smaller than the horizontal length scale for the deformation of the shell ∼3 cm, making this a satisfactory approximation to the point force assumed theoretically. Experiments were conducted at room temperature and the ball was supported by a wooden shelf with a cut-out hole to ensure alignment of the pole with the indentor.) The force required to impose this displacement was measured continuously using a force gauge (Andilog centor). Force–displacement curves for a range of internal pressures demonstrate that for small displacements the measured force is approximately linear in displacement with a prefactor that depends on the internal pressure (figure 2b).

For the theoretical formulation of the problem, we start from the equations of axisymmetric plate theory modified to incorporate the finite radius of curvature of the shell. These equations are well known [23] and, in the polar geometry of interest here, take the form

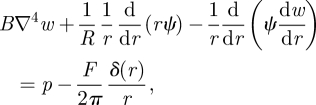2.1

and

2.2

where w(r) is the vertical displacement of the membrane (from the spherical state) and ψ is the derivative of the Airy stress function, so that σ_θθ =ψ′ and σ_rr = ψ/r where ()′ denotes differentiation with respect to r. We use a Dirac δ-function to represent the point forcing at the origin and have chosen the sign convention so that positive F acts in the opposite direction to the pressure, p. We thus expect positive forces to produce negative displacements.

3. Small indentation

For the case of no applied point force, F = 0, we anticipate that w = w_∞, a constant. Substituting this ansatz into equation (2.1), we find that

3.1

The shell is therefore in a uniform state of stress in which σ_θθ = σ_rr = σ_∞ = pR/2. To consider small deformations from this state, it is natural to perturb the base state given by equation (3.1), letting w → w + w_∞ and ψ → ψ + σ_∞r. At leading order, we eliminate ψ from equation (2.1) by using equation (2.2) to find that the displacement of the shell is governed by

3.2

We note that a balance between the term representing bending and the linear restoring force gives rise to a natural bending length scale,

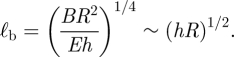3.3

The appropriate solution of equation (3.2) subject to w(0) = −w₀ is

3.4

where

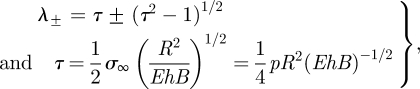3.5

and K₀(x) is the modified Bessel function of zeroth order [24]. We note that the coefficients of the K₀ terms in equation (3.4) are chosen such that there is no logarithmic singularity close to the point of indentation. The parameter τ represents a dimensionless pressure. It is a simple matter to calculate the force by integrating equation (3.2) once to give F = k₁w₀ where

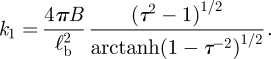3.6

In figure 3, we show the value of k₁ determined from Abaqus simulations for a range of values of the dimensionless pressure τ and compare it to the prediction in equation (3.6). In addition, the experimental effective stiffness, k₁, was determined by a linear fit on all data with w₀ < h/2. (We shall see that equation (3.6) is only valid in the limit 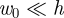.) The dependence of the measured values of k₁ on τ is plotted with the theoretical curve and numerical points in figure 3 and show that the measured stiffness is in good agreement with that expected from the theoretical analysis. The range of pressures used in our experiments are such that the Pezzi ball is a strongly pressurized shell (i.e. 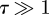), in which limit we find

3.7

Figure 3.

Small indentation. The dependence of the dimensionless shell stiffness k₁ ℓ_b²/B on the dimensionless pressure τ, which is defined in equation (3.5). The solid curve shows the theoretical prediction (3.6), which is approximated by the result of Reissner [13], k₁∼8B/ℓ_b², for τ ≪ 1 (dashed line) and by equation (3.7) for τ ≫ 1 (dotted curve). Open points show the results from simulations with shell thicknesses h = 2 mm (blue squares) and h = 5 mm (red circles). All other material properties are as in figure 2a. Solid points (green triangles) show experimental results obtained using a Pezzi ball with error bars given by repeated trials at different loading speeds. (Online version in colour).

We note that for 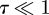we recover the unpressurized result of Reissner [13], which in our notation reads . These asymptotic results are shown in figure 3 for completeness. We also note that the result, equation (3.7), is similar to that obtained from a simplified analysis of the indentation of a cylindrical cell [8], albeit with a different prefactor. This similarity is to be expected on dimensional grounds. Finally, the force law f = k₁w₀ is expected to hold provided the effects of geometrical nonlinearities are relatively small, i.e. that the first term on the right-hand side of equation (2.2) dominates the second term. Quantitatively, this requires that .

4. Large indentation

We now consider an indentation . In this regime, we must carefully account for geometrical nonlinearities. Numerical simulations suggest that the force–displacement curve temporarily loses its linearity but ultimately regains it, albeit with a different stiffness, i.e. F ∼ k₂w₀. To understand this behaviour, it is important to consider the fully nonlinear problem described by equations (2.1) and (2.2). However, to simplify the analysis we neglect the effect of bending stiffness, the biharmonic term in equation (2.1). The coefficient of the bending term in equation (2.1) is a fraction τ⁻² of the other terms and hence this approximation is valid provided that 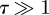. With this simplification, we find that the shell equations may be integrated once and simplified to give

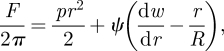4.1

and

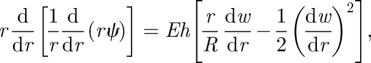4.2

where we have used the behaviour ψ ∼ pRr/2 as r → ∞ to eliminate the constant that arises upon integrating equation (2.2). Having neglected the influence of the bending stiffness on this problem, a new length scale

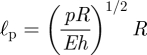4.3

emerges from a balance between in-plane stretching and the geometric stretching caused by the internal pressure.

We note that it is possible to transform equations (4.1) and (4.2) into a single equation for the stress function ψ by eliminating dw/dr from equation (4.2) using equation (4.1), as has been done previously for problems in planar membrane theory [25,26]. However, here we leave the equations in the above form and solve them numerically, using the Matlab routine bvp4c, subject to the boundary conditions

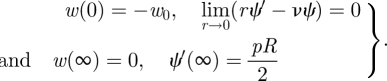4.4

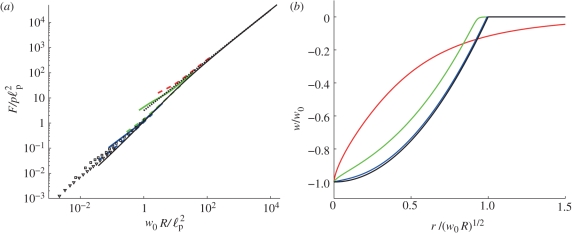
The second boundary condition corresponds to the condition of zero horizontal displacement at the origin [27]. The force F is determined as part of the solution to this problem. Its dependence on the imposed displacement w₀ is shown as the solid black curve in figure 4a and is compared with the simulation results obtained from Abaqus, shown by the coloured curves, as well as experimental results, shown by points. This comparison shows good agreement between the theoretical result, simulations and experiment with the discrepancies accounted for by our neglect of the bending stiffness, B, in this membrane model.

Figure 4.

Large indentation. (a) Force F required to give an imposed displacement w₀. The results of simulations with R = 1 m, E = 70 GPa and v = 0.3 are shown as coloured curves for different internal pressures p (blue, p = 10 MPa; green, p = 1 MPa; red, p = 0.1 MPa) and shell thicknesses h (dashed curves represent h = 2 mm, solid curves h = 5 mm). The solid black curve gives the membrane prediction obtained by solving equations (4.1) and (4.2), while the dotted black line gives the asymptotic result (4.8). The experimental results of figure 2b are also shown for p = 1.2 KPa (squares) and p = 5.4 KPa (triangles). (b) Rescaling of the deformation profile suggested by equation (4.7). The numerical results of the membrane model for w₀ R/ℓ_p² = 1 (red), 10² (green) and 10⁴ (blue) demonstrate that for w₀ R/ℓ_p² ≫ 1 we recover the inverted spherical cap profile (4.7), shown as the solid black curve.

Figure 4a suggests that in the limit of very large displacements we find . To understand this behaviour for large forces, we introduce the dimensionless force . We also rewrite equation (4.1) by introducing dimensionless variables 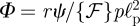, 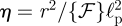and 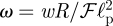to find that

4.5

which may then be used to rewrite equation (4.2) as

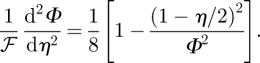4.6

In the limit 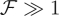equation (4.6) takes the usual form of a boundary layer equation with a small parameter, 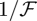, multiplying the highest order derivative. Far away from the point of indentation, we expect that the left-hand side of equation (4.6) can be approximated by 0, giving Φ ≈ |1–η/2|. Substituting this into equation (4.5), we find then that ω = 0 for η > 2 and ω = η–2 for η < 2. Upon rewriting ω = η–2 in dimensional terms and requiring that w(0) = –w₀ we find that in the limit the deformation of the shell is described by

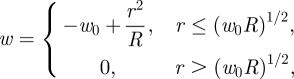4.7

which is simply the inverted spherical cap found by Pogorelov [14] for the case of unpressurized shells—also commonly known as ‘mirror buckling’. This shape is shown in rescaled form in figure 4b as the solid black curve demonstrating that the numerical solution of the membrane models (4.1) and (4.2) are well approximated by this result for 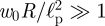. We note that in equation (4.7) the shell is only deformed for r < (w₀R)^1/2—the flat regions for r > (w₀R)^1/2 in figure 4b indicate that the shell is not deformed in this region.

The above analysis also demonstrates that F ∼ πpRw₀. Alternatively, we may understand the linear force law that is observed in this regime by noting that the decrease in volume of the shell caused by this deformation is 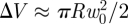and hence that the work done by the loading force in compressing the gas within the shell, 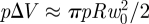. Differentiating this expression with respect to w₀, we find that the applied force

4.8

The asymptotic result (4.8) is confirmed by the numerical solution of the membrane models (4.1) and (4.2), as shown by the dotted black line in figure 4a.

5. Discussion and applications

We have studied the indentation of a pressurized elastic shell and shown that the force–displacement curve exhibits two linear regimes (at small and large deflections compared with the thickness h). For strongly pressurized shells, we found that F ∼ k₁w₀ for 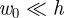and F ∼ k₂w₀ for where

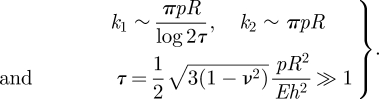5.1

We validated these analytical results using finite-element simulations and macroscopic experiments. The analytical understanding of these two regimes gained here may be used to determine both p and Eh² using data from a single indentation experiment in which both k₁ and k₂ are measured. This is in contrast to previous techniques [20], which required a single stiffness to be measured in two different experimental geometries in combination with numerical simulation. Our technique is particularly useful when it is the internal swelling pressure (or osmotic pressure) that is to be measured, since the result in equation (5.1) shows that the stiffness k₂ depends only on this pressure and the radius of the capsule. We note that the experiments of Gordon et al. [20] appear to be precisely in this regime since, using their estimates, the parameter 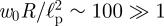. Using the asymptotic result (5.1), we find that their experimental data suggest internal pressures ranging from 15 to 120 Pa (assuming a capsule radius of 100 µm). This is in reasonable agreement with the values given by them (100–500 Pa) but is less sensitive to errors in fitting since it is not necessary to estimate the elastic properties of the shell as well.

Our results may also be applied to understand recent experiments [22] on yeast cells, Saccharomyces cerevisiae, in which indentation with an AFM tip was used to determine changes in the cell's stiffness as the osmotic pressure of the external medium was varied. These experiments were performed for indentations of the order of the wall thickness (maximum indentation ≈50 nm compared with a typical wall thickness [6] h ≈ 70 nm) and hence the measured stiffness corresponds to k₁ in our notation. The cell wall of yeast is known to be permeable allowing material to flow out of the cell and equilibrate non-osmotic pressure differences [28]. Although this flow could in principle be modelled [28], the relatively small size of indentations, together with the experimental observation that results are unchanged upon varying the indentation speed, suggest that the assumption made in our analysis of constant pressure difference during indentation is satisfactory. Other complications include the layered structure of the yeast cell wall, with not all layers contributing equally to its mechanical strength [29], and the potentially complicated constitutive law relating stresses and strains. Nevertheless, the application of the theoretical understanding developed from the idealized model presented in this paper gives us a starting point for extracting characteristic moduli and values for the internal osmotic pressure.

The principle result of the indentation experiments of Arfsten et al. [22] is that the value of k₁ depends on the osmotic pressure of the external medium (figure 5a). Furthermore, they found that above a critical external osmotic pressure, P_ext = 2.1 MPa, this stiffness becomes significantly smaller. From this observation, it was concluded that the cell is effectively deflated when P_ext = 2.1 MPa and hence that the internal osmotic pressure of the cell is P_int = 2.1 MPa. Strictly speaking, this value is the maximal osmotic pressure that the cell can generate. Our analysis suggests that, as the pressure difference decreases, a residual stiffness should remain and be explained by the analysis of Reissner [13]. Using this result and typical estimates for the thickness of the cell wall h ≈ 70 nm and cell radius R ≈ 2.75 µm from the literature [6], we take the measured upper and lower bounds for k₁ (see dashed lines in figure 5a) and estimate that 12 MPa ≤ E ≤ 46 MPa. This value is reasonably consistent with values determined previously [5,30] and also gives ℓ_p ≈ 2 µm and ℓ_b ≈ 200 µm, which are both significantly larger than the AFM tip used (≲15 nm) justifying our approximation of a point force. With this value of E, the theory developed here, more specifically equation (3.6), can be used to estimate the internal pressure required to obtain the observed values of k₁. The results of this calculation are shown in figure 5b and indicate that as the external pressure is increased so the internal pressure is actively increased to maintain a certain degree of turgor, i.e. an internal osmotic pressure that is higher than that of the external medium. Beyond P_int = 0.6 MPa the cell becomes unable to maintain turgor.

Figure 5.

(a) Raw results of measurements of k₁ for yeast cells in media of different osmotic pressure reported previously [22]. Measurements over many cells were found to follow a lognormal distribution and hence were summarized by the median value (crosses) and the 68.3% confidence interval, corresponding to 1 s.d., for log k₁ (error bars) [22]. Dashed lines show the minimum and maximum values of k₁ taken to estimate Young's modulus E, see text. (b) Dependence of the internal pressure of these yeast cells on the external osmotic pressure based on the results of this paper. Here, we have used the data at larger external pressure to determine Young's modulus of the cell wall and then to estimate the pressure difference felt by the cell at lower external osmotic pressures, thereby inferring the internal pressure.

We find a typical value of turgor of 0.1–0.2 MPa, which is consistent with experiments using different methodologies [30,31], which found turgor pressures in the range 0–1 MPa. Finally, we note that for these experiments 0 ≲ τ ≲ 10 and so it is necessary to make use of the full analytical expression (3.6). This is particularly important for explaining the presence of a residual stiffness when the yeast cell is unable to maintain turgor (for external pressures P_ext ∼ 0.6 MPa). As Arfsten et al. [22] surmised, the presence of this stiffness demonstrates that the role of bending effects cannot be neglected as turgor decreases—an assumption that is often made in simplified models of cell indentation [8,9].

We anticipate that our analytical results, and particularly the asymptotic results (5.1) for strongly pressurized shells, could provide a standard tool for the mechanical characterization of pressurized shells in a range of biological applications, such as the measurement of the properties of capsules and walled cells. Other features of the indentation of pressurized shells may also aid this aim. For example, under large deformations pressurized shells are subject to an azimuthal buckling instability that leads to the formation of a large number of wrinkles with a well-defined length. The number of wrinkles as well as their length could thus be used for the mechanical characterization of shells [32,33]. A full study of this wrinkling is currently underway.