Emergence of coherent structures and large-scale flows in motile suspensions

Abstract

The emergence of coherent structures, large-scale flows and correlated dynamics in suspensions of motile particles such as swimming micro-organisms or artificial microswimmers is studied using direct particle simulations. A detailed model is proposed for a slender rod-like particle that propels itself in a viscous fluid by exerting a prescribed tangential stress on its surface, and a method is devised for the efficient calculation of hydrodynamic interactions in large-scale suspensions of such particles using slender-body theory and a smooth particle-mesh Ewald algorithm. Simulations are performed with periodic boundary conditions for various system sizes and suspension volume fractions, and demonstrate a transition to large-scale correlated motions in suspensions of rear-actuated swimmers, or Pushers, above a critical volume fraction or system size. This transition, which is not observed in suspensions of head-actuated swimmers, or Pullers, is seen most clearly in particle velocity and passive tracer statistics. These observations are consistent with predictions from our previous mean-field kinetic theory, one of which states that instabilities will arise in uniform isotropic suspensions of Pushers when the product of the linear system size with the suspension volume fraction exceeds a given threshold. We also find that the collective dynamics of Pushers result in giant number fluctuations, local alignment of swimmers and strongly mixing flows. Suspensions of Pullers, which evince no large-scale dynamics, nonetheless display interesting deviations from the random isotropic state.

1. Introduction

Recent experiments on the dynamics of suspensions of self-propelled micro-organisms have uncovered new and fascinating hydrodynamic phenomena (e.g. [1–4]). For example, dense suspensions of swimming bacteria, such as Escherichia coli or Bacillus subtilis, exhibit complex flows characterized by large-scale vortices and jets [2,5–8]. These flows are a consequence of the activity of the self-propelled particles and often take place on length scales that greatly exceed the particle dimensions, and involve velocities much higher than the single micro-organism swimming speed [2]. Other peculiar phenomena that have been observed include the formation of spatial inhomogeneities [2,4], locally correlated motions [8–10], enhanced particle diffusion, enhanced fluid mixing and passive tracer diffusion [1,11–13]. Synthetic non-biological microswimmers that move autonomously [14–19] or semi-autonomously [20,21] have been fabricated and studied, but as yet have not been deployed (to our knowledge) to study collective hydrodynamic interactions. Perhaps this is because of the difficulty of manufacturing such devices in sufficient numbers, though this ability appears to be improving (e.g. [22]).

Attempts at understanding the mechanisms behind these experimental observations have included various types of particle simulations. Hernández-Ortiz et al. [23] developed a ‘minimal’ swimmer model, in which particles are represented as rigid dumbbells that exert two equal and opposite localized forces on the fluid, thus creating the far-field force dipole a swimming particle induces as a result of self-propulsion. With this model, they were able to reproduce features of the experiments, including correlated motions at high concentrations and enhanced tracer diffusion [23,24]. Pedley and coworkers developed detailed Stokesian dynamics simulations of ‘squirmers’, which propel as a result of a prescribed surface slip velocity, and also reported motile particle and tracer diffusion [25,26] and the development of coherent structures in their suspensions [27,28]. Recently, we also developed a detailed model, based on slender-body theory, in which hydrodynamically interacting rod-like particles propel themselves by exerting a prescribed tangential stress on their surfaces [29]. We observed large-scale flows taking place near the system size in semi-dilute suspensions of rear-actuated particles, resulting in an enhancement of the mean swimming speed and in strong motile particle diffusion at long times.

While particle simulations are most easily compared with experimental data, they do not easily provide analytical insight into the physical mechanisms at play. To this end, continuum mean-field theories have also been proposed, which couple conservation equations for the distribution of particle conformations to the governing equations for the fluid flow via an effective particle stress tensor modelling the effects of the force dipoles exerted by the particles on the surrounding fluid. Such a model was proposed by Simha & Ramaswamy [30], who extended phenomenological equations for liquid crystals to account for active stresses, and used them to investigate the stability of aligned suspensions. Similar models were also more recently developed by Aranson et al. [31], Wolgemuth [32], Baskaran & Marchetti [33,34] and Mishra et al. [35]. Because these often included ad hoc terms accounting for near-field steric interactions, the precise role played by hydrodynamic interactions in the dynamics of these suspensions remained unclear.

We recently developed a first-principles mean-field kinetic theory to study hydrodynamic interactions in these suspensions [36,37]. There, a conservation equation for the distribution of particle positions and orientations is coupled to the Stokes equations for the fluid flow, itself driven by an effective ‘active stress’ corresponding to the individual force dipoles resulting from particle self-propulsion. We performed linear stability analyses and nonlinear simulations to investigate the system's dynamics. Linear stability analysis for a uniform and isotropic suspension of Pusher particles predicts a long-wave spatial instability at a critical wavenumber k_c. This result was obtained independently and using a similar theory by Subramanian & Koch [38], who also included the effects of bacterial tumbling. Further, this linear instability does not yield concentration fluctuations, but rather growth of the effective particle stress, which can be interpreted as a local nematic order parameter. In other words, weak fluctuations in the distribution of the particle configurations will amplify and yield local alignment at short times. Beyond the wavenumber k_c, a more detailed analysis of the linear problem by Hohenegger & Shelley [39] revealed that both suspensions of Pushers and Pullers are neutrally stable in the absence of rotational diffusion, and stable otherwise.

A measure of the importance of hydrodynamic interactions is the effective volume fraction of swimmers ν = Ml³/V where M is the total number of swimmers in the system volume V and l is the particle half-length [40]. A useful non-dimensionalization of the kinetic theory uses the length and time scales l_c = l/ν and t_c = l_c/U₀ where U₀ is the isolated swimmer speed. After rescaling, the remaining system parameters are an O(1) signed active stress coefficient, normalized system size and two dimensionless diffusion coefficients. In our discrete rod simulations [29], we found that into the semi-dilute regime (ν ≈ 1), the rotational diffusivity scaled linearly with ν while translational diffusivity scaled inversely as ν⁻¹. In such a case, or in the absence of diffusion, the above scaling leaves the dimensionless diffusion coefficients in the kinetic theory dependent only upon swimmer length and speed, and ν appears only in the rescaled system size. The instability criterion on the critical wavenumber k_c may then be written succinctly in terms of system size L = V^1/3 and ν as [39]

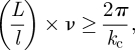1.1

where the non-dimensional k_c has no dependence on ν or L. Equation (1.1) shows that an instability will occur in Pusher suspensions when, for a fixed system size, the concentration exceeds a threshold value or, conversely, for a fixed concentration, when the system size exceeds a critical value. Note that because they included a model for orientation relaxation as a result of bacterial tumbling, Subramanian & Koch [38] obtained a slightly different criterion on the concentration that does not involve the system size.

In our previous work [37], we also derived an equation of evolution for the system configurational entropy, which is an energy-like quantity measuring the size of fluctuations relative to the uniform, isotropic state. It predicts that for suspensions of Pullers, fluctuations will decay away monotonically. For Pushers, entropy evolution is a balance of decay induced by diffusive mechanisms and growth from power input to the system by the swimmers. To investigate the long-time dynamics in these suspensions, large-scale simulations of the kinetic equations were performed [36,37,41]. For Pushers, they confirmed the criterion for instability predicted by the linear analysis, and that concentration fluctuations do grow as a result of nonlinearities. In the nonlinear regime, the dynamics were found to be characterized by the quasi-periodic formation and break-up of concentration patterns whose magnitude is controlled by diffusion, accompanied by complex unsteady flows qualitatively reminiscent of turbulence. These flows, in turn, were shown to result in very efficient fluid mixing achieved by large-scale stretching and folding of fluid elements. These dynamics were also reflected in the configurational entropy of the system, which showed persistent fluctuations about a long-time elevated mean. For Pullers, initial fluctuations showed no persistence, even for large amplitude data, and decayed monotonically.

The predictions of the kinetic model are qualitatively consistent with experimental observations, which suggest that large-scale flows and correlated motions occur only above a critical particle concentration [4,6–8]. However, they are yet to be tested quantitatively against particle simulations, which are arguably more controlled than biophysical experiments. In our previous particle simulations [29], large-scale flows and complex concentration patterns were reported in suspensions of Pushers, though the onset for these flows and patterns was not explicitly investigated. In this paper, we perform additional simulations using the same model (described in §2 and in the electronic supplementary material) with the specific aims of determining the conditions for these effects to arise and of testing the theoretical prediction of equation (1.1). We also analyse more precisely the characteristics of these flows, such as their effect on number density fluctuations, particle velocities, fluid mixing and passive tracer diffusion (§3). These results confirm the instability criterion of equation (1.1), with reasonable agreement with the numerical value of the critical effective volume concentration predicted by the kinetic model. We also find some interesting departures from the kinetic model, such as signs of the approaching transition through small-scale correlated particle motions even in the stable regime. Conclusions and directions for future work are discussed in §4.

2. Simulation method

The simulation method is described in detail in the electronic supplementary material and is only summarized here. We simulate periodic suspensions of M identical rod-like particles of length 2l, centre of mass x_i, and director p_i (i ∈ [1, … , M]), using the method developed in our previous work [29]. We assume that the particles propel themselves by exerting a prescribed tangential stress over half of their body, while the other half is subject to the standard no-slip boundary condition. This model may be considered a coarse-grained model for ciliated micro-organisms, or organisms that propel themselves by propagating shape deformations along their body. We assume that the particles have a high aspect ratio, and therefore use slender-body theory to model their motion [42]. Particle motions are coupled within the slender-body formulation via the incompressible disturbance velocity field u(x) induced by the other swimmers in the fluid, which accounts for hydrodynamic interactions and is calculated in the low-Reynolds-number regime using the Green's function for the Stokes flow. This results in a large-scale coupled system of integral equations which is solved with periodic boundary conditions using a spectral expansion of the disturbance velocities using Legendre polynomials [43], together with a smooth particle-mesh Ewald algorithm [44] for the efficient evaluation of hydrodynamic interactions. We consider two types of swimming particles: Pushers, for which the shear stress actuation occurs on the rear half of the particle, with the no-slip boundary condition on the front half; and Pullers, for which the actuation occurs at the front, with no-slip at the rear. The reader is referred to the electronic supplementary material for more details on the single-particle models and simulation method.

In the discussion below, lengths, velocities and times are made dimensionless using the particle length 2l, isolated swimming velocity U₀, and time-scale 2l/U₀. Unless otherwise noted, all the simulations described were performed in a periodic cubic box of linear dimension L = 10, with unit-length particles of aspect ratio 10. Volume concentrations are measured using the effective volume fraction ν = Ml³/V, for which ν ≈ 1 corresponds to a semi-dilute suspension [40].

3. Results

3.1. Particle distributions

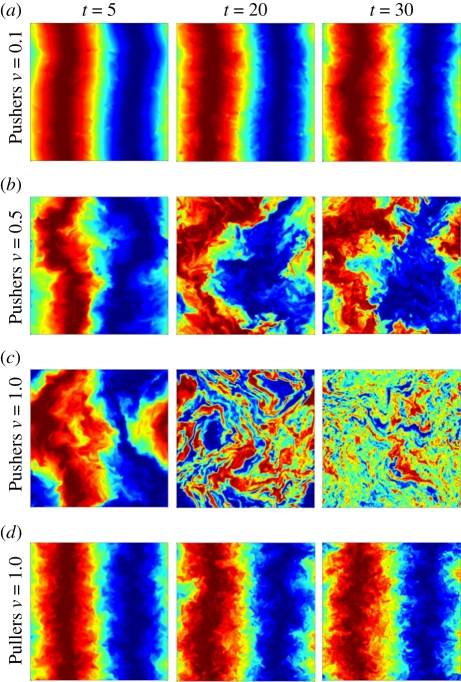
Figure 1 (see also the electronic supplementary material, Movie) shows typical late-time particle distributions in three simulations of Pusher suspensions, at effective volume fractions ν = 0.1, 0.5 and 1.0, as well as one simulation of a Puller suspension at ν = 1.0. In all cases, the initial distribution at t = 0 is taken to be random and isotropic. At the low volume fraction of ν = 0.1 (figure 1a), the Pusher particle distribution still appears to be random at t = 50, with no clear density fluctuations or correlated particle motions. The situation changes slightly at ν = 0.5, where suspensions of Pushers start exhibiting correlated motions, as demonstrated for instance by the local alignment of the particles, which was characterized in our previous work [29] and further here. Weak density fluctuations are also visible. At the yet higher concentration of ν = 1.0 (figure 1c), correlated motions become very clear, in particular in the accompanying movie (electronic supplementary material). The dynamics are found to be characterized by the formation of large rafts of particles—‘coherent structures’ of no fixed membership—that swim with velocities significantly larger than the isolated swimming speed. These rafts are typically slightly denser than the mean, and are surrounded by regions of clarified fluid. These effects are not observed in the case of Pullers (figure 1d), where the particle distribution remains apparently random and isotropic, and particle motions seem only weakly affected by interactions.

Figure 1.

Particle distributions at t = 0 (initial random distribution) and t = 50, in suspensions of Pushers at (a) ν = 0.1, (b) ν = 0.5, (c) ν = 1.0 and (d) in a suspension of Pullers at ν = 1.0. The simulations were performed in a cubic cell of linear dimension L = 10, but the above figures only show a section of dimensions 10 × 10 × 3. Also see the accompanying online movie (electronic supplementary material). (Online version in colour.)

As we proceed to show below, this transition to collective swimming, which appears to occur in suspensions of Pushers at ν ≈ 0.5, is especially visible in the particle velocity and passive tracer statistics. We also demonstrate that this transition does not occur in suspensions of Pullers, where the apparent effects of hydrodynamic interactions remain weak regardless of volume fraction.

3.2. Emergence of large-scale flows

Typical late-time fluid disturbance velocity fields from the simulations of figure 1 are shown in figure 2. At low volume fractions, the velocity fields only show small-scale fluctuations corresponding to the disturbances induced by individual particles. These fluctuations are weak and only significant in the direct vicinity of the particles owing to their fast decay as the inverse square separation distance from the particle of interest. The velocity fields significantly change in suspensions of Pullers when ν ≈ 0.5, as they start exhibiting correlated jets and vortices that occur on length scales significantly larger than the particle size; these become especially clear when ν reaches 1 in figure 2c, when strong jets and vortices are observed. These flow fields are qualitatively very similar to those previously observed in dense suspensions of the swimming bacterium B. subtilis, which is indeed a Pusher (e.g. [2,4]), as well as in previous simulations of Pusher suspensions [23,24,29]. Such large-scale flows, however, are never observed in simulations of Pullers regardless of volume fraction: the velocity fields instead remain uncorrelated, with only small-scale fluctuations corresponding to the disturbances induced by individual particles (figure 2d).

Figure 2.

Typical velocity fields in a plane in suspensions of Pushers at (a) ν = 0.1, (b) ν = 0.5, (c) ν = 1.0 and (d) in a suspension of Pullers at ν = 1.0. The simulations were all performed in a cubic cell of linear dimension L = 10.

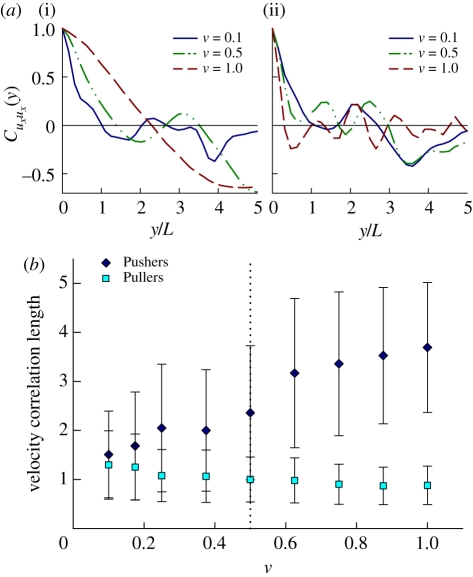
These observations are quantified in figure 3, which shows, for various volume fractions, sample spatial autocorrelation functions and the extracted correlation lengths, for the disturbance velocity field. At low volume fractions, velocity fields are correlated on a length scale of approximately 1, the length of one swimmer. For Pushers, this correlation length increases with volume fraction, especially for ν∼0.5, reaching a value of approximately 4, close to half the simulation box size. This increase is not observed in suspensions of Pullers, where the correlation lengths instead remain close to 1 but decrease slightly with ν.

Figure 3.

(a) Typical spatial autocorrelation functions of the x component of the fluid disturbance velocity field along the y-direction in suspensions of Pushers (i) and Pullers (ii). (b) Velocity correlation length (mean value over many samples, with standard deviation error bars) versus effective volume fraction ν. The correlation length is defined as the position of the first minimum in a velocity autocorrelation function. (Online version in colour.)

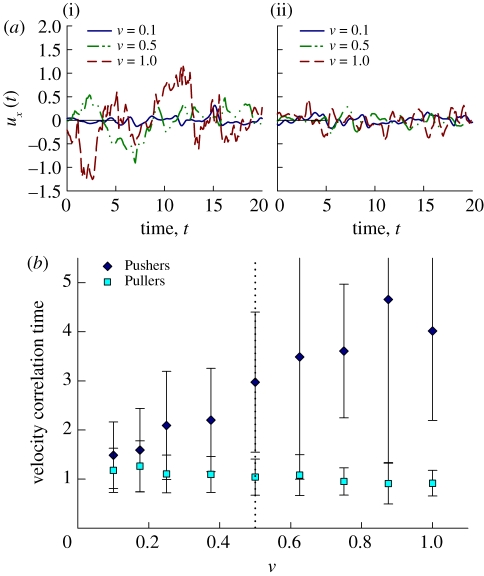
Similar observations can be made for the time evolution of the velocity fields. Figure 4a shows typical time traces of the x component of the disturbance velocity field, for both Pushers and Pullers, at an arbitrary fixed location in the simulation box. At low volume fractions, the velocity is found to rapidly fluctuate around a mean of zero. When ν increases in suspensions of Pushers, the magnitude and duration of the oscillations significantly increases. Such is not the case in suspensions of Pullers, where increasing ν has no discernible effect on the velocity time trace. These observations are also reflected in figure 4b which shows correlation times for the disturbance velocity field. At low volume fractions, velocity fields are correlated on a time of ≈1, which is the time it takes for a particle to swim a distance equal to its length. When ν increases, the correlation time increases in suspensions of Pushers, reaching values close to 5, which is the time for a particle to swim half the box dimension; this increase does not occur in suspensions of Pullers.

Figure 4.

(a) Sample time traces of the x component of the fluid velocity at an arbitrary spatial point in suspensions of Pushers (i) and Pullers (ii). (b) Velocity correlation time (mean value over many sample spatial points, with standard deviation error bars) versus effective volume fraction ν. The correlation time is defined as the position of the first minimum in a velocity time-trace autocorrelation. (Online version in colour.)

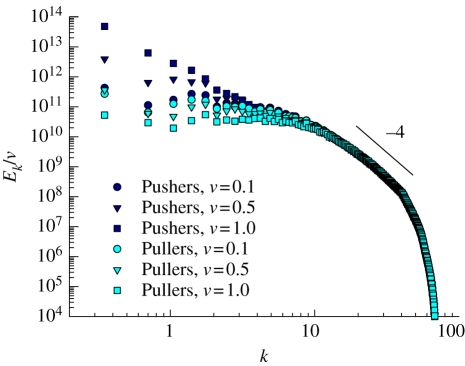
The disturbance velocity fields in the simulations are further characterized in figure 5 by their spatial power spectra, shown for Pushers and Pullers at various concentrations. Interestingly, the high-wavenumber behaviour is found to be universal in all simulations, particularly after division by ν, regardless of the swimming mechanism or the volume fraction, and is characterized by an apparent power-law decay (that said, the supporting range in k is a decade at most). The same behaviour was also found in synthetic isotropic suspensions. A simple analysis predicts a k⁻⁴ decay by describing a rod-like swimmer as a zero-mean distribution of Stokeslets aligned along its axis. If the Stokeslet strength has jumps along the rod or is not zero at the ends (i.e. if the periodic extension has jumps; also, see figure 2a,b of electronic supplementary material for the distributions relevant here), this will produce a k⁻⁶ decay in the squared Fourier amplitude of the velocity field. When spherically integrated over shells in k-space to produce the energy spectrum, a k⁻⁴ decay results. A set of M randomly oriented and placed rods yields an energy spectrum decaying again as k⁻⁴ and with a prefactor scaling with M, as is consistent with collapse of the spectra at high wavenumbers through division by ν.

Figure 5.

Power spectra, normalized by effective volume fraction ν, of the disturbance fluid velocity fields induced by suspensions of Pushers and Pullers at various concentrations. All simulations are performed in a cubic cell of linear dimension L = 10. (Online version in colour.)

The behaviour at low wavenumbers is not universal, and changes significantly with both swimming mechanism and volume fraction. At low volume fractions (e.g. ν = 0.1), the energy associated with low values of k is somewhat flat and is approximately the same for both Pushers and Pullers. For Pullers, as ν is increased, the spectrum more or less keeps its shape though it decreases in magnitude. For Pushers, the lower k spectrum significantly increases as ν reaches 0.5, and then increases by up to three orders of magnitude at ν = 1.0. In the latter case there is no flatness of the spectrum, and the kinetic energy is largest at the largest scale, showing what might be another, albeit slower, power-law decay towards the region of universal behaviour.

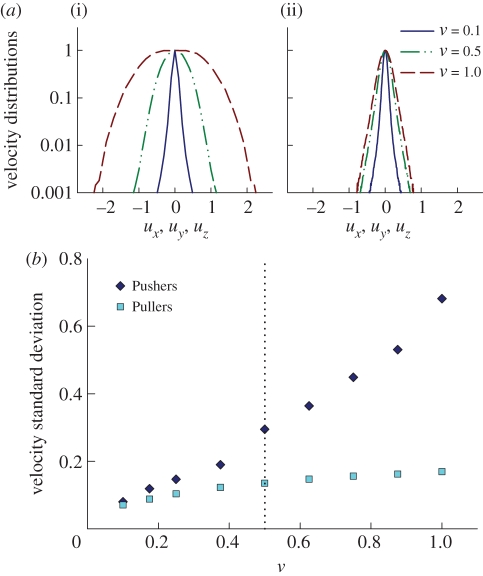
Figure 6a plots the probability distribution function (PDF) of fluid velocities at various volume fractions for both Pushers and Pullers. These show that fluid velocities generally increase as ν increases, but are significantly weaker in suspensions of Pullers than for Pushers. The distributions are also strongly non-Gaussian. For dilute random suspensions of particles, Rushkin et al. [45] argue that the tails of velocity PDFs are governed by the divergence of an appropriate Green's function for the Stokes equations. They predict and confirm that for a suspension of the alga Volvox carteri the PDF tail decays as u⁻⁴ due to V. carteri having a gravitationally induced Stokeslet. For dilute suspensions of either Pushers or Pullers we find a range with u^−α decay where α ≈ 3.5, which is faster than that predicted with a pure force dipole (u^−5/2). We suspect that this difference arises from the far-field dipole in our model being induced by a line of Stokeslets distributed along the rods. Numerical artefacts in producing the disturbance velocity field from the rod positions and force distributions may also play a role. At higher concentrations, the Pusher PDF is very flat at its centre, reflecting the loss of disorder through collective behaviour. Conversely, the Puller PDF becomes more Gaussian at higher ν as is consistent with synthetic velocity fields produced from uniform isotropic suspensions of either Pushers or Pullers. The dependence on volume fraction is further illustrated in figure 6b, showing the standard deviation of the distributions versus ν. This standard deviation increases strongly with the onset of collective motion in suspensions of Pushers, whereas the increase is weak for Pullers. As we show in §3.6, the strong flows occurring in concentrated Pusher suspensions will have a significant impact on fluid mixing.

Figure 6.

(a) Fluid velocity distributions in suspensions of Pushers (i) and Pullers (ii) at various volume fractions. (b) Standard deviation of the fluid velocities versus effective volume fraction ν in suspensions of Pushers and Pullers. (Online version in colour.)

3.3. Active input power from swimming

As each swimmer traverses the system, it inputs power to the fluid, which is offset by viscous dissipation. For a suspension of slender rods the total input power is given by

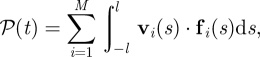3.1

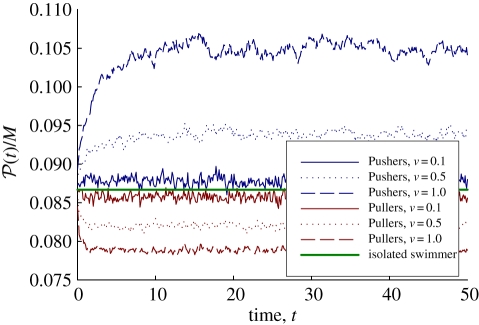
where v is the surface velocity of a rod, f the force per unit length it exerts upon the fluid and s the arclength along the rod centre-line. This quantity has contributions from the single swimmer motility as well as collective effects. Figure 7 shows the average power input per swimmer, 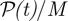, over time. The solid line denotes the base-state power input by a single swimmer moving in the computational box and averaged over swimmer orientation. Each initially isotropic suspension starts with its average input power near the base-state value. For Pullers, the dynamics leads to a decrement in 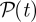that increases with volume concentration. Nonetheless, as we shall see in the next section, the long-time state remains nearly indistinguishable from that of uniform isotropy (at least by the statistical measures that we use). For Pushers, there is instead an increment in input power over the base value particularly with the emergence of large-scale flows at higher concentrations. The input power increment is particularly interesting as it is this quantity that in the kinetic theory increases the system's configurational entropy [37]. The observed dynamics in figure 7 are also consistent with those observed from nonlinear simulations of the kinetic theory for both Pushers and Pullers (see [37], figures 11–13). Increases in configurational entropy reflect increased fluctuations, either in concentration or orientation, relative to the uniform isotropic state, which we now examine.

Figure 7.

Total input power per particle 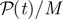defined in equation (3.1) as a function of time in suspensions of Pushers and Pullers at various volume fractions. (Online version in colour.)

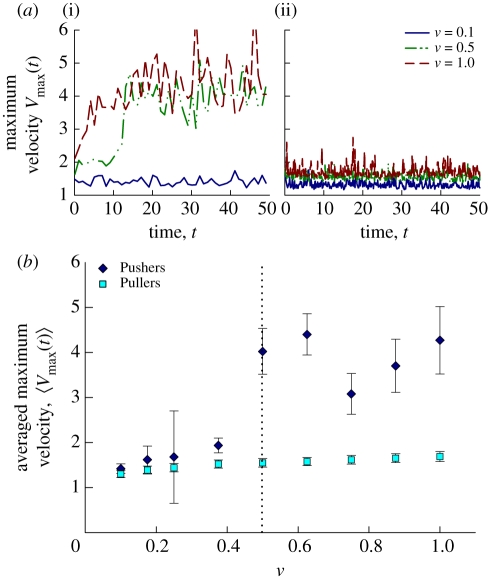
Figure 11.

(a) Maximum particle velocity V_max(t) as a function of time in suspensions of Pushers (i) and Pullers (ii). Solid line, ν = 0.1; dashed-dotted line, ν = 0.5; dashed line, ν = 1.0. (b) Time average of the maximum particle velocity at steady-state versus effective volume fraction ν. (Online version in colour.)

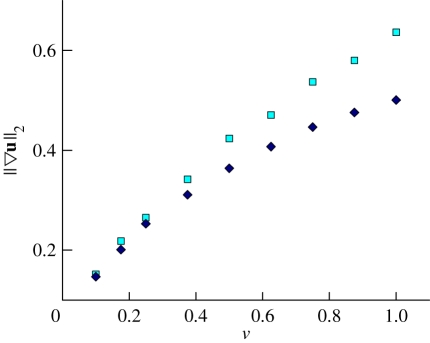
Figure 13.

The time-averaged L₂ norm 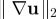of the disturbance velocity gradient as a function of ν for both Pushers (squares) and Pullers (diamonds). (Online version in colour.)

3.4. Density fluctuations and orientation correlations

The transition to collective swimming and large-scale flows described above is also associated with an increase in density fluctuations in the suspensions. This was previously predicted theoretically by Simha & Ramaswamy [30], who suggested that the standard deviation of the number of particles in a three-dimensional region containing 〈N〉 particles on average should grow as 〈N〉^5/6. Density fluctuations were also observed in the nonlinear kinetic simulations of Saintillan & Shelley [36,37], where they were explained as a consequence of the propulsion of the particles, which swim toward and aggregate in regions of negative divergence of the concentration-weighted director field [37].

To quantify the density fluctuations observed in figure 1, we consider particle occupancy statistics in figure 8. Given a small cubic interrogation cell of fixed volume 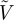, the mean number of particles inside the cell is expected to be 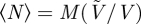. When such a cell is placed at an arbitrary position inside the simulation box, it will contain a number N of particles that may differ from the expected value of 〈N〉 as a result of fluctuations. The distribution P(N) of this number of particles therefore characterizes the magnitude of density fluctuations at a given scale. In a uniformly random suspension, the distribution is expected to be given by the Poisson distribution

3.2

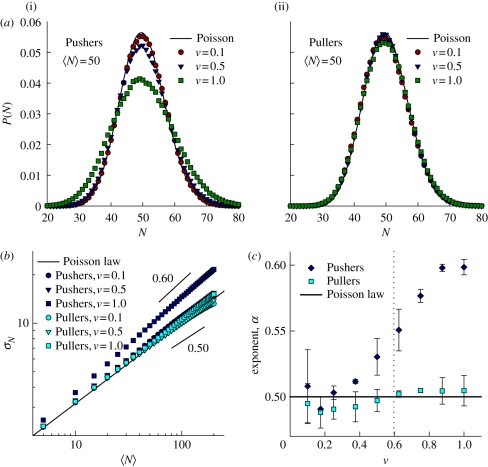
with a standard deviation of σ_N = 〈N〉^1/2. Figure 8a shows steady-state distributions P(N) in suspensions of Pushers and Pullers at two different concentrations, for an interrogation cell containing 〈N〉 = 50 particles on average, and compares these distributions to the Poisson distribution of equation (3.2). In the case of Pushers (figure 8a(i)), the distributions are found to depart from and be wider than the Poisson distribution, suggesting that density fluctuations are larger than in a random suspension, in agreement with our previous observations in figure 1. The distributions are also found to widen with increasing ν, suggesting that density fluctuations become more significant at high volume fractions. These effects are not observed in suspensions of Pullers (figure 8a(ii)), where the distributions remain close to the Poisson distribution even as ν increases.

Figure 8.

(a) Particle occupancy distributions for 〈N〉 = 50 in suspensions of Pushers (i) and Pullers (ii), at various volume fractions. The distributions are compared with the Poisson distribution of equation (3.2). (b) Standard deviation σ_N of P(N) versus 〈N〉, which exhibits a power-law dependence σ_N ≈〈N〉^α, with an exponent of 1/2 for a random suspension with Poisson statistics. (c) Exponent α versus effective volume fraction ν. (Online version in colour.)

Figure 8b shows the dependence of the standard deviation σ_N versus the mean 〈N〉. A power-law dependence σ_N = 〈N〉^α is found in all cases, with an exponent α which is close to the expected value of 1/2 for a Poisson distribution, but increases beyond this value in concentrated suspensions of Pushers. This is confirmed in figure 8c, showing the exponent α versus ν for both Pushers and Pullers. In suspensions of Pullers, α remains close to 1/2 regardless of volume fraction. Such is not the case with Pushers, where α increases to reach a value of approximately 0.60 at ν = 1.0. This increase confirms the existence of large density fluctuations in Pusher suspensions above the transition to collective swimming. Yet, the measured exponent of 0.60 remains significantly lower than the exponent of 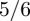predicted by Simha & Ramaswamy [30]. While this discrepancy may be a consequence of the small system sizes or relatively low volume fractions considered here, their estimate follows from considering the response of a linear phenomenological model to stochastic forcing.

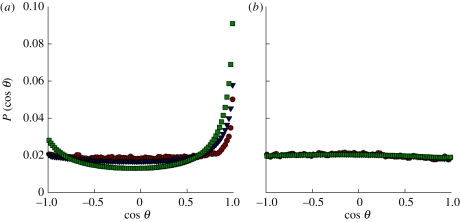
Figure 9 studies the local alignment of swimmers by plotting the normalized distribution of angles θ between pairs of rods separated by a body length or less. Pullers show a very slight departure from isotropy towards orthogonality at all concentrations. Pushers at high concentration show a pronounced tendency towards polar alignment—swimming in the same direction—with this peak diminishing but persisting even at low concentrations. Similar observations had been made in our previous work [29].

Figure 9.

The distribution of inner-products p_i · p_j = cos θ averaged over swimmer pairs within one rod length of each other, in suspensions of (a) Pushers, and (b) Pullers, at various volume fractions. Filled circles, ν = 0.1; filled triangles, ν = 0.5; filled squares, ν = 1.0. (Online version in colour.)

3.5. Particle velocities

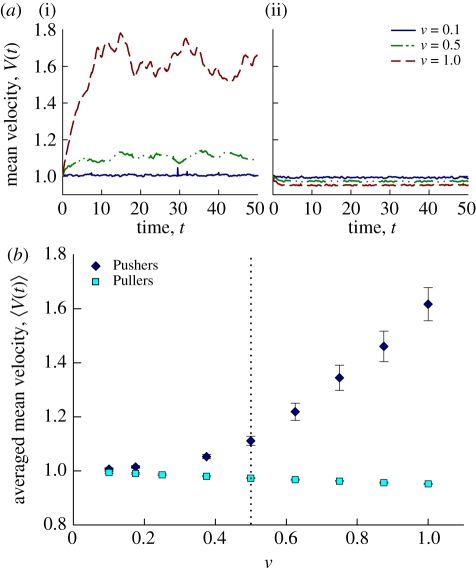
The transition to coherent motions and large-scale flows has a strong impact on particle velocity statistics, as illustrated in figures 10 and 11, showing mean and maximum particle velocities from the simulations. As shown in figure 10, in suspensions of Pushers the mean particle velocity increases well above the isolated swimming speed of 1 as the volume fraction increases. This increase is not observed for Pullers, where the mean velocity in fact decreases slightly below 1. These effects are clearest in figure 10b, showing the time-averaged mean velocity versus volume fraction: the mean velocity is seen to sharply increase in suspensions of Pushers beyond ν ≈ 0.5, whereas it slightly decreases in suspensions of Pullers. These observations are also consistent with our previous study [29].

Figure 10.

(a) Mean particle velocity V(t) as a function of time in suspensions of Pushers (i) and Pullers (ii). Solid line, ν = 0.1; dashed-dotted line, ν = 0.5; dashed line, ν = 1.0. (b) Time average of the mean particle velocity at steady-state versus effective volume fraction ν. (Online version in colour.)

Similar trends are observed in the maximum particle velocity, as shown in figure 11. In suspensions of Pushers, this maximum velocity is again seen to increase with the volume fraction, to reach a temporal mean value of ≈4 above ν ≈ 0.5, while the increase in suspensions of Pullers remains negligible. Occasionally, the maximum velocity in concentrated suspensions of Pushers reaches values as high as 6 or 7: these values are to be compared with experimentally measured velocities in suspensions of swimming bacteria, which have been reported to increase by up to a factor of 10 with respect to the isolated bacterium velocity [2,6].

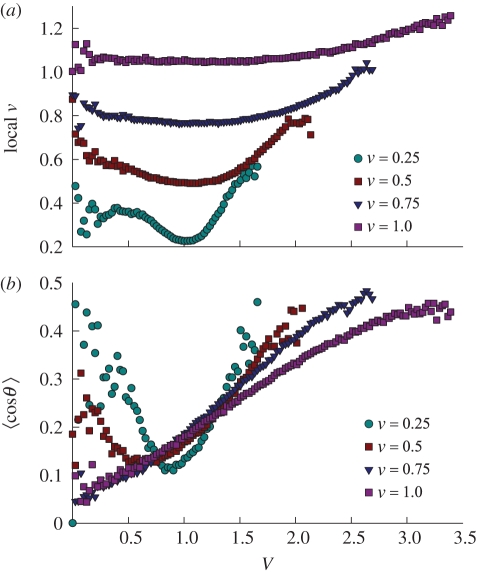
The origin of these large particle velocities in the more concentrated Pusher suspensions is made clearer in figure 12, which examines their relation to the local particle density and alignment. Specifically, figure 12a shows the local value of ν, measured in a sphere of radius 1 enclosing a particle, as a function of the velocity of that particle. While the variations of the local density remain weak (in agreement with the observations made in figure 8), a trend is visible showing that high particle velocities are associated with high local values of ν. Similarly, figure 12b shows the relation between the velocity of a particle and the local polar order parameter, defined as the mean value of cos θ within a distance of 1 from the particle centre. Again, high particle velocities are strongly correlated with larger values of 〈cos θ〉, corresponding to particles that are aligned with and pointing in the same direction as their neighbours. This local polar alignment was characterized in our previous work [29], where it was found that particle orientations and directions are strongly correlated in suspensions of Pushers, with a correlation length scale that exceeds the particle dimension. In other words, particles achieve high velocities through hydrodynamic interactions when they have many neighbours and when they are aligned with these neighbours: this effect is therefore directly enhanced by the formation of coherent structures and clusters described in §3.1 and 3.4.

Figure 12.

(a) Local effective volume fraction, measured in a sphere of radius 1 surrounding a given particle, as a function of the velocity of that particle, in suspensions of Pushers at various mean volume fractions. (b) Local polar order parameter 〈cos θ〉, defined as the mean value of the cosine of the angle θ between the particle of interest and the particles located within a distance of 1 from its centre, as a function of the velocity of that particle, in suspensions of Pushers at various volume fractions. (Online version in colour.)

One measure that shows little if any trace of the emergence of large-scale flows is the long-time diffusive behaviour of individual swimmers. In our previous simulation study [29], we calculated both their translational and rotational effective diffusivities. We found that up to ν ≈ 1, the rotational diffusion d increased linearly with ν. The translational diffusion D varied inversely with d (and hence with ν) following closely the prediction D = U₀²/6d obtained using Brenner's generalized Taylor dispersion theory [46] (we note that above ν = 1, we observe a saturation in diffusivities while preserving consistency with Brenner's predicted relation). We find very similar results here (not shown here; see figure 5 of Saintillan & Shelley [29]). While this is consistent with pair interactions inducing shifts in orientation, estimates of Subramanian & Koch [38] suggest that this mechanism is too weak to yield the diffusion coefficients that we measured. This suggests instead that the relevant mechanism involves the growth of the background velocity gradients which induce particle rotation (say, via Jeffery's equation in the dilute regime). This expectation is supported by figure 13 which shows the monotonic growth of 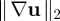(time-averaged) as a function of ν. As with the swimmers' coefficients of effective diffusion, little if any sign is apparent of a transition in flow behaviour.

3.6. Fluid mixing and diffusion of passive particles

With the emergence of the large-scale time- and space-correlated dynamics of collective swimming of Pushers, we also observe the emergence of disturbance flows that can be efficient fluid mixers. This is illustrated in figure 14, and its electronic supplementary material (movie), that shows the evolution of a scalar field s(x,y,z,t) driven by the background velocity fields such as those shown in figure 2. This coloured scalar begins with a one-dimensional sinusoidal distribution s(x,y,z,0) = sin(2πx/L) (with L = 10 the linear system size), and the figure and movie (electronic supplementary material) show its evolution on a planar slice set at constant z. These simulations were performed by advecting (coloured) passive Lagrangian particles with the background fluid velocity, and then interpolating their scalar field values back to a Cartesian grid for analysis.

Figure 14.

Evolution of a scalar field s(x,y,z,t), which is initially given by a one-dimensional sinusoidal distribution s(x,y,z,0) = sin(2πx/L) and is passively advected by the velocity fields of figure 2. The figure only shows a planar slice at constant z. The different rows correspond to Pushers at effective volume fractions (a) ν = 0.1, (b) ν = 0.5, (c) ν = 1.0 and (d) Pullers with ν = 1.0. Also see the accompanying online movie (electronic supplementary material). (Online version in colour.)

Figure 14a is for Pushers at low volume concentration (ν = 0.1). What these images, and particularly the movie (electronic supplementary material), show is the rough preservation of the sinusoidal form of the scalar field, and that the very slow fluid mixing observed there is driven by individual, effectively uncorrelated swimmers dragging fluid across the box. This begins to change for Pushers at ν = 0.5 (figure 14b). Large-scale fluid flows are beginning to emerge and, through their mixing, are destroying the sinusoidal form of the scalar colour field. The final case of ν = 1.0 for Pushers, shown in figure 14c, shows the early emergence of large-scale flows and subsequent rapid and dramatic mixing across the system. Figure 14d is the same high concentration simulation with ν = 1.0, but for Pullers. As for the low concentration simulation of Pushers, the sinusoidal form is roughly preserved and the effect of individual swimmers is seen in dragging fluid across the box. This mixing is again very slow due to the lack of large-scale flows.

Strongly mixing flows were also observed by Saintillan & Shelley [36,37] in their two-dimensional kinetic theory simulations. We follow that work by quantifying the rapidity and degree of mixing using the ‘multiscale mixing norm’ W[s] defined by Mathew et al. [47] as

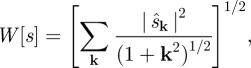3.3

where 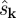is the Fourier transform of the scalar field s at wave vector k. Roughly, each quadrupling in the number of interleaving folds of the scalar field by the fluid velocity yields a halving of W.

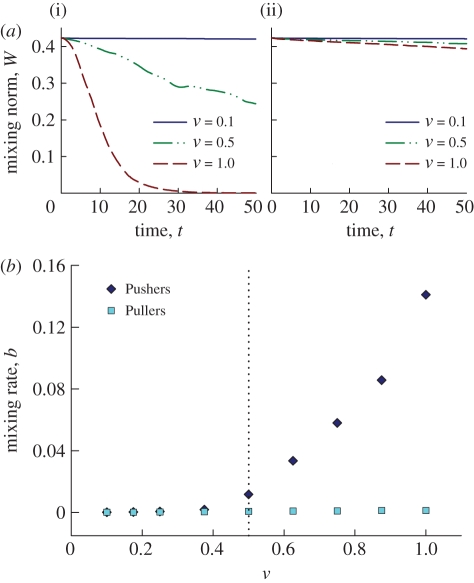
The time evolution of W is shown in figure 15a for both Pushers and Pullers. Figure 15a(i) for Pushers is in accordance with figure 14a–c: at low volume concentration, W decreases very little in time, indicating very little mixing; at the intermediate concentration of ν = 0.5, W shows a more rapid decrease to about 1/2 of its initial value over the course of the simulation. Again, the high concentration case for Pushers is markedly different. The norm W now shows an exponential decrease in value once the instability from uniform isotropy is fully developed, and it halves in value in approximately five time units, or the time for a single swimmer to traverse half the computational box. Conversely, suspensions of Pullers show extremely slow decrease in W (figure 15a(ii)).

Figure 15.

(a) Time evolution of the mixing norm W[s] defined in equation (3.3), in suspensions of Pushers (i) and Pullers (ii) at various volume fractions. (b) Mixing rate b, defined as the asymptotic rate of decrease in W with time (corresponding to a fit of the form W[s] ∼ exp(−bt)), as a function of effective volume fraction ν in suspensions of Pushers and Pullers. Filled diamonds, Pushers; filled squares, Pullers. (Online version in colour.)

We define the rate of mixing b as the asymptotic rate of decrease in W with time. That is, we assume W[s] ∼ exp(−bt), and determine b through a least-squares fit of ln W. This is shown in figure 15b. As expected, b is close to zero for suspensions of Pullers at all simulated volume concentrations, and for Pushers at small volume concentration. It shows a bifurcation to growth for ν ≈ 0.5.

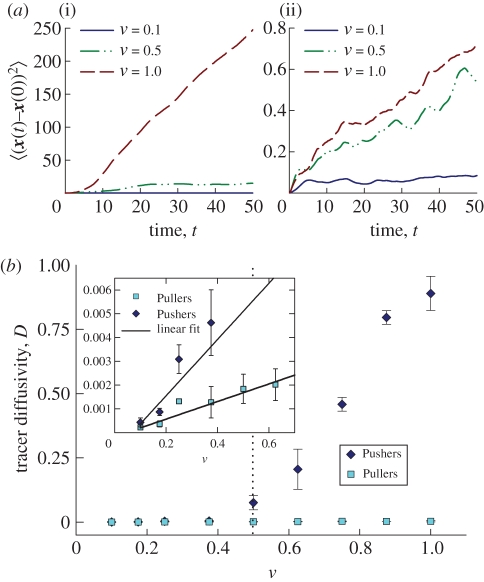
As a measure of global transport of fluid elements, we calculate the diffusivities of the field of advected particles making up the scalar field. Figure 16a shows the field-averaged mean-square displacement relative to initial position, as a function of time. As expected, the emergence of large-scale flows from isotropy for Pushers leads, at the highest volume concentration ν = 1.0, to a linear growth in time. For Pullers, an apparently linear growth also emerges with increases in ν, but with a slope that is two orders of magnitude smaller. Again, this difference arises from the differing mechanisms of fluid mixing presented by the two systems. For Pushers, the larger effective diffusivities are driven by large-scale time-dependent flows, while for Pullers they are associated with the slow mixing due to fluid being dragged by individual swimmers. From the mean-square displacements, figure 16b shows the estimated particle diffusivity. As expected, for Pullers the effective diffusivity is very small for all values of volume concentration, especially relative to Pushers at high concentration. It also follows a linear increase with ν over the whole range of concentrations we investigated (inset of figure 16b), which is consistent with previous experimental [12], theoretical [48–50] and computational studies [23,26]. For Pushers, there is again an evident bifurcation, at approximately ν = 0.5, from small diffusivities to much larger values that show an approximately linear increase in ν.

Figure 16.

(a) Mean-square displacements 〈(x(t) − x₀)²〉 of passive tracer particles advected by the disturbance velocity fields in suspensions of Pushers (i) and Pullers (ii). (b) Effective passive tracer diffusivities, obtained from the data of (a), as functions of the effective volume fraction ν in suspensions of Pushers and Pullers. Inset: passive tracer diffusivities as functions of ν for Puller suspensions. This growth (slope 3.7 × 10⁻³) is much smaller than that for subthreshold Pusher suspensions (slope 1.2 × 10⁻²). (Online version in colour.)

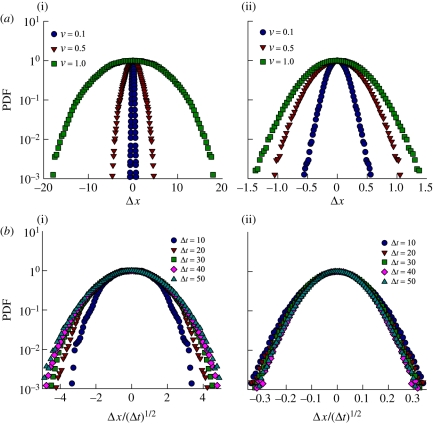
More information on passive tracer dynamics is provided in figure 17, showing probability distribution functions of tracer displacements. Figure 17a shows the distribution functions for both Pushers and Pullers at Δt = 20 and at different volume fractions. As expected, we find that the distributions widen as ν increases, as a result of the stronger disturbance flows driven by the swimmers; we also find that displacements are significantly larger for Pushers than for Pullers. Upon rescaling of Δx with Δt^1/2 in figure 17b, we find that the distributions for a given volume fraction all collapse at late times (large Δt), which is consistent with a long-time diffusive motion for the tracers. Note that the distributions are very well captured by Gaussians in the case of Pullers, though they tend to have faster-decaying tails in the case of Pushers. This observation differs from the experimental results of Leptos et al. [12], who looked at tracer displacements in suspensions of Chlamydomonas reinhardtii, a Puller micro-alga, and found that the distributions of displacements exhibited strongly non-Gaussian exponential tails. Such is not the case in our simulations. A possible source of discrepancy is the difference in the near-field velocities induced by the swimmers, which are likely to play an important role in the tracer diffusivities as argued by Leptos et al. [12] and Lin et al. [50].

Figure 17.

(a) Probability distribution functions for tracer displacements Δx in the x-direction after a time Δt = 20, in suspensions of Pushers (i) and Pullers (ii) at various volume fractions. (b) Rescaling of the distributions in terms of Δx/Δt^1/2 for Pushers and Pullers at an effective volume fraction of ν = 1.0. (Online version in colour.)

3.7. Effect of system size

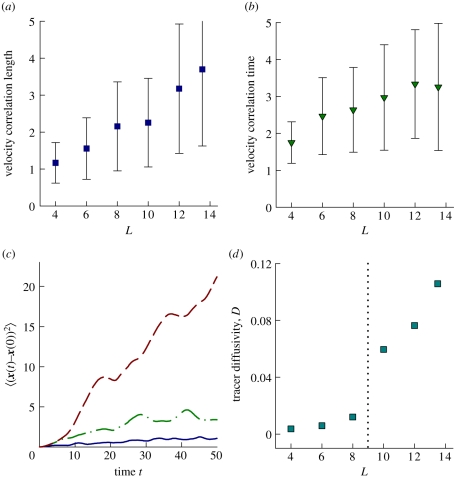
All the simulations described so far were performed in a cubic cell of fixed linear dimension L = 10, in which the number of particles was varied in order to vary the effective volume fraction ν. In these simulations, we observed that increasing ν at that fixed system size results in a transition from uncorrelated to correlated motions in suspensions of Pushers, at a critical volume fraction of the order of 0.5. According to the criterion of equation (1.1), a similar transition should occur when the system size is varied at a fixed volume fraction. To test this prediction, simulations were performed at a fixed volume fraction of ν = 0.5, in simulation cells of various sizes ranging from L = 4 to 13.5. A transition is again observed in suspensions of Pushers, with correlated motions and large-scale flows only occurring above a critical system size of order L ≈ 10. This transition is illustrated in figure 18, which shows results on velocity correlation lengths and times, and on passive tracer diffusivities. While the correlation lengths and times show a gradual increase with system size L with no clear transition at a critical system size, tracer diffusivities are very weak in small systems and sharply increase as L exceeds ≈ 10, which corresponds to the onset of large-scale flows in the suspensions. Again, no such transition is observed in suspensions of Pullers (not shown). These observations, together with those of the previous sections, are consistent with the instability criterion (1.1) derived from the kinetic model of Saintillan & Shelley [36,37] and Hohenegger & Shelley [39].

Figure 18.

(a) Velocity correlation lengths and (b) velocity correlation times in suspensions of Pushers at a fixed effective volume fraction ν = 0.5 in simulation cells of various sizes L. (c) Mean-square displacements 〈(x(t) − x₀)²〉 of passive tracer particles advected by the disturbance velocity fields in suspensions of Pushers at a fixed effective volume fraction ν = 0.5 in simulation cells of various sizes L. Solid line, L = 4; dashed-dotted line, L = 8; dashed line, L = 12. (d) Effective passive tracer diffusivities, obtained from the data of (c), as functions of the system size L in suspensions of Pushers at an effective volume fraction of ν = 0.5. (Online version in colour.)

4. Concluding remarks

Our main finding is identifying a transition from weakly correlated to correlated dynamics in suspensions of Pusher particles, which occurs when the product of concentration and system size exceeds a fixed threshold. No such transition was observed in suspensions of Pullers. The transition, as we showed, is characterized by a qualitative change in the dynamics of the system, with the emergence of strong large-scale chaotic flows that correlate on the system size, giant number fluctuations in the particle configurations, enhanced particle velocities (by up to a factor of 5) and input power, efficient fluid mixing, and enhanced passive tracer diffusion. Similar transitions have been previously reported in experiments on bacterial suspensions, where large-scale flows and collective dynamics have been shown to occur only above a critical concentration [4,7]. Curiously, quantities associated with the background fluid velocity fields show smoother variation with concentration or system size. This includes velocity correlation lengths and times, and the (time-averaged) L₂ norm of the velocity gradient, which is associated with the long-time diffusion of motile particles.

This transition is consistent with the prediction of our previous kinetic theory [36,37,39], according to which instabilities should arise in suspensions of Pusher particles when the criterion of equation (1.1) is met. In a system of fixed size L = 10, Hohenegger & Shelley [39] predict a somewhat higher value of the threshold ν, approximately 0.9, than the value of 0.5 that we find here. However, the kinetic theory is derived under assumptions such as several invocations of separation of scale, no direct rod–rod interactions and no finite-number effects. All of these assumptions were violated in the simulations given the computational constraints on system size and particle number, and were particularly evident in the various subthreshold correlations measured in Pusher suspensions.

While Puller suspensions maintained near isotropy and uniformity (as predicted by the kinetic theory) by all of our statistical measures, they also showed some departures such as in the power input and variation of the velocity gradient L₂ norm with concentration. We point out that in our model, there is a form of flow reversibility: by changing the sign of the motive stress, Pushers become Pullers and will retrace their paths backwards in time. This aspect also underlies the change in suspension stability with swimmer type.

Finally, both the kinetic theory and the present simulations clearly demonstrate that the emergence of collective dynamics is primarily a hydrodynamic effect due to interactions between the particles via their long-range flow disturbances, as both studies focused on the dilute to semi-dilute regimes and completely neglected short-range steric interactions. This conclusion differs from that of other previous studies (e.g. [4,31,33–35]), which explained collective dynamics as a result of excluded volume, causing particles to locally align at high concentrations; this effect is however negligible in the suspensions we considered in this work, which all had volume fractions well below the critical value for the isotropic-nematic transition for rod suspensions [40].