Boundary conditions of patient-specific fluid dynamics modelling of cavopulmonary connections: possible adaptation of pulmonary resistances results in a critical issue for a virtual surgical planning

Abstract

Cavopulmonary connections are surgical procedures used to treat a variety of complex congenital cardiac defects. Virtual pre-operative planning based on in silico patient-specific modelling might become a powerful tool in the surgical decision-making process. For this purpose, three-dimensional models can be easily developed from medical imaging data to investigate individual haemodynamics. However, the definition of patient-specific boundary conditions is still a crucial issue. The present study describes an approach to evaluate the vascular impedance of the right and left lungs on the basis of pre-operative clinical data and numerical simulations. Computational fluid dynamics techniques are applied to a patient with a bidirectional cavopulmonary anastomosis, who later underwent a total cavopulmonary connection (TCPC). Multi-scale models describing the surgical region and the lungs are adopted, while the flow rates measured in the venae cavae are used at the model inlets. Pre-operative and post-operative conditions are investigated; namely, TCPC haemodynamics, which are predicted using patient-specific pre-operative boundary conditions, indicates that the pre-operative balanced lung resistances are not compatible with the TCPC measured flows, suggesting that the pulmonary vascular impedances changed individually after the surgery. These modifications might be the consequence of adaptation to the altered pulmonary blood flows.

1. Introduction

Among the clinical requirements identified in the Roadmap to the Virtual Physiological Human (STEP Consortium, Seeding the EuroPhysiome: A Roadmap to the Virtual Physiological Human; http://www.europhysiome.org/roadmap/) are those for customized therapies and for decision-making systems. Such requirements have become increasingly important in paediatric cardiac surgery for the treatment of congenital malformations, which has been evolving very rapidly in recent years.

The surgical repairs that have been developed often involve major reconstructive procedures, creating a totally new circulation. The so-called ‘Fontan circulation’ refers to a cardiovascular configuration resulting from a group of operations used to bypass the non-functional right heart [1]. In such a univentricular circulation, the blood returning from the body reaches the lungs via direct blood vessel connections without a pumping chamber.

Different surgical procedures have been developed to create the Fontan circulation. One of these procedures is the total cavopulmonary connection (TCPC) [2]. In the TCPC, the superior and the inferior venae cavae (SVC and IVC, respectively) are directly connected to the right pulmonary artery, the latter by means of an intra-atrial or extracardiac tunnel. This final configuration is often obtained through an intermediate stage, the bidirectional cavopulmonary anastomosis (BCPA), where only the SVC is connected to the right pulmonary artery. The two surgical stages (BCPA and TCPC) lead to peculiar geometries (T-shaped and cross-shaped, respectively), which are associated with unusual fluid dynamics. Major problems possibly affecting the univentricular circulation are related to energy losses and blood distribution from the body into the lungs. The absence of a functioning right ventricle limits the energy available for pulmonary blood flow.

A number of studies have used in vitro and in silico flow modelling to evaluate the fluid dynamics of these operations in an effort to construct cavopulmonary anastomotic designs that minimize energy dissipations and properly balance the pulmonary flow distribution. A thorough review of the literature is reported in DeGroff [3]. Among the most recent studies investigating congenital heart diseases, it is worth remembering those which adopt a multi-scale (or multi-domain) approach, coupling the solution at the boundaries of the three-dimensional model of the surgical region with a lumped parameter model (LPM; i.e. zero-dimensional [4–6]) or one-dimensional model [7] of the remainder of the cardiovascular system. The main advantages of this approach are that both local and global haemodynamics can be monitored at the same time, and boundary conditions for the post-operative three-dimensional model are provided by the LPM.

Helping cardiac surgeons to design the most effective TCPC by means of a patient-specific ‘virtual surgery’ simulation is a tough challenge for bioengineers. A patient-specific model should be developed first that represents the pre-operative three-dimensional geometry (i.e. the BCPA) with patient-specific boundary conditions properly provided by an LPM representing the remainder of the cardiovascular system. On the basis of this multi-scale model, selected surgical options could be assessed by creating different post-operative models with the IVC connected to the BCPA and simulating the TCPC scenario [8].

However, a number of critical issues need to be emphasized: (i) the creation of a pre-operative multi-scale model using patient-specific data; (ii) the simulation of the surgeon's activity and the reproduction of the anatomical features produced by the surgical procedure; (iii) the potential change in the cardiovascular network parameters following surgery, owing to vascular self-regulation and adaptation to new local haemodynamics. The first point requires parameter identification based on patient-specific pre-operative data, whereas the other two points involve modelling for prediction of future scenarios. These issues pose a significant threat to the reliability of virtual surgery.

In the present study, the validation issue is analysed with regard to a set of multi-scale simulations for a single patient undergoing a TCPC, based on detailed pre-operative and post-operative anatomical and flow data. Left and right pulmonary impedances are estimated for the BCPA configuration and their applicability to the TCPC model is investigated. The aims of this work are to investigate possible unbalanced lung resistances in our BCPA patient, and to verify whether pulmonary resistances have changed after the TCPC has been created.

2. Material and methods

2.1. Magnetic resonance and catheterization data

A single patient, who had undergone a BCPA at the age of 10 months and a TCPC with a 20 mm extracardiac conduit at the age of 4 years, was enrolled in this study. Cardiac catheterization and magnetic resonance (MR) scans in the presence of the BCPA was carried out immediately prior to the patient undergoing the TCPC. MR scanning was also performed one month after the surgery, whereas catheterization was not. A complete set of tomographic images of the cavopulmonary connections was acquired using a 1.5 T MR scanner (General Electrics, Milwaukee, WI, USA). Anatomical slices were obtained with in-plane resolution of approximately 1 × 1 mm and slice thickness of 2 mm. This was achieved with a 256 × 256 matrix size and a 28 × 28 cm field of view. A commercially available gradient echo velocity mapping sequence, triggered by the electrocardiogram, was used to measure the blood flow rates in the caval veins and pulmonary arteries. Figure 1 plots the volume flow tracings throughout a cardiac cycle in the pre- and post-operative situations for the patient. The mean flow rates over the cardiac cycle are reported in table 1, together with the pressure values obtained during the cardiac catheterization. Presumably because of measurement errors, a slight difference was observed between the mean flow rate entering the anastomotic region and that in the pulmonary artery. However, the percentage discordance (ΔQ%) was lower than 8 per cent, which is in agreement with previously published data on TCPC [9,10].

Figure 1.

Time tracings of the (a) pre-operative and (b) post-operative blood volume flow rates measured over a cardiac cycle using MR. (a) Closed diamonds, Q_SVC; open squares, Q_LPA; open diamonds, Q_RPA. (b) Filled squares, Q_IVC; filled diamonds, Q_SVC; open squares, Q_LPA; open diamonds, Q_RPA.

Table 1.

Clinically measured quantities. ΔQ% = 2(Q_SVC−Q_LPA−Q_RPA)/(Q_SVC + Q_LPA + Q_RPA) for BCPA. ΔQ% = 2(Q_SVC + Q_IVC−Q_LPA−Q_RPA)/(Q_SVC + Q_IVC + Q_LPA + Q_RPA) for TCPC. Both flow rates and pressures are mean values over a cardiac cycle. Flow time tracings are reported in figure 1. n.a., not available.

	blood flow rates (cm3 s−1)					blood pressures (Pa)
	QSVC	QIVC	QLPA	QRPA	% error ΔQ%	pPA-cath	pAt-cath
BCPA	24.87	14.75	13.45	13.47	−7.9	1733	1200
TCPC	18.20	11.83	13.27	17.40	−2.1	n.a.	n.a.

2.2. Multi-scale models

On the basis of the available clinical information, both pre-operative and post-operative three-dimensional in silico models were built. The models were constructed by means of Amira software (Visage Imaging Inc., San Diego, CA, USA) using 39 and 54 axial slices for the BCPA and TCPC conditions, respectively. The ‘region growing’ segmentation algorithm available in Amira was used to detect the contours of the region of interest. This region was selected by defining a range of grey values, the boundaries of the range being the lower and upper threshold values. After selecting the region of interest, a three-dimensional model of the structure was obtained by means of pattern recognition and interpolation algorithms. A set of aligned contours was extracted and the surfaces obtained were converted into the model used for the computational fluid dynamics (CFD) simulations, by means of smoothing algorithms (see http://www.amira.com/images/stories/pdf/41/amiraUsersGuide.pdf).

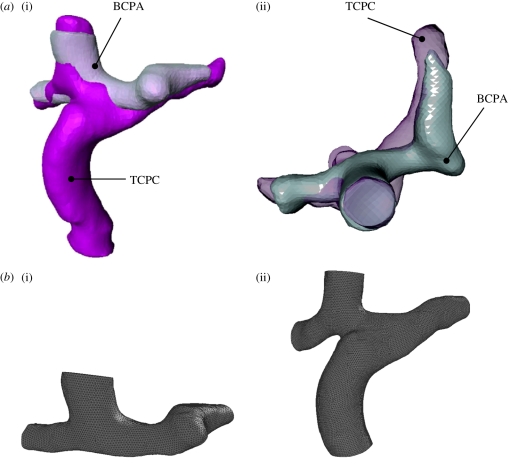
Figure 2a shows the reconstructed BCPA and TCPC geometries. The models are superimposed to allow a comparison and to show the anatomical changes following surgical IVC connection. Before meshing the models, particular care was used to cut the pulmonary arteries in the two models at exactly the same extent, upstream from the first branches.

Figure 2.

(a) Reconstructed geometries of the BCPA and TCPC. (i) Frontal and (ii) transverse views. The two geometries are superimposed to demonstrate the changes resulting from the TCPC surgery. (b) Meshed geometries of the BCPA (i) and TCPC (ii) three-dimensional models used in the in silico simulations.

The models were then meshed with the Gambit commercial package (ANSYS, Canonsburg, PA, USA) and an unstructured grid was used, made of tetrahedral elements. A mesh sensitivity analysis was carried out on the models by doubling the mesh size and checking that the resulting pressure difference values throughout the models did not change by more than 2 per cent. The adopted BCPA and TCPC meshes contained approximately 600 000 and 835 000 elements, respectively (figure 2b).

An LPM was then coupled to the three-dimensional models to set the outflow boundary conditions in a number of multi-scale simulations described in the following sections. The LPM used included two impedances, Z_r and Z_l, representing the right and left branches of the pulmonary vascular impedance. They were connected to the outlet cross sections of the three-dimensional model and to a constant-pressure reservoir (p_At-cath) accounting for the left atrial pressure measured during cardiac catheterization (figure 3). Each impedance was split into two series components: an R,L,C, block reproducing the remaining pulmonary arterial bed, followed by an R,C block accounting for the pulmonary venous side. A total of five parameter values (R₁, C₁, L, R₂, C₂) were to be defined for both the left and right lung models (a subscript l or r in the following, respectively). As an alternative, the following five parameters, which are a combination of the previous ones, may be considered:

Figure 3.

Scheme of the adopted multi-scale model: the three-dimensional model is connected to two lumped impedances (Z_r and Z_l) representing the lung vasculature. p_RPA and p_LPA indicate the mean pressures at the two outlet sections of the three-dimensional model; Q_RPA and Q_LPA are the right and left pulmonary flow rates. The lumped impedances are connected to a constant-pressure generator corresponding to the left atrium. p_At-cath is the mean atrial pressure measured during cardiac catheterization.

Patient-specific values were properly evaluated for R_tot and C_tot of the two lungs as illustrated in the following sections, while simplifying assumptions were made for the three remaining parameters. Namely, it was assumed that ρ_R = 0.7, ρ_C = 0.3 and τ = 0.00625 s for both lungs, on the basis of values adopted in previous LPM models of pulmonary vasculature [11–13] and clinical measurements [14].

2.3. Computational fluid dynamics simulations

Detailed blood flow fields were calculated by solving the Navier–Stokes equations governing unsteady flow of an incompressible, non-Newtonian fluid using a commercial code based on the finite volume method (Fluent package; ANSYS).

The vessel walls were considered to be rigid and impermeable with no-slip boundary conditions, while blood was treated as a homogeneous incompressible fluid with a density equal to 1060 kg m⁻³. A non-Newtonian Carreau model [15] was used to define the dynamic viscosity μ of blood,

2.1

where λ = 3.313 s, n = 0.3568, μ₀ = 56 cP and μ_∞ = 3.45 cP, with μ and expressed in centipoise and per second, respectively.

Four different kinds of simulations were carried out:

1. a steady-state simulation with the BCPA three-dimensional model to evaluate left and right pulmonary resistances;

2. unsteady simulations with the BCPA multi-scale model to find left and right pulmonary compliances;

3. an unsteady simulation with the TCPC multi-scale model to predict the post-operative hemodynamics;

4. an unsteady simulation with the TCPC three-dimensional model to verify the suitability of pre-operative pulmonary impedances as boundary conditions after surgery.

In the following, details of these four steps are described.

2.3.1. Step (i)

As the first step, a single steady-state simulation was performed imposing a flow ratio as the outflow boundary condition for the stand-alone BCPA three-dimensional model. This simulation allowed us to assess patient-specific values for the total left and right pulmonary resistances (R_tot-l and R_tot-r).

Boundary flow conditions were imposed according to the time-averaged values measured by MR scanning (table 1). Namely, a flat velocity profile corresponding to the SVC flow was imposed at the model inlet, while a flow ratio was set at the two pulmonary outlets (LPA and RPA). The Fluent Outflow Boundary option was used, which specifies zero normal gradient (i.e. Neumann conditions) for all velocity components, where the solver extrapolates the required information from the interior and applies an overall mass balance correction [16]. A segregated solver and the SIMPLE algorithm for pressure–velocity coupling were used. The upwinding method of the second order for momentum and standard discretization for pressure were chosen, while convergence criteria were set to 10⁻⁶.

Cardiac catheterization provided atrial (p_At-cath) and pulmonary arterial (p_PA-cath) mean pressures (table 1). However, available catheterization data did not include the values of left and right pulmonary pressures. Conversely, the CFD simulations allow one to compute the pressure gradients throughout the model. On the basis of the known pressure value at a fixed point, pressures can be calculated at all the other points. In this study, p_PA-cath was used as the reference pressure to evaluate the pressures at the model outlets (p_LPA and p_RPA). The measured value was associated with a spherical region of the model, and pressure differences between the average value in the sphere and the average value at each outlet section were evaluated (Δp_l for the LPA, and Δp_r for the RPA outlet sections), as shown in figure 4a. Patient-specific values of p_LPA and p_RPA (i.e. in agreement with pressures and flows measured clinically) were then simply evaluated, combining the measured p_PA-cath and the computational results in terms of Δp_l and Δp_r, as follows:

2.2

Figure 4.

(a) p_PA-cath is the mean pulmonary pressure measured during cardiac catheterization. This value was associated with a spherical region in the model, and used as the reference pressure to evaluate the values at the outlets (p_LPA and p_RPA). Pressure differences between p_PA-cath and the average value at each outlet section (Δp_l for the LPA, and Δp_r for the RPA outlet sections) were evaluated through step (i). (b) Three different spherical regions (3 mm radius) were considered at three adjacent positions within the pulmonary arteries as possible measurement locations for p_PA-cath: medial (corresponding to the main pulmonary artery closure), left and right (9 mm laterally to the medial location).

However, a degree of uncertainty generally exists about the location in the pulmonary artery where pressure is recorded during patient catheterization. Hence, we considered three different spherical regions (3 mm radius), at three adjacent positions within the pulmonary arteries (indicated as ‘medial’, corresponding to the main pulmonary artery closure; ‘left’ and ‘right’, 9 mm laterally to the medial location; figure 4b), as possible measurement locations. Three different values for both p_LPA and p_RPA were thus calculated (equation (2.2)) according to the sphere under consideration.

In the case of steady flow conditions, the LPM describing the lung vasculature can be simply described by the total left and right pulmonary resistances, R_tot-l and R_tot-r, respectively. Assuming a linear flow–pressure relationship, three different patient-specific values for both R_tot-l and R_tot-r were then calculated according to the p_LPA and p_RPA values, as follows:

2.3

where Q_LPA and Q_RPA are the mean volume flow rates measured in the pulmonary arteries.

2.3.2. Step (ii)

For the second step, the estimated total resistances were applied as outlet boundary conditions in the presence of pulsatile flow, by running a number of unsteady simulations with the BCPA multi-scale model. These simulations allowed us to find total compliance values (C_tot-l and C_tot-r) compatible with the (measured) pre-operative pulmonary flow tracings.

The MR-based volume flow curve was imposed at the SVC inlet, and outlet impedances according to figure 3 were used. The measured mean atrial pressure was imposed as a downstream condition of the pulmonary lumped impedances. Resistance and inertance values (R_1r, R_2r, L_r and R_1l, R_2l, L_l; table 2) were deduced from R_tot-r and R_tot-l according to the above described values of ρ_R and τ, and used in each pulsatile simulation. With regard to vascular distensibility, the value of the total pulmonary compliance was manually tuned, in the range from zero (no distensibility) to a maximum value reported for children with congenital heart diseases (0.033 cm³ Pa⁻¹, [17]), in order to obtain a good match between the computed flow time tracings and those measured with MR at the two pulmonary outlets. The C_tot-r/C_tot-l ratio was kept constant and equal to (R_tot-r/R_tot-l)^−0.75 according to proper scaling rules [18]. Moreover, C_tot-r and C_tot-l were distributed among the two blocks of the right and left lung models, respectively (C_1r, C_2r and C_1l, C_2l; table 2), according to the assumed ρ_C.

Table 2.

Values of the patient-specific pulmonary lumped parameters obtained from the BCPA model simulations at steps (i) and (ii), and used for the TCPC multi-scale model simulation at step (iii). C values are reported in cm³ Pa⁻¹; R values in Pa s cm⁻³; L values in Pa s² cm⁻³.

impedances	parameters	values
left lung	C1l	0.50 × 10−3
	R1l	26.32
	Ll	0.17
	C2l	1.20 × 10−3
	R2l	11.28
right lung	C1r	0.46 × 10−3
	R1r	29.68
	Lr	0.18
	C2r	1.09 × 10−3
	R2r	12.72

The time integration technique used to solve the Navier–Stokes equations for the three-dimensional domain was the implicit backward Euler method with a fixed time step equal to 10⁻⁴ s and a segregated solver. The ordinary differential equation system resulting from the LPM was solved with the explicit Euler method, implemented in the Fluent code by means of a user-defined function. Three cardiac cycles were simulated to guarantee a stable solution. The time required for the simulation of a cardiac cycle was about 12 h, using an Intel Core 2 Duo (3 GHz) personal computer.

2.3.3. Step (iii)

An additional pulsatile simulation was executed for the TCPC multi-scale model using the parameter values assessed as pre-operative outlet boundary conditions, to verify whether they could be correctly used in the post-operative model too. In other words, the aim of this simulation was to assess potential changes in the pulmonary vascular resistances of the patient under consideration that may have occurred after TCPC surgery.

The post-operative MR-based volume flow curves were imposed at the SVC and IVC inlets and the above evaluated pre-operative left and right pulmonary impedances were used. Again, the computed flow time tracings at the two pulmonary outlets were compared with those measured with MR. Moreover, the power dissipation p_diss across the model over a cardiac cycle was calculated as in Dubini et al. [19],

where ρ is the blood density, is the mean square velocity and p_i is the mean pressure on the ith inlet/outlet section.

2.3.4. Step (iv)

Finally, the TCPC haemodynamics occurring when the inlet and outlet flow rates are equal to the measured ones was evaluated by a pulsatile simulation using the stand-alone three-dimensional model. The measured LPA flow tracing was imposed at the corresponding outlet to reproduce the post-operative MR-based pulmonary flow split. The power dissipation across the model was calculated (likewise step (iii)) as a term of comparison for the above described multi-scale simulation.

3. Results

Figure 5 shows the pressure field and the pathlines of the BCPA model in the steady-state simulation. The pressure distribution shows that an overpressure occurs at the pulmonary inferior wall, where the SVC stream impacts on the vessel, while pressure progressively decreases moving towards the pulmonary outlets. The particle path plot shows some secondary motions throughout the pulmonary arteries. Furthermore, a recirculation zone occurs in the medial region, within the protuberance left after the closure of the main pulmonary artery, with a slight increase in pressure. Nevertheless, the pressure drop across the model is relatively small (118 Pa) in comparison with the difference between p_PA-cath and p_At-cath (533 Pa according to table 1). Furthermore, pressure differences among the three considered spheres do not exceed 45 Pa.

Figure 5.

Results from the steady-state simulation (step (i)) with the BCPA model: pressure colour maps with reference (a) zero pressure at the LPA outlet and (b) pathlines colour coded according to velocity.

The evaluated right and left pulmonary resistances are quite similar (42.4 ± 1.7 versus 37.6 ± 1.6 Pa s cm⁻³, mean ± s.d. of three spheres under consideration). Moreover, the possible influence of the location of the p_PA-cath measurement (‘medial’, ‘left’ or ‘right’) is very limited in the current patient (s.d. lower than 5% of resistances mean values), owing to quite low pressure gradients throughout the BCPA model. The mean values of the calculated resistances were then adopted as R_tot-r and R_tot-l in the pulsatile simulations with the BCPA multi-scale model.

In figure 6, the tracings of blood volume flows at the two pulmonary outlets computed for three different values of pulmonary compliances (indicated as ‘null’, dashed lines; ‘high’, thin solid lines; and ‘intermediate’, thick solid lines) are compared with those measured in the patient (lines with filled squares). After compliance tuning, ‘intermediate’ values for pulmonary compliances were assumed to be representative of the pulmonary vascular distensibility in the pre-operative condition, owing to the satisfactory matching in terms of mean and max–min flow values with MR data in the pulmonary arteries. Hence, the corresponding set of lumped parameters (table 2) was used for the outlet boundary conditions in the pulsatile simulation with the TCPC multi-scale model, too.

Figure 6.

Results from the multi-scale pulsatile simulations (step (ii)) with the BCPA model and different values of pulmonary compliances. The computed flow rates at (a) the LPA and (b) RPA outlets according to compliance values (‘null’ compliance, dashed lines; ‘high’ compliance, thin solid lines; and ‘intermediate’ compliance, thick solid lines) are compared with the MR measured tracings (lines with filled squares).

Results show (figure 7) that the pulmonary flows computed with the TCPC multi-scale model largely differ from the measured time tracings. The multi-scale model predicted a flow split slightly in favour of the left lung (52.3% of caval flow), which disagrees with the measured flow repartition (only 43.3% of caval flow to the left lung).

Figure 7.

Results from the multi-scale pulsatile simulation (step (iii)) with the TCPC model coupled to the pre-operative left and right pulmonary impedances (table 2). The computed flow rates at the LPA and RPA outlets (Q_LPA-CFD and Q_RPA-CFD; solid lines) show a clear discrepancy with MR measured tracings (Q_LPA and Q_RPA; lines with squares and diamonds).

Figure 8 shows the flow field calculated by the TCPC multi-scale model (step (iii)) compared with that obtained by imposing the measured outlet flow conditions (step (iv)) at three relevant instants of the cardiac cycle. Results from the multi-scale simulation indicated that, if the post-operative left and right pulmonary impedances are derived from the pre-operative situation, for the investigated case, the LPA receives flow from both caval veins, while the RPA is roughly perfused only by blood coming from the SVC. On the contrary, in the simulation in step (iv) in the presence of the clinically measured pulmonary flow split, both venae cavae supply blood to the RPA. Consequently, the calculated power dissipations were also different, showing higher values for the multi-scale simulation (1.35 versus 1.08 mW).

Figure 8.

Back views of the SVC (yellow) and IVC (red) flow distributions computed at three different instants in the cardiac cycle in the simulation with the TCPC multi-scale model (step (iii), top), and in that obtained by imposing the measured pulmonary flow split (step (iv), bottom).

4. Discussion

Nowadays, virtual surgery based on in silico patient-specific modelling is a powerful tool for clinical use because it can help surgeons in the decision-making process, improving haemodynamic outcomes and reducing errors during complex surgery [8]. This could be even more important for paediatric surgical operations to treat congenital heart diseases. However, the reliability of virtual surgical predictions is a critical issue since a true validation is unfeasible owing to the lack of detailed patient information after surgery. Indeed, post-TCPC MR scanning and cardiac catheterization are not performed when they are considered to be unnecessary from a clinical point of view, owing to their cost and invasiveness. Hence, to date no studies have attempted to validate the predictions of virtual surgery owing to the lack of post-operative data.

In the present study, the availability of both pre-operative and post-operative data in a single clinical case allowed us to focus on anatomical changes and possible adaptation of lung impedances after TCPC surgery. Therefore, it was possible to partially tackle the above validation issues and to highlight a number of important concerns in the development of patient-specific pre-operative models.

4.1. Set-up of the pre-operative model

Pre-operative left and right lung impedances were estimated with an approach similar to that adopted by Spilker & Taylor [20] to identify the lumped parameters to be used as outlet boundary conditions of three-dimensional cardiovascular models. They emphasized that estimating the correct values for the downstream resistances and impedances of multiple outlets is essential to build an effective patient-specific pre-operative vascular model. Patient-specific parameters were deduced on the basis of increasingly enriched simulations (steady-state, pulsatile, … , etc.) and assumptions about vascular lumped parameters—namely resistance ratios and time constants. Differently from the approach of Spilker & Taylor [20], consisting in an automatic parameter optimization to achieve the desired features of pressure and flow waveforms, we adopted a manual tuning.

The estimated values of the whole resistances of the left and right lungs showed a slight difference (about 12%) in our patient (37 versus 42 Pa s cm⁻³), despite the calculated LPA and RPA mean volume flows being identical. Indeed, blood flow distribution from the SVC to the lungs is driven by the resistances created by local phenomena in the BCPA region and by distributed pressure losses across the lung vasculature. Multi-scale modelling is thus necessary to account for the former, through the three-dimensional model, and the latter, through the LPM. The presence of an only small imbalance in the individual lung resistances in the investigated patient is consistent with several assumptions of equal lung resistances used in the literature [19,21,22]. However, it can be expected that such a hypothesis would not be realistic in a patient with asymmetrical lung development. Hence patient-specific values should be identified.

Another critical point is the uncertainty in the calculation of patient-specific resistances imposed at the outlets of the three-dimensional model, using pressure values from cardiac catheterization and MR volume flow rates [23,24]. Indeed, the present study indicates that different resistances may be calculated according to the assumed location of pressure measurement. However, the outcomes of the resistance uncertainty depend on the pressure distribution throughout the model. When pressure gradients are small, as in the investigated clinical case, the calculated resistances show a negligible variability (around 5%), but when large pressure gradients across the cavopulmonary connection occur (e.g. in the presence of unilateral pulmonary stenosis, [7]), significantly different values of resistances may be obtained. This uncertainty about boundary conditions could pose a major limitation to the subsequent virtual surgery simulation.

The pre-operative model should also include patient-specific pulmonary compliances. The study by Vignon-Clementel et al. [25], which thoroughly investigated outflow boundary conditions for three-dimensional finite-element modelling of blood flow in arteries, showed that a change in the downstream vascular compliance produces a significant modification of three-dimensional outflow and pressure tracings. The present work confirmed that the introduction of compliances in the LPM pulmonary impedances leads to a better prediction of the flow tracings in comparison with pure resistance outlet boundary conditions (figure 6). Therefore, tuning of the parameter values is necessary to find the patient-specific values of the pulmonary compliances. The compliance values obtained for the investigated clinical case (table 2) are consistent with the range measured in children with congenital heart diseases (0.4–6.2 ml m⁻² mm Hg⁻¹, [17]).

Of note is the fact that, in the present study, the LPA and RPA boundaries were located before pulmonary artery branching, resulting in what may be seen as a simpler geometry than that used by other authors who considered multi-branched Fontan models [5,24]. Such models were constructed using MR angiography with intravenous administration of a gadolinium-based contrast agent, which allows one to identify even small pulmonary branches. In the present work, as well as in other similar studies [26,27], MR angiographic methods were not used and, therefore, simpler anatomical models were reconstructed, owing to the fact that gadolinium contrast is not systematically administered to younger patients in the clinical centre providing the imaging data. Although multi-branched three-dimensional models account for a larger number of pulmonary arterial branches, the compliance properties of such vascular portions are not considered, while they might be important for the hemodynamics in the surgical region. Moreover, a downstream impedance has to be evaluated for each outlet, after making an arbitrary assumption on the individual branch flows. On the contrary, by cutting the model immediately before the first left or right pulmonary bifurcation, it is possible to account for the compliance of the downstream arteries using proper lumped parameters. Nevertheless, in these simpler models, the velocity profiles close to the outlets could differ from the actual ones, owing to the proximity of the prescribed boundary conditions.

4.2. Suitability of the pre-operative pulmonary impedances for post-operative predictions

Provided that the patient-specific BCPA multi-scale model was built, virtual surgery can be performed, reproducing the surgical IVC connection, to obtain a TCPC model geometry for post-operative model simulations [8]. However, the present study did not perform virtual surgery, since we focused on comparing the actual reconstructed anatomies. Superimposing the BCPA and TCPC three-dimensional models (figure 2) showed that changes also occurred after TCPC surgery in the SVC connection, probably owing to vessel distortion and synthetic conduit attachment. This finding highlights the difficulty in accurately reproducing the post-operative anatomy based on the pre-operative anatomy.

A further concern also arose regarding the suitability of using the pre-operative LPM for post-operative simulations. Our multi-scale simulation indicated that the use of the estimated pre-operative impedances coupled with the real post-operative anatomy would lead to slightly higher left pulmonary flow (52.3% of caval flow). This was largely expected, considering the pre-operative data (almost equal left and right pulmonary resistances with perfectly balanced flow) and the surgical connection of the IVC exhibiting an extracardiac tube markedly directed towards the LPA. In contrast, the measured in vivo flows showed a TCPC flow repartition clearly favourable to the RPA (56.7% of caval flow). In our opinion, the unexpected clinically observed behaviour (post-operative Q_RPA higher than Q_LPA) demonstrates that the pulmonary resistances in the patient under investigation changed when passing from the BCPA to the TCPC configurations. Although the left and right post-operative resistances could not be evaluated in the present study because post-operative measurements of pressures were not available, our results suggest that R_tot-r of the patient became lower than R_tot-l after the TCPC. During the month that elapsed between the surgery and the MR measurements, individual pulmonary resistances probably adapted to the new fluid dynamic configuration, though we cannot deduce whether R_tot-r had decreased or R_tot-l had increased. Looking at the streamlines obtained from the simulation with pre-operative pulmonary impedances (‘predicted’ in figure 8), it appears that only a small fraction of the IVC flow is directed towards the RPA. This situation, which is representative of the period immediately after the surgery, may have led to pulmonary arteriovenous malformations (AVMs) in the right lung, and thus to a decrease in the right lung resistance, as appears from the ‘MR-based’ simulation. However, AVM aetiology remains largely unanswered.

Along the same lines, a recent study [28] proved that pathological flow alters the balance of factors responsible for the pulmonary vascular tone. Indeed, it seems that both high and low shear stresses associated with a non-physiological pulmonary flow may favour prolonged vasoconstriction and enhanced vascular resistance, owing to a lower production of vasodilators and a higher expression of contractile proteins. Moreover, animal and clinical studies provide evidence of pulmonary vascular resistance modifications after Fontan repairs [29,30]. Local abnormal flows, as may occur in patients with surgical corrections of congenital heart diseases, might selectively cause mid/long-term adaptation processes in the different pulmonary branches, thus varying local and global pulmonary resistances. Hence, vascular adaptation mechanisms should be included in the multi-scale models for use in virtual surgery. In a very recent study [31], the short-term responses of the heart, coronary vascular beds and arterial system to physiological changes owing to light exercise have been investigated in a multi-domain closed-loop model of the cardiovascular system. Conversely, to the best of our knowledge, mid/long-term adaptation processes have not been taken into account in CFD patient-specific models for virtual surgical planning.

In conclusion, although the analysis was conducted on a single patient, and model simplifications were introduced (namely, rigid vessel walls, and respiratory effects were disregarded), the present study indicates that:

• — patient-specific pre-operative models for simulating cavopulmonary connection fluid dynamics can be created on the basis of the routine clinical data—nevertheless, measurement uncertainties (pressure and flow data) should be carefully managed;

• — the pre-operative models should be built according to a multi-scale approach, including both a three-dimensional geometry of the investigated surgical region and a simplified, patient-specific description (e.g. LPM) of the other parts of the circulation;

• — the (pre-operative) creation of the post-operative three-dimensional model simulating the surgical connection of a vessel or synthetic tube is difficult since vascular distortion probably occurs;

• — the results of post-operative in silico simulations and the prediction of both local and global haemodynamics may be significantly worse if vascular adaptation processes are not considered.

Virtual planning of surgical corrections, despite its rapid improvements and increasing popularity in recent years, still appears to be a very challenging task. In particular, a deep understanding of adaptive and auto-regulatory phenomena seems necessary to make these models applicable to realistic scenarios in the treatment of congenital heart disease.

A lot of detailed clinical information needs to be collected both pre- and post-operatively. The young age of the patients and the relative invasiveness of the examinations severely limit this necessity. For this reason, a Trans-Atlantic Network of Excellence has been recently granted by Fondation Leducq to explore and possibly define corrective actions to address this important point in the treatment of congenital heart disease.