Multi-scale simulations of the dynamics of in-stent restenosis: impact of stent deployment and design

Abstract

Neointimal hyperplasia, a process of smooth muscle cell re-growth, is the result of a natural wound healing response of the injured artery after stent deployment. Excessive neointimal hyperplasia following coronary artery stenting results in in-stent restenosis (ISR). Regardless of recent developments in the field of coronary stent design, ISR remains a significant complication of this interventional therapy. The influence of stent design parameters such as strut thickness, shape and the depth of strut deployment within the vessel wall on the severity of restenosis has already been highlighted but the detail of this influence is unclear. These factors impact on local haemodynamics and vessel structure and affect the rate of neointima formation. This paper presents the first results of a multi-scale model of ISR. The development of the simulated restenosis as a function of stent deployment depth is compared with an in vivo porcine dataset. Moreover, the influence of strut size and shape is investigated, and the effect of a drug released at the site of injury, by means of a drug-eluting stent, is also examined. A strong correlation between strut thickness and the rate of smooth muscle cell proliferation has been observed. Simulation results also suggest that the growth of the restenotic lesion is strongly dependent on the stent strut cross-sectional profile.

1. Introduction

Coronary heart disease (CHD) is the most common cause of death in Europe, being responsible for approximately 1.9 million deaths per year [1]. Atherosclerosis, the most common form of CHD, is associated with the build-up of atheromatous plaque within the wall of the coronary arteries. Presence of such plaques may lead to a significant decrease in luminal cross-sectional area (a stenosis) and reduce the blood supply to the heart. The current intervention of choice for many symptomatic patients is stent-assisted balloon angioplasty. In this procedure, a tubular mesh-like structure (stent) is deployed within the vessel at the site of the stenosis. Once deployed, the stent behaves as a mechanical scaffold, compressing the plaque and eliminating the possibility of vessel collapse. While this generally results in a successful outcome, in-stent restenosis (ISR), an excessive re-growth of tissue within the stented segment of the artery associated with the injury caused by the stent deployment, is still a negative aspect of the procedure [2–4]. The process of restenosis involves a cascade of complex biological and physical interactions that are activated in response to stent-induced arterial wall damage. Denudation of endothelial cells and the rupture and/or stretch of the elastic laminae, media and adventitia after stent deployment act as stimuli to initiate the development of ISR [5]. The process can be categorized as a sequence of events starting with an initial instantaneous thrombosis formation in response to arterial injury and progressing to an inflammatory stage, granulation tissue development, smooth muscle cell proliferation, extracellular matrix (ECM) deposition, and ultimately remodelling of the neointima and vascular wall [6,7]. A detailed description of the underlying biological processes has been presented by Evans et al. [8].

It is widely accepted that the development of restenosis is regulated by a number of key factors, including the severity of injury, inter-strut spacing, strut thickness, stent length, stented segment compliance [7,9,10]. All of these factors have profound effects on flow haemodynamics and wall shear stress (WSS) distribution across the stented segment [11,12]. A decreased restenosis rate has been observed with the use of drug-eluting stents (DES), which are coated with anti-mitogenic or anti-proliferative drugs to inhibit smooth muscle cell proliferation and neointimal growth [13]. Despite a growing trend for the use of DES as the stent of choice in comparison with bare metal stents (BMSs), late in-stent thrombosis (IST) and lack of re-endothelialization are the major drawbacks associated with the use of DES [9,13,14].

The degree of injury caused by the implantation of a stent has been observed as an independent determinant to estimate the amount of restenosis in an experimental study carried out in pigs [15]. The extent of vascular injury is estimated from the penetration depth of the struts into the tissue; a deeper deployment depth implies a larger injury. In the current study, we have used the Gunn Injury Score system that defines the degree of injury according to the angle of the internal elastic lamina (IEL) at the point of strut impact, the rupture of the IEL or, in the extreme, rupture of external elastic lamina (EEL). Gunn applied this to categorize injury arising from the deployment of a stent in the porcine implant model [16].

In previous work, we modelled ISR as a complex multi-scale system [8], and realized a coupled multi-scale simulation of a simplified version of this model in two dimensions using porcine coronary arteries [17]. In the present work, the overall dynamical response of the porcine coronary artery ISR model is studied in detail, as well as the influence of different stent geometries on the simulated ISR. The rationale for choosing to simulate ISR in a porcine artery is based on the fact that an extensive literature from clinical and experimental studies performed on pigs is available to us, whereas there is no similar time-series data available for human implants. Moreover, the pig exhibits similarities with the human case in terms of coronary anatomic structure and vessel sizes and, most importantly, in terms of the response to arterial injury caused by the penetration of a stent into the vessel wall [18]. The primary difference between the pig and human is the rate of ISR development. In pigs, the normal time span of restenotic lesion development is about 60 days with a peak smooth muscle cell proliferation at around 20 days, whereas in the human, ISR development extends to six months with the proliferation rate peaking at around two months [18,19]. There is some literature showing the influence of strut thickness on the progression of angiographic and clinical ISR in humans, but such data are relatively sparse [10,20–22]. The main conclusion from clinical trials is the impact of strut thickness. This is an independent predictor of ISR, with thin struts resulting in a lower incidence of restenosis as well as lower late luminal loss when compared with the results observed for thick struts [10,12,22].

In the current study, we report results produced by our two-dimensional multi-scale ISR model. The effect of strut thickness on the development of restenosis was investigated using two BMSs of different strut thickness. The deployment depth was varied, and the number of neointimal cells was measured as a function of time. The resulting growth curves were fitted to a logistic function, and the simulated ISR characterized by just two parameters. The percentage of proliferating vascular smooth muscle cells (SMCs) was also measured as function of time. Where possible, our results were compared against the available porcine model in vivo dataset. The paper concludes with a discussion on the validity of the current model, and suggestions for improvements. The implications of this work for further understanding of ISR are also discussed.

2. Computational model

ISR is a multi-science multi-scale phenomenon linking a series of processes which can be described in terms of biology, physics and chemistry. Evans et al. [8] formulated an extended multi-scale model for ISR based on the Complex Automata (CxA) paradigm [23–25], where a multi-scale system is modelled as a collection of single-scale models coupled through the scales. Caiazzo et al. [17] simplified the original model for ISR to one where single-scale models for blood flow, vascular SMCs and drug diffusion communicate with each other via smart conduits. These single-scale models operate on different temporal and spatial scales. A MUltiScale Coupling Library and Environment (MUSCLE) was used to set up and launch the simulation as a CxA [26]. Here we consider the two-dimensional version of this model.

We will now briefly describe the model for ISR. For all details, we refer to Caiazzo et al. [17]. During the stent deployment process, stretch was induced in the vessel wall by deploying a stent, modelled as a single two-dimensional strut, to a specific depth into the vessel wall. Next, the IEL was ruptured based on the hoop strain and longitudinal strain threshold criteria. As a result of IEL rupture, vascular SMCs were exposed to the blood flow and, according to contact inhibition criteria in the SMC biological model, only exposed cells are able to proliferate. Blood flow was modelled as a homogeneous, incompressible, Newtonian fluid using a Lattice Boltzmann method. SMC hyperplasia in a non-axisymmetric geometry was simulated via an agent-based model where each SMC is modelled as an individual agent. A biological solver controlled the progression of SMC proliferation, which was regulated through a cell cycle based on a set of biological rules. The biological rules were based on contact inhibition (presence of neighbouring cells), WSS thresholds and, in the case of a DES, drug concentration thresholds. A physical solver, based on agent–agent interaction potentials, was used to simulate the structural dynamics of the SMCs. The process of drug elution and subsequent diffusion of the drug into the vessel wall was modelled by solving an anisotropic diffusion equation using a finite difference scheme. A detailed description of all single-scale models as well as their mutual couplings has been published by Caiazzo et al. [17].

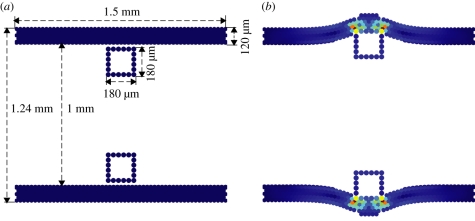
In the present study, we considered a vessel of segment length 1.5 mm and width 1.24 mm with a wall thickness of 120 µm as a benchmark geometry (figure 1). Wall thickness was obtained from an existing archive of in vivo porcine data [16]. Models were prepared by deploying two, square cross-section, bare metal struts, into the vessel wall (figure 1). We examined the influence of strut thickness and cross-sectional profile on neointimal proliferation. Where strut thickness is denoted as D, a thin strut has a strut thickness of D = 90 µm, whereas the thicker strut has a thickness of D = 180 µm. Both struts were deployed into the vessel at depths over the range of 70–130 µm. We also considered a square DES strut deployed to a depth of 90 µm. Additionally, we changed the shape of the bare metal strut to a rounded strut with a base length of 180 µm and height of 90 µm.

Figure 1.

SMC domain. (a) Domain before deployment of thick stent struts (D = 180 µm). (b) Domain after strut deployment to a depth of 90 µm into the tissue (SMCs coloured according to the structural stress).

WSS is known to be a key parameter in the process of re-endothelialization and neointimal formation, resulting in a higher neointimal growth in the regions of low WSS [27,28]. Steady-state blood flow simulations, with a constant flow rate, were carried out using a fluid of constant viscosity, μ = 4 mPa.s, density ρ = 1000 kg m⁻³ and Re = 120. The rationale for maintaining a constant flow rate is based on the normal physiological reaction of the cardiovascular system to a moderate stenosis. This assumption served to increase the WSS as the lumen narrowed and fits well with the published theory that a blood vessel remodels in response to changes in fluid forces until these forces are normalized [29,30].

3. Results

A previous publication presented preliminary results of the two-dimensional ISR model [31] obtained at a very early stage of model development. Further tuning of the model parameters such as WSS, drug concentration and contact inhibition was carried out within the COAST (www.complex-automata.org) consortium (data not shown). This parameter tuning allowed us to investigate the relationship between the injury index and the restenotic lesion growth by exploring the predictive power of our model.

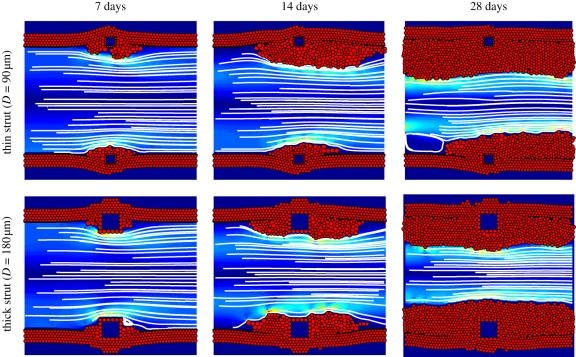
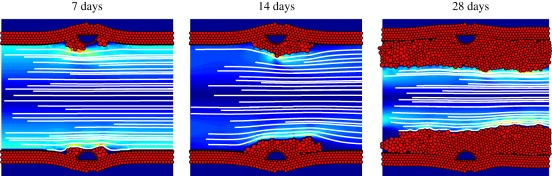
In the present study, we performed simulations for two strut sizes (D = 90 and 180 µm) deployed at four different depths (70, 90, 110 and 130 µm). Each simulation was repeated five times to obtain the mean and standard deviation of the neointimal growth measurement. Figure 2 shows a detailed visualization of the simulated ISR response as a function of time post deployment, for small and large struts, deployed to a depth of 90 µm. While there is a considerable smooth muscle cell response in both cases, the thicker strut (D = 180 µm) produced a larger amount of neointima when compared with the thin strut (D = 90 µm). An asymmetric proliferation was observed between the upper and lower halves of the thin strut geometry (figure 2). This asymmetry occurs mainly owing to the random selection of the biological state of each cell after the stent deployment.

Figure 2.

Simulation results for the thin strut (D = 90 µm) and the thick strut (D = 180 µm), both deployed to a depth of 90 µm, at 7, 14 and 28 days after stent deployment. The SMCs are shown as red circles and the square struts as blue squares surrounded by red obstacle agents. In the lumen, blood flow is visualized by streamlines, and the colours represent the shear stress, ranging from 0 Pa (dark blue) to 60 Pa (dark red).

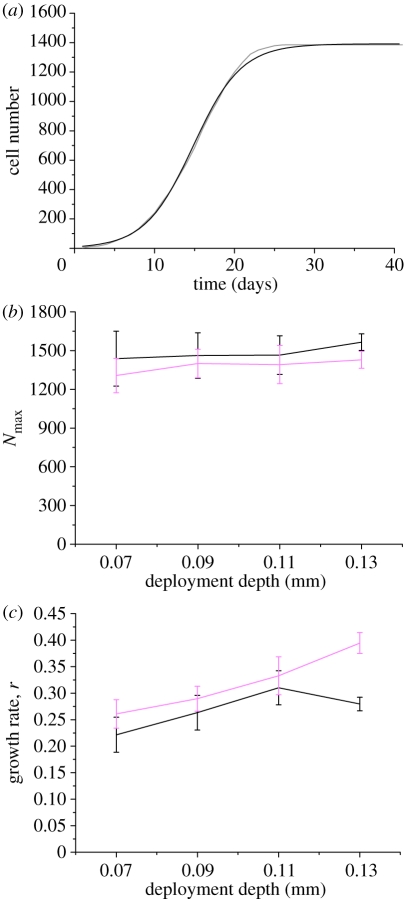
For each simulation, we measured the number of neointimal SMCs (N) as a function of time (t) after stent deployment. Figure 3a shows N(t) for a thick strut (D = 180 µm) deployed at a depth of 90 µm. The dynamics of the simulated ISR response bear a close resemblance to a logistic growth curve, i.e. an initial exponential growth phase, followed by a slowing down of the growth and final settling to a maximum number of neointimal cells N_m. In all cases studied, the number of neointimal cells as function of time exhibited this type of dynamics (data not shown).

Figure 3.

(a) Nonlinear logistic curve-fitting of neointimal cell number from a thick strut (D = 180 µm; grey line) deployed at a depth of 90 µm. Logistic fit represented as black line. (b) Curve-fitting parameters N_max and (c) growth rate ‘r’ are plotted with respect to different deployment depths for both strut sizes. Black line, D = 90 µm; pink line, D = 180 µm.

In logistic growth, a population is modelled as

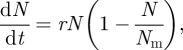3.1

where r is the growth rate. If N₀ is the initial number of cells, equation (3.1) can be solved analytically, yielding

3.2

We performed nonlinear fits of the logistic growth dynamics (equation (3.2)) to the measured neointimal growth, resulting in fitted values for the model parameters N₀, N_m and r. The curve-fitting was carried out using the Levenberg–Marquardt algorithm [32] to optimize parameter values in an iterative process. We kept N₀ = 10 based on our assumption that the SMCs, which are exposed to blood after the removal of endothelial cells, act as proliferative neointimal cells. In the current simulations, we observed that for the majority of cases, the number of exposed SMCs was approximately 10 ± 2. We therefore chose N₀ = 10 as an average initial cell number to perform curve-fitting. For the case reported in figure 3a, this fitting procedure resulted in N_m = 1392 and r = 0.33. The best-fit curve has a very close agreement to the measured data and is also shown in figure 3a. The quality of the fitted curve was calculated by means of an R² test, this gave a value of R² = 0.997. Similar good fits were obtained for all other experiments (data not shown). Using this procedure, we were able to better study and compare the simulated ISR as a function of parameters such as deployment depth, and strut size or shape. The results are summarized in figure 3b,c, which shows N_m and r as a function of deployment depth for both strut sizes.

Figure 3b demonstrates that the final endpoint of restenosis is approximately constant (±10%) for both strut sizes. We obtained a standard deviation by averaging the results from five runs per parameter set (deployment depth, strut thickness). This was used as an input to the fitting routine. The combined error (from standard deviation and fitting error) is plotted as an error bar for each simulation set. The major difference that can be observed from figure 3b is the effect of the thin strut, which results in a higher number of neointimal cells in comparison with the thick strut. The fitted growth rates including error bars from thin strut simulations were plotted and compared with the growth rate curve for neointimal formation in thick strut simulations (figure 3c). The assessment of the simulation results demonstrates that a thinner strut results in slightly higher N_max (approx. 100–150 SMCs) but lesser growth rate when compared with thicker strut. This difference in the N_max is owing to the fact that the thin strut occupies less space and provides more room for SMCs to proliferate. Moreover, the data also suggest that deployment depth correlates with the growth rate; when the strut is deployed further into the vessel wall, a larger neointimal growth rate is observed. The only exception to this was for a thin strut deployed to a depth of 130 µm.

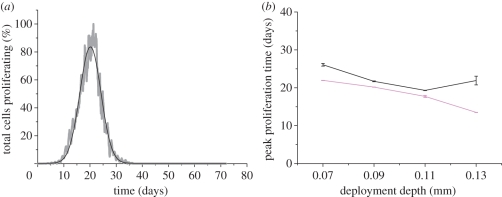
Another useful metric for use in qualitative comparison, is the normalized peak absolute growth fraction (NPAGF) as defined by Schwartz et al. [19]. NPAGF is the product of growth fraction (cells in mitosis phase/total cell number), divided by the maximum value of growth fraction across the series. This value indicates the time point at which the greatest numbers of cells are proliferating. Figure 4a shows the NPAGF curve for a thick strut, deployed to a depth of 90 µm. It is clear from this curve that peak proliferation occurs at around 22 days.

Figure 4.

(a) Normalized peak proliferation curve from the thick strut (D = 180 µm; grey line) deployed at 90 µm. The fitted Gaussian curve (black line) highlights the time at which maximum proliferation occurred. (b) Peak proliferation time plotted against deployment depth for both strut sizes. Black line, D = 90 µm; pink line, D = 180 µm.

The fluctuations seen in the NPAGF curve are owing to the presence of discrete events (mitosis of cells). To better estimate the time where maximum proliferation is occurring, we fitted a Gaussian function (figure 4a) to obtain peak proliferation time (T_peak). Figure 4b shows the resulting peak proliferation time as a function of deployment depth. A downward trend of the peak proliferation time was observed with an increase in the deployment depth for both strut thicknesses, except the thin strut that was deployed at 130 µm. Analysis of figure 4b also suggests that the thick strut is associated with a lower peak proliferation time at all deployment depths.

We also examined the effect of a drug eluted from the thick strut (D = 180 µm) deployed at a depth of 90 µm. The results were obtained by applying the curve-fitting techniques explained above (table 1). A nominal drug concentration threshold of 0.4 was used. For more details about drug concentration, we refer to Caiazzo et al. [17]. Data from a DES simulation indicate a delay in the overall neointimal growth process when compared with the results obtained for a similar bare metal strut. Table 1 also includes the results for a bare metal strut with rounded cross-section deployed to a depth of 90 µm. A reduction in the growth rate, resulting in a late peak proliferation time was observed when compared with bare metal square strut. The morphological images from rounded strut simulation are also shown in figure 5 in order to allow the reader to understand the strut shape and its effect on the neointimal growth.

Table 1.

Results from different strut type (BMS and DES) and strut shape (square and rounded).

strut type (D = 180 µm)	Nmax	growth rate (r)	Tpeak (days)
square bare metal	(1.4 ± 0.11) × 103	0.29 ± 0.024	20 ± 0.03
square drug eluting	(1.3 ± 0.10) × 103	0.22 ± 0.016	26 ± 0.36
rounded bare metal	(1.4 ± 0.13) × 103	0.23 ± 0.022	25 ± 0.33

Figure 5.

Simulation results of a rounded strut deployed at 90 µm, showing neointimal growth after 7, 14 and 28 days after the stent deployment.

3.1. In vivo dataset

We have access to a unique archive of histological sections from stented porcine coronary arteries collated from a number of experimental studies over the last decade [33–38]. The archive contains transverse sections from over 500 porcine arteries in which stents of several different designs have been deployed. For the present study, we selected transverse sections derived from more than 50 arteries harvested at 6 h, 14, 21 and 28 days after the deployment of a bare metal BiodivYsio stent. An average of 10 struts was present in each section. Each of these struts was individually scored using the Gunn Injury Score [16] according to the degree of injury they imposed on the artery. These data were used to generate a database relating the degree of injury caused by stent strut deployment, to the neointimal thickness observed at the various time points after stenting. Figure 6 summarizes these results, showing averages and standard deviations of the full set of available histological measurements. The time points in figure 6 were determined by the availability of samples. The neointimal thickness measured at 6 h does not specifically correspond to a SMC-rich neointima, but represents a measurement of thrombus which forms immediately after stent deployment. Analysis of the in vivo dataset shows that an increase in injury score correlates with increased neointimal thickness (figure 6). The decrease at 28 days could be related to vessel remodelling, a process which is not considered in our current computational model.

Figure 6.

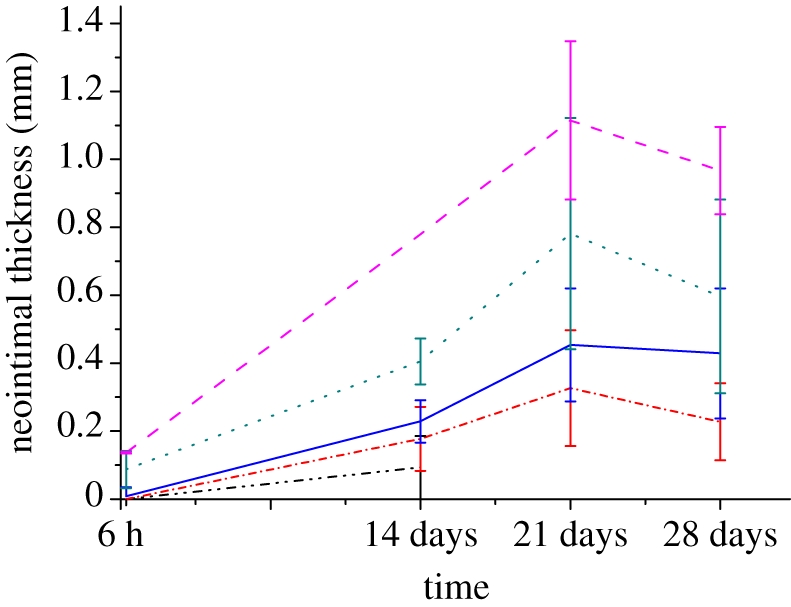
Neointimal thickness as a function of time after stent deployment. The mean and standard deviation of the neointimal measurements are plotted at 6 h, 14, 21 and 28 days post-stent deployment. The data show a positive correlation between neointimal thickness and the Gunn injury scores. Black dashed-dotted line, injury score 0; red dashed-dotted line, injury score 1; blue solid line, injury score 2; green dotted line, injury score 3; pink dashed line, injury score 4.

4. Discussion

We report a series of simulations investigating the relationship between an injury index (in our case, deployment depth) and ISR growth. Despite the limited amount of quantitative literature available to model such complex phenomena, our results show a good qualitative correlation with the available experimental, clinical and in vivo data, as will be discussed below. We showed results from simulations deploying two different strut sizes at four deployment depths into the tissue (figure 3) and interpreted the simulation results with two parameters using logistic curve fitting, summarizing the neointimal growth curves in terms of a growth rate ‘r’ and a maximum of smooth muscle cells N_m.

As there are no experimental or clinical investigations available measuring detailed time-response curves as illustrated in figure 3, and showing the impact of injury on the growth rate of neointima in the initial few weeks, it is far from trivial to compare our model results against in vivo data. The effect of strut thickness on ISR has been assessed in human clinical trials [20–22,39]. The observed angiographic and clinical restenosis growth measured at six months' follow-up suggests that a thicker strut is associated with greater neointimal growth. However, this effect was not observed in the output of simulations shown in figure 3b where the number of smooth muscle cells (N_m) is almost constant, irrespective of strut size. In our model, SMCs proliferation is inhibited when the WSS exceeds a preset threshold. As the blood flux through the vessel is kept constant, a decreasing lumen diameter owing to ISR results in a gradual increasing WSS, and the threshold value is reached at a more or less constant diameter (see also figure 2), independent of strut size or deployment depth. As it is clear from both clinical data and the porcine data reported in figure 6, such constant endpoint is not realistic and is a flaw of our current model. Despite this obvious problem in the long-term dynamics of our model, it does provide more insight to the initial short-time dynamics and provides the capability for investigating different hypotheses. According to our simulation results, a thicker strut results in a faster neointimal growth (figure 3c) in the initial few weeks, which might explain the greater neointimal growth reported in clinical trials at six months post implantation.

Schwartz et al. [19] published NPAGF data calculated for several studies carried out in rats, pigs and humans. There is an excellent agreement when we compare the values of NPAGF from the computational output (figure 4a) to those published by Schwartz et al. As it is not possible to determine the strut deployment depth or injury level achieved in the porcine model used by Schwartz to generate the data, it is difficult to make a direct comparison. However, the values of NPAGF calculated from our simulation data are comparable to those produced by Schwartz, showing a peak in proliferation at around 20 days (figure 4a). The lack of detail provided by Schwartz regarding the precise experimental conditions under which the data were generated highlights the need for better quantitative experimental data regarding IEL rupture and the need for improved documentation of experimental conditions. The most apparent qualitative difference in comparison with Schwartz' data is the asymmetry of the curve where a long tail has been observed by Schwartz, showing that the proliferation process continues for a longer period. This is not the case in our model where we commonly observed a symmetrical curve. This difference could be in part owing to our stopping conditions where an increase in the WSS threshold stops the whole process of neointimal thickening. The simulation results also predict that the peak proliferation occurs earlier in case of deep injury/stretch (figure 4b).

Another important finding of the current study is the effect of deep injury caused by the stent on the development of neointimal growth. If we ignore the limitation of the final endpoint, then the computational output follows the same qualitative patterns as the in vivo data; the degree of SMC proliferation increases with the degree of injury caused by stent deployment (figures 3c and 6). There is one exception for a thin strut (D = 90 µm) where a reduction in the growth rate was observed at a deployment depth of 130 µm. The in vivo data (figure 6) indicate a decrease in the neointimal thickness measured after 28 days. This may be related to vessel remodelling; a feature which is not captured in the present computational model. Moreover, a clear correlation of this decrease with our simulation output is currently restricted owing to the endpoint limitation. We aim to reinvestigate this after implementing a remodelling kernel in our CxA simulations.

Endothelial cell injury and disfunction play a critical role in the pathogenesis of several cardiovascular diseases including atherosclerosis [40]. It is generally accepted that injury caused by stent deployment results in the denudation or dysfunction of endothelial cells [41] and re-endothelialization has been observed to play an important role in halting the progression of stent-induced neointimal growth [27]. In the current scenario, our model is dependent on a premise that the initial injury/stretch instigates the process of neointimal growth [5,16] and that the growth process stops in the presence of high WSS. WSS has been identified as a key player in the process of re-endothelialization and neointimal formation. Delayed re-endothelialization and greater neointimal growth seem to be associated with regions of low WSS [27,28]. The effect of WSS on the ISR has also been investigated by De Santis et al. [42], where a WSS-based algorithm was used to simulate vessel remodelling. Results show that a high value of WSS was observed throughout the final remodelled geometry. This investigation highlights the importance of WSS with respect to ISR and describes WSS as a valuable predictor of the final lumen geometry. This effect can also be observed in our simulations where a high WSS threshold stops the whole neointimal growth process. It should be noted however that in the current study we have assumed steady flow conditions. A next step will be to study SMC behaviour under pulsatile flow conditions, taking into account the oscillatory shear by defining an appropriate oscillatory shear index threshold.

DES have been shown to reduce restenosis [13]. This effect is quite prominent in our simulations (table 1) showing an inhibition of SMC proliferation, which results in a delayed response of the whole process of neointimal growth. Preliminary results from a round cross-section BMS strut also showed a decrease in the growth rate, resulting in a delayed neointimal growth. A reason suggested to explain this delayed growth is that the rounded shape results in a more stable flow within the artery lumen thus minimizing or eliminating the effect of flow recirculation [9].

In summary, our single-scale models, especially the SMC model, are still at an early stage of development and require further improvement. In the near future, we will also run simulations with the three-dimensional version of the model (thus taking into account realistic shapes of the stent, and shape and curvature of the vessel), coupling more single-scale kernels (e.g. thrombosis, cell signalling, vessel remodeling, etc.) to capture, more closely the behaviour of this complex phenomenon. Such three-dimensional simulations will require high-end distributed multi-scale computing capabilities, as currently being developed within the MAPPER project (www.mapper-project.eu). However, despite the need for an improved three-dimensional model, we should not disregard the importance and relevance of the current two-dimensional model. We will continue to use the two-dimensional model for rapid testing of new hypotheses. Further refinement of this will enable us to test different hypotheses and provide greater insights into the time-dependent behaviour of ISR. Refinement of the current two-dimensional model will include implementation of pulsatile flow as well as the integration of an improved tissue model containing additional levels of complexity. For example, addition of an endothelium, ECM and the EEL. It may even be useful to investigate the effect of vessel remodelling in the two-dimensional model as the effect of this is not well known.

Fitting the data to a logistic growth function helped us to characterize the dynamic response in terms of growth rate. Although we do not claim that ISR is a logistic growth process, this characterization in terms of r and N_max may prove useful in the preclinical testing of stent designs, and may eventually provide a predictive tool for use in the clinical setting. We will therefore continue to calculate the restenotic lesion growth rate r as a function of strut thickness, deployment depth and strut shape. Experimental studies providing a measure of ISR as a function of time would allow further validation of our models, and more importantly, would enable us to test the hypothesis that the complex ISR response can be characterized by just a small set of parameters, as in logistic growth.