A thermodynamical model for stress-fiber organization in contractile cells

Abstract

Cell mechanical adaptivity to external stimuli is vital to many of its biological functions. A critical question is therefore to understand the formation and organization of the stress fibers from which emerge the cell’s mechanical properties. By accounting for the mechanical aspects and the viscoelastic behavior of stress fibers, we here propose a thermodynamic model to predict the formation and orientation of stress fibers in contractile cells subjected to constant or cyclic stretch and different substrate stiffness. Our results demonstrate that the stress fibers viscoelastic behavior plays a crucial role in their formation and organization and shows good consistency with various experiments.

The ability of biological tissues to adapt and respond to external mechanical stimuli is at the heart of a variety of biological phenomena, such as morphogenesis,¹ wound healing,² or cancer dynamics.^{3, 4, 5} This behavior arises from the capacity of certain cells (i.e., fibroblasts) to generate a network of contractile stress fibers (SFs), which attach to the surrounding extra-cellular matrix (ECM) via focal adhesions (FAs). This dynamic structure enables cells to sense their mechanical environment and react to any changes in stretch, stress, or stiffness by applying contractile forces, which ultimately results in ECM deformation and remodeling.^{6, 7} Numerous experimental and theoretical efforts have been directed toward explaining the biophysical mechanisms underlying the structural reorganization of SFs in different mechanical environments.⁸ Experiments on epithelial cells and fibroblasts have demonstrated that contractility and SF density increase with substrate stiffness while SF alignment is strongly influenced by substrate anisotropy.^{9, 10} In addition, SFs were shown to align in or perpendicular to the direction of maximum stretch respectively for constant or cyclic stretch.^{11, 12, 13} To explain the latter, Wang and co-workers¹⁴ proposed a physical model in which perturbations in the SFs strain energy are assumed to cause their disassembly and were able to accurately predict SFs orientations in the case of uniaxial cyclic stretch. More recently, Stamenovitch et al.¹⁵ used the Maxwell stability criteria on the global mechano-chemical energy of the SF-FA complex to find SFs orientation in cells subjected to constant uniaxial stretch. While those models were successful at capturing the alignment of SFs with respect to stretch, the effect of the substrate stiffness was not considered.

The present work addresses this issue by formulating a general thermodynamical model that captures key mechanisms of SF organization in contractile cells on substrate of variable stiffness and subjected to arbitrary stretching conditions. The model is based on the experimental observations that contractile stress promotes assembly and stabilizes existing SFs^{16, 17} while the elastic deformation of SFs causes their disassembly.¹⁸ We show here that by considering these two fundamental mechanisms along with the viscoelasticity of SFs,¹⁹ it is possible to predict the density and principal orientation of SFs in cells that are subjected to a variety of mechanical environments.

For the purpose of this study, a cell is considered as a solution (the cytosol) in which a population of soluble contractile units isotropically distributed (made of actin and myosin) coexist with their polymerized form (SFs), consisting of long filaments of polar volume fraction ${\phi }_{\alpha }^{\mathit{sf}}$, with α the angle that characterizes the direction of SFs. The chemical stability of unassembled and assembled contractile units may be written in terms of their respective chemical potentials μ^cu and ${\mu }_{\alpha }^{\mathit{sf}}$ as follows:^{20, 21, 22}

$${\mu }^{\mathit{cu}}={\mu }_0^{\mathit{cu}}+k\mathrm{\Theta }\ln {\phi }^{\mathit{cu}},$$ (1)

$${\mu }_{\alpha }^{\mathit{sf}}={\mu }_0^{\mathit{sf}}+k\mathrm{\Theta }(\ln {\phi }_{\alpha }^{\mathit{sf}}+a_{\mu }{\left(\frac{{\phi }_{\alpha }^{\mathit{sf}}}{{\phi }^{*}}\right)}^{\frac{5}{4}})+{\mu }_{\alpha }^{\mathit{sf},\mathit{mech}},$$ (2)

where k is the Boltzmann constant, Θ is the absolute temperature, and α denotes quantities evaluated in the α-direction. The first term in Eqs. 1, 2 denotes the reference chemical potential, while the second term represents the entropy of configuration. The overlapping volume fraction φ* and the a_μ coefficient are correction terms for the mixing entropy of semi-dilute polymers, which have not been determined for actin solutions. They are neglected in the present work since their role is not expected to impact the general results of this study. To capture the influence of stress and strain on SF stability, the chemical potential ${\mu }_{\alpha }^{\mathit{sf}}$ possesses a mechanical contribution ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ (Ref. ²⁰)

$${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}=\frac{V_{\mathit{cu}}}{T}{\int }_0^T(-{\sigma }^{*}{\varepsilon }_{\alpha }+\frac{1}{2}{E}_{\mathit{sf}}(\omega ){\varepsilon }_{\alpha }^2)\mathit{dt},$$ (3)

where T is a stretch cycle period and V_cu is the volume of a contractile unit. The first term in the integral corresponds to the lost free energy due to acto-myosin contraction (σ*) and captures the fact that contractility has a stabilizing effect on SFs, as found in experimental studies.^{16, 17} In contrast, the second (positive) term contributes to SFs dissociation due to an increase in their elastic energy during stretch ε_α in direction α. Furthermore, a key component of the proposed model is the dependency of elastic modulus E_sf on the stretching frequency ω to capture the viscoelasticity of SFs. Here, we describe SF stiffening with loading frequency ω with a function E_sf(ω) of the form²³

$$E_{\mathit{sf}}(\omega )=E_l+E_v\log (1+9\omega ),$$ (4)

where E_l and E_v characterize the static and dynamic stiffnesses of SFs at frequency ω = 1 Hz, respectively. Without loss of generality, we assume here that cells are subjected to sinusoidal strain variation ${\varepsilon }_{\alpha }={\overline{\varepsilon }}_{\alpha }+{\tilde{\varepsilon }}_{\alpha }\cos (2\pi t/T)$, which, when substituted in Eq. 3, leads to the following mechano-chemical potential:

$${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}=\frac{(E_l+E_v\log (1+9\omega ))}{2}({\overline{\varepsilon }}_{\alpha }^2+\frac{{\tilde{\varepsilon }}_{\alpha }^2}{2})-{\sigma }^{*}{\overline{\varepsilon }}_{\alpha }.$$ (5)

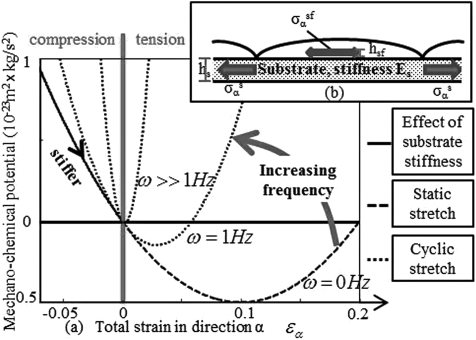
The above expression describes how contractile stress as well as static and cyclic stretch influences the chemical stability of SFs (Fig. 1a). At high frequency (1 Hz cyclic stretch), SFs appear stiffer, and the disassembling elastic energy $1/2E_{\mathit{SF}}(\omega ){\varepsilon }_{\alpha }^2$ is predominant over the contractile work. A rise in the stretch amplitude therefore increases the mechano-chemical potential ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ and has a disassembling effect on the SFs. Inversely, at a low frequency (ω → 0), softer SFs emphasizes the stabilizing role of contractile stress σ*, resulting in SF stabilization with increasing stretch. However, as stretch increases above a critical value at which ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ is minimum $({\varepsilon }_{\alpha }^{\mathit{crit}}={\sigma }^{*}/E_l)$, the stored elastic energy becomes dominant and SFs fall into a disassembly regime.

Figure 1.

(Color online) Mechano-chemical potential ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ in direction α as a function of strain for different stretch frequencies (a). SFs assemble in direction α when ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ decreases, and disassemble when ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ increases. Mechanical equilibrium at angle α (b).

To assess the behavior of our thermodynamical model, we consider a system made of a confluent population of cells adhering to a homogeneously deforming thin substrate (Fig. 1b) whose linear elasticity is governed by its Young’s modulus E and Poisson’s ratio ν. In these conditions, the state of any material point in the system is given by chemical and mechanical equilibrium as

$$(a){\mu }_{\alpha }^{\mathit{sf}}={\mu }^{\mathit{cu}}\forall \alpha \in [0,\pi ],(b)\sum _{\beta =s,\mathit{sf}}{\sigma }^{\beta }=\overline{\sigma },$$ (6)

where $\overline{\sigma }$ denotes the externally applied stress and the internal stress arises from a combination of substrate elasticity and SF contractility. Following standard elasticity theory, the components of the substrate stress are written as ${\sigma }_{\mathit{ij}}^s=E/(1+\nu ){\epsilon }_{\mathit{ij}}+E\nu /((1+\nu )(1-2\nu )){\delta }_{\mathit{ij}}{\epsilon }_{\mathit{kk}}$, where δ_ij is the Kronecker delta. In contrast, the directional SF stress is evaluated in specific direction α and is comprised of both a contractile and a passive elastic components weighted by the polar volume fraction as follows: ${\sigma }_{\alpha }^{\mathit{sf}}={\phi }_{\alpha }^{\mathit{sf}}({\sigma }^{\star }+E_{\mathit{sf}}(\omega ){\varepsilon }_{\alpha })$. Using expressions (1) and (2) in (6) and invoking mass conservation between SF and unassembled contractile units allows us to solve for the volume fraction of SF and soluble contractile units as follows:

$${\phi }_{\alpha }^{\mathit{sf}}={\phi }^{\mathit{cu}}\mathit{exp}(-\frac{{\mu }_0^{\mathit{sf}}-{\mu }_0^{\mathit{cu}}+{\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}({\varepsilon }_{\alpha })}{k\mathrm{\Theta }}),$$ (7)

$${\phi }^{\mathit{cu}}=\phi -\frac{1}{\pi }{\int }_0^{\pi }{\phi }_{\alpha }^{\mathit{sf}}d\alpha ,$$ (8)

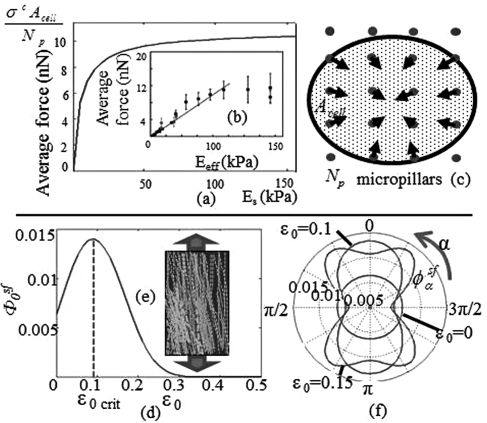
where φ is the total volume fraction of contractile units (assembled and unassembled) in the cell (taken to be 5% in this paper). These nonlinear equations can be solved numerically to determine the direction and density of SF in cells subjected to various mechanical environments. In our computations, a set of commonly accepted material parameters was chosen: the temperature is 310 K, the SF stiffnesses E_l and E_v are 100 kPa,²⁴ and the isometric contractile stress generated by a SF through acto-myosin interaction σ* is estimated to be 10 kPa (obtained with a tensile force of 300 pN (Ref. ²⁵) and a cross sectional area of 0.03 μm² (Ref. ²⁶)). Furthermore, SF contractile units are of the same length of a SF sarcomere (1μm) and of diameter 10 nm. The difference in the reference chemical potential ${\mu }_0^{\mathit{sf}}-{\mu }_0^{\mathit{cu}}$ is set to −4kΘ such that the average force on micropillars generated by the isotropic contractile stress of the cell σ^c = φ^sfσ^* on a very stiff substrate matches the one from,¹⁰ i.e., $\simeq 10-11\mathrm{nN}$.

We now propose to use the model to investigate the influence of substrate stiffness on cell contraction. Considering a free-standing isotropic substrate $(\overline{\sigma }=0)$ of thickness h_s and writing the projection of the mechanical equilibrium Eq. 6 in the α-direction, the strain ε_α is found to be

$${\varepsilon }_{\alpha }=\frac{-{\phi }_{\alpha }^{\mathit{sf}}{\sigma }^{\star }{h}_{\mathit{sf}}}{{\mathit{Eh}}_s/((1+\nu )(1-2\nu ))+{\phi }_{\alpha }^{\mathit{sf}}{E}_{\mathit{sf}}(\omega )h_{\mathit{sf}}},$$ (9)

where h_SF denotes the thickness of SFs. Using Eq. 9 in Eqs. 7, 8, one can find the density ${\phi }_{\alpha }^{\mathit{sf}}$ and contractile stress ${\phi }_{\alpha }^{\mathit{sf}}{\sigma }^{\star }$ in terms of substrate stiffness E. The model predicts a pronounced nonlinear relation between contractile stress ${\phi }_{\alpha }^{\mathit{sf}}{\sigma }^{\star }$ and substrate stiffness (Fig. 2a), characterized by an asymptotic value, which corresponds to SF volume fraction of 4% for very large substrate stiffness. This behavior is explained by the fact that contractile strain −ε_α decreases with substrate stiffness, which induces SF stabilization at high stiffness (see Fig. 1a). The predicted isotropic SF volume fraction and stiffness-contraction relation qualitatively matches with experimental trends¹⁰ as shown in Fig. 2b. Note that the discrepancy between the initial slopes of the curves likely arises from phenomena that are not accounted for in the present model, including bio-chemical signals and the strain dependency of sarcomere contraction.

Figure 2.

(Color online) Effect of an isotropic substrate stiffness increase on cell contractility as predicted by (a) the model and (b) experimental methods.¹⁰ (c) Schematic representation of experimental set up in Ref. 10, with $N_p\simeq 100$. The effect of constant stretch on the volume fraction of SF ${\phi }_0^{\mathit{sf}}$ in direction α = 0 is shown in (d), and (e) shows the orientation and disassembly of myofibrils (when overstretched)¹¹ with the arrows representing the direction of stretch. (f) is the angular distribution.

Let us now turn to the case where cells are subjected to substrate deformation. Experimentally, SFs in contractile cells such as fibroblasts or myofibrils have been shown to preferably align in the direction of stretch for constant loading.^{11, 27} To replicate the constant substrate stretch condition, we impose a state of uniaxial strain ${\overline{\epsilon }}_{11}$ to the substrate such that the angular stretch in a cell is written ${\varepsilon }_{\alpha }={\overline{\varepsilon }}_{\alpha }={\overline{\varepsilon }}_{11}((1+\nu ){\cos }^2(\alpha )-\nu )$. This expression is then substituted in Eqs. 7, 8 to derive the angular variation of SF density ${\phi }_{\alpha }^{\mathit{sf}}$. As shown in Fig. 2, the model predicts a strong alignment of SFs in direction of stretch (Fig. 2f). However, once the critical strain is reached, SFs lose stability and start disassembling with stretch. This behavior can be understood by observing the curve corresponding to ω = 0 Hz in Fig. 1a where ${\phi }_{\alpha }^{\mathit{sf},\mathit{mech}}$ successively goes through assembling and disassembling phases (Fig. 2d) as strain increases and has been experimentally observed in myofibrils (Fig. 2e).^{11, 28}

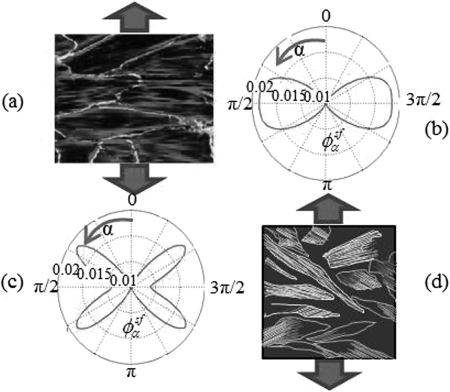
In the case of cyclic stretch, the angular strain in a cell becomes ${\varepsilon }_{\alpha }={\overline{\varepsilon }}_{\alpha }+{\tilde{\varepsilon }}_{\alpha }\cos (2\pi t/T)$ with ${\tilde{\varepsilon }}_{\alpha }={\tilde{\varepsilon }}_{11}((1+\nu ){\cos }^2(\alpha )-\nu )$ and ${\tilde{\varepsilon }}_{11}$ the applied cyclic uniaxial strain. Conversely to the case of constant stretch, experimental observations have shown that SFs align in the direction of minimum stretch, i.e., at a 90° angle for a substrate’s Poisson’s ratio ν = 0 (no transverse compression)¹² or at a 60° angle for incompressible substrates (ν = 0.5)¹³ (Fig. 3). Indeed, introducing the cyclic stretch term ${\tilde{\varepsilon }}_{\alpha }$ and a higher frequency ω in Eq. 5 increases the SF’s viscoelastic stiffness and the contribution of the elastic energy in the SF’s mechano-chemical potential ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ and results in a more convex function ${\mu }_{\alpha }^{\mathit{sf},\mathit{mech}}$ (curve corresponding to ω = 1 Hz in Fig. 1a). This causes the strain to have a disassembling effect on SFs and leads to high SF density in directions of minimum strain, i.e., 90° for ν = 0 and 60° for ν = 0.5. The predicted SF distributions in the case of cyclic stretching shown in Fig. 3 are amenable to direct comparison with the experimental images of Refs. ^{12, 13}.

Figure 3.

(Color online) Effect of cyclic stretching for ν = 0 (b) (experimental result (a) from Ref. 18) and ν = 0.5 (c) (experimental result (d) from Ref. 13).

To summarize, this Letter presented a thermodynamical model that aims at describing the formation and distribution of SFs when subjected to various mechanical stimuli. Model contributions are two-folds; first by incorporating a mechanical contribution into the chemical potential of SFs, the formulation enables a natural coupling between chemical stability and stress/strain states in SFs. Second, the approach revealed the importance of a viscoelastic description of SFs to accurately describe their rate-dependent behavior under constant or cyclic stretching. It also shows that, while choosing physiological parameters consistent with experimental data, the hypotheses by which SFs are stabilized by contractile stress and disassembled by their elastic energy give results that concur with experimental observations in all the cases tested.