Forced wave motion with internal and boundary damping

Abstract

A d’Alembert-based solution of forced wave motion with internal and boundary damping is presented with the specific intention of investigating the transient response. The dynamic boundary condition is a convenient method to model the absorption and reflection effects of an interface without considering coupled PDE’s. Problems with boundary condition of the form $\frac{\partial w}{\partial z}+\tilde{\alpha }\frac{\partial w}{\partial t}=0$ are not self-adjoint which greatly complicates solution by spectral analysis. However, exact solutions are found with d’Alembert’s method. Solutions are also derived for a time-harmonically forced problem with internal damping and are used to investigate the effect of ultrasound in a bioreactor, particularly the amount of energy delivered to cultured cells. The concise form of the solution simplifies the analysis of acoustic field problems.

INTRODUCTION

Acoustics are widely used for measurement or mechanical stimulation in medicine, non-destructive testing, refining processes, chemical reactors and many other applications. The utility of ultrasound (US) as an imaging tool has greatly impacted the field of diagnostic imaging^{1, 2, 3, 4} and the development of novel sophisticated imaging modalities continue to enhance the role of ultrasound in diagnosis. Applications of ultrasound are not restricted to imaging, but also find extensive usage in therapeutic applications as in physiotherapy⁵ and the use of high-amplitude acoustic shock wave to disintegrate kidney stones (lithotripsy).⁶ Emerging applications of ultrasound include the use of high intensity focused ultrasound in the non-invasive treatment of tumors.^{6, 7, 8} More research is in progress to fully understand and develop the use of ultrasound in the delivery of drugs and genetic material, thrombolysis and tumor therapy.^{9, 10}

The response of biological tissue to US exposure depends on the location, function as well as on the acoustic and biological properties of the exposed tissue.^{10, 11} A wide variety of biological ultrasound effects have been documented both in vivo and in vitro.^{10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21} Particularly, studies in the last ten years have shown that cells maintained in in vitro cultures can be stimulated by ultrasound^{15, 16, 17, 18, 22} and this feature has been exploited to build bioprocessing systems that aim to generate tissue engineered cellular constructs.

Mathematical models of varying complexity have been used to simulate the different processes.²³ Although this paper focuses on acoustic waves specifically, the theory applies to all physical phenomena described by the one-dimensional linear wave equation. Propagation of waves through different media usually requires the solution of coupled partial differential equations (PDE’s). It is a simple exercise to calculate the steady-state response of a system forced by a harmonic function (that is, where the time-dependence is of the form $e^{j\omega t}$, thus transforming the wave equation into the Helmholtz equation²⁴). However, we are specifically interested in the transient acoustic response to assess the effects of pulsed ultrasound, or continuous ultrasound with dynamic frequency and/or amplitude modulation. Calculating the transient response to arbitrary forcing functions is much more difficult and one must usually resort to spectral or numerical methods. The dynamic boundary causes the partial differential equation to be nonselfadjoint. Consequently, the eigenfunctions required by the spectral analysis will not be orthogonal and may indeed form an ill-conditioned basis.²⁵ This reduces (and in special cases, eliminates) the ability of spectral methods to describe wave motion.

Instead, we present an analytical method for solving the one dimensional linear wave equation by modeling the effects of absorption and reflection at the media interfaces using a dynamic boundary condition. Van Rensburg et al.²⁵ has shown that exact solutions are found with d’Alembert’s method. The paper by Van Rensburg et al.²⁵ is unique in its application of the d’Alembert method on a finite domain. We extend the method to account for forcing and internal damping. Finally, the solution is applied to ultrasonic waves in a bioreactor for the purposes of tissue engineering.

MATHEMATICAL MODEL

Justification of the dynamic boundary condition

In this section, we present the validity and physical interpretation of the dynamic boundary condition used to account for the absorption and reflection of acoustic waves at a media interface. The acoustic wave equation in inviscid fluids may be approximated by the linearization of the continuity (Eq. 1) and momentum balance (Eq. 2) equations as well as the compressibility equation of state (Eq. 3):²⁴

$$\frac{\partial \rho }{\partial t}+{\rho }_0\nabla ·\overrightarrow{w}=0,$$ (1)

$${\rho }_0\frac{\partial \overrightarrow{w}}{\partial t}+\nabla p=0,$$ (2)

$$p=K\frac{\rho }{{\rho }_0}.$$ (3)

In the linearization, ρ and p are the acoustic density and pressure variations respectively, such that $p_{\mathit{abs}}=p+p_0$ (similarly for $p_{\mathit{abs}}$). The velocity is given by the vector $\overrightarrow{w}$ and the bulk modulus by K. We can substitute Eq. 3 in Eq. 1, take the gradient of Eq. 1 and the time derivative of Eq. 2 and rearrange to obtain Eq. 4:

$$\frac{{\partial }^2\overrightarrow{w}}{\partial t^2}-\frac{K}{\rho }{\nabla }^2\overrightarrow{w}=\frac{{\partial }^2\overrightarrow{w}}{\partial t^2}-c^2{\nabla }^2\overrightarrow{w}=0.$$ (4)

Equation 4 is the linear wave equation. In one dimension, the problem is solvable using d’Alembert’s method, which states that the solution has the form given by Eq. 5:

$$w(z,t)=w_R(z-\mathit{ct})+w_L(z+\mathit{ct}),$$ (5)

where $w_R\left(\xi \right)$ and $w_L\left(\xi \right)$ are arbitrary functions describing the profile of the right- and left-traveling wave, respectively. The one-dimensional form of the wave equation is applicable to waves traveling down a solid bar, vibrating strings, etc. In acoustics, the one-dimensional wave equation is appropriate when evaluating plane waves. It is common practice to represent complex waves (such as the beams generated by transducers) as an infinite series of plane waves.²⁶ The problem is solved for each individual plane wave, and the beam is reconstructed using these solutions.

Next, we calculate the first partial derivatives with respect to time and position, Eqs. 6, 7:

$$\frac{\partial w}{\partial t}=-c(w{\text{'}}_R(z-\mathit{ct})-w{\text{'}}_L(z+\mathit{ct})),$$ (6)

$$\frac{\partial w}{\partial z}=w{\text{'}}_R(z-\mathit{ct})+w{\text{'}}_L(z+\mathit{ct}).$$ (7)

The prime indicates the derivative w.r.t the argument, $w\text{'}\left(\xi \right)=\frac{\mathit{dw}}{d\xi }$. The pressure is given by rearranging Eq. 2 to give Eq. 8:

$$p=-{\rho }_0\int \frac{\partial w}{\partial t}\mathit{dz}={\rho }_{0}c\int (w{\text{'}}_R(z-\mathit{ct})-w{\text{'}}_L(z+\mathit{ct}))\mathit{dz}=Z(w_R(z-\mathit{ct})-w_L(z+\mathit{ct})).$$ (8)

The quantity $Z={\rho }_{0}c$ is known as the acoustic impedance. If the right-traveling wave impinges on a surface at $z=L$, it will create a (left-traveling) reflected wave and a (right-traveling) transmitted wave. The boundary conditions are continuity of pressure (Eq. 9) and velocity (Eq. 10):

$$w_R(L-c_{1}t)+w_L(L+c_{1}t)=w_T(L-c_{2}t),$$ (9)

$$Z_1(w_R(L-c_{1}t)-w_L(L+c_{1}t))=Z_2{w}_T(L-c_{2}t).$$ (10)

The subscripts 1 and 2 refer to the first and second medium and $w_T$ refers to the transmitted wave. We can combine Eqs. 9, 10 to eliminate $w_T$ as shown in Eq. 11 (we drop the arguments $(L-c_{1}t)$ and $(L+c_{1}t)$ for brevity):

$$(w_R+w_L)-\frac{Z_1}{Z_2}(w_R-w_L)=0.$$ (11)

Since Eq. 11 must be true for $z=L$ and all times $t>0$, we take the time derivative of Eq. 11 to get Eq. 12:

$$\frac{\partial }{\partial t}[(w_R+w_L)-\frac{Z_1}{Z_2}(w_R-w_L)]=0\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\Rightarrow (w{\text{'}}_R-w{\text{'}}_L)-\frac{Z_1}{Z_2}(w{\text{'}}_R+w{\text{'}}_L)=0.$$ (12)

Substituting Eq. 6 and Eq. 7 into Eq. 12 gives the dynamic boundary condition Eq. 13:

$$\tilde{\alpha }\frac{\partial w}{\partial t}+\frac{\partial w}{\partial z}=0;\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\tilde{\alpha }=Z_2/c_1{Z}_1.$$ (13)

If the equations are rendered dimensionless by $u=w/c_1$, $\tau ={\mathit{tc}}_1/L$, and $x=z/L$, then we have Eq. 14:

$$\alpha \frac{\partial u}{\partial \tau }+\frac{\partial u}{\partial x}=0;\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\alpha =Z_2/Z_1.$$ (14)

In this form, α is simply the ratio of acoustic impedances for fluids 1 and 2.

D’Alembert solution for an arbitrary forcing function and no internal damping

It is important to note that the procedure described in this section can be used to find the solution to the problem with dynamic boundaries on either side of the domain. It is even possible to calculate the response of multiple acoustic layers to an arbitrary input by coupling the dynamic boundaries. For the examples to follow, we will only consider the simplest case where no waves are entering the domain from the dynamic boundary, which is true when the second medium is sound-absorbing or semi-infinite. We seek the transient response of a dimensionless, linear acoustic wave as described by Eq. 15:

$$\begin{array}{c}\multicolumn{1}{c}{\frac{{\partial }^{2}u}{\partial {\tau }^2}-\frac{{\partial }^{2}u}{\partial x^2}=0\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}0<x<1,\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\tau >0u(x,0)=f\left(x\right)\frac{\partial u}{\partial \tau }(x,0)=v\left(x\right)u(0,\tau )=\phi \left(\tau \right)\alpha \frac{\partial u}{\partial t}(1,\tau )+\frac{\partial u}{\partial x}(1,\tau )=0.}\end{array}$$ (15)

Define the functions $g_1\left(x\right)$ and $g_2\left(x\right)$ as extensions of $\frac{1}{2}f\left(x\right)$ and $\frac{1}{2}h\left(x\right)$, respectively, where $h\text{'}\left(x\right)=v\left(x\right)$, on the infinite domain $x\in (-\infty ,\infty )$. The solution to the problem posed in Eq. 15 is given by Eq. 16:

$$u(x,\tau )=g_1(x+\tau )+g_1(x-\tau )+g_2(x+\tau )\mathrm{-}\mathrm{\hspace{1em}}{g}_2(x-\tau ),$$ (16)

Substituting Eq. 16 into the boundary condition at $x=0$ we can obtain recursive formulas for the extension functions, shown in Eqs. 17, 18:

$$u(0,\tau )=g_1\left(\tau \right)+g_1(-\tau )+g_2\left(\tau \right)-g_2(-\tau )=\phi \left(\tau \right),$$

Thus, let:

$$g_1(-\tau )=\phi \left(\tau \right)-g_1\left(\tau \right),$$ (17)

and

$$g_2\left(\tau \right)=g_2(-\tau ).$$ (18)

Similarly, if we apply Eq. 16 at $x=1$, we obtain the recursive formulas given by Eqs. 19, 20:

$$\begin{array}{c}\multicolumn{1}{c}{u_x(1,\tau )+\alpha u_{\tau }(1,\tau )=\left(\begin{array}{c}\multicolumn{1}{c}{[g{\text{'}}_1(1+\tau )+g{\text{'}}_1(1-\tau )+g{\text{'}}_2(1+\tau )-g{\text{'}}_2(1-\tau )]}\\ \multicolumn{1}{c}{+\alpha [g{\text{'}}_1(1+\tau )-g{\text{'}}_1(1-\tau )+g{\text{'}}_2(1+\tau )+g{\text{'}}_2(1-\tau )]}\end{array}\right)=0,}\end{array}$$

which leads to

$$g{\text{'}}_1(1+\tau )=-ag{\text{'}}_1(1-\tau ),$$ (19)

and

$$g{\text{'}}_2(1+\tau )=ag{\text{'}}_2(1-\tau ).$$ (20)

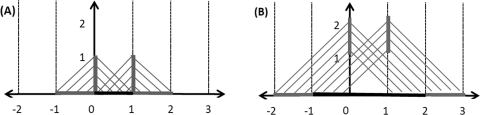
Note that the prime indicates differentiation. The constant $a=\frac{1-\alpha }{1+\alpha }=\frac{z_1-z_2}{z_1+z_2}$ is the reflection coefficient. Furthermore, $g_1\left(x\right)=\frac{1}{2}f\left(x\right)$ and $g_2\left(x\right)=\frac{1}{2}h\left(x\right)$ are defined on $x\in [0,1]$ by the initial conditions. Since $f\left(x\right)$ and $v\left(x\right)$ are defined on the interval $x\in [0,1]$, Eqs. 17, 18, 19, 20 can be used to extend the functions to $x<0$ and $x>1$ and still satisfy the boundary conditions. The method is illustrated in Fig. 1.

Figure 1.

(Color online) Diagram showing the dependency of $g_1\left(x\right)$ on the forcing function and initial condition. (a) $u(0,\tau )=\phi \left(\tau \right)$ on $\tau \in [0,1]$ depends on $g_1\left(x\right)$ for $x\in (-1,1)$. However, since $g_1\left(x\right)=\frac{1}{2}f\left(x\right)$ on $x\in (0,1)$ is defined, one can calculate $g_1\left(x\right)$ on $x\in (-1,0)$ using Eq. 17. Similarly, Eq. 19 can be used to calculate $g_1\left(x\right)$ on $x\in (1,2)$. (b) This method is then repeated to calculate $g_1\left(x\right)$ on $x\in (-2,-1)\cup (2,3)$.

Let $x=k+\epsilon$, where $k\in \mathbb{Z}$ and $\epsilon \in (-1,1)\subset \mathbb{R}$ (e.g., if $x=-2.43$, then $k=-2$ and $\epsilon =-0.43$). Equations 17, 18, 19, 20 provides a recursive method for determining $g_1\left(x\right)=g_1(k+\epsilon )$ and $g_2\left(x\right)=g_2(k+\epsilon )$. By iteratively applying Eqs. 17, 18, 19, 20 and through extensive algebraic manipulation, we arrive at the extension functions as given by Eqs. 21, 22:

$$g_1\left(x\right)=\{\begin{array}{c}\multicolumn{1}{c}{-\frac{x}{\left|x\right|}[\sum _{n=H\left(x\right)}^{\frac{\left|k\right|-1}{2}}\left[{(-a)}^n\phi (\left|x\right|-2n)\right]+\frac{{(-a)}^{\frac{\left|k\right|+1}{2}}}{2}f(1-|x-k|)]\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}k\hspace{1em}\mathrm{is}\hspace{1em}\mathrm{odd}}\\ \multicolumn{1}{c}{\frac{-x}{\left|x\right|}[\sum _{n=H\left(x\right)}^{\frac{\left|k\right|}{2}}\left[{(-a)}^n\phi (\left|x\right|-2n)\right]-\frac{{(-a)}^{\frac{\left|k\right|}{2}}}{2}f\left(|x-k|\right)]\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}k\mathrm{\hspace{1em}}\mathrm{is}\hspace{1em}\mathrm{even}}\end{array},$$ (21)

$$g_2\left(x\right)=\{\begin{array}{c}\multicolumn{1}{c}{\frac{{(-a)}^{\frac{\left|k\right|+1}{2}}}{2}h(1-|x-k|)\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}k\mathrm{\hspace{1em}}\mathrm{is}\mathrm{\hspace{1em}}\mathrm{odd}}\\ \multicolumn{1}{c}{\frac{{(-a)}^{\frac{\left|k\right|}{2}}}{2}h\left(|x-k|\right)\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}k\mathrm{\hspace{1em}}\mathrm{is}\mathrm{\hspace{1em}}\mathrm{even}}\end{array}.$$ (22)

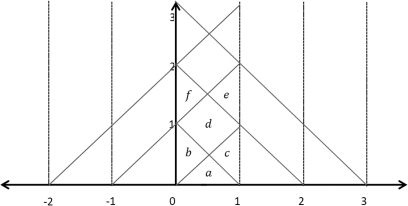
Note that the lower bound of summation is given by the Heaviside function $H\left(x\right)=0$ if $x<0$ and $H\left(x\right)=1$ if $x\ge 0$. The implications of this method are illustrated in Fig. 2 below.

Figure 2.

(Color online) The τ-x plane, divided into regions determined by its dependency on the function $f\left(x\right)$.

The τ-x plane is divided into regions on Fig. 2. In region a, the solution depends only on the initial conditions $u(x,0)$ and $u_{\tau }(x,0)$. In region b, the effect of the forcing function appears, which corresponds mathematically to $g_1\left(x\right)$ and $g_2\left(x\right)$ on $x\in [-1,0]$. In region c, the initial wave is reflected, corresponding to $g_1\left(x\right)$ and $g_2\left(x\right)$ on $x\in [1,2]$. In region d, both the reflected wave and the forcing function contribute. For example, in region d, where $(x+\tau )\in [1,2]$ and $(x-\tau )\in [-1,0]$, the solution has the form given by Eq. 23:

$$\begin{array}{c}\multicolumn{1}{c}{u(x,\tau )=g_1(x+\tau )+g_1(x-\tau )+g_2(x+\tau )\mathrm{-}\mathrm{\hspace{1em}}{g}_2(x-\tau )=\phi (\tau -x)+\frac{a}{2}(f(2-(x+\tau ))-h(2-(x+\tau )))\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}-\frac{1}{2}(f(\tau -x)+h(\tau -x)).}\end{array}$$ (23)

The first term in Eq. 23 is the forcing function. The second term presents the two waves that have been reflected at the dynamic boundary (note the reflection coefficient a). Similarly, the last term represents the waves that have been reflected of the left hand boundary.

The extension functions given by Eqs. 21, 22 simplify if $u(x,0)=u_{\tau }(x,0)=0$ (in practice, the medium is usually initially at rest). The initial condition terms can be neglected completely and Eq. 21 reduces to Eq. 24, while Eq. 22 is equal to zero:

$$\begin{array}{c}\multicolumn{1}{c}{g_1\left(x\right)\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}=-\frac{x}{\left|x\right|}(\phi \left(\left|x\right|\right)H(-x)+\sum _{n=1}^{\infty }\left[{(-a)}^n\phi (\left|x\right|-2n)H(\left|x\right|-2n)\right]).}\end{array}$$ (24)

Substituting Eq. 24 into Eq. 16, the solution is given by Eq. 25:

$$u(x,\tau )=\hspace{1em}\phi (\tau -x)H(\tau -x)+\sum _{n=1}^{\infty }{(-a)}^n\times \left(\begin{array}{c}\multicolumn{1}{c}{\phi (\tau -(2n+x))H(\tau -(2n+x))}\\ \multicolumn{1}{c}{-\phi (\tau -(2n-x))H(\tau -(2n-x))}\end{array}\right).$$ (25)

To summarize this section, the solution of Eq. 15 is given by Eqs. 21, 22. The solution can be further simplified if $u(x,0)=u_{\tau }(x,0)=0$, and this solution is given by Eq. 25.

D’Alembert solution for a time-harmonic forcing function and internal damping

Damping is introduced by adding a third, mixed derivative term to the linear wave equation, as shown by Eq. 26, which is known as the linearized Kuznetsov equation:27²⁷

$$\frac{{\partial }^{2}u}{\partial {\tau }^2}-\frac{{\partial }^{2}u}{\partial x^2}=\beta \frac{{\partial }^{3}u}{\partial x^2\partial t}.$$ (26)

The dimensionless parameter $\beta =(\frac{4}{3}\nu +\frac{{\mu }_B}{{\rho }_0}+(\gamma -1)\kappa )/\mathit{cL}$ is the diffusivity of sound,²⁷ with $\nu ,{\mu }_B$, and κ being the kinematic viscosity, bulk viscosity and thermal diffusivity respectively and $\gamma =c_P/c_V$ is the adiabatic index. The mixed derivative term $u_{\mathit{xx}\tau }$ describes the internal damping and the change in the propagation speed due to damping, which depends on the spectrum of the wave. Here we present analytical solutions for the special case where the forcing function is given by $\phi \left(\tau \right)=e^{j\omega \tau }$ and the initial conditions are zero, i.e., $u(x,0)=u_{\tau }(x,0)=0.$ To accommodate internal damping, we replace $\phi (x,\tau )$ in Eq. 25 with ${\phi }^{*}(x,\tau )=e^{j(\omega \tau -\mathit{kx})}$, where $k\in \mathbb{C}$.

The solution consists of two parts corresponding to the right- and left-traveling waves ($u_R$ and $u_L$, respectively, Eq. 27). The first term in Eq. 27 represents a wave emanating from $x=0$ that has not been reflected at the dynamic boundary $x=1$. The first term in the summation represents waves that have traveled a distance of $2n+x$, while the second term represents waves that have traveled a distance of $(2n-1)+(1-x)=2n-x$:

$$\begin{array}{cc}\multicolumn{1}{c}{u(x,\tau )=\hspace{1em}}& (e^{-\mathit{jkx}}H(\tau -\frac{\mathrm{Real}\{k\}}{\omega }x)\hfill \\ +\sum _{n=1}^{\infty }{(-a)}^n[\begin{array}{c}\multicolumn{1}{c}{e^{-\mathit{jk}(2n+x)}H(\tau -\frac{\mathrm{Real}\{k\}}{\omega }(2n+x))}\\ \multicolumn{1}{c}{-e^{-\mathit{jk}(2n-x)}H(\tau -\frac{\mathrm{Real}\{k\}}{\omega }(2n-x))}\end{array}])e^{j\omega t}.\hfill \end{array}$$ (27)

The physical wave is given by the real part of Eq. 27. Each term in Eq. 27 must satisfy the Kuznetsov equation. Upon substitution of any one of these terms into the differential equation and separating real and imaginary terms, one can solve for the complex wave number k using Eq. 28:

$$k=\hspace{1em}\omega (\frac{\beta \omega }{\sqrt{(2(1+{(\beta \omega )}^2)({(1+{(\beta \omega )}^2)}^{\frac{1}{2}}-1))}}-\frac{j}{\sqrt{(2(1+{(\beta \omega )}^2))}}).$$ (28)

Extension to an arbitrary forcing function and internal damping

The solution above is specific to a time-harmonic forcing function. However, any function on $\tau \in (-\infty ,\infty )$ can be represented using a Fourier integral $f\left(\tau \right)={\int }_{-\infty }^{\infty }\stackrel{\wedge }{f}\left(\omega \right)e^{j\omega \tau }d\omega$, hence the solution can be represented by a similar integral form, $u(x,\tau )={\int }_{-\infty }^{\infty }\stackrel{\wedge }{f}\left(\omega \right)\stackrel{\wedge }{u}(x,\tau ;\omega )d\omega$, where $\stackrel{\wedge }{u}(x,\tau ;\omega )$ is the solution to the system forced by $\phi \left(\tau \right)=e^{j\omega \tau }$ given by Eq. 27.

RESULTS

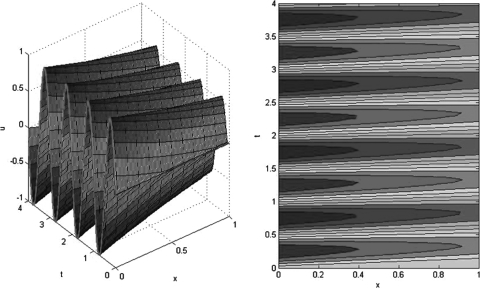
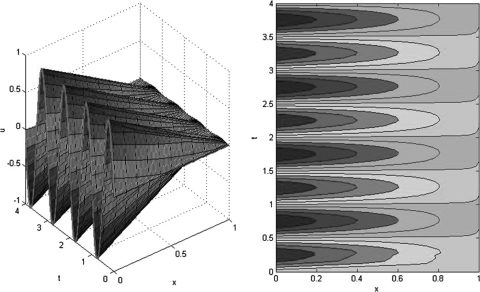
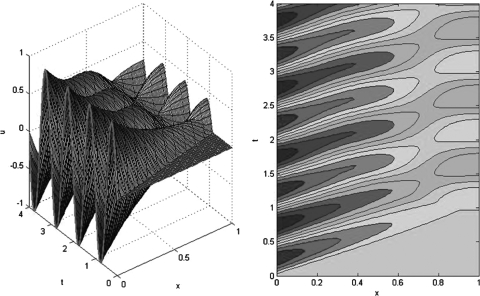
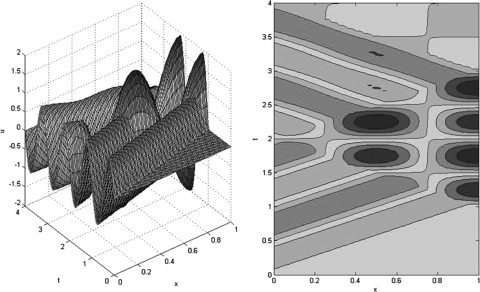
In Figs. 3456 we present solutions, given by Eq. 27 for various values of α and β; the forcing function is $\phi \left(\tau \right)=\mathit{sin}\left(2\pi \tau \right)$. For the special case $\alpha =1$, the wave is completely absorbed at the dynamic boundary as shown in Fig. 3. The internal damping coefficient is extremely large in this case. The value of β has a strong effect on the wave speed and the amount of damping. When α is large, the right-hand side boundary approximates a fixed boundary condition ($u(1,\tau )=0$), the result is shown in Fig. 4. Figures 34 show the case where β is large, corresponding to a high wave speed and reasonably high damping. The high wave speed can clearly be seen from the contour graphs in Figs. 34. Maximum damping occurs if $\lambda \beta =1$, or $\beta =1/2\pi$ in this case—the results are shown in Fig. 5, where the wave amplitude is reduced by nearly 90% across the length of the medium. Further decreasing β results in a decrease in damping and the wave speed approaches the normal speed of sound, as shown in Fig. 6. For small values of α, conditions of a free boundary are approached. In Figs. 56 the results are shown for $\alpha =0.01$, and $\beta =\frac{1}{2\pi }$ and $\beta =0.01$, respectively.

Figure 3.

(Color online) $\alpha =1,\beta =10$. No reflection occurs at the interface when $\alpha =1$. The slight decrease in the wave amplitude is purely due to damping.

Figure 4.

(Color online) $\alpha =100,\beta =10$. The high value of α forces the boundary at $x=1$ to be nearly constant. The wave has a high speed and minimal damping.

Figure 5.

(Color online) $\alpha =0.01,\beta =1/2\pi$. When α is small, the right-hand boundary is free, causing the reflected wave to enforce the oncoming wave. Damping is maximized when $\lambda \beta =1$. The wave speed has decreased, approaching the normal speed of sound.

Figure 6.

(Color online) $\alpha =0.01,\beta =0.001$. For small values of β, damping is negligible and the wave speed is equal to the normal speed of sound. Strong interference patterns caused by the free boundary are clearly visible from the contour graph.

Applications

Transient response

As discussed in Sec. 1, ultrasound may be used to stimulate cells for tissue engineering, and the various ultrasonic regimes used for stimulation requires analysis of the transient phase of the acoustic response. In Table TABLE I. we list typical parameter values for ultrasound stimulation of cells. The forcing function is sinusoidal and has the form $\phi \left(t\right)=A\mathit{sin}\left(\omega t\right)$.

TABLE I.

Parameters for ultrasound stimulation of cells.

Parameter	Value	Parameter	Value
A	$0.1\mathrm{\hspace{1em}}\mu \mathrm{m}$	ρ	$1000\mathrm{\hspace{1em}}\mathrm{kg}/{\mathrm{m}}^3$
ω	$5\mathrm{\hspace{1em}}\mathrm{MHz}$	c	$1484\mathrm{\hspace{1em}}\mathrm{m}/\mathrm{s}$
L	$1.4\mathrm{\hspace{1em}}\mathrm{cm}$	μ	$8.4\times {10}^{-4}\mathrm{\hspace{1em}}\mathrm{Pa}\mathrm{·}\mathrm{s}$
a	$2.5$	b	$1.12\times {10}^{-5}\hspace{1em}{\mathrm{m}}^2/\mathrm{s}$

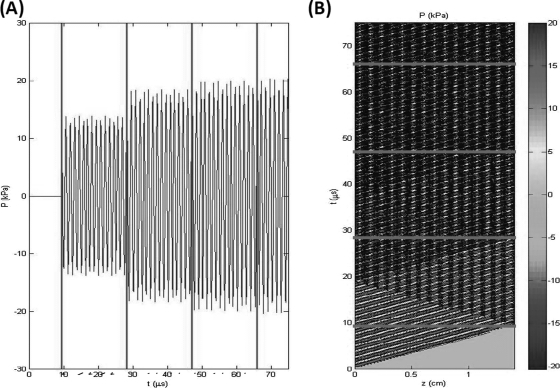
Using these parameters, the velocity u and the pressure fluctuations $\tilde{P}=P-P_0$ have been calculated. In Fig. 7 the pressure fluctuations are shown for the first 75 μs. At the dynamic boundary ($x=1$), four distinct phases of the pressure are noted. These phases correspond to the time it takes a traveling wave to reach the dynamic boundary, $t^{*}=\frac{L}{c}$. Initially, the pressure is equal to zero when $t<t_1=t^{*}$. After the first wave has reflected from the boundary, it interferes destructively with the incoming wave. The destructive interference is clearly seen in Fig. 7b as a lighter triangle when $10\mathrm{\hspace{1em}}\mu \mathrm{s}<t<20\mathrm{\hspace{1em}}\mu \mathrm{s}$.

Figure 7.

(Color online) (a) The pressure fluctuations at the dynamic boundary ($z=1.4\mathrm{\hspace{1em}}\mathrm{cm}$) is shown over a time period of $75\mathrm{\mu }\mathrm{s}$. Four different phases, each with increasing average pressure amplitude, can clearly be seen. Each phase corresponds to the time it takes a reflected wave to reach the boundary $(t_1=\frac{L}{c},t_2=\frac{3L}{c},t_3=\frac{5L}{c}$ and $t_4=\frac{7L}{c})$. (b) The contour graph clearly shows the effect of the destructive interference of the reflected wave in the regions $t_1<t<t_2$ and $t_2<t<t_3$. When $t>t_3$, the pressure amplitude reaches a steady state.

The pressure amplitude remains around $P_1\approx 13.8\mathrm{\hspace{1em}}\mathrm{kPa}$ for time $t_1<t<t_2=3t^{*}$. When $t=3t^{*}$, the wave that has been reflected from the dynamic boundary has been reflected off the forcing boundary again and has reached the dynamic boundary a second time. This adds to the pressure amplitude and $P_2\approx 18.5\mathrm{\hspace{1em}}\mathrm{kPa}$. This happens a third time, when $t<t_3=5t^{*}$ and the pressure amplitude is increases to $P_3\approx 20.0\mathrm{\hspace{1em}}\mathrm{kPa}$. After this final increase, subsequent reflections have little effect and the solution reaches a steady state. Pressures waves with an amplitude of $20.0\mathrm{\hspace{1em}}\mathrm{kPa}$ produce average intensities of 0.027 W/cm².

The example above clearly demonstrates the extended d’Alembert’s method’s value in predicting the transient response to ultrasonic stimulation. For the specific parameters given in Table TABLE I., the acoustic field approached its steady state response within $t=5t^{*}$. This information is useful when using ultrasound for mechanical stimulation of cells using either pulsed or continuously modulated ultrasound and may potentially be applied to ultrasonic imaging as well.

Energy and energy dissipation

The dimensionless energy in the system at any moment in time is given by Eq. 29:²⁵

$$E_T\left(t\right)=\frac{1}{2}({\int }_0^1{\left(u_t\right)}^2+\hspace{1em}{\left(u_x\right)}^2\mathit{dx}).$$ (29)

The energy that is transferred to the system by the actuator $E_A\left(t\right)$ equals the total energy in the system $E_T\left(t\right)$ plus the energy that is dissipated at the boundary $E_B\left(t\right)$ and the energy that is dissipated into thermal energy $E_g\left(t\right)$. Using this relation, we obtain Eq. 30:

$$E_A\left(t\right)-E_B\left(t\right)-E_Q\left(t\right)=\frac{1}{2}({\int }_0^1{\left(u_t\right)}^2+\hspace{1em}{\left(u_x\right)}^2\mathit{dx}).$$ (30)

Since the system is non-adiabatic, the temperature rise in the medium is less than the amount of energy dissipated. Therefore, a system that is perfectly insulated to thermal energy losses will provide a conservative estimate (upper bound) on the temperature rise in the medium.

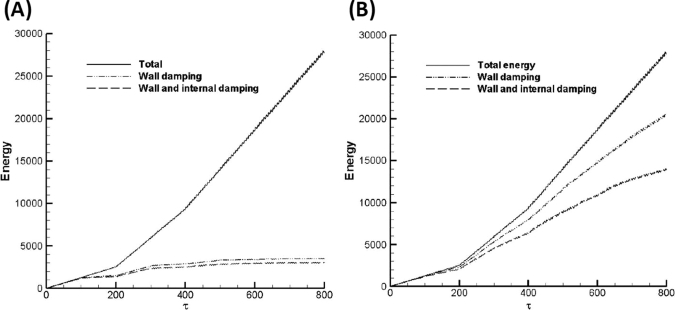
In Figs. 8a, 8b, the energy plots are shown for $\alpha =2.5$ and $\alpha =25$, respectively. In each figure three curves are shown:

• Total energy in the system with no dissipation, $E_T=E_A$ (solid curve);

• Total energy in the system with losses due to wall damping, $E_T=E_A-E_B$ (dash-dot curve);

• Total energy in the system with wall and internal damping, $E_T=E_A-E_B-E_Q$ (dash curve).

Figure 8.

Total energy in the system (scaled). Three cases are presented: forcing only with $\beta =0$, and $\alpha \to \infty$ (i.e. $\alpha =-1$) shown as the solid line, only wall damping ($\beta =0$), shown as the dash-dot line and the dash-line presents the case of wall damping and internal damping ($\beta =5\times {10}^{-5}$). (a) When $\alpha =2.5$, wall damping is the primary method of energy dissipation. (b) Much less energy is dissipated by the dynamic boundary when $\alpha =25$.

The properties of Table TABLE I. have been used. Significantly more energy is absorbed at the wall when $\alpha =2.5$; this result is evident from the difference between the total energy curve and the wall damping curve in Fig. 8a compared to the difference for Fig. 8b. Also, the total energy with wall damping approaches a plateau for $\alpha =2.5$. A relatively small amount of energy (difference between the two lower curves) is dissipated as thermal energy. When the wall damping is reduced, i.e., $\alpha =25$, the total energy with damping continues to increase over time, albeit at a reduced rate compared to the undamped case. The amount of energy that is dissipated as thermal energy, is much higher than for the case $\alpha =2.5$.

If the actuator is powered for 50 s, then the total energy in the system can be estimated from extrapolating the curves shown in Figs. 8a, 8b. The temperature rise after 50 s is calculated from the difference between the extrapolated values total energy with wall damping and total energy with wall and internal damping. In the case of $\alpha =25$ and $\beta =5\times {10}^{-5}$, the temperature rise is about 21 °C. It needs to be pointed out that the temperature rise does not account for heat losses at the lateral walls of the acoustic chamber. Further, the dissipated energy is calculated as thermal energy of the water only and temperature rises of the chamber walls are neglected. All of these omissions will lead to significant lower temperature increases in practical situations. If a more realistic value of $\beta =5\times {10}^{-6}$ is used for the Kuznetsov damping coefficient and $\alpha =25$ then the temperature rise is only 3 °C after 50 s.

CONCLUSIONS

In summary, analytical solutions for a periodically forced problem with internal and boundary damping have been presented. If internal damping is negligible, the solution is given by Eq. 25 for an arbitrary forcing function. The solution given by Eq. 27 for a complex exponential forcing function also accounts for internal damping. The analytical solutions have the following advantageous:

• The model allows for the prediction of the transient response of an inviscid fluid to initial conditions and arbitrary forcing functions at the boundary;

• The dynamic boundary eliminates the need to solve two coupled PDE’s with jump-conditions at the interface to determine the reflection and absorption effects;

• The model incorporates internal damping, which allows application to a wide variety of problems;

• Since the solution is analytical, it is not computationally intensive or error prone;

• The solution accurately captures the characteristics of the nonselfadjoint problem, overcoming the short-comings of spectral methods.

The model was used to investigate the effect of ultrasound on a tissue engineering bioreactor. The time to reach steady state was determined, as well as the energy absorption by the fluid and at the bioreactor wall. The concise form of the solution simplifies further analysis of acoustic field problems.