Robust Statistical Fusion of Image Labels

Abstract

Image labeling and parcellation (i.e. assigning structure to a collection of voxels) are critical tasks for the assessment of volumetric and morphometric features in medical imaging data. The process of image labeling is inherently error prone as images are corrupted by noise and artifacts. Even expert interpretations are subject to subjectivity and the precision of the individual raters. Hence, all labels must be considered imperfect with some degree of inherent variability. One may seek multiple independent assessments to both reduce this variability and quantify the degree of uncertainty. Existing techniques have exploited maximum a posteriori statistics to combine data from multiple raters and simultaneously estimate rater reliabilities. Although quite successful, wide-scale application has been hampered by unstable estimation with practical datasets, for example, with label sets with small or thin objects to be labeled or with partial or limited datasets. As well, these approaches have required each rater to generate a complete dataset, which is often impossible given both human foibles and the typical turnover rate of raters in a research or clinical environment. Herein, we propose a robust approach to improve estimation performance with small anatomical structures, allow for missing data, account for repeated label sets, and utilize training/catch trial data. With this approach, numerous raters can label small, overlapping portions of a large dataset, and rater heterogeneity can be robustly controlled while simultaneously estimating a single, reliable label set and characterizing uncertainty. The proposed approach enables many individuals to collaborate in the construction of large datasets for labeling tasks (e.g., human parallel processing) and reduces the otherwise detrimental impact of rater unavailability.

I. Introduction

Numerous clinically relevant conditions (e.g., degeneration, inflammation, vascular pathology, traumatic injury, cancer, etc.) correlate with volumetric or morphometric features as observed on magnetic resonance imaging (MRI). Quantification and characterization as well as potential clinical use of these correlations requires the labeling or delineation of structures of interest. The established gold standard for identifying class memberships is manual voxel-by-voxel labeling by a neuroanatomist, which can be exceptionally time and resource intensive. Furthermore, different human experts often have differing interpretations of ambiguous voxels (e.g., 5-15% coefficient of variation for multiple sclerosis lesions [1] or 10-17% by volume for tumor volumes [2]). Therefore, pursuit of manual approaches is typically limited to either (1) validating automated or semi-automated methods or (2) the study of structures for which no automated method exists. An often understood objective in manual labeling is for each rater to produce the most accurate and reproducible labels possible. Yet this is not the only possible technique for achieving reliable results. Kearns and Valiant first posed the question whether a collection of “weak learners” (raters that are just better than chance) could be boosted (“combined”) to form a “strong learner” (a rater with arbitrarily high accuracy) [3]. The first affirmative response to this challenge was proven one year later [4] and, with the advent of AdaBoost [5], boosting became widely practical and is now in widespread use.

Statistical boosting methods have been previously proposed to simultaneously estimate rater reliability and true labels from complete datasets created by several different raters or automated methods [6-9]. Typically, there are very few raters available in brain imaging research, and raters are generally considered to be superior to “weak learners.” Warfield et al. presented a probabilistic algorithm to estimate the “ground truth” segmentation from a group of expert segmentations and simultaneously assess of the quality of each expert [6]. A similar approach was presented by Rohlfing et al. [8]. These maximum likelihood/maximum a posteriori methods (hereafter referred to as Simultaneous Truth and Performance Level Estimation, STAPLE [7]) increase the accuracy of a single labeling by combining information from multiple, potentially less accurate raters (as long as the raters are independent and collectively unbiased). The framework has been widely used in multi-atlas segmentation [10-12] and has been extended to be applicable to continuous (scalar or vector) images [13, 14].

For practical purposes and ultimately more widespread application, the existing STAPLE framework has several limitations. First, existing descriptions of STAPLE require that all raters delineate all voxels within in a given region. In practice, it is often difficult to achieve this requirement since different sets of raters may delineate arbitrary subsets of a population of scans due to limitations on rater availability or because of the large scale of the study. Second, raters are often requested to label datasets more than once in order to establish a measure of intra-rater reliability; but STAPLE is not set up to use these multiple ratings when estimating the true label set. It is possible to account for multiple delineations by the same rater; however, the traditional STAPLE model forces these delineations to be treated as separate raters entirely. Third, raters are often divided into a class of “experts” whose performances are previously characterized and “novices” whose performances have yet to be established. Yet STAPLE has no explicit way to incorporate prior performance estimates within its estimation framework. We find that the new formulae to address these concerns involve only small changes to the summand subscripts appearing in the original algorithm, which might be viewed as a relatively minor contribution. The equations, however, remain optimal relative to the maximum likelihood criterion of STAPLE, an important condition that neither heuristic nor ad hoc modification of the equations would guarantee. Thus, both the equations comprising the new algorithm that can be implemented under these common conditions and the fact of their optimality are important contributions of this work.

Another criticism of the STAPLE framework is that it can produce dramatically incorrect label estimates in some scenarios, particularly when raters are asked to delineate small or thin structures and/or when there are too few raters or raters with highly inaccurate segmentations. The cause of this type of failure has been interpreted as an estimation instability due to the presence of anatomical structures with small or heterogeneous volumes [12]. For example, the top row of Figure 1 illustrates a brain segmentation model (A) and a seemingly reasonable observation (B); yet when several observations are statistically combined (C), the result is worse than that from an individual rater. These catastrophic errors are referred to as the label inversion problem associated with STAPLE. The result of the label inversion problem is that STAPLE converges to a highly undesired local optimum due to the fact that the raters are highly inaccurate. One of the major contributions of this paper is the development of a technique to help alleviate the label inversion problem. Yet, as Figure 1 also shows in (D)-(F), this catastrophic label fusion behavior does not occur using the same label fusion approach but similarly distributed label models and rater reliabilities. Such varied performance on similar problem types could explain both the successful (e.g., [6, 7, 13]) and less-than-stellar (e.g., [12]) literature reports regarding the utility of STAPLE. Nevertheless, there has been contention about the comparison performed in [12] as it compares STAPLE using a global prior to an algorithm that is initialized in a spatially varying manner.

Figure 1.

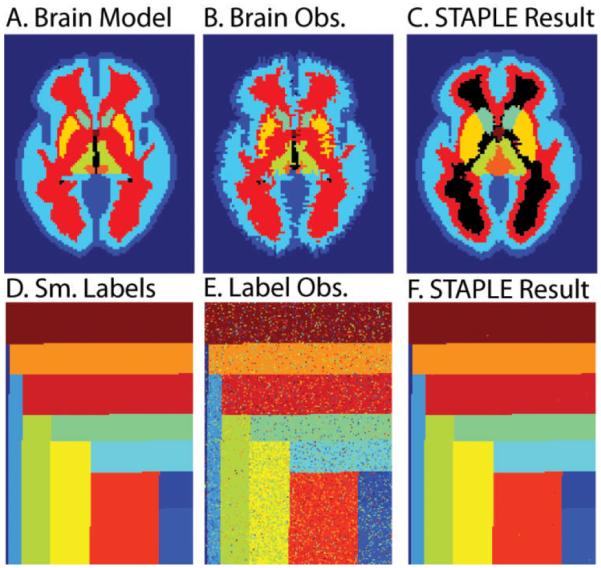
Characteristic STAPLE failure and success. For truth label models (one slice shown in A&D), fusion of multiple sets of reasonable quality random observations (such as in B&E) can lead to decreased performance (such as in C) as seen through the dramatic label inversion problem. A collection of 50 raters of quality similar to the observation seen in (B) were used to generate the estimate seen in (C). This catastrophic segmentation error occurred between 10% and 20% of the time the simulation was run. However, this behavior is not ever present, even for models with small regions (as illustrated in the label fusion in F). Note B&E were observed with the same rater reliabilities and C&F were each fused with three observations per voxel.

In this paper, we present and evaluate Simultaneous Truth and Performance Level Estimation with Robust extensions (STAPLER) to enable use of data with missing labels (i.e., partial label sets in which raters do not delineate all voxels), repeated labels (i.e., labels sets in which raters may generate repeated labels for some, or all, voxels), and training trials (i.e., label sets in which some raters may have known reliabilities — or some voxels have known true labels). The incorporation of training data is equivalent to defining a data-driven a priori distribution on rater reliability, which also may be generated using “catch trials” against ground truth labels during routine labeling of other data sets. We consider this information ancillary as it does not specifically relate to the labels on structures of interest, but rather to the variability of individual raters. We therefore extend the STAPLE label fusion methodology to include explicit, exogenously defined priors, and this capability can be used to successfully counter the irregular estimation behavior described above.

STAPLER simultaneously incorporates all label sets from all raters in order to estimate a maximum a posteriori estimate of both rater reliability and true labels. In this paper, the impacts of missing and training data are studied with simulations based on two models of rater behavior. First, the performance is studied using voxel-wise “random raters” whose behaviors are described by confusion matrices (i.e., probabilities of indicating each label given a true label). Second, we develop a more realistic set of simulations in which raters make more mistakes along the boundaries between regions. Using these models within a series of simulation studies, we demonstrate the ability of a priori probability distributions (“priors”) on the rater reliabilities to stabilize the estimated label sets by conditioning the rater reliability estimates. We present simulations to characterize the occurrence of catastrophic failures of label fusion and show that priors on rater reliabilities can rectify these problems. The performance of STAPLER is characterized with these simulated rater models in simulations of cerebellar and brain parcellation.

For all presented experiments, we exclude consensus background regions as proposed in [15]; however, we are specifically considering minimally trained raters and large numbers of participants, so there are essentially no voxels (0.61% for the empirical data in Section I) for which there is consensus among all raters. For almost every slice, someone (sometimes many people) executed the incorrect labeling task. Because of the scenarios we consider, the use of specific consensus regions within the target is impossible. Furthermore, there has been exciting work using multi-atlas registration using residual intensities [16] and a plethora of voting methods using intensity information (reviewed in [17]). However, these approaches are not appropriate for the problem under consideration because we consider only manual raters in scenarios in which intensity information may or may not be relevant to their task.

Most closely related to this work, is the idea proposed by Commowick et al. [18] in which a parametric prior on the performance level parameters is examined. This approach operates under the assumption that the performance level parameters are distributed as a Beta distribution and can be extended to multi-label case in a straightforward iterative method. This technique has been shown to provide a stabilizing influence on STAPLE estimates. On the other hand, STAPLER provides an explicit method of taking into account training data and provides a non-parametric approach to the problem. Moreover, STAPLER was developed with the intent of utilizing data contributed by minimally trained raters and training data is essential in terms of estimating accurate performance level parameters. The approach proposed by Commowick et al. is mainly aimed at easing the duties of highly trained expert anatomists so that the burden of segmenting all structures is dramatically lessened.

II.Theory

A. Problem Statement

Consider an image of N voxels and the task of determining the correct label for each voxel. Let $\tilde{N}$ be the number of voxels for which the true label is known (i.e. training voxels), $\widehat{N}$ be the number of voxels for which truth is unknown (i.e. testing voxels) and these quantities are such that they sum to N (i.e. $\tilde{N}+\widehat{N}=N$). For notational purposes, let N, $\tilde{\mathit{N}}$, and $\widehat{\mathit{N}}$ be the sets of all voxels, training voxels and testing voxels, respectively. The set of labels, L, represents the set of possible values that a rater can assign to all N voxels. Also consider a collection of R raters that observe a subset of N, where it is permissible for each rater to observe voxel i ∈ N more than once. The scalar D_ijr represents the r^th observation of voxel i by rater j, where D_ijr ∈ {∅,0,1, …,L − 1}. Note, if rater j did not observe voxel i for the r^th time then D_ijr = ∅. Let T be a vector of N elements that represents the hidden true segmentation, where T_i ∈ {0,1, …, L − 1}.

B. The STAPLER Algorithm

The STAPLER algorithm provides 3 basic extensions to the traditional STAPLE algorithm. These extensions are 1) the ability to take into account raters that did not observe all voxels, 2) the ability to take into account raters that observed certain voxels more than once and 3) the ability to take into account training data (or catch-trials). The theory is presented alongside the traditional STAPLE approach so that the extensions are made clear.

As with [7], the algorithm is presented in an Expectation Maximization (EM) framework, which breaks the computation into the E-step, or the calculation of the conditional probability of the true segmentation, and the M-step, or the calculation of the rater performance parameters. In the E-step we calculate $W_{si}^{\left(k\right)}$ which represents the probability that voxel i has true label s on the k^th iteration of the algorithm. In the M-step we calculate ${\theta }_{j{s}^{\prime }s}^{\left(k\right)}$ which represents the probability that rater j observes label s′ when the true label is s on the k^th iteration of the algorithm.

C.E-step – Calculation of the conditional probability of the true segmentation

In the traditional STAPLE approach, it is guaranteed that all raters delineated all voxels exactly once and the conditional probability of the true segmentation is given by:

$$\begin{array}{cc}\hfill W_{si}^{\left(k\right)}\equiv & p\left(T_i=s\mid {\mathit{D}}_i,{\theta }^{\left(k\right)}\right)\hfill \\ \hfill =& \frac{p(T_i=\mathrm{s}){\Pi }_j{\theta }_{j{s}^{\prime }s}^{\left(k\right)}}{{\sum }_{n}p(T_i=n){\Pi }_j{\theta }_{j{s}^{\prime }n}^{\left(k\right)}}\hfill \end{array}$$ (1)

where a s′ is the label decision by rater j at voxel i, p(T_i = s) is prior on the label distribution, the denominator simply normalizes the probability such that ${\Sigma }_s{W}_{si}^{\left(k\right)}=1$.

In the present (STAPLER) scenario, raters are allowed to observe all voxels any number of times (including zero). In this case, it can be shown using a straightforward derivation that the correct expression for this conditional probability is found by simply adjusting the product terms to exclude unobserved data points and adding an additional product term to account for multiple observations of the same voxel:

$$\begin{array}{cc}\hfill W_{si}^{\left(k\right)}\equiv & p\left(T_i=s\mid {\mathit{D}}_i,{\theta }^{\left(k\right)}\right)\hfill \\ \hfill =& \frac{p(T_i=\mathrm{s}){\Pi }_{\mathrm{r}}{\Pi }_{j:D_{ijr}\ne \varnothing }{\theta }_{j{s}^{\prime }s}^{\left(k\right)}}{{\sum }_{n}p(T_i=n){\Pi }_{\mathrm{r}}{\Pi }_{j:D_{ijr}\ne \varnothing }{\theta }_{j{s}^{\prime }n}^{\left(k\right)}}\hfill \end{array}$$ (2)

where s′ is the r^th observed label value by rater j at voxel i and ∅ indicates that rater j did not observe voxel i for the r^th time. The product over all r makes it possible to take into account raters that either did not observe voxel i, or observed it multiple times. Note that for both Eqs. (1) and (2), only the values of $i\in \tilde{\mathit{N}}$ are iterated over as the true label value for $i\in \widehat{\mathrm{N}}$ is already known. In other words, $W_{si\in \tilde{\mathit{N}}}=I(T_i=s)$ where I is the indicator function.

D.M-step – Calculation of the rater performance parameters

Next, we consider how the presence of incomplete, over-complete and training data affect the calculation of the performance level parameters. In [7], the update equation for parameter estimates (for all raters observing all voxels and with no “known” data) was shown to be:

$${\theta }_{j{s}^{\prime }s}^{(k+1)}=\frac{{\Sigma }_{i:D_{ij}=s^{\prime }}{W}_{si}^{\left(k\right)}}{{\Sigma }_i{W}_{si}^{\left(k\right)}}$$ (3)

where the denominator simply normalizes the equation such that ${\Sigma }_{s^{\prime }}{\theta }_{j{s}^{\prime }s}^{(k+1)}=1$. Additionally, it is important to note that this implementation has no way of taking into account training data, thus the summations are only iterated over $i\in \widehat{\mathit{N}}$.

To extend in this framework to the STAPLER case, we perform three modifications. First, we only iterate over voxels that were observed by the rater. Second, we iterate multiple times over voxels that were observed more than once by the same rater. Lastly, instead of iterating only over the testing data, we iterate over all i ∈ N. The result of performing these modifications is shown to be:

$${\theta }_{j{s}^{\prime }s}^{(k+1)}=\frac{{\Sigma }_{i\in \mathit{N}}{\Sigma }_{\mathrm{r}}I(D_{ijr}=s^{\prime })W_{si}^{\left(k\right)}}{{\Sigma }_{i\in \mathit{N}}{\Sigma }_{\mathrm{r}}I(D_{ijr}\ne \varnothing )W_{si}^{\left(k\right)}}$$ (4)

where the numerator iterates over all observations by rater j that were equal to label s′ and the denominator is a normalizing factor that iterates over all observed voxels by rater j. Note that the calculation includes both the training data and the testing data. However, the true segmentation for the training data is assumed to be known. Thus, it is straightforward to compute the true rater performance for the training data and only iterate over the testing data like the technique seen in Eq. (3).

$$\begin{array}{cc}\hfill {\theta }_{j{s}^{\prime }s}^{(k+1)}=& \frac{{\Sigma }_{i\in \tilde{\mathit{N}}}{\Sigma }_{\mathrm{r}}I(D_{ijr}=s^{\prime }\cap T_i=s)+{\Sigma }_{i\in \widehat{\mathit{N}}}{\Sigma }_{\mathrm{r}}I(D_{ijr}=s^{\prime })W_{si}^{\left(k\right)}}{{\Sigma }_{i\in \tilde{\mathit{N}}}{\Sigma }_{\mathrm{r}}I(D_{ijr}\ne \varnothing \cap T_i=s)+{\Sigma }_{i\in \widehat{\mathit{N}}}{\Sigma }_{\mathrm{r}}I(D_{ijr}\ne \varnothing )W_{si}^{\left(k\right)}}\hfill \\ \hfill =& \frac{{\tilde{N}}_{js}{\tilde{\theta }}_{j{s}^{\prime }s}+{\Sigma }_{i\in \widehat{\mathit{N}}}{\Sigma }_{\mathrm{r}}I(D_{ijr}=s^{\prime })W_{si}^{\left(k\right)}}{{\tilde{N}}_{js}{\Sigma }_{s^{\prime }}{\tilde{\theta }}_{j{s}^{\prime }s}+{\Sigma }_{i\in \widehat{\mathit{N}}}{\Sigma }_{\mathrm{r}}I(D_{ijr}\ne \varnothing )W_{si}^{\left(k\right)}}\hfill \end{array}$$ (5)

where ${\tilde{\mathrm{N}}}_{\mathrm{j}\mathrm{s}}$ is the number of times rater j observed label s in the training data, and ${\tilde{\theta }}_{j{s}^{\prime }s}$ is the observed performance parameters from the training data. Note, in situations where $\tilde{N}\gg \widehat{N}$ (i.e. significantly more training data than testing data) then it is unlikely that the testing data would dramatically change the performance level estimates.

In Eq. (5), we consider what happens when training data is available that is, when the reliabilities of a rater have been separately estimated in a previous experiment or when it is otherwise reasonable to assume prior knowledge of a rater’s reliabilities. Training data may be included in Eq. (5) as the introduction of data that has been labeled by a rater of known reliability. If the rater represents a gold standard, then the associated confusion matrix is the identity matrix, but one can use a “less than perfect” confusion matrix if the training data “solution set” has imperfections i.e., if the experimental truth had been learned by STAPLE (or STAPLER). The inclusion of training data in Eq. (5) can be viewed as an empirical (i.e., non-parametric) prior on the rater reliabilities. When no data is recorded for a rater, the empirical distribution defines the rater’s reliability. As more data is acquired, the impact of the empirical prior diminishes. We can generalize the impact of empirical training data on the estimation of rater reliability through incorporation of an exogenously generated prior probability distribution. For example, training data from a canonical, or representative, rater may be used in place of explicit training data. Alternatively, an explicit prior may be introduced by incorporation of data motivated by a theoretical characterization of raters for a given task.

It is important to address the fact that in realistic situations it is unlikely that raters would exhibit temporally or spatially constant performance. This idea has been addressed through implementations that ignore consensus voxels [19] and a more recently proposed idea in which spatial quality variations are taken into account using multiple confusion matrices per rater [20]. STAPLER idealizes the situation by assuming that rater performance is consistent enough such that the training data is an accurate depiction of a given rater’s performance. From our initial experimentation, this assumption seems to be only slightly violated on empirical data. Nevertheless, addressing spatial and temporal rater consistency variation is a fascinating area of continuing research.

E. Modification of the Prior Label Probabilities

There are several possible ways one could model theunconditional label probabilities (i.e., the label priors as opposed to the rater priors, described above). If the relative sizes of the structures of interest are known, a fixed probability distribution could be used. Alternatively, one could employ a random field model to identify probable points of confusion (as in [7]). The simpler models have the potential for introducing unwanted bias while field based models may suffer from slow convergence. Here, we use an adaptive mean label frequency to update the unconditional label probabilities:

$$p{(T_i=s)}^{k+1}=\frac{{\Sigma }_{i\in \widehat{\mathrm{N}}}{\mathrm{W}}_{si}^{\left(k\right)}}{\widehat{\mathrm{N}}}$$ (6)

This simple prior avoids introducing substantial label volume bias, as would occur with a fixed (non-adaptive) or equal probability prior. By introducing this prior Eq. (2) is now modified to be

$$W_{si}^{\left(k\right)}=\frac{p{(T_i=\mathrm{s})}^{\left(k\right)}{\Pi }_{\mathrm{r}}{\Pi }_{j:D_{ijr}\ne \varnothing }{\theta }_{j{s}^{\prime }s}^{\left(k\right)}}{{\sum }_{n}p{(T_i=n)}^{\left(n\right)}{\Pi }_{\mathrm{r}}{\Pi }_{j:D_{ijr}\ne \varnothing }{\theta }_{j{s}^{\prime }n}^{\left(k\right)}}$$ (7)

where the a priori distribution is modified at each iteration.

While we believe it is unlikely to occur in practice, it is possible in principle that using this iterative global prior may prevent STAPLER from converging. This would occur if the estimation was constantly oscillating between conflicting estimations for the performance levels and the true segmentation. We have seen more accurate estimations of the true segmentation occur using this prior; however, if convergence issues occur we suggest using the traditional global prior described in [7].

III. Methods and Results

A. Terminology

In the following, we investigate the performance of STAPLE and STAPLER when used with label observations from different categories of possible underlying “true” distributions and from different classes of raters. We use several levels of randomization in order to model and evaluate the different scenarios, and proper interpretation of our results requires a common and consistent terminology throughout:

• A label is an integer valued category assigned to an anatomical location (e.g., pixel or voxel).

• A label set is a collection of labels that correspond to a set of locations in a dataset (typically, associated via spatial extent – e.g., an image).

• A truth model for a label set defines the true labels for each anatomical location.

• A generative label model is a definition for the probability of observing a particular label set.

• A family of generative label models defines a series of related generative label models.

• A rater is an entity (typically a person or simulated person) who reports (observes) labels.

• A rater model characterizes the stochastic manner in which a rater will report a label given a true value of a label for a particular location.

Since we are considering STAPLE and STAPLER approaches without the use of spatial regularization, the relative order of a label within a label set—i.e., its particular spatial arrangement or location—does not impact statistical fusion. Therefore, the label size, volume, or area is simply the number of pixels or voxels, and this number also directly corresponds to label probability.

B. Data

Imaging data were acquired from two healthy volunteers who provided informed written consent prior to the study. A high resolution MPRAGE (magnetization prepared rapid acquired gradient echo) sequence was acquired axially with full head coverage (149×81×39 voxels, 0.82×0.82×1.5 mm resolution). In order to generate realistic simulated label sets, ground truth labels were established by an experienced human rater who labeled the cerebellum from each dataset with 12 divisions of the cerebellar hemispheres (see Figures 3B and 4A) [21, 22]. For additional experiments the a topological brain atlas with 12 topologically correct brain, cerebellar, and brainstem labels was used as a truth model [23].

Figure 3.

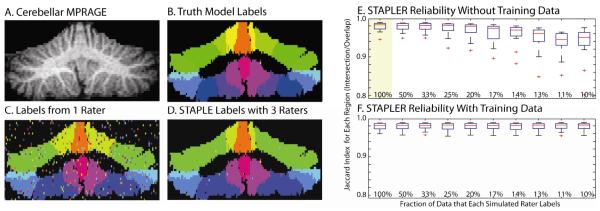
Simulations with voxel-wise random raters. Coronal sections of the three-dimensional volume show the high resolution MRI image (A), manually drawn truth model (B), an example delineation from one random voxel-wise rater (C), and the results of a STAPLE recombination of three label sets (D). STAPLER fuses partial label sets, but performance degrades with decreasing overlap (E). With training data (F), STAPLER performance is consistent even with each rater labeling only a small portion of the dataset. Box plots in E and F show mean, quartiles, range up to 1.5σ, and outliers. The highlighted plot in E indicates the simulation for which STAPLER was equivalent to STAPLE--i.e., all raters provide a complete set of labels.

Figure 4.

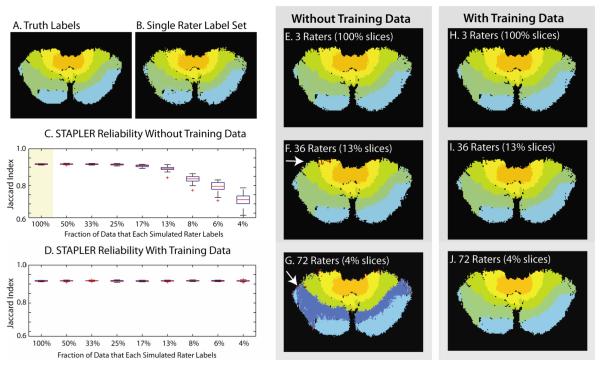
Simulations with boundary random raters. Axial sections of the three-dimensional volume show the manually drawn truth model (A) and sample labeling from a single simulated rater (B) alongside STAPLER fused results from 3, 36, and 72 raters producing a total of 3 complete labeled datasets without training data (E-G) and with training data (H-J). Note that boundary errors are generated in three-dimensions, so errors may appear distant from the boundaries in cross-sections. Boundary errors (e.g., arrow in F) increased with decreasing rater overlap. Label inversions (e.g., arrow in G) resulted in very high error with minimal overlap. As with the voxel-wise rater model (Figure 3), STAPLER fuses partial label sets, but performance degrades with decreasing overlap (C). With the addition of training data (D), STAPLER sustains performance even with each rater labeling only a small portion of the dataset.

Simulated label sets were derived from simulated raters using a Monte Carlo framework. Two distinct models of raters (described below) were evaluated as illustrated in Figure 2 and described below.

Figure 2.

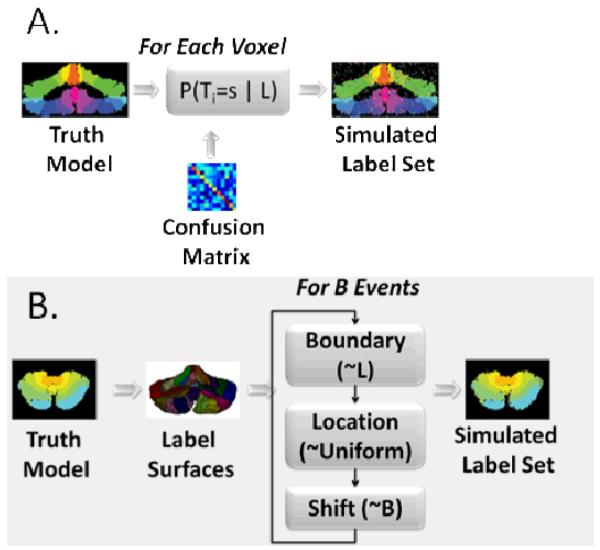
Random rater models. In a voxel-wise model (A), the distribution of label probabilities depends on the underlying true label, but does not depend on the local neighborhood or spatial position. In a boundary random rater model (B), errors are uniformly distributed on the boundaries between regions. Sampling of boundary errors is done iteratively with replacement and model updating so that it is possible for cumulative errors to shift the boundary by multiple voxels in any location. The “For B Events” panel indicates that the procedure is performed for all boundary voxels. Boundary surfaces are stored at voxel resolution on a Cartesian grid.

In the first model (“voxel-wise random rater,” see Figure 2A), each rater was assigned a confusion matrix such that the i,jth element indicates the probability that the rater would assign the jth label when the ith label is correct. Label errors are equally likely to occur throughout the image domain and exhibit no spatial dependence. The background region is considered a labeled region. This is the same model of rater performance as employed by the STAPLE (or STAPLER) statistical framework. To generate each pseudo-random rater, a matrix with each entry corresponding to a uniform random number between 0 and 1 was created. The confusion matrix was generated by adding a scaled identity matrix to the randomly generated matrix and normalizing column sums to one such that the mean probability of true labels was 0.93 (e.g., the mean diagonal element was 0.93). Ten Monte Carlo iterations were used for each simulation.

In the second model (“boundary random raters”, see Figure 2B), errors occurred at the boundaries of labels rather than uniformly throughout the image domain. Three parameters describe rater performance: r, l, and b. The scalar r is the rater’s global, true positive fraction. The boundary probability vector l encodes the probability, given an error occurred, that it was at the ith boundary. Finally the vector b describes the error bias at every boundary which denotes the probability of shifting a boundary toward either bounding label. For an unbiased rater, b_i = 0.5, ∀i. Twenty-five Monte Carlo iterations were used for each simulation. To generate a pseudo-random rater, the boundary probability vector was initialized to a vector with uniform random coefficients and normalized to sum to 1. To generate a simulated random dataset with a given boundary rater, the voxel-wise mask of truth labels was first converted into a set of boundary surfaces. Then, the following procedure was repeated for (1 – r) ∣B∣ iterations (where B is the set of all boundary voxels).

• A boundary surface (a pair of two labels) was chosen according to the l distribution. If the boundary did not exist in the current dataset, a new boundary surface was chosen until it did exist.

• A boundary point within the chosen surface was selected uniformly at random for all boundary points between the two label sets.

• A random direction was chosen Bernoulli(b_i) to determine if the boundary surface would move toward the label with the lower index or the label with the high index.

• The set of boundary voxels was updated to reflect the change in boundary position. With the change in labels, the set of boundary label boundary pairs was also updated.

In this study, the mean rater performance was set to 0.8 and the bias term was set to 0.5. These settings were chosen as we felt it was a realistic model of unbiased rater performance. Note that the boundary probability vector, l, was randomly initialized for each rater, which helps ensure that each rater is still unique in the manner in which they observe each voxel.

C.Implementation and Evaluation

STAPLER was implemented in Matlab (Mathworks, Natick, MA). The implementations of STAPLE and STAPLER presented in this manuscript are fully available via the “MASI Label Fusion” project on the Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC, www.nitrc.org/projects/masi-fusion). The random rater framework and analysis tools were implemented in the Java Image Science Toolkit (JIST, http://www.nitrc.org/projects/jist/ [24, 25]). All studies were run on a 64 bit 2.5 GHz notebook with 4 GB of RAM. As in [7], simultaneous parameter and truth level estimation was performed with iterative expectation maximization.

Simulation experiments with random raters were performed with a known, true ground truth model. The accuracy of each label set for Simulations 1 and 2 was assessed relative to the truth model with the Jaccard similarity index [26, 27] for each labeled region:

$${\mathrm{J}}_{\mathrm{T}}(\mathrm{X},\mathrm{Y})=\frac{\mid \mathrm{X}\cap \mathrm{Y}\mid }{\mid \mathrm{X}\cup \mathrm{Y}\mid }=\frac{{\sum }_{{\mathrm{X}}_{\mathrm{i}}=\mathrm{T}\text{and}{\mathrm{Y}}_{\mathrm{i}}=\mathrm{T}}1}{{\sum }_{{\mathrm{X}}_{\mathrm{i}}=\mathrm{T}\text{or}{\mathrm{Y}}_{\mathrm{i}}=\mathrm{T}}1}$$ (8)

where X is either an individual or reconstructed label set and Y is the true label set. Bars indicate set cardinality. For Simulation 3 the Dice Similarity Coefficient (DSC) [28] is used to analyze the accuracy of each label set:

$${\mathrm{DSC}}_{\mathrm{T}}(\mathrm{X},\mathrm{Y})=\frac{2\mid \mathrm{X}\cap \mathrm{Y}\mid }{\mid \mathrm{X}\mid +\mid \mathrm{Y}\mid }=\frac{2\left({\sum }_{{\mathrm{X}}_{\mathrm{i}}=\mathrm{T}\text{and}{\mathrm{Y}}_{\mathrm{i}}=\mathrm{T}}1\right)}{{\sum }_{{\mathrm{X}}_{\mathrm{i}}=\mathrm{T}}1+{\sum }_{{\mathrm{Y}}_{\mathrm{i}}=\mathrm{T}}1}$$ (9)

where X and Y are defined in the same manner as Eq. (8). The Jaccard index and DSC range from 0 (indicating no overlap between label sets) to 1 (indicating no disagreement between label sets). Multiple label accuracy assessment techniques were used to diversify the presentation of our analysis.

D.Simulations 1 and 2: Fusion of Incomplete and Over-Complete Datasets

Simulated label sets were generated according to the characteristic label sets and randomized rater distributions. For each rater model (voxel-wise random raters and boundary random raters), the following set of experiments was carried out. Traditional STAPLE was first evaluated by combining labels from 3 random raters (Eqns. (1) and (3)). Each of the three synthetic raters was modeled as having labeled one complete dataset. STAPLER was evaluated by labels from three complete coverages where M total raters were randomly chosen to perform each coverage (Eqns. (2) and (5)). Each rater delineated approximately 1/M^th (i.e., each rater labels between 50% and 4% of slices with the total amount of data held constant), where M is the number of raters used to observe each coverage. Note that all simulations were designed such that each voxel was labeled exactly three times; only the identity of the simulated rater who contributed these labels randomly varied.

Next, the advantages of incorporating training data were studied for both rater models by repeating the STAPLER analysis with all raters also fully labeling a second, independent test data set with known true labels (Eqns. (2) and (5)). Note, when M=1 (i.e. each rater labeled the whole brain) and no training data is used STAPLER is equivalent to STAPLE. In these simulations, explicit rater priors (e.g., priors not implied by training data) were not used. The procedure was repeated either 10 or 25 times (as indicated) and the mean and standard deviation of overlap indices were reported for each analysis method. As in the first experiment, all simulations were designed such that each voxel was labeled exactly three times; only the identity of the simulated rater who contributed these labels varied.

E. Simulation 1 Results: Incomplete Label Fusion with Voxel-Wise Random Raters

For a single voxel-wise random rater, the Jaccard index was 0.67±0.02 (mean ± standard error across all regions over simulated datasets, one label set is shown in Figure 3C). The traditional STAPLE approach with three raters visually improved the consistency of the results (one label set is shown in Figure 3D), and the average Jaccard index increased to 0.98±0.012 (first column of Figure 3E). In the remaining experiments, the traditional STAPLE algorithm cannot be used in a volumetric manner; although each voxel is labeled exactly three times, the number of raters from which each label is selected is greater than 3, and therefore STAPLER must be used. As shown in Figure 3E, STAPLER consistently resulted in Jaccard indexes above 0.9, even when each individual rater labeled only 10 percent of the dataset. Additionally, the STAPLER performance where each rater only observed a third of the dataset (3^rd column Figure 3E) resulted in an equivalent performance (in terms of Jaccard index) to the STAPLE approach (1^st column Figure 3E). As the fraction of the data observed decreased beyond a third, the STAPLER performance saw a slowly degraded performance. For all STAPLER simulations, use of multiple raters improved the label reliability over that which was achievable with a single rater (Figure 3E).

As shown in Figure 3F, use of training trials greatly improved the accuracy of label estimation when many raters each label a small portion of the data set (Figure 3E). No appreciable differences were seen when the number of raters providing the same quantity of total data were varied (as indicated by the consistent performance across labeling fraction).

Lastly, it is important to note that, as with [12], a large number of observations by raters were fused (e.g. more than 35). Theoretically, it is possible for dramatic numerical instability issues to occur using double precision arithmetic with this many raters. However, the authors of this paper did not see any evidence of mathematical instability during the writing of this manuscript.

F. Simulation 2 Results: Incomplete Label Fusion with Boundary Random Raters

For a single boundary random rater, the Jaccard index was 0.83±0.01 (representative label set shown in Figure 4B). Using three raters in a traditional STAPLE approach increased the average Jaccard index to 0.91±0.01 (one label set shown in Figure 4E). As shown in Figure 4C, the STAPLER approach led to consistently high Jaccard indexes with as low as 25 percent of the total dataset labeled by each rater. However, with individual raters generating very limited data sets (<10%), STAPLER yielded Jaccard indexes lower than that of a single rater—clear evidence that use of multiple raters can be quite detrimental if there is insufficient information upon which to learn their reliabilities. In a further analysis of this scenario, we found that the off-diagonal elements of the estimated confusion matrices become large and result in “label switching” (seen in Figure 4C and E-G). This behavior was not routinely observed in the first experiment, but is one factor that led toward increased variability of Jaccard index in the second experiment (see outlier data points in Figure 3E).

As shown in Figure 4D and H-J, use of data from training trials alleviates this problem by ensuring that sufficient data on each label from each rater is available. The Jaccard index showed no appreciable differences when raters labeled between 4 percent and 100 percent of the dataset. We also observed that the artifactual, large off-diagonal confusion matrix coefficients were not present when training data were used. This is strong evidence that use of training data stabilizes the reliability matrix estimation process and can be a key factor in label estimation when using large numbers of “limited” raters.

G.Simulation 3: Relationship between Positive Predictive Value and Fusion Accuracy

In this simulation, we investigate the causes of the major failures of STAPLE and attempt to relate it back to a single metric. We propose that the positive predictive value (PPV) associated with the raters for each label could serve as a predictor for the quality relationship between STAPLE, Majority Vote and STAPLER. We define the positive predictive value for rater j as the probability that a given voxel has true label s, given that the rater observed label s′. Note, this is closely related (Bayes rule) to the values of the performance level parameters (confusion matrices) where each element represents the probably that rater j observes labels s’ given that the true label is s.

In order to assess this relationship, we apply STAPLE, STAPLER and Majority Vote to simulated label sets corresponding to a model in which there is one large label (80% of the total volume) and eight small labels (each corresponding to 2.5% of the total volume). The total volume was 100×100×25 voxels. A collection of five raters were used for all experiments. All raters observed each voxel exactly once. In a series of 20 experiments, PPV was linearly varied between 0.2 and 0.9. For each experiment, 10 Monte Carlo iterations were used with raters constructed such that simulated confusion matrices were randomly constructed with the specified PPV. All raters were equally likely to miss at all voxels (i.e. the STAPLE model of rater behavior). The implementation of STAPLER used a collection of training data that was the same size as the testing data. Thus, when calculating the STAPLER performance level parameters, the training estimate provided an approximately 50% bias to final performance level estimates on the testing data. Matlab code to perform the construction of random rater construction is included in the indicated repository.

H.Simulation 3 Results: Exploring Rater Priors and STAPLE’s Modes of Failure

The results (in terms of fraction voxels correct) for Majority Vote, STAPLE and STAPLER with respect to the PPV are presented in Figure 5. STAPLER outperforms both STAPLE and Majority Vote for all presented PPV’s. Interestingly, for PPV’s less than 0.7 Majority Vote consistently outperforms STAPLE. Two-sided t-tests were performed to assess differences between experiments. The reason for this is mainly attributed to the fact that STAPLE is unable to converge to an accurate estimate of the performance level parameters. However, by utilizing the training data STAPLER is able to provide a much more accurate estimate of the true segmentation. Unfortunately, for low PPV’s the performance of all three algorithms is quite poor.

Figure 5.

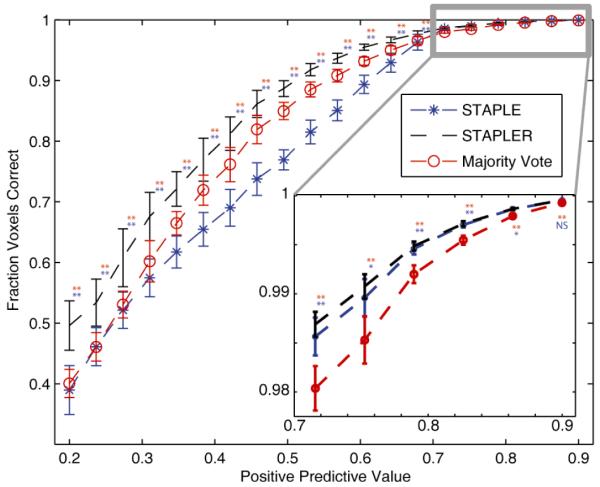
Relationship between the accuracy of fusion algorithms and positive predictive value (PPV). The accuracy of STAPLE, STAPLER and Majority Vote were assessed with respect to the PPV. The PPV presented is the same for all 5 raters in each experiment with 10 Monte Carlo iterations per PPV. The confusion matrices were constructed as to maintain the PPV for each rater. Each rater was equally likely to make a mistake at all voxels (i.e. the STAPLE model of rater behavior holds). The results of a two-sided t-test can be seen next to each of the data points, where red corresponds to the test between STAPLER and majority vote, and blue corresponds to the test between STAPLER and STAPLE. Note, ** indicates p < 0.001, * indicates p < 0.05, and NS indicates that the results were not significant. The results indicate that for PPV’s less than 0.7 Majority Vote consistently outperforms STAPLE despite the fact that the expected STAPLE of model of rater behavior holds. STAPLER outperforms the other algorithms for all PPV’s. The inlay shows that for PPV’s between 0.7 and 0.9 (generally considered the normally operating range) STAPLE is nearly as good as STAPLER and outperforms Majority Vote.

The results seen in the inlay on Figure 5 are in line with the traditionally presented results when comparing STAPLE and Majority Vote. As expected, for higher PPV’s STAPLE begins to outperform majority and is able to improve the quality of the performance level estimates used to estimate the true segmentation. STAPLER is consistently equal or better quality than STAPLE. The prior for both STAPLE and STAPLER was set based upon the empirically observed frequencies because the true prior would not be available in practice. This small simulation is consistent with more complete characterizations comparing STAPLE with voting approaches (see review in [17]). The additional use of training data in STAPLER enables more accurate determination of the prior and yields more consistent results.

I. Empirical Example of STAPLER

Finally, quantitative differences between STAPLE and STAPLER were assessed in the practical setting of collaborative labeling of the cerebellum with a high resolution MPRAGE (magnetization prepared rapid acquired gradient echo) sequence. Whole-brain scans of two healthy individuals (after informed written consent prior) were acquired (182×218×182 voxels), and each slice was cropped to isolate the posterior fossa. Both datasets were manually labeled by a neuroanatomical expert in a labor intensive process (approximately 20 hours each). One dataset was designated for training and one for testing. The training data was implemented as catch-trials so the raters were unaware when they were performing training or testing data. Axial cross sections were created and presented for labeling for both data sets. Thirty-eight undergraduate students were recruited as raters. For the axial set, raters labeled between 5 and 75 slices (training: 521 total) and between 10 and 100 slices (testing: 545 total). The raters participated at will for various lengths of time and labeled randomized image sections. As such, overlap of slice contributions between raters was sparse and STAPLE could not be used to simultaneously statistically fuse all data. To compensate, STAPLE was applied on a slice-by-slice basis while STAPLER was applied simultaneously to all data. For comparison, majority vote was also performed.

J. Empirical Example Results

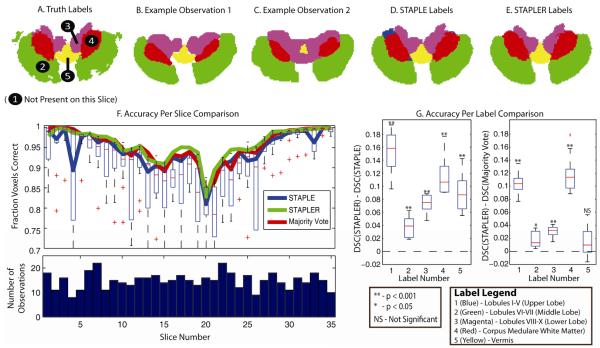
Figures 6A-C present representative slices from the truth model and example observations of that slice from the minimally trained undergraduate students, respectively. We are specifically considering collaborative labeling by minimally (poorly) trained raters, so individual observations vary dramatically. Figure 6D-E present representative STAPLE and STAPLER estimates, respectively. The top portion of Figure 6F presents the accuracy of the estimation (in terms of fraction voxels correct) for STAPLE, STAPLER and the individual observations. It is important to note, however, that STAPLER is consistently as good as or better than the upper quartile of the observations and also outperforms STAPLE for all slices. The bottom part of Figure 6F presents a histogram indicating the number of observations per slice. On average there were about fifteen observations per slice. As with Figure 5, Majority Vote lies largely between the STAPLER and STAPLE approaches. Lastly, Figure 6G represents the accuracy of the algorithms on a per label basis (excluding background) in terms of the DSC. STAPLER significantly outperforms STAPLE on all labels (two-sided t-test), and is significantly better than majority vote on all labels except the vermis. This is mainly because of the fact that STAPLER is able to construct a significantly more accurate estimate of the performance level parameters because of the ability to take into account incomplete, over-complete and training data all at once.

Figure 6.

Empirical experiment using axial cross-section of cerebellar data to assess the performance of STAPLE (on a slice-by-slice basis) and STAPLER (volumetric fusion). The representative slices shown in (A) – (C) present an example truth model, and observations by minimally trained undergraduate students, respectively. The slices seen in (D) and (E) are the estimated labels by STAPLE and STAPLER, respectively. The plot on the top of (F) shows the accuracy on a per slice basis of the observations (box plots) STAPLER (green), STAPLE (blue), and majority vote (red). The histogram on the bottom of (F) shows the number of observations per slice. Lastly, the plot seen in (G) shows the difference in DSC between STAPLER, STAPLE, and majority vote on a per label basis. The legend for these label numbers can be seen at the bottom of (G).

IV. Discussion

STAPLER extends the applicability of the STAPLE technique to common research situations with missing, partial, and repeated data, and facilitates use of training data and reliability priors to improve accuracy. These ancillary data are commonly available and may either consist of exact known labels or raters with known reliability. A typical scenario would involve a period of rater training followed by their carrying out a complete labeling on the training set. Alternatively, a model (parametric or empirical) of a typical rater could be used to stabilize rater reliability estimates. Only then would they carry out independent labeling of test data. STAPLER was successful both when simulated error matched modeled errors (i.e., the voxel-wise model) and with more realistic, boundary errors, which is promising for future application to work involving efforts of large numbers of human raters. STAPLER extensions are independent of the manifold of the underlying data. These methods are equally applicable to fusion of volumetric labels [29-31], labeled surfaces [32, 33], or other point-wise structures.

With the newly presented STAPLER technique, numerous raters can label small, overlapping portions of a large dataset, which can be recombined into a single, reliable label estimate, and the time commitment from any individual rater can be minimized. This enables parallel processing of manual labeling and reduces detrimental impacts should a rater become unavailable during a study. Hence, less well trained raters who may participate on a part-time basis could contribute. As with STAPLE, both the labels and degrees of confidence on those labels are simultaneously estimated, so that subsequent processing could make informed decisions regarding data quality. Such an approach could enable collaborative image labeling and be a viable alternative to expert raters in neuroscience research.

Decreases in reliability with low overlap were observed with STAPLER. This may arise because not all raters have observed all labels with equal frequency. For smaller regions, some raters may have observed very few (or no data points). During estimation, the rater reliabilities for these “under seen” labels can be very noisy and lead to unstable estimates, which can result in estimation of substantial off-diagonal components of the confusion matrix (i.e., overestimated error probabilities). These instabilities were to be resolved through inclusion of training data; the use of training data effectively places a data-adaptive prior on the confusion matrix. Since each rater provides a complete dataset, each label category is observed by each rater for a substantial quantity of voxels. Hence, the training data provide evidence against artifactual, large off-diagonal confusion matrix coefficients and improves estimation stability. Furthermore, without missing categories, there are no undetermined confusion matrix entries.

The inclusion of priors on rater reliability can be seen as forming a seamless bridge between pure STAPLE approaches (in which reliability is estimated) and weighted voting (which use external information to establish relative weights). The former can be considered optimal when raters are heterogeneous and sufficient data are available, while the latter are well-known to be stable. In the proposed approach, the reliability priors have an impact inversely proportional to the amount of data present for a particular label.

The characterization of STAPLE failure according to the positive predictive value (as opposed to simply region size) opens significant opportunities for predicting when additional regularization might be needed. Intuitively, positive predictive value is a natural metric for assessing the likelihood of STAPLE failure. With low positive predictive value, each label observation provides little information. For a constant overall true positive rate, the average positive predictive value across voxels is constant; however, the positive predictive value across labels can vary substantially due to heterogeneous region volume, rater reliability, or relative proportion of observations per label class. We found that for five raters, low positive predictive values STAPLE is generally outperformed by Majority Vote, while for moderate positive predictive values (between 0.7 and 0.9 - generally considered to be the expected operating range), STAPLE is shown to outperform Majority Vote.

Evaluation of STAPLER with heterogeneous labeled datasets is an active area of research. Improvements in Jaccard index in the boundary rater model were less than that in the voxel-wise random rater model (from 0.83 to 0.91 versus 0.67 to 0.98). In the voxel-wise rater example, both the estimation and underlying error models were the same. In the boundary rater model, the model used during estimation was only a loose approximation of the underlying mechanism. This result provides an indication that simple rater confusion models may still be effective in practice (with human raters) when difficult to characterize interdependencies that might exist between rater confusion characteristics, the data, and temporal characteristics.

As with the original STAPLE algorithms, STAPLER can readily be augmented by introducing spatially adaptive, unconditional label probabilities, such as with a Markov Random Field (MRF). Yet, inclusion of spatially varying priors in statistical fusion is widely discussed, but rarely used. Spatially varying prior parameters were suggested for STAPLE in the initial theoretical presentation by Warfield et al [1]. However, almost uniformly, literature reports using STAPLE have ignored spatial variation and instead opted for a single global parameter (e.g., [1-10]). Hence, application of spatially varying priors remains a tantalizing and important area of potential growth, but it is beyond the scope of the present paper. This work provides an important and necessary “stepping stone” in the direction of spatially varying priors. When we and/or others provide a more solid foundation for the incorporation of spatially varying priors, the present paper will provide an existing approach in scenarios where data are missing or redundant and for cases where consensus data are unavailable due to either poorly trained or large numbers of raters.

Biography

Bennett A. Landman (M’01–S’04–M’08) was born in San Francisco, California and studied electrical engineering and computer science (BS’01 and MEng’02) at the Massachusetts Institute of Technology (Cambridge, MA). After returning from industry, he pursued a doctoral degree in biomedical engineering at Johns Hopkins University (Baltimore, MD).

In 1999, he joined ViaSense, Inc., a startup company in Emeryille, CA, and continued full-time as a research engineer after his undergraduate graduation. In 2003, he became a Senior Software Engineer at Neurobehavioral Research, Inc., Corte Madera, CA. In 2008, he joined Johns Hopkins as an Assistant Research Professor in the Department of Biomedical Engineering. Since January 2010, he has been an Assistant Professor in the Department of Electrical Engineering at Vanderbilt University (Nashville, TN). His research concentrates on analyzing large-scale cross-sectional and longitudinal neuroimaging data. Specifically, he is interested in population characterization with magnetic resonance imaging (MRI), multi-parametric studies (DTI, sMRI, qMRI), and shape modeling.

Dr. Landman is a member of the SPIE and international society for magnetic resonance in medicine (ISMRM).