Efficacy of Phototherapy for Newborns with Hyperbilirubinemia: A Cautionary Example of an Instrumental Variable Analysis

Abstract

Background

Use of instrumental variables is gaining popularity as a method of controlling for confounding by indication in observational studies of treatments.

Objectives

To illustrate how unmeasured instrument-level treatment substitution can distort effect size estimates using as an example an instrumental variable analysis of phototherapy for neonatal jaundice.

Design

Retrospective cohort study.

Setting

Northern California Kaiser Permanente Hospitals.

Patients

The authors studied 20,731 newborns ≥2000 g and ≥35 weeks' gestation born 1995–2004 with a “qualifying” total serum bilirubin (TSB) level within 3 mg/dL of the 2004 American Academy of Pediatrics (AAP) phototherapy threshold who did not have a positive direct antiglobulin test.

Measurements

The intervention was inpatient phototherapy within 8 hours of the qualifying TSB. The outcome was a TSB level exceeding the AAP exchange transfusion threshold <48 hours from the qualifying TSB. The instrumental variable was a measure of the frequency of phototherapy use at the newborn's birth hospital. The unmeasured substituted treatment was supplementation with infant formula, assessed by chart review in a sample from the same cohort.

Results

In total, 128 infants (0.62%) exceeded the exchange transfusion threshold. Logistic and propensity analyses yielded crude odds ratios of ∼0.5 for phototherapy efficacy, decreasing to ∼0.2 with control for confounding by indication. Instrumental variable analyses suggested much greater phototherapy efficacy (e.g., odds ratios of 0.02–0.05). However, chart reviews revealed greater use of infant formula (which also lowers bilirubin levels) in hospitals that used more phototherapy (r = 0.56; P = 0.02), an association not present at the individual level (r = 0.13).

Conclusions

Instrumental variable analyses may provide biased estimates of treatment efficacy if there are cointer-ventions or confounders associated with treatment at the level of the instrument, even when these associations may not exist in individuals.

Background

Although jaundice in newborns is common and generally benign, very high total serum bilirubin (TSB) levels can injure the newborn's central nervous system.^1,2 For this reason, TSB levels in jaundiced newborns are followed and sometimes treated with either phototherapy or exchange transfusion if they are at risk of rising to or have already reached potentially dangerous levels. The American Academy of Pediatrics (AAP) has published guidelines³ that suggest TSB levels at which phototherapy and exchange transfusions are recommended for term and late preterm newborns. However, no randomized trials have quantified the efficacy of these interventions at the TSB levels at which they are currently recommended. Even a randomized trial of phototherapy, which is done much more commonly than exchange transfusion, would be difficult to do because relevant outcomes, such as a TSB level exceeding the AAP's threshold for exchange transfusion, are rare^4,5 and because there are ethical obstacles to randomizing newborns not to receive a therapy recommended by the AAP.

We recently reported a historical cohort study that took advantage of practice variation in the use of phototherapy in the Northern California Kaiser Permanente Medical Care Program (NC-KPMCP). We estimated the efficacy of phototherapy at preventing significant hyperbilirubinemia in infants with TSB levels within 3 mg/dL of the AAP's phototherapy threshold.⁶ We found that inpatient phototherapy was effective in newborns who did not have a positive direct antiglobulin test (DAT), with a multivariate odds ratio of 0.16 (95% confidence interval [CI], 0.07–0.34). However, we did not have data on breastfeeding or formula use for that study. Because continuing exclusive breastfeeding is a risk factor for subsequent hyperbilirubinemia,⁷ we reasoned that phototherapy was more indicated and therefore might be more commonly used in infants continuing to breastfeed exclusively. Thus, we expected that the effect of not having breastfeeding data might be residual confounding by indication, which would cause the observed odds ratio to be falsely high.

Analyses using propensity scores^8,9 and instrumental variables^10–12 are alternatives to standard multivariable models for estimating effects of treatments in observational studies. Instrumental variables differ from the other techniques in that they may allow control for unmeasured confounding variables.^13–15 A good instrumental variable is one that is strongly associated with the treatment of interest (in this case, timely inpatient phototherapy) but not independently associated with the outcome (in this case, a TSB level exceeding the AAP's exchange transfusion threshold within 48 hours). Because of considerable seemingly random variability in the use of phototherapy at different NC-KPMCP facilities,^16,17 we hypothesized that the rate of phototherapy use at the infant's birth hospital might be a good instrumental variable and that use of this technique would provide estimates of treatment efficacy less attenuated by confounding by indication than traditional logistic regression or propensity score analyses. However, our instrumental variable analysis produced what we believe are implausibly low odds ratios. In this report, we compare results of our instrumental variable analyses with those obtained using logistic regression and propensity score analyses and show how an association between formula supplementation and phototherapy use at the hospital level may have led to exaggerated estimates of phototherapy efficacy in the instrumental variable analyses.

Methods

Overall Design, Birth Cohort, and Institutional Review Board Approval

We identified subjects and electronic data for this retrospective cohort study from the cohort of infants born alive in 12 NC-KPMCP hospitals from 1 January 1995 to 31 December 2004 whose birth weight was ≥2000 g and whose gestational age was ≥35 weeks (N = 281,898), as previously described.⁶ This project was approved by the NC-KPMCP Institutional Review Board for the Protection of Human Subjects and by the University of California, San Francisco Committee on Human Research.

Study Subjects

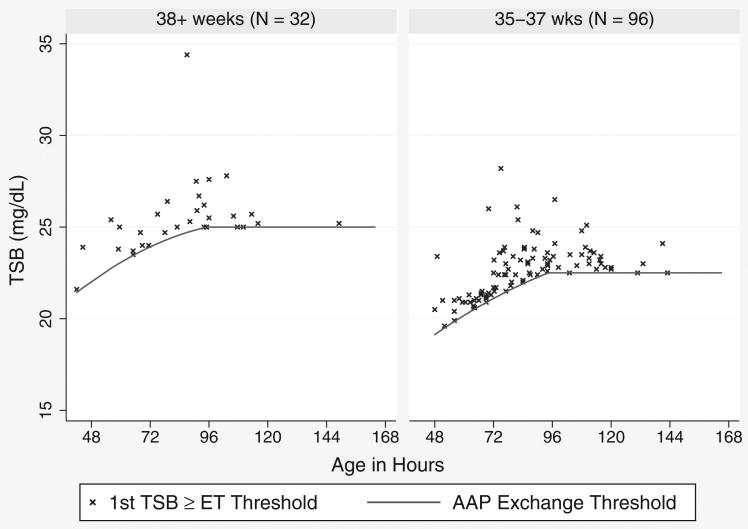
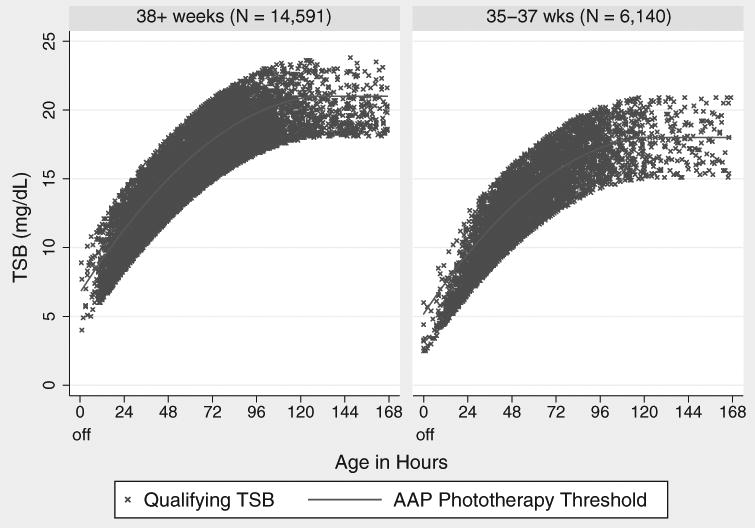
We chose subjects who were reasonable candidates for phototherapy, based on the 2004 AAP hyperbilirubinemia treatment guidelines. These guidelines are summarized in 2 figures, one for phototherapy and one for exchange transfusion. Each figure has TSB treatment threshold lines for infants in 3 risk groups, defined by gestational age (<38 weeks or ≥38 weeks) and the presence of hemolysis or other signs of significant illness. Because we previously found diminished efficacy of phototherapy in DAT-positive infants,⁶ we excluded infants with a positive DAT. Therefore, our study population was divided into the AAP's low- and medium-risk groups based only on whether the gestational age was ≥38 or <38 weeks. For each infant, we then compared all TSB levels to the treatment guidelines and included infants with a TSB level within 3 mg/dL of the AAP phototherapy threshold for their age and gestational age group. For each newborn, we considered the first such TSB the qualifying TSB. We excluded infants if their TSB was already declining, if they did not have a subsequent documented decline in their TSB, or if a conjugated or direct bilirubin level at the time of the qualifying TSB was ≥2.0 mg/dL. Figure 1 shows the qualifying TSB levels and AAP phototherapy thresholds by ages of the included subjects.

Figure 1. Qualifying total serum bilirubin (TSB) levels and American Academy of Pediatrics (AAP) phototherapy guidelines.

Predictor Variables

Covariables

We obtained maternal and infant demographic data, bilirubin levels, hospitalizations, and procedures from NC-KPMCP databases. Because of its strong association with both phototherapy use and the outcome, a key calculated predictor variable was the difference between the newborn's qualifying TSB and the TSB level at which the AAP recommends phototherapy for infants of that age and risk group, which we coded with indicator variables in 1-mg/dL categories (e.g., −3.0 to −2.1 mg/dL, −2.0 to −1.1 mg/dL, etc.).

Intervention

The intervention was receipt of hospital phototherapy within 8 hours of the qualifying TSB. Because timing of hospital phototherapy was not available electronically, we assumed it began 1 hour after admission for readmissions with a procedure code for phototherapy. As previously described,⁶ we assumed all phototherapy during the birth hospitalization began within 8 hours of the qualifying TSB, our a priori point for dichotomizing timely phototherapy. For ease of exposition, hospital phototherapy within 8 hours as defined above may be referred to simply as phototherapy in this article. We treated home phototherapy as a potential confounder and considered it to have been given within 1 day of the qualifying TSB if a home phototherapy unit was delivered on the same day or the day after the qualifying TSB.

Instrumental variables

We used 2 similar instrumental variables. Both were proportions of infants who had a qualifying TSB level 0 to 0.9 mg/dL above the AAP phototherapy threshold for their risk group who received hospital phototherapy within 8 hours of their qualifying TSB level. For the first instrumental variable, we used the proportion for the infant's hospital of birth. The second instrumental variable used the proportion for both hospital and year of birth. Because the AAP guideline takes the newborn's TSB, age, and gestational age into account, these instruments should depend primarily on different propensities to use phototherapy across hospitals and years, rather than on differences in the distribution of these potential confounding variables.

Outcome Variable

Our outcome variable was a TSB level that reached the AAP exchange transfusion threshold within 48 hours of the qualifying TSB.⁶ For TSB levels that exceeded the exchange threshold >48 hours after the qualifying TSB, we estimated the time that the exchange threshold was crossed by assuming a linear increase in TSB levels between the last TSB level below and the first TSB level above the threshold. The TSB levels of the infants who developed the outcome, along with the AAP exchange thresholds for each gestational age group, are shown in Figure 2.

Figure 2. Total serum bilirubin (TSB) levels of infants who exceeded American Academy of Pediatrics (AAP) exchange transfusion (ET) thresholds within 48 hours of their qualifying TSB.

Statistical Analysis

We used SAS (SAS Corporation, Cary, NC) to create data sets from NC-KPMCP databases and Stata 11 for all analyses (Stata Corp, College Station, TX). We used 4 methods to estimate the effect of receiving phototherapy within 8 hours of the qualifying TSB on crossing the exchange threshold within 48 hours. In each method, we adjusted for all of the same covariates included in our earlier analysis,⁶ including qualifying TSB level, sex, birth weight, gestational age in weeks, age in hours, and receipt of phototherapy at home. We then compared this fully adjusted result with those obtained when we omitted all covariates except for birth facility.

The first analysis used standard logistic regression, as in our earlier work.⁶ Standard model checks were performed, including the Hosmer-Lemeshow goodness-of-fit statistic, for nonlinearity (on the logit scale) of the effect of birth weight (the sole continuous covariate), and whether omission of interactions affected the odds ratio (OR) for phototherapy. The second analysis replaced adjustment variables with propensity scores, using logistic regression to control only for the quintile of the fully or minimally modeled propensity score. Overlap of propensity scores for the treated and untreated infants was assessed graphically.

Our third method used a bivariate probit regression model, now the standard instrumental variable approach for data where both the outcome and the exposure of interest are binary. In brief, this approach assumes that the 2 observable binary variables (outcome and intervention) are manifestations of a corresponding pair of unobserved, correlated, bivariate normal latent variables, with the manifest variable taking on a value of 1 if the latent variable was positive and 0 otherwise. More formally, the bivariate probit model can be written as

$$\begin{array}{c}{\text{ETL}}_{\text{i}}={\beta }_0+{\beta }_{\text{T}}{\text{PT}}_{\text{i}}+{\text{z}}_{\text{i}}^{\text{'}}{\beta }_{\text{Z}}+{\varepsilon }_{\text{i}}\hfill \\ {\text{PTL}}_i={\gamma }_0+{\gamma }_{\text{IV}}{\text{IV}}_{\text{i}}+{\text{z}}_{\text{i}}^{\text{'}}{\gamma }_{\text{Z}}+{\text{v}}_{\text{i}}\hfill \end{array},$$ (1)

where ETL_i and PTL_i are, respectively, the latent values determining the probabilities of exceeding the exchange threshold and receiving phototherapy for the ith infant; PT_i is indicator for receipt of phototherapy; IV_i is the value of the instrumental variable for the ith infant; z_i is a vector of additional covariates; ε_i and ν_i are normally distributed error terms (with means 0, variances 1, and correlation ρ); and the βs and γs are parameters to be estimated from the data. If there is uncontrolled confounding in the multivariate analysis, the 2 error terms have a nonzero correlation. This forms the basis of a formal likelihood ratio test on the adequacy of control for confounding in the multivariate logistic and propensity score models.

It can be shown¹⁸ that by accounting for the correlation between the 2 latent variables, the bivariate probit model removes the influence of unmeasured confounders and enables estimation of causal effects—assuming that the instrument has no effect on the outcome except through its influence on the exposure. This analysis was implemented using the biprobit command in Stata 11.

For comparison, we also fit models using the ivprobit command in Stata 11. That model assumes a latent variable for the outcome, exceeding the threshold, as in (1), but assumes that a linear regression model holds directly for PT_i (as opposed to a linear regression for PTL_i as in (1)). The linear regression assumption for PT_i is a dubious one since it is binary.

In addition, we used the standard linear instrumental variables method (ivregress in Stata 11) appropriate for data where both the outcome and exposure are themselves correlated normal variables with means depending on exposure, covariates, and the instrument as in the bivariate probit analysis. Again, accounting for the correlation between the exposure and the instrument is the means by which this analysis removes unmeasured confounding, provided the instrumental variable assumptions are met. Because our outcome and exposure were binary, the normality assumptions implicit in this approach hold approximately at best.

The instrumental variable analyses do not provide odds ratios comparable to the summary effect measures provided by the standard logistic and propensity score analyses. To address this difficulty and to summarize the results of each analysis using common metrics, we calculated marginal estimates of the odds ratio and absolute risk reduction for all 4 methods. To do this, the predicted probability of crossing the exchange transfusion threshold was calculated twice for each newborn from the model estimates: first, as if the newborn had received phototherapy within 8 hours and, second, as if he or she had not. Both sets of estimated probabilities were then averaged across all newborns whose qualifying TSB levels were greater than or equal to the AAP phototherapy threshold. These calculations were implemented using the margins command in Stata 11 (details in the appendix). The averages represent clinically relevant estimates of the expected failure rates if all qualifying infants were, and respectively were not, treated with phototherapy within 8 hours. Marginal odds ratios and absolute risk reductions were then calculated from the 2 summary failure rates. However, the marginal odds ratios based on the linear instrumental variable (ivregress command) results were negative and are not presented.

Assuming confounding has been successfully controlled by the analysis, the marginal odds ratios and absolute risk reductions are interpretable as average causal effects. For the standard logistic and propensity score analyses, this assumption is, at best, plausible only for the fully adjusted analyses, but it may hold for both the minimally and fully adjusted instrumental variables analyses.

Finally, bias-corrected bootstrap estimates and confidence intervals were calculated for the marginal odds ratios and absolute risk reductions estimated by each of the minimally and fully adjusted analyses. In some cases, these confidence intervals were asymmetric on the log odds scale because bootstrap confidence intervals circumvent the assumption of approximate normality of the distribution of the log odds ratio, unlike the confidence intervals typically produced by statistical software. Effect size estimates using propensity scores and instrumental variables were recalculated in each of the 500 bootstrap samples.

To investigate possible hospital-level confounding by formula use, we used data from a previously reported nested case control study of infants with TSB levels of 17 to 22.9 mg/dL, in which the cases were those that developed TSB levels ≥25 mg/dL.⁷ One variable in that study, obtained by chart review, was whether infants were given any formula after their qualifying TSB. In that study, formula use was associated with a ∼50% decrease in the risk of the outcome (reported previously as an odds ratio of 2.03 for continuing exclusive breastfeeding).⁷ We correlated formula use with phototherapy use both at the individual level and at the hospital level using controls from this data set. We did not include cases because they would be expected to be unrepresentative (i.e., less likely to have received formula) and made up only 0.4% of the population at risk.

Results

Demographic characteristics of the 4584 infants who did and the 16,147 who did not receive hospital phototherapy within 8 hours of their qualifying TSB are compared in Table 1. Infants who received home phototherapy only (n = 677) or hospital phototherapy more than 8 hours after their qualifying TSB (n = 1538) are included in the group that did not receive timely inpatient phototherapy. Infants who received phototherapy within 8 hours were more likely to be <38 weeks' gestation, which explains their lower qualifying TSB levels, since phototherapy is recommended at lower levels if the gestational age is <38 weeks. However, as expected, their levels tended to be higher in relation to the phototherapy guideline. The qualifying TSB levels of the 20,731 infants eligible for the study are shown in Figure 1, along with the AAP phototherapy thresholds for the 2 different risk groups, defined by gestational age <38 weeks and ≥38 weeks.

Table 1. Characteristics of Infants Who Did and Did Not Receive Inpatient Phototherapy Within 8 Hours of Their Qualifying TSB Level.

	Inpatient Phototherapy within 8 Hours				Total	P Value
	No.	% or SD	Ye s	% or SD
Total No.	16,147		4584		20,731
Maternal age, y	29.3	6.0	29.6	6.1	29.3	<0.001
Male sex	9275	57.4%	2741	59.8%	12,016	0.004
Race						<0.001
White	6472	40.1%	1998	43.6%	8470
Asian	4455	27.6%	1166	25.4%	5621
Latino	3611	22.4%	938	20.5%	4549
Other	708	4.4%	211	4.6%	919
Black	616	3.8%	206	4.5%	822
Unknown	285	1.8%	65	1.4%	350
Gestational age, wk	38.5	1.6	37.9	2.0		<0.001
<38 weeks	4240	26.3%	1900	41.4%	14,591	<0.001
≥38 weeks	11,907	73.7%	2684	58.6%	6140
Birth weight, g	3.354	0.53	3.22	0.66		<0.001
Qualifying TSB level, mg/dL	15.05	3.44	13.45	3.73		<0.001
Age at qualifying TSB level, h, mean ± SD	67.9	40.9	49.2	0.3		<0.001
Maximum TSB	17.9	2.6	16.4	2.7		<0.001
Difference between qualifying TSB and AAP phototherapy threshold, mg/dL						<0.001
–3 to –2.1	4510	27.9%	933	20.4%	5443
–2 to –1.1	4127	25.6%	889	19.4%	5016
–1 to –0.1	3149	19.5%	863	18.8%	4012
0 to 0.9	2122	13.1%	754	16.4%	2876
1.0 to 1.9	1425	8.8%	633	13.8%	2058
2.0 to 2.9	814	5.0%	512	11.2%	1326
Home phototherapy (ever)	755	4.7%	107	2.3%	862	<0.001

AAP, American Academy of Pediatrics; TSB, total serum bilirubin.

Use of phototherapy varied by hospital of birth (Table 2); the proportion receiving phototherapy within 8 hours of the qualifying TSB (our first instrumental variable) varied from 11% to 42% when the TSB was from 0 to 0.9 mg/dL above the AAP phototherapy threshold. Similarly, phototherapy use for infants with TSB levels in that range varied by year of birth, from 18.5% in 1995 to 37.2% in 2003, so that the hospital and year-specific rate (our second instrumental variable) varied from 3% to 62%. Differences in phototherapy use within 8 hours by hospital of birth for infants with TSB levels 0 to 0.9 mg/dL above the AAP phototherapy threshold persisted after adjusting for infants' age, gestational age, and other covariates, as shown in Table 2.

Table 2. Variation in Use of Inpatient Phototherapy within 8 Hours by Birth Hospital for Infants 0 to 0.9 mg/dL above the AAP Phototherapy Threshold.

Hospital	Total No.	Qualifying TSB 0 to 0.9 mg/dL above AAP Guideline		PT if TSB 0 to 0.9 mg/dL above AAP Guideline		Crude OR for PT	Adjusteda OR for PT	95% CI for Adjusted OR	P Value
		No.	%	No.	%
A	754	123	16	22	18	0.30	0.33	0.19–0.58	<0.001
B	2869	452	16	118	26	0.49	0.57	0.41–0.78	<0.001
C	434	49	11	14	29	0.55	0.49	0.24–1.03	0.059
D	1106	98	9	33	34	0.70	0.58	0.35–0.97	0.040
E	2078	271	13	56	21	0.36	0.25	0.17–0.37	<0.001
F	1436	221	15	59	27	0.50	0.44	0.30–0.65	<0.001
G	1548	281	18	38	14	0.22	0.19	0.13–0.30	<0.001
H	1102	137	12	43	31	0.63	0.60	0.39–0.95	0.028
J	2313	342	15	39	11	0.18	0.18	0.12–0.27	<0.001
K	1967	264	13	79	30	0.59	0.59	0.41–0.84	0.004
L	2156	150	7	48	32	0.65	0.63	0.41–0.98	0.039
M	2968	488	16	205	42	1.00 (ref)	1.00 (ref)	—	—
Total	20731	2876	14	754	26

AAP, American Academy of Pediatrics; CI, confidence interval; OR, odds ratio; PT, phototherapy threshold; TSB, total serum bilirubin.

^aOR adjusted for year of birth, maternal age, race, sex, birth weight, gestational age, qualifying TSB (6 categories), and age at qualifying TSB (5 categories).

A total of 113 untreated infants (0.70%) and 15 treated infants (0.33%) developed the outcome (i.e., had TSB levels exceeding the AAP's exchange level at <48 hours). These levels were generally only a few mg/dL above the exchange level and occurred between 60 and 120 hours of age (Figure 2). Although only 30% of the infants included in the study were born at less than 38 weeks' gestation, this group made up 75% of those who developed the outcome. This occurred not because their TSB levels were higher but because the AAP exchange transfusion threshold is lower for infants born at <38 weeks (Figure 2).

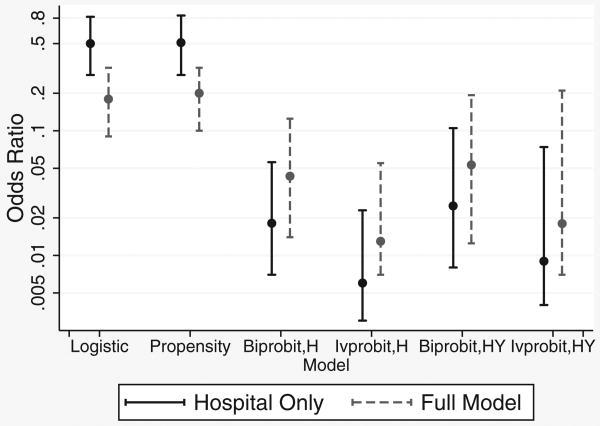
Marginal odds ratios for logistic regression, propensity score, and the probit instrumental variable analyses are compared in Figure 3. When confounding variables were omitted from logistic and propensity analyses, odds ratios were about 0.5. With control for confounding by indication, the fully adjusted marginal odds ratio for the logistic analysis (0.18) is close to the 0.16 we previously reported. The propensity score analysis yielded similar results (OR = 0.5 with hospital only in the propensity score, decreasing to 0.2 in the fully adjusted model). This latter analysis revealed that there were only 10 outcomes in the bottom 2 propensity quintiles, of which only one was in a treated patient, making odds ratios in the lower quintiles unstable.

Figure 3. Odds ratios and 95% confidence intervals for phototherapy controlling for hospital only or all known confounders (full model), by multivariate model. Biprobit and ivprobit models use instrumental variables based on either phototherapy use by birth hospital (H) or by both birth hospital and year (HY).

Using a fully adjusted version of the bivariate probit model, (1), there was evidence for a remaining correlation between the error terms, ε_i and ν_i (P = 0.02), suggesting the presence of unmeasured confounders in the logistic and propensity analysis and lending support for an instrumental variables analysis. Point estimates of the odds ratios from the probit instrumental variable analyses based on hospital of birth were much lower than those from the logistic model and propensity score analysis, somewhat more resistant to omission of confounding variables, and less precisely estimated. Using an instrument based on both year and hospital of birth increased the odds ratios somewhat but greatly increased the width of the confidence intervals, especially in the ivprobit model (Figure 3).

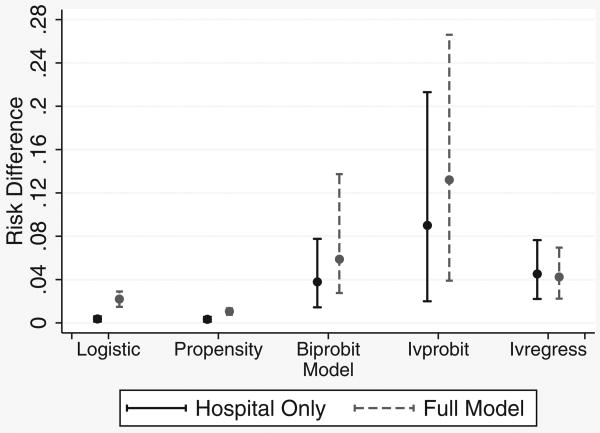
Estimates for risk differences showed the same pattern, with both probit and linear estimates for the risk difference greater than estimates from logistic regression or propensity score analysis, with much wider confidence intervals, especially for the ivprobit model (Figure 4). The linear estimate was only minimally affected by omission of confounding variables. Results for the instrument based on both hospital and year of birth (not shown) were similar.

Figure 4. Risk differences and 95% confidence intervals for phototherapy controlling for hospital only or all known confounders (full model). Instrumental variables were based on hospital of birth only; see text.

Our model adequacy checks revealed little cause for concern. The Hosmer-Lemeshow goodness-of-fit statistic for the logistic model was not statistically significant (P = 0.13), despite the large sample size. The effect of birth weight showed some signs of non-linearity, but representing the birth weight effect with a flexible spline function left the odds ratio for phototherapy unchanged. We tested a large number of 2-way interactions, each at a nominal significance level of 0.1. Two interactions gave P values less than 0.05: a mild interaction of age when the infant first came within 3 mg/dL of the AAP phototherapy threshold and phototherapy and an interaction of birth weight and gestational age. Inclusion of the interaction between birth weight and gestational age made no difference to the odds ratio for phototherapy, and the interaction with age at qualifying bilirubin arose because of an odds ratio slightly above 1 for a single age category with sparse data. There was good overlap of the propensity scores in the treated and untreated infants.

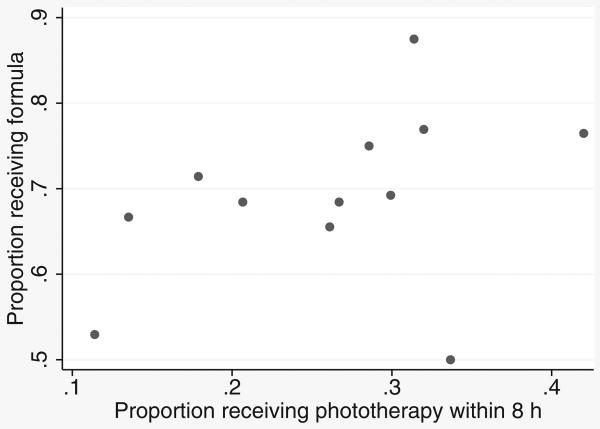
The fact that the odds ratio from the bivariate probit model was much lower than from the logistic and propensity models led us to investigate the possibility of confounding at the hospital level that did not exist at the individual level. We found that although at the individual level, phototherapy use was only weakly associated with formula use (r = 0.13), at the hospital level, hospitals with higher rates of phototherapy use also had higher rates of formula use (Figure 5; r = 0.56; P < 0.001).

Figure 5. Association between receiving inpatient phototherapy and receiving formula after the qualifying total serum bilirubin level in the 12 study hospitals.

Discussion

In this historical cohort study, all methods of analysis suggested that inpatient phototherapy was highly effective for treatment of neonatal jaundice. Traditional logistic regression analyses and analyses using propensity scores gave similar results, with odds ratios in the 0.15 to 0.2 range, whereas the odds ratios from the instrumental variable analyses based on the probit model were much lower (about 0.02–0.05). Both the probit and linear models gave large risk differences; the probit results seem particularly implausible.

In our previous report on the efficacy of phototherapy in this cohort,⁶ we discussed two main limitations: 1) probable misclassification of exposure, due to limitations of electronic data for determining which infants were treated with phototherapy within 8 hours, and 2) possible residual confounding by indication, as could occur if, for example, infants at higher risk of subsequent hyperbilirubinemia due to continued exclusive breastfeeding were more likely to be treated with phototherapy. Both types of errors would be expected to bias the odds ratio toward 1; the fact that the odds ratio was 0.16 suggested neither was a significant problem. We undertook the current analysis expecting that the instrumental variable approach would yield somewhat lower odds ratios than previously reported because they should be less affected by uncontrolled confounding by indication.

Our instrumental variable analyses illustrated some strengths and weaknesses of that approach. The log odds ratios from the probit model were only slightly less affected by omission of known confounding variables than the traditional logistic regression or propensity score analyses, and confidence intervals were much wider. Only with the linear model were the effect size estimates with and without inclusion of confounders almost equal. However, when outcomes are rare (as in the present study), the relationship between risk differences obtained from additive models and odds ratios or risk ratios is highly unstable¹⁸: attempts to obtain marginal odds ratios from linear models as we originally planned gave nonsensical results.

Perhaps the most interesting result is what we believe are implausibly low odds ratios for phototherapy in the probit analyses. A falsely low odds ratio for a treatment in an observational study (i.e., an odds ratio suggesting the treatment is more effective than it really is) suggests that compared with those not treated, those receiving the treatment had lower levels of some risk factors or higher levels of some protective factors that were not in the model. The main candidate in this case is a lower level of exclusive breastfeeding (i.e., greater use of infant formula) among those treated with phototherapy.

Our initial supposition was that because infants receiving formula would be at lower risk of subsequent hyperbilirubinemia, phototherapy would be less indicated for them, and hence they would be less likely to receive it. However, another possibility is that when clinicians or parents are worried about hyperbilirubinemia, they might tend to treat with both phototherapy and formula supplementation. Our data suggest that at the level of individual patients, this was not a strong association: clinicians who are concerned about jaundice might treat with phototherapy or formula, but treating with one did not make it much more likely that the infant would receive the other. However, at the hospital level, the association was stronger (Figure 5), suggesting that hospitals where there is more concern about bilirubin may be more likely to use both phototherapy and formula, even though they may not use both for the same newborn. This would lead to a falsely low odds ratio for phototherapy in instrumental variable analyses because the lower rate of the outcome among infants born in hospitals that use more phototherapy is due not just to their greater likelihood of receiving phototherapy but also to their greater likelihood of receiving formula. Because formula use is not included in the model, all of the bilirubin-lowering effect of differential formula use across hospitals is attributed to the difference in phototherapy use, thus creating an artificially optimistic estimate for the effect of phototherapy.

This example provides a nice illustration of the meaning and limitations of an instrumental variable analysis. Results of such analyses are probably best interpreted using if-then statements. In this example, the statement would be “if all of the differences across hospitals in the risk of the outcome (adjusting for other known confounding factors) in newborns with TSB levels above the phototherapy threshold were due to differences in the use of phototherapy, then the average causal effect of phototherapy would be reflected in the odds ratios of 0.02 to 0.05.” When phrased this way, it is clear that although instrumental variables analyses are resistant to confounding, investigators and consumers of such analyses must be vigilant to the possibility that there may be associations of the instrument with the outcome in ways not mediated by the treatment. In our case, this arose because of confounding at the level of the instrument. In particular, this example illustrates the need to be aware of the possibility of treatment substitution—for example, in this case, hospitals in which there was a greater level of concern about neonatal jaundice may have been more likely to use formula or phototherapy, even though individual newborns who received one were not more likely to receive the other.

Several previous studies have reported results of instrumental variable analyses and propensity score or standard multivariable models for the same research question.^9,19–26 Results of standard multivariable analyses and propensity analyses are almost always similar to one another, which is not surprising since both rely on confounding variables having been measured. Where instrumental variable analyses have differed from the other 2 techniques, the difference has been attributed to better²⁰ but still incomplete²⁴ control for unmeasured confounders. We did not find previous reports highlighting unrealistically optimistic estimates of effect from instrumental variable analyses attributed either to differential use of cointerventions or choice of instrument, as we report here.

We conclude that phototherapy was a highly effective treatment for neonatal jaundice in the term and near-term newborns in this study. Although instrumental variable analyses may produce estimates of treatment efficacy that are less affected by uncontrolled confounders, our results illustrate that different analytic techniques can provide different results and that investigators must be cautious about the possibility of confounding or cointerventions at the level of the instrument, even when these may not occur at the individual level.