Nonparametric Independence Screening in Sparse Ultra-High Dimensional Additive Models

Abstract

A variable screening procedure via correlation learning was proposed in Fan and Lv (2008) to reduce dimensionality in sparse ultra-high dimensional models. Even when the true model is linear, the marginal regression can be highly nonlinear. To address this issue, we further extend the correlation learning to marginal nonparametric learning. Our nonparametric independence screening is called NIS, a specific member of the sure independence screening. Several closely related variable screening procedures are proposed. Under general nonparametric models, it is shown that under some mild technical conditions, the proposed independence screening methods enjoy a sure screening property. The extent to which the dimensionality can be reduced by independence screening is also explicitly quantified. As a methodological extension, a data-driven thresholding and an iterative nonparametric independence screening (INIS) are also proposed to enhance the finite sample performance for fitting sparse additive models. The simulation results and a real data analysis demonstrate that the proposed procedure works well with moderate sample size and large dimension and performs better than competing methods.

1 Introduction

With rapid advances of computing power and other modern technology, high-throughput data of unprecedented size and complexity are frequently seen in many contemporary statistical studies. Examples include data from genetic, microarrays, proteomics, fMRI, functional data and high frequency financial data. In all these examples, the number of variables p can grow much faster than the number of observations n. To be more specific, we assume log p = O(n^a) for some a ∈ (0, 1/2). Following Fan and Lv (2009), we call it non-polynomial (NP) dimensionality or ultra-high dimensionality. What makes the under-determined statistical inference possible is the sparsity assumption: only a small set of independent variables contribute to the response. Therefore, dimension reduction and feature selection play pivotal roles in these ultra-high dimensional problems.

The statistical literature contains numerous procedures on the variable selection for linear models and other parametric models, such as the Lasso (Tibshirani, 1996), the SCAD and other folded-concave penalty (Fan, 1997; Fan and Li, 2001), the Dantzig selector (Candes and Tao, 2007), the Elastic net (Enet) penalty (Zou and Hastie, 2005), the MCP (Zhang, 2010) and related methods (Zou, 2006; Zou and Li, 2008). Nevertheless, due to the “curse of dimensionality” in terms of simultaneous challenges on the computational expediency, statistical accuracy and algorithmic stability, these methods meet their limits in ultra-high dimensional problems.

Motivated by these concerns, Fan and Lv (2008) introduced a new frame-work for variable screening via correlation learning with NP-dimensionality in the context of least squares. Hall et al. (2009) used a different marginal utility, derived from an empirical likelihood point of view. Hall and Miller (2009) proposed a generalized correlation ranking, which allows nonlinear regression. Huang et al. (2008) also investigated the marginal bridge regression in the ordinary linear model. These methods focus on studying the marginal pseudo-likelihood and are fast but crude in terms of reducing the NP-dimensionality to a more moderate size. To enhance the performance, Fan and Lv (2008) and Fan et al. (2009) introduced some methodological extensions including iterative SIS (ISIS) and multi-stage procedures, such as SIS-SCAD and SIS-LASSO, to select variables and estimate parameters simultaneously. Nevertheless, these marginal screening methods have some methodological challenges. When the covariates are not jointly normal, even if the linear model holds in the joint regression, the marginal regression can be highly nonlinear. Therefore, sure screening based on nonparametric marginal regression becomes a natural candidate.

In practice, there is often little prior information that the effects of the covariates take a linear form or belong to any other finite-dimensional parametric family. Substantial improvements are sometimes possible by using a more flexible class of nonparametric models, such as the additive model $Y={\sum }_{j=1}^p{m}_j\left(X_j\right)+\epsilon$, introduced by Stone (1985). It increases substantially the flexibility of the ordinary linear model and allows a data-analytic transform of the covariates to enter into the linear model. Yet, the literature on variable selection in nonparametric additive models are limited. See, for example, Koltchinskii and Yuan (2008), Ravikumar et al. (2009), Huang et al. (2010) and Meier et al. (2009). Koltchinskii and Yuan (2008) and Ravikumar et al. (2009) are closely related with COSSO proposed in Lin and Zhang (2006) with fixed minimal signals, which does not converge to zero. Huang et al. (2010) can be viewed as an extension of adaptive lasso to additive models with fixed minimal signals. Meier et al. (2009) proposed a penalty which is a combination of sparsity and smoothness with a fixed design. Under ultra-high dimensional settings, all these methods still suffer from the aforementioned three challenges as they can be viewed as extensions of penalized pseudo-likelihood approaches to additive modeling. The commonly used algorithm in additive modeling such as backfitting makes the situation even more challenging, as it is quite computationally expensive.

In this paper, we consider independence learning by ranking the magnitude of marginal estimators, nonparametric marginal correlations, and the marginal residual sum of squares. That is, we fit p marginal nonparametric regressions of the response Y against each covariate X_i separately and rank their importance to the joint model according to a measure of the goodness of fit of their marginal model. The magnitude of these marginal utilities can preserve the non-sparsity of the joint additive models under some reasonable conditions, even with converging minimum strength of signals. Our work can be regarded as an important and nontrivial extension of SIS procedures proposed in Fan and Lv (2008) and Fan and Song (2010). Compared with these papers, the minimum distinguishable signal is related with not only the stochastic error in estimating the nonparametric components, but also approximation errors in modeling nonparametric components, which depends on the number of basis functions used for the approximation. This brings significant challenges to the theoretical development and leads to an interesting result on the extent to which the dimensionality can be reduced by nonparametric independence screening. We also propose an iterative nonparametric independence screening procedure, INIS-penGAM, to reduce the false positive rate and stabilize the computation. This two-stage procedure can deal with the aforementioned three challenges better than other methods, as will be demonstrated in our empirical studies.

We approximate the nonparametric additive components by using a B-spline basis. Hence, the component selection in additive models can be viewed as a functional version of the grouped variable selection. An early literature on the group variable selection using group penalized least-squares is Antoniadis and Fan (2001) (see page 966), in which blocks of wavelet coefficients are either killed or selected. The group variable selection was more thoroughly studied in Yuan and Lin (2006), Kim et al. (2006), Wei and Huang (2007) and Meier et al. (2009). Our methods and results have important implications on the group variable selections, as in additive regression, each component can be expressed as a linear combination of a set of basis functions, whose coefficients have to be either killed or selected simultaneously.

The rest of the paper is organized as follows. In Section 2, we introduce the nonparametric independence screening (NIS) procedure in additive models. The theoretical properties for NIS are presented in Section 3. As a methodological extension, INIS-penGAM and its greedy version g-INIS-penGAM are outlined in Section 4. Monte Carlo simulations and a real data analysis in Section 5 demonstrate the effectiveness of the INIS method. We conclude with a discussion in Section 6 and relegate the proofs to Section 7.

2 Nonparametric independence screening

Suppose that we have a random sample ${\left\{({\mathbf{X}}_i,Y_i)\right\}}_{i=1}^n$ from the population

$$Y=m\left(\mathbf{X}\right)+\epsilon ,$$ (1)

in which X = (X₁, … , X_p)^T, ε is the random error with conditional mean zero. To expeditiously identify important variables in model (1), without the “curse-of-dimensionality”, we consider the following p marginal nonparametric regression problems:

$$\underset{f_j\in L_2\left(P\right)}{\min }E{\left(Y-f_j\left(X_j\right)\right)}^2,$$ (2)

where P denotes the joint distribution of (X, Y) and L₂(P) is the class of square integrable functions under the measure P. The minimizer of (2) is f_j = E(Y|X_j), the projection of Y onto X_j. We rank the utility of covariates in model (1) according to, for example, $E{f}_j^2\left(X_j\right)$ and select a small group of covariates via thresholding.

To obtain a sample version of the marginal nonparametric regression, we employ a B-Spline basis. Let S_n be the space of polynomial splines of degree l ≥ 1 and {Ψ_jk, k = 1, … , d_n} denote a normalized B-Spline basis with ∥Ψ_jk∥_∞ ≤ 1, where ∥ · ∥_∞ is the sup norm. For any $f_{nj}\in {\mathcal{S}}_n$, we have

$$f_{nj}\left(x\right)=\sum _{k=1}^{d_n}{\beta }_{jk}{\Psi }_{jk}\left(x\right),1\le j\le p,$$

for some coefficients ${\left\{{\beta }_{jk}\right\}}_{k=1}^{d_n}$. Under some smoothness conditions, the non-parametric projections ${\left\{f_j\right\}}_{j=1}^p$ can well be approximated by functions in ${\mathcal{S}}_n$. The sample version of the marginal regression problem can be expressed as

$$\underset{f_{nj}\in {\mathcal{S}}_n}{\min }{\mathbb{P}}_n{\left(Y-f_{nj}\left(X_j\right)\right)}^2=\underset{{\beta }_j\in {\mathbb{R}}^{d_n}}{\min }{\mathbb{P}}_n{\left(Y-{\Psi }_j^T{\beta }_j\right)}^2,$$ (3)

where Ψ_j ≡ Ψ_j(X_j) = (Ψ₁(X_j), ⋯ , Ψ_dn(X_j))^T denotes the d_n dimensional basis functions and ${\mathbb{P}}_{n}g(\mathbf{X},Y)$ is the expectation with respect to the empirical measure ${\mathbb{P}}_n$, i.e., the sample average of ${\left\{g({\mathbf{X}}_i,Y_i)\right\}}_{i=1}^n$. This univariate nonparametric smoothing can be rapidly computed, even for NP-dimensional problems. We correspondingly define the population version of the minimizer of the componentwise least square regression,

$$f_{nj}\left(X_j\right)={\Psi }_j^T{\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}E{\Psi }_{j}Y,j=1,\cdots ,p.$$

where E denotes the expectation under the true model.

We now select a set of variables

$${\widehat{\mathcal{M}}}_{{\nu }_n}=\{1\le j\le p:{\parallel {\widehat{f}}_{nj}\parallel }_n^2\ge {\nu }_n\},$$ (4)

where ${\parallel {\widehat{f}}_{nj}\parallel }_n^2=n^{-1}{\sum }_{i=1}^n{\widehat{f}}_{nj}{\left(X_{ij}\right)}^2$ and ν_n is a predefined threshold value. Such an independence screening ranks the importance according to the marginal strength of the marginal nonparametric regression. This screening can also be viewed as ranking by the magnitude of the correlation of the marginal nonparametric estimate ${\left\{{\widehat{f}}_{nj}\left(X_{ij}\right)\right\}}_{i=1}^n$ with the response ${\left\{Y_i\right\}}_{i=1}^n$, since ${\parallel {\widehat{f}}_{nj}\parallel }_n^2={\parallel Y{\widehat{f}}_{nj}\parallel }_n$. In this sense, the proposed NIS procedure is related to the correlation learning proposed in Fan and Lv (2008).

Another screening approach is to rank according to the descent order of the residual sum of squares of the componentwise nonparametric regressions, where we select a set of variables:

$${\widehat{\mathcal{N}}}_{{\gamma }_n}=\{1\le j\le p:u_j\le {\gamma }_n\},$$

with $u_j={\min }_{{\beta }_j}{\mathbb{P}}_n{(Y-{\Psi }_j^T{\beta }_j)}^2$ is the residual sum of squares of the marginal fit and γ_n is a predefined threshold value. It is straightforward to show that $u_j={\mathbb{P}}_n(Y^2-{\widehat{f}}_{nj}^2)$. Hence, the two methods are equivalent.

The nonparametric independence screening reduces the dimensionality from p to a possibly much smaller space with model size $\mid {\widehat{\mathcal{M}}}_{\nu n}\mid$ or $\mid {\widehat{\mathcal{N}}}_{\gamma n}\mid$. It is applicable to all models. The question is whether we have mistakenly deleted some active variables in model (1). In other words, whether the procedure has a sure screening property as postulated by Fan and Lv (2008). In the next section, we will show that the sure screening property indeed holds for nonparametric additive models with a limited false selection rate.

3 Sure Screening Properties

In this section, we establish the sure screening properties for additive models with results presented in three steps.

3.1 Preliminaries

We now assume that the true regression function admits the additive structure:

$$m\left(\mathbf{X}\right)=\sum _{j=1}^p{m}_j\left(X_j\right).$$ (5)

For identifiability, we assume ${\left\{m_j\left(X_j\right)\right\}}_{j=1}^p$ have mean zero. Consequently, the response Y has zero mean, too. Let ${\mathcal{M}}_{\star }=\{j:E{m}_j{\left(X_j\right)}^2\ge 0\}$ be the true sparse model with non-sparsity size $s_n=\mid {\mathcal{M}}_{\star }\mid$. We allow p to grow with n and denote it as p_n whenever needed.

The theoretical basis of the sure screening is that the marginal signal of the active components $(\parallel f_j\parallel ,j\in {\mathcal{M}}_{\star })$ does not vanish, where ${\parallel f_j\parallel }^2=E{f}_j^2$. The following conditions make this possible. For simplicity, let [a, b] be the support of X_j.

1. The nonparametric marginal projections ${\left\{f_j\right\}}_{j=1}^p$ belong to a class of functions $\mathcal{F}$ whose rth derivative f^(r) exists and is Lipschitz of order α:

   $$\mathcal{F}=\left\{f(\cdot ):\mid f^{\left(r\right)}\left(s\right)-f^{\left(r\right)}\left(t\right)\mid \le K{\mid s-t\mid }^{\alpha },\text{for}s,t\in [a,b]\right\}$$

   for some positive constant K, where r is a non-negative integer and α ∈ (0, 1] such that d = r + α ≥ 0.5.

2. The marginal density function g_j of X_j satisfies 0 < K₁ ≤ g_j(X_j) ≤ K₂ < ∞ on [a, b] for 1 ≤ j ≤ p for some constants K₁ and K₂.

3. ${\min }_{j\in {\mathcal{M}}_{\star }}$ E{E(Y|X_j)²} ≥ c₁d_nn^−2k, for some 0 < k < d/(2d + 1) and c₁ > 0.

Under conditions A and B, the following three facts hold when l ≥ d and will be used in the paper. We state them here for readability.

• Fact 1. There exists a positive constant C₁ such that (Stone, 1985)

  $${\parallel f_j-f_{nj}\parallel }^2\le C_1{d}_n^{-2d}.$$ (6)
• Fact 2. There exists a positive constant C₂ such that (Stone, 1985; Huang et al., 2010)

  $$E{\Psi }_{jk}^2\left(X_{ij}\right)\le C_2{d}_n^{-1}.$$ (7)
• Fact 3. There exist some positive constants D₁ and D₂ such that (Zhou et al., 1998)

  $$D_1{d}_n^{-1}\le {\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)\le {\lambda }_{\max }\left(E{\Psi }_j{\Psi }_j^T\right)\le D_2{d}_n^{-1}.$$ (8)

The following lemma shows that the minimum signal of ${\left\{\parallel f_{nj}\parallel \right\}}_{j\in {\mathcal{M}}_{\ast }}$ is at the same level of the marginal projection, provided that the approximation error is negligible.

• Lemma 1. Under conditions A–C, we have

  $$mi{n}_{j\in {\mathcal{M}}_{\ast }}{\parallel f_{nj}\parallel }^2\ge c_1\xi d_n{n}^{-2\kappa },$$

  provided that $d_n^{-2d-1}\le c_1(1-\xi )n^{-2k}∕C_1$ for some ξ ∈ (0, 1).

A model selection consistency result can be established with nonparametric independence screening under the partial orthogonality condition, i.e., $\{X_j,j\notin {\mathcal{M}}_{\star }\}$ is independent of $\{X_i,i\in {\mathcal{M}}_{\star }\}$. In this case, there is a separation between the strength of marginal signals ∥f_nj∥² for active variables $\{X_j;j\in {\mathcal{M}}_{\star }\}$ and inactive variables $\{X_j,j\notin {\mathcal{M}}_{\star }\}$, which are zero. When the separation is sufficiently large, these two sets of variables can be easily identified.

3.2 Sure Screening

In this section, we establish the sure screening properties of the nonparametric independence screening (NIS). We need the following additional conditions:

• D∥m∥_∞ < B₁ for some positive constant B₁, where ∥ · ∥_∞ is the sup norm.
• EThe random error ${\left\{{\epsilon }_i\right\}}_{i=1}^n$ are i.i.d. with conditional mean zero and for any B₂ > 0, there exists a positive constant B₃ such that E[exp(B₂|ε_i|)|X_i] < B₃.
• FThere exist a positive constant c₁ and ξ ∈ (0, 1) such that $d_n^{-2d-1}\le c_1(1-\xi )n^{-2\kappa }∕C_1$.

The following theorem gives the sure screening properties. It reveals that it is only the size of non-sparse elements s_n that matters for the purpose of sure screening, not the dimensionality p_n. The first result is on the uniform convergence of ${\parallel {\widehat{f}}_{nj}\parallel }_n^2$ to ∥f_nj∥².

Theorem 1. Suppose that Conditions A, B, D and E hold.

1. For any c₂ > 0, there exist some positive constants c₃ and c₄ such that

   $$\begin{array}{c}\hfill P\left(\underset{1\le j\le p_n}{\max }\mid {\parallel {\widehat{f}}_{nj}\parallel }_n^2-{\parallel f_{nj}\parallel }^2\mid \ge c_2{d}_n{n}^{-2k}\right)\hfill \\ \hfill \le p_n{d}_n\left\{(8+2d_n)\exp \left(-c_3{n}^{1-4\kappa }{d}_n^{-3}\right)+6d_n\exp \left(-c_{4}n{d}_n^{-3}\right)\right\}.\hfill \end{array}$$ (9)
2. If, in addition, Conditions C and F hold, then by taking ν_n = c₅d_nn^−2k with c₅ ≤ c₁ξ/2, we have

   $$P({\mathcal{M}}_{\ast }\subset {\widehat{\mathcal{M}}}_{\nu n})\ge 1-s_n{d}_n\left\{(8+2d_n)\text{exp}\left(-c_3{n}^{1-4\kappa }{d}_n^{-3}\right)+6d_n\text{exp}\left(-c_{4}n{d}_n^{-3}\right)\right\}.$$

Note that the second part of the upper bound in Theorem 1 is related to the uniform convergence rates of the minimum eigenvalues of the design matrices. It gives an upper bound on the number of basis d_n = o(n^1/3) in order to have the sure screening property, whereas Condition F requires d_n ≥ B₄n^2k/^(2d+1), where B₄ = (c₁(1 − ξ)/C₁)^−1/(2d+1).

It follows from Theorem 1 that we can handle the NP-dimensionality:

$$\log p_n=o(n^{1-4\kappa }{d}_n^{-3}+n{d}_n^{-3}).$$ (10)

Under this condition,

$$P({\mathcal{M}}_{\ast }\subset {\widehat{\mathcal{M}}}_{{\nu }_n})\to 1,$$

i.e., the sure screening property. It is worthwhile to point out that the number of spline basis d_n affects the order of dimensionality, comparing with the results of Fan and Lv (2008) and Fan and Song (2010) in which univariate marginal regression is used. Equation (10) shows that the larger the minimum signal level or the smaller the number of basis functions, the higher dimensionality the nonparametric independence screening (NIS) can handle. This is in line with our intuition. On the other hand, the number of basis functions can not be too small, since the approximation error can not be too large. As required by Condition F, d_n ≥ B₄n^2k/(2d+1); the smoother the underlying function, the smaller d_n we can take and the higher the dimension that the NIS can handle. If the minimum signal does not converge to zero, as in Lin and Zhang (2006), Koltchinskii and Yuan (2008) and Huang et al. (2010), then k = 0. In this case, d_n can be taken to be finite as long as it is sufficiently large so that minimum signal in Lemma 1 exceeds the noise level. By taking d_n = n^1/(2d+1), the optimal rate for nonparametric regression (Stone, 1985), we have log p_n = o(n^{2(d−1)/(2d+1)}). In other words, the dimensionality can be as high as exp{o(n^{2(d−1)/(2d+1)})}.

3.3 Controlling false selection rates

The sure screening property, without controlling false selection rates, is not insightful. It basically states that the NIS has no false negatives. An ideal case for the vanishing false positive rate is that

$$\underset{j\notin {\mathcal{M}}_{\ast }}{\text{max}}{\parallel f_{nj}\parallel }^2=o\left(d_n{n}^{-2\kappa }\right)$$

so that there is a gap between active variables and inactive variables in model (1) when using the marginal nonparametric screener. In this case, by Theorem 1(i), if (9) tends to zero, with probability tending to one that

$$\underset{j\notin {\mathcal{M}}_{\ast }}{\text{max}}{\parallel {\widehat{f}}_{nj}\parallel }_n^2\le c_2{d}_n{n}^{-2\kappa },\text{for}\text{any}{c}_2>0.$$

Hence, by the choice of ν_n as in Theorem 1(ii), we can achieve model selection consistency:

$$P({\widehat{\mathcal{M}}}_{{\nu }_n}={\mathcal{M}}_{\ast })=1-o\left(1\right)$$

We now deal with the more general case. The idea is to bound the size of the selected set by using the fact that var(Y) is bounded. In this part, we show that the correlations among the basis functions, i.e., the design matrix of the basis functions, are related to the size of selected models.

Theorem 2. Suppose Conditions A–F hold and var(Y) = O(1). Then, for any ν_n = c₅d_nn^−2k, there exist positive constants c₃ and c₄ such that

$$P[\mid {\widehat{\mathcal{M}}}_{{\nu }_n}\mid \le {\rm O}\left\{n^{2\kappa }{\lambda }_{\text{max}}(\sum )\right\}]\ge 1-p_n{d}_n\left\{(8+2d_n)\text{exp}(-c_3{n}^{1-4\kappa }{d}_n^{-3})+6d_n\text{exp}(-c_{4}n{d}_n^{-3})\right\},$$

where Σ = EΨΨ^T and Ψ = (Ψ₁ ⋯ , Ψ_pn)^T.

The significance of the result is that when λ_max(Σ) = O(n^τ), the selected model size with the sure screening property is only of polynomial order, whereas the original model size is of NP-dimensionality. In other words, the false selection rate converges to zero exponentially fast. The size of the selected variables is of order O(n^{2k + τ}. This is of the same order as in Fan and Lv (2008). Our result is an extension of Fan and Lv (2008), even in this very specific case without the condition 2κ + τ < 1. The results are also consistent with that in Fan and Song (2010): the number of selected variables is related to the correlation structure of the covariance matrix.

In the specific case where the covariates are independent, then the matrix Σ is block diagonal with j-th block Σ_j. Hence, it follows from (8) that ${\lambda }_{\max }\left(\Sigma \right)=O\left(d_n^{-1}\right)$.

4 INIS Method

4.1 Description of the Algorithm

After variable screening, the next step is naturally to select the variables using more refined techniques in the additive model. For example, the penalized method for additive model (penGAM) in Meier et al. (2009) can be employed to select a subset of active variables. This results in NIS-penGAM. To further enhance the performance of the method, in terms of false selection rates, following Fan and Lv (2008) and Fan et al. (2009), we can iteratively employ the large-scale screening and moderate-scale selection strategy, resulting in the INIS-penGAM.

Given the data {(X_i, Y_i)}, i = 1, ⋯ , n, for each component f_j(·), j = 1, ⋯ , p, we choose the same truncation term d_n = O(n^1/5). To determine a data-driven thresholding for independence screening, we extend the random permutation idea in Zhao and Li (2010), which allows only 1 − q proportion (for a given q ∈ [0, 1]) of inactive variables to enter the model when X and Y are not related (the null model). The random permutation is used to decouple X_i and Y_i so that the resulting data (X_π(i), Y_i) follow a null model, where π(1), ⋯ , π(n) are a random permutation of the index 1, ⋯ , n. The algorithm works as follows:

• Step 1: For every j ∈ {1, ⋯ , p}, we compute

  $${\widehat{f}}_{nj}={\text{argmin}}_{f_{nj}\in {\mathcal{S}}_n}{\mathbb{P}}_n{\left(Y-f_{nj}\left(X_j\right)\right)}^2,\text{for}1\le j\le p.$$

  Randomly permute the rows of X, yielding $\tilde{\mathbf{X}}$. Letω_(q) be the q^th quantile of $\{{\parallel {\widehat{f}}_{nj}^{\ast }\parallel }_n^2,j=1,2,\cdots ,p\}$, where

  $${\widehat{f}}_{nj}^{\ast }={\text{argmin}}_{f_{nj}\in {\mathcal{S}}_n}{\mathbb{P}}_n{\left(Y-f_{nj}\left({\tilde{X}}_j\right)\right)}^2.$$

  Then, NIS selects the following variables:

  $${\mathcal{A}}_1=\{j:{\parallel {\widehat{f}}_{nj}^{\ast }\parallel }_n^2\ge {\omega }_{\left(q\right)}\}.$$

  In our numerical examples, we use q = 1 (i.e., take the maximum value of the empirical norm of the permuted estimates).

• Step 2: We apply further the penalized method for additive model (penGAM) in Meier et al. (2009) on the set ${\mathcal{A}}_1$ to select a subset ${\mathcal{M}}_1$. Inside the penGAM algorithm, the penalty parameter is selected by cross validation.

• Step 3: For every $j\in {\mathcal{M}}_1^c=\{1,\cdots ,p\}\setminus {\mathcal{M}}_1$, we minimize

  $${\mathbb{P}}_n{\left(Y-\sum _{i\in {\mathcal{M}}_1}{f}_{ni}\left(X_i\right)-f_{nj}\left(X_j\right)\right)}^2,$$ (11)

  with respect to $f_{ni}\in {\mathcal{S}}_n$ for all $i\in {\mathcal{M}}_1$ and $f_{nj}\in {\mathcal{S}}_n$. This regression reflects the additional contribution of the j-th components conditioning on the existence of the variable set ${\mathcal{M}}_1$. After marginally screening as in the first step, we can pick a set $\mathcal{A}2$ of indices. Here the size determination is the same as in Step 1, except that only the variables not in ${\mathcal{M}}_1$ are randomly permuted. Then we apply further the penGAM algorithm on the set ${\mathcal{M}}_1\bigcup {\mathcal{A}}_2$ to select a subset ${\mathcal{M}}_2$.

• Step 4: We iterate the process until $\mid {\mathcal{M}}_l\mid \ge s_0$ or ${\mathcal{M}}_l={\mathcal{M}}_{l-1}$.

Here are a few comments about the method. In Step 2, we use the penGAM method. In fact, any variable selection method for additive models will work such as the SpAM in Ravikumar et al. (2009) and also the adaptive group LASSO for additive models in Huang et al. (2010). A similar sample splitting idea as described in Fan et al. (2009) can be applied here to further reduce false selection rate.

4.2 Greedy INIS (g-INIS)

We now propose a greedy modification to the INIS algorithm to speed up the computation and to enhance the performance. Specifically, we restrict the size of the set ${\mathcal{A}}_j$ in the iterative screening steps to be at most p₀, a small positive integer, and the algorithm stops when none of the variables is recruited, i.e., exceeding the thresholding for the null model. In the numerical studies, p₀ is taken to be one for simplicity. This greedy version of the INIS algorithm is called “g-INIS”.

When p₀ = 1, the g-INIS method is connected with the forward selection (Efroymson, 1960; Draper and Smith, 1966). Recently, Wang (2009) showed that under certain technical conditions, forward selection can also achieve the sure screening property. Both g-INIS and forward selection recruit at most one new variable into the model at a time. The major difference is that unlike the forward selection which keeps a variable once selected, g-INIS has a deletion step via penalized least-squares that can remove multiple variables. This makes the g-INIS algorithm more attractive since it is more flexible in terms of recruiting and deleting variables.

The g-INIS is particularly effective when the covariates are highly correlated or conditionally correlated. In this case, the original INIS method tends to select many unimportant variables that have high correlation with important variables as they, too, have large marginal effects on the response. Although greedy, the g-INIS method is better at choosing true positives due to more stringent screening and improves the chance of the remaining important variables to be selected in subsequent stages due to less false positives at each stage. This leads to conditioning on a smaller set of more relevant variables and improve the overall performance. From our numerical experience, the g-INIS method outperforms the original INIS method in all examples in terms of higher true positive rate, smaller false positive rate and smaller prediction error.

5 Numerical Results

In this section, we will illustrate our method by studying the performance on the simulated data and a real data analysis. Part of the simulation settings are adapted from Fan and Lv (2008), Meier et al. (2009), Huang et al. (2010), and Fan and Song (2010).

5.1 Comparison of Minimum Model Size

We first illustrate the behavior of the NIS procedure under different correlation structures. Following Fan and Song (2010), the minimum model size(MMS) required for the NIS procedure and the penGAM procedure to have the sure screening property, i.e., to contain the true model ${\mathcal{M}}^{\ast }$, is used as a measure of the effectiveness of a screening method. We also include the correlation screening of Fan and Lv (2008) for comparison. The advantage of the MMS method is that we do not need to choose the thresholding parameter or penalized parameters. For NIS, we take d_n = [n^1/5] + 2 = 5. We set n = 400 and p = 1000 for all examples.

Example 1. Following Fan and Song (2010), let ${\left\{X_k\right\}}_{k=1}^{950}$ be i.i.d standard normal random variables and

$$X_k=\sum _{j=1}^s{X}_j{(-1)}^{j+1}∕5+\sqrt{1-\frac{s}{25}{\epsilon }_k}k=951,\cdots ,1000,$$

where ${\left\{{\epsilon }_k\right\}}_{k=951}^{1000}$ are standard normally distributed. We consider the following linear model as a specific case of the additive model: Y = β*^T X + ε, in which ε ~ N(0, 3) and β* = (1, −1, ε)^T has s non-vanishing components, taking values ±1 alternately.

Example 2. In this example, the data is generated from the simple linear regression Y = X₁+X₂+X₃+ε, where ε ~ N(0, 3). However, the covariates are not normally distributed: {X_k}_k≠2 are i.i.d standard normal random variables whereas $X_2=-\frac{1}{3}{X}_1^3+\tilde{\epsilon }$, where $\tilde{\epsilon }~N(0,1)$. In this case, E(Y|X₁) and E(Y|X₂) are nonlinear.

The minimum model size(MMS) for each method and its associated robust estimate of the standard deviation(RSD = IQR/1.34) are shown in Table 1. The column “NIS”, “penGAM”, and “SIS” summarizes the results on the MMS based on 100 simulations, respectively for the nonparametric independence screening in the paper, penalized method for additive model of Meier et al. (2009), and the linear correlation ranking method of Fan and Lv (2008). For Example 1, when the nonsparsity size s > 5, the irrepresentable condition required for the model selection consistency of LASSO fails. For these cases, penGAM fails even to include the true model until the last step. In contrast, the proposed nonparametric independence screening performs reasonably well. It is also worth noting that SIS performs better than NIS in the first example, particularly for s = 24. This is due to the fact that the true model is linear and the covariates are jointly normally distributed, which implies that the marginal projection is also linear. In this case, NIS selects variables from pd_n parameters whereas SIS selects only from p parameters. However, for the nonlinear problem like Example 2, both nonlinear method NIS and penGAM behave nicely, whereas SIS fails badly even though the underlying true model is indeed linear.

Table 1.

Minimum model size and robust estimate of standard deviations (in parentheses).

Model	NIS	PenGAM	SIS
Ex 1 (s = 3; SNR ≈ 1:01)	3(0)	3(0)	3(0)
Ex 1 (s = 6; SNR ≈ 1:99 )	56(0)	1000(0)	56(0)
Ex 1 (s = 12; SNR ≈ 4:07)	66(7)	1000(0)	62(1)
Ex 1 (s = 24; SNR ≈ 8:20)	269(134)	1000(0)	109(43)
Ex 2 (SNR ≈ 0:83)	3(0)	3(0)	360(361)

5.2 Comparison of Model Selection and Estimation

As in the previous section, we set n = 400 and p = 1000 for all the examples to demonstrate the power of our newly proposed methods INIS and g-INIS. Here in the NIS step, we fix d_n = 5 as in the last subsection. The number of simulations is 100. Here, we use five-fold cross validation in Step 2 of the INIS algorithm. For simplicity of notations, we let

$$g_1\left(x\right)=x,g_2\left(x\right)={(2x-1)}^2,g_3\left(x\right)=\frac{\sin \left(2\pi x\right)}{2-\sin \left(2\pi x\right)}$$

and

$$g_4\left(x\right)=0.1\sin \left(2\pi x\right)+0.2\cos \left(2\pi x\right)+0.3\sin {\left(2\pi x\right)}^2+0.4\cos {\left(2\pi x\right)}^3+0.5\sin {\left(2\pi x\right)}^3.$$

Example 3. Following Meier et al. (2009), we generate the data from the following additive model:

$$Y=5g_1\left(X_1\right)+3g_2\left(X_2\right)+4g_3\left(X_3\right)+6g_4\left(X_4\right)+\sqrt{1.74}\epsilon$$

The covariates X = (X₁, ⋯ , X_p)^T are simulated according to the random effect model

$$X_j=\frac{W_j+tU}{1+t},j=1,\cdots ,p,$$

where W₁, ⋯ , W_p and U are i.i.d. Unif(0, 1) and ε ~ N(0, 1). When t = 0, the covariates are all independent, and when t = 1 the pairwise correlation of covariates is 0.5.

Example 4. Again, we adapt the simulation model from Meier et al. (2009). This example is a more difficult case than Example 3 since it has 12 important variables with different coefficients.

$$\begin{array}{cc}\hfill Y& =g_1\left(X_1\right)+g_2\left(X_2\right)+g_3\left(X_3\right)+g_4\left(X_4\right)\hfill \\ \hfill & +1.5g_1\left(X_5\right)+1.5g_2\left(X_6\right)+1.5g_3\left(X_7\right)+1.5g_4\left(X_8\right)\hfill \\ \hfill & +2g_1\left(X_9\right)+2g_2\left(X_{10}\right)+2g_3\left(X_{11}\right)+2g_4\left(X_{12}\right)+\sqrt{0.5184}\epsilon ,\hfill \end{array}$$

where ε ~ N(0, 1). The covariates are simulated as in Example 3.

Example 5. We follow the simulation model of Fan et al. (2009), in which Y = β₁X₁ + β₂X₂ + β₃X₃ + β₄X₄ + ε is simulated, where ε ~ N(0, 1). The covariates X₁, ⋯ , X_p are jointly Gaussian, marginally N(0, 1), and with $\mathrm{corr}(X_i,X_4)=1∕\sqrt{2}$ for all i ≠ 4 and corr(X_i, X_j) = 1/2 if i and j are distinct elements of {1, ⋯ , p}\{4}. The coefficients β₁ = 2, β₂ = 2, β₃ = 2, β₄ = $-3\sqrt{2}$, and β_j = 0 for j > 4 are taken so that X₄ is independent of Y, even though it is the most important variable in the joint model, in terms of the regression coefficient.

For each example, we compare the performances of INIS-penGAM, g-INIS-penGAM proposed in the paper, penGAM(Meier et al., 2009), and ISIS-SCAD (Fan et al., 2009) which aims for sparse linear model. Their results are shown respectively in the rows “INIS”, “g-INIS”, “penGAM” and “ISIS” of Table 2, in which the True Positives(TP), False Positives(FP), Prediction Error(PE) and Computation Time (Time) are reported for each method. Here the prediction error is calculated on an independent test data set of size n/2.

Table 2.

Average values of the numbers of true (TP) and false (FP) positives, prediction error (PE), and Time (in seconds). Robust standard deviations are given in parentheses.

Model	Method	TP	FP	PE	Time
Ex 3(t = 0) (SNR ≈ 9.02)	INIS	4. 00(0. 00)	2.58(2.24)	3. 02(0. 34)	18. 50(7. 22)
	g-INIS	4. 00(0. 00)	0. 67(0. 75)	2. 92(0. 30)	25. 03(4. 87)
	penGAM	4. 00(0. 00)	31. 86(23. 51)	3. 30(0. 40)	180. 63(6. 92)
	ISIS	3. 03(0. 00)	29.97(0.00)	15.95(1.74)	12. 95(4. 18)
Ex 3(t = 1) (SNR ≈ 7.58)	INIS	3. 98(0. 00)	15.76(6.72)	2. 97(0. 39)	78. 80(26. 91)
	g-INIS	4. 00(0. 00)	0. 98(1. 49)	2. 61(0. 26)	33. 89(9. 99)
	penGAM	4. 00(0. 00)	39. 21(24. 63)	2. 97(0. 28)	254. 06(13. 06)
	ISIS	3. 01(0. 00)	29.99(0.00)	12. 91(1. 39)	18. 59(4. 37)
Ex 4(t = 0) (SNR ≈ 8.67)	INIS	11. 97(0. 00)	3.22(1.49)	0.97(0.11)	73.60(25.77)
	g-INIS	12. 00(0. 00)	0. 73(0. 75)	0.91(0.10)	160. 75(19. 94)
	penGAM	11. 99(0. 00)	80. 10(18. 28)	1. 27(0. 14)	233. 72(10. 25)
	ISIS	7.96(0.75)	25.04(0.75)	4.70(0.40)	12. 89(5. 00)
Ex 4(t = 1) (SNR ≈ 10.89)	INIS	10. 01(1. 49)	15.56(0.93)	1.03(0.13)	125.11(39.99)
	g-INIS	10. 78(0. 75)	1.08(1.49)	0.87(0.11)	156. 37(28. 58)
	penGAM	10. 51(0. 75)	62. 11(26. 31)	1. 13(0. 12)	278.61(16.93)
	ISIS	6.53(0.75)	26.47(0.75)	4.30(0.44)	17.02(4.01)
Ex 5 (SNR ≈ 6.11)	INIS	3. 99(0. 00)	21.96(0.00)	1. 62(0. 18)	94. 50(7. 12)
	g-INIS	4. 00(0. 00)	1. 04(1. 49)	1. 16(0. 12)	39.78(12.45)
	penGAM	3. 00(0. 00)	195. 03(21. 08)	1.93(0.28)	1481. 12(181. 93)
	ISIS	4. 00(0. 00)	29.00(0.00)	1.40(0.17)	17. 78(3. 85)

First of all, for the greedy modification, g-INIS-penGAM, the number of false positive variables is approximately 1 for all examples and the number of false positive for both INIS-penGAM and ISIS-SCAD are much smaller than that for penGAM. In terms of false positives, we can see that in Examples 3 and 4, INIS-penGAM and penGAM have similar performance, whereas penGAM misses one variable most of the time in Example 5. The linear method ISIS-SCAD missed important variables in the nonlinear models in Examples 3 and 4.

One may notice that in Example 4 (t = 1), even INIS and g-INIS miss more than one variables on average. To explore the reason, we took a close look at the iterative process for this example and find out the variable X₁ and X₂ are missed quite often. The explanation is that although the overall SNR (Signal to Noise Ratio) for this example is around 10.89, the individual contributions to the total signal vary significantly. Now, let us introduce the notion of individual SNR. For example, var(m₁(X₁))/var(ε) in the additive model

$$Y=m_1\left(X_1\right)+\cdots +m_p\left(X_p\right)+\epsilon$$

is the individual SNR for the first component under the oracle model where m₂, ⋯ , m_p are known. In Example 4 (t = 1), the variance of all 12 components are as follows:

1	2	3	4	5	6	7	8	9	10	11	12
0.08	0.09	0.21	0.26	0.19	0.20	0.47	0.58	0.33	0.36	0.84	1.03

We can see that the variance varies a lot among the 12 components, which leads to very different marginal SNRs. For example, the individual SNR for the first component is merely 0.08/0.518 = 0.154, which is very challenging to be detected. With the overall SNR fixed, the individual SNRs play an important role in measuring the difficulty for selecting individual variables

In the perspective of the prediction error, INIS-penGAM, g-INIS-penGAM and penGAM outperforms ISIS-SCAD in the nonlinear models whereas their performances are worse than ISIS-SCAD in the linear model, Example 5. Overall, it is quite clear that the greedy modification g-INIS is a competing variable selection method in ultra-high dimensional additive models where we have very low false selection rate, small prediction errors, and fast computation.

5.3 d_n and SNR

In this subsection, we conduct simulation study to investigate the performance of INIS-penGAM estimator under different SNR settings using different number (d_n) of basis functions.

Example 6. We generate the data from the following additive model:

$$Y=3g_1\left(X_1\right)+3g_2\left(X_2\right)+2g_3\left(X_3\right)+2g_4\left(X_4\right)+C\sqrt{3.3843}\epsilon ,$$

where the covariates X = (X₁, ⋯ , X_p)^T are simulated according to Example 3. Here C takes a series of different values (C² = 2, 1, 0.5, 0.25) to make the corresponding SNR = 0.5, 1, 2, 4. We report the results of using number of basis functions d_n = 2, 4, 6, 8, in Tables 4 and 5 in the Appendix.

From Table 4 in the Appendix where all the variables are independent, both methods have very good true positives under various SNR when d_n is not too large. However, for the case of SNR = 0.5 and d_n = 16, the INIS and penGAM perform poorly in terms of low true positive rate. This is due to the fact that when d_n is large, the estimation variance will be large and this makes it difficult to differentiate the active variables from inactive ones when the signals are weak.

Now let us have a look at the more difficult case in Table 5 (in the Appendix) where pairwise correlation between variables is 0.5. We can see that INIS have a competitive performance under various SNR values except when d_n = 16. When SNR = 0.5, we can not achieve sure screening under the current sample size and configuration for the aforementioned reasons.

5.4 An analysis on Affymetric GeneChip Rat Genome 230 2.0 Array

We use the data set reported in Scheetz et al. (2006) and analyzed by Huang et al. (2010) to illustrate the application of the proposed method. For this data set, 120 twelve-week-old male rats were selected for tissue harvesting from the eyes and for microarray analysis. The microarrays used to analyze the RNA from the eyes of these animals contain over 31,042 different probe sets (Affymetric GeneChip Rat Genome 230 2.0 Array). The intensity values were normalized using the robust multi-chip averaging method (Irizarry et al., 2003) method to obtain summary expression values for each probe set. Gene expression levels were analyzed on a logarithmic scale.

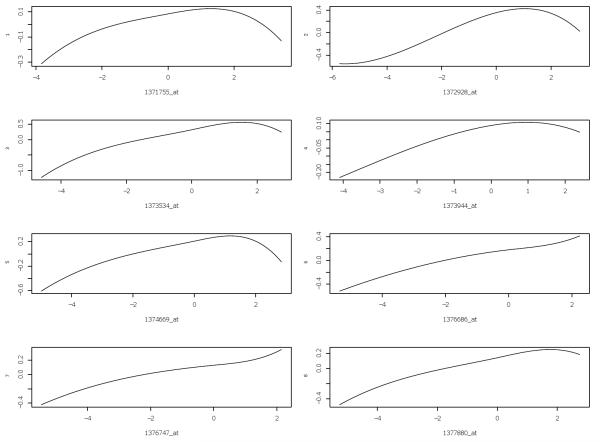
Following Huang et al. (2010), we are interested in finding the genes that are related to the gene TRIM32, which was recently found to cause Bardet-Biedl syndrome (Chiang et al., 2006), and is a genetically heterogeneous disease of multiple organ systems including the retina. Although over 30,000 probe sets are represented on the Rat Genome 230 2.0 Array, many of them are not expressed in the eye tissue. We only focus on the 18975 probes which are expressed in the eye tissue. We use our INIS-penGAM method directly on this dataset, where n = 120 and p = 18975, and the method is denoted as INIS-penGAM (p = 18975). Direct application of penGAM approach on the whole dataset is too slow. Following Huang et al. (2010), we use 2000 probe sets that are expressed in the eye and have highest marginal correlation with TRIM32 in the analysis. On the subset of the data (n = 120, p = 2000), we apply the INIS-penGAM and penGAM to model the relation between the expression of TRIM32 and those of the 2000 genes. For simplicity, we did not implement g-INIS-penGAM. Prior to the analysis, we standardize each probe to be of mean 0 and variance 1. Now, we have three different estimators, INIS-penGAM (p = 18975), INIS-penGAM (p = 2000) and penGAM (p = 2000). The INIS-penGAM (p = 18975) selects the following 8 probes: 1371755_at, 1372928_at, 1373534_at, 1373944_at, 1374669_at, 1376686_at, 1376747_at, 1377880_at. The INIS-penGAM (p = 2000) selects the following 8 probes: 1376686_at, 1376747_at, 1378590_at, 1373534_at, 1377880_at, 1372928_at, 1374669_at, 1373944_at. On the other hand, the penGAM (p = 2000) selects 32 probes. The residual sum of squares (RSS) for these fittings are 0.24, 0.26 and 0.1 for INIS-penGAM (p = 18975), INIS-penGAM (p = 2000) and penGAM (p = 2000), respectively.

In order to further evaluate the performances of the two methods, we use cross-validation and compare the prediction mean square error (PE). We randomly partition the data into a training set of 100 observations and a test set of 20 observations. We compute the number of probes selected using the 100 observations and the prediction errors on these 20 test sets. This process is repeated 100 times. Table 3 gives the average values and their associated robust standard deviations over 100 replications. It is clear in the table that by applying the INIS-penGAM approach, we select far fewer genes and give smaller prediction error. Therefore, in this example, the INIS-penGAM provides the biological investigator a more targeted list of probe sets, which could be very useful in further study.

Table 3.

Mean Model Size (MS) and Prediction Error (PE) over 100 repetitions and their robust standard deviations(in parentheses) for INIS (p = 18975), INIS (p = 2000) and penGAM (p = 2000).

Method	MS	PE
INIS (p = 18975)	7.73(0.00)	0.47(0.13)
INIS (p = 2000)	7.68(0.75)	0.44(0.15)
penGAM (p = 2000)	26.71(14.93)	0.48(0.16)

6 Remarks

In this paper, we studied the nonparametric independence screening (NIS) method for variable selection in additive models. B-spline basis functions are used for fitting the marginal nonparametric components. The proposed marginal projection criteria is an important extension of the marginal correlation. Iterative NIS procedures are also proposed such that variable selection and coefficient estimation can be achieved simultaneously. By applying the INIS-penGAM method, we can preserve the sure screening property and substantially reduce the false selection rate. A greedy modification of the method g-INIS-penGAM is proposed to further reduce the false selection rate. Moreover, we can deal with the case where some variable is marginally uncorrelated but jointly correlated with the response. The proposed method can be easily generalized to generalized additive model with appropriate conditions.

As the additive components are specifically approximated by truncated series expansions with B-spline bases in this paper, the theoretical results should hold in general and the proposed framework can be readily adaptive to other smoothing methods with additive models (Horowitz et al., 2006; Silverman, 1984), such as local polynomial regression (Fan and Jiang, 2005), wavelets approximations(Antoniadis and Fan, 2001; Sardy and Tseng, 2004) and smoothing spline (Speckman, 1985). This is an interesting topic for future research.

7 Proofs

Proof of Lemma 1.

By the property of the least-squares, E(Y − f_nj)f_nj = 0 and E(Y − f_nj)f_nj = 0. Therefore,

$$E{f}_{nj}(f_j-f_{nj})=E(Y-f_{nj})f_{nj}-E(Y-f_j)f_{nj}=0.$$

It follows from this and the orthogonal decomposition f_j = f_nj + (f_j − f_nj) that

$${\parallel f_{nj}\parallel }^2={\parallel f_j\parallel }^2-{\parallel f_j-f_{nj}\parallel }^2$$

The desired result follows from Condition C together with Fact 1.

The following two types of Bernstein’s inequality in van der Vaart and Wellner (1996) will be needed. We reproduce them here for the sake of read-ability.

Lemma 2 (Bernstein’s inequality, Lemma 2.2.9, van der Vaart and Wellner (1996)). For independent random variables Y₁, ⋯ , Y_n with bounded ranges [−M, M] and zero means,

$$P(\mid Y_1+\cdots +Y_n\mid >x)\le 2\text{exp}\{-x^2∕\left(2(v+Mx∕3)\right)\}$$

for v ≥ var(Y₁ + ⋯ + Y_n).

Lemma 3 (Bernstein’s inequality, Lemma 2.2.11, van der Vaart and Wellner (1996)). Let Y₁, ⋯ , Y_n be independent random variables with zero mean such that E|Y_i|^m ≤ m!M^m−2v_i/2, for every m ≥ 2 (and all i) and some constants M and v_i. Then

$$P(\mid Y_1+\cdots +Y_n\mid >x)\le 2\text{exp}\{-x^2∕\left(2(v+Mx)\right)\},$$

for v ≥ v₁ + ⋯ v_n.

The following two lemmas will be needed to prove Theorem 1.

Lemma 4. Under Conditions A, B and D, for any δ > 0, there exist some positive constants c₆ and c₇ such that

$$P(\mid ({\mathbb{P}}_n-E){\Psi }_{jk}Y\mid \ge \delta n^{-1})\le 4\text{exp}(-{\delta }^2∕2(c_{6}n{d}_n^{-1}+c_7\delta )),$$

for k = 1, ⋯ , d_n, j = 1, ⋯ , p.

Proof of Lemma 4.

Denote by T_jki = Ψ_jk(X_ij)Y_i − EΨ_jk(X_ij)Y_i. Since Y_i = m(X_i) + ε_i, we can write T_jki = T_jki1 + T_jki2, where

$$T_{jki1}={\Psi }_{jk}\left(X_{ij}\right)m\left(X_i\right)-E{\Psi }_{jk}\left(X_{ij}\right)m{\left(\text{X}\right)}_i,$$

and T_jki2 = Ψ_jk(X_ij)ε_i.

By Conditions A, B, D and Fact 2, recalling ∥Ψ_jk∥_∞ ≤ 1, we have

$$\mid T_{jki1}\mid \le 2B_1,\mathrm{var}\left(T_{jki1}\right)\le E{\Psi }_{jk}^2\left(X_{ij}\right)m_i{\left(X_{ij}\right)}^2\le B_1^2{C}_2{d}_n^{-1}.$$ (12)

By Bernstein’s inequality (Lemma 2), for any δ₁ > 0,

$$P(\mid \sum _{i=1}^n{T}_{jki1}\mid >{\delta }_1)\le 2\exp \left(-\frac{1}{2}\frac{{\delta }_1^2}{n{B}_1^2{C}_2{d}_n^{-1}+2B_1{\delta }_1∕3}\right).$$ (13)

Next, we bound the tails of T_jki2. For every r ≥ 2,

$$\begin{array}{cc}\hfill E{\mid T_{jkt2}\mid }^r& \le E\mid {\Psi }_{jk}{\left(X_{ij}\right)}^2\mid E({\mid {\epsilon }_i\mid }^r\mid X_i)\hfill \\ \hfill & \le r!B_2^{-r}E{\mid {\Psi }_{jk}\left(X_{ij}\right)\mid }^{2}E\text{exp}(B_2\mid {\epsilon }_i\mid \mid X_i)\hfill \\ \hfill & \le B_3{C}_2{d}_n^{-1}r!B_2^{-r},\hfill \end{array}$$

where the last inequality utilizes Condition E and Fact 2. By Bernstein’s inequality (Lemma 3), for any δ₂ > 0,

$$P(\mid \sum _{i=1}^n{T}_{jki2}\mid >{\delta }_2)\le 2\exp \left(-\frac{1}{2}\frac{{\delta }_2^2}{2n{B}_2^{-2}{B}_3{C}_2{d}_n^{-1}+B_2^{-1}{\delta }_2}\right).$$ (14)

Combining (13) and (14), the desired result follows by taking $c_6=\max (B_1^2{C}_2,2B_2^{-2}{B}_3{C}_2)$ and c₇ = max(2/3B₁, $B_2^{-1}$.

Throughout the rest of the proof, for any matrix A, let $\parallel \mathbf{A}\parallel =\sqrt{{\lambda }_{\max }\left({\mathbf{A}}^T\mathbf{A}\right)}$ be the operator norm and ∥A∥_∞ = max_i,j |A_ij| be the infinity norm. The next lemma is about the tail probability of the eigenvalues of the design matrix.

Lemma 5. Under Conditions A and B, for any δ > 0,

$$P(\mid {\lambda }_{\text{min}}\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)-{\lambda }_{min}\left(E{\Psi }_j{\Psi }_j^T\right)\mid \ge d_n\delta ∕n)\le 2d_n^2\text{exp}\left\{-\frac{1}{2}\frac{{\delta }^2}{C_{2}n{d}_n^{-1}+\delta ∕3}\right\}.$$

In addition, for any given constant c₄, there exists some positive constant c₈ such that

$$P\left\{\mid \parallel {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel -\parallel {\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \mid \ge c_8\parallel {\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \right\}\le 2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right).$$ (15)

Proof of Lemma 5.

For any symmetric matrices A and B and any ∥x∥ = 1, where ∥ · ∥ is the Euclidean norm,

$$X^T(A+B)x=X^{T}AX+X^{T}BX\ge \underset{\parallel X\parallel =1}{min}{X}^{T}AX+\underset{\parallel X\parallel =1}{\text{min}}{X}^{T}BX.$$

Taking minimum among ∥x∥ = 1 on the left side, we have

$$\underset{\parallel X\parallel }{\text{min}}{X}^T(A+B)X\ge \underset{\parallel X\parallel =1}{\text{min}}{X}^{T}AX+\underset{\parallel X\parallel =1}{\text{min}}{X}^{T}BX,$$

which is equivalent to λ_min(A + B) ≥ λ_min(A) + λ_min(B).

Then we have

$${\lambda }_{\text{min}}\left(\text{A}\right)\ge {\lambda }_{\text{min}}\left(\text{B}\right)+{\lambda }_{\text{min}}(\text{A}-\text{B}),$$

which is the same as

$$\lambda (\text{A}-\text{B})\le {\lambda }_{\text{min}}\left(\text{A}\right)-{\lambda }_{\text{min}}\left(\text{B}\right).$$

By switching the roles of A and B, we also have

$${\lambda }_{\text{min}}(\text{B}-\text{A})\le {\lambda }_{\text{min}}\left(\text{B}\right)-{\lambda }_{\text{min}}\left(\text{A}\right)$$

In other words,

$$\mid {\lambda }_{\min }\left(\mathbf{A}\right)-{\lambda }_{\min }\left(\mathbf{B}\right)\mid \le \max \{\mid {\lambda }_{\min }(\mathbf{A}-\mathbf{B})\mid ,\mid {\lambda }_{\min }(\mathbf{B}-\mathbf{A})\mid \}$$ (16)

Let ${\mathbf{D}}_j={\mathbb{P}}_n{\Psi }_j{\Psi }_j^T-E{\Psi }_j{\Psi }_j^T$. Then, it follows from (16) that

$$\mid {\lambda }_{\min }\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)-{\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)\mid \le \max \{\mid {\lambda }_{\min }\left({\mathbf{D}}_j\right)\mid ,\mid {\lambda }_{\min }(-{\mathbf{D}}_j)\mid \}.$$ (17)

We now bound the right-hand side of (17). Let ${\mathbf{D}}_j^{(i,l)}$ be the (i, l) entry of D_j. Then, it is easy to see that for any ∥x∥ = 1,

$$\mid {\mathbf{x}}^T{\mathbf{D}}_j\mathbf{x}\mid \le {\parallel {\mathbf{D}}_j\parallel }_{\infty }{\left(\sum _{i=1}^{d_n}\mid x_i\mid \right)}^2\le d_n{\parallel {\mathbf{D}}_j\parallel }_{\infty }.$$ (18)

Thus,

$${\lambda }_{\text{min}}\left({\text{D}}_j\right)=\underset{\parallel X\parallel =1}{\text{min}}{X}^T{D}_{j}X\le d_n{\parallel D_j\parallel }_{\infty }$$

On the other hand, by using (18) again, we have

$${\lambda }_{\text{min}}\left({\text{D}}_j\right)=-\underset{\parallel X\parallel =1}{\text{max}}(-X^T{D}_{j}X)\ge -d_n{\parallel D_j\parallel }_{\infty }.$$

We conclude that

$$\mid {\lambda }_{\text{min}}\left({\text{D}}_j\right)\mid \le d_n{\parallel D_j\parallel }_{\infty }.$$

The same bound on |λ_min(−D_j)| can be obtained by using the same argument. Thus, by (17), we have

$$\mid {\lambda }_{\min }\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)-{\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)\mid \le d_n{\parallel {\mathbf{D}}_j\parallel }_{\infty }.$$ (19)

We now use Bernstein’s inequality to bound the right-hand side of (19). Since ∥Ψ_jk∥_∞ ≤ 1, and by using Fact 2, we have that

$$\text{var}\left({\Psi }_{jk}\left(X_j\right){\Psi }_{jl}\left(X_j\right)\right)\le E{\Psi }_{jk}^2\left(X_j\right){\Psi }_{jl}^2\left(X_j\right){\Psi }_{jl}^2\left(X_j\right)\le E{\Psi }_{jk}^2\left(X_j\right)\le C_2{d}_n^{-1}.$$

By Bernstein’s inequality (Lemma 2), for any δ > 0,

$$P(\mid ({\mathbb{P}}_n-E){\Psi }_{jk}\left(X_j\right){\Psi }_{jl}\left(X_j\right)\mid >\delta ∕n)\le 2\exp \left\{-\frac{\delta 2}{2(C_{2}n{d}_n^{-1}+\delta ∕3)}\right\}.$$ (20)

It follows from (19), (20) and the union bound of probability that

$$P(\mid {\lambda }_{min}\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)-{\lambda }_{\text{min}}\left(E\Psi \text{j}{\Psi }_j^T\right)\mid \ge d_n\delta ∕n)\le 2d_n^2\text{exp}\left\{\frac{{\delta }^2}{2(C_{2}n{d}_n^{-1}+\delta ∕3)}\right\}.$$

This completes the proof of the first inequality.

To prove the second inequality, let us take $\delta =c_g{D}_{1}n{d}_n^{-2}$ in (20), where c₉ ∈ (0, 1). By recalling Fact 3, it follows that

$$P(\mid {\lambda }_{\min }\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)-{\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)\mid \ge c_9{\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right))\le 2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right),$$ (21)

for some positive constant c₄. The second part of the lemma thus follows from the fact that λ_min(H)⁻¹ = λ_max(H⁻¹), if we establish

$$P\left(\mid {\left\{{\lambda }_{\min }\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)\right\}}^{-1}-{\left\{{\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)\right\}}^{-1}\mid \ge c_8{\left\{{\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)\right\}}^{-1}\right)\le 2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right),$$ (22)

by using (21), where c₈ = 1/(1 − c₉) − 1.

We now deduce (22) from (21). Let $A={\lambda }_{\min }({\mathbb{P}}_n{\Psi }_j,{\Psi }_j^T)$ and $B={\lambda }_{\min }\left(E{\Psi }_j{\Psi }_j^T\right)$. Then A > 0 and B > 0. We aim to show for a ∈ (0,1),

$$\mid A^{-1}-{\text{B}}^{-1}\mid \ge c{B}^{-1}\text{implies}\mid A-B\mid \ge aB,$$

where c = 1/(1 − a) − 1.

Since

$$\mid A^{-1}-B^{-1}\mid \ge (1∕(1-a)-1)B^{-1},$$

we have

$$A^{-1}-B^{-1}\le -(1∕(1-a)-1)B^{-1},\text{or}\ge (1∕(1-a)-1)B^{-1}.$$

Note that for a ∈ (0, 1), we have 1 − 1/(1 + a) < 1/(1 − a) − 1. Then it follows that

$$A^{-1}-B^{-1}\le -(1-1∕(1+a))B^{-1},\text{or}\ge (1∕(1-a)-1)B^{-1}.$$

which is equivalent to |A – B| ≥ aB.

This concludes the proof of the lemma.

Proof of Theorem 1.

We first show part (i). Recall that

$${\parallel {\widehat{f}}_{nj}\parallel }_n^2={\left({\mathbb{P}}_n{\Psi }_{j}Y\right)}^T{\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}{\mathbb{P}}_n{\Psi }_{j}Y,$$

and

$${\parallel f_{nj}\parallel }^2={\left(E{\Psi }_{j}Y\right)}^T{\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}E{\Psi }_{j}Y.$$

Let ${\mathbf{a}}_n={\mathbb{P}}_n{\Psi }_{j}Y$, ${\mathbf{B}}_n={\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}$, a = EΨ_jY. and $\mathbf{B}={\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}$. By some algebra,

$${\text{a}}_n^T{\text{B}}_n{\text{a}}_n-{\text{a}}^T\text{Ba}={({\text{a}}_n-\text{a})}^T{\text{B}}_n({\text{a}}_n-\text{a})+2{({\text{a}}_n-a)}^T{\text{B}}_n\text{a}+a_n^T({\text{B}}_n-\text{B})a,$$

we have

$${\parallel {\widehat{f}}_{nj}\parallel }_n^2-{\mid \mid f_{nj}\mid \mid }^2=S_1+S_2+S_3,$$ (23)

where

$$\begin{array}{cc}\hfill S_1& ={({\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y)}^T{\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}({\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y),\hfill \\ \hfill S_2& =2{({\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y)}^T{\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}E{\Psi }_{j}Y,\hfill \\ \hfill S_3& ={\left(E{\Psi }_{j}Y\right)}^T({\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}-{\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1})E{\Psi }_{j}Y.\hfill \end{array}$$

Note that

$$S_1\le \parallel {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \cdot {\parallel {\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y\parallel }^2.$$ (24)

By Lemma 4 and the union bound of probability,

$$P({\parallel {\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y\parallel }^2\ge d_n{\delta }^2{n}^{-2})\le 4d_n\exp (-{\delta }^2∕2(c_{6}n{d}_n^{-1}+c_7\delta )).$$ (25)

Recall the result in Lemma 5 that, for any given constant c₄, there exists a positive constant c₈ such that

$$P\left\{\mid \parallel {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel -\parallel {\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \mid \ge c_8\parallel {\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \right\}\le 2d_n^2\text{exp}\left(-c_{4}n{d}_n^{-3}\right).$$

Since by Fact 3,

$$\Vert {\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\Vert \le D_1^{-1}{d}_n,$$

it follows that

$$P\left\{\Vert {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\Vert \ge (c_8+1)D_1^{-1}{d}_n\right\}\le 2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right).$$ (26)

Combining (24)–(26) and the union bound of probability, we have

$$P(S_1\ge (c_8+1)D_1^{-1}{d}_n^2{\delta }^2∕n^2)\le 4d_n\exp (-{\delta }^2∕2(c_{6}n{d}_n^{-1}+c_7\delta ))+2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right).$$ (27)

To bound S₂, we note that

$$\begin{array}{cc}\hfill \mid S_2\mid & \le 2\parallel {\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y\parallel \cdot \parallel {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}E{\Psi }_{j}Y\parallel \hfill \\ \hfill & \le 2\parallel {\mathbb{P}}_n{\Psi }_{j}Y-E{\Psi }_{j}Y\parallel \cdot \parallel {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \cdot \parallel E{\Psi }_{j}Y\parallel .\hfill \end{array}$$ (28)

Since by Condition D,

$${\parallel E{\Psi }_{j}Y\parallel }^2=\sum _{k=1}^{d_n}{\left(E{\Psi }_{jk}Y\right)}^2=\sum _{k=1}^{d_n}{\left(E{\Psi }_{jk}m\right)}^2\le \sum _{k=1}^{d_n}{B}_1^{2}E{\Psi }_{jk}^2\le B_1^2{C}_2,$$ (29)

it follows from (25), (26), (28), (29) and the union bound of probability that

$$\begin{array}{cc}\hfill & P(\mid S_2\mid \ge 2(c_8+1)D_1^{-1}{C}_2^{1∕2}{B}_1{d}_n^{3∕2}\delta ∕n)\hfill \\ \hfill & \le 4d_n\exp (-{\delta }^2∕2(c_{6}n{d}_n^{-1}+c_7\delta ))+2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right).\hfill \end{array}$$ (30)

Now we bound S₃. Note that

$$S_3={\left(E{\Psi }_{j}Y\right)}^T{\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\left(E-{\mathbb{P}}_n\right){\Psi }_j{\Psi }_j^T{\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}E{\Psi }_{j}Y.$$ (31)

By the fact that ∥AB∥ ≤ ∥A∥ · ∥B∥, we have

$$\mid S_3\mid \le \parallel ({\mathbb{P}}_n-E){\Psi }_j{\Psi }_j^T\parallel \cdot \parallel {\left({\mathbb{P}}_n{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \cdot \parallel {\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\parallel \cdot {\parallel E{\Psi }_{j}Y\parallel }^2.$$ (32)

For any ∥x∥ = 1 and d_n-dimensional square matrix D,

$$\Vert \left({\mathbb{P}}_n-E\right){\Psi }_j{\Psi }_j^T)\Vert \le d_n{\parallel ({\mathbb{P}}_n-E){\Psi }_j{\Psi }_j^T\parallel }_{\infty }.$$ (33)

Therefore, ∥D∥ ≤ d_n∥D∥_∞. We conclude that

$${\text{X}}^T{\text{D}}^T\text{DX}=\sum _i{\left(\sum _j{d}_{ij}{x}_j\right)}^2\le {\parallel \text{D}\parallel }_{\infty }^2{d}_n{\left(\sum _{j=1}^{d_n}\mid x_i\mid \right)}^2\le d_n^2{\parallel \text{D}\parallel }_{\infty }^2.$$

By (20), (26), (29), (32), (33) and the union bound of probability, it follows that

$$\begin{array}{cc}\hfill & P(\mid S_3\mid \ge (c_8+1)D_1^{-2}{B}_1^2{C}_2{d}_n^3\delta ∕n)\hfill \\ \hfill & \le 2d_n^2\exp (-{\delta }^2∕2(c_{6}n{d}_n^{-1}+c_7\delta ))2d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right).\hfill \end{array}$$ (34)

It follows from (23), (27), (30), (34) and the union bound of probability that for some positive constants c₁₀, c₁₁ and c₁₂,

$$\begin{array}{cc}\hfill & P\left(\mid {\parallel {\widehat{f}}_{nj}\parallel }_n^2-{\parallel f_{nj}\parallel }^2\mid \ge c_{10}{d}_n^2{\delta }^2∕n^2+c_{11}{d}_n^{3∕2}\delta ∕n+c_{12}{d}_n^3\delta ∕n\right)\hfill \\ \hfill & \le (8d_n+2d_n^2)\exp (-{\delta }^2∕2(c_{6}n{d}_n^{-1}+c_7\delta ))+6d_n^2\exp \left(-c_{4}n{d}_n^{-3}\right).\hfill \end{array}$$ (35)

In (35), let $c_{10}{d}_n^2{\delta }^2∕n^2+c_{11}{d}_n^{3∕2}\delta ∕n+c_{12}{d}_n^3\delta ∕n=c_2{d}_n{n}^{-2k}$ for any given c₂ > 0, i.e., taking $\delta =n^{1-2k}{d}_n^{-2}{c}_2∕c_{12}$, there exist some positive constants c₃ and c₄ such that

$$P(\mid {\parallel {\widehat{f}}_{nj}\parallel }_n^2-{\parallel f_{nj}\parallel }^2\mid \ge c_2{d}_n{n}^{-2\kappa })\le (8d_n+2d_n^2)\text{exp}(-c_3{n}^{1-4\kappa }{d}_n^{-3})+6d_n^2\text{exp}(-c_{4}n{d}_n^{-3}).$$

The first part thus follows the union bound of probability.

To prove the second part, note that on the event

$$A_n\equiv \{\underset{j\in {\mathcal{M}}_{\ast }}{\text{max}}\mid {\parallel {\widehat{f}}_{nj}\parallel }_n^2-{\parallel f_{nj}\parallel }^2\mid \le c_1\xi d_n{n}^{-2\kappa }∕2\},$$

by Lemma 1, we have

$${\parallel {\widehat{f}}_{nj}\parallel }_n^2\ge c_1\xi d_n{n}^{-2\kappa }∕2,\text{for all}j\in {\mathcal{M}}_{\star }.$$ (36)

Hence, by the choice of 03BD;_n we have ${\mathcal{M}}_{\star }\subset {\widehat{\mathcal{M}}}_{{\nu }_n}$. The result now follows from a simple union bound:

$$P\left(A_n^c\right)\le s_n\left\{(8d_n+2d_n^2)\text{exp}\left(-c_3{n}^{1-4\kappa }{d}_n^{-3}\right)+6d_n^2\text{exp}\left(-c_{4}n{d}_n^{-3}\right)\right\}.$$

This completes the proof.

Proof of Theorem 2. The key idea of the proof is to show that

$${\parallel E\Psi Y\parallel }^2=O\left({\lambda }_{\max }\left(\Sigma \right)\right).$$ (37)

If so, by definition and ∥Ψ_jk∥_∞ ≤ 1, we have

$$\sum _{j=1}^{p_n}{\parallel f_{nj}\parallel }^2\le \underset{1\le j\le p_n}{\text{max}}{\lambda }_{\text{max}}\left\{{\left(E{\Psi }_j{\Psi }_j^T\right)}^{-1}\right\}{\parallel E\Psi Y\parallel }^2={\rm O}\left(d_n{\lambda }_{max}\left(\Sigma \right)\right).$$

This implies that the number of {j : ∥f_nj∥² > εd_nn^−2k} can not exceed O(n^2k λ_max(Σ)) for any ε > 0. Thus, on the set

$$B_n=\{\underset{1\le j\le p_n}{\text{max}}\mid {\parallel {\widehat{f}}_{nj}\parallel }_n^2-{\parallel f_{nj}\parallel }^2\mid \le \epsilon d_n{n}^{-2\kappa }\},$$

the number of $\{j:{\parallel {\widehat{f}}_{nj}\parallel }_n^2\ge 2\epsilon d_n{n}^{-2k}\}$ can not exceed the number of {j: ∥f_nj∥² > εd_nn^−2k}, which is bounded by O{n^2k λ_max(Σ)}. By taking ε = c₅/2, we have

$$P[\mid {\widehat{\mathcal{M}}}_{\nu n}\mid \le O\left\{n^{2\kappa }{\lambda }_{\max }\left(\Sigma \right)\right\}]\ge P\left(B_n\right).$$

The conclusion follows from Theorem 1(i).

It remains to prove (37). Note that (37) is more related to the joint regression rather than the marginal regression. Let

$${\alpha }_n={\mathrm{argmin}}_{\alpha }E{\left(Y-{{\Psi }^T}_{\alpha }\right)}^2,$$

which is the joint regression coefficients in the population. By the score equation of α_n, we get

$$E\Psi (Y-{\Psi }^T{\alpha }_n)=0.$$

Hence

$${\parallel E\Psi Y\parallel }^2={\alpha }_n^{T}E\Psi {\Psi }^{T}E\Psi {\Psi }^T{\alpha }_n\le {\lambda }_{\max }\left(\Sigma \right){\alpha }_n^{T}E\Psi {\Psi }^T{\alpha }_n,$$

Now, it follows from the orthogonal decomposition that

$$\mathrm{var}\left(Y\right)=\mathrm{var}\left({\Psi }^T{\alpha }_n\right)+\mathrm{var}(Y-{\Psi }^T{\alpha }_n).$$

Since var(Y) = O(1), we conclude that var(Ψ^T α_n = O(1), i.e.

$${\alpha }_n^{T}E\Psi {\Psi }^T{\alpha }_n=O\left(1\right).$$

This completes the proof. □.

Figure 1.

Fitted regression functions for the 8 probes that are selected by INIS-penGAM (p = 18975).

A APPENDIX: Tables for Simulation Results of Section 5.3

Table 4.

Average values of the numbers of true (TP), false (FP) positives, prediction error (PE), computation time (Time) for Example 6 (t = 0). Robust standard deviations are given in parentheses.

SNR	dn	Method	TP	FP	PE	Time
0.5	2	INIS	3.96(0.00)	2.28(1.49)	7.74(0.79)	16.09(5.32)
		penGAM	4.00(0.00)	27.85(16.98)	8.07(0.92)	354.46(31.48)
	4	INIS	3.93(0.00)	2.29(1.68)	7.90(0.81)	21.68(8.95)
		penGAM	3.99(0.00)	25.61(13.62)	8.21(0.84)	421.17(35.71)
	8	INIS	3.81(0.00)	2.59(2.24)	8.16(1.08)	33.10(15.79)
		penGAM	3.95(0.00)	34.59(20.34)	8.49(0.82)	484.17(179.70)
	16	INIS	3.38(0.75)	2.02(1.49)	8.60(1.13)	42.69(20.13)
		penGAM	3.74(0.00)	33.48(23.88)	9.04(0.93)	685.97(267.43)
1.0	2	INIS	4.00(0.00)	2.16(2.24)	3.98(0.34)	16.03(5.74)
		penGAM	4.00(0.00)	26.51(14.18)	4.20(0.46)	284.85(20.30)
	4	INIS	4.00(0.00)	2.08(1.49)	3.97(0.45)	20.80(8.57)
		penGAM	4.00(0.00)	28.33(15.49)	4.24(0.47)	362.02(81.43)
	8	INIS	4.00(0.00)	2.72(2.24)	4.04(0.43)	35.79(18.38)
		penGAM	4.00(0.00)	36.50(21.83)	4.37(0.47)	427.60(152.53)
	16	INIS	4.00(0.00)	1.80(1.49)	4.26(0.45)	46.81(21.47)
		penGAM	4.00(0.00)	38.60(19.78)	4.80(0.57)	595.87(197.06)
2.0	2	INIS	4.00(0.00)	2.03(2.24)	2.12(0.17)	15.92(5.42)
		penGAM	4.00(0.00)	25.89(13.06)	2.25(0.24)	235.69(13.32)
	4	INIS	4.00(0.00)	2.38(2.24)	2.06(0.22)	23.54(9.08)
		penGAM	4.00(0.00)	30.37(17.16)	2.21(0.26)	341.13(19.44)
	8	INIS	4.00(0.00)	2.79(2.24)	2.03(0.21)	38.56(19.58)
		penGAM	4.00(0.00)	38.51(16.42)	2.24(0.26)	396.84(20.51)
	16	INIS	4.00(0.00)	1.77(1.49)	2.17(0.25)	48.40(24.65)
		penGAM	4.00(0.00)	42.58(16.60)	2.54(0.30)	540.89(165.39)
4.0	2	INIS	4.00(0.00)	2.06(2.24)	1.19(0.13)	17.74(6.42)
		penGAM	4.00(0.00)	28.57(14.37)	1.27(0.15)	213.43(12.09)
	4	INIS	4.00(0.00)	2.33(1.49)	1.09(0.10)	23.28(9.37)
		penGAM	4.00(0.00)	30.75(17.35)	1.18(0.14)	300.69(12.21)
	8	INIS	4.00(0.00)	2.88(2.24)	1.02(0.12)	39.21(19.17)
		penGAM	4.00(0.00)	40.51(17.54)	1.14(0.14)	340.06(11.49)
	16	INIS	4.00(0.00)	1.72(1.49)	1.10(0.12)	49.79(25.78)
		penGAM	4.00(0.00)	45.77(19.03)	1.33(0.16)	481.19(141.51)

Table 5.

Average values of the numbers of true (TP), false (FP) positives, prediction error (PE), computation time (Time) for Example 6 (t = 1). Robust standard deviations are given in parentheses.

SNR	dn	Method	TP	FP	PE	Time
0.5	2	INIS	3.35(0.75)	33.67(8.96)	9.49(1.28)	196.87(91.48)
		penGAM	3.10(0.00)	17.74(15.11)	7.92(0.89)	1107.78(385.95)
	4	INIS	3.02(0.00)	20.22(2.43)	8.70(1.14)	109.51(56.11)
		penGAM	2.78(0.00)	15.91(10.07)	7.99(0.91)	734.08(227.55)
	8	INIS	2.51(0.75)	10.48(0.75)	8.37(0.89)	65.12(16.64)
		penGAM	2.59(0.75)	16.47(9.70)	8.13(0.90)	624.31(56.23)
	16	INIS	2.10(0.00)	4.47(0.75)	8.44(1.00)	46.84(15.61)
		penGAM	2.41(0.75)	15.56(10.63)	8.42(0.97)	786.45(244.02)
1.0	2	INIS	3.83(0.00)	32.46(9.70)	4.86(0.60)	164.97(64.14)
		penGAM	3.64(0.75)	24.61(21.08)	4.19(0.49)	849.23(294.03)
	4	INIS	3.56(0.75)	20.53(1.68)	4.42(0.52)	118.14(43.97)
		penGAM	3.46(0.75)	22.07(16.04)	4.18(0.49)	614.93(97.36)
	8	INIS	3.09(0.00)	10.67(0.75)	4.28(0.49)	71.16(32.10)
		penGAM	3.12(0.00)	19.92(10.63)	4.30(0.50)	548.60(33.88)
	16	INIS	2.68(0.75)	4.18(0.75)	4.45(0.52)	46.08(15.35)
		penGAM	2.95(0.00)	16.39(11.19)	4.57(0.55)	710.56(199.86)
2.0	2	INIS	3.99(0.00)	29.45(11.57)	2.55(0.38)	139.67(70.45)
		penGAM	3.97(0.00)	36.57(22.57)	2.25(0.28)	626.84(210.44)
	4	INIS	3.93(0.00)	19.12(3.73)	2.26(0.24)	111.01(21.82)
		penGAM	3.91(0.00)	31.31(20.52)	2.19(0.23)	481.87(52.11)
	8	INIS	3.50(0.75)	10.29(0.75)	2.21(0.23)	78.06(32.23)
		penGAM	3.71(0.75)	27.06(19.03)	2.28(0.29)	448.38(26.63)
	16	INIS	2.93(0.00)	4.07(0.00)	2.42(0.32)	51.69(1.10)
		penGAM	3.22(0.00)	19.51(12.13)	2.53(0.30)	661.93(46.27)
4.0	2	INIS	4.00(0.00)	29.47(11.38)	1.45(0.21)	144.22(72.54)
		penGAM	4.00(0.00)	37.27(20.71)	1.27(0.17)	533.98(69.29)
	4	INIS	3.99(0.00)	17.36(5.22)	1.17(0.12)	102.97(32.71)
		penGAM	4.00(0.00)	38.71(20.34)	1.16(0.11)	403.32(28.29)
	8	INIS	3.78(0.00)	10.00(0.00)	1.13(0.16)	88.79(12.02)
		penGAM	3.99(0.00)	41.42(15.86)	1.19(0.13)	402.92(16.94)
	16	INIS	3.02(0.00)	3.98(0.00)	1.36(0.15)	49.13(1.85)
		penGAM	3.72(0.75)	29.58(19.40)	1.43(0.18)	556.31(35.48)